Introduction

Noise manifests itself and influences the dynamics of cellular systems at various spatial scales1,2,3,4,5. Of particular interest and acknowledged importance are concentration fluctuations stemming from the random timing of unimolecular and bimolecular chemical events. The ratio of the standard deviation to the mean of these fluctuations roughly scales as the inverse square root of the average number of molecules6, hence its importance to the dynamics of intracellular pathways since many chemical species are present in low numbers per cell7.

Given a particular biochemical pathway of interest, noise can be further categorized as that coming from sources external to the pathway and that originating from the individual reactions constituting the pathway. A ubiquitous source of external noise is the mechanism by which molecules are input or injected into a biochemical pathway. The classical model for this is a Poisson process in which a single molecule is injected at random points in time. However, numerous experimental studies over the past decade have shown that such a description is often inaccurate8,9,10,11,12.

Injection events have at least two physical interpretations for models of intracellular dynamics; injection can describe protein expression when modelling a biochemical pathway in the cytosol, whereas for pathways in membrane-bound subcellular compartments injection events can describe transport of molecules into the compartment by diffusive or active transport. A number of studies have confirmed that protein expression occurs in sharp and random bursts8,9. The bursts are found to be exponentially distributed and the expression events are temporally uncorrelated. The origin of these bursts can be explained by a simple mechanism. For bacteria and yeast, the lifetime of mRNA is typically short compared to that of proteins. In its short lifetime, each mRNA is translated into a number of protein molecules leading to random uncorrelated bursty events of protein production10. Although such protein expression is the best studied example of burstiness in protein production, it is not the only one. It has recently been found that protein translocation to the nucleus in response to an extracellular stimulus in budding yeast also occurs in sharp bursts11; indeed these bursts may be even more influential than those in protein expression since the mean size of the translocation bursts are estimated to be hundreds of molecules whereas those stemming from protein expressions are of the order of few tens or less9,12.

It is interesting to ponder what effects burstiness in protein production has on the steady-state properties and dynamics of the downstream biochemical pathway into which it feeds. Intuitively, a bursty input mechanism introduces a larger degree of noise to the downstream pathway than a non-bursty one. Indeed, this increase in noise has been quantified in very simple scenarios where the downstream pathway involves protein decay via a first-order process; for a bursty production mechanism, it was found that the Fano factor (variance of number fluctuations divided by the mean of molecule numbers) is equal to 1 plus the mean burst size, whereas for a non-bursty mechanism the Fano factor is 112,13. It is expected that this noise amplification occurs for all species' concentrations in more complex downstream pathways; from this point of view, bursting appears to be deleterious to the precise orchestration of cellular function. Consequently one might expect the cell to have developed downstream mechanisms to reduce or control such unwanted noise.

In this article we challenge this notion by demonstrating the non-intuitive effects of bursty inputs on noise-induced concentration oscillations. We compare the stochastic properties of two identical biochemical pathways, in one of which the protein is produced via a non-bursty input mechanism and in the other via a bursty input mechanism where the number of molecules per burst are distributed according to a general probability distribution. The mean rates of protein production are chosen to be the same in the two pathways and hence, according to the deterministic rate equation formalism, the two systems are characterized by the same steady-state concentrations. However, we show that there exist pronounced differences in the noise-induced oscillations generated by bursty and non-bursty systems and that the crucial non-dimensional parameter distinguishing the two is the sum of the mean and the Fano-factor of the burst size probability distribution. By deriving necessary conditions for noise-induced oscillations in the two systems we demonstrate a method of classifying simple biochemical circuits by their response to input bursting.

Results

A general framework for assessing the effects of bursty protein production

In this section we introduce the two-system setup which we will use to study the effects of bursting on the fluctuations in downstream pathways.

Consider a two species system in which both species are injected into a pathway and subsequently interact via a number R of downstream reactions. The non-bursty version of this system can be schematically represented as:

where Xi denotes species i, sij and rij (i = 1, 2) are the integer stoichiometric coefficients and hj and kj are the associated rate constants of the jth input and jth processing (downstream) reaction respectively.

A bursty input version of this system can also be envisaged as follows:

where qi(m) is the probability that the input burst size is m for species Xi and is a proportionality constant such that is an input rate constant. The integer constants M1 and M2 are the maximum burst sizes for species X1 and X2 respectively.

In the limit of large molecule numbers, the time evolution of the mean concentrations for the two systems is given by the conventional rate equations:

where the first terms describe the input reactions and the second terms describe the processing reactions. The vector is the concentration vector for bursty (b) and non-bursty, i.e., single-molecule input (s) systems. The processing rates are given by where Sij = rij − sij are the elements of the stoichiometric matrix. The factors μ1 and μ2 are the mean input burst size for species X1 and X2 respectively, i.e., . Note that the input rates hi and may be constants, e.g., when modelling diffusive transport, or functions of the concentrations, e.g., when modeling repression or activation of gene transcription.

If the two systems have the same initial conditions and if the mean number of molecules injected per unit time is the same, i.e., if , , then they are indistinguishable from measurements of their mean concentrations, i.e., for all times. Given this condition, it can be shown (see Methods) using the linear-noise approximation (LNA)14 that the time-evolution equations for the probability distribution of concentration fluctuations about the mean concentration solution of the above rate equations are given by:

where is the noise about the mean concentration of species Xi, is the second moment of the distribution of bursts, is the Jacobian matrix (describing linear stability) of the two rate equations above and . Note that since the bursty and non-bursty input systems have the same vector of mean concentrations and the same Jacobian (under the condition of equal mean input rates), we have denoted these as and J respectively, for both systems.

An inspection of the Fokker-Planck equations, Eqs. (5) and (6), shows that they have the same drift terms but different diffusion terms. This implies that while the bursty and non-bursty systems have the same mean concentrations, their fluctuation properties are different. The crucial set of non-dimensional parameters determining the differences in the fluctuations between the bursty and non-bursty input systems are:

where is the variance of the probability distribution of the bursts in species Xi. When ηi = 1 then the differences between the Fokker-Planck equations for the bursty and non-bursty input systems vanish. As expected, this occurs in the limit that the variance approaches zero and the mean burst size is one. As discussed in the Introduction, experiments show that the mean burst size is larger than one and hence we shall exclusively consider ηi > 1. The implication of equation (7) is that the larger is η1 − 1, the larger are the expected differences in the fluctuation properties of the downstream pathways in the two systems. For example for a Poissonian distribution of bursts, it is found ηi − 1 = μi whereas for a geometric distribution of bursts we have ηi − 1 = 2μi and hence we expect the burstiness-induced effects to be more prominent for systems with the latter burst input.

We finish this section by noting that we now have a convenient analytical setup with which to understand the effects of burstiness on the fluctuations of a downstream pathway. In the next sections we use the Fokker-Planck equations to understand how the fluctuations from bursty input change the downstream pathway's ability to generate noise-induced oscillations.

Necessary conditions for bursty input alteration of the oscillatory properties of the downstream pathway

In the setup described in the previous section, the bursty and non-bursty input systems are indistinguishable from a rate equation perspective and hence it follows that the deterministic dynamics of the two systems, including their ability to generate deterministic oscillations (limit cycles) are one and the same. However it is well appreciated that noise can induce oscillations in systems whose rate equations predict none. Given that the noise in the bursty and non-bursty input systems is different, it is plausible that the noise-induced oscillations displayed by both systems can also be different. In what follows we use the Fokker-Planck equations of the last section to probe this question.

We consider a general two variable Fokker-Planck equation with linear drift and diffusion coefficients of the form:

One can use this equation to derive an equation for the power spectrum of the fluctuations in the number of molecules of species Xi () and this is found to be15:

where , α2 is the same as α1 but with 1 and 2 interchanged, βi = Dii, p = [Det(J)]2 and q = [Tr(J)]2 − 2Det(J). Here Tr and Det refer to the matrix trace and determinant respectively. The power spectrum of the fluctuations in a given species is the Fourier transform of the autocorrelation function of the fluctuations of that species. Hence for a system in steady-state conditions, a peak in the power spectrum of a species at some frequency ω indicates a noise-induced oscillation of the same frequency in the concentration fluctuations of that species16. The sharpness of the peak indicates the quality of the oscillation; see Ref. 15 for a detailed discussion of quality measures for noisy oscillators.

By comparing Eqs. (5) and (6) with the general form equation (8), we can deduce that the power spectrum of the fluctuations in the bursty and non-bursty input systems are given by equation (9) with and respectively. These two spectra we shall refer to as and respectively.

By differentiating and with respect to ω, we can find the sufficient conditions for the power spectra to have a maximum, i.e., for the two systems to exhibit noise-induced oscillations. If q < 0, it can be shown that both and display a peak in their power spectrum; hence in this case burstiness does not lead to any qualitative change in the oscillatory properties of the downstream pathway. However for q > 0 the situation is more interesting. The positive q condition describes downstream pathways which, when parameterized, are far from a Hopf bifurcation17; the equilibrium is described by a node (which satisfies Tr[J]2 > 4Det(J)) or by a focus close to the node-focus borderline in phase space (which satisfies 2Det(J) < Tr[J]2 ≤ 4Det(J)). In this case the conditions for noise-induced oscillations in the concentration of species X1 in the bursty and non-bursty input systems are different and given by

respectively. The parameter θ1 is a function of the Jacobian elements only and is given by:

The conditions for noise-induced oscillations in species X2 are as above but with 1 and 2 interchanged. Note that although not explicitly shown, the elements of the D and J matrices in Eqs. (10)–(12) are functions of the mean concentration vector .

Hence for q > 0 we can identify three distinct cases: (i) , (ii) and (iii) . These are illustrated in Fig. 1. For case (i) either both systems display no oscillations or they both show noise-induced oscillations. For case (ii), there is the possibility of a special regime () in which the non-bursty input system displays noise-induced oscillations but the bursty input system does not. For case (iii), there is the possibility of a special regime () in which the non-bursty input system displays no oscillations but the bursty input system exhibits noise-induced oscillations. Hence burstiness has no effect in case (i), may cause destruction of noise-induced oscillations in case (ii) and may promote noise-induced oscillations in case (iii).

Figure 1
figure 1

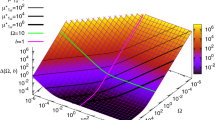
The impact of burstiness in the input reaction on the oscillatory properties of species X1 in a two species downstream pathway.

The figure illustrates the three possibilities: Case I in which both bursty and non-bursty input systems have qualitatively similar oscillatory properties, i.e., both and have a peak or not; Case II in which there is the possibility that the non-bursty input system displays noise-induced oscillations while the bursty input system does not (peak in only); Case III in which there is the possibility that the bursty input system displays noise-induced oscillations while the non-bursty input system does not (peak in only). The parameters , and θ1 are defined in the main text by Eqs. (10)–(12) respectively. Burstiness in the input reactions has no effect in Case I, is deleterious in Case II (BDO – bursting destroys oscillations) and promotes noise-induced oscillations in Case III (BIO – bursting induces oscillations).

Full size image

Note that is only a necessary condition for the destruction of noise-induced oscillations by burstiness in the input reactions; sufficient conditions ensue when we further have () which may not be always possible to satisfy. Similarly should be construed as a necessary condition for the creation of noise-induced oscillations by burstiness in the input reactions.

By inspection of Eqs. (10)–(11), we can make further specific statements regarding the importance of burstiness in the input reactions to the oscillatory dynamics of the two species pathway:

  • If the species X2 does not activate or inhibit X1, i.e., J12 = 0, then and hence burstiness in the inputs of X1 or X2 do not cause a qualitative change in the oscillatory dynamics of X1. Thus it is clear that bursting on its own is insufficient to affect oscillatory dynamics, rather an interplay of bursting with a downstream pathway featuring the interaction of two or more species is required.

  • For all other (i.e., J12 ≠ 0) pathways, an increase in the input burstiness of species X2 (for example by increasing the variance of the burst fluctuations at constant burst size mean) always increases the term . Thus, since it is possible to induce the condition but not the condition , bursting in species X2 may destroy noise-induced oscillations in species X1 but can never promote noise-induced oscillations in species X1.

  • For pathways that obeys the condition , an increase in the input burstiness of species X1 decreases the term . Thus, since it is possible to induce the condition , bursting in species X1 for these pathways may promote noise-induced oscillations in species X1. An exemplary class of such pathways are those in which the reactions are stoichiometrically uncoupled () but kinetically coupled (J12 ≠ 0), i.e., in each reaction there is only a net change in the number of molecules of one species yet the kinetics of the two species are coupled (see the Applications section for examples)18.

In the next section we investigate the effects of input bursting in exemplary biochemical circuits, in particular verifying our theoretical prediction that burstiness in the input reactions can both promote and destroy noise-induced oscillations far from the Hopf bifurcation. We conclude here by highlighting a simple four point recipe, provided in the Methods section, which can be used to calculate the necessary conditions derived in this section for any two species biochemical circuit.

Applications

Modified brusselator

Here we consider a modified form of the Brusselator19, which was introduced by Tyson and Kauffman in an early attempt to model dynamics within the process of mitosis. The non-bursty reaction scheme for this model is:

As previously explained, the bursty input version of this scheme having the same mean concentrations as the non-bursty version involve replacing the input reaction by the set of reactions , , , ......., , where M1 is some positive integer representing the maximum input burst size, q1(m) is the probability of an input burst of size m in species X1 and is the mean burst size.

The quantities (for i = 1, 2) which determine the necessary conditions for promotion or destruction of noise-induced oscillations by burstiness can be computed by following a four step recipe (see the Methods section). Here we simply state the results:

where and Λ2 = k2/k3 are non-dimensional parameters of the system. Thus we have and for η1 > 1, i.e., for all possible distributions of the burst size with mean burst size greater than 1. These are Case III and Case II in Fig. 1 respectively, implying necessary conditions for bursting in the input to promote noise-induced oscillations in species X1 and for it to destroy noise-induced oscillations in species X2.

We investigated these predicted phenomena in further detail as follows. We chose the burst size distribution such that it was geometric with a mean burst size μ1 = 12 (and hence η1 = 25; see equation (7) and the discussion which follows it) and varied Λ1 and Λ2 over the range 10−3 to 103. The geometric distribution is the discrete analog of the exponential distribution which has been measured in experiments9 and has also been predicted from theory13. For each parameter set we deduced the nature of the stable steady-state from linear stability analysis (focus, i.e., Tr[J] < 0, Det[J] > 0 and Tr[J]2 < 4Det(J) or node, i.e., Tr[J] < 0, Det[J] > 0 and Tr[J]2 > 4Det(J)17) and also checked if there is a peak at some non-zero frequency in the LNA power spectrum as given by equation (9) (which implies noise-induced oscillations). The results for both species X1 and X2 are shown in Fig. 2. The red regions in Figs. 2 (a) and (b) denote the regions in parameter space where there are noise-induced oscillations in species X1 for non-bursty and bursty input systems respectively. Similarly the blue regions in Figs. 2 (c) and (d) denote the regions in parameter space where there are noise-induced oscillations in species X2 for non-bursty and bursty input systems respectively. Notice that in accordance with the predictions based on the necessary conditions discussed in the previous paragraph, we find that the burstiness in the input reaction promotes noise-induced oscillations in X1 (increased area of red region in Fig. 2 (b) compared to Fig. 2(a)) and destroys noise-induced oscillations in X2 (decreased area of blue region in Fig. 2 (d) compared to Fig. 2 (c)). One also notices that the changes mainly occur in regions of parameter space characterized by a node and not by a focus (dotted region), which is consistent with the earlier prediction that burstiness has an important effect in systems far from the Hopf bifurcation.

Figure 2
figure 2

The impact of burstiness in the input reaction on the existence of noise-induced oscillations for the modified Brusselator model.

The regions in Λ1–Λ2 space are numbered as follows: (0) unstable, (1) node with noise-induced oscillations (NIO), (2) focus with NIO, (3) node with no NIO and (4) focus with no NIO. Solid black lines bound the regions of different linear stability: the dotted region corresponds to the stable focus regime; white regions correspond to the stable node regimes and the grey region is where the fixed point is unstable (including the limit cycle regime). The red regions in (a) and (b) show the parameter space region where there are noise-induced oscillations in the concentration of species X1 for the non-bursty input and bursty-input versions of the modified Brusselator respectively. The blue regions in (c) and (d) imply the same but for species X2. The burst input distribution is geometric with mean burst size μ1 = 12. A comparison of (a) and (b) shows that burstiness in the input reaction promotes noise-induced oscillations in X1 while a comparison of (c) and (d) shows that it destroys them in X2. Note that the regions where most of these effects occur are not dotted, indicating that they are stable node steady-states.

Full size image

In Fig. 3 (a) and (c) we show the power spectra calculated from the LNA and from stochastic simulations for two points in Λ1–Λ2 space for which the LNA analysis of Fig. 2 predicted that burstiness in the input reaction should promote and destroy noise-induced oscillations respectively. The simulations confirm the predicted phenomena by showing that the spectra of X1 and X2 exhibit the appearance and disappearance of a peak at a non-zero frequency respectively, when bursting in the input reaction is turned on. It is also shown that the phenomena are more pronounced for geometric burst size distributions rather than for Poisson ones of the same mean burst size; this is since given the same mean, the width of the former distribution is larger than that of the latter. In Fig. 3 (b) and (d) we show the quality factor of the noise-induced oscillations as a function of the mean burst size μ1. The quality factor is defined as , where is the frequency at which maximum power is obtained and Δω99% is the difference of the frequencies at which the power takes 99% of its maximum value; this measure was introduced in15 and shown to be highly reflective of the rhythmicity visible in a time series of noise-induced oscillations. For these far-from Hopf oscillations the maximum possible value of Q99% is ≈ 5 (Ref 15). Of particular interest is the saturation observed in Fig. 3 (b) which implies that there are limits to how much burstiness in the input reaction can improve the quality of noise-induced oscillations. This also means that in the limit of large burst sizes the quality of noise-induced oscillations is independent of the precise type of the burst size distribution.

Figure 3
figure 3

Verification of LNA predictions by stochastic simulations.

In (a) and (c) we plot the power spectra of the concentration fluctuations in X1 and X2 respectively using the LNA (solid lines) and also from stochastic simulations using the stochastic simulation algorithm (data points). Note that in (a) burstiness in the input reaction promotes noise-induced oscillations (induces a peak in the spectrum of X1) and in (c) it destroys them (removes the peak in the spectrum of X2 for non-bursty input). In (b) and (d) we plot the quality of the noise-induced oscillations whose spectra are shown in (a) and (c) respectively. See text for definition of the quality factor Q99%. Note that the quality of the noise-induced oscillations can only be improved by burstiness in the input reaction to a certain extent (saturation of Q99% with mean burst size μ1). The constants are (a) h1Ω NA = 1000 molecules s−1, k1 = 2.805 × 1011 M−2 s−1, k2 = 0.375 s−1 and k3 = 0.25 s−1; (b) h1Ω NA = 500 molecules s−1, k1 = 6.528 × 1010 M−2 s−1, k2 = 0.01 s−1 and k3 = 1 s−1. The compartment volume in each case is Ω = 3 × 10−15 l, which gives mean molecule numbers of (a) molecules and (b) molecules. Note that the units for concentration, time and frequency ω are Molar (M), second (s) and radians per second (rad s−1) respectively. See Methods for a discussion of biologically relevant parameter ranges.

Full size image

Other simple circuits

Next we report the results of a detailed investigation of the effect of burstiness on the oscillatory properties of 8 biochemical pathways. The reaction schemes for the latter including their rate equations and the non-dimensional parameters characterizing the steady-state behavior are shown in Table I. Note that for the gene circuits we have set some of the rate constants to 1; the model's behavior can then be described by at most three non-dimensional parameters which considerably simplifies our analysis.

Table 1 Details of the eight chemical reaction systems studied. The symbol ϕi denotes the concentration of species Xi and are the molar gene concentrations (see Methods). The upper four circuits feature input burstiness in only one species while the lower four feature input burstiness in both species
Full size table

Next we used the four point calculational recipe in the Methods section to obtain the quantity for each of these 8 pathways. The sign of this quantity determines which of the three cases shown in Fig. 1 each pathway falls into and hence constitutes necessary conditions for promotion and destruction of noise-induced oscillations in species X1 by bursting. The expressions for are shown in the second column of Table II. It is simple to determine the sign of this quantity since all constants a1 to a8 are positive, as are Λ1, Λ2 and Λ3 and η1, η2 > 1 (mean burst size is greater than 1). If the sign can take negative values then Case III is possible; if the sign can take positive values then Case II is possible. Which case can be displayed by each pathway is shown in columns 4 and 6 of Table II. Notice that 6 out of 8 pathways can display Case III behavior, i.e., bursting may induce oscillations; 6 out of 8 pathways can display Case II behavior, i.e., bursting may destroy oscillations; 4 out of 8 pathways can display both Case II and Case III behavior, i.e., bursting may promote or destroy oscillations.

Table 2 The effect of bursting in the input reactions on the eight chemical systems shown in Table I. The sign of determines whether the model exhibits Case III or Case II behaviour (see Fig. 1), i.e., the necessary conditions for burstiness to promote or destroy noise-induced oscillations respectively (fourth and sixth columns of the table). Determining whether input bursting can in fact promote or destroy oscillations requires the full condition that θ1 is large enough; the columns ‘BIO Observed’ and ‘BDO Observed’ are the results of our numerical investigation to this end (see text for details). The upper four circuits feature input burstiness in only one species, the lower four feature input burstiness in both species. Note that ai are positive constants
Full size table

As we have shown the simple necessary conditions are very easily determined in practice and give a quick indication of whether input burstiness could cause a qualitative change in oscillatory behaviour in a system. However these conditions are not sufficient by themselves to prove that the systems do actually display the burstiness-induced destruction or promotion of noise-induced oscillations. As previously explained and shown in Fig. 1, one needs to further determine if θ1 falls in the correct range of values. This is considerably more involved analytically and hence we determine it numerically by an extensive parameter scan.

The parameter scan algorithm involved the following steps. We randomly picked 105 sets of non-dimensional parameters (the Λi's in Table I are uniformly distributed in log-space over the range [10−3, 103] and the burstiness parameters ηi are uniformly distributed integers in the range [1, 25]) for which the system has a steady-state. For each of the models, this chosen range of non-dimensional kinetic parameters falls within the biologically relevant range for sub-cellular processes (see Methods). For each parameter set we calculated the quantities q, θ1, and . If q < 0 then for this parameter set both bursty and non-bursty input systems display noise-induced oscillations. If q > 0, then θ1, and are used to obtain which case and which particular region of the case shown in Fig. 1 describes the system's behavior for the chosen parameter set. These classifications are recorded for each parameter set.

Information regarding whether the sufficient conditions were found to be satisfied or not is reported in columns 5 and 7 of Table II. A more detailed classification is shown in bar chart form in Fig. 4 for six of the eight pathways in Table I. Note that the two remaining pathways (One Gene Model B and Two Gene Model C) are similar in behaviour to Two Gene Model A and hence not shown in the latter figure. At least one of Case II or Case III behaviour was possible for each model. The necessary conditions for bursts destroying or promoting noise-induced oscillations were also sufficient, with three exceptions: One Gene Model B, Two Gene Model A and Two Gene Model C. Interestingly, these three exceptions are unique among the models in that they are the only ones which cannot exhibit noise-induced oscillations for any parameter choices for both bursty and non-bursty systems.

Figure 4
figure 4

Numerical investigation into the effect of bursting in the input reactions on six of the eight biochemical models shown in Table I. See main text for details of the numerical algorithm used.

q < 0 refers to the cases close to the Hopf bifurcation where both bursty and non-bursty input systems show noise-induced oscillations. Cases I, II and III are for q > 0 (far from Hopf bifurcation) described in Fig. 1. Ticks/crosses indicate that noise-induced oscillations are/are not observed for both bursty and non-bursty-input systems. BDO and BIO refer to the cases where burstiness destroys or promotes noise-induced oscillations, i.e., the behavior of the two systems is different. The heights of the bars for each behavior are directly proportional to the fraction of the 100, 000 parameter sets which exhibit that behavior.

Full size image

We noticed that the effect of burstiness on each system was strongly linked to two main features: (a) whether burstiness is possible in one or both species; and (b) the pathway's feedback motif, as described by the signs of the off-diagonal elements of the Jacobian matrix (column 3 in Table II). The three exceptional models (One Gene Model B, Two Gene Model A and Two Gene Model C) which never exhibited noise-induced oscillations and for which the necessary conditions for bursts destroying or promoting noise-induced oscillations did not also translate to sufficient conditions, all feature either mutual promotion or mutual inhibition between the two species.

Models with negative feedback, whereby one species promotes the other and that species inhibits the first (indicated by different signs on the off-diagonals of J) were sensitive to burstiness destroying or promoting noise-induced oscillations. When burstiness is possible in both species (Autocatalysis and Two Gene Model B), necessary conditions for both BIO and BDO can be satisfied and BIO and BDO were indeed observed. Therefore, our results suggest that the combination of a negative feedback motif and burstiness in both species allows a wide range of bursting-induced oscillatory behaviour. When burstiness is only possible in one of the species, the matching of necessary and sufficient conditions is again observed, but here the asymmetry of the Jacobian is important; when J12 is positive (Brusselator) the necessary conditions indicate that burstiness tends to destroy noise-induced oscillations in X1, but when J12 is negative (Trimerization and One Gene Model A) the necessary conditions indicate that noise tends to promote noise-induced oscillations in X1.

Although the regions of parameter space for which bursts promote or destroy noise-induced oscillations is quite small in some models, e.g., Two Gene Model B, we note that this region can be considerably enlarged by choosing a smaller range for the burstiness parameters (e.g. if η1 and η2 are fixed to 25 and 2 respectively rather than the range [1, 25] used in our parameter scan). The fact that a large proportion of the considered pathways display burstiness alteration of the noisy oscillatory dynamics suggests that such phenomena may be common in many biochemical systems.

Discussion

In this paper we have shown using the LNA that burstiness in the input reactions can have a considerable impact on the oscillatory properties of the downstream pathway. In particular we showed that for two identical pathways, one with bursty and one with non-bursty input, the two pathways may differ in their ability to produce noise-induced oscillations. We derived necessary conditions for the burstiness to promote oscillations and for the burstiness to destroy oscillations and confirmed the existence of these phenomena using stochastic simulations. Our work is the first to investigate the effect of burstiness on the noisy oscillatory dynamics of biochemical pathways; previous work focused on deriving expressions for the steady-state distributions (or the moments) of protein concentrations in the presence of bursting10,20,21,22 and on elucidating the link between circuit architecture and the susceptibility to bursts in gene expressions23.

We note that our analysis is based on the LNA which is a good approximation when describing pathways involving small levels of noise, i.e., pathways characterized by a sufficiently large number of molecules. This is not always the case since a number of species inside cells occur in small molecule numbers7. Our theory can be extended to account for such cases by considering higher-order terms than the LNA in the system size expansion of the master equation24,25,26. Preliminary investigations show that in non-bursty systems if the LNA predicts a peak in the power spectrum of fluctuations for systems far from the Hopf bifurcation then the spectrum calculated from stochastic simulations shows a peak even if the molecule numbers are very small (see Fig. 6 in15); the quality of the oscillations may, however, be lower than that predicted by the LNA. Hence we expect the consideration of terms of higher order than the LNA to have little or no effect on the necessary conditions derived in this paper since these are specifically for the existence or non-existence of a peak in the power spectrum.

Our results can also be interpreted in the context of single cell rhythms, as follows. Rate equation models are typically constrained to experimental measurements from an ensemble of cells, e.g.27. They are only accurate models of single-cell pathway dynamics when the cells are dynamically non-coupled and each cell is characterized by negligible noise. Hence, experimentally observed oscillating concentrations correspond to rate equation predictions of limit cycles and experimentally observed constant concentrations correspond to rate equation predictions of steady-state conditions in single cells. However, when noise is non-negligible each realization of the stochastic simulation algorithm provides the behavior of a particular cell in the ensemble28 and the power spectrum provides information of the rhythmicity present at the single-cell level. From this point of view, the noise-induced oscillations described in this article correspond to the biological scenario where ensemble level experiments suggest that cells are non-oscillatory while in reality non-synchronized rhythms are present in each cell. This phenomenon has been experimentally observed by comparing ensemble and single cell measurements29. In this context, our bursty and non-bursty systems correspond to two independent populations of non-coupled cells, in one of which the oscillatory pathway has a bursty production of proteins and in the other it does not. At the ensemble level both populations appear non-oscillatory and indistinguishable (both their rate equations have the same steady-state) but at the single cell level they are sometimes distinguishable since bursts can either promote or destroy single cell rhythms (noise-induced oscillations).

We finish by discussing how our theoretical results could be experimentally tested. The procedure consists of three parts: (i) the synthetic engineering of one of the pathways considered in this paper in a single cell; (ii) the variation of burstiness in protein production at fixed protein production rates; (iii) the measurement of single cell power spectra of protein fluctuations in the synthetic pathway. Points (i) and (iii) have been done in various contexts; see for example30,31. Point (ii) is the subtlest of the three as it requires regulation of burstiness at the gene level. A rate equation analysis of the the standard linear model of gene expression8 leads to the conclusion that whenever the mRNA lifetime is much shorter than that of proteins (the typical case in bacteria and yeast), the overall rate of protein production is equal to the product of the transcription and translation rates divided by the rate of mRNA degradation while the burst size is equal to the translation rate divided by the mRNA degradation rate. Thus one can conclude that by varying the transcription and translation rates independently, it is possible to increase the burst size at a constant overall rate of protein production and to hence test our predictions. A method to achieve this has been reported in Ref 8 and hence it follows that the results of our theory can be tested by currently available experimental techniques.

Methods

Stochastic analysis via the Linear-noise approximation (LNA)

The stochastic dynamics of any chemical system in a well-mixed compartment are described by chemical master equations14 which for the non-bursty and bursty systems shown in schemes (1) and (2) take the respective form:

where Pb/s(n1, n2, t) is the probability that there are n1 molecules of species X1 and n2 molecules of species X2 at time t for the bursty input (b) and non-bursty, i.e., single-molecule input (s) systems, Ω is the volume of the compartment in which the downstream pathway operates, Sij = rij − sij are the elements of the stoichiometric matrix, is the step operator which when it acts on some function w(ni) gives w(ni + j) and is the microscopic rate function for the jth processing reaction which is given by14:

Note that the first term in each of the master equations above describes the input reactions while the second term describes the processing reactions.

These master equations are typically unsolvable except in special cases (see for example32) or for the case where all processing reactions are first-order33, a very restrictive assumption given that most interactions inside a cell involve the binding of two molecules. We circumvent this problem by using the LNA of the master equation, a well known technique14 which approximates the master equation by a Fokker-Planck equation with linear drift and diffusion coefficients. This approximation is valid for an arbitrarily complex monostable reaction system provided the fluctuations about the mean concentrations are quite small, i.e., provided the molecule numbers are not too small. The general formalism has been described in34; here we simply state the relevant results when the LNA is applied to the master equations (16) and (17).

Within the LNA, the time evolution of the mean concentrations for the two systems is given by the conventional rate equations, Eqs. (3) and (4), in the main text. The LNA analysis also shows that the Fokker-Planck equations describing the probability distribution of concentration fluctuations about the mean concentration solution of the above rate equations are given by:

where is the noise about the mean concentration of species Xi, is the second moment of the distribution of bursts, , are the Jacobian matrices (describing linear stability) of the two rate equations, Eqs. (3) and (4) and .

Enforcing the condition of equal mean input rates for the bursty and non-bursty systems, i.e., , Eqs. (19)–(20) simplify to Eqs. (5)–(6) in the main text.

Four step recipe for calculating the necessary conditions for burstiness-induced effects in a two-species system

Step 1

By comparison of the particular system under study with the general form of the non-bursty input system described by scheme (1), one deduces the stoichiometric coefficients sij and rij and constructs the elements of the stoichiometric matrix Sij = rij − sij of the downstream pathway where i varies between 1 and 2 and j varies between 1 and the total number R of downstream reactions.

Step 2

Write down the rate equations , where . Solve these equations with the time derivative set to zero to obtain the steady-state concentrations .

Step 3

Calculate the elements of the Jacobian matrix . Calculate the elements of the diffusion matrix of the downstream pathway . Calculate the elements of the diffusion matrices of the downstream path for bursty and non-bursty input: and .

Step 4

Calculate using their definitions in Eqs. (10)–(11) and from the sign of this quantity identify which of the three cases illustrated in Fig. 1 the system under study falls in.

Four step recipe applied to the modified Brusselator

Here we show in detail the steps of the calculational recipe as applied to the modified Brusselator studied in the Results section.

Step 1

Comparison of the modified Brusselator reaction scheme (13) with that in (1) shows that the stoichiometric coefficients are: s11 = 1, s21 = 2, r11 = 0, r21 = 3 for the first downstream reaction 2X2 + X1 → 3X2; s12 = 1, s22 = 0, r12 = 0, r22 = 1 for the second downstream reaction X1 → X2 and s13 = 0, s23 = 1, r13 = 0, r23 = 0 for the third downstream reaction X2 → Ø. Hence the stoichiometric matrix of the downstream pathway reads:

Step 2

Next one uses the stoichiometric information of Step 1 to write the functions and and hence the rate equations are dtϕ1 = h1 + g1 and dtϕ2 = g2 which have a steady-state solution ϕ2 = h1/k3 and .

Step 3

Using the functions g1 and g2 obtained in Step 2, the steady-state concentration solutions also obtained in Step 2 and the stoichiometric information obtained in Step 1, we can now calculate the three relevant matrices:

where and Λ2 = k2/k3 are non-dimensional parameters of the system.

Step 4

Using the three matrices calculated in the previous step and the definitions in Eqs. (10)–(11) we can finally calculate the two quantities relevant to deduce the necessary conditions:

Calculation of numerical power spectra of the modified Brusselator

Firstly, SBML reaction models were created describing the non-bursty input and bursty input versions of the modified Brusselator (reaction scheme (13)). The upper burst size for Poisson or Geometric burst distributions is unbounded, meaning that to be exact an infinite number of input reactions is required in the simulation. For the chosen distributions (with mean burst size equal to 12 molecules) we truncated this to a maximum input burst size of 160 molecules. A simple python script was used to generate such a large reaction scheme. After parameterizing the models with the values given in the legend of Fig. 3, the models were simulated using the exact stochastic simulation implementation in the freely available software iNA (intrinsic noise analyser)35.

For a single realization of the stochastic simulation algorithm, the number of molecules ni(t) of species i over some time interval T was regularly sampled at L discrete points separated by Δt, such that T = (L − 1)Δt. The time interval T has to be chosen much larger than the time taken for the simulations to reach steady-state. Subsequently the steady-state mean is subtracted such that one is left with a time series of fluctuations about the mean. The power spectrum estimate (the periodogram) is then obtained by a discrete Fourier transform of this time series (See Appendix C of Ref. 15 for further details). The choices of sampling parameters for the spectra in Fig. 3a and Fig. 3c were Δt = 0.1059 s, L = 600 and Δt = 0.5296 s, L = 600 respectively. Since the variance of the spectrum estimate is known to be high, the final numerical power spectral density estimates plotted in Fig. 3 were obtained by averaging over 2000 periodograms, each corresponding to an independent realization of the stochastic simulation algorithm.

Use of biologically relevant parameter ranges

Parameters for the 8-pathway numerical investigation

In our numerical investigation of the eight biochemical pathways we used the range [10−3, 103] for each of non-dimensional parameters Λi. As we now show, this range falls within the biologically relevant ranges for each of the circuits. The pathways feature zeroth order, unimolecular, bimolecular and trimolecular reactions. The range of the rate constants for each of these reactions is as follows.

  1. 1

    Input reaction (zeroth order): We infer this rate as lying in the range [10−16 M s−1, 10−10 M s−1] from the rate of protein production in mammalian cells, as calculated from the product of mRNA copy numbers (1–1000) and the rate of production of proteins per mRNA per hour (1–1000)36 factored by Avogadro's constant NA and the typical volume of a mouse fibroblast NIH3T3 cell (Ω ≈ 3 × 10−12 litres)37.

  2. 2

    Unimolecular reaction (first order): In the same study36 protein half lives were found to vary from 1–1000 hours, from which the range of protein degradation rates can be calculated via k = ln(2)/t1/2 to be of the order [10−4 s−1, 10−1 s−1].

  3. 3

    Bimolecular reaction (second order): For bimolecular reaction rates we use the wide range of enzyme-substrate association rates which are roughly given by the measured range of the ratio of the catalytic rate to the Michaelis-Menten constant: [103 M−1s−1, 107 M−1s−1]38.

  4. 4

    Trimolecular reaction (third order): The unit of the rate constant for such a reaction is M−2s−1. Hence we can estimate this rate by dividing the bimolecular rate constant by a concentration. Using the range of bimolecular rate constants stated above and the range of typical intracellular concentrations (nanomolar to micromolar), we estimate the range of trimolecular rate constants to be [109 M−2s−1, 1016 M−2s−1].

Using the above ranges one can calculate the range of the non-dimensional parameters in Table I. For example for the first non-dimensional parameter of the autocatalysis reaction, Λ1, the input rate constants h1 and h2 could vary to give the range of possible values:

and for the second non-dimensional parameter we have the range:

Hence one can see that the range used in our simulations for non-dimensional parameters Λi ∈ [10−3, 103] is a subset of the ranges calculated using typical rate constant values.

Note that in the models where genes are explicitly shown (such as One Gene Model A) the relevant input rate parameters k0 or were chosen such that the typical input range hi ∈ [10−16 M s−1, 10−10 M s−1] describes the basal expression rate where is the molar concentration of a single gene.

Parameters for the modified Brusselator model

For input rates to the modified Brusselator model (Fig. 3) we considered the alternative scenario in which proteins are transported into the cell, instead of being expressed in the cell. Transporter proteins are known to transport a large range of ions and molecules across the cell membrane at rates typically in the range [102 molecules s−1, 104 molecules s−1]39. Converting our input hi parameters into these units requires us to write input rates as hiΩ NA, where Ω is the volume of a cell and NA is Avogadro's constant. The input rates used in our study of 1000 and 500 molecules s−1 were chosen to fall within this biologically relevant range. The volume Ω was chosen to be equal to 3 × 10−15 litres, i.e., roughly that of a typical bacterial cell. Unimolecular and trimolecular rate constants were motivated as for the other models discussed above.

Equipment and settings

Image generation

  • Fig. 2 was created using Maple (to draw the correct boundary lines), with axis labels, area patterns/colours and numerical annotations added using Inkscape.

  • Fig. 3 was created using Maple, with axis labels and legend annotations added in Inkscape.

  • Fig. 4 was created using Maple, with axis labels, bar chart colours and text annotations added using Inkscape. The circuit diagrams were also added using Inkscape.