Abstract
The largest cities, the most frequently used words, the income of the richest countries and the most wealthy billionaires, can be all described in terms of Zipf’s Law, a rank-size rule capturing the relation between the frequency of a set of objects or events and their size. It is assumed to be one of many manifestations of an underlying power law like Pareto’s or Benford’s, but contrary to popular belief, from a distribution of, say, city sizes and a simple random sampling, one does not obtain Zipf’s law for the largest cities. This pathology is reflected in the fact that Zipf’s Law has a functional form depending on the number of events N. This requires a fundamental property of the sample distribution which we call ‘coherence’ and it corresponds to a ‘screening’ between various elements of the set. We show how it should be accounted for when fitting Zipf’s Law.
Similar content being viewed by others
Introduction
Zipf’s Law1,2,3, usually written as  where x is size, k is rank, and xM is the maximum size in a set of N objects, is widely assumed to be ubiquitous for systems where objects grow in size or are fractured through competition4,5,6. These processes force the majority of objects to be small and very few to be large. Income distributions are one of the oldest exemplars first noted by Pareto7 who considered their frequencies to be distributed as a power law. City sizes, firm sizes and word frequencies4,8,9 have also been widely used to explore the relevance of such relations while more recently, interaction phenomena associated with networks (hub traffic volumes, social contacts10,11) also appear to mirror power law-like behavior. Zipf’s Law has rapidly gained iconic status as a ‘universal’ for measuring scale and size in such systems, notwithstanding the continuing debate as to the appropriateness of the power law (or ‘1/k’ behavior) and the mixed empirical evidence which remains controversial3,4.
where x is size, k is rank, and xM is the maximum size in a set of N objects, is widely assumed to be ubiquitous for systems where objects grow in size or are fractured through competition4,5,6. These processes force the majority of objects to be small and very few to be large. Income distributions are one of the oldest exemplars first noted by Pareto7 who considered their frequencies to be distributed as a power law. City sizes, firm sizes and word frequencies4,8,9 have also been widely used to explore the relevance of such relations while more recently, interaction phenomena associated with networks (hub traffic volumes, social contacts10,11) also appear to mirror power law-like behavior. Zipf’s Law has rapidly gained iconic status as a ‘universal’ for measuring scale and size in such systems, notwithstanding the continuing debate as to the appropriateness of the power law (or ‘1/k’ behavior) and the mixed empirical evidence which remains controversial3,4.
Here we argue that the very definition of the objects comprising the system in the first place has to be undertaken with extreme care12. Many real systems do not show true power law behavior because they are incomplete or inconsistent with the conditions under which one might expect power laws to emerge13. We will show that the origin of 1/k behavior is considerably more subtle than expected at first sight and than is usually stated in the scientific literature. Here we report on a surprising and usually ignored property which points to the fundamental importance of the nature or the ‘coherence’ of the sample (or sub-sample) of objects or events defining systems of interest whose objects may follow a perfect Zipf’s Law or may markedly deviate from it. The vision proposed here provides new perspectives on the meaning and interpretation of the informative content of Zipf’s Law and we propose an analysis to extract new and useful information from this novel property.
A spectacular and surprising consequence of the coherence characterizing Zipfian sets is that in general Zipf’s Law does not hold for subsets or a union of Zipfian sets. In fact, for subsets, some missing elements inevitably produce deviations from a pure Zipf Law’s in the subset, especially when these ‘holes’ occur for the largest elements of the original set with this problem being crucial for the leading elements of the set such as the largest cities in a country. Similarly a union or aggregation of Zipfian sets does not inherit the coherence property of the original sets because replicas or very similarly sized elements destroy any integration in the aggregate sets. The reason why word distributions are not good candidates to test for coherence as are city, firm and income distributions is that subsets of a text such as a paragraph or chapter tend to be coherent set and thus it is harder to see deviations from Zipf’s Law.
Cities in the US and the EU provide impressive concrete examples of such an argument. While Zipf’s Law holds approximately for the city sizes of each European country (France, Italy, Germany, Spain, etc), it completely fails in the aggregated sets, that is in the EU. Conversely the size of US cities compose a near Zipfian set, in contrast to the sets composed of the cities from a single state such as California, New York State, Illinois, Massachusetts. These cannot be represented by a Zipf’s Law. These two examples also suggest to us that this coherence or integration property must be linked to the evolution of the elements of the Zipfian set. In fact, historically, the geographic level for Europe, at which an integrated evolution is observed, is the national state, while in the US, the whole confederation, not each independent state, has collectively and organically evolved towards a distribution of cities that follows Zipf’s Law. From this perspective, the US is an organic, integrated economic federation, while the EU has not yet become so and shows little convergence to such an economic unit.
In some specific cases, we can give more concrete and simpler interpretations of the coherence of a Zipfian set. In Fig. 1, we present the evolution of the rank-size rule for the Gross Domestic Product (hereafter GDP) of the top 100 national economies from 1900 to 2008. It appears that the more the world’s economies become globalized, the more their national GDP compose a Zipfian set. Therefore, we speculate that the Zipfian Law we observe for the GDP and its consequent higher degree of coherence in time, is a reflection of the globalization process which is forcing a full integration of the world’s economy. Krugman14 suggests that the world economy suddenly became more integrated by the start of the First World War but then departed from this in the 1920s. The distribution of GDP in 1914 suggests a little more coherence than 1900 and we might expect to see a little volatility in the movement to and from a more globalized world when we examine this data at a finer temporal resolution.
Zipf’s Law for National Gross Domestic Products 1900-2008.
The Gross Domestic Products of nations appear to show a more and more a Zipfian behavior over the last one hundred years. We propose a fascinating interpretation of this evidence in terms of globalization. In fact we have said that a set is Zipfian if there exists an internal coherence among its elements. As the world has become more fully globalized, we observe that Zipf’s Law holds for an increasing number for countries. In fact in 2000 and 2008 we observe that not only the highest GDPs satisfy Zipf’s Law (red line) but also the top fifty economies and that the rank at which the deviation from a Zipf’s Law behavior starts increases in time, suggesting the idea that world economic system is getting more and more coherent, i.e. globalized. Globalization is making the world fully coherent/integrated with respect to the richness distribution among its units (i.e. countries) while this degree of integration has not yet been reached by the world’s national populations (see Fig. 3). Sources: Wikipedia: various pages on GDP http://en.wikipedia.org/wiki/List_of_countries_by_GDP_(nominal) and http://en.wikipedia.org/wiki/List_of_regions_by_past_GDP_(PPP).
We briefly anticipate that the mathematical meaning of the coherence of a Zipfian set can be made more cogent by considering a different problem which we call the ‘backward problem’: how should we generate a distribution that reproduces Zipf’s Law? As we will see in more detail in the argument that follows, we will find that the distribution explicitly depends on the number of elements in the set. This implies that the distribution must change at each draw of a new element in order to take into account the internal coherence which holds among Zipfian elements. Furthermore we show that there exists a more fashionable way of considering the dependence of the distribution on the size of the set in terms of a screening effect of the largest elements of a Zipfian set. We will call this the ‘New York effect’, which implies that in a Zipfian set, we cannot draw two or more ‘New York’s’, for we would destroy the coherence of the set if we did. In short a Zipfian set cannot contain such replicas.
Results
For richer or poorer: the coherence of the sample
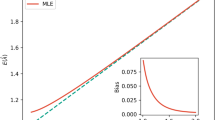
Our thesis is remarkably easy to demonstrate. Consider the income of 20 people whose distribution satisfies Zipf’s Law and where the maximum income  is $1m. If we consider a sub-sample of the first 10 persons (the richest), then this sub-sample will certainly satisfy the same Zipf’s Law. However when we consider the second group of 10 persons (the poorest), the incomes of the first two persons are $1m/11 and $1m/12, while the ratio of the second to the first is 11/12, very different from the first two incomes in the richest set whose ratio is 1/2. These differences apply to all the other corresponding ratios between successive objects in the two subsets. In Fig. 2, we elaborate this example first by ranking the incomes of the 390 billionaires resident in the US in 2010 (from the Forbes List15) whose incomes, once ordered, approximately follow Zipf’s Law. This provides a highly graphic demonstration that by partitioning two sets generated from one law, two laws are necessary to explain their resulting parts. This point has extremely wide ramifications for all work on scaling systems and power laws in general, rank size and Zipfian relations in particular. There is little evidence in the literature that the importance of this point has been grasped, or if it has, it has been widely ignored.
is $1m. If we consider a sub-sample of the first 10 persons (the richest), then this sub-sample will certainly satisfy the same Zipf’s Law. However when we consider the second group of 10 persons (the poorest), the incomes of the first two persons are $1m/11 and $1m/12, while the ratio of the second to the first is 11/12, very different from the first two incomes in the richest set whose ratio is 1/2. These differences apply to all the other corresponding ratios between successive objects in the two subsets. In Fig. 2, we elaborate this example first by ranking the incomes of the 390 billionaires resident in the US in 2010 (from the Forbes List15) whose incomes, once ordered, approximately follow Zipf’s Law. This provides a highly graphic demonstration that by partitioning two sets generated from one law, two laws are necessary to explain their resulting parts. This point has extremely wide ramifications for all work on scaling systems and power laws in general, rank size and Zipfian relations in particular. There is little evidence in the literature that the importance of this point has been grasped, or if it has, it has been widely ignored.
Zipf’s Law for the Richest Billionaires in the United States.
The richest 390 persons in the US are billionaires whose wealth we plot against their rank as the uppermost set of points (the first 195 richest being grey circles, the second 195 poorest being red circles). The second set is the sub-sample that we translate to the original ranks and plot as the set of red circle points below the diagonal straight line which is the pure Zipf plot associated with  . The inset is a pure Zipf plot dimensioned to the entire set of 390 billionaires and the poorest sub-sample of 195. (Source: Forbes Listhttp://www.forbes.com/).
. The inset is a pure Zipf plot dimensioned to the entire set of 390 billionaires and the poorest sub-sample of 195. (Source: Forbes Listhttp://www.forbes.com/).
To explore its implications, from an elementary analysis of the N objects in the full sample, we select an ordered sub-sample of all objects below the rank k = k*. We examine this set as a rank-size law where the new rank  is defined in terms of the original rank k as
is defined in terms of the original rank k as  . The sub-sample now follows the relation
. The sub-sample now follows the relation

where the new maximum is  and where the last expression holds when
and where the last expression holds when  . Noting that in the original set, the ratio of successive sizes is
. Noting that in the original set, the ratio of successive sizes is  , in the sub-sample this ratio is
, in the sub-sample this ratio is  which shows quite clearly that the second set does not follow the same rank size rule as the initial set. In fact for the subdivision in Fig. 2 where we divide the top 390 billionaires into the first richest 195 and the second ‘poorest’, the ratio of the first to the second in the second set, expressed in terms of the rescaled rank
which shows quite clearly that the second set does not follow the same rank size rule as the initial set. In fact for the subdivision in Fig. 2 where we divide the top 390 billionaires into the first richest 195 and the second ‘poorest’, the ratio of the first to the second in the second set, expressed in terms of the rescaled rank  , is
, is  which is very different from the expected ratio of 0.5 for a pure Zipf’s Law. In the inset, we also show the same failure for the second ordered set (red dots) which occurs when the rank size is based on a pure Zipf’s Law dimensioned to the same income data.
which is very different from the expected ratio of 0.5 for a pure Zipf’s Law. In the inset, we also show the same failure for the second ordered set (red dots) which occurs when the rank size is based on a pure Zipf’s Law dimensioned to the same income data.
An analogous problem arises if we consider two independent sets where  holds for each which we then aggregate. It is clear that Zipf’s Law cannot hold for the aggregated set. For instance, if we consider two replicas of the same set, then the union of the two replicas cannot be described by the same law. Such elementary examples show, in a rather dramatic way, the crucial role played by a property of internal consistency or completeness of the total set under examination which we call ‘coherence’. A thorough examination and some reflection on empirical applications of Zipf’s Law, particularly to social systems, suggests that many applications to date are based on systems where the data is incomplete in some obvious way16. This is particularly so for city size distributions where arbitrary subdivisions of countries and cities are often used and where there is some evidence that systems that are developing independently, as for example for cities within a well-defined political or economic jurisdiction, are then aggregated into sets that ignore such entities. This is always the case when, for example, we examine world cities17. These issues elevate consistency in system and object definition into a new open problem we will address here. Thus for Zipf’s Law to hold, a set of objects must not contain replicas of the kind just noted, nor must the Law be applied to a sample of objects or events that is less than the whole, unless the sampling is able to anticipate the structure of the whole. This, as we will see, is a powerful and difficult criterion to meet.
holds for each which we then aggregate. It is clear that Zipf’s Law cannot hold for the aggregated set. For instance, if we consider two replicas of the same set, then the union of the two replicas cannot be described by the same law. Such elementary examples show, in a rather dramatic way, the crucial role played by a property of internal consistency or completeness of the total set under examination which we call ‘coherence’. A thorough examination and some reflection on empirical applications of Zipf’s Law, particularly to social systems, suggests that many applications to date are based on systems where the data is incomplete in some obvious way16. This is particularly so for city size distributions where arbitrary subdivisions of countries and cities are often used and where there is some evidence that systems that are developing independently, as for example for cities within a well-defined political or economic jurisdiction, are then aggregated into sets that ignore such entities. This is always the case when, for example, we examine world cities17. These issues elevate consistency in system and object definition into a new open problem we will address here. Thus for Zipf’s Law to hold, a set of objects must not contain replicas of the kind just noted, nor must the Law be applied to a sample of objects or events that is less than the whole, unless the sampling is able to anticipate the structure of the whole. This, as we will see, is a powerful and difficult criterion to meet.
Why we need more than a power law
When we say “There is more than a power law in Zipf”, we mean that although an underlying power law distribution is certainly necessary to reproduce the asymptotic behavior of Zipf’s Law at large values of rank k, any random sampling of data does not lead to Zipf’s Law and the deviations are dramatic for the largest objects. We will see that coherence in the entire dataset is necessary which may be interpreted in terms of screening among different objects, an effect that is beyond the underlying power law distribution. It implies that any system which obeys this law must have internal consistency in its size distribution or its sample. In this quest, it is worth noting that Benford’s Law which reveals the dominance of small numbers with properties akin to a power law, does not suffer from these problems of sampling, for any random subset, union of sets, or aggregation would still meet Benford’s Law18. In this sense, we consider Zipf’s Law to be much more subtle and informative than Benford’s in that the system of interest used to demonstrate Zipf’s Law is of crucial importance to the relevance, hence applicability of the law.
Let us consider N objects (cities, word frequencies, etc.) distributed according to the probability density  . In sorting the size of these objects, the rank k associated with the size x(k) corresponds to the probability of finding k−1 objects larger than x(k), between x(k) and the maximum value xM. Then for rank k we can write
. In sorting the size of these objects, the rank k associated with the size x(k) corresponds to the probability of finding k−1 objects larger than x(k), between x(k) and the maximum value xM. Then for rank k we can write

where  and we assume
and we assume  . From Eq.(2), it is easy to derive the rank size law as
. From Eq.(2), it is easy to derive the rank size law as  from which Zipf’s Law is recovered when
from which Zipf’s Law is recovered when  . However, this argument only holds for large values of k because we assume
. However, this argument only holds for large values of k because we assume  . If we do not ignore xM, accept that it is finite in a realistic case and set
. If we do not ignore xM, accept that it is finite in a realistic case and set  , we then explicitly define the normalization constant C from the boundary values of the support
, we then explicitly define the normalization constant C from the boundary values of the support  of p(x) in Eq.(2) as
of p(x) in Eq.(2) as  . Using C, we can then define the most appropriate rank size rule for empirical analysis as
. Using C, we can then define the most appropriate rank size rule for empirical analysis as

As expected, the rank size rule in Eq.(3) behaves asymptotically as 1/k but for small values of k which is the region we tend to be mostly interested in, the behavior of Eq.(3) shows a deviation from a pure Zipf’s Law due to the constant term C/xM present in the denominator. The value of this constant also sets the rank  above which x(k) can be approximated by 1/k and below which the rank size law deviates from a pure 1/k Zipf’s Law.
above which x(k) can be approximated by 1/k and below which the rank size law deviates from a pure 1/k Zipf’s Law.
A clear demonstration of the importance of this constant and its effect on large values in a typical size distribution is illustrated in Fig. 3 where we plot the rank order of the population of the top 61 world cities. The broken red line is a graphical representation of the rank size rule from Eq.(3) which is based on a random sampling from the density function x−2 where we used the size of the largest and the smallest cities in the set to estimate xM and xm. Its closeness to the observed population points is obvious but this is in stark contrast to the pure Zipf’s Law  which is the solid black line from which the actual data and modified Zipf’s Law in Eq.(3) differ. The rank
which is the solid black line from which the actual data and modified Zipf’s Law in Eq.(3) differ. The rank  and this immediately shows that for the top 18 cities (which in fact comprise almost half the total population, 200m out of some 400m), Zipf’s Law is entirely inappropriate.
and this immediately shows that for the top 18 cities (which in fact comprise almost half the total population, 200m out of some 400m), Zipf’s Law is entirely inappropriate.
Rank Size of World Cities and Deviation from Zipf’s Law.
The top 61 ‘world cities proper’ normalized as  plotted in the grey squares are used to compute the modified rank size equation Eq.(3) – dashed red line – compared to the pure rank size equation
plotted in the grey squares are used to compute the modified rank size equation Eq.(3) – dashed red line – compared to the pure rank size equation  which is the solid black line. Note the value of
which is the solid black line. Note the value of  , below which values do not accord to Zipf’s Law in contrast to those above. The data is from the compilation of 65 separate databases (Sources: Wikipediahttp://en.wikipedia.org/wiki/List_of_cities_proper_by_population).
, below which values do not accord to Zipf’s Law in contrast to those above. The data is from the compilation of 65 separate databases (Sources: Wikipediahttp://en.wikipedia.org/wiki/List_of_cities_proper_by_population).
Moreover the shape of Eq.(3) reveals a subtle problem with respect to the question of deviations from a pure Zipf’s Law. In fact the rank-size law found in Eq.(3) can be either concave or convex (in log-log scale) for different values of the parameters. This means that there exists a combination of the parameters for which the rank size in Eq.(3) behaves as a pure Zipf’s Law (i.e.  ). However, this is only an accidental result due to the specific dependence of the shape of Eq.(3) on the parameters.
). However, this is only an accidental result due to the specific dependence of the shape of Eq.(3) on the parameters.
We can make this point more cogently by underlining the fact that a mechanism which is able to recover the 1/k behavior only asymptotically completely misses the significant features of a Zipfian set of values. In fact the largest values of this set (i.e. those values corresponding to small values of k) are actually the main expression of what we have called ‘coherence’ or consistency of the sample. In Fig. 1, we have seen that the problem of sample coherence is particularly important for the biggest values with the largest value in fact defining the entire rank-size law. Therefore the rank  of an independent sampling cannot be interpreted as the breakpoint in the scale at which an adequately approximated mechanism exists to explain Zipf’s Law because these values are indeed the core of the problem addressed here.
of an independent sampling cannot be interpreted as the breakpoint in the scale at which an adequately approximated mechanism exists to explain Zipf’s Law because these values are indeed the core of the problem addressed here.
The deviations most clearly observed in the rank size law of world city sizes in Fig. 3 imply that this data set is an assemblage of objects that do not form a coherent system. From casual but informed evidence, we believe that the system of cities has not matured to the point where these world cities are truly competing with one another for scarce resources19 and thus cannot ever give rise to anything like a pure Zipf’s Law. In short, world city populations have not yet ‘globalized’ sufficiently to form part of an integrated system (unlike national GDP in Fig. 1) and thus are more likely to represent Zipfian distributions that apply to country or region-wide systems of cities that have in fact evolved in more integrated ways17. In Fig. 3, the deviations from Zipf’s Law are related to the fact that we are looking at the wrong ‘scale’ at which to observe the coherence of the sample. The right scale is more likely to be at the country level at which Zipf’s Law approximately holds for many countries as we show in Fig. 4 and below in Fig. 6 (although there are exceptions such as the UK).
Rank-Size Laws Illustrating Different Degrees of Coherence.
Top Left: Rank-size for the largest world cities showing the absence of truly global cities which have developed in relation to all other cities. Therefore the world is not a coherent/fully integrated system and represents the wrong scale at which city size samples must be aggregated to obtain a Zipf’s Law. Instead Nigeria (green solid line) shows a nearly perfect Zipfian behavior. Nigeria which is separate from the rest of Africa, represents a city system which has developed more uniformly in a more integrated fashion, The Nigeria rank size law has been rescaled for clarity; Centre Left: Rank-size of the fifty largest European continental cities (i.e. the European part of Russia and UK are excluded). As in the case of the world cities, we observe absence of coherence at this geographical scale; Bottom Left: River formations are mainly due to geographical and morphological constraints on the Earth’s surface. Hence a Zipf’s Law is not expected and in fact the river rank size rule is well approximated by the curve (dashed black line), predicted by an independent sampling procedure without any screening effect; Top Right: For the frequency of words in the Corpus of Contemporary American English, a quasi-perfect Zipf’s Law is observed over the 2000 (and more) most used words. Linguistic systems are fully coherent with respect to our interpretation of Zipf’s Law. Centre Right: If we rank the Gross Domestic Product (GDP) of world countries, we observe a Zipfian behavior for the 30 richest. Bottom Right: As for words, a Zipf’s Law also appears in the frequency of usage of Python modules in a computer science project domain. Sources: Nigeria from the Mathematica database see Fig. 5 ; the top 61 country populations is from Wikipedia, see Fig. 2 ; the top 50 continental European city populations from http://www.citymayors.com/features/euro_cities.html; the top 161 river lengths from Wikipedia http://en.wikipedia.org/wiki/List_of_rivers_by_length; top 2000 COCA words from http://corpus.byu.edu/coca/; GDP from Wikipedia http://en.wikipedia.org/wiki/List_of_countries_by_GDP_(nominal); the frequency of Python module usage from http://www.algorithm.co.il/blogs/math/python-module-usage-statistics/
Real (Zipfian) and Sampled Theoretical Rank-Size Law.
Left (a): Eight sets of samples of 250 cities each drawn using the random conditioning algorithm explained in the text, rescaled in order to have the same maximum value and compared with a pure Zipf’s Law (black solid line). In the inset, we report the average rank-size law (dashed orange line) of 200 simulated countries from which the eight reported in the main box are extracted. We compare this with the rank-size rule produced by independent random samplings (red dashed line) and with the average over the 16 countries of panel b) (maroon solid line). We observe that the conditioned sampling algorithm produces a striking result very close to a pure Zipf ‘s Law (blue solid line). Right (b): Rank-size rules for the cities in 16 world countries collapsed in order to have the same maximum values and comparable with Zipf’s Law for the same (black solid line) (Source: Wolfram Mathematica online database).
The implications in all this are that departures from Zipf’s Law might represent some quantitative indicator of the lack of integration (or cohesion) although this is a speculation beyond our immediate concern here. It is worth noting from Fig. 3 that Zipf’s Law works extremely well for the largest values in many phenomena as in countries where cities have developed in a more integrated manner. Nigeria is a good example which during its major growth period was relatively isolated globally (see Fig. 4) and therefore this country exhibits a nearly perfect Zipf’s Law or, with respect to our interpretation, a high degree of coherence favored by the isolated growth. For many other size-frequency distributions shown in Fig. 4, we can also report phenomena where coherence is not expected and where indeed Zipf’s Law is not observed.
In fact, many applications of Zipf’s Law reveal a severe lack of coherence in their data and lead, as in the world city data set in Fig. 3 and Fig. 6, to the bigger question: what is missing? To address this in a slightly more oblique fashion, we will now proceed in a somewhat different way. In order to appreciate the importance of this problem, we will define a backwards relation such that, given a rank-size law, this would define the corresponding distribution as

where  ; x(k) is now given and p(x) is the probability density function we are searching for. We can easily solve Eq.(4) recalling that
; x(k) is now given and p(x) is the probability density function we are searching for. We can easily solve Eq.(4) recalling that  where
where  is the cumulative distribution associated with p(x) and inverting x(k). Obviously if we invert Eq.(3) and insert it in Eq.(4), we retrieve
is the cumulative distribution associated with p(x) and inverting x(k). Obviously if we invert Eq.(3) and insert it in Eq.(4), we retrieve  but the important point that we want to stress is that in solving Eq.(4), any dependence on N vanishes. This means that the rank-size rule changes its shape, varying the number, for instance, of cities but the underlying p(x) does not change whatsoever for N. Equivalently we can say that to obtain Eq.(3), the number of cities N and the normalization constant C are independent.
but the important point that we want to stress is that in solving Eq.(4), any dependence on N vanishes. This means that the rank-size rule changes its shape, varying the number, for instance, of cities but the underlying p(x) does not change whatsoever for N. Equivalently we can say that to obtain Eq.(3), the number of cities N and the normalization constant C are independent.
Instead when we deal with a pure Zipfian rank-size rule  we find that
we find that

We obtain p(x) by differentiating Eq.(5) with respect to x to get

As expected, we find that the underlying inverse square pdf must be one of the ingredients in order to obtain Zipf’s Law. But the dependence on N does not vanish anymore. This point is now much subtler than the previous one. In fact we find that the normalization in Eq.(6) must explicitly depend on the number of cities, that is  . In practice in order to obtain a pure Zipf’s Law, this means that the range of definition of p(x) depends on the number of elements in the sample. This is linked to the observation made before that there exists a particular combination of parameters for which Eq.(3) reduces to a pure Zipf’s Law. The backward problem shows that in the framework of independent samplings, we have to set N according to the range of the pdf or the range according to N. We can see this dependence between C and N as a consequence of the coherence that a Zipfian sample must have. However, rather than adopt this somewhat artificial combination of parameters in Eq.(3), we now argue that this coherence can be interpreted in a different context in a more fashionable and natural way.
. In practice in order to obtain a pure Zipf’s Law, this means that the range of definition of p(x) depends on the number of elements in the sample. This is linked to the observation made before that there exists a particular combination of parameters for which Eq.(3) reduces to a pure Zipf’s Law. The backward problem shows that in the framework of independent samplings, we have to set N according to the range of the pdf or the range according to N. We can see this dependence between C and N as a consequence of the coherence that a Zipfian sample must have. However, rather than adopt this somewhat artificial combination of parameters in Eq.(3), we now argue that this coherence can be interpreted in a different context in a more fashionable and natural way.
A simple model for coherence: conditioned sampling
Instead of varying the range of the original power law  , we propose that a screening or conditioning effect should be introduced into the selection procedure with respect to our framework. The basic idea behind such a concept can be exemplified using the distribution of city sizes in the US. Suppose that at a certain point, we extract ‘New York City’ from our 1/x2 distribution. After such an event in a random sampling, there is still a probability that ‘Another New York City’ could be drawn from the distribution. In reality of course, such an event cannot happen because the largest cities screen one another with respect to their growth dynamics.
, we propose that a screening or conditioning effect should be introduced into the selection procedure with respect to our framework. The basic idea behind such a concept can be exemplified using the distribution of city sizes in the US. Suppose that at a certain point, we extract ‘New York City’ from our 1/x2 distribution. After such an event in a random sampling, there is still a probability that ‘Another New York City’ could be drawn from the distribution. In reality of course, such an event cannot happen because the largest cities screen one another with respect to their growth dynamics.
A simple way to introduce such an effect is to make the sampling conditional. Then after a certain value is extracted, a section of the distribution around this value is thence excluded from the density. We show this schematically in Fig. 5. In essence, we draw the size of the first object x1 from the density  that is normalized over the range
that is normalized over the range  . The section to remove around x1 varies from x1min to x1max and these bounds are computed so that the area of the removed section is A
. The section to remove around x1 varies from x1min to x1max and these bounds are computed so that the area of the removed section is A

The area A of the forbidden section is a priori arbitrary and we fix it to be equal to 1/N where N is the total number of extractions. This slice  is then removed meaning that the subsequent object of size x2 must be not be drawn from this area. The number of elements drawn can be larger than N even if the area A = 1/N because the forbidden area can be partially overlapping. The computation proceeds recursively in this fashion until the required number of objects has been sampled as implied in Fig. 5.
is then removed meaning that the subsequent object of size x2 must be not be drawn from this area. The number of elements drawn can be larger than N even if the area A = 1/N because the forbidden area can be partially overlapping. The computation proceeds recursively in this fashion until the required number of objects has been sampled as implied in Fig. 5.
Successive Conditioned Draws.
When we extract an object (or a city size) such as x1, we remove a section (blue slice in panel 1) of the probability density around the drawn value. See the text for the details of how to compute the slice to remove (Eq.7). Then the density moves to the reduced distribution in panel 2 from which the next object is drawn in the same way with the slice associated with x2 being removed in panel 3.
In Fig. 6(a), we show a series of samples, normalized with respect to their maximum values where the scaling is close to Zipf’s Law but where their position, hence actual populations are heavily influenced by the lower ranked, larger-sized draws. In Fig. 6(b), we show real data which corresponds to the city size distributions for several different countries20. The sampled and real distributions in Fig. 6 are sufficiently different en masse to indicate that many real city size distributions are incoherent in comparison to their theoretical equivalents21. In Fig. 6(b), there are some countries such as the UK, Russia, Iran and to a lesser degree France, where the capital cities exercise a primate city effect which indicates extreme concentration compared to other elements in their size distributions. Explanations for these deviations are loose: cities serving empires beyond their national boundaries and highly centralized administrations, are obvious explanations. Most other countries reveal the opposite in that their largest cities have lesser sizes than might be expected if Zipf’s Law were to play out exactly. We also consider that screening of one object with respect to another occurs at different hierarchical levels. Thus we consider that conditional sampling of the data and exploration of the extent to which cities screen one another is key to an understanding of city size relations.
Discussion
This situation forces conceptual problems of a new type because up to now, most researchers dealing with this problem have attempted to develop a theory for Zipf’s Law which is to be found in the underlying distribution 1/x2. In fact we now see clearly that such a theory cannot be developed without considering the problem of the sample coherence which in cities, income distributions and in many other systems whose signatures are believed to be described by power laws, will always show itself up as the phenomenon we have referred to as screening. The question of defining each individual object also effects the coherence of the system because if objects are split and disaggregated, or indeed merged and aggregated, their order changes. Such can easily happen when we deal with objects that are defined by social practice and are human artifacts such as cities22 or firms23. As we consider Zipf’s Law to be the ultimate signature of an integrated system (say, for instance, the world’s economy in terms of GDP as in Fig. 1), it is important to devise general models which include coherence in a simple but generic way. In this line of reasoning, coherence and screening could be the result of some kind of optimization in growth processes or of an optimal self-organization mechanism of the system with respect to some (finite) resources. This must be the next step in providing new and novel perspectives on this entire area of study.
References
Zipf, G. K. Human behavior and the principle of least effort (Addison-Wesley, Cambridge, MA, 1949).
Saichev, A., Malevergne, Y. & Sornette, D. Theory of Zipf’s law and beyond (Lecture Notes in Economics and Mathematical Systems 632, Springer, Heidelberg, Germany, 2010).
Google Scholar returned 620 papers with ‘Zipf’ in the title and over 46,300 with reference to ‘Zipf’ (accessed July 30, 2012).
Clauset, A., Shalizi, C. R., & Newman, M. E. J. Power-law distributions in empirical data. SIAM Review 51, 661–703 (2009).
Blank, A. & Solomon, S. Power laws in cities population, financial markets and internet sites: Scaling and systems with a variable number of components. Physica A 287, 279–288 (2000).
Lotka, A. J. The frequency distribution of scientific production. Journal of the Washington Academy of Sciences 16, 317–323 (1926).
Pareto, V. Manual of political economy (English translation, Ann S. Schwier, 1971, Augustus M. Kelley Publishers, New York, 1906).
Gabaix, X. Zipf’s law for cities: An explanation. Quarterly Journal of Economics 114, 739–767 (1999).
Axtell, R. L. Zipf distribution of U.S. firm sizes. Science 293, 1818–1820 (2001).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286. 509–512 (1999).
Barabási, A.-L. The origin of bursts and heavy tails in human dynamics. Nature 435, 207–211 (2005).
Perline, R. Strong, weak and false inverse power laws. Statistical Science 20, 68–88 (2005).
Montroll, E. W. & Schlesinger, M. F. On 1/f noise and other distributions with long tails. Proceedings of the National Academy of Sciences USA 79, 3380–3383 (1982).
Krugman, P. The great illusion, The New York Times, August 15, A17 (2008), available at http://www.nytimes.com/2008/08/15/opinion/15krugman.html?_r=0 accessed 5/10/2012.
Forbes Lists. http://www.forbes.com/wealth/forbes-400 accessed 28/9/2010.
Eeckhout, J. Gibrat’s law for (all) cities. American Economic Review 94, 1429–1451 (2005).
Rose, A. K. Cities and countries. Journal of Money, Credit and Banking 38, 2225–2245 (2006).
Pietronero, L., Tosatti, E., Tosatti, V. & Vespignani, A. Explaining the uneven distribution of numbers in nature: the laws of Benford and Zipf. Physica A 293, 297–304 (2001).
Sassen, S. The global city: New York, London, Tokyo (Princeton University Press, Princeton, NJ, 2001).
Rosen, K. T. & Resnick, M. The size distribution of cities: An examination of the Pareto law and primacy. Journal of Urban Economics 8, 165–186 (1980).
Soo, K. T. Zipf's law for cities: A cross country investigation. Regional Science and Urban Economics 35, 239–263 (2005).
Cheshire, P. Trends in sizes and structure of urban areas. Handbook of Regional and Urban Economics, 3, 1339–1373 (1999).
Stanley, M. H. R., Buldyrev, S. V., Havlin, S., Mantegna, R. N., Salinger, M. A. & Stanley, H. E. Zipf plots and the size distribution of firms. Economics Letters 49, 453–457 (1995).
Acknowledgements
LP and MC thank FET Open Project FOC nr. 255987 for partial support. MB thanks the EPSRC Complexity in the Real World (ENFOLDing EP/H02185X/1) Project for partial support.
Author information
Authors and Affiliations
Contributions
LP and MB developed the logic for these ideas, MC developed the formal analysis and with MB explored the data. All three authors were involved in writing the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Cristelli, M., Batty, M. & Pietronero, L. There is More than a Power Law in Zipf. Sci Rep 2, 812 (2012). https://doi.org/10.1038/srep00812
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00812
This article is cited by
-
Defining a city — delineating urban areas using cell-phone data
Nature Cities (2024)
-
The Base-e Representation of Numbers and the Power Law
Circuits, Systems, and Signal Processing (2021)
-
Demography and the emergence of universal patterns in urban systems
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.