Introduction

Mechanical metamaterials1,2,3,4,5,6,7,8,9,10,11 have been of widespread attraction over the past few decades as a result of their unusual, but often desirable, mechanical properties12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43. Such properties are, in general, not found in natural materials, but are the results of specific approaches to the internal structural design of mechanical metamaterials. Among such properties, negative Poisson’s ratio has been of widespread interest within the scientific community, with metamaterials with such a property known as ‘auxetics’. This property is unusual and counter-intuitive, given that Poisson’s ratio, ν, is in the range −1 < ν < 0.5 for conventional isotropic materials, and in the range −∞ < ν < ∞ for anisotropic materials1,3,44,45,46,47,48,49,50,51. Auxetic materials benefit from enhanced shear moduli, indentation resistance, and fracture toughness, and can achieve extremely large strains and shape changes in comparison with conventional materials52,53. As a result, a considerable number of analytical, numerical, and experimental studies have been devoted to the design and analysis of auxetic metamaterials in recent years1,2,3,54,55,56.

A well-known family of auxetic metamaterials is the pivotally-interconnected assemblies of polygons, first introduced by Ronald D. Resch in 196557. He devised a design principle enabling the construction of various geometric arrangements of articulated, identical polygonal units (or elements), where each unit is connected to its neighbours by rotational hinges at its corners. Assuming the polygonal units to be perfectly rigid, these structures deform by the rotation of the rigid units rather than any deformation of these units. In 2000, Grima and Evans58 revived the attention of the scientific community to Resch’s invention by highlighting the auxetic behaviour (with ν = −1) of such assemblies. Since then, in particular, assemblies with square elements have been welcomed by scientists59,60,61,62,63,64,65,66,67,68,69,70,71,72 with a diverse range of proposed applications, e.g. in the development of novel medical stents73,74,75,76,77,78,79, deformable batteries80, and flexible electronics81.

Several recent developments of Resch’s interconnected assemblies considered ‘hierarchical’ generalisations of these structures45,75,80,82,83,84,85,86,87,88. In hierarchical structures/materials, a distinct structural pattern repeats in different scales89, that is why they are also called ‘multiscale’ structures/materials7. Many materials in nature—e.g. bone, nacre, diatoms, and spider silk—have hierarchical structures, resulting in some beneficial mechanical properties such as increased toughness and resistance to crack propagation90,91,92,93,94.

In general, by increasing the level of the hierarchy, the number of degrees of freedom (DoFs) of a pivotally-interconnected hierarchical structure will increase82,85. Seifi et al.82 introduced the method of rotate-and-mirror (RAM) to limit the number of DoFs when the hierarchical level increases. However, it was concluded that this method is only able to generate hierarchical assemblies with odd-numbered modules (e.g., the module in the upper part of Fig. 1a), whereas even-numbered modules (e.g., the module in the upper part of Fig. 1b) must be avoided. Hereafter, we call hierarchical assemblies generated based on the former sort of module ‘odd-numbered assemblies’ (‘ONAs’), and those generated based on the latter sort of module ‘even-numbered assemblies’ (‘ENAs’). Here we focus on tackling the problem of synchronous deployment of RAM-generated ENAs of square units.

Fig. 1: Generating hierarchical levels using the method of rotate-and-mirror (RAM) and simulating the motion of each element.
figure 1

This diagram demonstrates how we generate the hierarchical level of Type I or/and Type II with a odd, and b even numbers of square elements. After generating each assembly, rotationally-neutral elements are labelled as grey elements. By removing a pair of red or yellow hinges, it is possible to contract the even-numbered assembly (ENA) of level 2. The red cross shows which pair of hinges should be removed in each ENA. c Schematic representation of the connecting hinges, represented by black circles, that facilitate the generation of the assembly of the next level of the hierarchy from the sub-assemblies represented by green circles.

Full size image

A range of ENAs was presented in several previous studies. For instance, Cho et al.85 used fractal-cuts to expand a sheet of material into a wider pattern with particular properties. Gatt et al.75 investigated the effect of stiffness of hinges on the degree of auxeticity of the hierarchical assemblies. They generated a level-3 ENA that was not able to be contracted completely (more information is provided in Supplementary Note 4, and also Supplementary Movie 4). Tang et al.95 studied the nonlinear stress-strain behaviour and phononic bandgaps of hierarchically cut thin sheets of elastomer as super‐stretchable mechanical metamaterials. Kunin et al.83 investigated the static and dynamic elastic behaviour of fractal-cut materials. Tang and Yin87 studied kirigami-based hierarchical auxetic sheets capable of achieving high stretchability and compressibility, and examined the effect of raising the hierarchal level on the stretchability of such metamaterials. Dudek et al.45 investigated the effect of the resistance of hinges on the final configuration and mechanical properties of ENAs. Kim et al.80 used the hierarchical fractal-cut method to produce a flexible auxetic battery. An et al.86 exploited kirigami for embedding an array of cuts into a thin plastic sheet to create an ENA of squares; they devised a type of programmable hierarchical metamaterial by tuning a set of geometric parameters associated with the pattern of cuts as well as the physical specifications of the thin sheet. Using hierarchical cuts, Han et al.81 developed high-performance conductors with biaxial mechanical stretchability and stable conductivity.

Here we use the method of RAM to generate hierarchical assemblies in which the level-(N − 1) assembly rotates by 0 < θ < 90°, followed by reflections with respect to the Y- and X-axes, respectively, to generate the level-N assembly. It should be noted that we choose θ = 45° as the rotational position to generate the models in their fully-expanded state, where the rotating direction can be either clockwise (CW) or counter-clockwise (CCW). We demonstrate that by applying the generation method RAM to even-numbered modules, some elements will undergo translational transformations (in addition to rotational transformations) during deformation. This observation inspired us to propose a new design approach, called the selective hinge removal (SHR) strategy, which facilitates the complete deployment of ENAs through removing selective hinges from their assemblies. We first present the method of identification of the hinges to be removed at each level of the hierarchy to ensure that the structure can be completely deployed. Subsequently, in order to evaluate Poisson’s ratio, three different methods are used to calculate the dimensions of the assemblies in two directions. These methods are as follows: (1) analytical models based on geometrical transformations, (2) numerical simulations using Working Model 2D, and (3) experimental measurements using physical models. Finally, we will present and discuss the variations of Poisson’s ratio for the ENAs of levels 1, 2, and 3.

Results

Generating ONAs

For generating the level-1 assembly, first, the square of level 0 should be rotated by +45° (or −45°). In this article, CW-rotating squares are coloured in orange, whereas CCW-rotating squares are coloured in blue. The next step is to mirror the rotated elements, followed by connecting them to each other by rotational hinges. At level 1, every square is connected to each of its neighbouring squares by only one hinge, enabling two connected squares to rotate in opposite directions. In Fig. 1a, b, hinges are represented by white small circles.

In the case of generating and deforming assemblies of level 2, ONAs are discussed first to investigate their translational elements and determine the difference between their behaviour with that of ENAs. For this purpose, the set of squares of level 1 rotates 45° (either CW or CCW), followed by a reflection with respect to the mirror lines (MLs), as shown by red dashed lines in Fig. 1a, b. Because the colours of the squares at the corner of the ONAs of level 1 are similar, the direction of rotation is not important. As illustrated in Fig. 1a, on both sides of the vertical and horizontal MLs, the structures are geometrically similar, but their corresponding squares have different colours, as a result of reflection transformations. In other words, if a square on one side of a ML is orange, its image on the other side will be blue, and vice versa.

In this paper, those elements that can only move on the XY-plane translationally are coloured in grey, which play an important role in the behaviour of such hierarchical structures. In the process of generating level-2 from the level-1 assemblies, after mirroring, there is a ‘labelling’ step as designated in Fig. 1a, b, where translational elements are labelled by grey ‘stickers’. To assign labels to appropriate elements, we first determine the colours of connected squares on the two sides of the horizontal and vertical MLs. At level 2, the colours of the squares which are in contact with the MLs are opposite (while they have the same rotational speed). Given that such elements are mutually connected by two hinges, they restrain the rotational DoF of each other, therefore should be labelled by ‘rectangular’ grey stickers. In other words, the rectangular labels indicate which squares should be identified as grey elements on the two sides of the MLs. As a consequence, these labelled squares will neutralise their corresponding homochromatic squares in the hierarchical assembly of the lower level, i.e. level 1. These neutralised squares are labelled by ‘small square’ grey stickers (see Supplementary Movie 1).

After labelling the level-2 ONAs and colouring the appropriate squares in grey, some orange and blue squares will remain in the structure, enabling the assembly to contract and expand. Figure 1a illustrates how the assemblies of level 2 can be contracted synchronously, shown in particular configurations with θ = 90°, 60°, 30°, and 0, where deployment angle θ is the angle between two adjacent squares at level 1. As can be seen from the two fully-contracted level-2 ONA models depicted in Fig. 1a, there is no difference between these two models, as one can be isometrically transformed into the other by a 90° rotation. As a result, the rotational direction of the level-1 structure during the generation process does not affect the final result in higher hierarchical levels. Conversely, in ENAs, the rotational direction of the assembly of level N − 1 determines the type of the assembly of level N. Depending on the colour of the first rotating square, in ENAs, two different types of assemblies will be achievable: (1) Type I, in which the first square is orange; and (2) Type II, in which the first square is blue.

Selective hinge removal (SHR) strategy for architecting ENAs

For ENAs, the generation process is, in general, similar to that of ONAs. However, unlike ONAs, after constructing the two types of level-2 structures for ENAs, the mirrored level-1 structures will be in contact with their neighbours through elements with opposite colours, connected by two hinges on the vertical or horizontal MLs (Fig. 1b). Therefore, as explained in the labelling step, these squares should be labelled with grey rectangular stickers. Every labelled square which is in contact with its neighbour with two hinges on the vertical ML will label its corresponding sub-assembly at level 1. This similarly applies to every square which is in contact with the horizontal ML. As a result, in the labelling step, the entire assembly will be labelled. In other words, after labelling an ENA of level 2, all the elements of the structure will become grey. Therefore, the ‘all-grey’ structure will be locked due to the absence of rotating elements (see Supplementary Movie 1). As a result, in order to revive the rotational elements of level 2, it is necessary to selectively remove hinges on the contact lines (edges) of the assemblies of level 1, which are located on the MLs associated with level 2. As a convention, we will not make any changes to the hinges located on the vertical ML. However, where there are two squares connected on the horizontal ML, one hinge should be removed from the pair. This enables the proper function of local rotating squares, and consequently those of the entire assembly. In this paper, the outer hinges on the horizontal ML are shown in red, whereas the inner hinges are depicted in yellow. As a result of particular arrangements of connections among blue and orange squares, in Type-I assemblies the red hinges must be removed, whereas in Type-II assemblies the yellow hinges are those to be removed. These alternations enable us to contract ENAs appropriately. In Fig. 1b, the deformation of models of level 2 is illustrated in particular deployment angles. Supplementary Movie 1 demonstrates the labelling process and reveals the differences between Type-I and Type-II assemblies.

Fertile versus barren ENAs

The next question is whether both types of ENAs of level 2 can generate the next hierarchical level. To deal with this problem, a simplified model is illustrated in Fig. 1c, where each green circle represents a level-(N − 1) structure, by assembling four of which, a level-N structure can be achieved. The black small circles denote the hinges that should be shared by a similar assembly to generate the next level of hierarchy, i.e. level N + 1. After being rotated by 45°, the hinges will be located in their correct positions. In Fig. 1c, the black circles are indicated on all of the final assemblies. By following them, it is possible to determine the capability of each structure for the generation of the next hierarchical level. We first start tracking these black circles in ONAs. As shown in Fig. 1a, after the completion of the deformation, the black dots will be located on the four vertices of the final models, which are larger squares ABCD and EFGH. Therefore, both final ONAs can generate level 3, because these hinges can be shared with their neighbouring assemblies to generate the next level of the hierarchy.

On the other hand, in ENAs, the locations of black hinges are not identical in the fully-closed configurations of Type I and II (squares IJKL and MNOP in Fig. 1b). More specifically, for Type-I assemblies, in which the red hinges are removed, the black hinges will be located on the four vertices of the 4 × 4 fully-contracted structure IJKL. As a result, Type I can generate the next level of the hierarchy because it can share these hinges to facilitate appropriate connectivities to generate the next level. On the contrary, in Type II, the black hinges are located on sides MN and OP of the corresponding fully-contracted structure, i.e. square MNOP, not on its vertices; consequently, the Type-II assembly cannot be the parent of level 3 because it is not able to appropriately share the black hinges with its neighbours. We call such a structure to be ‘barren’ because it is unable to produce the next level of the hierarchy. (See Supplementary Movie 1 to track the positions of the black circles).

Generalized generation process of ENAs

The deployment of Type-I and -II assemblies of levels 3 and 4 are illustrated in Fig. 2a, b, respectively. In Fig. 2, all squares are coloured in green, denoting elements with unspecified motion, where the role of black dots is similar to that of Fig. 1c. By tracking the black dots in Type-I assemblies of both levels 3 and 4, it can be observed that at θ = 0, the black hinges will be located on the four vertices of fully-contracted squares ABCD and IJKL. They also appear on the upper and lower sides of the two squares (i.e., sides AD, BC, IL, and JK), facilitating hinge-sharing to generate the next level of the hierarchy. Therefore, Type-I assemblies of levels 3 and 4 are able to generate their next levels. As illustrated in Fig. 2, Type-I assemblies of level 3 can generate two types of level-4 assemblies depending on which direction it is rotated while mirroring. It is also shown how the Type-I assembly of level 3 rotates in the deployment process of an assembly of level 4, and how its black hinges make appropriate connections. A red dashed ML is added as a guideline to the figures to indicate the rotation direction of the assembly. On the contrary, by investigating the Type-II assemblies of levels 3 and 4, it can be understood that when the structures are fully-contracted (squares EFGH and MNOP), the black hinges are located on the right and left sides of the contracted models (i.e. EF and GH at level 3, and MN and OP at level 4), not on their vertices. As mentioned earlier, these hinges cannot be shared with similar structures to generate the next level of the hierarchy; consequently, such Type-II assemblies with removed inner hinges turn out to be barren.

Fig. 2: The generation flowchart of hierarchical even-numbered assemblies (ENAs).
figure 2

Contraction phases of a level-3, and b level-4 assemblies of Types I and II (in the figures, L(N) denotes level N). c Representations of Type-I and Type-II assemblies of level N, where the CW- and CCW-rotated assemblies are indicated by ACW and ACCW, respectively. d Generalized generation flowchart of ENAs. To generate the next levels of the hierarchy, only Type-I assemblies of the previous levels can be used, because all Type-II assemblies are barren.

Full size image

The two types of assemblies at each level of the hierarchy are schematically represented in Fig. 2c, where circles represent assemblies (corresponding to grey circles in Fig. 2a, b). There is an arrow in each circle that indicates the rotation direction of the assembly; CW- and CCW-rotated assemblies are indicated by ACW and ACCW, respectively. The pairs of white hinges located on the vertical MLs will be retained because they connect the sub-assemblies of lower levels to form the assemblies of higher levels. On the other hand, hinges located on the horizontal MLs are shown in either yellow or red. More specifically, in Type-I assemblies, yellow and red hinges represent those which are to be retained and removed, respectively. In contrast, in Type-II assemblies, red hinges are retained whilst yellow hinges are removed.

A generalized generation flowchart of hierarchical ENAs is shown in Fig. 2d, where the assemblies of level N − 1 are shown by pink-shaded circles which consist of the assemblies of the lower level. As explained before, the Type-II assembly of level N − 1 cannot generate the next level, whereas the Type-I assembly of level N − 1 can generate assemblies of both Types I and II at level N which are depicted by light grey circles. At this level, the Type-I assembly will generate Types-I and -II assemblies of level N + 1, but the Type-II assembly is barren. The deployment sequence of hierarchical assemblies of Types I and II by up to level 5 are shown in Supplementary Figs. 8 and 9, respectively.

In-plane Poisson’s ratio of ENAs

As a result of alterations in the connectivity of elements in ENAs, their Poisson’s ratios vary as a function of deployment angle θ. More specifically, depending on the configuration, their Poisson’s ratio can be positive or negative, or tend to positive or negative infinity. In this section, we present the method of determining Poisson’s ratio for such structures by up to level 3. In order to achieve this aim, the first step is to find \({X}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\), which represent the dimensions of a level-N assembly at a deployment angle θ, in the X- and Y-directions, respectively. To this end, three different methods are used in this paper (see Fig. 3). The first method is analytical based on geometrical relations; the second method relies on the numerical data extracted from motion simulations; and as the third method, and to verify the analytical and numerical results, we experimentally measure the values of \({X}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) in some particular deployment angles of the physical models. By inputting the data of \({X}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) at each hierarchical level, it is possible to find the corresponding amount of true (i.e., logarithmic) strain using Eqs. (1) and (2); finally, Poisson’s ratio in the two directions can be calculated from Eqs. (3) and (4), as follows:

$${\varepsilon }_{Y}^{({{{\rm{C}}}})}(\theta )={\int }_{{Y}_{90}}^{{Y}_{\theta }}\left(\frac{dY}{Y}\right)=\,{{{{\mathrm{ln}}}}}\,\left(\frac{{Y}_{\theta }}{{Y}_{90}}\right)\;{{{{{\rm{and}}}}}}\;{\varepsilon }_{X}^{({{{\rm{C}}}})}(\theta )={\int }_{{X}_{90}}^{{X}_{\theta }}\left(\frac{dX}{X}\right)=\,{{{{\mathrm{ln}}}}}\,\left(\frac{{X}_{\theta }}{{X}_{90}}\right),$$
(1)
$${\varepsilon }_{Y}^{({{{\rm{E}}}})}(\theta )={\int }_{{Y}_{0}}^{{Y}_{\theta }}\left(\frac{dY}{Y}\right)=\,{{{{\mathrm{ln}}}}}\,\left(\frac{{Y}_{\theta }}{{Y}_{0}}\right)\;{{{{{\rm{and}}}}}}\;{\varepsilon }_{X}^{({{{\rm{E}}}})}(\theta )={\int }_{{X}_{0}}^{{X}_{\theta }}\left(\frac{dX}{X}\right)=\,{{{{\mathrm{ln}}}}}\,\left(\frac{{X}_{\theta }}{{X}_{0}}\right)$$
(2)
$${\nu }_{XY}^{({{{\rm{C}}}})}(\theta )=-\,\frac{{\varepsilon }_{Y}^{({{{\rm{C}}}})}(\theta )}{{\varepsilon }_{X}^{({{{\rm{C}}}})}(\theta )}\;{{{{{\rm{and}}}}}}\;{\nu }_{YX}^{({{{\rm{C}}}})}(\theta )=-\,\frac{{\varepsilon }_{X}^{({{{\rm{C}}}})}(\theta )}{{\varepsilon }_{Y}^{({{{\rm{C}}}})}(\theta )},$$
(3)
$${\nu }_{XY}^{({{{\rm{E}}}})}(\theta )=-\,\frac{{\varepsilon }_{Y}^{({{{\rm{E}}}})}(\theta )}{{\varepsilon }_{X}^{({{{\rm{E}}}})}(\theta )}\;{{{{{\rm{and}}}}}}\;{\nu }_{YX}^{({{{\rm{E}}}})}(\theta )=-\,\frac{{\varepsilon }_{X}^{({{{\rm{E}}}})}(\theta )}{{\varepsilon }_{Y}^{({{{\rm{E}}}})}(\theta )},$$
(4)

where superscripts (C) and (E) denote contraction and expansion, respectively, and θ is in degrees. It should be noted that, in this study, we calculate the ‘accumulated logarithmic’ Poisson’s ratio rather than the ‘instantaneous’ Poisson’s ratio. The reason behind such a choice of Poisson’s ratio is provided in Supplementary Note 5 and Supplementary Fig. 12.

Fig. 3: Geometric variations during deformations for ENAs of levels 2 and 3 in terms of deployment angle θ.
figure 3

The analytical results are compared with numerical and experimental results. At 60°, it is shown how Xθ and Yθ (i.e., the distance between red circles in the X- and Y-directions, respectively) are divided into smaller, measurable segments on the plan views of the experimental models. The analytical and numerical results are represented continuously, whereas the experimental results are measured at different deployment angles from 90° to zero in increments of 10°.

Full size image

In the analytical method, we can find equations relating \({X}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) by considering the parallelism or perpendicularity of the edges with respect to the MLs of different levels (see Supplementary Fig. 1). To calculate \({X}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) at each level, they should be divided into measurable segments, indicated by red lines in Fig. 3. In other words, the distance between the two red points, shown for each level, is divided into smaller line segments that can be calculated geometrically. By increasing the level of the hierarchy, the number of these segments will rise considerably; however, thanks to the mirror symmetry of the assemblies, it is sufficient to perform calculations in each coordinate direction for only a half of each model. These equations enable us to find the dimensions of a model as a function of deployment angle θ. The calculations using this method are explained in detail for the hierarchical structures of levels 1, 2, and 3 in Supplementary Note 1 (including Supplementary Figs. 2–6), with the final equations given here. Considering a0 to be the side length of the basic square of level 0, the side length of the basic square associated with each level N, denoted by aN, can be expressed as:

$${a}_{N}=\,\frac{{a}_{0}}{{2}^{N}},$$
(5)

where N is the level of the hierarchy. For level 1, we will have:

$${X}_{\theta }^{{{{{{\rm{L}}}}}}(1)}={Y}_{\theta }^{{{{{{\rm{L}}}}}}(1)}={a}_{0}\left(\cos \left(\frac{\theta }{2}\right)+\,\sin \left(\frac{\theta }{2}\right)\right).$$
(6)

For level 2, we will obtain:

$${X}_{\theta }^{{{{{{\rm{L}}}}}}(2)}=\frac{{a}_{0}}{2}(2+\,\sin \theta ),$$
(7)
$${Y}_{\theta }^{{{{{{\rm{L}}}}}}(2)}=\frac{{a}_{0}}{2}(\,2\,\sin \theta +\,\cos \theta +1).$$
(8)

Finally, for level 3, the equations will be as follows:

$${X}_{\theta }^{{{{{{\rm{L}}}}}}(3)}=\frac{{a}_{0}}{4}\left(5\,\sin \left(\frac{\theta }{2}\right)+4\,\cos \left(\frac{\theta }{2}\right)+\,\sin \left(\frac{3\theta }{2}\right)\right),$$
(9)
$${Y}_{\theta }^{{{{{{\rm{L}}}}}}(3)}=\frac{{a}_{0}}{4}\left(2\,\sin \left(\frac{\theta }{2}\right)+4\,\cos \left(\frac{\theta }{2}\right)+2\,\sin \left(\frac{3\theta }{2}\right)+2\,\sin \theta \,\sin \left(\frac{\theta }{2}\right)\right).$$
(10)

Given that the side lengths of the fully-contracted structures are equal to a0, and assuming a0 = 24 cm in this research, parameters a2 and a3 will be 6 and 3 cm, respectively, according to Eq. (5).

An alternative method to calculate the instantaneous dimensions of the structures during deformation is to exploit the numerical data obtained from motion simulations. To this end, the structures were modelled and simulated (materials and methods; motion simulation), the results of which are compared with those of the analytically-derived equations. As can be seen from Fig. 3, the results of both methods are exactly compatible for levels 2 and 3. Furthermore, to verify the analytical/numerical results, experimental models were fabricated and tested (Materials and Methods; Physical models), where the dimensions of the models were calculated at different deployment angles from 90° to zero in increments of 10° (i.e., 90°, 80°, 70°, …, and 0). Subsequently, these experimental results were compared with the analytical/numerical data. As shown in Fig. 3, the error is within the range of ±3%, so it can be concluded that these results are in very good agreement with our analytical/numerical data.

Since in this study we consider the deformation of the assemblies over a period of time during which the structure undergoes a ‘large’ (i.e., ‘geometrically nonlinear’) deformation, the accumulated Poisson’s ratio might be different in tension and compression. Therefore, in this section, we demonstrate that the ENAs show different mechanical properties during the contraction and expansion processes, and calculate Poisson’s ratios for both cases. Because we create the structures in their fully-expanded configurations, the investigation of Poisson’s ratio diagrams starts with contraction and continues with expansion. During contraction, the deployment angle runs from θ = 90° to θ = 0. On the contrary, during expansion, the deformation starts at the θ = 0 and ends at θ = 90°. In Fig. 4, the yellow squares represent the initial dimensions of the structures. Importantly, if any of the two dimensions of the model at a position is equal to the side length of the yellow squares, the corresponding deployment angle will be a critical angle in the diagram of Poisson’s ratio because it would tend to infinity (Supplementary Movie 2).

Fig. 4: In-plane Poisson’s ratio in hierarchical ENAs of levels 2 and 3.
figure 4

a, b Plots of the strains and Poisson’s ratio of the contraction of the level-2 structure. c, d Plots of the strains and Poisson’s ratio of the expansion of the level-2 structure. e, f Plots of the strains and Poisson’s ratio of the contraction of the level-3 structure. g, h Plots of the strains and Poisson’s ratio of the expansion of the level-3 structure. 3D assemblies are used to exhibit the deformation of the models. Yellow squares represent the initial dimensions of the structures; when during the deformation process any of the two instantaneous dimensions of the structures are equal to the respective dimensions of the yellow squares, the corresponding deployment angle is a critical angle.

Full size image

The geometric behaviour of the level-1 assembly was previously investigated58, so here we only report the results for the assemblies of levels 2 and 3. Also, in Fig. 4, only the assemblies of Type I are illustrated, because they can be the parents of the next level. Nevertheless, it is important to note that Poisson’s ratio is similar at each level of the hierarchy for structures of Type I and Type II, the difference between which is only the order of connecting the CW and CCW assemblies (Fig. 2c). Therefore, \({X}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\theta }^{{{{{{\rm{L}}}}}}(N)}\), and consequently Poisson’s ratios, are equal in both types. The variations of strains in each direction, i.e. εX and εY, in terms of deployment angle θ, are shown in Fig. 4 (see also Supplementary Movie 2 for more information).

Contraction and expansion processes of level-2 ENAs

As shown in Fig. 4a, at the onset of contraction, εY gradually increases while εX is ~0, making vXY drop form +∞ gradually (Fig. 4b). At θ = 54.0°, the strains are equal in magnitude but opposite in sign, leading to \({\nu }_{XY}={\nu }_{YX}=1\). Importantly, \(\theta =36.3^\circ\) is a critical angle for the structure where \({Y}_{36}^{{{{{{\rm{L}}}}}}(2)}={Y}_{90}^{{{{{{\rm{L}}}}}}(2)}\), resulting in \({\varepsilon }_{Y}={\nu }_{XY}=0\); however, vYX tends to +∞ and −∞ at the left and right sides of this point, respectively. In fact, the structure exhibits auxetic behaviour only starting from this angle towards complete contraction where \({\nu }_{XY}={\nu }_{YX}=-1\).

$$\mathop{{{{{\mathrm{lim}}}}}}\limits_{\theta \to {(90^\circ )}^{-}}{\nu }_{XY}=+\infty ,$$
(11)

and

$$\mathop{{{{{\mathrm{lim}}}}}}\limits_{\theta \to {(36.3^\circ )}^{+}}{\nu }_{YX}=+\infty \;{{{{{\rm{and}}}}}}\;\mathop{{{{{\mathrm{lim}}}}}}\limits_{\theta \to {(36.3^\circ )}^{-}}{\nu }_{YX}=-\infty .$$
(12)

On the other hand, we can observe a different behaviour from the level-2 structure during expansion. At the commencement of the expansion process, as shown in Fig. 4c, εY is twice as εX, so initially we have \({\nu }_{XY}=-2\) and \({\nu }_{YX}=-0.5\). However, as the structure starts to expand, the difference between the two strains gradually reduces and eventually the model will have a negative Poisson’s ratio of −1 at 90°, i.e. at its fully-expanded configuration. Hence, during the entire expansion process, the level-2 structure shows auxetic behaviour. Importantly, in the expansion of the level-2 structure, there are no critical angles, because the values of \({X}_{\theta }^{{{{{{\rm{L}}}}}}(2)}\) and \({Y}_{\theta }^{{{{{{\rm{L}}}}}}(2)}\) are never equal to \({X}_{0}^{{{{{{\rm{L}}}}}}(2)}\) and \({Y}_{0}^{{{{{{\rm{L}}}}}}(2)}\), respectively.

Contraction and expansion processes of level-3 ENAs

In the contraction of the level-3 structure, deformation starts with a Poisson’s ratio of −1 in both directions, i.e. \({\nu }_{XY}={\nu }_{YX}=-1\) at \(\theta =90^\circ\) (Fig. 4f); however, as deformation continues, we can observe that \(\theta =64.7^\circ\) and 49.2° are two critical angles for the system as we have:

$$\mathop{{{{{\mathrm{lim}}}}}}\limits_{\theta \to {(64.7^\circ )}^{+}}{\nu }_{XY}=-\infty \;{{{{{\rm{and}}}}}}\;\mathop{{{{{\mathrm{lim}}}}}}\limits_{\theta \to {(64.7^\circ )}^{-}}{\nu }_{XY}=+\infty ,$$
(13)
$$\mathop{{{{{\mathrm{lim}}}}}}\limits_{\theta \to {(49.2^\circ )}^{+}}{\nu }_{YX}=+\infty \;{{{{{\rm{and}}}}}}\;\mathop{{{{{\mathrm{lim}}}}}}\limits_{\theta \to {(49.2^\circ )}^{-}}{\nu }_{YX}=-\infty .$$
(14)

As can be seen from Fig. 4f, if Poisson’s ratio in one direction tends to infinity, the corresponding Poisson’s ratio in the other direction will be zero. Between 90° and 64.7°, the structure is auxetic; this is because vYX approaches −∞, whilst vYX has finite negative values approaching zero. From 64.7° to 49.2°, εY is positive whilst εX is negative, so the structure is not auxetic in this range. Then at the right of 64.7°, vYX tends to +∞, whereas vYX is zero. Similarly, at the left of 49.2°, vYX tends to +∞, whereas vYX is zero. Importantly, at θ = 55.5°, we have \({\varepsilon }_{Y}=-{\varepsilon }_{X}\) (i.e. \({\nu }_{XY}={\nu }_{YX}=1\)), so the Poisson’s ratio curves cross each other at this angle. Between 49.2° and zero, the dimensions of the model decrease in both directions, therefore εX and εY are both negative, so the structure shows auxetic behaviour. As can be seen from Fig. 4e, f, during the final 20° of deformation, the plots of εX and εY tend to overlap, ending up with \({\nu }_{XY}={\nu }_{YX}=-1\) at \(\theta =90^\circ\). In the expansion of the level-3 structure, as shown in Fig. 4g, εX and εY are always positive, so the structure is always auxetic in both directions, with the initial and final Poisson’s ratios of −1. The slight gap between the plots of vYX and vYX (Fig. 4h) is a result of the selective removal of hinges in ENAs which facilitates the deployment of the assemblies.

Discussion

As revealed earlier in this study, the ONAs created using the method of RAM have deployment behaviours different from those of the ENAs created by this method. In this paper, by a detailed investigation of the transformation behaviour of each element in the ENAs, we devised a new design strategy, called ‘SHR’, allowing these assemblies to contract and expand, without which the ENAs are ‘locked’ and their elements have only translational motion.

To figure out which hinges should be removed, we demonstrated that two types (i.e., Type I and Type II) of assemblies can be generated at each level of the hierarchy. We observed that Type-I assemblies can be the parents of higher hierarchical levels, whereas Type-II assemblies are barren structures which cannot produce any assemblies of a higher level. For example, an assembly presented in ref. 75, which is similar to a Type-II ENA in this research, was used to generate the next levels of the hierarchy. As explained and discussed in Supplementary Note 4 and visualised in Supplementary Movie 4, the higher-level assemblies generated based on the Type-II ENAs are not able to undergo a complete deployment cycle (see also Supplementary Figs. 10 and 11).

To evaluate and validate the Poisson’s ratio of the hierarchical assemblies, three different methods were utilised to determine the dimensions of the structures during the process of deployment. As depicted in Fig. 3, the numerical results of motion simulation and the analytical outputs of the mathematical model were fully compatible. Moreover, experimental results based on physical models acceptably validated the analytical/numerical data with an error within the range of ±3%. Sources of error affecting the experimental results include: (1) the use of polyurethane foams in the fabrication of the physical models, in which the elements are not perfectly rigid and the hinges are not ideal rotational mechanisms; and (2) the manual actuation of the models by two people with imperfect synchronisation.

Results from the current study revealed that Poisson’s ratio changes as a function of deployment angle in the ENAs of levels 2 and 3 of the hierarchy. It is already known that at level 1, Poisson’s ratio is −1 throughout the deformation process58. In contrast, at level 2, due to the selective removal of hinges, Poisson’s ratio not only changes as a function of deployment angle, but also its variation curves in the contraction process are completely different from those of the expansion process. Normally, Poisson’s ratio is the same in tension and compression at any specific point in time, but if the deformation is considered over a period of time (i.e., when the accumulated Poisson’s ratio is calculated), the diagrams of Poisson’s ratio will be different during expansion and contraction. Importantly, at some particular deployment angles during the contraction of the ENAs of levels 2 and 3, the instantaneous dimensions of the models will be equal to their initial values. Therefore, at these critical angles, corresponding to the vertical asymptotes in Fig. 4b, f, Poisson’s ratio tends to infinity in one direction while it is zero in the other direction. Between these critical angles, the models do not show auxetic behaviour.

Conclusions

In summary, we have established a systematic design strategy for ENAs based on the selective removal of rotational hinges, resulting in fully-deployable structures, which were not achievable with previously known methods. Furthermore, we demonstrated that there is a significant difference in the deployment behaviour of ONAs and ENAs. The obtained diagrams of Poisson’s ratio versus the deployment angle in pivotally-interconnected assemblies showed that this index can have different finite or infinite values.

As a result of the findings of this research, now both odd- and even-numbered hierarchical assemblies can be generated theoretically by level N, where N is an arbitrary natural number. While we have presented the results by up to level 3, one can perform this study by level N using the method introduced in this paper (Supplementary Note 1). In this sense, we have enlarged the design space of functional pivotally-interconnected mechanical metamaterials which could be used by researchers and designers for various applications including the development of novel reconfigurable structures, medical devices, flexible electronics, and deformable batteries.

Materials and methods

Mathematical modelling

Object-oriented programming was used to generate hierarchical structures in Delphi, where each hierarchical level is considered as an object or class, and a new class is added to update the code for generating the next level of the hierarchy. The governing equations were derived for the hierarchical structures of levels 1, 2, and 3 (for details, see Supplementary Note 2), resulting in the development of the application software ‘HiElm’ (standing for ‘hierarchical elements’) which provides a graphical user interface (GUI) to simulate the behaviour of the structures (Supplementary Software 1). The algorithm is divided into two main parts: (1) the generation of the hierarchical levels, which is the same as the procedure illustrated in Fig. 2d, and (2) the geometric transformations of units, in which a rotation is applied to the ‘parent’ of each level, that is a large square containing all the small squares associated with that level. Parent units are illustrated as grey squares in Fig. 5, in which the colour of their borders represents their rotational direction (orange: CW; blue: CCW). For all the three levels, only Type-I ENAs are presented in HiElm.

Fig. 5: The method of hinging in HiElm.
figure 5

a–c Depict the hinging method at levels 1, 2, and 3, respectively. On the right-hand side of each part (corresponding to each level), it is shown how \(\varDelta {X}^{{{{{{\rm{L}}}}}}(N)}\) and \(\varDelta {Y}^{{{{{{\rm{L}}}}}}(N)}\) are calculated during deformation, where φ is the rotation angle of respective parent (grey) squares, and dashed lines represent mirror lines.

Full size image

As can be seen from Fig. 5 and Supplementary Fig. 7, the rotation of the parent squares is around their centroids which are represented by black circles. Although the deployment angle is 0 < θ < 90°, the rotation angle of the parent squares is 0 < φ < 45° (the rotation angle of the 45°-rotated parent squares changes from 45° to zero). Importantly, the distance between the centroids and the vertical/horizontal MLs is always constant. The second measurable distance is between the centroids and the farthest point of each assembly along the X- and Y- directions denoted by \({X}_{\varphi }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\varphi }^{{{{{{\rm{L}}}}}}(N)}\), respectively, where φ is the rotation degree of the parent square and N is the level of the hierarchy. The derivations of \({X}_{\varphi }^{{{{{{\rm{L}}}}}}(N)}\) and \({Y}_{\varphi }^{{{{{{\rm{L}}}}}}(N)}\) up to three levels of the hierarchy are presented in Supplementary Note 2 (see Supplementary Figs. 2–6). The final relations are provided as Eqs. (15)–(25). By calculating the values of \(\varDelta {X}_{\varphi }^{{{{{{\rm{L}}}}}}(N)}\)and \(\varDelta {Y}_{\varphi }^{{{{{{\rm{L}}}}}}(N)}\), it is possible to find the exact position of the centroids of squares at each deployment angle.

Level 1

$${X}_{\varphi }^{{{{{{\rm{L}}}}}}(1)}={a}_{0}\frac{\sqrt{2}}{4}\,\cos \left(\frac{\pi }{4}-\varphi \right)$$
(15)
$$\Delta {X}_{\varphi }^{L(1)}={X}_{45}^{L(1)}-{X}_{\varphi }^{L(1)}={a}_{0}\frac{\sqrt{2}}{4}\left(1-\,\cos \left(\frac{\pi }{4}-\varphi \right)\right)$$
(16)
$$\Delta {Y}_{\varphi }^{{{{\rm{L}}}}(1)}=\Delta {X}_{\varphi }^{{{{\rm{L}}}}(1)}$$
(17)

Level 2

$${X}_{\varphi }^{{{{{{\rm{L}}}}}}(2)}=\frac{{a}_{0}}{4}(\sin \varphi \,\cos \varphi +1)$$
(18)
$$\Delta {X}_{\varphi }^{{{{{{\rm{L}}}}}}(2)}={X}_{45}^{{{{{{\rm{L}}}}}}(2)}-{X}_{\varphi }^{{{{{{\rm{L}}}}}}(2)}=\frac{{a}_{0}}{4}\left(\frac{1}{2}-\,\sin \varphi \,\cos \varphi \right)$$
(19)
$${Y}_{\varphi }^{{{{{{\rm{L}}}}}}(2)}=\frac{{a}_{0}}{4}({\sin }^{2}\varphi +\,\cos (2\varphi )+\,\sin (2\varphi ))$$
(20)
$$\Delta {Y}_{\varphi }^{{{{{{\rm{L}}}}}}(2)}={Y}_{45}^{{{{{{\rm{L}}}}}}(2)}-{Y}_{\varphi }^{{{{{{\rm{L}}}}}}(2)}=\frac{{a}_{0}}{4}\left(\frac{3}{2}-{\sin }^{2}\varphi -\,\cos (2\varphi )-\,\sin (2\varphi )\right)$$
(21)

Level 3

$${X}_{\varphi }^{{{{{{\rm{L}}}}}}(3)}=\frac{{a}_{0}}{8}(\sin (2\varphi )\cos \varphi +2\,\sin \varphi +2\,\cos \varphi )$$
(22)
$$\Delta {X}_{\varphi }^{{{{{{\rm{L}}}}}}(3)}={X}_{45}^{{{{{{\rm{L}}}}}}(3)}-{X}_{\varphi }^{{{{{{\rm{L}}}}}}(3)}=\frac{{a}_{0}}{8}\left(\frac{5\sqrt{2}}{2}-\,\sin (2\varphi )\cos \varphi -2\,\sin \varphi -2\,\cos \varphi \right)$$
(23)
$${Y}_{\varphi }^{{{{{{\rm{L}}}}}}(3)}=\frac{{a}_{0}}{8}(\sin (2\varphi )\sin \varphi +2\,\cos \varphi +\,\sin \varphi +\,\sin (3\varphi ))$$
(24)
$$\Delta {Y}_{\varphi }^{{{{{{\rm{L}}}}}}(3)}={Y}_{45}^{{{{{{\rm{L}}}}}}(3)}-{Y}_{\varphi }^{{{{{{\rm{L}}}}}}(3)}=\frac{{a}_{0}}{8}\left(\frac{5\sqrt{2}}{2}-\,\sin (2\varphi )\sin \varphi -2\,\cos \varphi -\,\sin \varphi -\,\sin (3\varphi )\right)$$
(25)

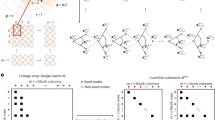
Interestingly, in pivotally-interconnected assemblies, square units can be replaced by alternative, convex or concave polygonal units. In this section, we have adapted some motifs from Persian-Islamic geometric patterns—known as ‘gereh’ (also written ‘girih’)—used in traditional Persian architecture96. To this end, two motifs are chosen from the ceiling decorative design of the palace ‘Hasht-Behesht’ located in Isfahan, Iran (Fig. 6a). The first gereh is an 8-pointed star called ‘Shamse’ (Fig. 6b) and the second gereh is a regular octagon known as ‘Setareh Chahar-Lenge’ (Fig. 6c).

Fig. 6: Hierarchical ENAs inspired by Persian-Islamic geometrical patterns and the software HiElm.
figure 6

a The ceiling of the palace ‘Hasht-Behesht’ located in Isfahan, Iran, constructed in the seventeenth century97. Schematics of the deployment of level-3 ENAs in which square units are replaced by b ‘Shamse’ and c ‘Setareh Chahar-Lenge’. d Graphical User Interface (GUI) of HiElm. In this application, in addition to square elements, four different Persian-Islamic motifs are provided which can be used to generate assemblies of up to level 3 of the hierarchy.

Full size image

In the application software HiElm provided as Supplementary Software 1, users can select different motifs and simulate the deployment of the hierarchical ENAs developed based on these motifs. An array of results within the GUI of HiElm is depicted in Fig. 6d.

Motion simulation

To simulate the deformation of the structures, the motion simulation software Working Model 2D was used, where rigid squares were connected to each other using frictionless hinges. Then, depending on the level of the hierarchy, a number of motors were added to each assembly. To run a synchronous simulation, the angular speed of all motors was considered to be 2° per second. The effect of gravity was assumed to be negligible.

Physical models

To simulate the rotational hinges and rigid squares, we fabricated a glued two-layer structure of polyurethane (PU) foams, where the first layer had a thickness of 10 mm and density of 45 kg m−3, and the second layer had a thickness of 20 mm and density of 25 kg m−3. The thickness of the hinges was considered to be 2.5 mm. The ENAs of levels 2 and 3 were designed in their fully-expanded configurations and cut using a CO2 laser cutting machine. Parameters a2 and a3 were considered to be 60 and 30 mm, respectively; therefore, the dimensions of both structures in their fully-contracted configurations were 240 mm (Fig. 7).

Fig. 7: Contraction of physical models made of polyurethane (PU) foams for the ENAs of levels 2 and 3.
figure 7

The models are depicted in the particular deployment angles of 90°, 60°, 30°, and 0.

Full size image

To limit the number of DoFs, the loci of the centroids of some squares were extracted from the motion simulations performed in Working Model 2D and cut using the CO2 laser cutter on square sheets of three-layered corrugated cardboard. Plastic straws were connected to the less dense foam layer at the centroids of the selected squares. By inserting the straws into their corresponding slots, the models were able to be contracted and expanded in a controlled way. Figure 7 and Supplementary Movie 3 show the deformation behaviour of Type-I ENAs of levels 2 and 3.