Orthogonal antiferromagnetism to canted ferromagnetism in CaCo₃Ti₄O₁₂ quadruple perovskite driven by underlying kagome lattices

Abstract

AA′₃B₄O₁₂ quadruple perovskites, with magnetic A′ and non-magnetic B cations, are characterized by a wide range of complex magnetic structures. These are due to a variety of competing spin-exchange interactions up to the fourth nearest neighbours. Here, we synthesize and characterize the magnetic behaviour of the CaCo₃Ti₄O₁₂ quadruple perovskite. We find that in the absence of an external magnetic field, the system undergoes antiferromagnetic ordering at 9.3 K. This magnetic structure consists of three interpenetrating mutually orthogonal magnetic sublattices. Under an applied magnetic field, this antiferromagnetic structure evolves into a canted ferromagnetic structure. In explaining these magnetic structures, as well as the seemingly unrelated magnetic structures found in other quadruple perovskites, we suggest a crucial role played by the underlying kagome lattices in these systems. All observed magnetic structures of these materials represent indeed one of the three possible ways to reduce spin frustration in the A′ site kagome layers. More specifically, our survey of the magnetic structures observed for quadruple perovskites AA′₃B₄O₁₂ reveals the following three ways to reduce spin frustration, namely to make each layer ferromagnetic, to adopt a compromise 120° spin arrangement in each layer, or to have a magnetic structure with a vanishing sum of all second nearest-neighbour spin exchanges.

Introduction

Oxide materials adopting the perovskite structure show a wide range of physical, magnetic, and chemical properties as a consequence of the wide chemical flexibility of these materials¹. This chemical flexibility is in part due to the ability of the network of corner-sharing octahedra in this structure to distort via twists and tilts to accommodate a wide range of cation sizes.

Of particular interest is the structure resulting from the a⁺a⁺a⁺ tilt system, which produces the so-called quadruple perovskite structure shown in Fig. 1a². This has the general formula AA′₃B₄O₁₂, where the A′ site in materials adopting this structure type is of the appropriate size to host transition metal cations in square-planar coordination.

Fig. 1: Crystal structure and experimental data collected from CaCo₃Ti₄O₁₂.

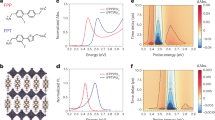
a Quadruple perovskite crystal structure. b Zero-field (ZFC) and field cooled (FC) magnetization data collected as a function of temperature from CaCo₃Ti₄O₁₂ under an applied field of 1 T. c Magnetization data collected as a function of field from CaCo₃Ti₄O₁₂. Observed (black), calculated (red), and difference (green) plots from the refinement of CaCo₃Ti₄O₁₂ against neutron powder diffraction data collected at d 300 K, e 1.6 K under 0 T, and f 1.6 K under 8 T. In d the upper set of tick marks corresponds to contributions from CaCo₃Ti₄O₁₂ and the lower set to contributions from the CoTiO₃ secondary phase. In e and f from top to bottom the tick marks correspond to: CaCo₃Ti₄O₁₂ nuclear and magnetic reflections and CoTiO₃ nuclear and magnetic reflections. The shaded regions correspond to contributions from the cryomagnet which were excluded from the refinement.

In materials with magnetic A′ and non-magnetic B cations, there are a range of competing interactions between the orthogonally arranged square-planar A′ sites that produce a wide variety of interesting emergent behaviour^{3,4,5,6,7,8,9,10}. For instance, both S = 1/2 Cu²⁺ in CaCu₃Ti₄O₁₂ and S = 2 Mn³⁺ in YMn₃Al₄O₁₂ exhibit long-range antiferromagnetic (AFM) ordering with T_N = 25 and 35 K respectively^3,4. In contrast, S = 1/2 Cu²⁺ spins in CaCu₃Sn₄O₁₂ and CaCu₃Ge₄O₁₂ order ferromagnetically (FM)¹¹. LaMn₃V₄O₁₂ with S = 5/2 Mn²⁺ shows a symmetry-breaking magnetic structure below T_N = 44 K in which the spins on neighbouring Mn sites are arranged at 60° to each other in planes perpendicular to the [111] direction⁷. CaCo₃V₄O₁₂ shows collinear ordering of all S = 3/2 Co²⁺ spins (T_N = 98 K), but arranged in two sublattices along two separate k-vectors^8,9. It is noted that the B cations of LaMn₃V^3.75+₄O₁₂ and CaCo₃V⁴⁺₄O₁₂ possess d-electrons, but they exhibit no magnetic moment likely due to the delocalization of these electrons^7,8,9. We recently reported the magnetic characterization of CaFe₃Ti₄O₁₂ with S = 2 Fe²⁺ at the A′ sites, which adopts an unusual AFM structure (T_N = 2.8 K) in which the moment direction depends on the orientation of the FeO₄ square plane¹⁰. The resulting arrangement consists of three interpenetrating sublattices each made up of the set of square planes sharing a common orientation. Under high applied magnetic field, CaFe₃Ti₄O₁₂ displays metamagnetic behaviour. Its magnetic structure switches to a canted FM state consisting of three FM sublattices (cFM phase)¹⁰.

Understanding the behaviour of these materials is complicated by a wide range of properties exhibited and a large number of competing interactions and electronic effects including Coulomb correlations, spin-orbit coupling, and orbital polarization. It is clear that first and second nearest neighbour (1NN and 2NN, respectively) interactions are not sufficient to explain the observed behaviour in these materials, and we must consider third and fourth neighbour spin exchanges (3NN and 4NN, respectively).

In this work, we prepare and characterize the quadruple perovskite CaCo₃Ti₄O₁₂ with Co²⁺ (S = 3/2) cations occupying the A′ sites, to find that it adopts an orthogonal magnetic structure similar to that observed for CaFe₃Ti₄O₁₂ with some key differences. We carry out DFT+U and DFT+U+SOC calculations to analyze the magnetic structure of CaCo₃Ti₄O₁₂. We show that various magnetic structures of quadruple perovskites are readily explained from the viewpoint of avoiding spin frustration in the underlying kagome spin lattices of their A′ cations.

Results and discussion

Initial characterization

Laboratory X-ray powder diffraction data collected from the products of reaction between CaTiO₃ and CoTiO₃ at 1600 °C and 13.5 GPa were consistent with the formation of a phase adopting the quadruple perovskite structure shown in Fig. 1a. A model based on the quadruple perovskite structure was refined against synchrotron X-ray powder diffraction data and produced excellent statistical and observed fits, confirming the material crystallizes in a cubic structure (space group Im−3) with a lattice parameter a = 7.4398(1) Å. Observed, calculated, and difference plots are shown in Supplementary Fig. 1a and the refined structural parameters are given in Supplementary Table 1.

Zero-field (ZFC) and field cooled (FC) magnetization data were collected from a sample under an applied field of 1 T and are shown in Fig. 1b. These contain a local maximum at T = 9.3 K consistent with an AFM transition. A fit of the ZFC data to the Curie–Weiss law (χ = C/(T−θ)) in the region 100 ≤ T (K) ≤ 300 yields values of C = 12.05(1) emu K mol⁻¹ and θ = −25.55(1) K. The calculated Curie constant yields an effective moment of µ_eff = 5.67(1) µ_B consistent with high-spin S = 3/2 Co²⁺, for which the theoretical spin-only moment would yield 3.87 µ_B. The higher-than-expected moment indicates the presence of an orbital contribution to the paramagnetic moment. Magnetization data collected above 10 K are linear through the origin. However, data collected at 2 K show an unusual shape consistent with metamagnetic behaviour with a transition at H_C ≈ 2.5 T Fig. 1c.

A model based on the quadruple perovskite structure could be refined against neutron powder diffraction data collected at 300 K to yield excellent calculated and observed fits. Plots of the refinement are shown in Supplementary Fig. 1b and the refined structural parameters are given in Supplementary Table 2. A small amount of CoTiO₃ (8.8% by weight) was included as a secondary phase. No antisite disorder was observed when the cation site occupancies were allowed to refine. Bond valence sums calculated from the refined structure yielded values of 1.849, 1.704, and 4.093 for Ca, Co, and Ti, respectively, confirming the composition as CaCo²⁺₃Ti⁴⁺₄O₁₂¹². The obtained compound thus contains magnetic Co²⁺ ions at the A′ site and nonmagnetic Ti⁴⁺ ions at the B site.

Zero-field magnetic structure

Low temperature neutron powder diffraction data were collected from CaCo₃Ti₄O₁₂ at 1.6 K under zero field. These data contained additional reflections consistent with long-range magnetic order. All the magnetic reflections which did not originate from the CoTiO₃ impurity could be indexed on the basis of a magnetic cell with a propagation vector k = (½, ½, ½) on the basis of the nuclear cell. This magnetic propagation vector is different from that found in CaFe₃Ti₄O₁₂ (k = (½, ½, 0)), indicating an overall different arrangement of magnetic moments in the two materials¹⁰. The highest symmetry magnetic structure (space group F_S23), which correctly accounted for the peak intensities, is shown in Fig. 2a.

Fig. 2: Magnetic structures of CaCo₃Ti₄O₁₂ and spin interactions in quadruple perovskites.

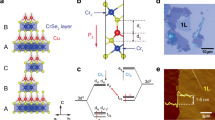
Refined magnetic structures of CaCo₃Ti₄O₁₂ at 1.6 K and under a 0 T and b 8 T. Red, blue, and green centres each correspond to a set of CoO₄ square planes sharing a common orientation. c J₁ exchange between 1NN. d Relative arrangement of 1NN centres in the 0 T magnetic structure of CaCo₃Ti₄O₁₂. e J₂ exchange between 2NN. f Relative arrangement of 2NN centres. g J₃ exchange between 3NN. h Relative arrangement of 3NN centres. i J₄ exchange between 4NN. j Relative arrangement of 4NN centres. k Three different J₄ interactions. l Moment directions considered during DFT calculations (detailed in the Supplementary Fig. 4). m Arrangement of the kagome layers along the [111] direction. n A kagome layer of J₂ spins perpendicular to [111]. o Projection view of two adjacent kagome layers of J₂ spins perpendicular to [111].

This structure consists of three interpenetrating magnetic sublattices corresponding to sets of CoO₄ square planes sharing a common orientation. It contains two different inequivalent Co sites, which were constrained to have the same moment M, allowing the structure to be refined using a single parameter (∣M∣). The refinement produced excellent calculated (χ² = 7.52) and observed fits (Fig. 1e) and resulted in a refined moment of 3.76 µ_B per Co centre. Full details of the refined structural model are given in Supplementary Table 3.

Under no applied magnetic field, CaCo₃Ti₄O₁₂ exhibits long range magnetic ordering with a transition temperature T_N = 9.3 K. The refined magnetic structure contains similarities to that observed previously in CaFe₃Ti₄O₁₂ (T_N = 2.3 K)¹⁰. Both structures consist of three mutually orthogonal AFM sublattices, each of which corresponds to the set of MO₄ square planes that share a common orientation (Fig. 2a). The difference between the two structures lies in the sign of one of the 4NN interactions between parallel MO₄ square planes. In the magnetic structure of CaCo₃Ti₄O₁₂, all three 4NN interactions are AFM while in CaFe₃Ti₄O₁₂ one of them (J₄(πCa), see below) is FM, resulting in the two different observed magnetic structures¹⁰.

High-field magnetic structure

Neutron powder diffraction data collected from CaCo₃Ti₄O₁₂ at 1.6 K and under an applied magnetic field of 8 T did not contain the magnetic reflections present in the data collected at 0 T, but did contain additional reflections relative to the data collected at 300 K. These could be indexed using a magnetic propagation vector k = (0, 0, 0). A model in which all Co moments are collinear could not account for the observed magnetic intensities. The R−3 model previously proposed for CaFe₃Ti₄O₁₂ at fields H ≥ 0.25 T (shown in Fig. 2b) was found to be compatible with the data¹⁰. This was refined against the data to yield good calculated (χ² = 8.95) and observed fits and yielded a moment of 3.04(1) µ_B per Co centre. Plots of the data are shown in Fig. 1f and refined parameters are given in Supplementary Table 4. However, a complete characterization of field-stabilized magnetic structure requires taking into account domain population and is better done on a single crystal.

Neutron powder diffraction data collected under applied fields H ≥ 2.5 T show a gradual suppression of the magnetic reflections originating from the AFM structure and the emergence of different magnetic reflections (Supplementary Fig. 2).

As in the AFM case, the magnetic structure of CaCo₃Ti₄O₁₂ under a high magnetic field consists of three sublattices that correspond to the square plane orientations (Fig. 2b, left). Within each sublattice, all moments are collinear and ferromagnetically ordered. However, the spins of all three FM sublattices are not collinear so as to reduce the magnetic dipole–dipole (MDD) interactions^13,14,15.

Spin exchanges

In order to understand the zero-field (F_S23) AFM structure of CaCo₃Ti₄O₁₂, we first consider Heisenberg (isotropic) spin exchange. The energy between two spins i and j is described by the Heisenberg exchange energy, $-{J}_{{ij}}\left({S}_{i}\cdot {S}_{j}\right)$^15,16,17. This energy vanishes for each 1NN exchange because the two spins involved in the exchange path are orthogonal, resulting in ${S}_{i}\cdot {S}_{j}=0$ (Fig. 2c, d). For the same reason, the exchange between 2NN also vanishes (Fig. 2e, f). The two spins in each 3NN are parallel and the exchange between these is therefore nonzero (Fig. 2g). However, in this structure, half of the 3NN paths have the spins ferromagnetically coupled, and the other half have the spins antiferromagnetically coupled (Fig. 2h). Thus, the sum of 3NN spin exchanges vanishes in this structure. That is to say, the AFM arrangement is not determined by 1NN, 2NN, or 3NN spin exchanges.

In cases when Heisenberg exchange fails to account for observed magnetic properties, it is common to consider Dzyaloshinskii-Moriya (DM, asymmetric) exchange between spin sites given by $-{D}_{{ij}}\cdot (S_{i}{\times {S}}_{j})$^15,16,17,18. This exchange is typically an order of magnitude weaker than the corresponding Heisenberg spin exchange. In this structure, the DM term for each 1NN path is zero as these centres lie on two orthogonal mirror planes, and no DM vector can be perpendicular to both. For the 2NN exchange paths, the individual DM terms are not necessarily zero, but the sum total of them is zero. Thus, the DM interactions cannot be responsible for the observed arrangement.

This prompted us to examine 4NN interactions (Fig. 2i, j). There are three kinds of 4NN interactions to consider as shown in Fig. 2k:

J₄(δM)Between two MO₄ planar units parallel to each other along a direction normal to the planes with an intermediate orthogonally oriented MO₄ unit.

J₄(πM)Between two coplanar MO₄ units along a direction ∥ to these with an intermediate orthogonal MO₄ unit.

J₄(πCa)Between two coplanar MO₄ units along a direction ∥ to these with an intermediate orthogonal Ca centre.

We evaluated the values of the 1NN, 2NN, and 3NN spin exchanges in CaCo₃Ti₄O₁₂ via energy mapping analysis based on first principles DFT calculations^{15,16,17,19,20,21,22,23}. Details of these calculations are given in the Supplementary Note 6. The ordered spin states that were used are defined in Supplementary Fig. 4. Our DFT+U calculations for CaCo₃Ti₄O₁₂ show that J₁ = 0.95 K, J₂ = −0.86 K, and J₃ = −0.64 K using U_eff = U − J = 4 eV. Namely, J₁ is FM while J₂ and J₃ are AFM, but all these spin exchanges are very weak. As already mentioned, these exchanges do not determine the AFM magnetic structure. We note that there were DFT studies on CaCu₃B₄O₁₂ (B = Ti⁴⁺, Ge⁴⁺, Sn⁴⁺) and CaCo₃V₄O₁₂^24,25.

We now examine the 4NN spin exchanges J₄(πCa), J₄(πM), and J₄(δM). To find how their values are affected by the orientation of the spins in each 4NN exchange path, we include spin-orbit coupling (SOC) in the DFT+U calculations. These DFT+U+SOC are simplified by employing the “dimer” model, in which all Co²⁺ ions except for those of the two CoO₄ square planes defining the 4NN spin exchange are replaced with nonmagnetic Zn²⁺ ions. Note that these correspond to the Co²⁺ ions located between the two CoO₄ square planes in J₄(πM) and J₄(δM). One needs to consider three different spin directions for the Co²⁺ ion of each CoO₄ square plane. One direction is perpendicular to the CoO₄ plane (⊥CoO₄). The in-plane spin orientation is not isotropic, so we distinguish two-moment directions: either parallel to the Co-Ca-Co direction (hereafter Co→Ca) or parallel to the Co-⊥Co-Co direction (hereafter Co→Co) (Fig. 2l and S4).

We examined AFM and FM arrangements for each combination of spin direction and 4NN exchange path. Our DFT+U+SOC calculations show that, for each spin orientation, the AFM coupling is more stable than the FM coupling in all three 4NN exchange paths. The relative energies calculated for the AFM states of each 4NN spin exchange path with three different spin orientations are summarized in Table 1. The results show that for each 4NN exchange path, the ||CoO₄ orientations are more stable than the ⊥CoO₄ orientation. Furthermore, of the two ||CoO₄ orientations, the one pointed along the Co→Ca direction is more stable as can be confirmed from the sum of the relative energies in Table 1. This is consistent with the experimentally observed magnetic structure.

Table 1 Calculated relative energies of CoO₄ dimers.

We now calculate the values of J₄(πCa), J₄(πM), and J₄(δM) based on their most stable spin orientations. Given the energy difference ΔE = E_AFM − E_FM = JS², where S = 3/2 for Co²⁺. Thus, from the ΔE values calculated, we obtain J₄(πCa) = −3.9 K, J₄(πM) = −0.3 K, and J₄(δM) = −2.0 K. All three 4NN spin exchanges are AFM with one particularly weak interaction. This is consistent with the fact that CaCo₃Ti₄O₁₂ undergoes an AFM ordering at a low temperature (i.e., T_N = 9.3 K).

Underlying kagome layers in quadruple perovskites

As described above, the AFM structure of CaCo₃Ti₄O₁₂ observed in the absence of external magnetic field is converted to the canted FM structure upon applying an external magnetic field. This is puzzling because the two magnetic structures appear quite unrelated. It is important to probe if the cause is hidden in plain view. We note that certain low-dimensional metals possessing several partially filled bands exhibit charge density wave instabilities although their individual Fermi surfaces do not show any observed nesting vectors. This puzzling observation is explained by the introducing concept of hidden Fermi surface nesting²⁶. We now show that the magnetic ions Co²⁺ of CaCo₃Ti₄O₁₂ form kagome layers perpendicular to the [111] direction, and the spin frustration of these underlying kagome layers not only provides a natural connection between the AFM structure and the canted FM structure of CaCo₃Ti₄O₁₂, but also may explain the variety of spin structures observed in A′-site magnetic quadruple perovskites. Notably, the Im−3 cubic crystal structure of CaCo₃Ti₄O₁₂ provides perfect kagome lattices with no distortion. Each nuclear unit cell will contain four sets of kagome layers perpendicular to the four body diagonal directions. However, due to the cubic symmetry, all of these are equivalent, indistinguishable, and related by rotations. We therefore only need to consider one set of kagome layers.

We note that the 2NN paths J₂, when extended, consist of kagome layers stacked along the [111] direction (Fig. 2m, n). Adjacent kagome layers interact via the 3NN exchange J₃ make the hexagram arrangement using half the (J₂, J₂, J₂) triangles as depicted in Fig. 2m, o. These underlying kagome layers play an important role in determining the magnetic structures of quadruple perovskites AA′₃B₄O₁₂. The high-field magnetic structure can be described as resulting from FM kagome layers in which all spins are oriented along the [111] direction and the moments canted with respect to the three-fold rotational axis. The senses of the spin canting between the two adjacent (J₂, J₂, J₂) triangles, connected by the J₃ paths, are opposite such that the two spins in each J₃ path are parallel to each other. It is important to notice that 2NN spin exchanges do not take place between NN kagome layers, but between 2NN kagome layers (Fig. 2e), which plays an important role in the magnetic structures of other quadruple perovskites.

We now consider the spin frustration that would result from AFM J₂ interactions. The ordered magnetic structures of quadruple perovskites under zero applied field show three different ways to relieve this spin frustration. The first is to have FM coupling within each kagome layer (made up of J₂) and AFM coupling between layers (through J₃). This is the arrangement observed in S = 1/2 CaCu₃Ti₄O₁₂³. Because of the AFM J₃ paths, every second layer will have the same spin arrangement, minimizing the frustration of the (J₂, J₂, J₂) triangles between every second J₂-kagome layers (Fig. 2e). The second way to reduce spin frustration is to have a compromise 120° spin arrangement. This is the situation observed in LaMn₃V₄O₁₂ with AFM coupling between adjacent layers⁷.

The third way to reduce the spin frustration is to have a magnetic structure with a vanishing sum of all J₂ exchanges. The Co²⁺ ions in the AFM structure of CaCo₃V₄O₁₂ are divided into two interpenetrating sublattices, in each of which the (J₂, J₂, J₂) triangles have equal numbers of (↑↑↓) and (↑↓↓) spin arrangements so that the sum of all J₂ spin exchanges vanishes⁹. In CaFe₃Ti₄O₁₂ and CaCo₃Ti₄O₁₂, the magnetic arrangement consist of three interpenetrating sublattices such that the spins on all J₂ paths are orthogonal to each other making the sum of all J₂ vanish¹⁰.

A canted FM (i.e., cFM) structure observed for CaFe₃Ti₄O₁₂ and CaCo₃Ti₄O₁₂ under high-field (Fig. 2b) is a combination of two different ways of reducing the spin frustration in the underlying kagome layers; one is a FM arrangement with spins oriented along the [111] direction, and the other is a compromise 120° spin arrangement with spins oriented perpendicular to the [111] direction. The FM arrangement is brought about by the external magnetic field, and the collinear spins of this arrangement become canted by introducing the compromise 120° spin arrangement. This spin canting is energy-lowering because it reduces the extent of the MDD interactions that occur among the collinear spins in the FM arrangement^13,14,15. In forming the cFM structure under high high-field, the spin exchanges J₂ and J₃, which are both are substantially AFM (Supplementary Table 7), play a major role. Under high-field, the spin moments are lined up with the field. Thus, when the spins are lined up along the [111] direction, the spins of each kagome lattice become ferromagnetically coupled leading to the collinear FM arrangement throughout the kagome lattices. This spin arrangement is energetically favourable in terms of avoiding spin frustration associated with the J₂ paths, but unfavourable in terms of MDD interactions. To reduce the latter, the spins of each kagome lattice cant by introducing a 120° compromise character such that the spins of the J₃-paths between adjacent kagome lattices are antiferromagnetically coupled to gain energy from the J₃ exchanges (Fig. 2m). This requires a “three-in” compromise arrangement in one spin triangle and a “three-out” compromise arrangement in the adjacent spin triangle (Fig. 2b). This explains why the canted spins are parallel in every second kagome lattices.

Conclusions

We prepared and characterized the quadruple perovskite CaCo₃Ti₄O₁₂ with S = 3/2 ions Co²⁺ at the square planar A′ sites. This material orders antiferromagnetically at T_N = 9.3 K to adopt a magnetic structure consisting of three interpenetrating mutually orthogonal magnetic sublattices. Each sublattice is made up of CoO₄ square planes possessing a common spin orientation. The formation of this AFM structure is not determined by the 1NN, 2NN, and 3NN spin exchanges, nor by DM interactions, but by the 4NN spin exchanges as well as SOC. The latter makes all spins lie in the plane of the CoO₄ units along the Co→Ca direction. It is important to note that the magnetic ions A′ of quadruple perovskites AA′₃B₄O₁₂, though cubic in structure, form kagome layers of 2NN spin exchange J₂ perpendicular to the [111] direction, and that minimization of spin frustration in the J₂-kagome layer is a common denominator for all different magnetic structures of AA′₃B₄O₁₂ in the absence and presence of external magnetic fields. There are three ways of relieving the spin frustration in these J₂-kagome layers; (1) to make each J₂-kagome layer FM, (2) to make J₂-kagome layer adopt a compromise 120° spin arrangement, or (3) to make the sum of all J₂ spin exchanges vanish. The first two ways are combined together in forming the canted FM structure of CaCo₃Ti₄O₁₂ and CaFe₃Ti₄O₁₂, which occurs to reduce the MDD interactions of the collinear spins in the pure FM structure.

Methods

Sample preparation

Samples of CaCo₃Ti₄O₁₂ were prepared from a 1:3 molar ratio of CaTiO₃ and CoTiO₃. CaTiO₃ was prepared from a mixture of CaCO₃ (99.5%) and TiO₂ (99.9%, dried at 900 °C) ground together using an agate mortar and pestle. The resulting powder was pressed into a pellet and fired at 1000 °C for 3 periods of 24 h with intermediate regrinding and repelletising steps. CoTiO₃ was prepared from a mixture of CoO (99.9%) and TiO₂ ground together, pelletised, and heated in a vacuum-sealed ampoule at 900 °C for 72 h.

The precursor mixture for CaCo₃Ti₄O₁₂ was ground together using an agate mortar and pestle and then ball milled using agate spheres for 2 h. The resulting powder was loaded into platinum capsules and treated at 1600 °C under 13.5 GPa for 1 h using a 6–8 cubic multianvil press. The pressure was released slowly after quenching to room temperature. In order to prepare a sufficient amount of material for neutron powder diffraction measurements, six samples (approx. 50 mg each) were prepared from a common precursor mixture. Laboratory X-ray diffraction data were collected using a Bruker D8 diffractometer and showed some of these contained a small amount of unreacted CoTiO₃ (<5% by mass). The sample containing the least amount of secondary phase was selected for magnetic and physical property measurements.

Diffraction experiments

Synchrotron X-ray powder diffraction data collected using the BL02-B2 beamline at Spring-8 synchrotron, Hyogo, Japan from a sample that did not show any peaks corresponding to unreacted precursors or unwanted secondary phases (shown in Supplementary Fig. 1a).

Neutron powder diffraction data were collected from a mixture of the products of five separate experimental runs using the ECHIDNA diffractometer at the OPAL reactor, Sydney, Australia²⁷. These samples were ground together using an agate mortar and pestle and pressed into a 5 mm diameter pellet. The pellet was placed in a vanadium can and fixed in place using a cadmium rod. Data suitable for structural characterization were collected at 300 K using a wavelength of 1.6215 Å. Data at low temperatures were collected using a cryomagnet and a wavelength of 2.4395 Å. Rietveld analysis was carried out using GSAS-II²⁸. Magnetic structure solutions were carried out using k-SUBGROUPSMAG as implemented in GSAS-II^28,29.

Magnetic property measurements

Magnetic property measurements were carried out using an MPMS-XL SQUID magnetometer.

DFT calculations

To determine the spin exchanges of CaCo₃Ti₄O₁₂, we carried out spin-polarized DFT+U calculations by using the frozen-core projector augmented plane wave (PAW) encoded in the Vienna ab Initio Simulation Package (VASP) and the PBE exchange-correlation functional^19,20,21,22. The electron correlation associated with the 3d states of Co was taken into consideration by DFT+U calculations with an effective on-site repulsion U_eff = U − J = 4 and 5 eV²³. All our DFT calculations used the plane wave cutoff energy of 450 eV, and the threshold of 10⁻⁶ eV for self-consistent-field energy convergence. We employed a set of (8 × 8 × 8) k-points for DFT+U calculations and a set of (4 × 4 × 4) k-points for DFT+U+SOC calculations³⁰.