Dynamics of inertialess sedimentation of a rigid U-shaped disk

Abstract

When particles sediment in a viscous fluid, the character of their trajectories depends sensitively on the particles’ shape. Here we study the sedimentation of U-shaped rigid disks in a regime where inertia can be neglected. We show that, unlike the case of planar disks which settle in a fixed orientation relative to the direction of gravity, U-shaped disks tend to perform a periodic sequence of pitching and rolling motions which cause their centre of mass to sediment along complex trajectories that range from quasi-periodic spirals to helices. Thus, we demonstrate that particles of achiral shape can sediment along chiral paths whose handedness is determined by their initial orientation rather than their geometry. Our analysis provides a framework in which to interpret the motion of sedimenting particles of arbitrary shape.

Introduction

The zig-zag trajectory of a sheet of paper settling to the ground under its own weight^1,2 is a familiar example of sedimentation, where the unsteady motion and complex trajectories of the sheet are dictated by inertial dynamics. By contrast, when inertia is negligible, gravity forces balance viscous drag and trajectories tend to be simpler: spheres descend vertically with constant velocity according to Stokes’ law, while rods, disks or ellipsoids follow oblique paths set by their initial orientation³.

The handling and processing of microscale materials, which is routinely performed in a liquid environment⁴, involves a rich variety of processes in the Stokes limit of vanishing inertia. Examples of sedimentation on the microscale include the segregation of graphene by centrifugation⁵, the preparation of graphene ink⁶, blood testing methods⁷, microalgae harvesting⁸, and the separation of microplastics from natural sediment^9,10.

Particle shape is a key factor in microhydrodynamics in the Stokes limit³. For non-colloidal spheres, complex sedimentation behaviour requires long-range hydrodynamic interactions that arise in suspensions¹¹. However, two identical but non-spherical particles such as rods, disks or hemispheres, can sediment along tumbling trajectories; on these, the two particles undergo in-phase periodic reorientations, accompanied by concomitant modulations in their sedimentation speed and separation distance¹².

Complex single-particle motion can arise in simple shear flow, where non-axisymmetric particles exhibit rotational motion characterised by a combination of chaotic and quasi-periodic orbits¹³. In contrast, to the best of our knowledge, screw motion is the most complex single-particle sedimentation behaviour reported in the literature, where the centre of mass of the particle follows a helical path while rotating at a constant angular velocity about the axis of sedimentation^14,15. These chiral particle paths are associated with chiral particle shapes, as shown theoretically in models of propellers¹⁶, helices¹⁷, and more generally particles with irregular shapes¹⁸. A direct comparison between experiments and a bead-spring model based on the Rotne–Prager–Yamakawa theory indicates that a symmetrically bent fibre, an achiral shape, sediments along a vertical path, whereas an asymmetrically bent fibre, a chiral shape, exhibits the complex reorientations associated with screw motion¹⁹. In this paper, we demonstrate that achiral particles can also sediment along chiral trajectories, whose handedness is determined by their initial orientation.

We select our rigid particle shape among the complex shapes which can spontaneously emerge when manipulating flexible fibres and membranes linked to applications from biology⁴ to nanomaterials⁵. Experiments and bead-spring models^20,21 have shown that a sedimenting flexible fibre gradually bends into a symmetric U-shape as it descends and reaches a steady sedimentation state akin to that of the symmetrically bent rigid fibre discussed above¹⁹. An initially crumpled elastic disk also relaxes into a symmetric U-shape (see the “Methods” section). We select this canonical achiral shape, which has two orthogonal planes of mirror symmetry, as our rigid particle.

In this paper, we explore the sedimentation of this U-shaped rigid disk in a regime where inertia can be neglected. We determine the mobility matrix of the disk from experimental data and use it to simulate the disk’s long-term behaviour in an unbounded fluid where the dynamics of any particle are fully characterised by a phase space spanned by two orientational degrees of freedom. We show that unlike U-shaped fibres, such U-shaped disks can exhibit a range of different spiralling motions including helical screw motion, despite their achirality. In so doing we provide a framework in which to interpret physically the motion of sedimenting particles of arbitrary shape.

Results and discussion

Experimental approach

We studied the sedimentation of our U-shaped disk in a Perspex tank of internal dimensions 90 × 40 × 40 cm³, filled to a height of 75 cm with silicone oil (Allcock & Sons, density ρ_f = 972.7 ± 0.5 kg m⁻³, dynamic viscosity μ = 1.02 ± 0.01 Pa s, refractive index n_f = 1.403 at the laboratory temperature of 22 ± 1 °C) (see Fig. 1a). The U-shaped disks were manufactured by accurately cutting on a lathe a thin polyamide nylon sheet (Goodfellow, thickness b = 236.7 ± 0.3 μm, density ρ_s = 1130 kg m⁻³, refractive index n_s = 1.53) sandwiched between two metal sheets, into a disk of radius R = 12.00 ± 0.05 mm. Each disk was then thermoformed into a U-shape with a radius of curvature at its centre, R_c = 6.3 mm (Fig. 1c), by placing it between the two faces of a milled aluminium mould which was in turn heated to 200 °C. We also performed a few experiments with a smaller, more strongly curved disk (R = 5.00 ± 0.05 mm, R_c = 1.05 mm).

Fig. 1: Experimental setup and particle geometry.

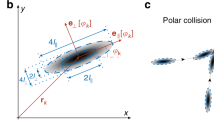
a Schematic of the experimental set-up (to scale) showing the sedimenting U-shaped disk. b Typical disk reconstructed from experimental visualisation. $(\hat{{{{{{{{\boldsymbol{x}}}}}}}}},\,\hat{{{{{{{{\boldsymbol{y}}}}}}}}},\,\hat{{{{{{{{\boldsymbol{z}}}}}}}}})$ are the unit vectors in the laboratory frame of reference (see (a)), while $({\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1},\,{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2},\,{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3})$ are the unit vectors of the disk’s body-fitted axes. We track two directed inclination angles: $\alpha =\arccos ({\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}.\hat{{{{{{{{\boldsymbol{z}}}}}}}}})\cdot {{{{{{{\rm{sign}}}}}}}}({\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}.\hat{{{{{{{{\boldsymbol{z}}}}}}}}})$ and $\beta =-\arcsin ({\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}.\hat{{{{{{{{\boldsymbol{z}}}}}}}}})$. c Edge-on view in the x₂−x₃ plane of the U-shaped disk (orange) showing a circle fitted to its central region (blue). We track the position of the centre of mass (CoM) in the laboratory frame, which is located off the surface of the disk.

Prior to each experiment, the tank was stirred vigorously using a two-blade propeller, taking care to avoid the entrainment of bubbles. This was necessary to homogenise small density variations, which arose because of residual temperature gradients and air entrainment. At the start of each experiment, we used a metre-long spatula to pick up the disk from the bottom of the tank and to position it centrally and ~10 cm below the surface. This location was chosen to minimise the effect of tank boundaries and upper free surface on the sedimentation. A 20 cm long rod was then inserted to manually adjust the disk’s initial orientation. Image recording with a top view camera (Fig. 1a) was initiated 20 s after removing the rod, which was sufficient for all fluid motion caused by the rod to subside.

The tank was illuminated with a full HD projector (Optoma HD143X) mounted sideways, which cast 20 stationary 290 μm-thick planes of light (41 in the experiments featuring the smaller disk) (see Fig. 1a). The sedimenting disk was illuminated by at most one plane at any time because the minimum spacing between the planes (29.5 mm in the centre of tank) was larger than the diameter of the disk. The disk traversed each plane of light without significant reorientation; therefore light scattered at the points of intersection with the plane and captured by a top-view camera at 15 frames per second (see inset of Fig. 1a for a typical raw image) could be used to reconstruct the shape and orientation of the disk. We used an auto-encoder to reconstruct the shape of the disk²² (see the “Methods” section). The reconstructed shape with R = 12.0 mm is shown in Fig. 1b (3D view) and Fig. 1c (edge-on projection). Reconstruction using the auto-encoder yields root-mean-square time fluctuations of 2% of the average curvature and 4% of the surface area A of the disk. The orientation of the disk in terms of the angles shown in Fig. 1b was reconstructed accurately to within ±1^∘. Challenges in the reconstruction of the smaller disk due to reduced image resolution meant that it was only used in a few experiments.

Experimental observations of the sedimenting U-shaped disk

Figure 2 shows representative trajectories of the disk’s centre of mass as it sediments through the tank, both as lines in three-dimensional space and their projection into the horizontal x−y plane. The maximum velocity (U ≃ 1.22 mm s⁻¹ for the disk with radius R = 12 mm) was measured when the disk sedimented in an edge-on orientation, i.e. when the body-fitted roll axis ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}$ (see Fig. 1b) was aligned with the direction of gravity. This corresponds to a maximum Reynolds number of Re = ρ_fUR/μ ≤ 0.014 ≪ 1, implying that inertia does not play an important role in this problem. Figure 2 shows that the disk does not sediment along straight trajectories. Unlike a flat disk which, at small Reynolds numbers, maintains constant orientation and hence a straight sedimentation trajectory³, our U-shaped disk reorientates continually with concomitant changes to its path, as illustrated by insets showing the disk’s orientation at selected points along trajectories.

Fig. 2: Experimental observations of the sedimentation of a U-shaped disk.

a Four example trajectories of a disk’s centre of mass and their horizontal projections in terms of scaled lab-frame coordinates (x/R, y/R, z/R). The disk has radius R = 12.0 mm, radius of curvature at its centre R_c = 6.3 mm and travels 30R in the z-direction. The bounding box is for visual aid and does not represent the boundary of the tank. For clarity, small differences in initial positions were removed by translating the trajectories to a common origin. b Trajectory from the experiment using the small disk with R = 5 mm and R_c = 1.05 mm, which covers 90R in the z-direction.

In Fig. 2a we compare the trajectories from our experiments, all performed with the disk of radius R = 12.0 mm. We released the disk from a range of initial orientations and recorded its trajectory over a vertical distance of 30 disk radii in the central region of the tank. The projection of the trajectories into the x−y plane shows that the lateral displacement of the disk varies considerably with its initial orientation. Furthermore, the disk undergoes very different reorientation sequences as it sediments along the various trajectories. To illustrate this we consider trajectory A for which the orientation of the disk starts from an inclined upside-down U orientation (see the green disks shown on the left of the figure). The disk rotates about its ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}$ (roll) axis until it approaches an upright U orientation while the roll axis itself maintains a strong and approximately constant inclination against the vertical. In contrast, along trajectory C the disk’s ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}$ (roll) axis is weakly inclined against the vertical and the disk reorientates via modest rotations about its pitch (${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}$) and roll (${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}$) axes, as shown by the purple disks next to the figure. We performed a total of 28 experiments with this disk but were unable to infer a pattern of reorientation dynamics from these observations alone.

Figure 2b shows the same data for the smaller disk (R = 5 mm) which we were able to observe over a vertical travelling distance of 90 disk radii. Starting from an upright-U orientation the disk primarily reorientates by pitching about its ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}$ axis until it reaches an edge-on orientation in which the roll axis ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}$ is approximately vertical. This is followed by rolling (about ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}$) which ultimately returns the disk to its original orientation relative to the direction of gravity. This suggests that the observed reorientation sequence would repeat if the experiment could accommodate an even larger vertical sedimentation distance. The switch from dominant pitching to rolling is accompanied by a near reversal in the direction of motion in the x−y plane. We also note that the disk’s continued change in orientation due to the rolling and pitching motion induces a net rotation about the z-axis in the lab frame of reference: while traversing the trajectory shown in Fig. 2b, the body-fitted ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}$-axis rotates by 235° about $\hat{{{{{{{{\boldsymbol{z}}}}}}}}}$.

Experimental trajectories in the body-fitted coordinate system

To characterise the disk’s orientation relative to the direction of gravity we introduce the angles α and β shown in Fig. 1b. The angle α measures the inclination of the normal to the disk, ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}$, against $\hat{{{{{{{{\boldsymbol{z}}}}}}}}}$, the vertical direction in the lab-frame; the angle β provides a measure of the inclination of the disk’s pitch-axis, ${\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}$ against $\hat{{{{{{{{\boldsymbol{z}}}}}}}}}$. Thus α = β = 0 corresponds to the disk in its upright-U orientation. Insets in Fig. 3a show schematics of pure pitching, which occurs for β = 0 as α is increased from 0 to 180°, and pure rolling, which is associated with angles β = α for α ≤ 90° and β = 180°−α for α > 90°. These lines of pure pitching and pure rolling bound a triangular region which contains all the possible orientations of the disk. Positive and negative values of α (or β) result in the same orientation relative to the direction of gravity, but with the direction of pitching (or rolling) reversed; for our disk which has two planes of symmetry these orientations are equivalent. Thus, we plot all results for α ≥ 0 and β ≥ 0 by reflecting all other data about α = 0 and β = 0.

Fig. 3: Phase-plane representation of the dynamics of the U-shaped disk in the body-fitted frame of reference.

a Phase plane trajectories of the larger and less curved disk (R = 12 mm and R_c/R = 0.52) with 3D insets to illustrate its orientation at various points. The arrows show the experimental data points (one colour per experiment, initial points encircled), which collectively form concentric orbits around a centre. The error bars indicate measurement uncertainties in the orientation of the disk. The grey lines are the predicted orbits obtained from fitting a mobility matrix. The red and pink boundaries are the heteroclinic orbits associated with the pure rotations shown in the inset and illustrated by schematics. b Phase plane trajectories of the smaller and more curved disk (R = 5 mm and R_c/R = 0.21) from Fig. 2b, showing concentric orbits around the centre at β_c ≈ 18°, which is twice the value for the less curved disk shown in (a).

The coloured arrows in Fig. 3a show the evolution of (α(t), β(t)) in the 28 experiments performed with the disk with R = 12.0 mm, starting from initial orientations identified by the circular symbols. Each experiment only produces a relatively short trajectory in the α−β plane but collectively they appear to form loops, suggesting that the sedimenting disk does indeed undergo a periodic reorientation as conjectured based on the trajectory of the smaller disk (R = 5 mm) shown in Fig. 2b. We also show three trajectories of this disk in Fig. 3b, which each indicate that a closed loop is associated with the sequence of pitching and rolling shown in Fig. 2b. The loops are concentric and appear to enclose a centre at (α_c, β_c) for which the disk’s orientation remains constant relative to the direction of gravity. For the larger disk, which has a radius of curvature R_c/R = 0.52, the centre is located at approximately (89°, 9°) (Fig. 3a), while trajectories of the more tightly curved small disk with R_c/R = 0.21 centre on approximately (80°, 18°) (Fig. 3b). For a perfectly symmetrically bent disk, we expect α_c = 90° for reasons of symmetry, and the experimental deviation indicates imperfections in the disk. Furthermore, measurements on a flatter disk (R_c/R = 1.19, also with R = 12 mm) gave β_c ≃ 6. 1°, which suggests that β_c increases with increasing curvature of the sheet.

Trajectory C in Fig. 2a was initiated close to this centre, with initial angles (α₀, β₀) = (84°, 8.4°), and thus, the disk only experienced a small reorientation via the combination of pitching and rolling. In contrast, for trajectory A which started from initial angles of (135.8°, 8.1°) we have a rolling-dominated reorientation, corresponding to an anti-clockwise motion through the upper part of the (α, β) diagram to (41.1°, 2.0°) by the end of the experiment.

Mobility matrix of the U-shaped disk

The experiments therefore strongly suggest that the sedimenting U-shaped disk undergoes a periodic motion, even though our observations are naturally limited by the finite vertical extent of the tank. However, the size of the disk was much smaller than the size of the container, and the disk was generally far from the container walls and the free surface in all the small-Reynolds number sedimentation experiments shown in Figs. 2 and 3. This suggests that it is possible to gain insight into the disk’s long-term behaviour by considering its sedimentation in an unbounded fluid at zero Reynolds number. In this case, the disk’s motion is fully determined by a 6 × 6 mobility matrix, M, whose constant entries depend only on the shape of the disk. This matrix relates the components of the velocity ${{{{{{{{\bf{U}}}}}}}}}^{(\infty )}={U}_{1}^{(\infty )}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}+{U}_{2}^{(\infty )}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}+{U}_{3}^{(\infty )}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}$ of the disk’s centre of mass and of the disk’s rate of rotation, ${\omega }^{(\infty )}={\omega }_{1}^{(\infty )}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}+{\omega }_{2}^{(\infty )}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}+{\omega }_{3}^{(\infty )}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}$, both expressed relative to the body-fitted axes, to the body force, ${{{{{{{\bf{F}}}}}}}}=-\pi {R}^{2}b({\rho }_{s}-{\rho }_{f})g\,\hat{{{{{{{{\boldsymbol{z}}}}}}}}}$, acting on the disk, where g is the gravitational acceleration. Given the disk’s two planes of symmetry, only a subset of the entries in M are nonzero²³, giving

$$\frac{1}{\mu }\left(\begin{array}{cccccc}{M}_{11}&0&0&0&{M}_{51}&0\\ 0&{M}_{22}&0&{M}_{42}&0&0\\ 0&0&{M}_{33}&0&0&0\\ 0&{M}_{42}&0&{M}_{44}&0&0\\ {M}_{51}&0&0&0&{M}_{55}&0\\ 0&0&0&0&0&{M}_{66}\\ \end{array}\right)\left(\begin{array}{c}{F}_{1}\\ {F}_{2}\\ {F}_{3}\\ 0\\ 0\\ 0\\ \end{array}\right)=\left(\begin{array}{c}{U}_{1}^{(\infty )}\\ {U}_{2}^{(\infty )}\\ {U}_{3}^{(\infty )}\\ {\omega }_{1}^{(\infty )}\\ {\omega }_{2}^{(\infty )}\\ {\omega }_{3}^{(\infty )}\\ \end{array}\right),$$

(1)

where we have written the body force as ${{{{{{{\bf{F}}}}}}}}={F}_{1}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}+{F}_{2}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}+{F}_{3}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}$ and exploited that there is no external torque acting on the disk. Note that, given this decomposition into the disk’s body-fitted axes, the components F_i vary as the disk reorientates relative to the laboratory frame.

We improved this basic model by approximately incorporating the leading-order interactions of the disk with the boundaries of the fluid domain. For this purpose, we recall that if a particle sediments in a semi-infinite fluid domain that is bounded by a single, infinite planar surface, located at a large distance, l, from the particle, the sedimentation velocity and rate of rotation predicted by Eq. (1) are changed by corrections δU_b(l) = δU_b0(l) + O(l⁻²) and δω_b = O(l⁻²)²⁴, where

$$\delta {{{{{{{{\boldsymbol{U}}}}}}}}}_{{\rm {b}}0}(l)=-\frac{1}{6\pi \mu l}k({{{{{{{\boldsymbol{F}}}}}}}}+({{{{{{{\boldsymbol{F}}}}}}}}.\hat{{{{{{{{\boldsymbol{n}}}}}}}}})\hat{{{{{{{{\boldsymbol{n}}}}}}}}}).$$

(2)

Here $\hat{{{{{{{{\bf{n}}}}}}}}}$ is the unit normal to the boundary, and the correction coefficient $k=\frac{9}{16}$ for solid walls and $\frac{3}{8}$ for free surfaces²⁵. We restrict ourselves to the O(l⁻¹) corrections which only affect the sedimentation velocity. Thus we model the disk’s motion using ω = ω^(∞) and U = U^(∞) + δU_c. We approximated δU_c by simply summing the contributions from the container walls and the free surface, i.e. $\delta {{{{{{{{\bf{U}}}}}}}}}_{c}({l}_{1},...,{l}_{6})=\mathop{\sum }\nolimits_{i = 1}^{6}\delta {{{{{{{{\bf{U}}}}}}}}}_{b0}({l}_{i},{\hat{{{{{{{{\boldsymbol{n}}}}}}}}}}_{i},{k}_{i})$, where the l_i are the instantaneous distances of the disk from the respective boundaries which have unit normal vectors ${\hat{{{{{{{{\boldsymbol{n}}}}}}}}}}_{i}$ and correction coefficients k_i.

Given the disk’s current orientation and the position of its centre of mass, r_CoM, Eq. (1) determines its instantaneous rate-of-rotation ω = ω^(∞) which reorientates the body-fitted axes according to

$$\frac{{\rm {d}}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}}{{\rm {d}}t}={\omega }_{3}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}-{\omega }_{2}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3},\quad \frac{{\rm {d}}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}}{{\rm {d}}t}={\omega }_{1}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}-{\omega }_{3}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1},\quad \frac{{\rm {d}}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}}{{\rm {d}}t}={\omega }_{2}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}-{\omega }_{1}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}.$$

(3)

Similarly, the centre of mass moves with the velocity U, so

$$\frac{{\rm {d}}{{{{{{{{\boldsymbol{r}}}}}}}}}_{{{{{{{{\rm{CoM}}}}}}}}}}{{\rm {d}}t}={U}_{1}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1}+{U}_{2}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2}+{U}_{3}{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3}.$$

(4)

We employed this model to determine the nonzero coefficients of the mobility matrix M by minimising the root-mean-square distance between the experimentally observed trajectories, ${{{{{{{{\boldsymbol{r}}}}}}}}}_{{{{{{{{\rm{C}}}}}}}}oM}^{{{{{{{{\rm{[exp]}}}}}}}}}(t)$, and the predictions for r_CoM(t) from our model. The latter was obtained by integrating the ODEs (3) and (4) with Mathematica’s NDSolve function, using initial conditions from the first data point in each experiment; the parameter fitting was done using the Barzilai–Borwein algorithm²⁶. This yielded M₁₁ = (96.5 ± 1.3) × 10⁻³/R, M₂₂ = (90.5 ± 1.5) × 10⁻³/R, M₃₃ = (74.7 ± 1.0) × 10⁻³/R, M₄₂ = (21.8 ± 1.6) × 10⁻³/R², M₅₁ = (0.50 ± 0.04) × 10⁻³/R², where R = 12.0 mm is the radius of the disk and the uncertainties obtained from the root-mean-square fit quantify the level of random error. The effect of boundary corrections on the mobility matrix was modest with individual matrix components differing by between 3% and 14% from those of the matrix fitted without correction. We note that the mobilities M₁₁ and M₂₂ are within 3% of the edge-on mobility of the flat disk³, while the broadside mobility M₃₃ is 20% larger. Since this difference brings the broadside-to-edge-on ratio of mobilities closer to unity, our disk has a narrower range of possible sedimentation velocities than a corresponding flat disk.

Long-term sedimentation trajectories

Having accounted for the tank boundaries and the free surface when determining the fitted mobility matrix, we can now use this matrix to simulate the sedimentation of our disk in an unbounded fluid by integrating the six ODEs (3) and (4). We note that for any particle sedimenting in an unbounded fluid, only two of the six unknowns are genuine degrees of freedom. This is because, in an unbounded fluid, a change in the initial position simply shifts the entire trajectory by a rigid body translation; similarly, a rotation about the direction of gravity subjects the particle’s trajectory and its orientation to a corresponding rigid body rotation. As a result, only the two degrees of freedom which describe the inclination of the disk are required to describe its dynamics. The angles α and β (or any other, equivalent, parametrisation of the disk’s inclination) therefore define a two-dimensional phase space which describes the dynamics of the disk sedimenting in an unbounded fluid.

This allows us to reinterpret Fig. 3 in the language of dynamical systems. The points (α, β) = (0°, 0°) and (180°, 0°) (corresponding to the upright-U and upside-down-U orientations, respectively), play the role of saddles which are connected by heteroclinic orbits along which the disk moves by pure pitching and rolling motions. We illustrate the trajectories of the disk’s centre of mass along these orbits in the laboratory frame in Fig. 4a–d. For this, we align the disk’s body-fitted axes $({\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{1},{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{2},{\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{3})$ with the lab axes (x, y, z) in the reference upright-U orientation. If we release the disk from a horizontal orientation with (α₀, β₀) = (0°, 0°) or (180°, 0°), it sediments purely vertically without any reorientation (Fig. 4a). If the disk is released from a near horizontal orientation (Fig. 4b, α₀ = 0.01°, β₀ = 0°), reorientation by pure pitching is accompanied by a translation in the x−z plane (i.e. normal to the pitching axis). The horizontal velocity decays as the disk approaches its upside-down-U orientation, and the total horizontal displacement remains finite. In Fig. 4b the disk drifts up to a maximum of 44.5R as it approaches α = 90° before returning to its original position in the x−y plane as α → 180°. Similarly, in Fig. 4c, a release from (α₀ = 179.9°, β₀ = 0°) causes a reorientation by pure rolling; this is accompanied by a translation in the z−y plane (normal to the rolling axis). The horizontal velocity decays as the disk approaches its upright-U orientation and it drifts laterally only by 0.74R before returning to its original xy-position. In Fig. 4d, we illustrate how the disk can alternate between pitching and rolling-dominated reorientations by releasing it from an initial orientation where it is rotated slightly about both the x and y axes (α₀ = 0.014°, β₀ = 0.010°). Initial pitching about the y-axis rotates the disk from its upright-U to an upside-down-U orientation; this is accompanied by a translation in the x-direction (as in Fig. 4b). The motion then becomes dominated by rolling about the x-axis, which returns the disk back to its upright-U orientation while translating in the y-direction (as in Fig. 4c), resulting in a cross-like projection of the trajectory into the x−y plane. Once the disk has returned close to its original orientation, the pitching/rolling cycle repeats. Note that the trajectory shows that the reorientation by rolling occurs much more quickly than that by pitching: the disk sediments over several thousand disk radii while pitching by ≈ 180°; the corresponding reorientation by rolling is complete within about 20 disk radii.

Fig. 4: Long-term trajectories of the U-shaped disk in the laboratory frame of reference.

a Vertical descent (α₀, β₀) = (0°, 0°). b Trajectory along the pure-pitching heteroclinic orbit ((α₀, β₀) = (0.01°, 0°)). c Trajectory along the pure-rolling heteroclinic orbit ((α₀, β₀) = (179.9°, 0.01°)). d Near-horizontal initial orientation (α₀, β₀) = (0.014°, 0.010°), with 0 < β₀ < α₀. e Helical sedimentation at the centre ((α₀, β₀) = (α_c, β_c)). Helical trajectories are spirals with a constant pitch. The trajectories, which cover vertical sedimentation distances of up to 8000 disk radii, are numerical predictions obtained using the experimentally determined mobility matrix. Projected trajectories are shown in the bottom x−y plane. The disks illustrate the orientation but are not drawn to scale.

The trajectories shown in the α−β phase plane in Fig. 3 are closed orbits, and therefore, all trajectories are uniquely determined by their initial conditions and equally likely to be observed experimentally if the initial conditions are random in α and β. However, because pitching occurs on a much longer timescale than rolling, the disk’s β angle rapidly decays towards zero far from the dynamic centre. The disk then undergoes a long period of near-pure pitching, during which very small differences in the β angle lead to very different orientations later in the trajectory. The sensitivity in this region of phase-space means that the outermost trajectories will not be experimentally observable in full. This is shown in Fig. 3b where the disk can be seen to be perturbed during the period of near-pure pitching due to unavoidable experimental fluctuations.

The grey lines in Fig. 3, which were obtained by numerically integrating the ODEs from a variety of initial conditions, provide a good representation of the experimental orbits. They represent closed orbits about a centre located at (α_c, β_c) = (90°, 8.6°), which is in excellent agreement with experimental observations. If the disk is released from an orientation in which (α₀, β₀) = (α_c, β_c), its orientation against the vertical axis remains constant. It sediments with a finite horizontal velocity but rotates about the z-axis at a constant rate, such that it rotates by 258.6° per period. The trajectory is therefore a helix (a spiral with constant pitch), as illustrated in Fig. 4e, which shows a left-handed helix with a radius of 0.255R. The spiral is left-handed when the product α₀β₀ > 0 and right-handed when α₀β₀ < 0.

Figure 5 shows the period of the orbits in the α−β plane, including values for the trajectories A and C shown in Fig. 2a and discussed in the context of Fig. 3. The period was obtained by starting the time-integration at α(t = 0) = α₀ = 90° for various values of β(t = 0) = β₀ ∈ [0°, 90°] and recording how long it takes for α(t) and β(t) to return to their original values. The period tends to infinity as we approach the pure pitching (β₀ → 0°) and pure rolling (β₀ → 90°) cases, consistent with the time required to traverse between two saddles in any phase space. We note that one complete loop through this heteroclinic pitching/rolling orbit would rotate the disk by 180° about the $\hat{{{{{{{{\boldsymbol{z}}}}}}}}}$ axis. This is because a 180° pure pitching motion followed by 180° of pure rolling returns the disk to its original orientation—but with its right and left sides exchanged. The symmetry of our disk renders this configuration indistinguishable from the reference state, though all material lines have rotated by 180° in the lab frame. We also observed experimentally that the period decreased with increasing curvature of the U-shaped disk. We found that for the flatter disk, the coupling terms governing the rate of reorientation are smaller and the period is longer, consistent with the limit of zero curvature, where the coupling terms tend to zero and the period tends to infinity (so that a flat disk sediments steadily). Hence, it was the cumulative effects of increased curvature and reduced disk size that enabled us to observe approximately one period of reorientation in Figs. 2b and 3b.

Fig. 5: Predicted dimensionless period of the orbits in the α−β plane, as a function of the initial value β₀ for a fixed initial value α₀ = 90°.

The period T is non-dimensionalised by the time it takes a rigid flat disk to descend vertically by one radius³. The points labelled A, C correspond to the trajectories shown in Fig. 2a.

Finally, we use the model to extend the trajectories observed experimentally and show a representative selection in Fig. 6. The blue points indicate trajectories of the disk’s centre of mass obtained in the experiments; they are closely matched by the computed trajectories (solid lines). We have seen that the velocity of the disk’s centre of mass and its rotation about the z-axis are enslaved to the orientational angles α and β which vary periodically. The net rotation about the z-axis during one period of the orbit in the α−β plane is generally not a rational fraction of 360°. Therefore, the disk’s motion tends to be quasi-periodic. The trajectory in Fig. 6a is close to a uniform spiral, while the trajectories in Fig. 6b–d are initiated at orientations increasingly distant from the centre (α_c, β_c). Their projection into the x−y plane results in increasingly distorted spirograph-like patterns, shown at the bottom of the plots. By Fig. 6d, the sequence of pitching and rolling motions occurs along approximately straight lines in the x−y plane as for the cross trajectory shown in Fig. 4d.

Fig. 6: Sedimentation of a U-shaped disk from experimental initial conditions in the laboratory frame of reference.

The blue circles indicate the experimental trajectories and the solid lines are numerical predictions, which cover vertical sedimentation distances of up to 3000 disk radii and which are obtained using the experimentally determined mobility matrix. Projected trajectories are shown in the bottom x−y plane. a (α₀, β₀) = (89.2°, −8.7°), b (α₀, β₀) = (93.4°, −9.3°), c (α₀, β₀) = (94.1°, −21.5°), d (α₀, β₀) = (135.9°, 8.0°) (trajectory A in Fig. 2a).

Conclusion

To summarise, we have used a combination of experiments and theoretical modelling to show that even in the absence of inertia, sedimentation of a non-planar particle can involve complex reorientation dynamics. For our U-shaped disk, periodic reorientation about the direction of gravity leads to chiral trajectories ranging from helix to quasi-periodic spirals. In these, the disk reorientates through sequences of pitching and rolling with a period which is incommensurate with that of rotation about the axis of gravity resulting in quasi-periodic motion. These modes of sedimentation preclude any net sideways drift so that a dilute suspension of such disks would not display any net horizontal dispersion. However, the reorientation period is typically long so that we need the particle to descend by more than 1000 radii to complete a full cycle. In spite of our particle’s two planes of symmetry (which make it identical to its mirror image and therefore non-chiral), it sediments along chiral trajectories. The handedness of these trajectories is set by the initial orientation alone and is determined by whether the initial angles (α, β) have the same or opposite signs. We use our particle to illustrate that any particle sedimenting in an unbounded fluid at zero Reynolds number has at most two degrees of (orientational) freedom. Hence, its most complex dynamics are limited to periodic behaviour and it cannot exhibit chaos. Our analysis provides the necessary framework in which to interpret physically the motion of sedimenting particles of arbitrary shape.

Methods

Reconstruction of the particle shape

The top-view movie of light scattered at the points of intersection with the planes of light from the full HD projector (Optoma HD143X) was used to reconstruct the particle shape. Most of the area of the translucent disk was visible to the camera regardless of orientation and shadows were weak enough not to affect the visualisation. By accounting for the refractions in the system and tracking which plane the disk crossed, we obtained a set of spatio-temporal data (x, y, z, t) for further analysis. We reconstructed the disk’s surface by fitting a parametric 2D surface evolving in time (i.e., a three-dimensional manifold embedded in a four-dimensional space) using an auto-encoder²⁷ which trained two neural networks: the encoder reduces the four-dimensional data to a three-dimensional latent space, and the decoder learns the parametrisation from the latent space back to the direct space. The disk’s shape was reconstructed only once; in subsequent experiments, experimental scans of the disk through each light sheet were fitted to the reconstructed disk shape using a least-square method optimised for the three translational and three rotational degrees of freedom; see Miara et al.²² for details of this method.

Estimate of the elastic deformation of the disk

We provide an upper bound estimate for the elastic deformation of our disk due to viscous loading. The total drag experienced by a disk of radius R and thickness b balances the body force ∣F∣ = πR²bΔρg. The upper bound for the bending moment is M < ∣F∣R. Considering the change in curvature in the x₂−x₃ plane, from Kirchoff–Love plate theory, in the case of pure bending, the deflection w is described by

$$\frac{{\partial }^{2}w}{\partial {x}_{2}^{2}}=\frac{M}{D}\,,$$

(5)

where $D=\frac{E{b}^{3}}{12(1-{\nu }^{2})}$ is the flexural rigidity of the disk. In the case of our Polyamide Nylon 6 disk (R = 0.012 m, Elastic modulus E = 2.8 ± 0.2 GPa, Poisson ratio ν = 0.39, thickness b = 236.7 ± 0.3 μm), the flexural rigidity is D = (3.65 ± 0.13) × 10⁻³ N m. When sedimenting in silicone oil Δρ = 157.3 kg m⁻³, the bending moment M < 1.98 × 10⁻⁶ N m. Thus, the viscous forces change the curvature of the disk by no more than 0.0005 m⁻¹ which is five orders of magnitude smaller than the curvature of the U-shaped disk (1/R_c = 159 m⁻¹). Hence, the disk may be considered rigid.

Sedimentation of an elastic sheet can also be described by the elasto-gravitational number B, i.e., the ratio of elastic forces to gravity forces given by,

$$B=\frac{D}{| {{{{{{{\boldsymbol{F}}}}}}}}| R}=\frac{E{b}^{2}}{12\pi (1-{\nu }^{2}){R}^{3}g{{\Delta }}\rho }=1840\pm 70.$$

For the flexible sheet shown in Fig. 7, B = 0.0134.

Fig. 7: Sedimentation of an elastic disk.

An elastic disk made of swollen silicone rubber (thickness b = 0.105 mm, radius R = 30 mm, Young’s modulus E = 882 kPa, Poisson ratio ν ≃ 0.5, excess density Δρ = 97 kg/m³) sediments in silicone oil. Starting from a crumpled shape at the top, the time sequence of images shows how the sheet unfolds and adopts a simple U-bent shape.