Introduction

Carbon nanotube (CNT)-reinforced composites have shown outstanding physical, mechanical, thermal and electrical properties over traditional structural materials, drawing interest from numerous researchers. CNTs are recognized as well suited to reinforce polymer composites due to their high elastic modulus and tensile strength and low density1,2,3,4. As a result, enthusiasm for research activities involving CNTs has been ignited in recent years. Wagner et al.5 performed tensile experiments on multi-walled carbon nanotubes (MWCNTs) and analysed the transformation of the elastic modulus and the break stress of nanoscale reinforced composites. Qian et al.6 developed homologous research two years later, noting that the addition of only 1% MWCNT to polystyrene significantly improved its polymeric mechanical properties. Fiedler et al.7 demonstrated the superiority of the CNTs as nanofillers in polymers and suggested that a distribution of CNTs should be concentrated or dispersed to realize the best possible properties. Han8 and Wan9 found that the introduction of low volume fractions of nanotubes in matrices can result in notable strengthening of the composite properties. Relative to micron-scale counterparts, the interfacial regions between the nanoparticles and the matrix are strongly reactive. Coleman et al.10 compared mechanical properties and various manufacturing processes of single-walled carbon nanotube (SWCNT)-reinforced composites to MWCNT-reinforced composites. However, the collective problems of dispersion and stress transfer still lack solutions.

To overcome these issues, functionalization through chemical procedures, for example, has been adopted by researchers. Functionally graded (FG) materials, which act as primitive thermal barrier materials in the aerospace industry, are widely known for their smooth and continuous variations in material properties. In this way, the integration of single materials with different properties can be improved, and the advantages of material properties can be combined11,12,13. Shen14 in 2009 first proposed a new distribution form with CNTs distributed in an FG manner in the matrix; the volume fraction of CNTs was assumed to vary along the thickness direction. The issue of nonlinear bending behaviour of functionally graded carbon-nanotube-reinforced composite (FG-CNTRC) plates was investigated in which a transverse uniform or sinusoidal load in thermal environments was taken into consideration. The results revealed that mechanical, electrical and thermal properties varied considerably with the FG distribution of CNTs.

CNT-reinforced composites, which are increasingly used, can be formed into structures such as beams, plates and shells. Beams are a fundamental and significant structure in comprehensive engineering applications in the fields of marine, aerospace, civil, and mechanical engineering, among others areas. In this regard, various studies have focused on dynamic characteristics analysis of beam structures to guide structurally reliable design of such engineering applications15,16,17,18,19,20. Incorporating first-order beam theory, Yas and Samadi21 adopted the generalized differential quadrature method to analyse the issue of vibrations and buckling of carbon-nanotube-reinforced composite (CNTRC) beams on elastic foundations. Four different CNT distributions were considered, and the material properties of the nanocomposites were obtained from the rule of mixtures. In light of the von Kármán geometric nonlinearity displacement–strain relationship and Euler beam theory, the linear and nonlinear vibration behaviours of CNT-reinforced FG composite beams were presented by Rafiee et al.22. Numerical results showed that an increase in the CNT volume fraction led to an increase in the nonlinear-to-linear frequency ratio and the natural frequencies. Lin and Xiang23,24 investigated the free-vibration characteristics of CNT-reinforced beams with soft-clamped and hard-clamped boundary conditions, with uniformly distributed (UD) CNTs and FG distribution being considered. The model was established based on first-order and third-order shear deformation elasticity theories and solved using the polynomial Ritz method. The research showed that ratios of nonlinear-to-linear frequency parameters and natural frequencies based on first-order and third-order shear deformation elasticity theories with soft-clamped boundary conditions showed manifest deviations. Ke et al.25 investigated the nonlinear vibration characteristics of FG-CNTRC beams with various boundary conditions using a direct iterative method. The influences of the vibration amplitude, volume fraction of CNTs, ratio of length to thickness, boundary conditions and CNT distribution were taken into account to characterize nonlinear vibration in the beams. The response of CNT-reinforced FG composite beams under low-velocity impact was first analysed by Jam and Kiani26. On the basis of first-order beam theory, the behaviour of FG-CNTRC beams exposed to the impact of a small mass was solved by means of the conventional polynomial Ritz method and the Runge–Kutta method. The peak contact force was found to be proportionate to the volume fraction of CNTs and inversely proportional to the temperature, while the contact time behaved oppositely.

With the rapidly increasing industrial use of composite materials, various numerical tools and theories have been promoted to analyse the mechanical behaviour of composite structures27,28,29,30. The problem of nonlinear vibration of composite plates reinforced by CNTs was presented by Wang31. The governing equation of the CNTRC plate was derived according to higher-order shear deformation theory, and the theoretical model was solved using the improved perturbation technique. Zhang et al.32 focused attention on the free-vibration characteristics of CNT-reinforced FG composite triangular plates and adopted the element-free IMLS-Ritz method based on first-order beam theory. In view of the first order shear deformation theory, Rafiee et al.33 employed the Galerkin method and the harmonic balance method to investigate initially imperfect piezoelectric composite plates reinforced by SWCNTs. The vibrational characteristics and buckling of an FGM microplate with two different supports were studied by Ke et al.34. Wang35,36 developed a unified semi-analytical approach and applied it to the issue of free-vibration analysis of FG-CNTRC structures of revolution, including spherical panels and doubly curved shells. The differential quadrature method and the Mindlin plate theory were applied in this research to enable scientific conclusions to be drawn. Based on the FEM and two types of shear deformation theory, Yas and Heshmati37 established an analytical model of a FG-CNTRC beam subjected to a moving load.

Numerous studies have been conducted to illustrate the vibrational characteristics of CNTRC beams. Nevertheless, the investigations mentioned above are limited to several representative boundary conditions. A diversity of boundary restraints leads to notable changes in the free-vibration characteristics. Relatively little study has addressed the free vibration of CNT-reinforced beams with elastic supports, although various possibilities of boundary conditions appear in engineering practice. Furthermore, most actual solution procedures are customized to restricted forms of certain classes at both ends of the beam. Consequently, existent contributions are urgently sought not only to guide engineering applications but also to enhance complementary research.

Aiming at satisfying practical needs, in this investigation, a unified and satisfactorily accurate method is presented for the free-vibration analysis of FG-CNTRC beams with arbitrary boundary conditions, including various classical boundary conditions and elastic supports. The modified Fourier method was first proposed by Li to analyse the vibration of a beam38 and was subsequently extended to plates39,40,41,42,43,44,45,46,47 and shells48,49,50,51,52,53. The two functions of displacement and two functions of rotation are expressed as a linear combination of an original Fourier cosine series expansion and two complementary auxiliary polynomial functions. The supplemental items are introduced to remove the potential discontinuities of displacement components and derivatives of displacement functions at the ends of the beam and to accelerate convergence of the solution procedures. Arbitrary boundary conditions can be conveniently achieved through assigning the appropriate stiffness to four sets of boundary springs at each edge of the CNTRC beam without updating the solution procedure.

In the present work, a strong-form solution procedure of the modified Fourier method is proposed and used to solve generalized eigenvalue problems directly by submitting a modified Fourier series to the governing equations and the boundary conditions. In addition, the results obtained from the Rayleigh–Ritz technique associated with the modified Fourier method are presented here as a weak-form solution for comparison. Numerical results calculated by the present method are checked against available results published in the open literature to evaluate accuracy and validity. New results in terms of frequency parameters and mode shapes of CNTRC beams with elastic boundary conditions are presented here to provide a benchmark for future researchers in this field.

Theory and formulation

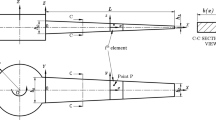
As depicted in Fig. 1, we consider a general CNT-reinforced composite beam with a rectangular cross section. A right-handed Cartesian coordinate system is established in which the length L, width b, and thickness h are respectively defined along the x-, y- and z-directions. The main purpose of this work is to investigate the CNTRC beam with arbitrary boundary conditions, and thus, two sets of linear springs (\({k}_{0,L}^{u}\) and \({k}_{0,L}^{w}\)) and two sets of rotational springs (\({K}_{0,L}^{s}\) and \({K}_{0,L}^{c}\)) are artificially introduced to simulate boundary restraint forces at the two ends of the beam. By assigning a suitable stiffness to the four sets of boundary springs, an arbitrary combination of classical and elastic boundary conditions can be realized. For example, if linear and rotational restraining spring coefficients at both ends are set to infinity (or a sufficiently large number in practical numerical simulations), the perfectly clamped boundary condition can be conveniently achieved.

Figure 1
figure 1

Geometry and coordinate system of a CNTRC beam. A right-handed Cartesian coordinate system is established in which the x-, y- and z-axes are taken along the length L, width b and height h of the beam, respectively. Four sets of springs (\({k}_{0,L}^{u}\), \({k}_{0,L}^{w}\), \({K}_{0,L}^{s}\) and \({K}_{0,L}^{c}\)) are artificially introduced to simulate boundary restraint forces at the two ends of the beam.

Full size image

It is assumed that the CNTRC beam consists of a polymer matrix mixture that can be generally treated as an isotropic material and CNTs. SWCNT reinforcements are placed along the length direction and are either UD or FG in the thickness direction. Four- types of FG distribution forms are taken into account, namely, FG-X, FG-O, FG-V and FG-\(\Lambda \), as illustrated in Fig. 2.

Figure 2
figure 2

Cross section of UD, FG-Λ, FG-V, FG-O and FG-X CNTRC beams.

Full size image

Regardless of the various distribution patterns of CNT reinforcement at the cross section, four types of FG-CNTRC beams are assumed to contain an equal CNT total weight of m tcnt and total CNT volume fraction V tcnt . The expressions of CNT volume fraction for different distributions can be written as:

$${\rm{UD}}:\,{V}_{cnt}={V}_{tcnt}$$
(1a)
$${\rm{FG}}\mbox{-}{\rm{X}}:\,{V}_{cnt}=4\frac{|z|}{h}{V}_{tcnt}$$
(1b)
$${\rm{FG}}\mbox{-}{\rm{V}}:\,{V}_{cnt}=(1+\frac{2z}{h}){V}_{tcnt}$$
(1c)
$${\rm{FG}}\mbox{-}{\rm{O}}:\,{V}_{cnt}=2-4\frac{|z|}{h}{V}_{tcnt}$$
(1d)
$${\rm{FG}}\mbox{-}{\rm{\Lambda }}:\,{V}_{cnt}=(1-\frac{2z}{h}){V}_{tcnt}$$
(1e)

The effective material properties of CNTRC beams, e.g., the Young’s modulus (E 11 and E 22), shear modulus (G 12) and Poisson’s ratios (v 12 and v 21), are estimated according to matching molecular dynamics simulation results based on the rule of mixtures, which can be expressed as follows:

$${E}_{11}={\eta }_{1}{V}_{cnt}{E}_{11}^{cnt}+{V}_{m}{E}^{m}$$
(2a)
$$\frac{{\eta }_{2}}{{E}_{22}}=\frac{{V}_{cnt}}{{E}_{22}^{cnt}}+\frac{{V}_{m}}{{E}^{m}}$$
(2b)
$$\frac{{\eta }_{3}}{{G}_{12}}=\frac{{V}_{cnt}}{{G}_{12}^{cnt}}+\frac{{V}_{m}}{{G}^{m}}$$
(2c)
$${V}_{m}=1-{V}_{cnt}$$
(2d)
$${\upsilon }_{12}={V}_{cnt}{\upsilon }_{12}^{cnt}+{V}_{m}{\upsilon }^{m}$$
(2e)
$${\upsilon }_{21}=\frac{{\upsilon }_{12}}{{E}_{11}}{E}_{22}$$
(2f)
$$\rho ={V}_{cnt}{\rho }^{cnt}+{V}_{m}{\rho }^{m}$$
(2g)

where \({E}_{11}^{cnt}\), \({E}_{22}^{cnt}\) and \({G}_{12}^{cnt}\) indicate the Young’s modulus along the longitudinal direction, Young’s modulus in the transverse direction and shear modulus of CNTs, respectively. E m and G m indicate the Young’s modulus and shear modulus of the isotropic matrix, respectively. \({\upsilon }_{12}^{cnt}\) and \({\rho }^{cnt}\) represent the Poisson’s ratio and mass density of CNT, respectively, and v m and \({\rho }^{m}\) are the corresponding properties of the matrix. V m represents the matrix volume fraction, and η j (j = 1, 2, 3) denotes the CNT efficiency parameters, which are determined from the results of molecular dynamics simulations.

The displacement field for the CNTRC beam under the assumptions of first-order shear deformation elasticity theory can be expressed as follows:

$$U(x,z,t)=u(x,t)+z\theta (x,t)$$
(3a)
$$V(x,z,t)=z\varphi (x,t)$$
(3b)
$$W(x,z,t)=w(x,t)$$
(3c)

where u and w are the axial and transverse displacements along the x- and z-directions in the middle surface, respectively, and \(\theta \) and \(\varphi \) represent the rotations of the normal to the section about the y- and x-axes, respectively.

The strain and curvatures are defined in terms of the mid-plane displacements and rotations as:

$${\varepsilon }_{x}=\partial u/\partial x+z\partial \theta /\partial x$$
(4a)
$${\gamma }_{xz}=\partial w/\partial x+\theta $$
(4b)
$${\gamma }_{xy}=z\partial \varphi /\partial x$$
(4c)
$${\varepsilon }_{x}^{0}=\partial u/\partial x$$
(4d)
$${k}_{x}=\partial \theta /\partial x$$
(4e)
$${k}_{xy}=\partial \varphi /\partial x$$
(4f)

The constitutive equations are given by:

$$\{\begin{array}{c}{N}_{x}\\ {N}_{y}\\ {N}_{xy}\\ {M}_{x}\\ {M}_{y}\\ {M}_{xy}\end{array}\}=[\begin{array}{cccccc}{A}_{11} & {A}_{12} & {A}_{16} & {B}_{11} & {B}_{12} & {B}_{16}\\ {A}_{{\rm{12}}} & {A}_{22} & {A}_{26} & {B}_{{\rm{12}}} & {B}_{22} & {B}_{26}\\ {A}_{{\rm{16}}} & {A}_{{\rm{26}}} & {A}_{66} & {B}_{{\rm{16}}} & {B}_{{\rm{26}}} & {B}_{66}\\ {B}_{11} & {B}_{12} & {B}_{16} & {D}_{11} & {D}_{12} & {D}_{16}\\ {B}_{{\rm{12}}} & {B}_{22} & {B}_{26} & {D}_{{\rm{12}}} & {D}_{22} & {D}_{26}\\ {B}_{{\rm{16}}} & {B}_{{\rm{26}}} & {B}_{66} & {D}_{{\rm{16}}} & {D}_{{\rm{26}}} & {D}_{66}\end{array}]\{\begin{array}{c}{\varepsilon }_{x}^{0}\\ {\varepsilon }_{y}^{0}\\ {\gamma }_{xy}\\ {k}_{x}\\ {k}_{y}\\ {k}_{xy}\end{array}\}$$
(5a)
$$\{\begin{array}{c}{Q}_{xz}\\ {Q}_{yz}\end{array}\}=[\begin{array}{cc}{A}_{55} & 0\\ 0 & {A}_{55}\end{array}]\{\begin{array}{c}{\gamma }_{xz}\\ {\gamma }_{yz}\end{array}\}$$
(5b)

in which \({\varepsilon }_{x}\) and γ xz denote the normal and shear strain, respectively. \({\varepsilon }_{x}^{0}\), \({\varepsilon }_{y}^{0}\) and γ xy represent the strain at the middle surface; k x , k y and k xy are the bending and twisting curvatures; N x , N y and N xy indicate the force resultants at the middle surface; M x , M y and M xy are the bending and twisting moment resultants; and Q xy and Q yz represent the shear force resultants.

Regarding the CNTRC beam, certain force and moment resultants, namely, N y , N xy , Q yz and M y , are equal to zero, while the corresponding strains \({\varepsilon }_{y}^{0}\), γ xy and curvature k y are assumed to be non-zero. Consequently, Eq. (5) can be expressed as:

$$\{\begin{array}{c}{N}_{x}\\ {M}_{x}\\ {M}_{xy}\end{array}\}=[\begin{array}{ccc}{\bar{A}}_{11} & {\bar{B}}_{11} & {\bar{B}}_{16}\\ {\bar{B}}_{11} & {\bar{D}}_{11} & {\bar{D}}_{16}\\ {\bar{B}}_{16} & {\bar{D}}_{16} & {\bar{D}}_{66}\end{array}]\{\begin{array}{c}\partial u/\partial x\\ \partial \theta /\partial x\\ \partial \varphi /\partial x\end{array}\}$$
(6a)
$${Q}_{xz}={A}_{55}{\gamma }_{xz}={A}_{55}(\partial w/\partial x+\theta )$$
(6b)

where

$$\begin{array}{c}[\begin{array}{ccc}{\bar{A}}_{11} & {\bar{B}}_{11} & {\bar{B}}_{16}\\ {\bar{B}}_{11} & {\bar{D}}_{11} & {\bar{D}}_{16}\\ {\bar{B}}_{16} & {\bar{D}}_{16} & {\bar{D}}_{66}\end{array}]=[\begin{array}{ccc}{A}_{11} & {B}_{11} & {B}_{16}\\ {B}_{11} & {D}_{11} & {D}_{16}\\ {B}_{16} & {D}_{16} & {D}_{66}\end{array}]-\\ \begin{array}{l}\end{array}[\begin{array}{ccc}{A}_{12} & {A}_{16} & {B}_{12}\\ {B}_{12} & {B}_{16} & {D}_{12}\\ {B}_{26} & {D}_{12} & {D}_{26}\end{array}]\,{[\begin{array}{ccc}{A}_{22} & {A}_{26} & {B}_{22}\\ {A}_{26} & {A}_{66} & {B}_{26}\\ {B}_{22} & {B}_{26} & {D}_{22}\end{array}]}^{-1}{[\begin{array}{ccc}{A}_{12} & {A}_{16} & {B}_{12}\\ {B}_{12} & {B}_{16} & {D}_{12}\\ {B}_{26} & {D}_{12} & {D}_{26}\end{array}]}^{T}\end{array}$$
(7)

The extensional stiffness coefficients A ij , coupling stiffness coefficients B ij , bending stiffness coefficients D ij (i, j = 1, 2, 6) and transverse shear stiffness A 55 are defined as functions of material properties, which can be written as:

$$({A}_{ij},{B}_{ij},{D}_{ij})={\int }_{-h/2}^{h/2}{\bar{Q}}_{ij}(1,z,{z}^{2})dz$$
(8a)
$${A}_{55}=\kappa {\int }_{-h/2}^{h/2}{\bar{Q}}_{55}dz$$
(8b)

where \(\kappa \) denotes the shear correction factor. The reduced stiffness coefficients \({\bar{Q}}_{ij}(i=1,2,6)\) are defined by the following equations:

$${Q}_{11}=\frac{{E}_{11}}{1-{\upsilon }_{12}{\upsilon }_{21}}$$
(9a)
$${Q}_{12}=\frac{{\upsilon }_{12}{E}_{22}}{1-{\upsilon }_{12}{\upsilon }_{21}}=\frac{{\upsilon }_{21}{E}_{11}}{1-{\upsilon }_{12}{\upsilon }_{21}}$$
(9b)
$${Q}_{22}=\frac{{E}_{22}}{1-{\upsilon }_{12}{\upsilon }_{21}}$$
(9c)
$${Q}_{66}={Q}_{55}={G}_{12}$$
(9d)
$${Q}_{16}={Q}_{26}=0$$
(9e)

With the aim of deriving the governing equations and boundary conditions of the CNTRC beam according to Hamilton’s principle, the energy expressions are defined as follows. The total linear elastic strain energy (U s ) function of the CNTRC beam can be expressed as

$$\begin{array}{rcl}{U}_{s} & = & \frac{b}{2}{\int }_{0}^{L}({N}_{x}{\varepsilon }_{x}^{0}+{M}_{x}{k}_{x}+{M}_{xy}{k}_{xy}+{Q}_{xz}{\gamma }_{xz})dx\\ & = & \frac{b}{2}{\int }_{0}^{L}\{\begin{array}{c}{\bar{A}}_{11}{({\varepsilon }_{x}^{0})}^{2}+2{\bar{B}}_{11}{\varepsilon }_{x}^{0}{k}_{x}+2{\bar{B}}_{16}{\varepsilon }_{x}^{0}{k}_{xy}+{\bar{D}}_{11}{({k}_{x})}^{2}\\ +2{\bar{D}}_{16}{k}_{x}{k}_{xy}+{\bar{D}}_{66}{({k}_{xy})}^{2}+{A}_{55}{({\gamma }_{xz})}^{2}\end{array}\}dx\end{array}$$
(10)

and the homologous kinetic energy (T) function is given by

$$\begin{array}{c}T=\,\frac{b}{2}{\int }_{0}^{L}{\int }_{-h/2}^{h/2}\rho ({\dot{u}}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2})dzdx\\ \,\,\,=\,\frac{b}{2}{\int }_{0}^{L}[{I}_{1}{({\dot{u}}_{0})}^{2}+{I}_{3}{(\dot{\theta })}^{2}+{I}_{3}{(\mathop{\varphi }\limits^{.})}^{2}+2{I}_{2}{\dot{u}}_{0}\dot{\theta }+{I}_{1}({\dot{w}}_{0})]dx\end{array}$$
(11)

in which the inertia terms can be written as

$$({I}_{1},{I}_{2},{I}_{3})={\int }_{-h/2}^{h/2}\rho (1,z,{z}^{2})dz$$
(12)

In addition, four sets of boundary springs are introduced at each end of the beam; the boundary springs deformation strain energy (U sp ) function is given by

$${U}_{sp}=\frac{1}{2}{[{k}_{0}^{u}{u}^{2}+{k}_{0}^{w}{w}^{2}+{K}_{0}^{c}{\theta }^{2}+{K}_{0}^{s}{\varphi }^{2}]}_{x=0}+\frac{1}{2}{[{k}_{L}^{u}{u}^{2}+{k}_{L}^{w}{w}^{2}+{K}_{L}^{c}{\theta }^{2}+{K}_{L}^{s}{\varphi }^{2}]}_{x=L}$$
(13)

and the Hamilton’s principle with regard to the arbitrary initial time t 1 and final time t 2 is given by

$$\delta {\int }_{{t}_{1}}^{{t}_{2}}(T-{U}_{s}-{U}_{sp})dt=0$$
(14)

Substituting Eqs (10), (11) and (13) into Eq. (14) and integrating by parts to eliminate the variational terms, the governing equations and boundary conditions can be obtained as follows:

$$\begin{array}{c}{\int }_{{t}_{1}}^{{t}_{2}}{\int }_{0}^{L}({\bar{A}}_{11}\frac{{\partial }^{2}u}{\partial {x}^{{\rm{2}}}}+{\bar{B}}_{11}\frac{{\partial }^{2}\theta }{\partial {x}^{{\rm{2}}}}+{\bar{B}}_{{\rm{16}}}\frac{{\partial }^{2}\varphi }{\partial {x}^{{\rm{2}}}}-{I}_{1}\frac{{\partial }^{2}u}{\partial {t}^{{\rm{2}}}}-{I}_{2}\frac{{\partial }^{2}\theta }{\partial {t}^{{\rm{2}}}})\delta udxdt\\ +{\int }_{{t}_{1}}^{{t}_{2}}{\int }_{0}^{L}({A}_{55}\frac{{\partial }^{2}w}{\partial {x}^{{\rm{2}}}}+{A}_{55}\frac{\partial \theta }{\partial x}-{I}_{1}\frac{{\partial }^{2}w}{\partial {t}^{{\rm{2}}}})\delta wdxdt\\ +{\int }_{{t}_{1}}^{{t}_{2}}{\int }_{0}^{L}({\bar{B}}_{11}\frac{{\partial }^{2}u}{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{11}\frac{{\partial }^{2}\theta }{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{{\rm{16}}}\frac{{\partial }^{2}\varphi }{\partial {x}^{{\rm{2}}}}-{A}_{55}\frac{\partial w}{\partial x}-{A}_{55}\theta -{I}_{2}\frac{{\partial }^{2}u}{\partial {t}^{{\rm{2}}}}-{I}_{3}\frac{{\partial }^{2}\theta }{\partial {t}^{{\rm{2}}}})\delta \theta dxdt\\ +{\int }_{{t}_{1}}^{{t}_{2}}{\int }_{0}^{L}({\bar{B}}_{16}\frac{{\partial }^{2}u}{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{16}\frac{{\partial }^{2}\theta }{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{{\rm{66}}}\frac{{\partial }^{2}\varphi }{\partial {x}^{{\rm{2}}}}-{I}_{3}\frac{{\partial }^{2}\varphi }{\partial {t}^{{\rm{2}}}})\delta \varphi dxdt-\\ {\int }_{{t}_{1}}^{{t}_{2}}[\begin{array}{c}({N}_{x}+{k}_{L}^{u}u){\delta u|}_{L}-({N}_{x}-{k}_{0}^{u}u){\delta u|}_{0}+({Q}_{xz}+{k}_{L}^{w}w){\delta w|}_{L}-({Q}_{xz}-{k}_{0}^{w}w){\delta w|}_{0}\\ +({M}_{x}+{K}_{L}^{c}\theta ){\delta \theta |}_{L}-({M}_{x}-{K}_{0}^{c}\theta ){\delta \theta |}_{0}+({M}_{xy}+{K}_{L}^{s}\varphi ){\delta \varphi |}_{L}-({M}_{xy}-{K}_{0}^{s}\varphi ){\delta \varphi |}_{0}\end{array}]=0\end{array}$$
(15)

Because of the arbitrariness of the virtual displacements δu and δw, only when the values of the virtual displacements coefficients are equal to zero is Eq. (15) tractable. The governing equations can be expressed in terms of the differentials of displacement components as

$${\bar{A}}_{11}\frac{{\partial }^{2}u}{\partial {x}^{{\rm{2}}}}+{\bar{B}}_{11}\frac{{\partial }^{2}\theta }{\partial {x}^{{\rm{2}}}}+{\bar{B}}_{{\rm{16}}}\frac{{\partial }^{2}\varphi }{\partial {x}^{{\rm{2}}}}={I}_{1}\frac{{\partial }^{2}u}{\partial {t}^{{\rm{2}}}}+{I}_{2}\frac{{\partial }^{2}\theta }{\partial {t}^{{\rm{2}}}}$$
(16a)
$${A}_{55}\frac{{\partial }^{2}w}{\partial {x}^{{\rm{2}}}}+{A}_{55}\frac{\partial \theta }{\partial x}={I}_{1}\frac{{\partial }^{2}w}{\partial {t}^{{\rm{2}}}}$$
(16b)
$${\bar{B}}_{11}\frac{{\partial }^{2}u}{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{11}\frac{{\partial }^{2}\theta }{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{{\rm{16}}}\frac{{\partial }^{2}\varphi }{\partial {x}^{{\rm{2}}}}-{A}_{55}\frac{\partial w}{\partial x}-{A}_{55}\theta ={I}_{2}\frac{{\partial }^{2}u}{\partial {t}^{{\rm{2}}}}+{I}_{3}\frac{{\partial }^{2}\theta }{\partial {t}^{{\rm{2}}}}$$
(16c)
$${\bar{B}}_{16}\frac{{\partial }^{2}u}{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{16}\frac{{\partial }^{2}\theta }{\partial {x}^{{\rm{2}}}}+{\bar{D}}_{{\rm{66}}}\frac{{\partial }^{2}\varphi }{\partial {x}^{{\rm{2}}}}={I}_{3}\frac{{\partial }^{2}\varphi }{\partial {t}^{{\rm{2}}}}$$
(16d)

and the general boundary conditions can be stated as

$$x=0:\{\begin{array}{c}{N}_{x}-{k}_{0}^{u}u=0\\ {Q}_{xz}-{k}_{0}^{w}w=0\\ {M}_{x}-{K}_{0}^{c}\theta =0\\ {M}_{xy}-{K}_{0}^{s}\varphi =0\end{array}$$
(17a)
$$x=L:\{\begin{array}{c}{N}_{x}+{k}_{L}^{u}u=0\\ {Q}_{xz}+{k}_{L}^{w}w=0\\ {M}_{x}+{K}_{L}^{c}\theta =0\\ {M}_{xy}+{K}_{L}^{s}\varphi =0\end{array}$$
(17b)

Therefore, all classical boundary conditions and elastic supports can be directly achieved by means of the artificial spring boundary technique to assign the rigidities of the boundary springs at a certain value.

The appropriate choice of admissible displacement functions plays a significant role to ensure the validity and accuracy of the proposed solution procedures. Eqs (16a–16d) indicate that the translation and rotations displacements of the CNTRC beam are required up to the second derivative. For the sake of satisfying the arbitrary boundary conditions at both ends of the beam, the displacements and rotational components are represented as 1D Fourier cosine series expansions with two supplemental auxiliary function terms. These terms are introduced to improve the convergence of the primary Fourier series representations and avoid the potential discontinuities of the displacement functions and their first-order derivatives at the boundaries. Accordingly, the functions of flexural displacements and rotation of the CNTRC beam can be universally expressed as

$$u(x)=\sum _{m=0}^{M}{A}_{m}\,\cos \,{\lambda }_{m}x+{a}_{1}{P}_{1}(x)+{a}_{2}{P}_{2}(x)$$
(18a)
$$w(x)=\sum _{m=0}^{M}{B}_{m}\,\cos \,{\lambda }_{m}x+{b}_{1}{P}_{1}(x)+{b}_{2}{P}_{2}(x)$$
(18b)
$$\theta (x)=\sum _{m=0}^{M}{C}_{m}\,\cos \,{\lambda }_{m}x+{c}_{1}{P}_{1}(x)+{c}_{2}{P}_{2}(x)$$
(18c)
$$\varphi (x)=\sum _{m=0}^{M}{D}_{m}\,\cos \,{\lambda }_{m}x+{d}_{1}{P}_{1}(x)+{d}_{2}{P}_{2}(x)$$
(18d)

where \({\lambda }_{m}=m\pi /L\). M represents the truncation number, A m, B m, C m and D m are the expansion coefficients of the standard Fourier series, and a i , b i and c i (i = 1, 2) denote the corresponding expansion coefficients of the auxiliary function P 1(x) and P 2(x), which are defined as:

$${P}_{1}(x)=x{(\frac{x}{L}-1)}^{2}$$
(19a)
$${P}_{2}(x)=\frac{{x}^{2}}{L}(\frac{x}{L}-1)$$
(19b)

According to the modified Fourier series, the free-vibration characteristics of the CNTRC beam can be solved by means of strong-form solution procedures and weak-form solutions, as described below. The strong-form solution procedure is given step by step as follows.

We rewrite Eq. (18) in matrix form as

$$\begin{array}{c}u(x)={{\bf{H}}}_{f}{\bf{A}}+{{\bf{H}}}_{a}{\bf{a}}\\ w(x)={{\bf{H}}}_{f}{\bf{B}}+{{\bf{H}}}_{a}{\bf{b}}\\ \theta (x)={{\bf{H}}}_{f}{\bf{C}}+{{\bf{H}}}_{a}{\bf{c}}\\ \varphi (x)={{\bf{H}}}_{f}{\bf{D}}+{{\bf{H}}}_{a}{\bf{d}}\end{array}$$
(20)

where

$${{\bf{H}}}_{f}=[\begin{array}{ccccc}\cos \,{\lambda }_{0}x, & \cdots & \cos \,{\lambda }_{m}x, & \cdots & \cos \,{\lambda }_{M}x\end{array}]$$
(21a)
$${{\bf{H}}}_{a}=[{P}_{1}(x),{P}_{2}(x)]$$
(21b)
$$\begin{array}{cc}{\bf{A}}={[\begin{array}{ccccc}{A}_{0}, & \cdots & ,{A}_{m} & \cdots & ,{A}_{M}\end{array}]}^{T} & {\bf{a}}={[{a}_{1},{a}_{2}]}^{T}\end{array}$$
(21c)
$$\begin{array}{cc}{\bf{B}}={[\begin{array}{ccccc}{B}_{0}, & \cdots & ,{B}_{m} & \cdots & ,{B}_{M}\end{array}]}^{T} & {\bf{b}}={[{b}_{1},{b}_{2}]}^{T}\end{array}$$
(21d)
$$\begin{array}{cc}{\bf{C}}={[\begin{array}{ccccc}{C}_{0}, & \cdots & ,{C}_{m} & \cdots & ,{C}_{M}\end{array}]}^{T} & {\bf{c}}={[{c}_{1},{c}_{2}]}^{T}\end{array}$$
(21e)
$$\begin{array}{cc}{\bf{D}}={[\begin{array}{ccccc}{D}_{0}, & \cdots & ,{D}_{m} & \cdots & ,{D}_{M}\end{array}]}^{T} & {\bf{d}}={[{d}_{1},{d}_{2}]}^{T}\end{array}$$
(21f)

Substituting Eqs (20) and (21) into Eq. (16), we obtain

$${{\bf{L}}}_{f}\,[\begin{array}{c}{\bf{A}}\\ {\bf{B}}\\ {\bf{C}}\\ {\bf{D}}\end{array}]+{{\bf{L}}}_{a}\,[\begin{array}{c}{\bf{a}}\\ {\bf{b}}\\ {\bf{c}}\\ {\bf{d}}\end{array}]-{\omega }^{2}\,({{\bf{M}}}_{f}\,[\begin{array}{c}{\bf{A}}\\ {\bf{B}}\\ {\bf{C}}\\ {\bf{D}}\end{array}]+{{\bf{M}}}_{a}\,[\begin{array}{c}{\bf{a}}\\ {\bf{b}}\\ {\bf{c}}\\ {\bf{d}}\end{array}])=0$$
(22)

in which

$$\begin{array}{c}{{\bf{L}}}_{i}=[\begin{array}{cccc}{L}_{11}{{\bf{H}}}_{i} & 0 & {L}_{13}{{\bf{H}}}_{i} & {L}_{14}{{\bf{H}}}_{i}\\ 0 & {L}_{22}{{\bf{H}}}_{i} & {L}_{23}{{\bf{H}}}_{i} & 0\\ {L}_{31}{{\bf{H}}}_{i} & {L}_{32}{{\bf{H}}}_{i} & {L}_{33}{{\bf{H}}}_{i} & {L}_{34}{{\bf{H}}}_{i}\\ {L}_{41}{{\bf{H}}}_{i} & 0 & {L}_{43}{{\bf{H}}}_{i} & {L}_{44}{{\bf{H}}}_{i}\end{array}](i=f,a)\\ {{\bf{M}}}_{i}=[\begin{array}{cccc}{M}_{11}{{\bf{H}}}_{i} & 0 & {M}_{13}{{\bf{H}}}_{i} & 0\\ 0 & {M}_{22}{{\bf{H}}}_{i} & 0 & 0\\ {M}_{31}{{\bf{H}}}_{i} & 0 & {M}_{33}{{\bf{H}}}_{i} & 0\\ 0 & 0 & 0 & {M}_{44}{{\bf{H}}}_{i}\end{array}](i=f,a)\end{array}$$
(23)

and the coefficients of the linear operator are defined as follows

$$\begin{array}{l}{L}_{11}={\bar{A}}_{11}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}},{L}_{13}={\bar{B}}_{11}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}},{L}_{14}={\bar{B}}_{{\rm{16}}}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}},\,{L}_{22}={A}_{55}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}},{L}_{23}={A}_{55}\frac{\partial }{\partial x}\\ {L}_{31}={\bar{B}}_{11}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}},{L}_{32}=-{A}_{55}\frac{\partial }{\partial x},{L}_{33}={\bar{D}}_{11}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}}-{A}_{55},{L}_{34}={\bar{D}}_{{\rm{16}}}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}}\\ {L}_{41}={\bar{B}}_{16}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}},{L}_{43}={\bar{D}}_{16}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}},{L}_{44}={\bar{D}}_{{\rm{66}}}\frac{{\partial }^{2}}{\partial {x}^{{\rm{2}}}}\\ {M}_{11}={M}_{22}=-{I}_{1},{M}_{13}={M}_{31}=-{I}_{2},{M}_{33}={M}_{44}=-{I}_{3}\end{array}$$
(24)

Similarly, substituting Eqs (20) and (21) into Eq. (17), the boundary conditions of CNTRC beams are stated as

$$[\begin{array}{c}{{\bf{L}}}_{f}^{bc0}\\ {{\bf{L}}}_{f}^{bcL}\end{array}]\,[\begin{array}{c}{\bf{A}}\\ {\bf{B}}\\ {\bf{C}}\\ {\bf{D}}\end{array}]+[\begin{array}{c}{{\bf{L}}}_{a}^{bc0}\\ {{\bf{L}}}_{a}^{bcL}\end{array}]\,[\begin{array}{c}{\bf{a}}\\ {\bf{b}}\\ {\bf{c}}\\ {\bf{d}}\end{array}]=0$$
(25)

where

$${{\bf{L}}}_{i}^{bc0}={[\begin{array}{cccc}{\bar{A}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x}-{k}_{0}^{u}{{\bf{H}}}_{i} & 0 & {\bar{B}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & {\bar{B}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x}\\ 0 & {A}_{55}\frac{\partial {{\bf{H}}}_{i}}{\partial x}-{k}_{0}^{w}{{\bf{H}}}_{i} & {A}_{55}{{\bf{H}}}_{i} & 0\\ {\bar{B}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & 0 & {\bar{D}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x}-{K}_{0}^{c}{{\bf{H}}}_{i} & {\bar{D}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x}\\ {\bar{B}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & 0 & {\bar{D}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & {\bar{D}}_{66}\frac{\partial {{\bf{H}}}_{i}}{\partial x}-{K}_{0}^{s}{{\bf{H}}}_{i}\end{array}]}_{x=0}(i=f,a)$$
(26a)
$${{\bf{L}}}_{i}^{bcL}={[\begin{array}{cccc}{\bar{A}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x}+{k}_{L}^{u}{{\bf{H}}}_{i} & 0 & {\bar{B}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & {\bar{B}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x}\\ 0 & {A}_{55}\frac{\partial {{\bf{H}}}_{i}}{\partial x}+{k}_{L}^{w}{{\bf{H}}}_{i} & {A}_{55}{{\bf{H}}}_{i} & 0\\ {\bar{B}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & 0 & {\bar{D}}_{11}\frac{\partial {{\bf{H}}}_{i}}{\partial x}+{K}_{L}^{c}{{\bf{H}}}_{i} & {\bar{D}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x}\\ {\bar{B}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & 0 & {\bar{D}}_{16}\frac{\partial {{\bf{H}}}_{i}}{\partial x} & {\bar{D}}_{66}\frac{\partial {{\bf{H}}}_{i}}{\partial x}+{K}_{L}^{s}{{\bf{H}}}_{i}\end{array}]}_{x=L}(i=f,a)$$
(26b)

Therefore, the expansion coefficients of the standard Fourier cosine series and corresponding auxiliary functions have a certain relationship according to the boundary conditions, which are expressed as:

$$[\begin{array}{c}{\bf{a}}\\ {\bf{b}}\\ {\bf{c}}\\ {\bf{d}}\end{array}]=-{[\begin{array}{c}{{\bf{L}}}_{a}^{bc0}\\ {{\bf{L}}}_{a}^{bcL}\end{array}]}^{-1}\,[\begin{array}{c}{{\bf{L}}}_{f}^{bc0}\\ {{\bf{L}}}_{f}^{bcL}\end{array}]\,[\begin{array}{c}{\bf{A}}\\ {\bf{B}}\\ {\bf{C}}\\ {\bf{D}}\end{array}]$$
(27)

Substituting Eqs (26) and (27) into Eq. (22), then multiplying the transpose of displacement functions matrix H f on the left side and integrating both sides of the equality from 0 to L with respect to x, the partial differential equations are transformed into a standard eigenvalue problem as follows:

$$({\bf{K}}-{\omega }^{2}{\bf{M}}){\bf{G}}=0$$
(28)

in which K and M are the stiffness matrix and mass matrix, respectively, G is a vector that contains all undetermined coefficients of the standard Fourier series, and these matrices can be written as:

$${\bf{K}}={{\bf{L}}}_{f}-{{\bf{L}}}_{a}{[\begin{array}{c}{{\bf{L}}}_{a}^{bc0}\\ {{\bf{L}}}_{a}^{bcL}\end{array}]}^{-1}\,[\begin{array}{c}{{\bf{L}}}_{f}^{bc0}\\ {{\bf{L}}}_{f}^{bcL}\end{array}]$$
(29a)
$${\bf{M}}={{\bf{M}}}_{f}-{{\bf{M}}}_{a}{[\begin{array}{c}{{\bf{L}}}_{a}^{bc0}\\ {{\bf{L}}}_{a}^{bcL}\end{array}]}^{-1}\,[\begin{array}{c}{{\bf{L}}}_{f}^{bc0}\\ {{\bf{L}}}_{f}^{bcL}\end{array}]$$
(29b)
$${\bf{G}}={[\begin{array}{cccc}{\bf{A}} & {\bf{B}} & {\bf{C}} & {\bf{D}}\end{array}]}^{T}$$
(29c)

The natural frequencies and modes of CNTRC beams can be obtained directly by solving the standard eigenvalue equation.

Exact solutions are often unavailable in complex vibration problems, and an approximate method is employed to complete the vibrational analysis. The Rayleigh–Ritz method associated with modified Fourier series, i.e., weak-form solution, is also presented below to compare with the strong-form solution.

In the Ritz-variational energy procedure, the accuracy of the solution will rest on how well the actual displacement can be faithfully represented by an appropriate admissible displacement field in general. Hence, auxiliary functions play a crucial role. The same displacement functions are selected for comparative purposes, and all expansion coefficients of the modified Fourier series can be regarded as generalized coordinates independently and equally.

With regard to free-vibration analysis, the Lagrange energy function of CNTRC beams consists of the strain energy, kinetic energy and boundary spring deformation strain energy as follows:

$$L=T-{U}_{s}-{U}_{sp}$$
(30)

Substituting Eqs (10), (11) and (13) into Eq. (30), minimizing the total expression of the Lagrange energy function via taking the derivatives of the equation with respect to the generalized coordinates and setting all expressions equal to zero to find the stationary value of the energy function, we obtain:

$$\frac{\partial L}{\partial {A}_{m}}=\frac{\partial L}{\partial {B}_{m}}=\frac{\partial L}{\partial {C}_{m}}=\frac{\partial L}{\partial {D}_{m}}=\frac{\partial L}{\partial {a}_{i}}=\frac{\partial L}{\partial {b}_{i}}=\frac{\partial L}{\partial {c}_{i}}=\frac{\partial L}{\partial {d}_{i}}=0,(i=1,2)$$
(31)

A total of 4(M + 3) linear algebraic equations for the undetermined coefficients are achieved, which can be added and represented in a matrix form as

$$({{\bf{K}}}^{\ast }-{\omega }^{2}{{\bf{M}}}^{\ast }){{\bf{G}}}^{\ast }=0$$
(32)

where G * indicates the undetermined coefficients column vector, K * is treated as the total stiffness matrix of the CNTRC beams and M * indicates the corresponding mass matrix. Their expressions can be written as:

$${{\bf{G}}}^{\ast }={[\begin{array}{c}\begin{array}{ccccc}{A}_{0}, & \cdots & ,{A}_{m} & \cdots & ,{A}_{M}\end{array}\begin{array}{ccccc},{a}_{1},{a}_{2},{B}_{0}, & \cdots & ,{B}_{m} & \cdots & ,{B}_{M},\end{array}{b}_{1},{b}_{2},\\ \begin{array}{ccccc}{C}_{0}, & \cdots & ,{C}_{m} & \cdots & ,{C}_{M}\end{array},{c}_{1},{c}_{2},\begin{array}{ccccc}{D}_{0}, & \cdots & ,{D}_{m} & \cdots & ,{D}_{M}\end{array},{d}_{1},{d}_{2}\end{array}]}^{T}$$
(33a)
$${{\bf{K}}}^{\ast }=[\begin{array}{cccc}{{\bf{K}}}_{uu} & 0 & {{\bf{K}}}_{u\theta } & {{\bf{K}}}_{u\varphi }\\ 0 & {{\bf{K}}}_{ww} & {{\bf{K}}}_{w\theta } & 0\\ {{\bf{K}}}_{u\theta }^{T} & {{\bf{K}}}_{w\theta }^{T} & {{\bf{K}}}_{\theta \theta } & {{\bf{K}}}_{\theta \varphi }\\ {{\bf{K}}}_{u\varphi }^{T} & 0 & {{\bf{K}}}_{\theta \varphi }^{T} & {{\bf{K}}}_{\varphi \varphi }\end{array}]$$
(33b)
$${{\bf{M}}}^{\ast }=[\begin{array}{cccc}{{\bf{M}}}_{uu} & 0 & {{\bf{M}}}_{u\theta } & 0\\ 0 & {{\bf{M}}}_{ww} & 0 & 0\\ {{\bf{M}}}_{u\theta }^{T} & 0 & {{\bf{M}}}_{\theta \theta } & 0\\ 0 & 0 & 0 & {{\bf{M}}}_{\varphi \varphi }\end{array}]$$
(33c)

The detailed expressions of the elements of K * and M * are listed in the Appendix. The Rayleigh–Ritz method associated with the modified Fourier series is equivalent to strong-form solution procedures to obtain the vibration results by solving a standard eigenvalue equation.

Numerical results and discussions

With the achievement of the theoretical formulation of the modified Fourier method mentioned above, selected numerical examples for the free-vibration analysis of CNTRC beams with arbitrary boundary conditions are presented to validate the feasibility, accuracy and efficiency of the proposed method. Several key parameters representing the vibrational characteristics of CNTRC beams, such as the L/h ratio, CNT volume fraction and boundary spring stiffness, are discussed, and new results and useful conclusions are obtained.

The following material properties for CNTs and PMMA matrixes are applied unless otherwise illustrated: E m = 2.5 GPa, v m=0.3, ρ m = 1150 kg/m3, \({E}_{11}^{cnt}=5645.6\) GPa, \({E}_{22}^{cnt}=7080\) GPa, \({G}_{12}^{cnt}=1944.5\) GPa, \({\upsilon }_{12}^{cnt}=0.175\) and \({\rho }^{cnt}=2100\) kg/m3. By matching with the results calculated from molecular dynamics simulations, three types of CNT efficiency parameters with special CNT volume fractions are given as: η 1 = 0.137, η 2 = 1.022 for V tcnt  = 0.12; η 1 = 0.142, η 2 = 1.138 for V tcnt  = 0.17; η 1 = 0.141, η 2 = 1.109 for V tcnt  = 0.28. In the absence of shear modulus results in molecular dynamics simulations, η 3 is defined as 0.7 η 2.

In addition, the non-dimensional frequency parameters of the natural frequency take the form of \(\Omega =\omega {L}^{2}\sqrt{{\rho }^{m}/({E}^{m}{h}^{2})}\) in the latter subsections unless otherwise stated. The corresponding boundary conditions at the ends of beam can be defined in terms of the spring stiffness as:

Clamped (C): \({k}_{0,L}^{u}={k}_{0,L}^{w}={K}_{0,L}^{c}={K}_{0,L}^{s}={10}^{15}\)

Simply supported (S): \({k}_{0,L}^{u}={k}_{0,L}^{w}={K}_{0,L}^{s}={10}^{15},{K}_{0,L}^{c}=0\)

Free (F): \({k}_{0,L}^{u}={k}_{0,L}^{w}={K}_{0,L}^{c}={K}_{0,L}^{s}=0\)

Elastically restrained case 1 (E1): \({k}_{0,L}^{u}={K}_{0,L}^{c}={K}_{0,L}^{s}=0,{k}_{0,L}^{w}={10}^{8}\)

Elastically restrained case 2 (E2): \({k}_{0,L}^{u}={K}_{0,L}^{s}=0,{k}_{0,L}^{w}={K}_{0,L}^{c}={10}^{8}\)

The rationality of these definitions of boundary conditions in terms of assigning spring stiffness will be established through numerical examples in subsequent studies. For brevity, symbolism is applied to illustrate the boundary condition of FG-CNTRC beams, e.g., SE1 indicates a beam with S (simply supported) and E1 (elastically restrained case 1) boundary conditions at = 0 and x = L, respectively.

Convergence and validation

As previously mentioned, modified Fourier series with infinite terms in the current solution framework are infinitely approximate in the real results. Nevertheless, the infinite terms must be numerically truncated in practical numerical simulations. Consequently, convergence studies are conducted to determine the number of series terms M used in the computation. The first four lowest frequency parameters Ω for perfectly clamped and simply supported FGV-CNT beams are considered in Table 1, in which the results obtained from strong-form solution procedures and the Rayleigh–Ritz method are given. Excellent convergence and satisfactory numerical stability of two types of current solutions can be observed. The frequency parameters Ω converge sharply as the number of series terms M increases from 4 to 15, and the results are almost invariant when the truncated number reaches a certain value (M = 10). Thus, unless otherwise illustrated, the truncated number was uniformly chosen as 10 in subsequent studies.

Table 1 Convergence of the first four lowest frequency parameters Ω for a perfectly clamped FGV-CNT beam (V tcnt  = 0.12, L/h = 10).
Full size table

With satisfactory results for the convergence studies of the FG-CNTRC beam, which is assumed to feature a perfectly clamped boundary condition at both ends, the numerical validity and rationality of the mentioned definition of the boundary conditions in terms of assigning boundary spring rigidities is evaluated in this section. The first three non-dimensional frequency parameters \(\bar{{\rm{\Omega }}}=\omega L\sqrt{{\rho }^{m}[1-{({\upsilon }^{m})}^{2}]/{E}^{m}}\) for FG-CNTRC beams with various CNT distributions and boundary conditions are compared with those reported in the publications of Lin et al.20 and Yas et al.18, as shown in Table 2 and Table 3.

Table 2 Comparison of the first three frequency parameters \(\bar{{\rm{\Omega }}}=\omega L\sqrt{{\rho }^{m}[1-{({\upsilon }^{m})}^{2}]/{E}^{m}}\) for FG-CNTRC beams with various CNT distributions and boundary conditions (L/h = 15, V tcnt  = 0.28).
Full size table
Table 3 Comparison of the first three dimensionless frequencies \(\bar{{\rm{\Omega }}}=\omega L\sqrt{{\rho }^{m}[1-{({\upsilon }^{m})}^{2}]/{E}^{m}}\) for FG-CNTRC beams with various CNT distributions and volume fractions (L/h = 15, C-S).
Full size table

The geometrical and material constants of the beams are provided as follows: L/h = 15, \({E}_{11}^{cnt}=600\) GPa, \({E}_{22}^{cnt}=10\) GPa, \({G}_{12}^{cnt}=17.2\) GPa, E m = 2.5 GPa, \({\upsilon }_{12}^{cnt}=0.19\), v m=0.3, \({\rho }^{cnt}=1400\) kg/m3, and \({\rho }^{m}=1190\) kg/m3. Table 2 presents the first three non-dimensional frequency parameters \(\bar{{\rm{\Omega }}}=\omega L\sqrt{{\rho }^{m}[1-{({\upsilon }^{m})}^{2}]/{E}^{m}}\) for UD-CNT, FGV-CNT and FGX-CNT beams with a total volume fraction V tcnt  = 0.28, and two classical boundary conditions are considered, namely, S-S and C-F. The solutions from the two present numerical approaches are in outstanding agreement with the results from Lin et al.20 and Yas et al.18.

The first three dimensionless natural frequencies \(\bar{{\rm{\Omega }}}=\omega L\sqrt{{\rho }^{m}[1-{({\upsilon }^{m})}^{2}]/{E}^{m}}\) for FG-CNTRC beams with C-S boundary conditions are presented in Table 3. The results in the present investigation are close to those in the references, and the two present numerical approaches are sufficiently accurate to enable vibrational characterization of FG-CNTRC beams subject to various boundary conditions. Moreover, a further comparison is explored to illustrate the applicability of the linear theories and assumptions in this investigation. Table 4 demonstrates the comparison of natural frequencies between the results calculated by the present method and those reported in studies54,55 that adopted first-order beam theory along with von Karman geometric nonlinearity.

Table 4 Comparison of the first three frequency parameters Ω of simply supported FG-CNTRC beam with various volume fractions (L/h = 25, h = 0.01).
Full size table

The first three frequency parameters Ω of simply supported FG-CNTRC beams with different volume fractions are presented in Table 4. Consistency can be observed between the calculated results and the data from the literature. Thus, the mentioned numerical examples indicate that the current solutions possess rapid convergence and satisfactory accuracy, which will be employed for calculating the results for the parametric studies in the following subsections.

Parametric studies

Tables 2–5 indicate the accuracy and convergence of the present solution. With enhanced confidence in the present solution approach, a variety of further results for FG-CNTRC beams with different boundary conditions and material and geometrical parameters are provided in this section to serve as benchmark solutions for potential studies. In addition, the frequencies calculated by the strong-form solution procedures are close to the results obtained using the Rayleigh–Ritz method. For brevity, only the results obtained from the strong-form solution procedures are included.

Table 5 First three frequency parameters Ω for FG-CNTRC beams with various CNT distributions (L/h = 10, V tcnt  = 0.12).
Full size table

Figure 3 illustrates the relationship between the first three frequency parameters Ω and the length-to-thickness ratio L/h for FG-CNTRC beams with various boundary conditions and CNT distributions. The total CNT volume fraction V tcnt is fixed at 0.17, and the length-to-thickness ratio varies from 0.5 to 4. All dimensionless frequencies increase with increasing length-to-thickness ratio. The fundamental parameter rises gradually with increasing L/h ratio; in contrast, the second and third frequency parameters increase sharply. Furthermore, the graphs provide notable results regarding the influence of CNT distributions. The frequency parameters of FG-XCNT beams are always larger than the results of other distributions and beams, with FGO-CNT distributions having the smallest values regardless of the boundary conditions. The same phenomenon can also be found in the following tables.

Figure 3
figure 3

The first three lowest frequency parameters Ω of FG-CNTRC beams with various length-to-thickness ratios. The total CNT volume fraction V tcnt is equal to 0.17, and the length-to-thickness ratio varies from 0.5 to 4. Three boundary conditions are considered: (a) F-F, (b) C-C, and (c) C-S.

Full size image

Table 5 shows the changes in the dimensionless frequencies of FG-CNTRC beams with various CNT distributions. The data in Table 5 lead us to conclude that the CNT distributions have a significant impact on the free-vibration characteristics of FG-CNTRC beams. Furthermore, symmetrical CNT distributions, i.e., FG-XCNT and FG-OCNT, play a notable role in changing the frequency parameters of the CNTRC beams relative to the uniform and asymmetric distributions through the beam thickness.

One of the primary purposes of this work is to investigate the free-vibration characteristics of FG-CNTRC beams with elastic boundary constraints. Accordingly, Fig. 4 illustrates the effects of four types of boundary spring parameters on the first three frequency parameters of FG-CNTRC beams with elastic supports. The total CNT volume fraction V tcnt and ratio L/h are 0.28 and 10, respectively. The UD-CNT, FGΛ-CNT and FGX-CNT beams are taken into consideration. The symbols Γ u , Γ w , Γ θ and Γ φ are defined to indicate the various kinds of boundary springs, and the boundary condition is defined as elastically restrained only at x = 0, where only one group of boundary springs is assigned to variable stiffness values ranging from 102 to 1016 and the other groups are assumed to be infinite while the other boundary is clamped at x = L.

Figure 4
figure 4

Variation of the first three dimensionless frequencies Ω versus the elastic restraint parameters for FG-CNTRC beams with various CNT distributions: (a) UD-CNT, (b) FGΛ-CNT, and (c) FGX-CNT. The symbols Γ u , Γ w , Γ θ and Γ φ denote the various types of boundary springs. The boundary conditions are considered to be elastically restrained at x = 0 and perfectly clamped at x = L.

Full size image

Figure 4 shows that the dimensionless frequency parameters remain stable as the restraint parameters Γ u and Γ φ change. In contrast, the dimensionless frequencies increase sharply as the restraint parameters Γ w and Γ θ increase from 106 to 1010. Furthermore, there is little variation in the frequency parameters beyond this range. In addition, the results confirm that the influence of the restraint parameter Г w is more easily detectable than that of Г θ . Therefore, the definition of the boundary conditions mentioned above in terms of assigning the values of boundary spring stiffness is reasonable to simulate the real restraints.

The next example is focused on the influence of the total CNT volume fraction on FG-CNTRC beams with classical and elastic boundary conditions. The material properties of the beams are provided as follows: \({E}_{11}^{cnt}=600\) GPa, \({E}_{22}^{cnt}=10\) GPa, \({G}_{12}^{cnt}=17.2\) GPa, E m = 2.5 GPa, \({\upsilon }_{12}^{cnt}=0.19\), v m = 0.3, \({\rho }^{cnt}=1400\) kg/m3, and \({\rho }^{m}=1190\) kg/m3. Table 6 indicates the changes in the value of the first three dimensionless frequencies \(\bar{{\rm{\Omega }}}=\omega L\sqrt{{\rho }^{m}[1-{({\upsilon }^{m})}^{2}]/{E}^{m}}\) of FG-CNTRC beams as the total CNT volume fraction V tcnt increases from 0.12 to 0.28. The frequency parameters uniformly increase as the total CNT volume fraction increases.

Table 6 First three dimensionless frequencies \(\bar{{\rm{\Omega }}}=\omega L\sqrt{{\rho }^{m}[1-{({\upsilon }^{m})}^{2}]/{E}^{m}}\) for FG-CNTRC beams with various total CNT volume fractions (L/h = 10).
Full size table

By introducing the shear correction factor \(\kappa \), the first-order shear deformation elasticity theories address the shortcomings of the Euler beam theory, which neglects the effects of transverse shear and rotary inertia. Note that all results in this study are based on the first-order beam theory and that it is necessary to study the influence of the shear correction factor on the free-vibration characteristics of FG-CNTRC beams.

Table 7 presents the fundamental frequency parameters Ω for FG-CNTRC beams in the case in which the shear correction factor increases from 0.1 to 0.9 and compares the results with those calculated by Lin21 based on third-order shear deformation elasticity theory. The beam material properties and geometrical parameters are the same as for the FG-CNTRC beams presented in Table 5, where two classical boundary conditions and three types of CNT distribution are considered. The figures reveal that the frequency parameters monotonically increase as the shear correction factor increases from 0.1 to 0.9. To make the frequency parameters consistent with the results based on third-order beam theory, the appropriate shear correction factor \(\kappa \) should be selected in calculations with regard to the different boundary conditions.

Table 7 Fundamental frequency parameters Ω for FG-CNTRC beams with various shear correction factors.
Full size table

Because the free-vibration results for FG-CNTRC beams with arbitrary boundary conditions are extremely limited in the literature, new results are calculated in Table 8 to provide reference data for practising engineers and to act as a benchmark for potential future studies. Finally, aiming at strengthening our understanding of vibration behaviours of FG-CNTRC beams, several selected mode shapes of the beams addressed in Table 8 are plotted in Fig. 5.

Table 8 Fundamental frequency parameters Ω for a FG-CNTRC beam with various boundary conditions.
Full size table
Figure 5
figure 5

The first three lowest mode shapes of a FGX-CNT beam with two typical elastic boundary conditions. Two beams are taken into account: (a) S-E1, L/h = 10, V tcnt  = 0.28 and (b) E2-E2, L/h = 10, V tcnt  = 0.28.

Full size image

Conclusions

An accurate method is developed for the vibration analysis of FG-CNTRC beams. The distribution of CNTs through the thickness of the beam is assumed to vary continuously and smoothly, and five types of distribution, namely, UD-CNT, FGΛ-CNT, FGV-CNT, FGO-CNT and FGX-CNT, are considered. Note that this approach can be uniformly and conveniently applied in vibrational analysis of FG-CNTRC beams with arbitrary boundary conditions, including general elastic boundary conditions. The general boundary conditions can be enforced using the artificial spring technique, in which boundary springs can be assigned any value of stiffness to simulate the real boundary conditions. The energy expressions of the FG-CNTRC beams are written as functions of four displacement components based on first-order shear deformation elasticity theory. Regardless of the boundary conditions, specific geometry and material properties, the displacements and rotational components of the beam are expressed as a superposition of the standard cosine Fourier series and two auxiliary functions. The introduced auxiliary terms are intended to remove potential discontinuous displacement functions and their derivatives at each edge and to ensure the convergence of the series expansions.

By submitting modified Fourier series to governing equations and boundary conditions, the strong-form solution procedure of the modified Fourier method is proposed. For comparison, the Rayleigh–Ritz technique associated with the modified Fourier method is also presented as a weak-form solution. Numerical results obtained by these two present methods are compared with the available results previously reported, and both accuracy and satisfactory convergence are observed. The free-vibration characteristics of FG-CNTRC beams are analysed with a variety of key parameters, for example, the L/h ratio, CNT volume fraction, CNT distribution, boundary spring stiffness and shear correction factor. New vibration results containing frequency parameters and mode shapes for the FG-CNTRC beams with classical boundary conditions and elastic supports are calculated to provide reference data for practising engineers and act as a benchmark for future studies.

Data availability statement

All data generated or analysed during this study are included in this published article.