Attosecond electron microscopy by free-electron homodyne detection

Abstract

Time-resolved electron microscopy aims to track nanoscale excitations and dynamic states of matter at a temporal resolution ultimately reaching the attosecond regime. Periodically time-varying fields in an illuminated specimen cause free-electron inelastic scattering, which enables the spectroscopic imaging of near-field intensities. However, access to the evolution of nanoscale fields and structures within the cycle of light requires sensitivity to the optical phase. Here we introduce free-electron homodyne detection as a universally applicable approach to electron microscopy of phase-resolved optical responses at high spatiotemporal resolution. In this scheme, a phase-controlled reference interaction serves as the local oscillator to extract arbitrary sample-induced modulations of a free-electron wavefunction. We demonstrate this principle through the phase-resolved imaging of plasmonic fields with few-nanometre spatial and sub-cycle temporal resolutions. Due to its sensitivity to both phase- and amplitude-modulated electron beams, free-electron homodyne detection measurements will be able to detect and amplify weak signals stemming from a wide variety of microscopic origins, including linear and nonlinear optical polarizations, atomic and molecular resonances, and attosecond-modulated structure factors.

Main

The desire to map the structure and dynamic evolution of materials on their intrinsic spatiotemporal scales of ångströms and attoseconds has been a major driving force behind methodological developments in condensed matter science. Although structural information is available from X-ray^1,2,3 and electron^4,5,6 imaging and diffraction, temporal resolution down to the attosecond regime is provided by a growing suite of methods in optical spectroscopy^7,8,9. Ultrafast electron microscopy combines the strengths of optical techniques with nanoscale spatial resolution^10,11,12,13 for imaging non-equilibrium phenomena such as structural phase transformations¹⁴, strain wave and polariton propagation^15,16. In this approach, electrons are synchronized with optical excitations driven by femtosecond laser pulses, commonly used to trigger dynamical processes in solids, nanostructures and molecules. The characterization of the associated microscopic couplings and correlations with ultimate spatiotemporal resolution will facilitate future applications in materials synthesis, energy conversion and light harvesting.

The response of a material to an optical stimulus includes both linear and nonlinear contributions^17,18, which intrinsically involve a temporal evolution shorter than the optical period^{19,20,21,22,23}. Pulses with a sub-cycle temporal structure are employed to probe such dynamics^24,25. For example, high-harmonic generation facilitates the creation of attosecond extreme ultraviolet pulses²⁶ or pulse trains^27,28 for spectroscopy. In electron microscopy, the generation of energy sidebands by coherent inelastic electron scattering^29,30,31 allows sub-cycle bunching of the electron beam through dispersive propagation^32,33, promising attosecond microscopy^{34,35,36,37,38,39} with high spatial resolution. Recent works demonstrated attosecond electron pulse trains within the stringent spatial constraints imposed by electron microscopes^35,39,40, whereas very recent breakthroughs enable nanometric attosecond imaging^41,42,43,44.

Results

The principle of free-electron homodyne detection

In this Article we introduce free-electron homodyne detection (FREHD) as a universal scheme for attosecond electron microscopy of arbitrary periodic sample responses. The technique is based on a nanoscale readout of coherent amplitude or phase modulations of the free-electron wavefunction. Not requiring a density structuring of the beam, FREHD will enable the spatially resolved mapping of sub-cycle optical, electronic or structural dynamics. We experimentally demonstrate the capabilities of this approach in the phase-resolved imaging of plasmonic near fields at the few-nanometre scale.

The method presented here transfers the notion of homodyne detection in optics and radiofrequency technology to electron beams, with conceptual similarities but also notable additional features. In optics, homodyne detection is frequently used to characterize states of light in relation to a local oscillator⁴⁵. Specifically, the signal to be probed is brought to interference with a reference wave derived from the same source (the local oscillator) by mixing both at a beam splitter. A key advantage of this scheme is sensitivity to the relative phase between the signal and the reference. Moreover, a coherent amplification of the signal of interest is accomplished using a sufficiently strong local oscillator, although shot-noise constraints for weak signals are generally known to remain in place⁴⁶ (Methods).

Analagously, FREHD facilitates the nanoscale probing of microscopic sample responses by an electron beam in a phase-resolved manner and with an added sensitivity to nonlinear sub-cycle temporal evolution. Figure 1 schematically illustrates the principle of the technique. We consider an optical excitation at a frequency ω that induces a response in an investigated specimen, generally containing contributions at both the fundamental driving frequency and its harmonics 2ω, 3ω, …, nω. An electron beam transmitted through or diffracted by the sample experiences a modulation governed by the detailed electronic and structural response to the excitation. For example, a time-periodic variation of the magnitude of the structure factor in a crystalline specimen⁴⁷ leads to amplitude modulation of the electron wavefunction along its propagation direction (Fig. 1, left). By contrast, phase oscillations of the structure factor—as well as localized optical near fields and nonlinear optical polarizations⁴⁸ with vector components along the beam path—result in a longitudinal phase (that is, momentum) modulation of the wavefunction by inelastic electron–light scattering (Fig. 1, right), as leveraged in photon-induced near-field electron microscopy^{11,29,30,31,32} (PINEM).

Fig. 1: Measurement of arbitrary amplitude and phase responses by free-electron homodyne detection.

Optical excitation of an investigated sample at frequency ω, inducing a response at the fundamental driving frequency and its harmonics. A transmitted or diffracted electron beam experiences modulation in its amplitude and/or phase, which traces the response. For example, a modulation of the magnitude of the structure factor $f(\bf{k})$ of a material leads to an amplitude modulation of a diffracted electron wavefunction (left), whereas localized optical fields and polarizations typically result in a phase modulation (right). A second interaction with a local oscillator—serving as a reference or mixer with variable phase—yields antisymmetric and symmetric signals, respectively, in the final electron kinetic energy spectrum, which is measured in this homodyne detection scheme.

Consequently, the electron wavefunction is modulated in its amplitude and/or phase upon traversing a sample plane at velocity v_e. These modulations are characterized by their strength and their phase with respect to the optical carrier wave. Specifically, an nth harmonic modulation of the electron wavefunction amplitude along the propagation direction z is described by multiplication with $[1+| {a}_{n}| \sin (n\omega z/{v}_{{{{\rm{e}}}}}+{\phi }_{a,n})]$. This modulation is fully determined by the complex coefficient ${a}_{n}=| {a}_{n}| \exp ({{{{i}}}}{\phi }_{a,n})$. Similarly, phase modulation is described by the complex coefficient ${g}_{n}=| {g}_{n}| \exp ({{{{i}}}}{\phi }_{g,n})$, which corresponds to multiplication of the electron wavefunction by $\exp [-2{{{{i}}}}| {g}_{n}| \sin (n\omega z/{v}_{{{{\rm{e}}}}}+{\phi }_{g,n})]$. Generally, combinations of both types of modulation at different harmonics are possible, and probably occur in diffractive probing of strongly light-driven charge densities^17,20. In the past, electron phase modulation was primarily considered, typically resulting in multiple higher-order sidebands in the electron energy spectrum^{11,29,32,49,50,51,52}. Yet, in direct analogy to radiofrequency technology, amplitude modulation is expected to produce a single pair of energy sidebands for each harmonic.

For illustration, we consider the sample responses g and a at the fundamental frequency only (dropping the index n). In the limit of weak interactions, these responses generate electron energy sidebands with populations P_±1 ∝ ∣g∣², ∣a∣² (for ∣g∣, ∣a∣ ≪ 1), which are separated from the initial beam energy by ±ℏω (refs. ^29,30,31,32). We are now interested in the quantitative and phase-resolved determination of these modulations, which constitute the attosecond sample response. This is achieved by inducing a subsequent coherent and phase-controllable light interaction with the electron beam, which serves as a local oscillator (that is, a reference) for the electron wavefunction modulations. Either amplitude or phase modulation could be used as the local oscillator, but, for simplicity and experimental practicality (that is, readily available through PINEM), we consider a phase-modulating local oscillator g_ref with a controllable phase ${\phi }_{{{{\rm{ref}}}}}=\arg \{{g}_{{{{\rm{ref}}}}}\}$. The local oscillator leads to final-state interference in the electron energy sidebands, in distinctive manners for amplitude and phase modulations. Specifically, the symmetric (S) and antisymmetric (A) components of the first-order sideband populations directly encode the phase- and amplitude-modulation response of the material, respectively. Approximated to first order in the strength of the reference, these independent FREHD signals become

$$S={P}_{+1}+{P}_{-1}\propto | g| | {g}_{{{{\rm{ref}}}}}| \cos \left({\phi }_{{{{\rm{ref}}}}}-{\phi }_{g}\right)+{{{\rm{const.}}}}$$

(1a)

$$A={P}_{+1}-{P}_{-1}\propto | a| | {g}_{{{{\rm{ref}}}}}| \cos \left({\phi }_{{{{\rm{ref}}}}}-{\phi }_{a}\right)+{{{\rm{const.}}}}$$

(1b)

These complementary dependencies arise from the varying symmetries of the complex sideband amplitudes produced by amplitude and phase modulation, as derived in Methods (see also Extended Data Fig. 1). A generalization of these expressions to arbitrary harmonic responses and references requires the application of free-electron quantum state reconstruction, as recently introduced in refs. ^35,53.

From a fundamental viewpoint, the described approach exploits the quantum coherence of sequential interactions with free-electron beams, which were previously demonstrated in the context of Ramsey-type phase control⁵⁴, used for the quantitative measurement of attosecond electron pulses³⁵, and underlined recent demonstrations of cathodoluminescence interference from sequential scatterings⁵⁵. Analogously, sequential interactions have been employed to create energy-filtered holograms of travelling surface plasmons⁵⁶. Harnessing such phase-locked interactions in a universally applicable microscopy scheme to retrieve sub-cycle information requires both high spatial resolution and a controlled means of varying the phase of the local oscillator in a way that is independent of the sample under investigation. In essence, such a technique must combine free-electron quantum state reconstruction (achieved so far only for collimated beams³⁵) with high spatial resolution.

Implementation of FREHD at high spatial resolution

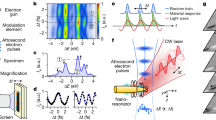
Next, we experimentally implement and demonstrate FREHD for resolving the plasmonic near-field evolution at a gold nanoprism with sub-cycle temporal (that is, phase) resolution using a 5 nm probe beam. The measurements are conducted at the Göttingen ultrafast transmission electron microscope (UTEM), which is equipped with a laser-triggered electron gun that generates photoelectron pulses for the femtosecond probing of structural, magnetic and optical excitations¹². Figure 2 illustrates the geometry employed in the experiment. As a key element, a custom-designed double specimen holder allows for the positioning of a reference membrane sample in proximity (here: 210 μm) below the specimen under investigation. (We note that placing the reference above the sample is of course equally possible. Generally, however, dispersive effects must be considered, which will differ in both scenarios.) Using a piezo actuator between the two arms of the double holder, the distance z between the sample and the reference membrane can be precisely controlled, as shown in Fig. 2a,b. A laser beam incident at −6° relative to the axis of the TEM column illuminates both the sample and reference, which are traversed by the 200 keV electron beam focused on the sample to a spot size of about 5 nm. The surface normal of the sample plane is tilted by about 13.2° from the electron beam, and away from the incident laser beam (Fig. 2c). This ensures that the optical phase fronts propagating at the vacuum speed of light match the modulations of the electron wavefunction, propagating at the electron group velocity v_e ≈ 0.695c₀ (refs. ^36,49,57). Thus, in the plane of the reference membrane (Fig. 2d), each part of the weakly conical electron beam interacts with the same optical phase.

Fig. 2: Implementation of FREHD at high spatial resolution.

a, Schematic of a focused electron beam and co-propagating laser beam traversing the sample and reference. A dedicated dual-plane holder allows for an independent vertical displacement of the reference (here, a silicon membrane). b, Side view of the piezo-controlled holder. c,d, Geometry of the experimental configuration (c). Focused to a 5 nm spot size at the sample, the electron beam has diverged to a beam diameter of about 13 μm at the reference. The sample is tilted by a predetermined angle to ensure electron–light phase matching. In this way, the phase fronts of the laser light and of the modulated electron wavefunction are matched at the reference membrane (see d). e, Top: stimulated inelastic scattering at an investigated nanostructure (here, a plasmonic nanoprism) leads to quantum-coherent electron phase modulation. The displacement of the reference plane controls the phase of the reference interaction ϕ_ref and the resulting final sideband populations. Bottom: the magnitude of the total phase modulation is measured by raster scanning, recording kinetic energy spectra at each in-plane position and for a set of reference phases. These interferograms yield a spatial map of the complex phase modulation induced by the sample.

As a model system to study nanometric optical excitations⁵⁸, we use a colloidal triangular gold nanoprism with a thickness of about 7 nm and a side length of 100 nm. Inelastic electron–light scattering at the optical near field of the nanoparticle induces a PINEM-type electron phase modulation with a spatially dependent coefficient g that is proportional to the local longitudinal electrical field E_z (Methods)^30,31. In scanning TEM, we raster the focused electron probe across the investigated gold nanoprism, and an electron kinetic energy spectrum is measured at every position to image the spatial distribution of the optical near field.

For a given point in the scanning routine, we observe an interaction-induced sinusoidal modulation of the electron wave with the reference phase, as sketched in Fig. 2e. This results from the coherent superposition of light–electron interactions taking place at the sample (coupling coefficient g) and at the reference membrane (coupling g_ref). Importantly, both modulations add up coherently⁵⁴ in the total coupling coefficient g_total = g + g_ref. The magnitude ∣g_total∣ of the total modulation governs the magnitude and number of populated sidebands and is directly obtained from fits to the measured spectra (Methods).

As the electron group velocity and the light phase velocity differ, changing the position of the reference plane Δz modifies the phase of the reference, which allows for cycling through constructive and destructive interference of both actions (2π phase change for Δz = 2.1 μm). We record electron spectra in raster scans of the sample plane for a discrete set of reference phases across a complete cycle, selected by displacements of the second membrane. These measurements yield a stack of ∣g_total∣ maps as a function of the reference phase (Fig. 2e).

Recording a complete interferogram (total electron–light coupling strength as a function of relative phase) for every lateral position yields

$$| {g}_{{{{\rm{total}}}}}{| }^{2}=| g{| }^{2}+| {g}_{{{{\rm{ref}}}}}{| }^{2}+2\,\gamma \,| g| | {g}_{{{{\rm{ref}}}}}| \cos \left({\phi }_{g}-{\phi }_{{{{\rm{ref}}}}}\right),$$

(2)

where ϕ_g − ϕ_ref denotes the phase difference between g and g_ref. A coherence factor (0 ≤ γ ≤ 1) is introduced here to account for imperfect interference conditions arising from amplitude or phase averaging (for example, due to polychromaticity of the laser during the two interactions, as shown in Extended Data Fig. 2, the finite size of the probe, dispersion effects and deviations from perfect velocity matching at different propagation angles). Strictly speaking, dispersive propagation between the interactions planes, leading to attosecond electron bunching^{33,35,36,37,39}, needs to be taken into account, but this only represents a small correction at the propagation distances and field strengths considered.

Attosecond evolution of a nanometric plasmonic field

Figure 3a shows images of the measured total interaction strength at four fixed reference phases across the full cycle. The interference of different plasmonic modes in the nanoprism leads to lobes and nodes at the nanoprism edge and centre. These features are generally aligned to the main axis of the weakly elliptical incident laser polarization (indicated in Fig. 3a, top left). Moderate birefringence in the pump beam path of the electron microscope leads to an ellipticity of the incident radiation on the nanoprism of about 0.25 ± 0.05, which we estimate by comparison with the simulation. It is apparent that the intensity of the lobes varies during the interference cycle, and maxima appear at different locations. Figure 3b displays phase-dependent total coupling strengths for the positions indicated both in Fig. 3a (bottom right) and in the dark-field image in Fig. 3c. The complex coupling coefficients are retrieved from fits to equation (2) at each pixel (solid lines in Fig. 3b). A uniform magnitude and phase of the reference (∣g_ref∣ = 0.370 ± 0.004, ϕ_ref = ± 0.1 rad), as well as a single coherence factor γ = 0.67, describe the entire dataset well. We obtain a coupling coefficient with ∣g∣ = 0.281 ± 0.017 and $\phi =(1.64\pm 0.034)\,{{{\rm{rad}}}}\widehat{\,=\,}(836\pm 18)\,{{{\rm{as}}}}$ in the peak of the excited plasmon mode (dark blue curve in Fig. 3b). The typical uncertainty in the phase determination at a single pixel in the region of the plasmonic peaks is about 45 mrad.

Fig. 3: Recorded FREHD interferograms for an optically excited gold nanoprism.

a, Spatial scans of the magnitude of the total phase modulation for four different values of the reference phase ϕ_ref. b, Interferograms (∣g_total∣² as a function of relative phase) at the pixel positions indicated by the colour-coordinated dots in a (bottom right) and c (solid lines, sinusoidal fits). c, Dark-field image of the nanoprism.

Figure 4 displays the complex response of the nanoprism in terms of its magnitude (Fig. 4a) and complex amplitude (Fig. 4b). Here, the depicted phase is shown relative to that of the silicon nitride (Si₃N₄) membrane supporting the nanostructure, and the substrate’s small uniform background coupling coefficient $g_{\rm{Si}_3N_4}$ = 0.091 is subtracted. The measurement clearly shows that the local maxima of the optical near field exhibit different optical phases. As they represent the complete information about the field, these measurements can be depicted in a time-domain sequence (Fig. 4c), illustrating the real part of the out-of-plane optical electric field ${E}_{z}\propto | g| \cos ({\phi }_{g}-\omega t)$ as frames of an attosecond movie. Notably, the handedness of the elliptical laser polarization appears as a time-dependent rotation of the maxima around the nanoprism.

Fig. 4: Measured electric field evolution at a gold nanoprism.

a,b, The interferogram analysis in Fig. 3 yields the magnitude (a) and complex amplitude (b) of the sample-induced phase modulation g. c, Temporal sequence of the out-of-plane electric field evolution within the optical cycle. d–f, Corresponding measurement for a weakly elliptical polarization state with the major axis rotated by 90°. The most pronounced maxima in both measurements are clearly aligned with the polarization angle. See Supplementary Videos 1 and 2 for the complete temporal evolution shown in c and f.

We repeat these measurements for an orthogonal incident polarization state, that is, with a rotation of the major polarization axis by 90° (Fig. 4d–f) and the opposite helicity, which clearly lead to pronounced oscillations along different axes of the nanoprism and an inversion of the apparent rotation angle of the near-field features. The experimental characterization of these complex electric near fields for two non-collinear polarizations constitutes a full polarization-dependent characterization of the near-field optical response. Hence, near fields resulting from arbitrary incident polarization states are immediately retrieved by a corresponding linear combination of these two measurement results.

Discussion

In the broader area of phase-resolved near-field imaging using scanning probe techniques^59,60,61, photoelectron emission^22,62,63, electron deflection⁶⁴ and Lorentz microscopy of optical fields⁴¹, as well as the control of quantum emitters⁶⁵, FREHD has a set of unique strengths. It is non-invasive, perfectly linear in its response, and allows for consistently high and practically sample-independent spatial resolution, which can be further correlated with detailed structural characterization of the specimen down to the atomic scale. Due to the direct dependence of the sideband populations on the electric field strength, FREHD can also provide calibrated quantitative values of the local field. Several spatial Fourier components of the field along the beam path would be required to determine the spatial field decay away from the structure, which could be attained by measurements at different electron velocities. Moreover, several propagation angles could be combined in a tomographic approach of the vectorial near field^63,66. A full reconstruction of the vectorial near field in three dimensions seems possible if using such data in conjunction with further physical constraints such as Maxwell’s equations and boundary conditions. Furthermore, the technique can be applied to recover sub-cycle fundamental and higher-harmonic phase profiles of any local field distribution, including orbital angular momentum states and topological near fields such as vortices²², skyrmions⁶³ and merons⁶⁷.

The approach is not limited to electromagnetic fields, but will rather detect any modulation imprinted onto an electron beam by an electronic or structural material response. Notably, this covers attosecond charge-density dynamics causing subtle light-driven changes of the structure factor⁴⁷ at the fundamental frequency and its harmonics. Extended Data Fig. 1 details the spectrally symmetric and antisymmetric contributions of amplitude and phase modulations at the fundamental and second-harmonic frequencies. The resulting characteristic phase-dependent signatures allow for an unambiguous determination of different amplitude and phase modulations, providing, for example, a retrieval of nonlinear polarizations⁴⁸, partial coherence or a complete quantum state reconstruction of free-electron density matrices^35,53.

Detecting such small modulations is facilitated by the intrinsic coherent amplification of the signal by the local oscillator, which follows from the linear (rather than quadratic) scaling of the sideband populations with modulation amplitude. For example, a weak modulation of g = 0.01—leading to only a P₁ ≈ 0.01% sideband population in the absence of a reference—can be amplified to an interferogram with sideband populations varying by 16.8% ± 0.6% (g_ref = 0.45). Depending on experimental conditions, such considerable amplifications render the detection of very weak objects feasible by overcoming given levels of background or detector noise. Broadly speaking, FREHD will greatly simplify reaching shot-noise (or quantum) limited detection of small signals. In direct analogy to optical homodyne detection⁴⁶ or interferometric single biomolecule imaging⁶⁸, under perfect detection conditions, the technique does not overcome the fundamental signal-to-noise limits of how many electrons are required to quantify the strength of a weakly scattering object (see considerations in Methods). Pixelated event-based detection, as utilized in our work, approaches unity quantum efficiency and features a practical absence of read and dark noise. Nonetheless, even with such detectors, physical backgrounds stemming from, for example, elastic and inelastic scattering cannot be completely avoided. Hence, there is a substantial practical advantage offered by coherent signal amplification, analogously to optical interferometric scattering microscopy⁶⁹. Ultimately, besides the benefit of phase sensitivity, these features may bring individual quantum systems, such as molecules, atoms or colour centres, closer to spectroscopically enhanced detection in electron microscopy.

In the present implementation, we measured quasi-periodic signals with a well-defined carrier frequency in a phase-resolved manner. In general, the approach can be translated to the detection of isolated attosecond responses of materials spanning a single optical cycle or less. To this end, the optical excitation and ideally also the electron pulse should be shorter than a single cycle, with a correspondingly large bandwidth. In this case, the measurement of sideband amplitudes would be replaced by overall shifts in the then continuous electron energy spectrum.

In conclusion, we present a general approach for attosecond phase-resolved electron microscopy at few-nanometre spatial resolution. Quantitative detection of wavefunction modulations imprinted onto a focused electron probe is achieved using a phase-matched local oscillator interaction at a movable reference plane. FREHD generalizes the high-resolution measurement of attosecond materials responses in electron microscopy, without a need for electron density bunching, and represents a first realization of a larger class of possible multidimensional optical spectroscopies that may enable the local readout of couplings, correlations and decoherence.

Methods

Samples and piezo double holder

The top sample consists of colloidal gold nanoprisms⁷⁰ drop cast onto a 50-nm-thick standard Si₃N₄ TEM membrane with a window size of 100 μm. The solution consists of nanoprisms with varying geometries, having slightly heterogeneous sizes and shapes with a typical thickness of about 7 nm. The nanoprism investigated in our experiments exhibits a side length of about 100 nm. Characterization via electron energy-loss spectroscopy in conventional TEM mode (continuous electron emission) identifies the energy of the edge and centre modes at 1.58 eV (785 nm) and 1.82 eV (681 nm), respectively. The corresponding spectra (Extended Data Fig. 3a) and maps at different energies (Extended Data Fig. 3b) are shown together with two dark-field micrographs (Extended Data Fig. 3c,d). The zero-loss peak has been deconvolved to reveal low-energy losses.

The bottom reference sample is a plain standard single-crystalline silicon membrane with a thickness of 30 nm and a window size of 500 μm. It acts like a mirror and produces a homogeneous reference near field. The reference sample is positioned 215 μm below the top sample membrane in a custom-designed double holder and can be translated by 2.2 μm relative to the top sample along the membrane’s normal (z-direction) by a preloaded, voltage-controlled piezo actuator.

Experimental geometry

The nanoprism sample and the reference plane are probed simultaneously in scanning TEM mode with 30 mrad semi-convergence angle of the electron beam, which is focused down to a 5 nm spot diameter on the nanoprism. These focussing conditions lead to an electron beam diameter of about 12.9 μm on the reference membrane.

The sample and reference planes are both excited with a laser incident at an angle of −6° relative to the electron beam axis. The whole sample holder is tilted along the holder axis by 13.2° from the perpendicular orientation to the electron beam axis (see Fig. 2c) to match the phase velocity of the laser excitation and the group velocity of the 200 keV electrons, resulting in a spatially homogeneous optical reference phase along directions normal to the electron beam.

Ultrafast transmission electron microscopy

The experiments were performed at the Göttingen UTEM¹². Photoelectron pulses are generated from a thermal Schottky field emitter tip using femtosecond laser pulses^12,71,72 (centre wavelength = 515 nm, pulse duration = 150 fs and repetition rate = 2 MHz) and accelerated to 200 keV. The electron pulse duration at the sample plane is governed by Coulomb interaction^73,74 leading to about 200 fs pulses under the given laser conditions. Laser excitation of the sample is provided by tunable-wavelength femtosecond pulses from an optical parametric amplifier (here at 960 nm central wavelength and 105 cm⁻¹ bandwidth) and polarization control via retarding quarter and half waveplates. To provide a time-homogeneous excitation for the duration of the electron pulses, the excitation pulses are stretched to a duration of about 600 fs using a dispersive SF6 glass rod (group delay dispersion (GDD) = 29,200 fs²). The resulting kinetic energy spectrum of the electrons induced by inelastic electron–light scattering is dispersed by a magnetic prism and recorded for each scanning position (pixel dwell time = 30 ms) with a hybrid pixel detector.

The acquisition of 64 px × 64 px with a short dwell time for the recording of the spectrum of 30 ms takes roughly 3 min per image and 50 min in total to record the full interference cycle at 16 different ϕ_ref. The resulting dataset consists of 65,536 spectrograms.

Homodyne detection of sub-cycle light-driven dynamics

Pump–probe studies of field-driven dynamics are usually performed by combining a harmonic optical excitation (light frequency ω) with probing pulses of durations below the optical cycle T = 2π/ω (for example, isolated pulses or pulse trains in the optical domain^7,75, and recently attosecond electron pulse trains^{35,36,37,44,76}). Sub-cycle light-driven dynamics can also be probed by reconstructing the full quantum state of a system using coherent excitation and probing schemes, thus giving access to its full temporal evolution, as performed for interferometric frequency-resolved optical gating or reconstruction algorithms such as SQUIRRELS for electrons³⁵. This concept is essential for FREHD (Fig. 1), which probes complex light-driven dynamics at the nanoscale by coherently modulating the electron wavefunction both at a sample (coupling g) and at a reference (coupling g_ref).

The near-field distribution $\bf{E}(x,y,z,t)={{{\rm{Re}}}}\,\{\bf{E}(x,y,z){\rm{e}}^{-{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}\}$ imprints a sinusoidal phase modulation onto the incident electron wavefunction Ψ_inc(z), such that the post-interaction wavefunction becomes

$${{{\varPsi }}}_{g}(z)=\exp \left[2{{{{i}}}}| g| \sin \left(\frac{\omega }{{v}_{{{{\rm{e}}}}}}z+{\phi }_{g}\right)\right]\ {{{\varPsi }}}_{{{{\rm{inc}}}}}(z),$$

(3)

where we work in the interaction picture. The interaction is described by the complex coupling parameter

$$g(x,y)=\frac{\rm{e}}{2\hslash \omega }\int\nolimits_{-\infty }^{\infty }{E}_{z}(x,y,z){\rm{e}}^{-{{{{i}}}}\omega \frac{z}{{v}_{{{{\rm{e}}}}}}}{{{\rm{d}}}}z,$$

(4)

which represents the spatial Fourier transform of the optical field along the electron beam direction at a spatial frequency ${{\Delta }}k=\frac{\omega }{{v}_{{{{\rm{e}}}}}}$, where v_e is the electron velocity^30,31. Incidentally, we define ${\phi }_{g}\equiv \arg \{-g\}$. Using the Jacobi–Anger relation, the electron wavefunction after inelastic electron–light scattering is made up of discrete sidebands labelled by an integer number N with each of them having an amplitude given in terms of a Bessel function J_N as³¹

$${{{\varPsi }}}_{g,N}={J}_{N}(2| g| ){\rm{e}}^{{{{{i}}}}N{\phi }_{g}}.$$

(5)

The total transmitted electron probability P is the same of contributions arising from the discrete harmonic sidebands as

$$P=\mathop{\sum }\limits_{N=-\infty }^{\infty }{P}_{N}=1,$$

(6)

where ${P}_{N}=| {{{\varPsi }}}_{g,N}{| }^{2}={J}_{N}^{2}(2| g| )$ is the intensity of sideband N. Obviously, ∣Ψ_g(z)∣ = 1 for all values of z, so there is only phase modulation of the electron density.

In the weak coupling regime (g ≪ 1), the wavefunction reduces to

$$\begin{array}{ll}{{{\varPsi }}}_{g}(z)&\approx \left[1+2{{{{i}}}}| g| \sin (\omega z/{v}_{{{{\rm{e}}}}}+{\phi }_{a})\right]\ {{{\varPsi }}}_{{{{\rm{inc}}}}}(z)\\ &=[1+g\,{\rm{e}}^{{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}-{g}^{* }{\rm{e}}^{-{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}]\ {{{\varPsi }}}_{{{{\rm{inc}}}}}(z),\end{array}$$

(7)

where the asterisk denotes the complex conjugate and we recover the Ψ_g,N coefficients for N = ± 1.

A situation in which we have amplitude modulation can be represented by a scattered wavefunction analogous to equation (3),

$${{{\varPsi }}}_{a}(z)=\exp \left[2| a| \cos \left(\frac{\omega }{{v}_{{{{\rm{e}}}}}}z+{\phi }_{a}\right)\right]\ {{{\varPsi }}}_{{{{\rm{inc}}}}}(z),$$

(8)

but now ∣Ψ_a(z)∣ oscillates with z, in contrast to ∣Ψ_g(z)∣. For weak coupling (a ≪ 1), we have

$$\begin{array}{ll}{{{\varPsi }}}_{a}(z)&\approx \left[1+2| a| \cos (\omega z/{v}_{{{{\rm{e}}}}}+{\phi }_{a})\right]\ {{{\varPsi }}}_{{{{\rm{inc}}}}}(z)\\ &=[1+a\,{\rm{e}}^{{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}+{a}^{* }{\rm{e}}^{-{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}]\ {{{\varPsi }}}_{{{{\rm{inc}}}}}(z),\end{array}$$

(9)

where $a=| a| {\rm{e}}^{{{{{i}}}}{\phi }_{a}}$. Note that the function $\cos \left(\frac{\omega }{{v}_{{{{\rm{e}}}}}}z+{\phi }_{a}\right)$ in equation (8) is general for harmonic modulation (for example, a sine modulation could be accommodated by redefining the phase ϕ_a).

To consider homodyne interferometric detection, we introduce a reference interaction characterized by a coupling coefficient g_ref that produces a phase modulation factor given by equation (7) with g substituted by g_ref. The total wavefunction resulting from the combination of all of these modulations (phase, amplitude and reference) can be understood as the convolution of different sidebands or, equivalently, it is the result of multiplying the incident wavefunction Ψ_inc(z) by a factor $\exp \left[2{{{{i}}}}| g| \sin (\omega z/{v}_{{{{\rm{e}}}}}+{\phi }_{g})+2| a| \cos (\omega z/{v}_{{{{\rm{e}}}}}+{\phi }_{a})+2{{{{i}}}}| {g}_{{{{\rm{ref}}}}}| \sin (\omega z/{v}_{{{{\rm{e}}}}}+{\phi }_{{g}_{{{{\rm{ref}}}}}})\right]$. Under the assumption of weak interactions, we Taylor-expand this expression again and retain only first-order terms in the exponent, so the total modulated wavefunction reduces to

$${{{\varPsi }}}_{{{{\rm{total}}}}}(z)\approx \left[1+(a+g+{g}_{{{{\rm{ref}}}}})\,{\rm{e}}^{{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}+{(a-g-{g}_{{{{\rm{ref}}}}})}^{* }{\rm{e}}^{-{{{{i}}}}\omega z/{v}_{{{{{\rm{e}}}}}}}\right]\ {{{\varPsi }}}_{{{{\rm{inc}}}}}(z).$$

The intensities of the first gain and loss sidebands (evolving as ${\rm{e}}^{{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}$ and ${\rm{e}}^{-{{{{i}}}}\omega z/{v}_{{{{\rm{e}}}}}}$ in the wavefunction, respectively) are then

$$\begin{array}{l}{P}_{+1}=| a+g+{g}_{{{{\rm{ref}}}}}{| }^{2},\\ {P}_{-1}=| a-g-{g}_{{{{\rm{ref}}}}}{| }^{2},\end{array}$$

which produce the signals

$$S={P}_{+1}+{P}_{-1}=4| g| | {g}_{{{{\rm{ref}}}}}| \cos ({{\phi }}_{{{{\rm{ref}}}}}-{{{\phi }}}_{g})+{{{\rm{constant}}}},$$

(10a)

$$A={P}_{+1}-{P}_{-1}=4| a| | {g}_{{{{\rm{ref}}}}}| \cos ({{\phi }}_{{{{\rm{ref}}}}}-{{{\phi }}}_{a})+4| a| | g| \cos ({{{\phi }}}_{g}-{{{\phi }}}_{a})+{{{\rm{constant}}}}$$

(10b)

in symmetric and antisymmetric detection channels. For a generic system in which both phase- and amplitude-modulation interactions are present, the symmetric channel thus allows obtaining the phase ϕ_g of the phase modulation component through equation (10a), and once this is determined, the antisymmetric channel (equation (10b)) can be used to retrieve ϕ_a. To simplify the discussion, in the main text we consider symmetric detection of phase-only modulation and antisymmetric detection of amplitude-only modulation (see equation (1a)).

This formalism can be depicted in quantum phase space and generalized to describe amplitude modulations, as shown in Extended Data Fig. 1. Different types of coherent sample interactions lead to phase-dependent signals, either in the symmetric or antisymmetric detection channels. In quantum phase space, the Wigner distribution W(x, p) describes an electron after optical modulation, with characteristic features arising, such as conjugate symmetric (for example, phase modulation) or symmetric (for example, amplitude modulation) sidebands. The phase-dependent spectrogram after the second interaction, accessible in a measurement, is obtained by convolution of the initial state with the second reference Wigner function W_ref(x, p) as S(E) = W(x, p) ∗ W_ref(x, p), where the asterisk indicates convolution. Noteworthy, dispersive propagation between sample interaction and reference leads to a shearing of W(x, p), which transforms an initial phase modulation into an amplitude modulation of the electron wavefunction, yielding sub-cycle density modulations and attosecond electron pulse trains³². Besides the possibility of a full quantum state reconstruction when combined with SQUIRRELS³⁵, FREHD offers fast and direct access to complex harmonic modulations of the electron state by measuring the symmetric P₁ + P₋₁ or antisymmetric P₁ − P₋₁ detection channels (weak signal and reference).

Fitting of PINEM spectra

The spectrum is described by equation (5), where each sideband is separated by an energy ℏω = 1.29 eV (the laser photon energy) and convolved with a zero-loss peak of the full-width at half-maximum (FWHM) taken as 0.6 eV. We fit each recorded spectrum to find the corresponding value of ∣g_total∣, taking the transmission and a shift of the zero-loss peak as fitting parameters.

Calibration of the reference phase

The reference phase is set by changing the z position of the reference membrane plane with a piezo actuator. The voltage operating the piezo actuator is applied in open-loop mode, requiring a position calibration. For positive voltages, the change in position depends linearly on the applied voltage. However, to extend the maximum range of motion in this experiment, we also operate the piezo at negative voltages, leading to a nonlinear dependence at the zero-voltage crossing, which is corrected during calibration using an error function in the range of the zero crossing. We calibrate both the width of the error function and the proportionality of the adjusted voltage to the resulting phase from a measurement with 61 phase steps between 0 and 2π. This calibration is evaluated in a region clearly separated from the nanoprism on the plain Si₃N₄ membrane, as shown in Extended Data Fig. 4. The proportionality and phase offset are determined by fitting a sinusoidal function to the measured interferogram, excluding data points at negative and low voltages (<20 V). The width of the error function is determined such that the measured values at negative and low voltages lie on the extrapolated sinusoidal fit.

Interferogram visibility

Geometric constraints and imperfections in the experiment are a source of phase averaging, and limit the visibility of the interferogram. These include minor deviations from perfect velocity matching at different propagation angles and finite size of the probe. Moreover, for the given excitation conditions with a chirped laser pulse, the coherence factor is reduced by the fact that the electrons interact with the pulse at two different times along its envelope. Consider laser pulses with a transform-limited pulse duration $\tau =\frac{{{{{\rm{FWHM}}}}}_{{{{\rm{Intensity}}}}}}{\sqrt{2\ln 2}}$ and an electric field envelope $e(t)={\exp }^{-{(t/\tau )}^{2}}$. Adding GDD to this pulse results in a time-dependent frequency, with the linear chirp given by $\omega (t)={\omega }_{0}+\frac{2C}{{\tau }_{C}^{2}}(t-{t}_{0})$, with the chirp parameter $C:=\frac{2{\phi }^{{\prime}{\prime}}}{{\tau }^{2}}$ and the chirped pulse length ${\tau }_{C}:=\tau \sqrt{1+{C}^{2}}$. The chirp parameter relates to the GDD by C = 2GDD/τ². The time-dependent phase ϕ(t) is given by

$$\begin{array}{l}\displaystyle \phi (t)=\int\,{{{\rm{d}}}}{t}^{{\prime} }\omega (t)=\int\,{{{\rm{d}}}}{t}^{{\prime} }{\omega }_{0}+\frac{2C}{{\tau }_{C}^{2}}{t}^{{\prime}}\\ \phi (t)={\omega }_{0}t+\dfrac{C}{{\tau }_{C}^{2}}{t}^{2}+{{{\rm{const.}}}}\end{array}$$

Each electron interacts two times with this electric field at the first and the second interaction plane. The time difference of these interactions with respect to the envelope results from the difference of electron group velocity and the light phase velocity co-propagating over the separation distance ${d}^{{\prime} }$.

$${{\Delta }}t=\frac{{d}^{{\prime} }}{{c}_{0}}\left(1-\frac{1}{{v}_{{{{\rm{e}}}}}/{c}_{0}}\right)$$

This time difference is fixed for all electrons in the pulse. However, as a result of the linear chirp of the laser pulse, the experienced phase difference between both interactions will vary for electrons arriving at different times with respect to the laser pulse envelope. The phase difference of the electric field at two times separated by Δt is given by

$$\begin{array}{l}\displaystyle {{\Delta }}\phi =\phi (t+{{\Delta }}t)-\phi (t)\\ {{\Delta }}\phi ={\omega }_{0}{{\Delta }}t+\dfrac{C}{{\tau }_{C}^{2}}({{\Delta }}{t}^{2}+2t{{\Delta }}t)\\ {{\Delta }}\phi =\dfrac{2C}{{\tau }_{C}^{2}}t{{\Delta }}t+{{{\rm{const.}}}}\\ {{\Delta }}\phi =\dfrac{t{{\Delta }}t}{\left(\frac{{\tau }^{4}}{4 {{{\rm{GDD}}}}}+{{{\rm{GDD}}}}\right)}+{{{\rm{const.}}}}\end{array}$$

The ensemble of electrons within the electron pulse is well described by a Gaussian pulse where the arrival time of the electron follows a normal distribution

$${t}_{{{{\rm{electron}}}}} \approx {{{\mathcal{N}}}}\left(0,{\sigma }_{{{{\rm{electron}}}}}^{2}\right).$$

In the experiment, we measure the ensemble and thus the cosine of phase differences

$$\begin{array}{l}\displaystyle {{\Delta }}\phi \approx {{{\mathcal{N}}}}\left(0,{\sigma }_{{{\Delta }}\phi }^{2}\right)\\ {\sigma }_{{{\Delta }}\phi }=\dfrac{2C}{(1+{C}^{2})}\dfrac{{{\Delta }}t}{{\tau }^{2}}{\sigma }_{{{{\rm{electron}}}}}\end{array}$$

The resulting contrast is given by the expectation value of the cosine

$$\gamma ={\mathbb{E}}[{I}_{{{{\rm{interference}}}}}]={\mathbb{E}}[\cos {{\Delta }}\phi ]={\rm{e}}^{-{\sigma }_{{{\Delta }}\phi }^{2}/2}.$$

(11)

For our experimental parameters with a bandwidth-limited laser pulse duration of 140 fs (FWHM), a GDD of 29,200 fs², and an electron pulse length of 200 fs (FWHM), we obtain a coherence factor γ = 0.69.

Boundary element method simulation

Electrodynamic simulations of the coupling coefficient g are performed using a boundary element method⁷⁷ (BEM) as implemented in the MNPBEM17 Matlab toolbox⁷⁸. For a metallic nanostructure of volume V delimited by a boundary ∂V and illuminated by a laser, the coupling coefficient in equation (4) can be written in terms of surface boundary sources as (H.L.-M. et al., manuscript in preparation)

$$g(\bf{R},\omega )=\frac{\rm{e}}{2\hslash \omega }{\displaystyle\oint }_{\partial V}{{{{\rm{d}}}}}^{2}\bf{s}\ U(\bf{s})\left[\frac{\omega }{c_0}{h}_{z}(\bf{s})-{q}_{z}\sigma (\bf{s})\right],$$

(12)

where c₀ is the speed of light in vacuum, U is an electron-generated scalar potential-like function, σ is the charge density and $h_z$ is the z-component of the current density induced at the nanostructure boundary, as obtained from BEM, and the electron velocity is taken along z. The nanoprism shape is extracted from experimental dark-field images using a distance regularized level set evolution algorithm (DRLSE)⁷⁹ that renders the 3D meshed surface shown in Extended Data Fig. 5a. We neglect the presence of the substrate, but incorporate it by redshifting the excitation and model the metal response through its frequency-dependent permittivity taken from optical data⁸⁰. The structure is illuminated by a light plane wave with an incidence angle of 20° with respect to the nanoprism normal, an amplitude of 0.08 V nm⁻¹ and a wavelength of 560 nm. This wavelength differs from the one used in experiment because the absence of the substrate in the simulations causes a blue shift of the plasmonic resonances. The solution of the full retarded Maxwell equations plugged in equation (12) leads to the maps shown in Extended Data Fig. 5b,c. We obtain a good qualitative agreement with the experimental data, although some discrepancies are to be expected due to the imprecise knowledge of the exact experimental parameters, for example geometry and exact resonance frequency of the sample, as well as angle and polarization of the excitation.

Shot-noise-limited detection of weak scatterers using FREHD

In light of the coherent amplification of weak signals discussed by us⁴² and others^43,81, it is instructive to discuss the role of shot noise in quantum-limited detection. Consider an electron scattering channel (for example, a PINEM sideband) characterized by a small amplitude g_total and a probability ∣g_total∣² ≪ 1. For N incident electrons, the expectation value of the number of counts in that channel is P = N∣g_total∣² with a standard deviation ${{\Delta }}P=\sqrt{N}| {g}_{{{{\rm{total}}}}}|$ associated with the corresponding Poissonian distribution. In a homodyne measurement approach^45,82, g_total = g + g_ref is the sum of an unknown specimen amplitude g and a known reference g_ref (added, for example, through a second coherent PINEM interaction, as considered in this work). In an experiment, we determine g from the measured P as $g=\sqrt{P/N}-{g}_{{{{\rm{ref}}}}}$ (assuming g and g_ref to be real and positive for simplicity), which is measured with an uncertainty ${{\Delta }}g\approx {{\Delta }}P/2\sqrt{NP}$. To determine g with precision η, we set Δg = ηg, which, using the equations above, leads to a number of incident electrons

$$N=\frac{1}{4{\eta }^{2}{g}^{2}}.$$

(13)

This amounts to N ≈ 2,500 required electrons for identifying a weak scatterer with g = 0.1 (that is, 1% scattering probability into the first sideband) at 10% precision (that is, η = 0.1). As N is independent of g_ref, it is evident that the homodyne approach does not reduce the number of electrons required to detect the weak signal under perfect shot-noise-limited conditions. Nonetheless, the above-mentioned substantial advantages under real conditions remain.