Main

Constantly promoting yield strength is a symbol of progress in advanced high-strength metallic materials1. However, a gain in yield strength is normally accompanied by a sacrifice in ductility2,3. In general, our goal is to raise the yield strength as much as we can and retain ductility as much as possible. Ductility depends on the work-hardening ability arising from dislocations to interact among themselves for the conventional forest hardening and with diverse microstructural heterogeneities to trigger further work hardening4, including nanoprecipitates5, nanotwins6 and heterointerfaces7, along with martensitic transformation8. The prerequisite for work hardening is dislocation production and accumulation. However, the higher the yield strength, the more difficult it will be to produce and even store dislocations in microstructures. This becomes pronounced particularly in alloys with an ultrahigh yield strength (UHYS), usually around 2 GPa.

Recently, respectable ductility is achieved in some conventional alloys and emerging multi-principal element alloys (MPEAs) with UHYS8,9,10,11,12,13. The low forest-hardening ability is typical of tensile deformation due to the far-inadequate dislocation production. To further intensify work hardening, additional contribution is indispensable by either martensitic transformation8,9 or nanoprecipitation10,11,12,13 or their combination8, promoting to replenish and accumulate the dislocations inside grains. Otherwise, irreversible necking will prematurely happen. Meanwhile, the aforementioned UHYS alloys are either metastable (apt to martensitic transformation8) or full of nanoprecipitates of extremely high density10,11,12,13. However, it is common in most alloys with neither nanoprecipitates nor martensitic transformation. Work hardening remains unsolved if these alloys are strengthened to UHYS levels.

Here we present a unique way of work hardening that harnesses premature necking during Lüders banding to induce the rapid multiplication of dislocations. The VCoNi MPEA is selected as the prototype14,15,16, having the local-chemical-order (LCO) regions as built-in heterogeneities17,18,19,20,21,22. We show that in addition to forest dislocation work hardening, the dislocations further interact with the LCO regions, promoting dislocation accumulation in ultrafine grains (UFGs) and consequently contributing to additional work hardening. Dual hardening effects restrain and stabilize the premature necking in reverse and then promote large ductility. Our results show that the LCO regions can serve as an alternative to nanoprecipitates, offering an opportunity to design and achieve unprecedented mechanical properties.

Microstructure characterization

We obtained the microstructure of face-centred-cubic (fcc)-structured UFGs by thermomechanical processing at 1,173 K for 150 s in the VCoNi alloy, similar to that reported previously20. The fcc UFGs are equiaxed and have an average size (\(\bar{d}\)) of 0.42 μm in the transmission electron microscopy (TEM) image (Fig. 1a). The plates of ordered L12 intermetallic compound (yellow arrows) appear in fcc grains. Figure 1a (inset) shows the superlattice spots (blue arrows) induced by L12 in the selected-area electron diffraction (SAED) pattern. The L12 plate consists of nano-lamellae, including the fcc structure, twin and stacking fault (SF), along with a minor amount of hexagonal close-packed (hcp) structure as seen in the high-angle annular dark-field (HAADF) image (Fig. 1b) and corresponding energy-dispersive X-ray spectroscopy mapping (Supplementary Fig. 1 and Supplementary Notes 1 and 2).

Fig. 1: Microstructure of VCoNi MPEA.
figure 1

a, Bright-field TEM image of equiaxed fcc grains. The yellow arrows denote L12 plates. The inset shows the SAED pattern with the [112] zone axis. The blue arrows indicate the extra reflections by L12. b, HAADF lattice image of one L12 plate, showing the nano-lamellae of fcc, twin and SFs, along with hcp-structured thin layers. Zone axis, [011]. c, Energy-filtered TEM dark-field image showing the LCO regions. The inset shows the SAED pattern. Zone axis, [112]. The blue arrows indicate the diffuse discs of superlattice scattering by LCO regions (one is circled). d, Overlay of two reconstructed lattice images of fcc lattice and LCO regions in green and yellow, respectively (left). GPA map of the data in the left panel (right). The alternative yellow and blue strips indicate the strain-field contrast of LCO regions. In the scale bar, ε denotes the lattice strain.

Full size image

The fcc grains also contain the LCO regions18,20 (Fig. 1c). Recently, the LCO regions have been gradually recognized as inherent heterogeneities in some MPEAs17,18,19,20,21,22. It is noted that we acknowledge the uncertainties and ongoing exploration on the structure of LCO regions23, which, however, should not influence the main conclusions here based on the evidence obtained by current techniques. The LCO regions are visible in fcc grains by using energy-filtered dark-field imaging (Fig. 1c). The statistical average size and volume fraction is 0.65 nm and 4%, similar to those previously reported20. By using the atomic-scale geometric phase analysis (GPA) mapping24, strain fields are determined by reconstructing two lattice images of the fcc matrix and LCO regions via individual reflections in the SAED pattern (Fig. 1c, inset) and overlaying them (Fig. 1d, left). The LCO region shows the strain-field contrast as an alternate yellow and blue stripe on the green fcc matrix in the GPA map20 (Fig. 1d, right).

Mechanical properties

The UFG VCoNi shows a respectable ductility (εu) of 16% and yield strength (σy, lower yield point) of 2 GPa at room temperature (298 K), as evident in the tensile engineering stress–strain (σe–εe) curve (Fig. 2a). Both εu and σy increase to around 20% and 2.2 GPa, respectively, during cryogenic deformation at liquid-helium (4 K) and liquid-nitrogen (77 K) temperatures (Fig. 2b). Here εu is conventionally regarded as the sum of the Lüders band (LB) propagation strain and the uniform strain when the LB arises8. The simultaneous increase in both εu and σy is the common feature during cryogenic deformation in fcc metals and alloys25,26. Importantly, the yield drop followed by a propagating LB consistently appear as an initial plastic response in three tensile curves (Fig. 2a,b (insets) and Supplementary Note 3).

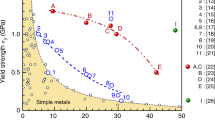
Fig. 2: Mechanical properties and strength–ductility balance at room and cryogenic temperatures.
figure 2

a,b, Tensile engineering stress–strain (σe–εe) curve at room (298 K) (a) and cryogenic (4 and 77 K) (b) temperatures. The square symbol indicates the ductility at the ultimate tensile strength. The inset in a shows an enlarged curve indicating the LB propagation followed by uniform elongation under work hardening. The arrow indicates the LB end. c,d, Yield strength (σy) and ductility (εu) balance at 298 K (c) and 77 and 4 K (d). Other data with UHYS are shown for comparison in c, including MPEAs (pink areas) and steels (blue area).

Full size image

Tailoring the microstructure gains a series of (σy, εu) balances at 298 K (Fig. 2c, seven blue balls). Extended Data Fig. 1 shows the corresponding σe–εe curves, along with the detailed microstructural characterization. These (σy, εu) balances are on par with those in other MPEAs and steels with UHYSs8,9,10,11,12,13,27,28,29,30. The cryogenic (σy, εu) synergy is prominent (Fig. 2d). It indicates that the VCoNi MPEA has suppressed the ductile-to-brittle transition that typically jeopardizes conventional steels usually with a body-centred-cubic and/or martensite phase. In this sense, the VCoNi MPEA combines the signature attribute of established alloys: desirable ductility in fcc alloys, which can be sustained to cryogenic temperatures, along with UHYS values known for advanced high-strength steels. Therefore, the VCoNi MPEA is a good candidate for cryogenic applications that need high strength and large ductility.

Premature necking and plastic responses

We first probed into the deformation physics behind Lüders banding in the present UHYS UFG. The key finding is the localized lateral shrinkage that appears at the LB front obtained from the digital-image-correlation (DIC) tensile test (Supplementary Fig. 2a1,2). The localized shrinkage is characterized by the shrinkage rate, v = (wt – wi)/Δt, where wi and wt are the initial and transient widths of the gauge section, respectively, and Δt is the time interval. The maximum value, vmax, locates at the LB front (Fig. 3a). Here vmax rapidly rises to the peak, then drops soon after yield drop and finally reaches a plateau during LB propagation. The following plateau (Fig. 3a, horizontal dashed line) is due to the Poisson’s ratio effect during uniform elongation. Both vmax peak and plateau during LB propagation are eight and two times that during uniform deformation, respectively, and even higher than that when final necking begins. This indicates that the localized shrinkage is essentially necking that keeps happening during LB propagation. Namely, premature necking has already happened at the LB front, yet with no sign left in the engineering stress–strain curve, unlike usual necking that shows a decrease in flow stress. Further, vmax shows a rapid drop from the peak followed by a stable plateau. This suggests that work hardening has been induced during LB propagation, restraining the premature necking (Supplementary Note 4).

Fig. 3: Premature necking at the LB front, plastic responses and dislocation multiplication.
figure 3

a, Maximum lateral shrinkage rate (vmax) induced by premature necking at the LB front, showing the steep rise to drop followed by the plateau during LB propagation. The dashed line indicates the shrinkage rate during uniform deformation. The square symbol indicates the onset of final diffuse necking. b, Change in stress state in the LB front region, showing three stress components at a tensile strain of 4%. The top and bottom panels show σyy, σxx and σzz along the length, width and thickness directions of the tensile sample, respectively. The arrow indicates the LB propagation direction towards the deformation-free gauge section. c, Change in stress triaxiality (η; top) and von Mises stress (σM; bottom) in the LB front region. The dashed line (top) shows the standard η value (1/3) during uniform deformation. d, Maximum strain gradient (λmax) at the LB front measured by the DIC test. The inset shows a snapshot of the full-field strain distribution at a strain of 4.0%. The arrow shows λmax at the LB front. e, Evolution of dislocation density ρ as a function of tensile strain measured by means of the synchrotron-based high-energy XRD in situ tensile testing. Note the rapid multiplication of ρ from the initial 2.6 × 1013 to 9.7 × 1014 m−2 at the LB front. f, Evolution of mobile dislocation density during uniform deformation (top) and GND density during LB propagation (bottom). For the data in the top panel, mean values ± standard error of the mean are presented on the basis of three stress-relaxation tensile tests.

Full size image

We then focus on two plastic responses inevitably induced by premature necking. The first is triaxial stress due to geometrical inhomogeneities at the LB front31. Three stress components are determined (Fig. 3b), that is, σxx, σzz and σyy, using finite-element-method (FEM) simulations (Supplementary Fig. 3a). This indicates a change in the stress state from uniaxial to triaxial in the LB front region, in contrast to an approximately uniaxial state on both sides. Further, the triaxial stress leads to an elevated von Mises stress (σM) in the LB front region (Fig. 3c, bottom). The triaxial stress state is characterized by the triaxiality parameter (η) defined as the hydrostatic press divided by σM (ref. 32). Here η varies from the least value of 0.26 to the largest value of 0.39 (Fig. 3c, top), relative to η of \(\tfrac{1}{3}\) by uniform shrinkage. Both maximum and minimum η are constant during LB propagation (Supplementary Fig. 3), indicating a stable triaxial stress state. The second is the strain gradient (λ) (ref. 33). Here λ arises from the macroscopic plastic incompatibility between the LB front region and remaining elastic section. Also, λ is defined as \(\tfrac{\partial \varepsilon }{\partial x}\), where ε is the longitudinal strain and x is the distance from the LB front. The maximum value, λmax, is located at the LB front and remains unchangeable during LB propagation (Fig. 3d). Both triaxial stress and strain gradient will facilitate to trigger dislocation production at the LB front.

Dislocation multiplication

We investigated the dislocation production at first by means of the synchrotron-based high-energy X-ray diffraction (XRD) in situ tensile testing (Extended Data Fig. 2a). The dislocation density (ρ) increases from the initial 2.6 × 1013 to 9.7 × 1014 m−2 once the LB front arrives and then to 1.2 × 1015 m−2 by the end of LB propagation; finally, it reaches 1.7 × 1015 m−2 when uniform deformation ends (Fig. 3e). The share of increment of ρ (Δρ) at the LB front is noteworthy, reaching ~80% during the LB propagation. Meanwhile, the dislocation multiplication rate (\(\dot{\rho }\)), calculated as Δρ/Δt, is 4.6 × 1013 m−2 s−1 at the LB front, which is 12 and 6 times quicker than that during the later LB propagation and uniform deformation, respectively. It follows that the dislocations rapidly multiply at the LB front where premature necking happens. Namely, necking promotes dislocation multiplication. Triaxial stress, along with an enhanced von Mises stress, facilitates to activate more slip systems and sources inside grains such that the dislocations multiply at a more rapid speed34. These dislocations are forest dislocations, also called statistically stored dislocations (SSDs)35. Most of them are initially mobile. We then measured the change in mobile dislocations density (\({\rho }_{{\rm{m}}}/{\rho }_{{{\rm{m}}}_{0}}\)) by stress-relaxation testing (Supplementary Fig. 4)36, where \({\rho }_{\mathrm{m}_{0}}\) and ρm are the initial and transient mobile dislocation density, respectively. The mobile dislocations, as the precondition of LB initiation8,31, accommodate not only highly accumulated strains at the LB front (Supplementary Fig. 2a4, top) but also uniform strains. Also, \({\rho }_{\mathrm{m}}/{\rho }_{\mathrm{m}_{0}}\) drops at first and then levels off during uniform deformation (Fig. 3f, top). This indicates the formation of mobile dislocations during LB propagation. We finally estimate the density of geometrically necessary dislocations (GNDs), ρGND, as λ/b (refs. 37,38), where b is the magnitude of Burgers vector (0.255 nm). The GNDs compensate for strain incompatibilities33, particularly offering local stress and extra work hardening7,39. Also, ρGND is 2.5 × 1011 m−2 during LB propagation (Fig. 3f, bottom), consistent with previously reported values40.

The dislocation behaviours were further investigated by site-specific TEM observations after an interrupted tensile testing. The dislocations are rapidly produced and accumulated in most grains once the LB front arrives (Fig. 4a and Supplementary Fig. 5), forming dislocation tangles and low-angle sub-boundaries (Fig. 4b,c, red arrows), along with small amounts of SFs (blue arrows). The weak-beam dark-field TEM image shows that dislocations prefer to tangle up and reside at the dislocation sub-boundaries (Fig. 4c), leaving less and less room in the grains to further accumulate dislocations. The dominant pattern is entangled dislocations by the end of LB propagation (Fig. 4d), which interact with and capture the remaining mobile dislocations to make them immobile. Besides, the high-resolution TEM lattice image shows a local dislocation density of 2.8 × 1015 m−2 after tensile deformation at 298 K (Fig. 4e), with the same order as that by XRD measurements (Fig. 3e). Also, ρ increases after cryogenic deformation at 77 K (Extended Data Fig. 3a1–4), with ρ as high as 8.8 × 1015 m−2 (Fig. 4f). The increased ρ value facilitates the simultaneous increase in strength and ductility (Fig. 2b). The large amount of SFs are visible after cryogenic deformation at 4 K (Extended Data Fig. 3b1–4). This is probably the reason for the serration flow at extremely low temperatures41.

Fig. 4: Dislocation behaviours in fcc grains and L12.
figure 4

a, Dislocation production inside fcc grains at the LB front after interrupted tensile testing at a strain of 5% (298 K). b,c, Weak-beam TEM bright-field (b) and dark-field (c) images of dislocations (298 K). The red arrows show the sub-boundaries of the dislocation cell. The blue arrows show the SFs. The dashed circle indicates the dislocation tangle. The bright contrast in c indicates dislocations. The inset in c shows the weak-beam g/3g pattern, with g = [11\(\bar{1}\)]. d, Weak-beam dark-field image. The dashed circle indicates dislocation tangles. e,f, High-resolution lattice images in fcc grains after tensile deformation at 298 and 77 K, respectively, showing dislocations. Zone axis, [110]. The ‘T’ symbols indicate extra half-plane of edge dislocation. The inset in e shows the Burgers circuit encircling one dislocation (T) having a Burgers vector of ½[1\(\bar{1}\)0]. g, HAADF image, showing nano-lamellar L12. Zone axis, [011]. The ⊥ symbol indicates the core of the Shockley partial. The red, blue, green and yellow lines indicate fcc-L12, twin, SF and hcp lattice, respectively. h, Lattice image showing the coherent L12/fcc-phase interface. Note the lattice rotation by 6.3° in L12.

Full size image

We also investigated the dislocation behaviours in the L12 plate. The electron concentration (e/a) is 8.43, which is calculated according to the chemical compositions of fcc-L12 (Supplementary Fig. 1a). Therefore, the L12 plate is hardly deformable based on the e/a criterion14. As expected, only a few Shockley partials are formed during plastic deformation and one is labelled by Τ (Fig. 4g), with the Burgers vector of the \(\tfrac{1}{6} < 2\bar{1}\bar{1} >\) type. It is observed further that the (1\(\bar{1}\)1) planes in fcc-L12 rotate by an angle of 6.3° (φ) to induce a shear strain (~tgφ) of 11% (Fig. 4h), that is, an equivalent strain of ~6%, whereas the L12/fcc-phase interface remains coherent. Accordingly, the L12 plates mainly accommodate the microscopic strains by lattice rotation and contribute little to work hardening (Supplementary Note 5).

Work hardening

We now place emphasis on work hardening that plays a decisive role in the restraint of premature necking. First, a microhardness increment (ΔH) appears as a gradient in the LB front region (Fig. 5a), well consistent with the rapid increase in ρ at the LB front (Fig. 3e and Supplementary Fig. 5). This signals that work hardening begins once the LB front arrives. Second, the cumulative work hardening can be described by the increment in flow stress as strain increases in the true stress–strain (σT−εT) curve (Fig. 5b). The increment during LB propagation, namely, ΔσLB, and that during uniform deformation, that is, ΔσUD, are 182 and 173 MPa, respectively. During these two stages, the corresponding forest stress increments induced by SSDs (Fig. 3e), ΔσSSDs, are only 110 and 80 MPa, which are calculated by the Taylor hardening law, that is, \({\Delta \sigma }_{{{\rm{SSDs}}}}=M\alpha \mu b(\sqrt{{\rho }_{{\rm{e}}}}-\sqrt{{\rho }_{{\rm{s}}}})\), where M is the Taylor factor (3); α is a constant (0.2); μ is the shear modulus (72 GPa); and ρs and ρe are the dislocation densities at the start and end of each stage, respectively. A non-negligible gap exists between the flow stress increment and forest stress increment in the two stages, which are 72 and 93 MPa, accounting for 40% and 54% in the flow stress increment, respectively. This indicates that the forest stress is only a part of the flow stress. Namely, forest dislocation hardening alone is inadequate to support the global work hardening in two stages.

Fig. 5: Work hardening.
figure 5

a, Gradient microhardness increment (ΔH) in the LB front area measured in the sample after an interrupted tensile strain of 4%. The arrow shows the direction of LB propagation. The dashed line shows the mean ΔH after tensile deformation. The mean values and error bands of the mean are presented on the basis of microhardness tests conducted at five positions with equal spacing along the width of the gauge section. b, Tensile true stress–strain (σT−εT) curve corresponding to the engineering (σe−εe) curve shown in Fig. 2a. The dashed line merely connects the start and end of LB propagation. Here ΔσLB and ΔσUD denote the increments in flow stress during LB propagation and uniform deformation, respectively. c, Mechanical hysteresis loop during an unload–reload cycle at an unload strain of 13.1%. d, Ratio of ΔσHDI to ΔσT (top) and that of ΘHDI to ΘT (bottom). Here σHDI and ΘHDI denote the HDI stress and HDI-stress-induced hardening rate, respectively, and σT and ΘT denote the true stress and global work-hardening rate, respectively. The mean values ± standard error of the mean are presented on the basis of three unload–reload tensile tests.

Full size image

We then find out the additional stress to compensate for the aforesaid stress gap by conducting an interrupted tensile test (Supplementary Fig. 6). An important finding is the mechanical hysteresis loop that repeatedly occurs during each unload–reload cycle. One loop is shown at an unload strain of 13.1% (Fig. 5c). The hysteresis loop is the characteristic mechanical response, indicating that both SSDs and GNDs simultaneously contribute to plastic deformation. To be specific, GNDs will induce a heterodeformation-induced (HDI) stress (σHDI) (refs. 7,39), serving as an essential supplement to ΔσSSDs. Accordingly, the flow stress increment during uniform deformation, ΔσT, is equal to ΔσSSDs plus ΔσHDI. The measured ΔσHDI accounts for ~51% in ΔσT (Fig. 5d, top), effectively filling in the aforementioned stress gap of 54%. Further, σHDI produces the HDI hardening, characterized by the hardening rate ΘHDI (∂σHDI/∂ε) (refs. 7,39). The global hardening rate ΘT is the sum of the hardening rates by SSDs and GNDs. It is visible that the percentage of ΘHDI reaches 50% (Fig. 5d, bottom). These results indicate the indispensable contribution of both σHDI and ΘHDI to the global flow stress and work hardening during uniform deformation. Because of the heterogeneous LB propagation, σHDI cannot be calculated. However, the decisive role of both σHDI and ΘHDI is certain during the LB deformation. This is due to the fact that the percentage of ΔσSSDs (110 MPa) is only ~60% of ΔσT (182 MPa). Accordingly, the forest hardening combines HDI hardening to slow down and stabilize the premature necking for the LB propagation and uniform elongation.

We finally return to seven data points (Fig. 2c) to demonstrate the effect of premature necking on work hardening (Fig. 6). The corresponding microstructures have similar tensile features and phase constituents (M1–M7; Extended Data Fig. 1) but different \(\bar{d}\) values in fcc grains. The mechanical parameters, including vmax, η and λ, were measured and tested (Supplementary Figs. 2b and 3b). The work-hardening exponent n is fitted by σ = k × εn, where k is a constant. Among them, vmax and \(\bar{d}\) deserve special mention. First, vmax shows dual effects. One is to signal the onset and degree of premature necking. The other is to trigger large Δρ and \(\dot{\rho }\), that is, the rapid multiplication of SSDs and GNDs. Namely, vmax arises from the lack of work hardening but produces—in reverse—the combined work hardening. In particular, the HDI hardening effectively makes up the deficiency of forest hardening (Fig. 5d, bottom). Second, \(\bar{d}\) is decisive to tailor work hardening. Here \(\bar{d}\) causes conflict between vmax and n. Specifically, the lower the value of \(\bar{d}\), the larger is the vmax value and lower is the value of n. Also, \(\bar{d}\) in M4 (Fig. 1a) is optimal for obtaining just the right work hardening to restrain and stabilize the LB, achieving respectable ductility along with the highest σy value (Fig. 2a). Yet, the decrease in \(\bar{d}\) in M2 and M3 makes an increased vmax and decreased n. Work hardening is insufficient and fracture happens during the LB propagation. Also, εLB drops and εUD is even lost. On the contrary, an increased \(\bar{d}\) in M5–M7 leads to decreased vmax and increased n. Compared with M4, M7 increases \(\bar{d}\) from 0.42 to 1.26 μm (Supplementary Note 6). The vmax peak in M7 is only half that in M4, still maintaining an almost unchangeable vmax plateau (Supplementary Fig. 2b5). This indicates that premature necking happens in M7. Also, Δρ decreases to 3.9 × 1014 m−2 during the LB propagation and increases to 21.7 × 1014 m−2 during the entire tensile deformation (Extended Data Fig. 2b3), along with a decreased \({\dot{\rm{\rho}}}\) value to 1.9 × 1013 m−2 s−1 at the LB front. All these changes are ascribed to an increased \(\bar{d}\) value in M7, leading to a decreased premature necking tendency. As a result, εLB drops and εUD rises, thereby increasing ductility. It follows that harnessing the premature instability is practical to achieve superior yield strength–ductility synergy.

Fig. 6: Work hardening for strength–ductility balance by harnessing premature necking.
figure 6

The x axis shows the yield strength (σy). Mx (top) indicate the seven microstructures (x = 1–7, corresponding to the seven data points shown in Fig. 2c and tensile stress–strain curves (Extended Data Fig. 1a)). The y axis shows the mechanical properties and parameters. The symbols indicate the measured data. The arrow shows the trend. Here \(\bar{d}\) indicates the average size of the fcc grains; vmax, the maximum lateral shrinkage rate at the LB front; n, work-hardening exponent; εLB, Lüders strain; εUD, uniform strain. Note the lost εUD (labelled by ×) due to direct fracture of the sample during LB propagation in both M2 and M3.

Full size image

Discussion and concluding remarks

HDI hardening is indispensable due to the HDI-hardening rate accounting for over 50% of the global hardening rate (Fig. 5, bottom). The local HDI stress causes the HDI hardening by GNDs (Supplementary Note 7)39. HDI stress is produced when a specific GND pattern, for example, a pile up and a group of loops, is blocked by either precipitates or grain boundaries39,42,43,44. However, small UFGs make these patterns of GNDs difficult to form. Meanwhile, the dislocations of mass multiplication rapidly evolve into tangles, usually having a negligible HDI stress39. Here we propose the LCO regions as the microstructural source for HDI stress. On one hand, the LCO regions are mechanically stable, rather than be destroyed by gliding dislocations, showing the almost unchangeable size and volume fraction before and after tensile deformation (Extended Data Fig. 1d5). On the other hand, the strain field is attached to an ordered LCO region (Fig. 1d), producing the strain-field interaction with gliding dislocations43. This scenario is consistent with that in an ordered precipitate of intermetallic phase, inducing the strain-field interaction with dislocations45,46,47,48. Conventionally, shearing is assumed as the interaction of LCO regions with gliding dislocations due to their tiny sizes. However, this incurs a problem that shearing cannot induce HDI stress, whereas bypassing can due to the constantly produced dislocation loops43,44. We propose that the HDI stress is induced by the strain-field interaction between dislocations and LCO region, or the cluster of LCO regions as a forest. To verify this (Supplementary Note 8), we conducted high-resolution TEM observations in fcc grains, showing several edge dislocations (extra half-planes labelled by yellow ‘Τ’ symbols) and LCO regions as evidenced by their characteristic electron diffraction43 (Extended Data Fig. 4a,b). The LCO regions (red spots) distribute on the fcc lattice (azury spots) in the overlay of two inverse Fourier transform images (Extended Data Fig. 4c). One edge dislocation (yellow-coloured Τ) inserts into the middle of the circled LCO region. The corresponding GPA map shows the coupling of the strain field between the LCO region and dislocations (Extended Data Fig. 4d). The average strain is 0.2% before tensile deformation, whereas it markedly rises to 6.9% after plastic deformation (Extended Data Fig. 4d, inset). The strain-field interaction induces an increased local strain near the LCO region. This indicates a trapping effect on moving dislocations when migrating through the strain field of LCO regions. By the definition of GND33, these dislocations that interact with LCO regions are GNDs compensating for local strain incompatibility. At this moment, an extra force, that is, HDI stress, is needed such that GNDs are de-trapped from the strain field and continue to move. The strain field, especially induced by the forest of LCO regions, will increase opportunities for GNDs to interact with each other. Therefore, extra HDI hardening is expected by the LCO regions.

In summary, here we show to exploit and stabilize premature necking during LB propagation to induce combined work hardening for ductility in MPEAs with UHYSs. These results help to understand and design the well-balanced strength and ductility and are easily transferable to other MPEAs containing the LCO regions as intrinsic heterogeneities.

Methods

Materials, processing and heat treatment

Nickel, cobalt and vanadium (all of them, >99.9% purity) were selected for the VCoNi alloy smelting. The ingot was cast into the mould of 130 mm diameter under an argon atmosphere by using the arc-melting technique. The ingot was turned upside down and then re-melted five times for chemical homogeneity. The ingot was hot forged at 1,423 K to the plate with a dimension of 12 × 100 × 600 mm3, homogenization treated in a vacuum at 1,373 K for 2 h, followed by quenching in water. Cold rolling was finally conducted with a 90% thickness reduction to obtain thin sheets of 1 mm thickness. Recrystallization annealing was conducted at 1,173 K for 150 s. The chemical composition was the equiatomic 33V–34Co–33Ni (atomic percentage) in this ternary VCoNi MPEA.

Microstructural characterization

XRD

XRD study was performed to obtain detailed information on the phase structure using a Rigaku SmartLab 9 X-ray diffractometer with Cu Kα radiation (λ = 1.5406 Å) at 35 kV. The mechanically polished samples were scanned through the 2θ range from 30.00° to 100.00° with a step size of 0.02° and counting time of 2 s. The volume fraction of L12 plates was determined by the relative integrated intensities of the characteristic diffraction peaks as follows49:

$${f}_{{\rm{L}}{1}_{2}}=\frac{\sum {{{I}}}_{{\rm{L}}{1}_{2}}}{\sum {{{I}}}_{{\rm{fcc}}}+\sum {{{I}}}_{{\rm{L}}{1}_{2}}},$$
(1)

where \(\sum {{{I}}}_{{\rm{fcc}}}\) and \(\sum {{{I}}}_{{\rm{L}}{1}_{2}}\) are the sum of the integrated intensities of the characteristic diffraction peaks, that is, (111), (200), (220) and (311) for fcc and L12, respectively.

SEM EBSD observation

The microstructural observation was conducted by using a high-resolution field-emission ZEISS GeminiSEM 300 scanning electron microscope (SEM) equipped with a fully automatic Oxford Instruments Aztec 2.0 electron backscatter diffraction (EBSD) system (Channel 5 software), with a scanning step of 40 nm during the EBSD acquisition. The high-angle grain boundaries were defined with a misorientation angle larger than 15°. The statistical mean grain size was obtained by measuring the original fcc grains, without the effect of subdivision by L12 plates inside the grain interiors.

TEM observation

Thin foils for TEM observations were mechanically polished to ~50 μm thickness and then punched to discs of 3 mm in diameter. The foils were perforated by twin-jet electron polishing with a solution of 20 vol% perchloric acid and 80 vol% acetic acid at –25 °C and a voltage of 50 mA. Atomic-resolution HAADF images were performed in an aberration-corrected scanning transmission electron microscope (FEI Titan Cubed Themis G2 300) operated at 300 kV, equipped with Super-X energy-dispersive X-ray spectroscopy with four window-less silicon-drift detectors. The thickness is around 30 nm in areas of TEM foils for the imaging of various LCO regions, especially energy-dispersive X-ray spectroscopy mapping.

The weak-beam TEM dark-field imaging was conducted to accurately determine the dislocation lines and their patterns. A weak beam refers to imaging under the diffraction contrast with reflection g set far off the Bragg condition. This weak-beam condition may effectively reduce the interference effects caused by the specimen thickness and dynamic scattering on the contrast of dislocation lines50,51. The bright contrast of dislocations emerges from an otherwise faint background. Here the g/3g condition, with g = 11\(\bar{1}\), has been employed to generate weak-beam dark-field images in fcc grains, which are recorded in an FEI Tecnai G2 F20 TEM instrument operated at 200 kV and an FEI Titan Cubed Themis G2 300 instrument operated at 300 kV.

The average size and spacing of LCO regions were measured in the energy-filtered dark-field TEM images and simultaneously in at least 20 inverse fast Fourier transform atomic-resolution TEM images. With the assumption of a uniform distribution of tiny LCO regions in three-dimensional space, the volume fraction (fV) of LCO regions is calculated as follows52,53:

$${f}_{{\rm{V}}}=\frac{\uppi }{4}\times \frac{1}{{\left[\frac{\lambda }{d\sqrt{2/3}}+1\right]}^{2}},$$
(2)

where d is the average size of the LCO regions and λ is the average interspacing.

Focused-ion-beam method

Thin TEM foils at the site-specific LB front were fabricated by liftouts and cross-section milling in an FEI Helios Nanolab G3 CX focused-ion-beam SEM device. The area of interest was selected and protected by platinum deposition. The initial milling was executed at a high ion-beam current (that is, ion beam parallel to the y axis), forming a film that was 10 μm wide (x direction), 10 μm high (y direction) and 2 μm thick (z direction). Then, this film was removed from the milled trench by using a micromanipulator and placed on a Cu grid. The film was further thinned gradually to avoid damaging by decreasing the ion-beam currents from 0.79 nA to 40 pA at a voltage of 30 kV until the thickness was less than 80 nm, which is suitable for TEM observations. The surface was finally cleaned to remove the damage of the ion beam at a relatively small voltage.

High-resolution TEM lattice-image-based GPA mapping

The GPA map shows the strain-field contours of the LCO regions on the basis of the change in lattice fringe spacing across the whole lattice image. The Fourier transform pattern related to different crystal planes (hkl) was obtained at first based on high-resolution lattice images with a specific zone axis. A perfect crystal lattice gives rise to sharply peaked frequency components, whereas the Bragg reflections broaden due to local lattice distortions. The VCoNi solution is a mixture of V, Co and Ni atoms, with an evidently differing atomic radius. In the normal direction of the close-packed (\(11\bar{1}\)) plane, tensile and compressive strain will be caused due to the local enrichment of larger V and smaller Co/Ni atoms, respectively. We placed a circular Gaussian mask on the reflection of (\(11\bar{1}\)) to obtain the strain map of close-packed planes20. The resolution was set at 0.25 nm to ensure the full display of lattice strain caused by LCO regions.

Mechanical tests

Uniaxial tensile test at room temperature

For the uniaxial tensile test, unload–reload test and stress-relaxation test, all the samples were dog-bone shaped, with a gauge section of 5 × 1 mm2 and 23 mm in length. The samples were cut from thin sheets of 1 mm thickness along the rolling direction. All the tensile tests at room temperature (298 K) were performed in an Instron 5967 machine at a strain rate of 5 × 10−4 s−1. The contacted extensometer was used to measure strains during tensile loading.

Tensile test at cryogenic temperatures

Tensile tests were conducted at a strain rate of 5 × 10−4 s−1 at both 77 and 4 K in a displacement-controlled mode in an electronic–mechanical test machine (MTS model SANS UTM 5305S, with a load capacity of 300 kN). A cryogenic-grade extensometer (Epsilon model 3542-010M-LT, with a gauge length of 10 mm) was used to record the full-range deformation. In particular, tensile tests at 4 K were conducted by immersing the whole specimen and test jigs into liquid helium in a home-made cryostat installed on the cross-beam of the test machine. All the interior components of the sample chamber were insulated by a high-purity copper radiation shield and multilayer insulation material, which effectively prevented liquid helium from evaporating. The liquid-helium level was monitored with a cryogenic liquid-level meter (Cryomagnetics model LM-500) and the liquid helium was refilled to maintain the defined level during the tensile process. A thermometer was installed on the inner wall of the sample chamber and the height of the thermometer was consistent with the tested sample, which was used not only to obtain accurate temperature but also to control the temperature inside the sample chamber.

Unload–reload tensile test

The testing was conducted to measure the HDI stress. The stretched specimen was subjected to successive cycles of unloading and reloading at several strains. The mechanical hysteresis loops appeared if GND-based heterodeformation happens. The HDI stress is calculated as follows54:

$${\sigma }_{{{\rm{HDI}}}}=\frac{\left({\sigma }_{{\rm{u}}}+{\sigma }_{{\rm{r}}}\right)}{2},$$
(3)

where σu and σr are the yield stresses on the unload and reload cycles, respectively, which were obtained from the hysteresis loops during each unload–reload cycle.

Synchrotron-based high-energy XRD in situ tensile test

The in situ tests were performed at the 11-ID-C beamline, Advanced Photon Source, Argonne National Laboratory. A monochromatic X-ray beam was used with an energy of 71.676 keV at a wavelength of 0.1173 Å. The beam size was 500 μm (along the width direction of the tensile sample) × 100 μm (along the longitudinal direction). The tensile tests were performed at room temperature and at a strain rate of 1 × 10−3 s−1. The gauge section was 10.0 (length) × 3.0 (width) × 0.5 (thickness) mm3. The engineering strain was measured from the cross-head displacement and corrected on the basis of the elasticity modulus. During tensile deformation, the scattering intensity was collected using a two-dimensional detector placed 1,770 mm from the tested sample. The two-dimensional diffraction data were transformed into a one-dimensional line profile by integrating over a ±5° azimuth range around the longitudinal direction and transversal direction of the specimen with GSAS-II software55. The crystallographic planes were determined from the diffraction patterns and lattice strains, εhkl, were calculated by the change in the corresponding interplanar spacing relative to the lattice spacing in the undeformed state as follows:

$${\varepsilon }_{{hkl}}=\frac{({d}_{{hkl}}-{d}_{{hkl}}^{0})}{{d}_{{hkl}}^{0}},$$
(4)

where \({d}_{{hkl}}^{0}\) is the d spacing of the (hkl) grain family at zero applied stress. The full-width at half-maximum of the physical lineshape for the tested sample was calibrated by extracting the instrumental broadening from the measured broadening as follows:

$${\rm{FWHM}}=\left[{\left({{\rm{FWHM}}}_{{{\rm{measured}}}}\right)}^{2}-{\left({{\rm{FWHM}}}_{{{\rm{instrumental}}}}\right)}^{2}\right].$$
(5)

The instrumental broadening was characterized using a near-perfect (broadening-free) CeO2 powder.

The dislocation density (ρ) was calculated from the synchrotron XRD profiles by using the modified William–Hall method56, assuming that the broadening of diffraction peaks is linked to the microstructural parameters including the average grain size (D) and ρ:

$$\Delta K\cong \frac{0.9}{D}+{\left(\frac{\uppi {A}^{2}{b}^{2}}{2}\right)}^{\frac{1}{2}}{\rho }^{\frac{1}{2}}\left(K{C}^{1/2}\right),$$
(6)

where

$$K=\frac{2\sin \theta }{\lambda }$$
(7)

and

$$\Delta {\rm{K}}=\frac{\cos \theta (\Delta 2\theta )}{\lambda }.$$
(8)

Also, θ is the diffraction angle at the exact Bragg position; λ, the X-ray wavelength; Δ2θ is the full-width at half-maximum of the diffraction peak at θ; A is a constant determined by the effective outer cutoff radius of dislocations (here we used A = 1 in the present study); b is the magnitude of Burgers vector (0.255 nm); and C is the average dislocation contrast factor57. For each (hkl) reflection, the value of C can be determined as

$$C={C}_{H00}\left\{1-q\left[\frac{{h}^{2}{k}^{2}+{k}^{2}{l}^{\;2}+{h}^{2}{l}^{\;2}}{{\left({h}^{2}+{k}^{2}+{l}^{\;2}\right)}^{2}}\right]\right\},$$
(9)

where CH00 and q are constants related to the anisotropic elastic constants (C11, C12 and C44) of the tested alloy. Also, CH00 and q depend on the elastic anisotropy Ai = 2C44(C11 – C12) and the ratio C12/C44.

$${C}_{H00}=a\left[1-\exp \left(-{A}_{i}/b\right)\right]+c{A}_{i}+d$$
(10)
$$q=a\left[1-\exp \left(-{A}_{i}/b\right)\right]+c{A}_{i}+d$$
(11)

For the present VCoNi alloy, elastic constants C11, C12 and C44 equal to 169, 82 and 96 GPa. The constants for the two groups, namely, a, b, c and d, are (0.1607, 1.8610, 0.0196 and 0.0928) and (4.6080, 0.8706, 0.0924 and –3.2550), and are used for the calculation of CH00 and q, respectively.

Stress-relaxation tensile testing

The aim of this test was to figure out the density evolution of mobile dislocations during tensile deformation. The specimen was first stretched at a strain rate of 5 × 10−4 s−1 to certain strain, whereas the cross-beam head was held to allow stress relaxation for 180 s. Then, this relaxed specimen was reloaded to the same stress level as before at a strain rate of 10−1 s−1 to conduct the second cycle of relaxation. In total, four cycles of repeated stress relaxation were carried out at each designed strain. The mobile dislocation density, \({\rho }_{\mathrm{m}}/{\rho }_{\mathrm{m}_{0}}\), exhibits an empirical power law with time (t) (ref. 36):

$$\frac{{\rho }_{\mathrm{m}}}{{\rho }_{\mathrm{m}_{0}}}={\left(\frac{{c}_{{\rm{r}}}}{t+{c}_{{\rm{r}}}}\right)}^{\frac{\beta }{1+\beta }},$$
(12)

where \({\rho }_{\mathrm{m}_{0}}\) is the dislocation density at the onset of each transient, cr is a time constant and β is a dimensionless immobilization parameter. The derivation of cr and β is described below.

A single stress-relaxation transient exhibits a logarithmic variation of stress drop with time elapsed. The apparent activation volume Va is determined by fitting the logarithmic stress-relaxation curve as

$$\Delta \tau (t)=-\frac{{k}_{{\rm{B}}}T}{{V}_{{\rm{a}}}}\,\mathrm{ln}\left(1+\frac{t}{{C}_{{\rm{r}}}}\right),$$
(13)

where Δτ(t) is the stress drop at time t, T is the temperature (Kelvin) and kB is the Boltzmann constant; consequently, time constant Cr and apparent activation volume Va are obtained. The physical activation volume V* is determined as

$${V}^{\,\ast }={k}_{{\rm{B}}}T\frac{\mathrm{ln}({\dot{\gamma }}_{i2}/{\dot{\gamma }}_{f\;1})}{\Delta {\tau }^{\,\ast }},$$
(14)

where \({\dot{\gamma }}_{i2}\) and \({\dot{\gamma }}_{f\;1}\) are the shear strain rate at the onset of relaxation 2 and the end of relaxation 1, respectively. Δτ* is the change in thermal component under relaxation condition:

$$\Delta {\tau }^{\ast }=(1+K/M\,)\Delta \tau,$$
(15)

where K can be approximated by the strain-hardening rate of the monotonic tensile curve, and M is the stiffness of the specimen−machine assembly. Additionally, the dimensionless immobilization parameter β can be determined as

$$\beta =\frac{\varOmega }{1+K/M}-1,$$
(16)

where parameter Ω can be expressed as

$$\varOmega =\frac{{V}_{{\rm{a}}}}{{V}^{\,\ast}}.$$
(17)

Finally, the density of mobile dislocations after relaxation can be obtained.

DIC-based in situ tensile test

This test was used to quantitatively measure the distribution of full-field strain during tensile deformation. The spot pattern was sprayed onto a white background on the specimen surface. The displacement of the pattern was tracked using a 1.2 megapixel charge-coupled device camera with a resolution of 2,848 × 2,848 pixels2 at 1 frame s−1. The recorded camera images were then analysed for local strains using ARAMIS v. 6.1 software. The strain contours were calculated with a spatial resolution of 275 nm pixel–1.

The strain gradient λ induced by the heterogeneous strain distribution is calculated as

$$\lambda =\frac{\partial \varepsilon }{\partial x},$$
(18)

where ε is the longitudinal strain measured by the DIC tensile testing and x is the distance from the LB front. Since the GNDs play a pivotal role in accommodating the local strain incompatibility, a classical method from the strain-gradient theory37,38 is used to estimate the GND density (ρGND) as follows:

$${\rho }_{{{\rm{GND}}}}=\frac{\lambda }{b},$$
(19)

where b is the magnitude of Burgers vector (0.255 nm).

Calculation of stress triaxiality by FEM simulation

The FEM calculation and simulation were carried out by means of the Abaqus/Standard code. The three-dimensional model was created according to the actual dimensions of the tensile specimen, and the simulated specimen was loaded in a similar way to real tensile testing. During the simulated testing, the upper grip of the model was fixed, whereas the lower grip was only allowed to move along the axial direction. The model was loaded on the lower-end surface to simulate the displacement-controlled tensile test. The analysis was set up in the large-deformation mode, static three-dimensional calculation with default stabilizing options and 41,124 hexahedral elements, type C3D20R (ref. 31). The reaction force on the lower-end surface and the elongation of gauge section were used to calculate the engineering stress and strain. A trigger element with a slightly lower strength of 75 MPa than all the other elements was severed as the starting point for LB propagation58. The simulation was regarded as reliable until the following targets are achieved: (a) the simulated engineering stress–strain relation achieved the best agreement with the experimental one; (b) the LB formation, propagation and subsequent uniform deformation were precisely reproduced.

The triaxiality parameter32 η is defined as the hydrostatic press (σH) divided by von Mises stress (σM):

$$\eta =\frac{{\sigma }_{{\rm{H}}}}{{\sigma }_{{\rm{M}}}},$$
(20)
$${\sigma }_{{\rm{H}}}=\frac{{\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}}{3},$$
(21)
$${\sigma }_{{\rm{M}}}=\sqrt{\frac{1}{2}\left[{\left({\sigma }_{1}-{\sigma }_{2}\right)}^{2}{+\left({\sigma }_{2}-{\sigma }_{3}\right)}^{2}+{\left({\sigma }_{3}-{\sigma }_{1}\right)}^{2}\right]},$$
(22)

where σ1, σ2 and σ3 are the principal stress values along the three stress directions.