Introduction

It has long been recognized that dimensionality plays an essential role in magnetic systems and can drastically influence their ordering behavior, low-energy excitations, and magneto-transport properties, due to delicate interplays of the different microscopic couplings between localized moments. In particular, studies of magnetism in two-dimensional (2D) systems within the regime of isotropic coupling have led to major conceptual advances including the Hohenberg–Mermin–Wanger theorem1,2 and Berezinskii–Kosterlitz–Thouless transition3,4,5. The former stipulates that Landau-type magnetic ordering is absent in rotationally invariant 2D systems, while the latter is manifested by distinctly new topological characteristics as the systems reduce their temperatures from the paramagnetic phase. Recent breakthrough advances in 2D ferromagnets of CrI3 and CrGeTe3, however, have unambiguously shown that the Hohenberg–Mermin–Wanger restriction can be lifted, thanks to sufficiently strong anisotropy in the exchange couplings6,7. These developments offer compelling opportunities for exploration of a broad wealth of exotic phenomena.

Anisotropic magnetic interactions can exist in various forms, but in essence are all rooted in spin-orbit coupling of electrons. Such anisotropies can be further classified into onsite and multi-site terms. The simplest onsite anisotropy is originated from the atomic-scale spin-orbit coupling that breaks the spatial rotational symmetry, favoring magnetization along a particular direction. Among the multi-site anisotropies, the celebrated example is the Dzyaloshinskii–Moriya interaction (DMI)8,9, favoring perpendicular mutual alignment between two localized moments. Past studies have shown that the DMI is essential in enabling the formation of various chiral or topological entities in magnetic systems, including chiral domain walls10, skyrmions11,12,13, and merons14. Yet given their inherent inversion symmetry, the DMI is largely absent in pristine monolayer CrI3 and CrGeTe3 at least at the nearest neighboring level15,16, and additional manipulations or materials modifications have to be invoked to break the inversion symmetry of such 2D magnets in order to induce significant DMI17,18,19,20,21.

In this paper, we use first-principles calculations to analyze the onsite and inter-site exchange anisotropies in a recently predicted monolayer magnet of CrMnI6, and reveal the striking coexistence of both giant DMI and strong XXZ-type biquadratic coupling. Qualitatively, the DMI is induced by the spontaneous in-plane inversion symmetry breaking in the bipartite system, which distinctly contrasts all the schemes to induce DMI via out-of-plane inversion symmetry breakings reported so far17,18,19,20,21, while the exotic XXZ-type biquadratic coupling is inherently tied to the high-spin state of the Mn sublattice. At a quantitative level, the large magnitudes of both anisotropic terms stem from the significant spin-orbit coupling within the system. Next, we use atomistic magnetics simulations to demonstrate the vital role of DMI in harboring topological bimeronic excitations, while the biquadratic coupling favors a Berezinskii–Kosterlitz–Thouless-like transition as the system reduces its temperature from the paramagnetic phase. These findings substantially enrich our understanding of the microscopic couplings in 2D magnets, which can be further exploited for various technological applications in memory devices.

Results

Giant DMI in the bipartite CrMnI6 monolayer

We first contrast two distinctive means of breaking inversion symmetry between two magnetic sites for inducing DMI. The scheme illustrated in Fig. 1a, which has been extensively implemented to 2D magnets, relies on breaking of the out-of-plane inversion symmetry via applying external electric field17, or building Janus structures18,19,20 or heterojunctions21. Whereas the strategy sketched in Fig. 1b, which breaks the in-plane inversion symmetry via involving two magnetic species, has not yet been exploited in 2D magnets and is the starting point of the present study. As a concrete example, Fig. 1c shows a CrMnI6 monolayer which can be obtained by substituting one sublattice of chromium in the CrI3 monolayer with manganese, and the ordered structure with bipartite spin lattice (3μB/Cr3+ and 4μB/Mn3+ respectively) as shown in Fig. 1d is energetically favored22. This intriguing 2D magnet composed of binary magnetic elements has been predicted as a magnetic topological insulator exhibiting the quantum anomalous Hall effect22. Beyond the nontrivial electronic band topology, the system may possess more direct and intriguing nontrivial magnetic properties in real space. Indeed, the structural symmetry is reduced from D3d to D3 upon substitution. Because of the concurrence of centro-asymmetry and large spin-orbit coupling, the system is expected to harbor pronounced DMI and potentially more exotic anisotropic couplings like the case of well-studied Kitaev magnets23.

Fig. 1: Inversion symmetry breaking schemes and geometric structure.
figure 1

a, b Schematics of two different approaches to induce DMIs in monolayer magnets (silver/green balls: magnetic cations, orange balls: nonmagnetic anions). a The prevailing strategy, relying on an effective vertical electric field Eeff. b Our strategy, by creating an asymmetric bipartite lattice. (c) Top view of the atomic structure of monolayer CrMnI6, showing the Cr and Mn ions centered in edge-sharing CrI6/MnI6 octahedra. d The honeycomb spin lattice with the exchange couplings indicated.

Full size image

To investigate the anisotropy of exchange couplings in the monolayer CrMnI6 system, we first assume an atomistic spin Hamiltonian with bilinear (BL) terms,

$$\begin{array}{lll}{H}_{BL}&=&-\mathop{\sum}\limits_{i}{A}_{i,zz}{S}_{iz}^{2}-\mathop{\sum}\limits_{i < j}{{{{\bf{S}}}}}_{i}{{{{\bf{J}}}}}_{ij}^{{{{\rm{sym}}}}}{{{{\bf{S}}}}}_{j}\\ &&-\mathop{\sum}\limits_{i < j}{{{{\bf{D}}}}}_{ij}\cdot ({{{{\bf{S}}}}}_{i}\times {{{{\bf{S}}}}}_{j})-{\mu }_{{{{\rm{B}}}}}\mathop{\sum}\limits_{i}{{{\bf{B}}}}\cdot {{{{\bf{S}}}}}_{i}.\end{array}$$
(1)

The first term represents the single-ion anisotropy, which is reduced to a single scalar due to the three-fold rotational symmetry of the system. The second and third terms correspond to the symmetric and antisymmetric (DMI) parts of the pairwise exchange couplings, respectively, covering the nearest neighbor (NN), next NN (NNN) and third NN (TNN) pairs as exemplified in Fig. 1d. The last term accounts for the Zeeman energy.

We perform density functional theory calculation with a mean-field onsite Coulomb repulsion correction for the localized d-orbitals (DFT+U), to attain the energetics of the monolayer CrMnI6 (see Methods section for details). For the magnetic degrees of freedom, we consider four specifically designed non-collinear spin configurations following the powerful four-state method24,25,26, from which the exchange parameters can be conveniently extracted with DFT accuracy15,24,27,28. The calculated bilinear exchange parameters are summarized in Table 1. One can see that the symmetric exchange couplings are predominantly ferromagnetic, but exhibit highly anisotropic characteristics, as reflected by the distinctly different diagonal values in the Jsym tensors and some non-vanishing off-diagonal components. For the antisymmetric part (DMI), more insights can be drawn regarding both directions and magnitudes. For directions, our calculated DM vectors are consistent with the Moriya’s rules29, namely, the symmetry-forbidden components are numerically negligible as well (<0.01 meV). For magnitudes, the dominant NN ∣D∣S1S2 = 0.63 meV, is comparable to those in Cr (I, Br)3 (0.61 meV) and Cr (I, Cl)3 (0.43 meV)19, but smaller than the magnitudes in Janus MnSeTe (2.14 meV) and MnSTe (2.63 meV)30. Practically, the ∣D∣/Jiso ratio31 is more widely used to evaluate the competition between the DMI and Jiso, which respectively favor canted and collinear alignments of the magnetic moments, with the trace average Jiso = Tr(Jsym)/3. For the considered predominant bilinear exchange coupling strengths, the ∣D∣/Jiso values reach 0.31 (NN Cr-Mn), 0.44 (Cr-Cr), and 0.82 (Mn-Mn) respectively. The first is comparable to the corresponding ratios in the prototypical Fe/Ir(111) system32, while the latter two are much larger. Such pronounced chiral exchange couplings may enable topological magnetic excitations, when proper magnetocrystalline anisotropy and/or magnetic field are present.

Table 1 Single-ion anisotropy and two-body exchange coupling strengths of the CrMnI6 monolayer (unit: meV).
Full size table

Magnetocrystalline anisotropy and anisotropic biquadratic coupling

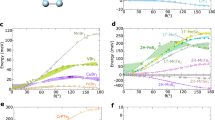
From the above discussions, another important physical aspect to investigate is the magnetocrystalline anisotropy energy (MAE), which indicates the easy magnetization orientations due to the interplay of multiple magnetic interactions. Our DFT+U calculations suggest that monolayer CrMnI6 favors in-plane magnetization, and the overall energy evolution trend can be qualitatively well reproduced by the bilinear model in Eq. (1) [Fig. 2a], indicating that the MAE partially stems from competition between bilinear interactions. On the other hand, there exists pronounced discrepancy at the quantitative level, which hints on the existence of some complex higher-order spin-spin interactions.

Fig. 2: Magnetic anisotropy.
figure 2

a Energy evolution of the FM configuration with rotating magnetization axis. b Energy evolution upon rotating spins of the Mn (Cr) sublattice from x (θ = 0∘) to z (θ = 90∘) synchronically while fixing spins of the Cr (Mn) sublattice along y. The energy differences between the DFT+U calculations and Eq. (1) are shaded in cyan.

Full size image

Given the protection of time-reversal symmetry33, the likely leading higher-order term is the biquadratic (BQ) coupling34,35,36,37,38,39. To reveal the potential existence and microscopic origin of such BQ interactions, we systematically investigate the element-resolved single-ion and pair-resolved ion-ion contributions. The single-ion and NN exchange coupling are both found to be bilinear (See Supplementary Note 1 and Supplementary Figs. 1–2 for details). Then we study the NNN pairs by rotating the spins of one sublattice synchronically from x to z while fixing the other sublattice magnetized along y. Note that the NNN exchange couplings are in essence the NN Cr-Cr or Mn-Mn exchange couplings within the respective sublattices. This rotation operation is valid as long as more distant Cr-Cr or Mn-Mn interactions are much weaker. By comparing the energy evolutions between the DFT+U and BL model calculations, we see quantitative consistency upon rotating spins of the Cr sublattice. In stark contrast, pronounced differences exist when the spins of the Mn sublattice are rotated [Fig. 2b], strongly pointing to the likely source of the MAE discrepancy shown in Fig. 2a. Microscopically, this contrast could originate from their different 3d-electron fillings in the presence of an octahedral crystal field [Fig. 1c]. Both ions have three d electrons occupying the low-lying t2g orbitals in the spin majority channel, while the Mn3+ ions (d4) have an extra d electron populating the higher-energy eg orbitals in the same spin channel. The exchange coupling of the eg electrons within a Mn-Mn pair in return gives rise to pronounced BQ spin-spin interaction.

We can now further improve the spin Hamiltonian in Eq. (1) on solid physics basis. Unlike earlier studied systems with isotropic BQ exchange couplings35,36,37,38,39, one distinctive feature of the present 2D system is that the BQ coupling must be highly anisotropic, because it contributes substantially to the MAE (It therefore should also differ from the recently reported chiral biquadratic interaction40, which is anisotropic but has zero contribution to MAE). Here, taking analogy to the simplest way of introducing exchange anisotropy in the bilinear regime37, and borrowing the wisdom of deriving XXZ-type effective spin-spin interactions41,42, we adopt a physically intuitive anisotropic form of BQ coupling,

$${H}_{BQ}=-\frac{1}{2}\mathop{\sum }\limits_{\langle \langle i,j\rangle \rangle }^{i,j\in {{{\rm{Mn}}}}}{({K}_{\perp }{S}_{ix}{S}_{jx}+{K}_{\perp }{S}_{iy}{S}_{jy}+{K}_{\parallel }{S}_{iz}{S}_{jz})}^{2},$$
(2)

with K⊥ and K∥ being the coefficients to be determined. With the inclusion of this BQ coupling, the energy evolution trend upon rotating the Mn sublattice spins can be significantly improved, as shown in Fig. 2b. As a crucial crosscheck, it also improves the description of the MAE quantitatively, as confirmed in Fig. 2a. The optimally compromised values of K⊥ and K∥ that can simultaneously improve the quantitative accuracies in both Fig. 2a and b is 0.2 and 0.1 meV1/2 respectively, constituting a BQ contribution to easy-in-plane magnetization. The BQ coefficient seems to be weak at the first glance, but given the large magnetic moments of Mn (S = 2), the BL [JisoS2 = 1.4 meV] and BQ [\({K}_{\perp }^{2}\)S4 = 0.64 meV] coupling strengths between NN Mn-Mn pairs are readily comparable. Note that the well-studied isotropic BQ coupling has been recognized to play an important role in the magnetic ground state, spin dynamics and fluctuation of layered magnetic systems35,36,37,38,39, and proved crucial in realizing the famous topological Haldane phase34. Here our work amounts to a concrete example of material hosting anisotropic high-order exchange couplings with pronounced strength, which also opens a new door to exploit unknown intricate exchange couplings via element mutation.

Bimeronic topological excitations and BKT-like transition

The BL-BQ spin Hamiltonian combining Eqs. (1) and (2) now provides an accurate description of the bipartite spin lattice of monolayer CrMnI6. The giant D/J ratios point to possible vortex excitations with spin chirality in the system (Supplementary Note 2 and Supplementary Fig. 3). To explore potential topological excitations, we carry out atomistic magnetics simulations by numerically integrating the Landau–Lifshitz–Gilbert (LLG) equation43, to model a fast cooling process from the paramagnetic state, and calculate the topological charge Q44 to trace the dynamic evolution of real-space geometric phase. As shown in Fig. 3a, Q fluctuates drastically during the initial transient period of the simulation, and then converges to lower values, indicating the emergence of topological chiral spin textures upon cooling. Furthermore, the snapshots in Fig. 3b, c clearly show the existence of vortex- or antivortex-like local excitations. Given that the material strongly favors in-plane magnetization, we assign these nontrivial magnetic structures to merons instead of skyrmions that require out-of-plane magnetization45. Specifically, we may have merons (Q = −1/2) and anti-merons (Q = 1/2), as well as their various paired forms (including bimerons with Q = −1, anti-bimerons with Q = 1, and meron plus anti-meron pairs with Q = 0). We also note that the integer pairing of two meronic excitations involving one vortex plus one antivortex, fulfills the generic vorticity conservation condition, which is analogous to the topological defects of a 2D system below the critical temperature of the Berezinskii–Kosterlitz–Thouless transition3,4,5. Such nontrivial chiral magnetic structures are observed in several independent simulations with different initial states and/or damping parameters, further confirming their intrinsic nature.

Fig. 3: Meronic excitations.
figure 3

a Evolution of the topological charge in an LLG simulation starting from a randomly magnetized configuration. b, c Snapshot configurations (top row) and topological charge distributions (bottom row).

Full size image

The DMI-enabled abundant nano-sized bimeronic excitations and the easy in-plane magnetization strongly enhanced by the BQ coupling are indicative of magnetic transition beyond Landau’s paradigm. To gain further insights into the magnetic critical behavior, we simulate the dynamics of the spin lattice under varying temperatures, with the thermal effect modeled by a stochastic magnetic fields scaled with temperature. To resolve the effect of the BQ coupling, simulations without and with the term described by Eq. (2) are performed separately. The results are summarized and exponentially fitted in Fig. 4, showing that the pronounced BQ coupling not only enhances the transition temperature of the system from ~30.7 K to ~35.1 K, but also alters the exponent depicting the critical behavior, β, from 0.290 to 0.235. The out-of-plane cores of the merons also exhibit shrinking size when the BQ coupling is included (Supplementary Fig. 4). Note that in the paradigmatic 2D XY model elucidating the Berezinskii–Kosterlitz–Thouless transition3,4,5, β = 3π2/128 ~ 0.23146. Here in monolayer CrMnI6, the in-plane and out-of-plane components of the Mn-Mn BQ coupling are both strong but anisotropic. Their uncompensated contribution enhances the easy-plane nature and renders the system a promising platform to exploit magnetic Berezinskii–Kosterlitz–Thouless physics with a critical temperature higher than the recently reported monolayer CrCl347.

Fig. 4: Critical behavior.
figure 4

Magnetic critical behavior of monolayer CrMnI6 simulated in the absence or presence of the identified anisotropic BQ coupling. The data points are from spin dynamics simulations while the curves are exponential fittings by using \(M(T)=M(0){(1-T/{T}_{C})}^{\beta }\).

Full size image

Discussion

Our work demonstrates the existence of biquadratic exchange couplings with distinctive anisotropic form in the bipartite CrMnI6 monolayer, and shows its essential influence on the low-energy excitation and critical behavior of the spin lattice. With these insights, it would be interesting to revisit existing magnetic materials for identifying potentially sizable anisotropic biquadratic exchange interactions, especially for those simultaneously harboring high-spin state and strong spin-orbit coupling. The former is universally required for biquadratic or even higher-order exchange interactions, while the latter is essential for inducing anisotropy. Contrasting the Cr and Mn sublattices of CrMnI6 in terms of the negligible and pronounced anisotropic biquadratic exchange couplings, it is natural to perceive that band-filling is also an important factor. The anisotropic biquadratic exchange coupling is expected to play an important role in predicting magnetic properties and interpreting experimental results when its energy scale is comparable with the anisotropy from the bilinear order (both single-ion and pairwise contribution), or even overwhelms the latter. Relevant phenomena for manifestation include the magnetic ground state, magnetocrystalline anisotropy, low-energy excitations, either collective (e.g. magnons) or solitonic (e.g. skyrmions or merons), and magnetic critical behavior of magnetic materials. On the theoretical side, it is convenient to contrast these properties with and without involving the anisotropic biquadratic term to quantify its influence, while on the experimental side, hints on its existence might arise from failure of interpreting some observations based solely on the bilinear spin model.

Summarizing, we have systematically investigated the single-ion, pairwise exchange, and magnetocrystalline anisotropy of monolayer CrMnI6, a recently predicted 2D magnet featured by in-plane inversion symmetry breaking that is distinctly different from the parental CrI3 and its existing Janus derivatives. The bipartite spin lattice of CrMnI6 enables coexistence of giant DMI and strong XXZ-type biquadratic coupling within the Mn sublattice with high-spin state. The interplay of anisotropic microscopic couplings gives rise to strongly preferred in-plane magnetization, facilitating the system to harbor nanometric bimeronic excitations and exhibit Berezinskii–Kosterlitz–Thouless-like critical behavior. Collectively, these central findings characterize CrMnI6 as an emergent versatile member in the family of 2D magnets for realizing intriguing topological magnetism and critical phenomena. The present study may also stimulate further interests in more in-plane inversion asymmetric 2D magnets containing multiple magnetic species and hosting unexplored anisotropic magnetic properties, given the recent progress in controllable growth of such compounds48.

Methods

Ab initio calculations

We perform first-principles calculations to determine the spin exchange interactions in CrMnI6 monolayer implementing the Vienna Ab initio Simulation Package (VASP)49. The projector augmented wave method50,51 is used and the energy cutoff for plane waves to expand the valence electron wave functions is 350 eV. The gradient-corrected functional parameterized by Perdew, Burke and Ernzerhof (PBE)52 is adopted to treat the electron exchange-correlation. A Γ-centered k-mesh is used to sample the Brillouin zone, with a grid density of 9 × 9 × 1, 4 × 4 × 1, and 2 × 2 × 1 for unit cell, 2 × 2, and 3 × 3 supercell respectively. Denser k-grids have been tested to ensure the convergence of calculated total energy and derived exchange parameters. A constrained magnetic field is imposed to guide the electronic state converging to the designated spin configurations53. A high accuracy energy convergence threshold of 10−7 eV/cell is implemented in the self-consistent calculations. To account for the strong onsite Coulomb repulsion of the d shell electrons of Cr and Mn ions, the rotationally invariant DFT+U scheme proposed by Dudarev et al.54 is implemented, with the effective U values being 2 and 4 eV respectively. A detailed discussion surrounding the influence of effective U values on the studied magnetic properties is presented in Supplementary Note 3 and Supplementary Figure 5. Visualization of crystal structure is enabled by VESTA55.

The parameterization of the bilinear spin model in Eq. (1) is accomplished by using the four-state method24,25,26. This method can delicately cancel out interactions with irrelevant spins and has been widely implemented for mapping the ab initio total energy to an effective spin Hamiltonian. The single-ion anisotropy and NN exchange couplings are calculated within the 2 × 2 supercell, while the NNN and TNN exchange couplings are calculated using the 3 × 3 supercell.

In our calculations, we constrain the orientations of the atomic magnetic moments to specific directions following the four-state method, and relax their magnitudes to converge the charge density to the constrained local minimum. We inspect the results from two aspects to warrant that the constrained-magnetism calculations have converged to the desired state. (1) The local magnetic moments obtained from the constrain-magnetism calculations have same amplitude as those of the unconstrained collinear case (3 and 4 μB for Cr3+ and Mn3+ respectively); (2) the penalty energy due to the constraint has been minimized to less than 0.02 meV by properly choosing the Lagrangian multiplier λ53. Specifically, for the CrMnI6 monolayer studied in the present work, our extensive testing calculations suggest that λ = 2 works very well in achieving convergence of both magnetic moments and penalty energy.

Atomistic LLG simulations

To explore potential chiral magnetic structures and their dynamics, we numerically integrate the LLG equation43

$$\frac{d{{{{\bf{n}}}}}_{i}}{dt}=-\frac{\gamma }{(1+{\alpha }^{2}){\mu }_{i}}[{{{{\bf{n}}}}}_{i}\times {{{{\bf{B}}}}}_{i}^{{{{\rm{eff}}}}}+\alpha {{{{\bf{n}}}}}_{i}\times ({{{{\bf{n}}}}}_{i}\times {{{{\bf{B}}}}}_{i}^{{{{\rm{eff}}}}})].$$
(3)

Here the subscript i indexes the spin sites; the first and second terms on the right-hand side represent respectively the precession and damping of the normalized local spin ni; γ is the electron gyromagnetic ratio, and α is the Gilbert damping parameter for which we take the value of 0.3 in our simulations. The local effective field \({{{{\bf{B}}}}}_{i}^{{{{\rm{eff}}}}}=-\partial H/\partial {{{{\bf{n}}}}}_{i}\) originates from both the intrinsic exchange couplings and external magnetic field.

We numerically integrate the LLG equation [Eq. (3)] with time to model the dynamics of localized spins formed by Cr + Mn honeycomb lattice. To tackle with the complex spin interaction as described by combining Eqs. (1) and (2), we have developed an in-house code56 based on Python and parallelized by message passing interface (MPI). The time step is set to δt = 1 fs and the Depondt modified Heun’s method57 is implemented for numerical integration so that the magnitudes of spins conserve throughout the simulations. Periodic boundary condition is applied in all simulations. The temporal effect is modeled by adding a thermal field to the local effective exchange field in Eq. (3), which scales with the temperature58

$${{{{\bf{B}}}}}_{i}^{th}=\sqrt{\frac{2\alpha {k}_{B}{\mu }_{i}}{\gamma \delta t}}{{{{\boldsymbol{\eta }}}}}_{i}(T)$$
(4)

Here ηi(T) is the white noise for spin site i, which obeys the normal random distribution and is updated for each time step; kB is the Boltzmann constant, T is the temperature in K, and other quantities follow Eq. (3). This modulation converts the LLG equation from deterministic to stochastic in the spirit of Langevin dynamics59.

In the atomistic LLG simulations, the spin lattice is modeled by a normalized vector field, namely, each classic spin is treated as a unit vector. The bipartite characteristic of the studied CrMnI6 monolayer is captured by the following technical treatments. (1) When calculating the effective exchange field \({{{{\bf{B}}}}}_{i}^{{{{\rm{exch}}}}}\), the single-ion anisotropy and bilinear exchange couplings are separately considered for the two sublattices to distinguish Cr and Mn, and the BQ-type exchange only exists in the Mn-sublattice following the first-principle results. The spin quantum numbers (S=3/2 for Cr and S=2 for Mn) are absorbed into the single-ion anisotropy and exchange-coupling parameters. (2) When calculating the torque induced by the external Zeeman fields \({{{{\bf{B}}}}}_{i}^{{{{\rm{ext}}}}}\) (including the stochastic field mimicking the thermal effect), the local moments of 3 and 4μB are multiplied for Cr3+ and Mn3+ respectively.

Calculation of topological charges

The topological charge Q depicts the evolution of geometric phase of chiral magnetic structures. In micromagnetic systems where the magnetization n(r) and its spatial gradients are continuous, the topological charge can be calculated by mapping the 2D spatial magnetization to the surface of a sphere13

$$Q=\frac{1}{4\pi }{\int}_{S}{{{\bf{n}}}}({{{\bf{r}}}})\cdot [{\partial }_{x}{{{\bf{n}}}}({{{\bf{r}}}})\times {\partial }_{y}{{{\bf{n}}}}({{{\bf{r}}}})]d{{{\bf{r}}}}.$$
(5)

In atomic magnetic lattices with discrete spin sites, Q is calculated by using the scheme proposed by Berg and Lüscher44,

$$Q=\frac{1}{4\pi }\mathop{\sum}\limits_{l}{A}_{l},$$
(6)

with

$$\cos \left(\frac{{A}_{l}}{2}\right)=\frac{1+{{{{\bf{n}}}}}_{i}\cdot {{{{\bf{n}}}}}_{j}+{{{{\bf{n}}}}}_{j}\cdot {{{{\bf{n}}}}}_{k}+{{{{\bf{n}}}}}_{k}\cdot {{{{\bf{n}}}}}_{i}}{2(1+{{{{\bf{n}}}}}_{i}\cdot {{{{\bf{n}}}}}_{j})(1+{{{{\bf{n}}}}}_{j}\cdot {{{{\bf{n}}}}}_{k})(1+{{{{\bf{n}}}}}_{k}\cdot {{{{\bf{n}}}}}_{i})}$$
(7)

where i, j, and k are indices of sites on a triangular plaquette from the Delaunay triangulation of the spin lattice, and Al is the solid angle measuring the relative canting of the three spins (See ref. 60 for detailed sketch).