Biquadratic exchange interactions in two-dimensional magnets

Abstract

Magnetism in recently discovered van der Waals materials has opened several avenues in the study of fundamental spin interactions in truly two-dimensions. A paramount question is what effect higher-order interactions beyond bilinear Heisenberg exchange have on the magnetic properties of few-atom thick compounds. Here we demonstrate that biquadratic exchange interactions, which is the simplest and most natural form of non-Heisenberg coupling, assume a key role in the magnetic properties of layered magnets. Using a combination of nonperturbative analytical techniques, non-collinear first-principles methods and classical Monte Carlo calculations that incorporate higher-order exchange, we show that several quantities including magnetic anisotropies, spin-wave gaps and topological spin-excitations are intrinsically renormalized leading to further thermal stability of the layers. We develop a spin Hamiltonian that also contains antisymmetric exchanges (e.g., Dzyaloshinskii–Moriya interactions) to successfully rationalize numerous observations, such as the non-Ising character of several compounds despite a strong magnetic anisotropy, peculiarities of the magnon spectrum of 2D magnets, and the discrepancy between measured and calculated Curie temperatures. Our results provide a theoretical framework for the exploration of different physical phenomena in 2D magnets where biquadratic exchange interactions have an important contribution.

Introduction

The finding of magnetism in atomically thin van der Waals (vdW) materials^1,2 has attracted an increasing amount of interest in the investigation of magnetic phenomena at the nanoscale³. Important in the understanding and applications of 2D vdW magnets in real technologies is the elucidation of fundamental interactions that determine their magnetic properties, such as the exchange interactions between the spins. These interactions govern the magnetic ordering and can be either symmetric, which determine collinear ferromagnets and anti-ferromagnets, or antisymmetric, which promote topological non-trivial spin textures, e.g. skyrmions. Higher-order exchange terms involving the hopping of two or more electrons play a pivotal role in the spin-ordering of low-dimensional nanostructures. For instance, biquadratic (BQ) exchange interactions are critical in the elucidation of the magnetic features of several systems, such as multilayer materials⁴, perovskites⁵, iron-based superconductors^6,7, iron tellurides⁸ and oxides⁹. Indeed, in materials where the exchange is for some reason weak¹⁰ (e.g., low-temperature magnets) BQ exchange has a particularly strong influence being the case of several 2D magnets discovered so far^11,12.

Here we identify that several families of 2D magnets including metals, insulators and small band gap semiconductors, develop substantially large BQ exchange interactions. The delicate interplay between the superexchange process through the non-magnetic atom and the Coulomb repulsion at neighboring spin-sites involving more than one electron induces sizable corrections to the total energy of the systems beyond bilinear spin models, e.g., Kitaev, Heisenberg, Ising. We developed a generalized non-Heisenberg spin Hamiltonian that includes both BQ and Dzyaloshinskii-Moriya interactions (DMI), providing a universal picture of the spin properties of 2D vdW magnets. We show that while BQ exchange interactions give substantial contributions to the thermal properties, such as in critical temperatures (T_c), non-collinear spin effects via DMI are negligible. The model also offers insights via analytical equations into the spin excitations of 2D materials as a general formalism is developed for materials that hold honeycomb crystal structure, ferromagnetism and out-of-plane easy axis in a universal basis. Our results provide the conceptual framework to understand a variety of 2D magnetic materials in a consistent way explaining numerous experimental observations, including controversies on the magnetic properties of CrI₃ or CrBr₃.

Results

Biquadratic exchange interactions

In order to calculate the different exchange contributions to the total energy at the level of first-principles methods (see Supplementary Sections 1–4 for details), we map the angular dependence of the spins S_j = μ_ss_j, where μ_s is the magnetic moment and ∣s_j∣ = 1, in the unit cell of the layered material^5,13,14 (Fig. 1a). We rotate the spins by θ between two known spin configurations: from ferromagnetic (FM) at θ = 0, to anti-ferromagnetic (AFM) at θ = 180^o. Small steps in θ generate a path of quasi-continuously configurations where both energy and magnetization are allowed to relax self-consistently without any fixed constraint on the direction. The resulting curve in energy includes contributions from bilinear (BL) exchanges up to higher-order terms, e.g., BQ exchange interactions. We used different supercells that resulted in no variations of the results. We quantify the contribution of each kind of interactions using the following non-Heisenberg spin Hamiltonian:

$${\mathcal{H}}=-\mathop {\sum}\limits_{ij}{J}_{ij}({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j})-\mathop {\sum}\limits_{ij}{\lambda }_{ij}{S}_{i}^{z}{S}_{j}^{z}-\mathop {\sum}\limits_{i}{D}_{i}{\left({{\bf{S}}}_{i}\cdot {{\bf{e}}}_{i}\right)}^{2}-\mathop {\sum}\limits_{ij}{K}_{ij}{\left({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\right)}^{2}$$

(1)

where J_ij and λ_ij are the isotropic and anisotropic BL exchanges between spins S_i and S_j on atomic sites i and j; D_i is the on-site anisotropy with easy axis e_i; and K_ij is the BQ exchange interactions which is due to electron hopping between two adjacent sites¹⁵. We restrict the discussions to first nearest-neighbor BQ interactions, that is, K_ij = K_bq, and K_ij = 0 otherwise. This assumption has been shown to be sufficient to study a variety of magnetic systems with higher-order exchanges^5,6,8,9. We can write Eq.(1) in a similar form separating the terms with angular and non-angular dependence as ${E}_{bq}^{tot}\left(\theta \right)={A}_{0}^{bq}+{A}_{1}^{bq}\cdot {S}^{2}\cos (\theta )+{A}_{2}^{bq}\cdot {S}^{4}{\cos }^{2}(\theta )$, where S is the spin moment. The different coefficients can be interpreted as the corresponding amount of BL (${A}_{1}^{bq}$) and BQ (${A}_{2}^{bq}$) exchanges, and the on-site energy as the spins are perpendicular to each other (${A}_{0}^{bq}$). Supplementary Section 4 gives a thorough discussion on these coefficients and how to extract analytical equations for their interpretation using Eq. (1). We extract ${A}_{0}^{bq}$, ${A}_{1}^{bq}$ and ${A}_{2}^{bq}$ from first-principles simulations for the variation of the total energy versus θ (Supplementary Section 5).

Fig. 1: Biquadratic exchange interactions in 2D magnets.

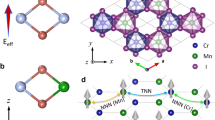
a Diagram of the rotation of spins S_i and S_j in the unit cell (defined by vectors a₁ and a₂) of a 2D magnet by a relative angle θ between them. Spins are rotated symmetrically in opposite directions from 0^o to 180^o. b–e Relative total energy (eV) as a function of θ(^o) for different monolayers of 2D magnets: trihalides (CrX₃, X = F, Cl, Br, I), metal tribromides (MBr₃, M = Mn, Cu, Fe, V), chromium based ternary tellurides (Cr₂X₂Te₆, X = Ge, P, Si), manganese based ternary chalcogenides (Mn₂P₂X₆, X = S, Se, Te), transition metal dichalcogenides (MnX₂, X = S, Se, Te) of different phases (2H, 1T) and an iron-based dichalcogenide (2H-FeS₂). The reference energy is taken at 0^o as the spins oriented at the same direction. Rotations can occur in-plane or out-of-plane with similar behavior. Symbols are calculated energies. Dashed lines correspond to a quadratic fitting using ${E}_{bq}^{tot}\left(\theta \right)={A}_{0}^{bq}+{A}_{1}^{bq}\cdot {S}^{2}\cos (\theta )+{A}_{2}^{bq}\cdot {S}^{4}{\cos }^{2}(\theta )$, while color filling areas indicate the deviation between the quadratic ${E}_{bq}^{tot}$ and a linear fitting using ${E}_{bl}^{tot}\left(\theta \right)={A}_{0}^{bl}+{A}_{1}^{bl}\cdot {S}^{2}\cos (\theta )$. Materials that show large deviation, such as CuBr₃ or 2H-FeS₂, develop large BQ exchange interactions. f Logarithm of the total energies (DFT) for the dataset in b–e, as a function of θ. Data analytics using polynomial regression (least-squares algorithm) in terms of linear (Q¹), quadratic (Q²) and cubic (Q³) approaches is evaluated over the calculated DFT energies (dots).

We apply this procedure for a total of 50 compounds including the most common 2D magnets studied up to date including several families of trihalides (MX₃, M = Ti, V, Cr, Mn, Fe, Ni, Cu; X = F, Cl, Br, I), metal tribromides (MBr₃, M = Mn, Cu, Fe, V), chromium based ternary tellurides (Cr₂X₂Te₆, X = Ge, P, Si), metal based ternary chalcogenides (M₂P₂X₆, M=V, Cr, Mn, Fe, Co, Ni; X = S, Se, Te), and transition metal dichalcogenides (MX₂, M = Co, Fe, V; X = S, Se, Te) of different phases (2H, 1T). Surprisingly, as the spins are spatially rotated away a sizable deviation from a $\cos \theta$-like behavior characteristic of BL exchange interactions (shaded area) is observed (Fig. 1b–e). The overall trend seems independent of the stoichiometric formula or the atomic elements composing the structure. The universal character of the higher-order exchange process in layered materials can be appreciated clearer in Fig. 1f where data-analytics using regression algorithms (linear, quadratic, cubic) was evaluated over the computed data. The best match between regression and DFT energies is for regressions beyond linear. This suggested that even more complex magnetic interactions may take place in 2D magnetic materials such as 3-, 4-spin interactions^16,17, and chiral biquadratic^18,19 which are not studied here. Materials with alike chemical environment (e.g., bond lengths, electron affinity, binding energy) such as CrI₃, CrBr₃ and CrCl₃ present close variation of the energy and consequently similar magnitudes of the BQ exchange (Table 1). Other compounds tend to gain energy with the spin rotation and stabilize in a different magnetic coupling, for instance, CrF₃ (Fig. 1b) becomes AFM ordered. This is also the case of Mn-based compounds, 2H-MnS₂, 2H-MnSe₂, MnPS₃, MnPSe₃ (Fig. 1d, e), which agreed with magnetometry measurements^20,21,22. It is noteworthy that CuBr₃ and 2H-FeS₂ have substantially larger magnitudes of BQ exchange (Table 1) comparable to more complex materials, i.e., ferropnictides, where spin and electronic correlations are known to play a key role in the determination of their superconducting and strongly-correlated properties²³. Both CuBr₃ and 2H-FeS₂ have relatively small BL exchange in the range of 5.87−6.88 meV with S = 1. For materials with small BL exchange higher-order exchange tends to be sizeable¹⁰. This result calls for further theoretical and experimental work on these two compounds whether unusual electronic interactions can be found. Furthermore, we noticed that several other compounds could not show a clear trend with θ apart from those where a specific magnetic ordering is stabilized, e.g., θ = 0, 180^o (Supplementary Section 6). Materials that are unable to stabilize different spin orientations are either due to strong magnetic anisotropy where a preferential spin orientation is too strong to be tilted (e.g. Ising magnets) or different spin solutions are not energetically stable ending up in non-magnetic phases²⁴.

Table 1 Calculated biquadratic exchange (K_bq) for several 2D magnetic materials with honeycomb (faint blue) and hexagonal (faint red) lattices using non-collinear ab initio methods as explained in the text.

We have also checked whether other models can give a sound description of the magnetic properties of the quadratic dependence of the energy as a function of θ. In particular, we considered two models: a Kitaev model^25,26, and a Heisenberg model including biquadratic on-site magnetic anisotropy. For the latter, the magnitudes of the biquadratic on-site anisotropies are several orders of magnitude smaller than BQ exchange within the range 3.87–14.32μeV (see details in Supplementary Section 7). For the former, there is no quadratic dependence on θ for the Kitaev model. We can expand the Kitaev Hamiltonian²⁵ assuming a rotation by angle θ between the spins to show that a fitting equation of the form of ${E}_{Kitaev}^{tot}\left(\theta \right)={B}_{0}+{B}_{1}\sin (2\theta )$ can be extracted (see details in Supplementary Section 8). These results suggest that BL models are insufficient to describe the magnetic features of 2D vdW magnets.

A Hubbard-based microscopic model

To understand the microscopic mechanism of the BQ exchange in 2D materials, we will use the following 2D half-filled Hubbard Hamiltonian applied to the honeycomb lattice (Fig. 2a, b):

$$H=-{t}_{eff}\mathop {\sum}\limits_{\langle ij\rangle ,\sigma }{c}_{i,\sigma }^{\dagger }{c}_{j,\sigma }+U\mathop {\sum}\limits_{i}{n}_{i\uparrow }{n}_{{\rm{i\downarrow }}}+\mathop {\sum}\limits_{i,\sigma }{\mu }_{i,\sigma }{n}_{i,\sigma },$$

(2)

where indices i and j denote the lattice sites, the d-spin states on the metal atoms (M_A,B) are labeled as σ = ↑, ↓, the sum <ij> is over the nearest neighbors and t_eff is the effective nearest neighbor hoping between M_A,B ions. t_eff is due to the hybridization between 3dⁿ and np orbitals (n = 2, 3, 4, 5 depending on the atomic element involved) at M_A,B and X atoms, respectively (Fig. 2b). The direct hopping between M_A,B scales with t_dd ~ r⁻⁵ and therefore for relatively big distances can be neglected¹⁵. U > 0 is the non-negative on-site Coulomb repulsion, ${c}_{i,\sigma }^{\dagger }$(c_i,σ) is the creation (annihilation) operator for a fermion with spin σ at site i, $n={c}_{i,\sigma }^{\dagger }{c}_{i,\sigma }$ is the density operator and μ_i,σ is the chemical potential which controls the filling of the bands. Second-order perturbation theory in Eq.(2), assuming U > > t_eff, gives the energy contributions of the Heisenberg exchanges^27,28:

$$\begin{array}{rcl}{J}_{{\rm{FM}}}^{(2)}&=&{t}_{eff}^{2}/(U-{U}_{ex})\\ {J}_{{\rm{AFM}}}^{(2)}&=&{t}_{eff}^{2}/(U+{U}_{ex})\\ {J}_{{\rm{bl}}}&=&{t}_{eff}^{2}\frac{2{U}_{ex}}{{U}^{2}\,-\,{U}_{ex}^{2}}\end{array}$$

(3)

where ${J}_{{\rm{FM}}}^{(2)}$ and ${J}_{{\rm{AFM}}}^{(2)}$ are the exchange energies for FM and AFM coupling at second-order, and the BL exchange is defined as ${J}_{{\rm{bl}}}={J}_{{\rm{FM}}}^{(2)}-{J}_{{\rm{AFM}}}^{(2)}$. U_ex is an energy correction for the internal spin exchange whether a spin flip is required during the hopping between M_A,B sites (Fig. 2b)²⁸. Such term can be used to stabilize or destabilize spin transfer through the M_A,B − X covalent bonds as the exchange occurs^15,28. If the electron-hopping is to an occupied orbital of the neighboring site, U_ex will favor AFM alignment of the two spins via a superexchange interaction (see Supplementary Section 9 for details). However, if the electron-hopping is to an unoccupied or a virtual state, a FM alignment will be favored by U_ex²⁹. The competition between the amount of energy U_ex to stabilize a specific coupling and the Coulomb repulsion U between the electrons at an energy state may compensate each other leading to a small value of J_bl. Indeed, several 2D magnets have shown low-temperature magnetism^1,2,12 which is directly related with the small magnitude of the exchange interactions. In this case, it is necessary to extend the perturbation in t_eff/U to fourth-order in Eq. (2) involving at least one electron from both M_A,B sites which resulted in¹⁵:

$$\begin{array}{rcl}{J}_{{\rm{FM}}}^{(4)}&\propto &{t}_{eff}^{4}/{(U-{U}_{ex})}^{3}\\ {J}_{{\rm{AFM}}}^{(4)}&\propto &{t}_{eff}^{4}/{(U+{U}_{ex})}^{3}\\ {K}_{{\rm{bq}}}&=&{t}_{eff}^{4}\frac{2(3{U}^{2}{U}_{ex}+{U}_{ex}^{3})}{{({U}^{2}-{U}_{ex}^{2})}^{3}}\end{array}$$

(4)

with ${K}_{{\rm{bq}}}={J}_{{\rm{FM}}}^{(4)}-{J}_{{\rm{AFM}}}^{(4)}$ being the BQ exchange energy. Both Eqs. (3)–(4) show that a competition between FM and AFM couplings takes place once the electrons are hopping between different spin sites. The stabilization of one or another magnetic order is determined by several factors such as the ligand-field splitting Δ₀ between t_2g and e_g states in the metal atom in the honeycomb lattice. As the filling of both type of states determines the magnitude of the 3d − sp hybridization between metals and ligands, we can approach Δ₀ ≈ U − U_ex being proportional to the bandgap of the material¹⁰. This condition is valid as long as the magnitudes of U and U_ex do not compete to each other. Since U_ex is an energy correction of spin stabilization, it should comply with Hund’s rule where unpaired spins occupy other states of the 3d shell (Fig. 2b). It has been shown that the role of high-order exchange interactions increases on reduction of the bandgap mediated by the non-magnetic atoms which is related to the ratio of BQ and BL exchanges^27,30. If we divide Eq. (4) and Eq. (3) and use the definition of Δ₀, we can write a direct relationship between the exchange interactions and the bandgap for 2D magnets as:

$${K}_{{\rm{bq}}}/{J}_{{\rm{bl}}}={t}_{eff}\frac{4{U}^{2}+{\Delta }_{0}^{2}-2U{\Delta }_{0}}{{\Delta }_{0}^{2}{\left(2U-{\Delta }_{0}\right)}^{2}}$$

(5)

This equation can be understood as a direct interplay between the Coulomb repulsion and the hopping of electrons between different sites subjected to the crystal field or bandgap of the material. We can consider two situations in Eq. (5): Δ₀ → 0 and Δ₀ → 2U which correspond to small and large bandgap materials, respectively. This resulted in:

$${K}_{{\rm{bq}}}/{J}_{{\rm{bl}}}\propto {t}_{eff}{\left.\frac{1}{{\left({\Delta }_{0}\right)}^{2}}\right|}_{{\Delta }_{0}\to 0}$$

(6)

$${K}_{{\rm{bq}}}/{J}_{{\rm{bl}}}\propto {t}_{eff}{\left.\frac{1}{{\left(2U-{\Delta }_{0}\right)}^{2}}\right|}_{{\Delta }_{0}\to 2U}$$

(7)

Fig. 2c shows the variation of K_bq/J_bl as a function of Δ₀ for the core of materials displaying BQ exchange interactions. Strikingly, both Eqs. (6)–(7) correctly describes the overall behavior observed in our simulations. Materials with similar bonding environment, for instance, either in terms of Cr (Mn) atoms follow an increase (decrease) of K_bq/J_bl with the bandgap, respectively. It is worth mentioning that as the compounds tend to a AFM spin alignment^10,29, i.e., CrF₃, they increase the value of K_bq/J_bl being the case within the Cr-based trihalide family (CrX₃, X = F, Cl, Br, I). There is also an abrupt change in behavior for narrow bandgap materials and metals with no dependence on Δ₀ (inset in Fig. 2c). These results indicate that one can design the amount of BQ exchange in a 2D magnet tuning its bandgap, for instance using an electric bias as recently used in CrI₃³¹.

Fig. 2: Bilinear (BL) and biquadratic (BQ) exchange interactions in 2D magnets.

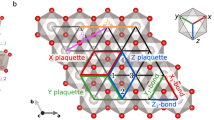
a Schematic of the BL exchanges at first (J₁), second (J₂) and third (J₃) nearest neighbors (NN), and BQ exchange (K_bq) at first NN. Single and double line diagrams represent BL and BQ exchanges, respectively. The two inequivalent magnetic sites in the honeycomb lattice are shown by faint blue (M_A) and faint red (M_B) dots. The blue orbits inside of the hexagons represent the magnetic flux ϕ generated by the second-NN Dzyaloshinskii-Moriya interactions (DMI), which breaks the inversion symmetry of the lattice. The dashed lines show the magnon hopping between second NN as the magnons gain a phase given by ϕ (see text). The lattice vectors u_i (i = 1, 2) and τ_j (i = 1, 2, 3) show the first and second NN on the lattice, respectively. b Zoom-in on the BQ exchange process involving two electrons between sites M_A and M_B with 3d^m electrons in the valence. The BQ exchange K_bq is mediated by non-magnetic atoms X with a valence given by np electrons, where n will depend on the atomic elements involved. An on-site Hubbard U term is at the M_A,B sites with U_ex representing the potential spin-splitting when the spins of the electrons involved in the BQ exchange align ferro- or anti-ferromagnetically (Supplementary Section 4). The difference between up and down spin coupling is given by 2U_ex. c K_bq/J_bl versus Δ₀(eV) for all materials displaying BQ exchange interactions. Magnetic atoms with similar chemical environment in terms of Coulomb repulsion, exchange interactions and valence follow alike behavior for K_bq/J_bl. For instance, Cr in blue and Mn in green (inset). Orange dots show materials with dissimilar electronic configurations but with Δ₀ = 0.

Thermal effects in 2D magnets

To verify whether BQ exchange interactions will have any effect on the thermal properties of 2D vdW magnets, we have implemented Eq. (1) within the Monte Carlo Metropolis algorithm with an adaptive move³². In the spin model we assume a classical spin vector S_i on each atomic site i. The quantization vector for the spin is a local quantity which intrinsically includes the effects of local thermal spin fluctuations, magnon processes and spin excitations. In our implementation the BQ exchange is quite general and can be applied to any pair-wise exchange interaction of arbitrary range. We also consider an additional term in Eq. (1) including the local Zeeman field B on the magnetic ions with a length of the local atomic moment μ_i arising from the BQ exchange interactions as:

$${\mathcal{H}}=-\mathop {\sum}\limits_{ij}{J}_{ij}({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j})-\mathop {\sum}\limits_{ij}{\lambda }_{ij}{S}_{i}^{z}{S}_{j}^{z}-\mathop {\sum}\limits_{i}{D}_{i}{\left({{\bf{S}}}_{i}\cdot {{\bf{e}}}_{i}\right)}^{2}-\mathop {\sum}\limits_{ij}{K}_{ij}{\left({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\right)}^{2}-\mathop {\sum}\limits_{i}{\mu }_{i}{{\bf{S}}}_{i}\cdot {{\bf{B}}}_{i}$$

(8)

For atomistic spin dynamics simulations, the effective field due to the biquadratic exchange are calculated via the first-derivative of Eq. (8) on the different spin components as:

$${H}_{bq,i}^{l}=-\frac{1}{{\mu }_{i}}\frac{\partial {\mathcal{H}}}{\partial {S}_{i}^{l}}=2{K}_{{\rm{bq}}}{S}_{j}^{l}\left({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\right)$$

(9)

where l = x, y, z represents the geometrical coordinates at the atomic sites i(j), and $({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j})={S}_{i}^{x}{S}_{j}^{x}+{S}_{i}^{y}{S}_{j}^{y}+{S}_{i}^{z}{S}_{j}^{z}$. The effective field ${H}_{bq,i}^{l}$ therefore contributes to the total field describing the time evolution of each atomic spin using the stochastic Landau-Lifshitz-Gilbert equation³³. We calculate up to third nearest-neighbors λ_ij and J_ij in Eq. (1) on a representative set of 2D magnets, e.g., Cr-based trihalide family (Table 2). Supplementary Section 10 gives a thorough discussion on the calculation of the exchange parameters. Figure 3 shows the behavior of the magnetization (M/M₀, where M₀ is the saturation magnetization at 0 K) and the logarithm of the magnetic susceptibility ($\mathrm{ln}\,\chi$) as a function of temperature T(K) for CrI₃, CrBr₃ and CrCl₃. Intriguingly, the inclusion of BQ exchange interactions give sizable thermal effects on both M/M₀ and $\mathrm{ln}\,\chi$ for all materials (Supplementary Section 11). By fitting the Monte Carlo simulations with ${\rm{M}}({\rm{T}})={{\rm{M}}}_{0}{\left(1-\frac{{\rm{T}}}{{{\rm{T}}}_{{\rm{c}}}}\right)}^{\beta }$ (where β is the critical exponent) we can notice that the Curie temperatures T_c changes by several Kelvins with the inclusion of BQ exchange interactions. The calculated magnitudes of T_c for CrI₃ and CrBr₃ approach closely those measured for both compounds with almost no difference (Fig. 3a–d). The lack of experimentally measured T_c for monolayer CrCl₃ unable us to make a clear comparison with our simulations. The different amount of nearest-neighbors at BL exchanges (from 1st to 3rd) also produces substantial effects even though not enough to reproduce the experimental values of T_c for CrI₃ and CrBr₃. It is worth mentioning that different groups have reported distinct magnitudes of T_c for CrBr₃^{34,35,36[,37,38,39}, which may be due to different factors such as sample quality, defects, and doping levels. We believe that our simulations still provide an accurate picture showing the effects of the underlying exchange interactions for these low-dimensional magnets at the limit of an ideal, pristine crystal (see Supplementary Section 12). Moreover, several other materials display larger values of BQ exchange interactions (Table 1) indicating that higher-exchange interactions should be taken into account on the description of their magnetic properties.

Table 2 Computed values of several magnetic quantities for CrX₃ (X = I, Br, Cl, F) at different number of nearest neighbors: isotropic (J₁, J₂, J₃) and anisotropic (λ₁, λ₂, λ₃) BL exchanges.

Fig. 3: Monte-Carlo simulations at different levels of theory including BL and BQ exchange interactions.

a, b Magnetization (M/M₀) and logarithm of the magnetic longitudinal susceptibility lnχ_m (a.u.) versus temperature (K), respectively, for monolayer CrI₃. Calculated and fitting curves using M/M${}_{{\rm{0}}}={(1-{{\rm{T/T}}}_{{\rm{c}}})}^{\beta }$ (where T_c and β are the critical temperature and coefficient, respectively) are shown by dots and solid lines, respectively, in a. Solid lines in b show the interpolation between points. Different curves correspond to different number of NN, from one up to third, taken into account in BL interactions: BL^1st (faint red), BL^1st,2nd,3rd (faint blue). Results including BQ exchange at first NN (BQ^1st) with different number of BL exchanges are shown in purple (BL^1st + BQ^1st) and faint green (BL^1st,2nd,3rd + BQ^1st). Critical temperatures (T_c) at each level of BL and BQ exchange interactions are indicated at b with the maximum magnitude of lnχ_m (a.u.) highlighted. Magnetic susceptibility is shown in logarithm scale for clarify. Experimental critical temperature (T${}_{{\rm{c}}}^{\exp }$) is included for comparison. c, d and e, f similar plots as in a, b, for CrBr₃ and CrCl₃, respectively. Critical exponents β extracted from the simulations for BL^1st,2nd,3rd + BQ^1st are β = 0.22, 0.24 and 0.28 for CrI₃, CrBr₃ and CrCl₃ respectively. Magnitudes of β for BL^1st,2nd,3rd are 0.25, 0.28 and 0.32 for CrI₃, CrBr₃ and CrCl₃ respectively.

Enhancement of magnetic stability

An outstanding remark on the existence of BQ interactions in 2D magnets is on the implications on their magnetic features. It is well known that several materials developed macroscopic properties due to this higher-order exchange interactions. From paramagnetic measurements of Mn⁺² ions in MgO⁹, up to different magnetic phases in oxides^5,13,40, it is not clear whether BQ exchange induces any significant role effect on basic properties, such as critical temperatures or stability. To understand the intrinsic effect of higher-order exchange interactions in the thermal features of 2D magnetic materials and provide a consistent description of the underlying spin interactions, we have developed an analytical model based on spin-wave theory^37,38. We generalized Eq. (1) to second order contributions on the magnetic anisotropies which resulted in:

$$\begin{array}{l}{\mathcal{H}}=-\mathop {\sum}\limits_{ij}{J}_{ij}({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j})-\mathop {\sum}\limits_{ij}{\lambda }_{ij}{S}_{i}^{z}{S}_{j}^{z}-\mathop {\sum}\limits_{i}{D}_{i}{\left({{\bf{S}}}_{i}\cdot {{\bf{e}}}_{i}\right)}^{2}\\ -\mathop {\sum}\limits_{ij}{K}_{ij}{\left({{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}\right)}^{2}-\mathop {\sum}\limits_{i}{D}_{i}^{bq}{\left({{\bf{S}}}_{i}\cdot {{\bf{e}}}_{i}\right)}^{4}-\mathop {\sum}\limits_{ij}{\lambda }_{ij}^{bq}{\left({S}_{i}^{z}{S}_{j}^{z}\right)}^{2}\end{array}$$

(10)

where ${D}_{i}^{bq}$ and ${\lambda }_{ij}^{bq}$ are the BQ on-site anisotropy and BQ anisotropic exchange, respectively. We replace the spin operators S_i,j in Eq. (10) by bosonic creation (${a}_{i}^{\dagger }$, ${b}_{i}^{\dagger }$) and annihilation (a_i, b_i) operators over the honeycomb sub-lattices ${\mathcal{A}}$ and ${\mathcal{B}}$ using Holstein-Primakoff transformations³⁸:

For $i\in {\mathcal{A}}$sublattice:

$$\begin{array}{rcl}{S}_{i}^{z}&=&(S-{a}_{i}^{\dagger }{a}_{i})\\ {S}_{i}^{+}&\approx &\sqrt{2S}{a}_{i}\\ {S}_{i}^{-}&\approx &{a}_{i}^{\dagger }\sqrt{2S}\end{array}$$

For$i\in {\mathcal{B}}$sublattice:

$$\begin{array}{rcl}{S}_{i}^{z}&=&(S-{b}_{i}^{\dagger }{b}_{i})\\ {S}_{i}^{+}&\approx &\sqrt{2S}{b}_{i}\\ {S}_{i}^{-}&\approx &{b}_{i}^{\dagger }\sqrt{2S}\end{array}$$

where we assume that ${a}_{i}^{\dagger }{a}_{i}< < S$ and ${b}_{i}^{\dagger }{b}_{i}< < S$ for small deviations of the spins from their ground state orientations. This gives (see Supplementary Section 13 for details):

$$\tilde{{\mathcal{H}}}=\mathop {\sum}\limits_{i}\left(2\tilde{D}S+Z\cdot S(\tilde{J}+\tilde{\lambda })\right)({b}_{i}^{\dagger }{b}_{i}+{a}_{i}^{\dagger }{a}_{i})-\tilde{J}S\mathop {\sum}\limits_{\langle ij\rangle }\left({a}_{i}^{\dagger }{b}_{j}+{b}_{j}^{\dagger }{a}_{i}\right)$$

(11)

where the sum over i and j runs over the sub-lattices and first nearest neighbors, respectively, and Z is the number of first nearest-neighbors. This procedure outlines a strong implication of the inclusion of higher-order exchange interactions in the description of the magnetic properties of 2D magnets. That is, the enhancement of several magnetic quantities:

$$\tilde{J}\approx J+2{S}^{2}\cdot {K}_{{\rm{bq}}}$$

(12)

$$\tilde{\lambda }\approx \lambda +2{S}^{2}\cdot {\lambda }^{{\rm{bq}}}$$

(13)

$$\tilde{D}\approx D+2{S}^{2}\cdot {D}^{{\rm{bq}}}$$

(14)

where λ^bq and D^bq are the BQ anisotropic exchanges, and the BQ on-site magnetic anisotropy, respectively, for first nearest neighbors. Incidentally Eqs. (12)–(14) yield several implications on the magnetic properties of the sheets, in particular, on the stabilization of magnetism in truly 2D. It is well known that in order to overcome thermal fluctuations that could destroy any magnetic order³⁹, sizable magnetic anisotropies need to be developed to gap the low-energy modes in the magnon spectra. That is, a spin wave gap needs to appear at the energy dispersion to act as a barrier to excitations of long-wavelength spin waves. We can show that the relation between the spin wave gap taken into account BQ exchange interactions (Δ_bq) and that at the level BL exchange (Δ_bl) for first-nearest neighbors is given by (see Supplementary Section 13):

$${\Delta }_{bq}={\Delta }_{bl}+4{S}^{3}({D}^{bq}+\frac{3}{2}{\lambda }^{bq})$$

(15)

where ${\Delta }_{bl}=2S\left[D+\frac{Z\lambda }{2}\right]$. By using some parameters for monolayer CrI₃ from Table 2, and approaching the second term in Eq. (15) as D^bq + 3λ^bq ≈ 10.72 μeV (see Supplementary Section 7) we can estimate Δ_bl = 0.81 meV and Δ_bq = 1.0 meV. The magnitude of Δ_bq is consistent with recent measurements of the magnon dispersion for bulk CrI₃, which a spin wave gap of approximately 1.3 meV was measured⁴⁰. Furthermore, the increment of the on-site and anisotropic magnetic anisotropies (Eqs. (13)–(14)) indicates that not only spin-orbit mechanisms are behind the substantial anisotropy in CrI₃ but rather higher-order exchange processes. Such BQ exchange-driven large magnetic anisotropy mechanism has been proposed for iron-based superconductors^7,23,41 which successfully described their magnetic properties. A direct consequence Eqs. (12)–(14) is the increment of Curie temperatures by factor r given by (see Supplementary Section 13):

$$r=\frac{{\tilde{T}}_{C}}{{T}_{C}}\approx \frac{\tilde{J}\mathrm{ln}\,(1+2\pi JS/{\Delta }_{bl})}{J\mathrm{ln}\,(1+2\pi {\tilde{J}S/{\Delta }_{bq})}}.$$

(16)

where ${\tilde{T}}_{C}$ and T_C are the Curie temperatures with and without BQ interactions, respectively. Including few values in Eq. (16), we can roughly estimate an enhancement of r ≈ 39% for monolayer CrI₃ which follows the Monte Carlo calculations (Fig. 3a, b). It is worth noticing that the model in Eq. (11), i) takes into account only first-nearest neighbors in the exchange interactions, and ii) we assume a mean-field approach in the solution of the non-linear Holstein-Primakoff transformation (e.g. magnon-magnon interactions) to simplify the complex mathematical terms, i.e. four-operator product. Supplementary Section 14 provides a full discussion on the details involved.

Describing topological spin excitations through BQ and DMI

An intriguing question that raised by the presence of BQ exchange interactions is whether they play an important role in the description of magnetic quasiparticles such as magnons and non-trivial spin textures in 2D vdw magnets. It has recently been shown using neutron scattering⁴⁰ that CrI₃ magnet shows topological spin-excitations with two distinctive magnon bands separated by a bandgap of 4 meV at the Dirac K-point. In spite of the clear demonstration that CrI₃ can not follow an Ising model as initially pointed out¹, these results indicate that non-Heisenberg interactions play an important role in the creation of spin-excitations in 2D magnetic materials. Since the gap opening at K is related with the inversion symmetry breaking and appearance of DMI, chirality becomes crucial in the discrimination of the magnon bound states. Moreover, it has become well established^23,42,43,44 that isotropic spin interactions at the level of the BL Heisenberg models do not capture all features in the energy dispersion of spin-excitations in magnetic materials. There are additional contributions through uniaxial anisotropies, next-nearest neighbor interactions and the delicate balance between them, that need to be considered. In order to account for all these quantities, we extended the model in Eq. (1) with the addition of DMI:

$${{\mathcal{H}}}_{{\rm{latt}}}={\mathcal{H}}+\mathop {\sum}\limits_{\langle \langle ij\rangle \rangle }{{\boldsymbol{A}}}_{ij}\cdot \left({{\bf{S}}}_{i}\times {{\bf{S}}}_{j}\right)$$

(17)

where A_ij is the DMI between spins S_i and S_j. For a honeycomb ferromagnetic layer, with an easy axis perpendicular to the surface (z-direction), there is no breaking of the inversion symmetry of the lattice at first nearest-neighbors, e.g., ${{\boldsymbol{A}}}_{ij}^{1st}=0$. However, contributions from the second nearest-neighbors become non-negligible as space inversion is not present. Therefore, we consider the DMI vector as A = ν_ijA^zz, where A_z is the magnitude of the DMI along of the easy-axis, and ν_ij = ±1 represents the hopping of spins at second nearest-neighbors from sites i to j and vice-versa, respectively (Fig. 2a). Similarly as shown above, we can use Holstein-Primakoff transformations for J_i > 0 to write Eq. (17) in terms of bosonic creation and annihilation operators (see details in Supplementary Section 15):

$${{\mathcal{H}}}_{latt}={{\mathcal{H}}}_{BL}+{{\mathcal{H}}}_{BQ}+{{\mathcal{H}}}_{DMI}$$

(18)

where we separate the terms due to BL exchange (${{\mathcal{H}}}_{BL}$), from those due to BQ (${{\mathcal{H}}}_{BQ}$) and DMI (${{\mathcal{H}}}_{DMI}$) which can be written as:

$${{\mathcal{H}}}_{BL}={H}_{D}+\mathop{\sum }\limits_{i = 1}^{3}{H}_{i}^{Isotropic}+\mathop{\sum }\limits_{i = 1}^{3}{H}_{i}^{Anisotropic}$$

(19)

$${H}_{BQ}=-12{K}_{bq}{S}^{4}-2{K}_{bq}{S}^{3}\left( \mathop {\sum}\limits_{\langle ij\rangle }\left({b}_{j}^{\dagger }{a}_{i}+{a}_{i}^{\dagger }{b}_{j}\right)-{Z}_{1}\mathop{\sum }\limits_{i\in {\mathcal{A}}}^{N/2}{a}_{i}^{\dagger }{a}_{i}-{Z}_{1}\mathop{\sum }\limits_{i\in {\mathcal{B}}}^{N/2}{b}_{i}^{\dagger }{b}_{i}\right)$$

(20)

$${{\mathcal{H}}}_{DMI}=i{A}_{z}S\left(\mathop{\sum }\limits_{\langle \langle ij\rangle \rangle \in {\mathcal{A}}}^{N/2}\left({a}_{i}^{\dagger }{a}_{j}-{a}_{j}^{\dagger }{a}_{i}\right)+\mathop{\sum }\limits_{\langle \langle ij\rangle \rangle \in {\mathcal{B}}}^{N/2}\left({b}_{i}^{\dagger }{b}_{j}-{b}_{j}^{\dagger }{b}_{i}\right)\right)$$

(21)

where H_D is the on-site anisotropy term, and ${H}_{i}^{Isotropic}$ and ${H}_{i}^{Anisotropic}$ are respectively the isotropic and anisotropic parts of the BL exchange Hamiltonian taken into account up to third nearest-neighbors (i = 1, 2, 3). The sum in 〈ij〉 runs over the first nearest-neighbors at both sublattices ${\mathcal{A}}$ and ${\mathcal{B}}$ while that on 〈〈ij〉〉 runs over the second nearest-neighbors specifically on either ${\mathcal{A}}$ or ${\mathcal{B}}$ lattice. We notice that the second nearest neighbors not only break the inversion symmetry of the honeycomb lattice but also generate a magnetic flux ϕ involving A_z and J₂ given by:

$$\phi =ta{n}^{-1}({A}_{z}/{J}_{2})$$

(22)

The magnetic flux (circular arrow) can be appreciated in Fig. 2a when the magnons (dashed lines) hop between the second nearest-neighbors. This process introduces a phase ϕ_ij = μ_ijϕ (μ_ij = ±1) in the magnons as they hop from a site i to j, and vice-versa. The different magnitudes of μ_ij determine whether the hopping follows the flux and consequently induces nontrivial topological properties (e.g. chirality) similarly as in the Haldane model^45,46 for fermions. The topological features of the magnon bands can be described in the k−space by using the Fourier transform of the creation (${a}_{{\boldsymbol{k}}}^{\dagger }$, ${b}_{{\boldsymbol{k}}}^{\dagger }$) and annihilation (a_k, b_k) operators in Eq. (18) as:

$${\mathcal{H}}={{\mathcal{H}}}_{0}+\mathop {\sum}\limits_{{\boldsymbol{k}}}\left({a}_{{\boldsymbol{k}}}^{\dagger }\quad {b}_{{\boldsymbol{k}}}^{\dagger }\right)\left(\begin{array}{cc}{h}_{0}({\boldsymbol{k}})+{h}_{z}({\boldsymbol{k}})&{h}_{x}({\boldsymbol{k}})-i{h}_{y}({\boldsymbol{k}})\\ {h}_{x}({\boldsymbol{k}})+i{h}_{y}({\boldsymbol{k}})&{h}_{0}({\boldsymbol{k}})-{h}_{z}({\boldsymbol{k}})\end{array}\right)\left(\begin{array}{c}{a}_{{\boldsymbol{k}}}\\ {b}_{{\boldsymbol{k}}}\end{array}\right)$$

(23)

where the different terms can be written as (see Supplementary Section 15 for details):

$$\begin{array}{rcl}{{\mathcal{H}}}_{0}= -2DS-3({J}_{1}+{\lambda }_{1}){S}^{2}-6({J}_{2}+{\lambda }_{2}){S}^{2}-12K{S}^{4}\\ {h}_{0}({\boldsymbol{k}})={\varepsilon }_{0}-4\sqrt{{({J}_{2}S)}^{2}+{({A}_{z}S)}^{2}}C({\boldsymbol{k}})\\ {\varepsilon }_{0}= 2DS+({J}_{1}+{\lambda }_{1}){Z}_{1}S+6K{S}^{3}+6({J}_{2}+{\lambda }_{2})S+3{J}_{3}S\\ {h}_{x}({\boldsymbol{k}})= -({J}_{1}+2K{S}^{2})S\mathop{\sum }\limits_{j = 1}^{3}\cos ({\boldsymbol{k}}\cdot {{\boldsymbol{\tau }}}_{j})-{J}_{3}S\mathop{\sum }\limits_{j = 1}^{3}\cos ({\boldsymbol{k}}\cdot ({{\boldsymbol{u}}}_{j}+{{\boldsymbol{\tau }}}_{j}))\\ {h}_{y}({\boldsymbol{k}})= -({J}_{1}+2K{S}^{2})S\mathop{\sum }\limits_{j = 1}^{3}\sin ({\boldsymbol{k}}\cdot {{\boldsymbol{\tau }}}_{j})-{J}_{3}S\mathop{\sum }\limits_{j = 1}^{3}\sin ({\boldsymbol{k}}\cdot ({{\boldsymbol{u}}}_{j}+{{\boldsymbol{\tau }}}_{j}))\\ {h}_{z}({\boldsymbol{k}})= 4\sqrt{{\left({J}_{2}S\right)}^{2}+{\left({A}_{z}S\right)}^{2}}S({\boldsymbol{k}})\end{array}$$

(24)

where $C({\boldsymbol{k}})=\cos (\phi )\mathop{\sum }\nolimits_{j = 1}^{3}\cos ({\boldsymbol{k}}\cdot {{\boldsymbol{u}}}_{j})$ and $S({\boldsymbol{k}})=\sin (\phi )\mathop{\sum }\nolimits_{j = 1}^{3}\sin ({\boldsymbol{k}}\cdot {{\boldsymbol{u}}}_{j})$. The vectors τ_j and u_j are respectively between 1^st and 2^nd nearest neighbors (Fig. 2a).

The eigenvalues of Eq. (23) can be written in terms of the lower and upper energy bands as:

$${E}^{\pm }={h}_{0}({\boldsymbol{k}})\pm \sqrt{{h}_{x}{\left({\boldsymbol{k}}\right)}^{2}+{h}_{y}{\left({\boldsymbol{k}}\right)}^{2}+{h}_{z}{\left({\boldsymbol{k}}\right)}^{2}}$$

(25)

Note that Eqs. (24) and (25) are general for any honeycomb material with ferromagnetic order, easy-axis perpendicular to the surface and develop DMI and BQ exchange interactions. For instance, we can use them to predict the energy dispersion of the magnon bands over the first Brillouin zone (BZ) of any 2D magnet, e.g., CrI₃. Figure 4a–e shows different levels of theory either using a simple XXZ model or including more sophisticated terms through the BQ exchange, DMI or simultaneously all of them. It is clear that XXZ models without any contribution from DMI (Fig. 4a–c) does not describe the gap opening at the Dirac points due to the breaking of the inversion symmetry. Moreover, a model at the level of XXZ + DMI as initially used to understand the magnon dispersion of CrI₃⁴⁰ does not capture entirely the full profile of the bands (Fig. 4d). The upper branch E⁺ becomes nearly flat with the increment of J₂ at the path K − M − K while the lower magnon branch E⁻ turns more curved. This picture modifies substantially when BQ exchange interactions are included in the XXZ + BQ + DMI model (Fig. 4e) as the magnon bands follow a similar curvature throughout the variation of J₂, although the upper branch at Γ increased to ${E}_{\Gamma }^{+}=$27.8 meV. A sound comparison between the XXZ + BQ + DMI model and the experimental results for CrI₃ is obtained (Fig. 4f) when J₁ is varied similarly (Fig. 4a) indicating that the first nearest-neighbors are important on the stabilization of ${E}_{\Gamma }^{+}$. It is worth mentioning that the value of the exchange interactions taken into account in the fitting of the neutron scattering spectra⁴⁰ do not separate BL contributions from BQ as shown in Eqs. (12)–(14). Hence, it is not known from the fitting procedure⁴⁰ what is the contribution of K_bq to the magnon dispersion. However, such separation can be clearly stated in our model as indicated in Fig. 4f. Furthermore, even though DMI is important for the gap opening at the Dirac point, it does not contribute to the magnitudes of the magnetization or critical temperatures for any 2D magnet with an out-of-plane easy-axis and ferromagnetic aligned spins (see details in Supplementary Section 15).

Fig. 4: Magnon spectra ω(meV) at different levels of theory for monolayer CrI₃.

a ω(meV) versus k at the first Brillouin zone (Γ − K − M − K − Γ) using a XXZ model. J₁ varies within 0–3.50 meV in steps of 0.5 meV from each curve (color map). b Similar as a, but with a fixed J₁ = 2.01 meV and varying J₂ within 0–0.30 meV (color map) in steps of 0.05 meV. c–e ω(meV) versus k for different models: XXZ including BQ exchange (XXZ+BQ), XXZ including DMI (XXZ+DMI), and XXZ including both BQ exchange and DMI (XXX+BQ+DMI). In these plots, J₁ = 2.01 meV, K_bq = 0.22 (on c and e), A_z = 0.31 meV⁴⁰ (on d and e) and J₂ varies within 0–0.30 meV. f Comparison between the XXZ+BQ+DMI model and the experimental data⁴⁰ recently measured for bulk CrI₃. We used as parameters: J₁ = 1.01 meV, J₂ = 0.10 meV, K_bq = 0.22 meV and A_z = 0.31 meV⁴⁰.

Discussion

In summary, we have shown the importance of biquadratic exchange interaction in the magnetic properties of 2D materials. We have described the phenomenology of such higher-order spin coupling, discussed its implications on several magnetic properties, and presented results at the level of non-collinear first-principles methods, Monte Carlo approximations and analytical models. The developed spin Hamiltonian including BQ exchange and DMI provided an accurate picture of topological spin-excitations on a generalized basis for any 2D magnet. Our results are particularly timely given the increasing interest in quantum materials, and we believe that our work will motivate the exploration of different exchange couplings and competition between critical phenomena⁴⁷.

The effects of the BQ exchange interactions proposed here should manifest in experimentally accessible temperature range. One indication is already the accurate reproduction of experimental Curie temperatures^1,35 including higher-order exchange which could not be obtained at the level of Ising, Heisenberg or Kitaev models. The magnitudes of BQ exchange can be in principle extracted from accurate hysteresis loops using phenomenological models^48,49. Importantly in such analysis are potential temperature variations of BL and BQ exchanges with layer thickness which may indicate tunable interlayer exchanges still to be explored in 2D magnets. Frustrated 2D Heisenberg models in the presence of BQ exchange interactions are also a non-trivial matter with a rich phase diagram involving incommensurate spin spirals, canted ferromagnetic states, quadrupolar phase or vertexes^23,50,51,52. As our results indicate that BQ exchanges are important for 2D magnets, possible ordered and disordered magnetic regimes may be stabilized in appreciable temperatures. Moreover, it is possible to enhance or suppress BQ interactions in Mott-Hubbard systems by applying external electric fields^53,54. Indeed, the control of the magnetic properties of CrI₃ using electrical means has already been demonstrated³¹. Therefore, this opens the prospect of a coherent transfer between spin and charge degrees of freedom using short laser pulses in nanosheets.

Methods

All methods can be found in Supplementary Materials.