Giant and controllable nonlinear magneto-optical effects in two-dimensional magnets

Abstract

The interplay of polarization and magnetism in materials with light can create rich nonlinear magneto-optical (NLMO) effects, and the recent discovery of two-dimensional (2D) van der Waals magnets provides remarkable control over NLMO effects due to their superb tunability. Here, based on first-principles calculations, we reported giant NLMO effects in CrI₃-based 2D magnets, including a dramatic change of second-harmonics generation (SHG) polarization direction (90°) and intensity (on/off switch) under magnetization reversal and a 100% SHG circular dichroism effect. We further revealed that these effects could not only be used to design ultra-thin multifunctional optical devices but also to detect subtle magnetic orderings. Remarkably, we analytically derived conditions to achieve giant NLMO effects and proposed general strategies to realize them in 2D magnets. Our work not only uncovers a series of intriguing NLMO phenomena but also paves the way for both fundamental research and device applications of ultra-thin NLMO materials.

Introduction

The interaction of light with polarization and magnetization in matters could create profound nonlinear magneto-optical (NLMO) phenomena, such as the magnetization-induced second-harmonics generation (MSHG) and the photocurrent generation^1,2,3. Among them, NLMO effects related to second-harmonics generation (SHG) have distinctive advantages in both magnetization detection and light modulation. As an all-optical probe characterized by higher-rank tensors, SHG-related NLMO measurement is nondestructive with high spatial and temporal resolution^4,5,6,7,8 and shows great promise to characterize structural and magnetic signals in 2D magnets^9,10,11. Moreover, the rotation angle of the SHG-related NLMO effect is independent of sample thickness¹², which is in clear contrast to the thickness-dependent linear magneto-optical Faraday angle and, therefore, has the potential to be used in miniature devices.

The most significant SHG signal originates from electric dipole transitions⁸, in which the breaking of the inversion (${{{\mathcal{P}}}}$) symmetry is necessary. ${{{\mathcal{P}}}}$ symmetry can be broken by either crystal or magnetic structures, generating the corresponding crystal SHG and MSHG. These two types of SHG are described by an i-type tensor χ_N, which has even-parity under time-reversal (${{{\mathcal{T}}}}$) operation, and a c-type tensor χ_M, which is ${{{\mathcal{T}}}}$-odd^{13,14,15,16,17}, respectively. Therefore, in non-centrosymmetric materials with ${{{\mathcal{T}}}}$ symmetry, only χ_N survives, and in non-centrosymmetric magnetic materials with space-time inversion (${{{\mathcal{PT}}}}$) symmetry, only χ_M survives (Detailed derivations are in Supplementary Note 1A). When both types of SHG coexist, that is, in materials with the simultaneous breaking of ${{{\mathcal{P}}}}$, ${{{\mathcal{T}}}}$ and ${{{\mathcal{PT}}}}$ symmetries, a class of specific NLMO effects arises due to the interference of χ_N and χ_M under ${{{\mathcal{T}}}}$-operation as

$${{{\bf{P}}}}(2\omega )\propto ({\chi }_{{{{\rm{N}}}}}\pm {\chi }_{{{{\rm{M}}}}}){{{\bf{E}}}}(\omega ){{{\bf{E}}}}(\omega )\,,$$

(1)

where E(ω) is the electric field of the incident light and P(2ω) is the nonlinear polarization. The ± represents the influence of ${{{\mathcal{T}}}}$-operation. We denoted this interference effect of χ_N and χ_M as the NLMO effect in the rest of the context. As illustrated in Fig. 1, The interference between the two types of SHG can change the intensity of second harmonic (SH) light through I(2ω) ∝ ∣P(2ω)∣² ∝ ∣χ_N ± χ_M∣². Thus, in magnets with comparable crystal SHG and MSHG, notable NLMO effects can emerge.

Fig. 1: Concept of NLMO effects.

Magnets with non-centrosymmetric crystal structures exhibit both the crystal SHG and the MSHG due to the simultaneous breaking of ${{{\mathcal{P}}}}$, ${{{\mathcal{T}}}}$ and ${{{\mathcal{PT}}}}$ symmetries. The crystal SHG is unaffected by the magnetization direction reversal while the MSHG changes the sign. Thus, the two terms can constructively (left panel) or destructively (right panel) interfere with each other for the positive and negative magnetization directions, respectively, which leads to NLMO effects. The red and blue arrows represent magnetic orders related by ${{{\mathcal{T}}}}$ operation.

However, experimentally observed NLMO effects in bulk materials are usually small^{6,12,18,19,20,21,22,23}, which seriously hinders the relevant research and applications of these effects. Additionally, a more profound theoretical understanding to explain and control the magnitude of NLMO effects is also absent. In contrast to bulk materials, recent experiments reveal many unusual SHG responses in two-dimensional (2D) materials, such as the large and tunable i-type SHG in MoS₂^24,25, NbOI₂/Cl₂ layers^26,27 and twisted h-BN^28,29, the giant pure c-type SHG in ${{{\mathcal{PT}}}}$-symmetric ultrathin CrI₃¹, MnPS₃³⁰ and CrSBr³¹, and the anomalous SHG of uncertain origin in MnBi₂Te₄ thin films³² and monolayer (ML) NiI₂³³. These inspiring advances, combined with the great tunability of atomically thin materials, made 2D materials an excellent platform for both fundamental research and the design of miniature devices based on NLMO effects.

In this work, based on the computational method developed in refs. ^34,35 and symmetry analysis, we investigated the NLMO effects of representative 2D magnets possessing both χ_N and χ_M, including trilayer ABA stacking CrI₃, ML Janus Cr₂I₃Br_3, and ML H-VSe₂. We analytically derived and numerically calculated the NLMO angle for linearly polarized incident light and the NLMO intensity asymmetry for circularly polarized incident light at different frequencies. Remarkably, we uncovered giant NLMO effects due to the maximal interference between comparable χ_N and χ_M in CrI₃-based 2D magnets, including a nearly 90° polarization rotation or an on/off switching of certain light helicity of SH light upon magnetization reversal and a maximal SHG circular dichroism (SHG-CD) effect within fixed magnetization. We also found that these NLMO effects are extremely sensitive to subtle changes in complex magnetic orders. Moreover, we revealed the influence of interlayer interaction, spin-orbit coupling (SOC), and synergistic effect of stacking and magnetic orders to NLMO effects and proposed strategies to achieve these giant NLMO effects in more 2D materials. Our work not only uncovered a series of giant NLMO effects and corresponding candidate materials but also provides strategies to manipulate these effects in other material systems, and further shed light on the application of NLMO effects in subtle magnetic orders detection and ultra-thin optical devices.

Results and discussion

Structures and SHG of representative 2D magnets

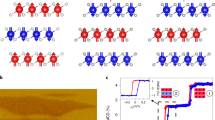
NLMO effects exist in magnetic materials without ${{{\mathcal{PT}}}}$ symmetry and therefore, we considered two typical ferromagnetic (FM) semiconductors in the monolayer limit, CrI₃ and H-VSe₂^{36,37,38,39,40,41,42}. ML VSe₂ is non-centrosymmetric with magnetic symmetry $\bar{6}{m}^{{\prime} }{2}^{{\prime} }$ when the magnetization is along the $\hat{z}$ axis. ML CrI₃ is centrosymmetric with magnetic symmetry $\bar{3}{m}^{{\prime} }$⁴³ and AB stacking bilayer CrI₃ has ${{{\mathcal{PT}}}}$ symmetry as shown in Supplementary Fig. 2; therefore, the ML does not have SHG, and the bilayer only has the MSHG χ_M. In the following, we used the strategy of multi-layer stacking and element replacement to break ${{{\mathcal{P}}}}$ and ${{{\mathcal{PT}}}}$ to enable NLMO effects in CrI₃-related materials. The simplest examples are ABA stacking trilayer CrI₃ with antiferromagnetic (AFM) interlayer coupling (denoted by ABA-AFM CrI₃) and ML Janus Cr₂I₃Br₃. Figure 2a, c, e shows the atomic and magnetic structures of ABA-AFM CrI₃, ML Cr₂I₃Br₃, and ML H-VSe₂ with their magnetic symmetries summarized in Table 1. Their band structures are shown in Supplementary Note 5.

Fig. 2: Atomic structures and SHG of the representative 2D magnets.

a, c, e Top and side views of ABA CrI₃ with AFM (↑↓↑) magnetic order, ML Cr₂I₃Br₃ and ML H-VSe₂ with FM (↑) magnetic order. The red/blue arrows represent the magnetic moment of each atom. b, d, f The real parts and the norm of SHG susceptibility tensor components. The red and blue lines represent the results of AFM (↑↓↑)/FM (↑) orders and their ${{{\mathcal{T}}}}$-related tAFM (↓↑↓)/tFM (↓) orders, respectively.

Table 1 Magnetic symmetries and symmetry properties of SHG tensor components of representative 2D magnets

Figure 2b, d, f shows the influence of ${{{\mathcal{T}}}}$ operation to different SHG components χ^abc(2ω; ω, ω) of the above mentioned materials. In the rest of the article, we used the shorthand notation χ^abc to represent χ^abc(2ω; ω, ω), where a, b, c are Cartesian directions. The two magnetic orders related by ${{{\mathcal{T}}}}$ symmetry are denoted as AFM/FM and tAFM/tFM, respectively. For SHG susceptibilities of trilayer CrI₃, we scissored the band gap to 1.5 eV, and our results show good agreement with the previous work⁴³ (Supplementary Fig. 3). Due to the C_3z symmetry in all three representative materials, each material has only two independent in-plane SHG components, that is χ¹¹¹ = −χ¹²² = −χ²¹² and χ²²² = −χ²¹¹ = −χ¹¹², where the subscripts 1 and 2 denote the Cartesian direction $\hat{x}$ and $\hat{y}$. Due to the presence of ${m}^{{\prime} }$ or ${2}^{{\prime} }$ symmetry in all three materials, one of the SHG components is ${{{\mathcal{T}}}}$-odd while the other is ${{{\mathcal{T}}}}$-even, as shown in the upper and middle panels of Fig. 2b, d, f. Generally, the even and odd quantities can coexist in the same tensor component, and in this case, ${\chi }_{{{{\rm{N}}}}}=(\chi +{{{\mathcal{T}}}}\chi )/2$, and ${\chi }_{{{{\rm{M}}}}}=(\chi -{{{\mathcal{T}}}}\chi )/2$, where ${{{\mathcal{T}}}}\chi$ is the SHG susceptibility of the time-reversal pair. The detailed expressions of χ_N and χ_M, as well as their symmetry requirements, are summarized in Supplementary Note 1. The parity of each component under ${{{\mathcal{T}}}}$ is also summarized in Table 1.

The bottom panel of Fig. 2b, d, f clearly shows that the relative values of ∣χ_N∣ and ∣χ_M∣ are distinctive in the three materials. Although ∣χ_M∣ exceeds ∣χ_N∣ in ABA-AFM CrI₃ at a wide frequency range and the opposite is observed in ML Cr₂I₃Br₃, there are still several intersections of ∣χ_N∣ and ∣χ_M∣. In contrast, ∣χ_N∣ is much larger than ∣χ_M∣ in ML H-VSe₂ without any intersections.

Giant NLMO effects of representative 2D magnets

The coexistence of χ_N and χ_M can induce a variety of NLMO effects. In the following, we calculated the SHG responses under the linearly and the circularly polarized light (LPL and CPL), with an emphasis on the role of different ratios of χ_N and χ_M to NLMO effects. Considering a normal incidence geometry where the material is in the xy-plane and the incident light propagates in the $-\hat{z}$ direction, the SHG polarization P(2ω) of 2D materials has been given in ref. ⁴³. As the intensity of the emitted SH light I(2ω) is proportional to ∣P(2ω)∣² and is commonly measured, we calculated ∣P(2ω)∣² to represent I(2ω).

For LPL characterized by ${{{\bf{E}}}}=E(\cos \theta ,\sin \theta )$, where θ denotes the angle between light polarization and the x-axis of the sample, we investigated the polarization-resolved SHG as a function of θ. The experiment measures the parallel (∣∣) and perpendicular (⊥) components of the SHG signal with respect to the direction of the incoming light polarization while the sample rotates with the angle θ. In the three representative materials, the SHG intensity at the parallel and perpendicular polarization directions can be written as⁴³

$$\begin{array}{ll}{I}_{| | }(\theta )&\propto | {\chi }^{111}\cos 3\theta -{\chi }^{222}\sin 3\theta {| }^{2}{E}^{4}\,,\\ {I}_{\perp }(\theta )&\propto | {\chi }^{111}\sin 3\theta +{\chi }^{222}\cos 3\theta {| }^{2}{E}^{4}.\end{array}$$

(2)

Both the parallel and perpendicular components exhibit sixfold sunflower-like patterns and differ only by a ±π/6 angle, as the black and red lines shown in Fig. 3b. In addition, the angle θ_m corresponding to the maximum (minimum) of I_∣∣ also corresponds to the minimum (maximum) of I_⊥.

Fig. 3: NLMO effects in representative 2D magnets.

a The NLMO angle and c NLMO intensity asymmetry as a function of frequency. The vertical dashed lines in the curves indicate the NLMO rotation is ill-defined at the corresponding frequencies, and the polarization-resolved SHG close to those frequencies in ABA-CrI₃ and ML Cr₂I₃Br₃ are shown in Supplementary Figs. 5a and 7a. b Change of polarization-resolved SHG under ${{{\mathcal{T}}}}$ operation at a LPL characteristic frequency ${\omega }_{{{{\rm{LPL}}}}}^{{\prime} }=1.71$ eV of ML Cr₂I₃Br₃. The yellow line marks one of the LPL incident angles where the maximal polarization direction change of SHG happens under ${{{\mathcal{T}}}}$ operation. d CPL SHG intensity of FM and tFM states of ML Cr₂I₃Br₃. The upper and lower panels are for incident helicity σ⁺ and σ⁻. The difference between the red and blue curves in each panel reflects the NLMO intensity asymmetry. For a particular magnetic order, the difference between the upper and lower panels reflects the magnitude of SHG-CD. The dashed yellow line indicates one of the CPL characteristic frequencies ω_CPL = 1.57 eV of ML Cr₂I₃Br₃. e Multi-degree controlling of NLMO in ML Cr₂I₃Br₃. For linearly-polarized incident light at polarization angle θ = π/12 + nπ/6 and frequency ${\omega }_{{{{\rm{LPL}}}}}^{{\prime} }$, ML Cr₂I₃Br₃ can act as a magneto-optical polarization switcher. For circularly polarized incident light at frequency ω_CPL, ML Cr₂I₃Br₃ can act as a magneto-optical switch for circularly polarized SH light or an optical filter for circularly polarized SH light with a particular helicity.

NLMO effects under LPL are reflected by comparing the polarization-resolved SHG patterns before and after ${{{\mathcal{T}}}}$ operation, which results from the sign reversal of χ_M. Under the symmetry of the three representative materials, this corresponds to a rotation of the polarization-resolved SHG pattern (Supplementary Figs. 5b and 7b), denoted as NLMO angle ${\theta }_{{{{\mathcal{T}}}}}$ (see details in Supplementary Note 2A), with the expression

$${\theta }_{{{{\mathcal{T}}}}}=2{\theta }_{{{{\rm{m}}}}}=-\frac{{\tan }^{-1}\left(\tan 2\delta \cos \Delta \varphi \right)}{3}+\frac{n\pi }{3}\,,$$

(3)

where n is an integer originated from the rotation symmetry of the pattern. $\tan \delta =\frac{| {\chi }^{111}| }{| {\chi }^{222}| }\in (0,+\infty )$ is the magnitude ratio of χ¹¹¹ and χ²²², and $\Delta \varphi =-i\left(\ln \frac{{\chi }^{111}}{| {\chi }^{111}| }-\ln \frac{{\chi }^{222}}{| {\chi }^{222}| }\right)\in (-\pi ,+\pi ]$ is the phase difference between χ¹¹¹ and χ²²². The range of δ is (0, π/2). Eq. (3) does not hold when ∣χ¹¹¹∣ = ∣χ²²²∣ and Δφ = ± π/2. In this situation, the polarization-resolved SHG is isotropic according to Eq. (2), therefore, it does not show any change under ${{{\mathcal{T}}}}$ operation.

The maximum NLMO angle can be achieved is ${\theta }_{{{{\mathcal{T}}}}}=\pi /6+n\pi /3$ with the condition

$$\left\{\begin{array}{l}| {\chi }^{111}| =| {\chi }^{222}| \,,\quad \\ \Delta \varphi \,\ne\, \pm \pi /2\,,\quad \end{array}\right.$$

(4)

and we denoted the corresponding frequency as the LPL characteristic frequency ω_LPL. At ω_LPL, the patterns of I_∣∣ and I_⊥ are swapped exactly, as shown in Fig. 3b, which results in a remarkable polarization change of the SH light. If the magnitude of I_∣∣ and I_⊥ differs greatly, the polarization of the SH light can rotate nearly π/2 under ${{{\mathcal{T}}}}$. The condition to achieve the π/2 polarization rotation at θ_m = π/12 + nπ/6 is

$$\left\{\begin{array}{l}| {\chi }^{111}| =| {\chi }^{222}| \,,\quad \\ \Delta \varphi =0\,{{{\rm{o}}}}r\,\pi \,,\quad \end{array}\right.$$

(5)

and the corresponding frequency is denoted as ${\omega }_{{{{\rm{LPL}}}}}^{{\prime} }$, which is a subset of ω_LPL. This condition is also graphically shown in the complex plane in Supplementary Fig. 1.

We numerically traced the ω-dependence of the NLMO angle ${\theta }_{{{{\mathcal{T}}}}}$ in the three representative materials, as shown in Fig. 3a. As highlighted by the dashed horizontal line, ${\theta }_{{{{\mathcal{T}}}}}$ close to π/6 + nπ/3 corresponds to the largest NLMO angle. Remarkably, ${\theta }_{{{{\mathcal{T}}}}}$ is giant in ABA-AFM CrI₃ and ML Cr₂I₃Br₃ at several ω_LPL frequencies. In contrast, ${\theta }_{{{{\mathcal{T}}}}}$ is always tiny in ML H-VSe₂. This distinction is consistent with their different ratio of ∣χ_N∣ and ∣χ_M∣ susceptibilities observed in Fig. 2b, d, f. Figure 3b shows the dramatic change of SHG light from perpendicular to parallel polarization direction for incident light at θ_m = π/12 (indicated by the yellow line) under ${{{\mathcal{T}}}}$ in this atomically thin Cr₂I₃Br₃ at ${\omega }_{{{{\rm{LPL}}}}}^{{\prime} }=1.71$ eV.

Next, we investigated the polarization and intensity of SH light under the illumination of the CPL. For the CPL characterized by E = E(1, ± i), where ±represents the left/right-handed (σ^±) CPL, the polarization of the SHG signal is

$${{{\bf{P}}}}(2\omega )=2{E}^{2}({\chi }^{111}\,\mp\, i{\chi }^{222})(1,\,\mp\, i)\,$$

(6)

according to Table 1. The SH light is also CPL with helicity opposite to the incident light. Furthermore, the intensity of the SH light depends on the helicity of the incident light, which is called the SHG-CD effect^44,45,46. The SHG-CD intensity asymmetry can be described by

$${\eta }_{{{{\rm{h}}}}}^{{{{\bf{M}}}}}=\frac{{I}^{+}({{{\bf{M}}}})-{I}^{-}({{{\bf{M}}}})}{{I}^{+}({{{\bf{M}}}})+{I}^{-}({{{\bf{M}}}})}\,,$$

(7)

where I⁺(M) is the SHG intensity generated by the magnetic order M when the helicity of the incident light is σ⁺.

${{{\mathcal{T}}}}$ operation can also change the intensity of the SH light with a certain helicity. We can define the NLMO intensity asymmetry at certain incident light helicity σ as

$${\eta }_{{{{\mathcal{T}}}}}^{\sigma }=\frac{{I}^{\sigma }(+{{{\bf{M}}}})-{I}^{\sigma }(-{{{\bf{M}}}})}{{I}^{\sigma }(+{{{\bf{M}}}})+{I}^{\sigma }(-{{{\bf{M}}}})}\,,$$

(8)

where the ±M states are ${{{\mathcal{T}}}}$-related, and I^σ(+M) is the SHG intensity generated by the +M magnetic order. The range of ${\eta }_{{{{\mathcal{T}}}}}^{\sigma }$ is [−1,1] and ${\eta }_{{{{\mathcal{T}}}}}^{\sigma }=\pm 1$ represents the situation in which an incident CPL with helicity σ can only generate SH light in the ±M magnetic states and is completely blocked in the opposite magnetic state. According to Eq. (6), the reversal of helicity and the reversal of magnetization are equivalent, and therefore the change of intensity under ${{{\mathcal{T}}}}$ operation can also be reproduced by changing the helicity of CPL at a fixed magnetization, i.e., ${\eta }_{{{{\mathcal{T}}}}}^{+}={\eta }_{{{{\rm{h}}}}}^{+{{{\bf{M}}}}}$.

The expression of the NLMO intensity asymmetry in our case is (derivation is in Supplementary Note 2B)

$${\eta }_{{{{\mathcal{T}}}}}^{\pm }=\mp \sin 2\delta \sin \Delta \varphi \,.$$

(9)

As long as Δφ ≠ nπ, the NLMO intensity asymmetry is always nonzero, and the intensity of the SH light is always magnetization-dependent. In general, the maximum $| {\eta }_{{{{\mathcal{T}}}}}^{\pm }| =1$ requires

$$\left\{\begin{array}{l}| {\chi }^{111}| =| {\chi }^{222}| \,,\quad \\ \Delta \varphi =\pm \pi /2\,,\quad \end{array}\right.$$

(10)

and we denoted the corresponding frequency as the CPL characteristic frequency ω_CPL. This condition is also graphically shown in the complex plane in Supplementary Fig. 1. It is worth noting that the ω_CPL is just where the ${\theta }_{{{{\mathcal{T}}}}}$ for LPL is ill-defined.

We numerically traced the ω-dependence of ${\eta }_{{{{\mathcal{T}}}}}^{+}(2\omega )$ in the three representative materials in Fig. 3c. Again, two CrI₃-based materials can achieve large ${\eta }_{{{{\mathcal{T}}}}}^{+}$ including ±1 at several frequencies while $| {\eta }_{{{{\mathcal{T}}}}}^{+}|$ is always below 0.4 in ML H-VSe₂. This contrast is another feature stemming from their distinct ratio of ∣χ_N∣ and ∣χ_M∣. We take ML Cr₂I₃Br₃ as an example to illustrate the intensity change of SH light under ${{{\mathcal{T}}}}$ operation for σ^± CPL in Fig. 3d. (The CPL SHG intensity of ABA-AFM CrI₃ and ML H-VSe₂ are shown in Supplementary Figs. 4 and 8). The vertical dash line in Fig. 3d highlights one of the frequencies ω_CPL at which the intensity of SHG changes between a considerable value and zero under ${{{\mathcal{T}}}}$ operation. The upper (σ⁺) and lower (σ⁻) panels of Fig. 3d look exactly the same, except the line colors are swapped, which reflects the equivalency of helicity and magnetization reversal. Other than that, the difference in the red (blue) line between the upper and lower panels in Fig. 3d also indicates that this material exhibits a 100% SHG-CD effect at ω_CPL.

The giant NLMO effects discovered in CrI₃-based materials enabled them to be used as magnetic-field-controlled atomically thin optical devices, as illustrated in Fig. 3e. Utilizing incident light at frequencies ${\omega }_{{{{\rm{LPL}}}}}^{{\prime} }$, they can serve as optical polarization switchers for LPL as they can rotate the polarization of SH light by nearly π/2. At the incident frequency ω_CPL, they are ideal magneto-optical switches for CPL due to their large ${\eta }_{{{{\mathcal{T}}}}}$. In addition, even without an external magnetic field, due to their large SHG-CD effects, they can serve as optical filters for CPL with a particular helicity.

It is worth noting that the above-discussed NLMO and SHG-CD effects are analyzed based on the nonlinear polarization P(2ω) generated in materials, and the intensity of radiation is estimated by I(2ω) ∝ ∣P(2ω)∣², which is not specific for the reflected or the transmitted SH light. The exact value of reflected and transmitted SH light can be obtained by solving Maxwell equations with corresponding boundary conditions⁴⁷. Although the SH light in reflection or transmission may have different intensities, the above-discussed NLMO and SHG-CD effects persist.

The materials we investigated so far have several particular symmetry features. In general, NLMO effects are highly sensitive to changes in magnetic orders and can be used as a powerful tool to distinguish subtle magnetic states. As an example, we considered a different magnetic order ↑↑↓ for ABA stacking trilayer CrI₃, which we denoted as the MIX state and its ${{{\mathcal{T}}}}$-pair state as tMIX. ABA-MIX CrI₃ and ABA-AFM CrI₃ have the same net magnetic moment and tensor components as Table 1 shows, and their linear optical responses are similar, as shown in Supplementary Note 4, which makes them difficult to be distinguished experimentally. However, in ABA-MIX CrI₃, each SHG tensor component contains both χ_N and χ_M and does not have a definite parity under ${{{\mathcal{T}}}}$, as shown in Fig. 4a. As a result, for LPL, the polarization-resolved SHG shows both rotation and magnitude change under ${{{\mathcal{T}}}}$ operation as shown at the bottom two plots in Fig. 4c. For CPL, the equivalence between helicity and magnetization reversal, i.e., ${\eta }_{{{h}}}^{+\mathbf{M}}={\eta }_{{{{\mathcal{T}}}}}^{+}$, is broken, as reflected by the remarkable difference between the upper and lower panels in Fig. 4b. Therefore, under the illumination of LPL (CPL) at ω_LPL (ω_CPL) for ABA-AFM CrI₃, we can observe notable differences between ABA-AFM CrI₃ and ABA-MIX CrI₃, as shown in Fig. 4c.

Fig. 4: SHG susceptibility, CPL SHG intensity and polarization-resolved SHG for ABA-MIX CrI₃.

a Real parts of SHG susceptibility tensor components of ABA-MIX CrI₃. Red and blue lines represent results for MIX(↑↑↓) and tMIX(↓↓↑) magnetic orders, respectively. b SHG intensity of MIX and tMIX magnetic orders of ABA-MIX CrI₃ under CPL illumination. The upper and lower panels are for incident helicity σ⁺ and σ⁻. The difference between the red and blue curves in each panel reflects the ${\eta }_{{{{\mathcal{T}}}}}$. For a particular magnetic order, the difference between the upper and lower panels reflects the magnitude of SHG-CD. c Polarization-resolved SHG of AFM, tAFM, MIX, and tMIX magnetic orders at one of the LPL frequency ${\omega }_{{{{\rm{LPL}}}}}^{{\prime} }$= 1.22 eV of ABA-AFM CrI₃. The red/blue arrow represents the magnetic moment in each CrI₃ layer.

In addition to the detection of full ordered magnetic ground states, the NLMO effects can also distinguish the influence from spin fluctuation at finite temperatures²² and spin canting caused by an external field, as shown in Supplementary Fig. 6.

Controllable NLMO effects of representative 2D magnets

The giant NLMO effects manifest many intriguing applications as we have learned from the above results, a necessary condition to achieve those effects is to have comparable ∣χ_N∣ and ∣χ_M∣. However, in real materials, ∣χ_N∣ and ∣χ_M∣ may differ greatly, which results in negligible NLMO effects. In the following, taking ABA-AFM CrI₃ as a model system, we demonstrated several strategies to enhance NLMO effects, in which χ¹¹¹ is the ${{{\mathcal{T}}}}$-odd term χ_M and χ²²² is the ${{{\mathcal{T}}}}$-even term χ_N as summarized in Table 1.

The strength of interlayer interaction has a great impact on properties of multilayer magnets^37,48,49; thus, we first investigated the influence of interlayer distance d in trilayer CrI₃, where d₀ is the interlayer distance of ABA-AFM CrI₃ at equilibrium. As shown in Fig. 5a, both ∣χ_M∣ and ∣χ_N∣ change with d, but ∣χ_N∣ is more sensitive to the variation of d. Therefore, a more comparable ∣χ_N∣ and ∣χ_M∣ can be realized by exerting hydrostatic pressure on multilayer CrI₃ along the z-axis in experiments, as shown in Fig. 5d.

Fig. 5: Design principles of NLMO effects.

The influence of interlayer spacing (a), SOC (b), and layer number (c) to ∣χ¹¹¹∣ which is the ${{{\mathcal{T}}}}$-odd term χ_M and ∣χ²²²∣ which is the ${{{\mathcal{T}}}}$-even term χ_N in ABA-AFM CrI₃ multilayers. The SHG tensor components of ABA-AFM CrI₃ with interlayer distance 0.9d₀ (d), ABA-AFM CrBr₃ (e) and 7L H-VSe₂ (f). The ${{{\mathcal{T}}}}$-odd component ∣χ²²²∣ in even-layer AFM CrI₃ is not shown.

Next, we investigated the influence of SOC on NLMO effects by artificially tuning the magnitude of SOC strength λ. As Fig. 5b shows, χ_M is sensitive to the change of λ while χ_N changes slightly. As ∣χ_M∣ is much larger than ∣χ_N∣ in ABA-AFM CrI₃, we replaced I by Br to reduce SOC and found ABA-AFM CrBr₃ possesses very comparable ∣χ_N∣ and ∣χ_M∣ in a broad frequency range, as shown in Fig. 5e.

Furthermore, we found stacking and magnetic orders can have synergistic effects on engineering the relative and absolute values of ∣χ_N∣ and ∣χ_M∣. As shown in Fig. 5c, in multilayer AB stacking AFM CrI₃, χ_N is forbidden in even-layer structures due to the presence of ${{{\mathcal{PT}}}}$ symmetry and remains almost the same in odd-layer structures, while χ_M increases with the layer number. The above observations can be simply understood as χ_N from each layer alternates the sign with similar magnitude, while χ_M from each layer has the same sign due to the ${{{\mathcal{PT}}}}$ symmetry between the A and the B layers²⁴. Inspired by this, as ∣χ_M∣ is much smaller than ∣χ_N∣ in ML H-VSe₂, we calculated the SHG susceptibility of 7-layer (7L) AA${}^{{\prime} }$-AFM H-VSe₂, which also has ${{{\mathcal{PT}}}}$ symmetry between A and A${}^{{\prime} }$ layers. As expected, the peak value of ∣χ_M∣ in 7L structure shown in Fig. 5f is almost 7 times that in ML H-VSe₂ (Fig. 2f) while its ∣χ_N∣ remains almost the same. ∣χ_N∣ and ∣χ_M∣ are comparable in 7L-AA${}^{{\prime} }$ stacking H-VSe₂, indicating it can host giant NLMO effects. Similarly, by tuning the stacking sequence and magnetic order, we can achieve ${{{\mathcal{P}}}}$, ${{{\mathcal{T}}}}$ or neither symmetry between neighboring layers and can realize an arbitrary control of the relative and absolute value of ∣χ_N∣ and ∣χ_M∣ (Supplementary Fig. 9).

To summarize, the simultaneous breaking of ${{{\mathcal{P}}}}$, ${{{\mathcal{T}}}}$ and their joint symmetry allows NLMO effects with the electric-dipole origin. In several representative 2D magnets with similar symmetry, we investigated and demonstrated NLMO angle ${\theta }_{{{{\mathcal{T}}}}}$ under LPL, NLMO intensity asymmetry ${\eta }_{{{{\mathcal{T}}}}}$ and SHG-CD η_h under CPL. In particular, we discovered promising candidates with giant NLMO effects, including a near 90° polarization rotation and an on/off switching of certain helicity of SH light upon magnetization reversal, as well as ±1 SHG-CD within a certain magnetic configuration. These giant NLMO effects in candidate 2D magnets can be used not only to design atomically thin NLMO devices such as optical polarization switchers, switches, and filters but also to detect subtle magnetic orders in multilayer magnets such as ABA CrI₃. We further derived that the comparable magnitude of ∣χ_N∣ and ∣χ_M∣ is indispensable to achieve giant NLMO effects. Lastly and most importantly, we found the interlayer distance, the magnitude of SOC, and the synergistic effect of stacking and magnetic orders could be used to control the relative and absolute magnitude of ∣χ_N∣ and ∣χ_M∣, which provides general design principles to achieve giant NLMO effects in 2D magnets. Our finding not only reveals several intriguing NLMO phenomena but also paves the way to achieve subtle magnetization detection, as well as giant and controllable NLMO effects in ultra-thin magneto-optical devices.

Methods

First-principles calculations

First-principles calculations were performed by Vienna Abinitio Simulation Package⁵⁰ with SOC included. The exchange-correlation function was parameterized in the Perdew–Burke–Ernzerhof form⁵¹, and the projector augmented-wave potential⁵² was used. For the 3d orbitals in magnetic ions Cr and V, the Hubbard U of 3³⁷ and 1.16 eV⁵³ were used. For layered materials, we used DFT-D3 form van der Waals correction without damping⁵⁴. The cut-off energy of plane waves was set to 450 and 500 eV for CrI₃-based materials and H-VSe₂-based materials, respectively. The convergence criterion of force was set to 10 and 1 meV Å⁻¹ for CrI₃-based materials and H-VSe₂-based materials, respectively. Total energy is converged within 10⁻⁶ eV. k-point samplings of 13 × 13 × 1 were used for CrI₃-based materials and 15 × 15 × 1 for H-VSe₂-based materials. Vacuum thickness of about 20 Å was used in the calculations of 2D materials.

SHG calculations

After getting the converged electronic structures, we generated the maximally localized Wannier functions using Wannier90⁵⁵ to build the tight-binding Hamiltonian and calculate optical responses³⁴. The ${{{\mathcal{T}}}}$ symmetry breaking is carefully treated in the calculations of SHG for magnets^35,56. We obtained 56 maximally localized orbitals for each layer of CrI₃ or Cr₂I₃Br₃ and 22 for each layer of H-VSe₂. The broadening factor of the Dirac delta function is taken to be 0.05 eV. We found that 50 × 50 × 1 and 150 × 150 × 1 k-mesh samplings are enough for the converged SHG susceptibilities for CrI₃-based materials and H-VSe₂-based materials. The band gap of trilayer CrI₃ has been scissored to 1.5 eV in the calculation of SHG susceptibility⁴³.