Interpretable machine-learning strategy for soft-magnetic property and thermal stability in Fe-based metallic glasses

Abstract

Fe-based metallic glasses (MGs) have been extensively investigated due to their unique properties, especially the outstanding soft-magnetic properties. However, conventional design of soft-magnetic Fe-based MGs is heavily relied on “trial and error” experiments, and thus difficult to balance the saturation flux density (B_s) and thermal stability due to the strong interplay between the glass formation and magnetic interaction. Herein, we report an eXtreme Gradient Boosting (XGBoost) machine-learning (ML) model for developing advanced Fe-based MGs with a decent combination of B_s and thermal stability. While it is an attempt to apply ML for exploring soft-magnetic property and thermal stability, the developed XGBoost model based on the intrinsic elemental properties (i.e., atomic size and electronegativity) can well predict B_s and T_x (the onset crystallization temperature) with an accuracy of 93.0% and 94.3%, respectively. More importantly, we derived the key features that primarily dictate B_s and T_x of Fe-based MGs from the ML model, which enables the revelation of the physical origins underlying the high B_s and thermal stability. As a proof of concept, several Fe-based MGs with high T_x (>800 K) and high B_s (>1.4 T) were successfully developed in terms of the ML model. This work demonstrates that the XGBoost ML approach is interpretable and feasible in the extraction of decisive parameters for properties of Fe-based magnetic MGs, which might allow us to efficiently design high-performance glassy materials.

Introduction

The continued growth in electrical power generation and distribution boosts the urgent demand of next-generation soft-magnetic materials for electric fields. Among these materials, Fe-based metallic glasses (MGs) are widely used in utility transformers due mainly to their low cost and core loss, and high saturation flux density B_s^{1,2,3,4,5,6,7,8,9,10}. Over the past decades, several Fe-based magnetic MGs and their composites, such as FINEMET¹¹, NANOPERM¹², and HITPERM¹³, have been successfully developed and commercialized, relying heavily on considerable ‘trial and error’ experiments^14,15,16,17. However, there exists a tradeoff between the soft-magnetic property and thermal stability for Fe-based MGs, i.e., the improvement in the soft-magnetic property is always accompanied by the deterioration of thermal stability^2,7. The main reason responsible for such tradeoff is that glass-forming elements are usually anti-magnetic. To address this critical issue, fully understanding the complicated interplay between glass formation and magnetic coupling is prerequisite, which actually makes the alloy design of soft-magnetic Fe-based BMGs extremely challenging. Therefore, it is of significance to establish a feasible model/principle to guide the design of Fe-based MGs based on intrinsic properties of their elemental constituents.

Machine-learning (ML) strategy enables the system to automatically learn and improve from knowledge and experiences in the field of artificial intelligence^18,19. Owing to the significant development in both hardware and software, ML has been becoming an attractive and powerful tool in the field of materials science^20,21,22. Considerable efforts have been devoted to developing advanced materials by ML, such as ceramic materials²³, high-entropy alloys²⁴, and oxide compounds²⁵. Recently, ML has been extended to the study of MGs, especially for predicting glass formation behaviors. Wang et al. have exploited the support vector machine (SVM) technique to predict glass formers²⁶, whilst Ward et al. have developed a model for pinpointing glass-forming compositions²⁷. These studies demonstrate that the materials discovery process could be significantly expedited and simplified if ML techniques are properly employed.

Although ML techniques have been applied to various materials, design of soft-magnetic Fe-based MGs still strongly depends on the “trial and error” method because of the lack of deep insights into this type of materials. Moreover, currently available ML models primarily focus on establishing the data relationship, rather than directly deriving fundamental physical mechanisms underlying the resultant relationship. In these cases, ML models are more like a “black box” rather than an alloy design theory with a simplistic scientific description. In this regard, some researchers recently have attempted to improve the interpretability of ML-based framework by clarifying the relationship between the intrinsic parameters and properties via introducing physical features into the ML process^28,29,30. For example, Weng et al. have constructed a simple descriptor with physical insight by symbolic regression ML model and successfully synthesized a series of oxide perovskites with good performance of oxygen evolution reaction activities²⁸. Obviously, these pioneering studies make ML models more feasible towards practical applications such as alloy design and performance optimization. Considering the research status of Fe-based MGs and inspired by previous work, here we aim to crack this hard nut by developing ML models for the property of interest, namely, identifying the most important parameters of soft-magnetic Fe-based MGs and composition-structure-property relationships in terms of intrinsic characteristics of constituents. The eXtreme Gradient Boosting (XGBoost) algorithm^31,32, which is a scalable tree boosting system and can be used for both classification and regression tasks, was used to study how composition and structural data relate to performance, and to quantitatively predict material properties based simply on their chemical composition. With this strategy, we can deduce the physics-based rules to clarify the data relationships and the related physical mechanism for Fe-based MGs, thus enabling efficient alloy design of advanced magnetic amorphous materials with desirable properties.

Results and discussion

Model optimization

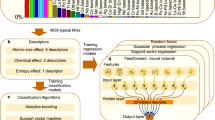
For data-driven materials research strategies, the dataset plays a significant role in developing models and subsequent prediction of properties. Figure 1 shows the schematic view of the ML process and framework for soft-magnetic Fe-based MGs. As shown in Fig. 1, it is mainly composed of five steps, including dataset preparation, feature selection, data processing by ML, prediction of properties of interest, and feedback.

Fig. 1: Schematic illustration of the ML flow chart for soft-magnetic Fe-based MGs.

FMG n, n and d present for the nth Fe-based MG, sequence number of alloys, and sequence number of features, respectively.

We compiled the data including composition and properties, B_s and crystallization temperature (T_x) for 252 Fe-based MGs [Supplementary data], which were previously reported in literature^{2,33,34,35,36,37,38,39,40,41,42,43,44,45}. Within the ML parlance, the former, i.e., the alloys, is referred to as “input”, and the latter, i.e., the properties such as B_s and T_x, is referred to as the “target” or “output”. Since the goal is to predict specific magnetic property and thermal stability at a high level of accuracy in a wide range of Fe-based composition space, all features should contain critical structural information at the atomic level that may determine the target properties. Here, the d-dimensional feature space is composed of the feature vector (also referred to as a descriptor) (F_i = F_i1, F_i2, F_i3, …, F_id) of each alloy. For soft-magnetic Fe-based MGs, there are many parameters that could affect soft-magnetic properties and thermal stability. At the moment, however, it is still a scientific challenge to quantitatively identify the importance of properties-related parameters. On the basis of this fact, we selected a total of 30 features (See “Methods” for detailed definition), such as valance electron concentration of system (VEC), valance electron concentration without consideration of Fe (VEC1) (see “Method” for more details), the electronegativity (χ), the averaged atomic radius difference (δ), the melting point (T_m) and the type of 25 elements utilized in the compositions (e.g., B, C, Al, Si, P, Cr, Mn, Fe, Co, Ni, Cu, and Zr).

For the XGBoost algorithm, the Scikit-Learn package in Python was used to develop the model for prediction. For the present dataset size (252 samples), k-fold cross validations (k = 5) were conducted firstly. The available data were divided into five equal-sized partitions, and five separate evaluation experiments were then performed. In the first evaluation experiment, the data in the 1st fold were used as the test set while the rest in the remaining k−1 folds were employed as the training set. A model was trained using the training set, and the relevant performance measures on the test set were recorded. Similarly, the second evaluation experiment was then performed using the data in the 2nd fold as the test set while those in the remaining k−1 folds as the training set. This process continues until five evaluation experiments have been completed and k sets of performance measures have been recorded. Finally, the k sets of the performance measures were aggregated to give one overall set of performance. The model attempts to identify the importance of features closely related to each attribute (the benchmark to guide the design of MGs) and to reduce the predication error as much as possible (i.e., the highest correlation coefficient R²). To do so, two model variables, i.e., Test Size and Max Depth, were adjusted to achieve desirable prediction results. Considering the application of soft-magnetic Fe-based MGs, we further optimized the XGBoost model based on two considerations; the first one is R² > 0.92 and the other is to offer high priority to B_s. Hence, we defined a parameter $R_{{\mathrm{all}}}^2 = 0.6R_{B_{\mathrm{s}}}^2 + 0.4R_{T_{\mathrm{x}}}^2$ as the indicator for evaluating the model performance. Figure 2 shows the heat map of prediction results of R² for B_s (Fig. 2a), T_x (Fig. 2b) and $R_{{\mathrm{all}}}^2$ (Fig. 2c), with different combinations of input parameters of Test Size and Max Depth. Based on the benchmark of $R_{{\mathrm{all}}}^2$, the optimal parameter value for the model is Test Size = 0.2 and Max Depth = 3. Additionally, we circularly exclude the least important feature from all 30 features and build a predictive model using only the remaining set of features. After 20 looping executions, the top ten important features were remained for each target property. Figure 3 shows the changes of $R_{B_{\mathrm{s}}}^2$, $R_{T_{\mathrm{x}}}^2$, and $R_{{\mathrm{all}}}^2$ with the increasing of feature numbers. It is seen that the model with 14 features can provide the best prediction result, i.e., the largest value of $R_{{\mathrm{all}}}^2$.

Fig. 2: Prediction from the ML model trained with different parameters.

Correlation coefficient (R²) for B_s (a) $R_{B_{\mathrm{S}}}^2$, for T_x (b) $R_{T_{\mathrm{x}}}^2$ and (c) $R_{{\mathrm{all}}}^2$. The best performance was identified to be the one with the largest $R_{{\mathrm{all}}}^2$, which is marked with blue star in (c).

Fig. 3: Correlation coefficient (R²) of the maximum saturation flux density (B_s) and crystallization temperature (T_x) as a function of the number of features.

The predictive model was constructed by the remaining set of features after circularly excluding the least important feature from all 30 features.

To obtain reasonable prediction, key features play a significant role in the ML-assisted design of soft-magnetic Fe-based MGs. Figure 4a shows the prediction values of B_s. As can be seen, $R_{B_{\mathrm{s}}}^2$ of the test sets for B_s can reach 0.934, even though the number of the training dataset is no more than two hundred. In the case of T_x, the $R_{T_{\mathrm{x}}}^2$ of the test set is even higher than that of $R_{B_{\mathrm{S}}}^2$, reaching 0.947 (shown in Fig. 4b). The origin of high accuracy of the model is attributed to the adoption of several methods to avoid overfitting for XGBoost algorithm. On the one hand, in the XGBoost framework, a group of functions are learnt by minimizing the regularized objective, and the additional regularization term is used to smooth the learnt weights. On the other hand, the XGBoost algorithm provides a shrinkage function, namely giving each leaf node an attenuation weight to prevent the issue of overfitting. In this case, the decreasing weight of a single tree can effectively reduces its impact on the final score and make it more flexible for next trees to improve performance of the ML model³¹.

Fig. 4: ML performance for soft-magnetic Fe-based MG data by the XGBoost model.

Prediction of the maximum saturation flux density (B_s) (a) and onset crystallization temperature (T_x) (b). Feature importance derived from the XGBoost model for B_s (c) and T_x (d).

Extraction of key features and revelation of physical mechanism

In addition to developing the predictive model with high accuracy, the XGBoost algorithm can also offer interpretation of the ML model by feature importance scores, which is one of the most distinctive advantages of this method and makes it much easier to visualize the relationship between the properties and the intrinsic features of soft-magnetic Fe-based MGs. Figure 4c and d demonstrate the feature importance score of different attributes for B_s and T_x, respectively. As for B_s, the most important attribute is the valance electron concentration without consideration of Fe, referred to VEC1 (Fig. 4c). One can also see from Fig. 4c that the importance score of the second-ranked feature, VEC, is just a little bit lower than that of VEC1. Except for these top two features, the importance scores of the others show sharp decline, indicating that there is a strong correlation between B_s and the first two features. In the case of T_x, a similar trend is found, but the top two features for T_x change to the averaged atomic radius difference (δ) and VEC. Since the feature importance does not provide a rule for choosing alloying elements directly, to make the ML model more interpretable and feasible in designing Fe-based MGs, we further extract the relationship between the basic characteristics of constituent elements and macroscopic properties in terms of the ML-provided intrinsic parameters as well as the physical metallurgy principles.

To check the validity of the selected features, we plotted a diagram of properties versus features based on all the datasets. Herein, the correlations between the top two features and properties are shown in Fig. 5. In the case of B_s, although a variety of studies have confirmed that B_s has a close relation with average VEC, how outer-shell electrons could possibly influence the B_s across various MGs is still far from being fully understood. As shown in Fig. 5b, the data have a scattered distribution without any specific trend. Nevertheless, if we exclude the coupling effects between the ferromagnetic elements (i.e., Fe, Co, Ni), namely, the Fe-based MGs containing no Co and Ni, a linear relation between VEC1 and B_s is clearly observed, as shown in Fig. 5a (indicated by the green elliptical dotted line). The fitting line of the data points corresponding to this specific family of Fe-based MGs by the least square method is expressed as follows (the yellow dash-dotted line in Fig. 5a):

$$B_{\mathrm{s}} = 2.32 - 0.998 \times {\mathrm{VEC}}1.$$

(1)

Fig. 5: Statistical analyses of experimental data for the saturation flux density.

a B_s versus VEC1, and (b) B_s versus VEC. The green elliptical dotted line in (a) encloses the Fe-based MGs without Co and Ni elements.

The intercept and slope of the fitting line is 2.32 and −0.998, respectively. Note that the intercept is quite close to the magnetic moment of pure Fe (2.2 μ_B) according to magnetic valence theory⁴⁶, indicating that the magnetic valence theory is still a good method to explain qualitatively the compositional dependence of B_s for the Fe-based MGs containing no Co and Ni due to its efficiency and simplicity. According to the charge transfer model⁴⁷, for Fe-metalloid magnetic MGs, the valence electrons of metalloid elements, such as electrons in s and p orbits, tend to transfer to the minority-spin band of Fe, resulting in the reduction of B_s. Equation (1) successfully reveals the transfer effects of this process, where the value of 2.32 represents the magnetic moment of pure Fe and −0.998 is a descriptor of the extent of charge transfer between metalloid elements and Fe atoms.

Now, we consider whether the correlation derived by the XGBoost ML method is physically sound in determining the target properties. In principle, according to the Slater-Pauling curve⁴⁶, the average magnetic moment of 3d-transitional-metal-based alloys is compositionally dependent and can be ascribed to the unpaired electron spins, which is affected by out-shell electrons. To realize glass formation in this type of Fe-based alloys, it is essential to add some glass-forming elements, especially those with negative mixing heat with Fe. Due to their strong affinity with Fe, addition of these alloying elements tends to form atomic pairs between them and Fe. Thus, the strong electron interactions between Fe and the glass-forming elements should be taken into account as far as the effective magneton number is considered.

Williams et al. have studied the magnetization of pure Fe, and given an empirical equation as follows⁴⁶:

$$\mu _{{\mathrm{pure}}{\mbox{-}}{\mathrm{Fe}}} = \left( {10.6 - n_{{\mathrm{pure}}{\mbox{-}}{\mathrm{Fe}}}} \right)\mu _{\mathrm{B}},$$

(2)

where μ_pure-Fe is the atomic magnetic moments of pure Fe, η_pure-Fe is the number of sp electrons of Fe (usually μ_pure-Fe equals 8), and μ_B is Bohr magneton. According to Eq. (2), nevertheless, the magnetization of Fe is determined to be 2.6 μ_B, which is larger than that of measured value 2.2 μ_B. In this case, this empirical equation is needed to be normalized as follows:

$$\mu _{{\mathrm{pure}}{\mbox{-}}{\mathrm{Fe}}} = \frac{{2.2}}{{2.6}}\left( {10.6 - n_{{\mathrm{pure}}{\mbox{-}}{\mathrm{Fe}}}} \right)\mu _{\mathrm{B}}.$$

(3)

As elaborated above, the sp orbitals of the metalloids have interactions with 3d electrons of Fe, which makes sp electrons of glass-forming elements transfer to minority-spin bands of Fe, leading to the increase of n in Eq. (3). Thus, the atomic magnetic moments of Fe-based MGs can be modified below:

$$\mu _{{\mathrm{amor}}{\mbox{-}}{\mathrm{Fe}}} = \frac{{2.2}}{{2.6}}\left[ {10.6 - \left( {n_{{\mathrm{pure}}{\mbox{-}}{\mathrm{Fe}}} + \mathop {\sum }x_in_i} \right)} \right]\mu _{{\mathrm{B}},}$$

(4)

where μ_amor-Fe is the atomic magnetic moments of Fe-based MGs, x_i and n_i are the atomic fraction and the number of sp electrons of the ith alloying element, respectively. Taking the n_pure-Fe value of 8 into Eq. (4), one can get the following expression:

$$\mu _{{\mathrm{amor}}{\mbox{-}}{\mathrm{Fe}}} = \left(2.2 - 0.846\mathop {\sum }x_in_i\right)\mu _{{\mathrm{B}}.}$$

(5)

As we can see from Fig. 5a, the linear fitting curve of Eq. (1) is quite comparable with Eq. (5), vividly verifying the validity of the established XGBoost ML model. From the perspective of ferromagnetic theory, B_s represents the density of magnetic dipoles in an alloy, which is correlated to magnetic moment ($\bar \mu$) and can be expressed as $B_{\mathrm{s}} = (c\bar \mu )\mu _{\mathrm{B}}$, where c is a constant⁴⁷. For soft-magnetic Fe-based MGs, the μ_amor-Fe can replace the $c\bar \mu$, and when not taking units into account, the B_s and μ_amor-Fe are equal to each other in value. Thus, by extraction of key parameters of Fe-based magnetic MGs using the XGBoost ML model, we successfully revealed the underlying physical origin of the B_s from the perspective of charge transfer and magnetic moment and deduced a general rule (i.e., Eq. (1)) to predict B_s, which can provide a scientific guidance for alloy design of Fe-based soft-magnetic MGs as long as Co and Ni are not involved.

In the case of thermal stability, crystallization processes of MGs are rather complicated, involving nucleation and growth of crystalline phases. The crystallization rate of glass-to-crystal transformation is commonly dominated by the nucleation rate and therefore depend not only on diffusivity, but also strongly on thermodynamic properties such as glass-crystal interfacial energy and the entropy of fusion⁴⁸.

As shown in Fig. 6, the crystallization temperature T_x is positively proportional to the averaged atomic radius difference (δ). From the perspective of topological criterion, which has been often used to understand the atomic structure and glass formation of MGs, atoms with significant size mismatch are in favor to form dense random packed atomic configuration⁴⁹. The constituent elements with the appropriate atomic size difference could stabilize the dense packing structure of MGs by forming various types of topological short-range orders. Thus, for Fe-based MGs, with the addition of either small (i.e., C, B, Si, and P) or large atoms (e.g., Hf, Ta, Y), the resultant dense packing structure can sufficiently stabilize the amorphous phase and restrain the nucleation and growth of crystallites, thus leading to a high crystallization temperature. On the other hand, from the kinetic point of view, thermal stability of MGs is closely related to the diffusion behavior of constituents. Numerous dense packing local structures existing in the glass matrix make the atomic diffusion more difficult during the crystallization process⁵⁰, thereby increasing the crystallization temperature.

Fig. 6: Statistical analysis of experimental data for T_x versus δ and VEC.

The crystallization temperature T_x is positively proportional to δ and negatively proportional to VEC.

In addition, our analysis also revealed that T_x is also negatively proportional to VEC, as shown in Fig. 6. In metallic materials, the valence electrons act like “glue”, bonding non-valence electrons and nuclei units together⁵¹. For Fe-based MGs, a high VEC value indicates a strong interaction between the principal element (i.e., Fe) and the alloying constituents, which may promote the formation of more pronounced chemical short-range orders (CSROs). Generally, CSROs are considered to be the precursor of nanocrystals in crystallization processes due to the similar constituent and topological structure^52,53. As a result, the CSRO can act as the preferential nucleation sites for primary crystalline phases usually observed in Fe-based MGs, such as α-Fe, Fe₂₃M_6, and α-Mn type phases². According to the heterogeneous nucleation theory⁵⁴, the existence of nucleation sites can decrease the activation energy for nucleation, which makes the crystallization easy and thus decreases the crystallization temperature. Thus, to achieve high thermal stability of Fe-based MGs, the elements with low valence electrons, such as B, C, Y, Zr, Hf, and Ta, should be selected in the first priority to lower the VEC and thus to enhance the T_x value.

As illustrated above, the T_x is strongly correlated with both δ and VEC. Therefore, the natural thought is to deduce a simple correlation of T_x with both δ and VEC based on the ML model. Figure 6 depicts all the data points of T_x, δ, and VEC of Fe-based MGs. It is seen that all these data collapse into a plane which can be described as follows:

$$T_{\mathrm{x}} = 1518.5 + 27.1 \times \delta - 123.7 \times {\mathrm{VEC}}.$$

(6)

The intercept and slope of δ and VEC for the fitting plane is 1518.5, 27.1 and −123.7, respectively. The linear fitting plane of Eq. (6) is consistent with the above discussion, verifying the validity of the key features determined by the XGBoost ML model. Thus, with the ML strategy, we deduced simple correlations between the properties, i.e., B_s (Eq. (1)) and T_x (Eq. (6)) for Fe-based magnetic MGs, enabling the possible efficient design of magnetic amorphous materials with desirable performance.

Experimental verification for the XGBoost model

Based on the above analysis, the current ML model hints us a general benchmark for the design of Fe-based MGs with good soft-magnetic properties and high thermal stability. Based on the simple guidelines in Eqs. (1) and (6), we can accelerate the selection of glass-forming elements and determine their desirable fractions to design Fe-based MGs with a combination of high B_s and T_x For demonstration, we have fabricated several different types of Fe-based MG ribbons, including Fe–B–Si–Zr and Fe–B–Si–Ta–Zr, and measured their B_s and T_x values by vibrating sample magnetometer (VSM) and differential scanning calorimetry (DSC), respectively. Moreover, to validate our XGBoost ML model, the predicted B_s of the designed alloys were also compared with the experimental results.

As shown in Fig. 7a, XRD patterns for all the as-spun ribbons of the designed MGs exhibit the typical amorphous feature which characterized by a broad diffuse peak at around 2θ = 45°. Figure 7b shows DSC traces of the as-spun ribbons at a heating rate of 0.33 K s⁻¹ while Fig. 7c presents the hysteresis loops of the as-spun ribbons at room temperature. The T_x and B_s values determined from the DSC curves and hysteresis loops, respectively, are summarized in Table 1. Figure 7d show the B_s and T_xfor the designed Fe-based magnetic MGs (without the addition of Co and Ni), in comparison to those reported previously. As can be seen from Fig. 7d and Table 1, the B_s and T_x values of designed Fe_73.8B_15.79Si_6.9Ta_0.75Zr_2.76 MG reaches 1.34 T and 865 K, respectively. Compared with the widely commercialized nanocrystalline material - FINEMET (Fe_73.5Si_13.5B₉Nb₃Cu₁), the soft-magnetic property and thermal stability of this particular Fe-based MG are much better. For another developed MG with a high Fe content, i.e., Fe_82.55B_13.79Si_0.9Zr_2.76, its B_s is over 1.6 T while the T_x value reaches 738 K, outperforming many counterparts with an Fe concentration over 80 at.%. Therefore, it is clear that based on the guidelines in Eqs. (1) and (6), we can quickly design soft-magnetic Fe-based MGs for different application purposes with different requirements of magnetic and thermal properties.

Fig. 7: Experimental validation of the ML prediction.

a XRD patterns, (b) DSC curves at a heating rate of 0.33 K s⁻¹, (c) the hysteresis loops, and (d) the B_s and T_x values of the designed soft-magnetic Fe-based MGs based on the ML model. Experimental data reported in the literature are also listed in (d) for comparison.

Table 1 Summary of VEC1, VEC, δ, onset temperature of crystallization (T_x), predicted onset temperature of crystallization (T_{x_cal}), saturation magnetization (B_s), and predicted saturation magnetization (B_{s_cal}) of the as-prepared Fe-based MGs.

Since the prediction criteria were based on the ML-determined important feature, checking the accuracy of Eqs. (1) and (6) can, in return, verify the validity of the XGBoost ML model used. For this purpose, the calculated saturation magnetization using Eq. (1) and crystallization temperature using Eq. (6), denoted by B_{s_cal} and T_{x_cal}, are also listed in Table 1. When comparing the calculated results and the experimental results, one can find that the prediction error is lower than 10% and 5% for B_s and T_x, respectively, indicating the accuracy and validity of Eqs. (1) and (6). Thus, these results verify that it is feasible and efficient for the property-orientated materials design strategy by combining ML and critical experiments to quickly develop Fe-based MGs with good soft-magnetic properties and thermal stability.

Methods

Data preparation

The dataset is consisted of 252 alloys with different compositions compiled from literature, with no consideration of fabrication methods utilized. For each alloy, it contains both intrinsic properties of alloys, such as concentration of the alloy, averaged atomic radius difference (δ), melting point (T_m), electronegativity (χ), and VEC, and macroscopic properties such as the crystalline temperature T_x and saturation flux density B_s. To build a ML model, it is important to select proper input and output parameters, corresponding to features and targets, respectively. For input descriptors, we selected compositions of alloys, δ, T_m, χ, and VEC as features, whilst T_x and B_s as targets. The averaged atomic radius difference, melting point, electronegativity and VEC of alloys are defined as follows:

$$\delta = \mathop {\sum}\limits_i {\left| {c_i(r_i - r_{{\mathrm{Fe}}})} \right|\,} ,$$

(7)

$$T_{\mathrm{m}} = \mathop {\sum}\limits_i {c_iT_{{\mathrm{m}}i},}$$

(8)

$$\chi = \mathop {\sum}\limits_i {c_i\chi _i} ,$$

(9)

$${\mathrm{VEC}}1 = \left(\mathop {\sum}\limits_i {c_iN_i} \right) - c_{{\mathrm{Fe}}}N_{{\mathrm{Fe}}},$$

(10)

$${\mathrm{VEC}} = \mathop {\sum}\limits_i {c_iN_i} ,$$

(11)

where c_i, r_i, T_mi, χ_i, and N_i are the concentration, atom radius, melting point, electronegativity and the number of valance electron of the ith element, respectively. $c_{{\mathrm{Fe}}}$, $N_{{\mathrm{Fe}}}$, and $r_{{\mathrm{Fe}}}$ are the concentration, number of valance electron and atom radius of Fe.

To fit the data in different ranges for the ML model, it is necessary to transform them to the same scale. For instance, the temperatures in features and targets fall into the range from 800 to >2000 K, whilst that of the averaged atomic radius difference ($\delta$) is less than $10^{ - 2}$. Thus, it is essential to scale these data by proper algorithm. There are many algorithms to achieve such a goal. Here we just used the most simplified one:

$$T^{\prime}_{\mathrm{m}} = \frac{{T_{\mathrm{m}}}}{{1000.0}},$$

(12)

$$\delta^{\prime} = \delta \times 100.0.$$

(13)

Then, the features and targets shall be split into a training subset and a testing subset for the subsequent ML.

Machine learning

XGBoost model

XGBoost is the abbreviation of eXtreme Gradient Boosting, which is a scalable algorithm based on tree boosting coined by Chen and Guestrin³¹. The XGBoost package provides both linear models and tree-based machine-learning algorithm, and supports classification, regression and ranking functions. Meanwhile, the extendibility of the package makes it possible for users to define their own objective functions if necessary. As described, for an input dataset $D = \{ \left( {x_i,y_i} \right)\}$, where $x_i$ is the training dataset of features associated with Fe-based MGs to predict the class label, $y_i$, a Classification and Regression Tree (CART) assigns a real score to each leaf, and the final score is obtained by summing up the prediction score for each CART and assessed by $K$ additive functions, which is shown in Eq. (14):

$$\widehat {y_i} = \mathop {\sum}\limits_{k = 1}^K {f_k(x_i)} ,\,f_k \in F,$$

(14)

where f_k is an independent tree structure with leaf weights and F is the space of all regression trees. To learn the final function applied in the ML framework, the regularized objective to minimize is given by Eq. (15):

$${\mathrm{Obj}}\left( \Theta \right) = \mathop {\sum}\limits_i^n l \left( {y_i,\widehat {y_i}} \right) + \mathop {\sum}\nolimits_k^K \Omega \left( {f_k} \right),$$

(15)

$l$ is a differentiable loss function, which measures the difference between the predicted $\hat y$ and the target $y_i$. ${{\Omega }}$ is the regularization term which penalizes the complexity $f$ of the model to prevent overfitting. The penalizing term is given by $\Omega \left( f \right) = \gamma T + \frac{1}{2}\lambda \mathop {\sum}\nolimits_{j = 1}^T {w_j^2}$, where $T$ and $w$ are the number of leaves and the score on each leaf, respectively. $\gamma$ and $\lambda$ are constants to control the degree of regularization. Meanwhile, the overfitting can also be prevented by two additional techniques, i.e., descriptor subsampling and shrinkage.

For a training dataset with vectors of features and corresponding class labels, the training procedure in XGBoost mainly includes scanning the best splitting point, choosing the descriptor with the best splitting point that optimizes the training objective, assigning prediction score to the leaves and pruning all negative nodes (nodes with negative gains) in a bottom-up order.

Since additive training is used, the prediction $\hat y$ at step $t$ is expressed as

$$\widehat {y_i}^{(t)} = \mathop {\sum}\limits_{k = 1}^K {f_k(x_i)} = \widehat {y_i}^{(t - 1)}.$$

(16)

And Eq. (15) can be written as

$${\mathrm{Obj}}\left( \Theta \right)^{(t)} = \mathop {\sum}\limits_i^n l ( {y_i,\widehat {y_i}^{\left( {t - 1} \right)} + f_t\left( {x_i} \right)} ) + {{\Omega }}\left( {f_t} \right).$$

(17)

By taking the Taylors expansion to the second order for the loss function, Eq. (15) can be further written as

$${\mathrm{Obj}}\left( \Theta \right)^{(t)} = \mathop {\sum}\limits_{i = 1}^n \left[l \left( {y_i,\widehat {y_i}^{\left( {t - 1} \right)} + g_if_t\left( {x_i} \right) + \frac{1}{2}h_if_t^2\left( {x_i} \right)} \right)\right] + {{\Omega }}(f_t),$$

(18)

where $g_i = \partial _{\widehat {y_i}^{\left( {t - 1} \right)}}l(y_i,\widehat {y_i}^{\left( {t - 1} \right)})$ and $h_i = \partial _{\widehat {y_i}^{\left( {t - 1} \right)}}^2l(y_i,\widehat {y_i}^{\left( {t - 1} \right)})$ are the first and second-order statistics on the loss function, respectively. A simplified objective function of Eq. (18) at the step t is as follows:

$${\mathrm{Obj}}\left( \Theta \right)^{(t)} = \mathop {\sum}\limits_{i = 1}^n {\left[ {g_if_t\left( {x_i} \right) + \frac{1}{2}h_if_t^2\left( {x_i} \right)} \right]} + \Omega \left( {f_t} \right).$$

(19)

By expanding the regularization term, the objective function is expressed as

$$\begin{array}{*{20}{l}} {{\mathrm{Obj}}\left( \Theta \right)^{\left( t \right)}} \hfill & = \hfill & {\mathop {\sum }\limits_{i = 1}^n \left[ {g_if_t\left( {x_i} \right) + \frac{1}{2}h_if_t^2\left( {x_i} \right)} \right] + \gamma T + \frac{1}{2}\lambda \mathop {\sum}\limits_{j = 1}^T {w_j^2} } \hfill \\ {\,} \hfill & = \hfill & {\mathop {\sum}\limits_{j = 1}^T {\left[ {(\mathop {\sum}\limits_{i{\it{\epsilon }}I_j} {g_i} )w_j + \frac{1}{2}(\mathop {\sum}\limits_{i{\it{\epsilon }}I_j} {h_i} + \lambda )w_j^2} \right] + \gamma T,} } \hfill \end{array}$$

(20)

where $I_j = \{ i\left| q \right.\left( {x_i} \right) = j\}$ is the instance set of leaf $j$. The optimal leaf weight, $w_j^ \ast$, and the optimal objective function are given by Eqs. (21) and (22), respectively:

$$w_j^ \ast = - \frac{{G_j}}{{H_j + \lambda }},$$

(21)

$${\mathrm{Obj}}^ \ast = - \frac{1}{2}\mathop {\sum}\limits_{j = 1}^T {\frac{{G_j^2}}{{H_j + \lambda }} + \gamma T,}$$

(22)

where $G_j = \mathop {\sum}\nolimits_{i{\it{\epsilon }}I_j} {g_i}$ and $H_j = \mathop {\sum}\nolimits_{i{\it{\epsilon }}I_j} {h_i}$.

Equation (23) is used to score a leaf node during splitting:

$${\mathrm{Gain}} = \frac{1}{2}\left[ {\frac{{G_L^2}}{{H_L + \lambda }} + \frac{{G_R^2}}{{H_R + \lambda }} - \frac{{(G_L + G_R)^2}}{{H_L + H_R + \lambda }}} \right] - \gamma .$$

(23)

The first, second, and third term of Eq. (23) are the score on the left, right, and the original leaf, respectively. Regarding to the final term, .., it is the regularization on the additional leaf.

Experiments

All alloy ingots of nominal compositions were prepared by arc-melting a mixture of constituent elements of Fe, B, Si, Ta and Zr with purity higher than 99.9 wt.% in a Ti-guttered argon atmosphere. Amorphous ribbons, typically 1–1.5 mm wide and 25–30 μm thick, were produced by the melt-spinning technique with a Cu-alloy wheel under an Ar atmosphere at a surface speed of 40 m s⁻¹. Thermal properties of all the as-spun ribbons were evaluated by differential scanning calorimetry (DSC) at a heating rate of 0.33 K s⁻¹ with argon as purging gas. Microstructures of the as-spun ribbons were identified by X-ray diffraction (XRD) with Cu Kα radiation. The saturation flux density (B_s) values of all the as-spun ribbons were characterized by a VSM under an applied field of −800 to 800 kA m⁻¹. In order to transform the value of B_s in unit of Tesla, the density of the rod specimens was measured by means of Archimedes’s method, and are listed in Table 1. Before the VSM tests, all the amorphous ribbons were annealed at 100 K below T_x to relieve internal stress.