Abstract
A critical ingredient for realising large-scale quantum information processors will be the ability to make economical use of qubit control hardware. We demonstrate an extensible strategy for reusing control hardware on same-frequency transmon qubits in a circuit QED chip with surface-code-compatible connectivity. A vector switch matrix enables selective broadcasting of input pulses to multiple transmons with individual tailoring of pulse quadratures for each, as required to minimise the effects of leakage on weakly anharmonic qubits. Using randomised benchmarking, we compare multiple broadcasting strategies that each pass the surface-code error threshold for single-qubit gates. In particular, we introduce a selective broadcasting control strategy using five pulse primitives, which allows independent, simultaneous Clifford gates on arbitrary numbers of qubits.
Similar content being viewed by others
Introduction
Building a fault-tolerant quantum computer requires the ability to efficiently address and control individual qubits in a large-scale system. Many leading experimental quantum information platforms, including trapped ions,1 electronic spins in impurities and quantum dots,2 and superconducting circuits,3 use qubits with level transitions in the microwave frequency domain. Addressing these transitions often involves expensive microwave electronics scaling linearly with the number of qubits. To move beyond the state-of-the-art in microwave-frequency quantum processors, such as those recently used for small-scale quantum error correction in superconducting circuits,4–6 it is beneficial to have a hardware-efficient control strategy that harnesses economies of scale. One approach, as proposed by Hornibrook et al.,7 is to use microwave pulses from a single control source for multiple qubits, requiring frequency-matched qubits and high-speed routing of pulses to separate control lines. The linear scaling of control equipment could then be reduced to a constant overhead for the most expensive resources.
Using control equipment for multiple qubits has previously been demonstrated for optical addressing in atomic systems, where qubits naturally have the same frequency.8–11 Such frequency reuse also becomes possible in circuit quantum electrodynamics12 in the context of fault-tolerant computation strategies that rely only on local interactions between qubits mediated by bus resonators.13–15 The natural isolation between different lattice sites allows the use of repeating patterns of qubit frequencies with selectivity provided by spatial separation. A tileable unit cell with a handful of qubit frequencies16 could, therefore, provide a promising route towards scalability. Crucially, this also solves the frequency-crowding problem that arises when trying to fit many distinct-frequency qubits within the finite useful bandwidth of the circuit-based devices, particularly for designs based on weakly anharmonic qubits where higher levels must also be avoided.17,18 Hornibrook et al.7 have recently demonstrated cryogenic switching matrix hardware for pulse distribution operating at 20 mK, triggered by a field-programmable gate array at 4 K. Cryogenic control equipment may shorten feedback latency and reduce wiring complexity across temperature stages, but the isolation and operational frequency range reported to date are insufficient for typical circuit quantum electrodynamics experiments. Simultaneous driving of multiple qubits with distinct frequencies using individually dedicated control hardware has already been demonstrated in a range of previous circuit quantum electrodynamics experiments.19,20 To date, however, simultaneous driving has not been demonstrated on same-frequency, solid-state qubits using shared microwave control hardware.
In this article, we demonstrate frequency reuse in an extensible solid-state multiqubit architecture. An extensible architecture harnessing frequency reuse has two key requirements: a method for distributing control pulses to multiple qubits with economical means to adapt the pulses for each qubit, and a multiqubit device containing same-frequency qubits with relevant connectivity and sufficient isolation between same-frequency qubits. To this end, we show independent simultaneous control of two same-frequency qubits with a room-temperature vector switch matrix (VSM) that we have developed. The VSM allows tailoring of control pulses to individual qubit properties, and routing of the pulses to either one or both of the qubits using fast digital markers. We develop several different approaches to selective pulse broadcasting, including a simple scheme for implementing independent Clifford control on an arbitrary number of qubits with a constant overhead in time. The device for this experiment is designed to allow testing in a circuit with the correct connectivity of a relevant surface-code lattice.21,22 Using randomised benchmarking (RB), we show that all control schemes exceed the fidelity threshold for surface code and are dominated by qubit relaxation. We also develop a method for measuring leakage to the second-excited state directly within the context of RB.23,24 We characterise the limitations of our system and find no major obstacles to scaling up to larger implementations.
Results
To demonstrate frequency reuse, we focus on a particular implementation of the surface code based on repeated tiling of a unit cell consisting of four qubits and two resonators13 (Figure 1). Each qubit couples to two resonators and each resonator couples to four qubits, requiring a minimum of four unique qubit frequencies at the operating point for single-qubit control. This ensures that same-frequency qubits are never coupled through a single resonator. Independent microwave control of same-frequency qubits requires a separate drive line for each. Such a line can be dedicated to each qubit,25 as used in this demonstration, or to each resonator26 to allow the driving of all four qubits coupled to it. This implementation of surface code requires two-qubit gates only between different-frequency qubits coupled to the same resonator and never between same-frequency qubits. Our two-qubit gates will be implemented using fast flux-bias lines,27 but in this article we focus on VSM-based single-qubit control. The higher-order coupling between same-frequency qubits (mediated by at least two resonators and one qubit at a different frequency) is only ever a disturbance and error source. Our device contains a small block of this surface code implementation, consisting of two same-frequency transmon qubits (QT and QB), which are connected to a third qubit (QM) via separate bus resonators (Figure 1). Together, the buses and QM, although not actively used throughout the experiment, provide a realistic operating environment for QT and QB.
Schematic of independent control of same-frequency qubits using a vector switch matrix (VSM). The device (grey-coloured box on right) connects two transmons with matched frequency (QT and QB: 6.220 GHz) indirectly through coupling buses and a third non-matched transmon (QM: 6.550 GHz). This provides the smallest relevant subunit of the four-frequency surface-code fabric illustrated above right (colours represent distinct qubit frequencies). The VSM (blue box) allows independent, simultaneous transmon control with tailored DRAG pulsing for each qubit through dedicated drive lines. The link between inputs and outputs can be switched on nanosecond timescales using the digital markers MT and MB (orange lines). Gaussian and derivative-of-Gaussian pulses are independently tuned in amplitude and phase for each input–output pair (top left).
To efficiently control multiple same-frequency qubits, we have designed a prototype room-temperature 4×2 (four input, two output) VSM that allows independent control of amplitude and phase for each of its input–output combinations. Fast marker-controlled digital switches enable routing of pulses to the qubits at nanosecond timescale, with approximately 50 dB isolation in the frequency range from 4 to 8 GHz (see Supplementary Material for additional data on VSM specifications). Because of the transmon’s weak anharmonicity,28 high-fidelity fast single-qubit control is achieved using the method of derivative-removal-via-adiabatic-gate (DRAG) pulsing, where the in-phase Gaussian pulse is combined with a quadrature derivative-of-Gaussian pulse.29,30 By directing the two constituent pulses of DRAG control to two of the four inputs of the VSM, this allows independent, in situ DRAG tuning for both same-frequency qubits using four AWG channels (two channels for IQ modulation of each constituent pulse; see Supplementary Material at [http://www.nature.com/npjqi] for additional data).
The first critical test of our control architecture is to assess the VSM’s ability to implement high-precision control of one qubit while leaving the other qubit idle. To do this, we use the standard technique of single-qubit RB based on Clifford gates,31–33 which allows the characterisation of control performance independently of state preparation and measurement errors. After initialising all qubits in the ground state by relaxation, we use the VSM to selectively apply random sequences of Cliffords gates to only one of the same-frequency qubits (Figure 2a,b), in each case measuring the effect on both qubits simultaneously via multiplexed readout.34,35 We decompose each gate into the standard minimal sequence of π and ±π/2 pulses around the x and y axes, requiring on average 〈Np〉=1.875 pulses per Clifford.24 This is in contrast to so-called ‘atomic pulses’,36 where the 24 single-qubit Cliffords can each be implemented with a single pulse. Each π and ±π/2 pulse is 16 ns long and separated by a 4 ns buffer from the next, for a total pulse time tp=20 ns. After applying a final Clifford that inverts the cumulative effect of all m previous Cliffords, the driven qubit is ideally returned to the ground state, but as a result of imperfections such as gate errors and decoherence the final ground-state population decays as a function of m. The decay rate can be related to the average fidelity per Clifford FC.31,32 From the RB data (Figure 2c,d), we extract the average Clifford fidelities for the two individually driven qubits to be 0.9982(2) (QT) and 0.9986(2) (QB). We compare these values with the expected average Clifford fidelities assuming only T1 decay:37
The similarity (Figure 2c,d) shows that the results are predominately limited by relaxation effects. The difference in performance between the two qubits is consistent with their different T1 times. It is consistent with previous RB demonstrations19 that we do not see a strong signature of pure dephasing in the fidelity. Further measurements show that driving both qubits simultaneously by the same pulse sequence (both markers on) does not significantly impact the performance (see Supplementary Material at [http://www.nature.com/npjqi] for additional data).
Single-qubit control of same-frequency qubits using the VSM. (a, b) Schematics showing DRAG pulses routed exclusively to either QT or QB using the corresponding markers (always on or off). (c, d) Characterisation of single-qubit control by randomised benchmarking (RB) of Clifford gates. Average populations of QT and QB in the ground, first- and second-excited states (〈P0〉, 〈P1〉 and 〈P2〉, respectively) as a function of the number of Clifford gates applied. Curves are best fits of single exponentials with offsets. Single-qubit Clifford fidelities for each qubit are extracted from the decay of ground-state populations. Both surpass the surface-code fault-tolerance threshold and are near T1-only relaxation-limited performance. (e, f) Expanded plots of second-excited state leakage during RB. Curves are best fits according to equation (2). (g, h) Cross-excitation of the undriven qubit resulting from control pulses applied to the driven qubit due to microwave leakage.
In a strictly two-level system, the measured ground- and excited-state populations averaged over many sequences (〈P0〉 and 〈P1〉) both converge to 0.5 for large m. For weakly anharmonic transmon qubits, leakage to the second-excited state can be an important additional source of gate error, which can lead to a shift of the asymptotic values away from 0.5. We address this issue by performing the RB protocol both with and without an additional final π pulse,38 which allows us to explicitly estimate the populations of the first three transmon states (see Supplementary Material at [http://www.nature.com/npjqi] for additional data). From the measured leakage populations 〈P2〉 (Figure 2e,f), we extract per Clifford leakage rates κ of 4.1(2)×10−6 (QT) and 1.3(4)×10−6 (QB) by fitting the following simple model to the data (see Supplementary Material at [http://www.nature.com/npjqi] for additional data):
where T2→1 is the second- to first-excited-state relaxation time. As these leakage rates are much smaller than the gate errors (1−FC), it is reasonable to neglect them when estimating the Clifford fidelity.
We next explore the effect of the single-qubit control pulses on the undriven qubit (Figure 2g,h). Although QT remains largely unaffected when driving QB, a substantial deviation from the ground state is measured in QB when driving QT. There are several possible mechanisms for cross-excitation in the system. Dominant on-chip sources include residual exchange interaction J between QT and QB (mediated by the bus resonators and QM), and cross-driving, resulting from uncontrolled parasitic couplings between each drive line and the untargeted qubit. As detailed in the 'Materials and Methods' section, measurements of these on-chip sources found J/2π≤36±1 kHz, and an asymmetric cross-driving that is stronger when QB is driven using the drive line of QT (−45 dB) than vice versa (−53 dB). This is larger than the dominant off-chip source of cross-excitation, the finite VSM isolation, which is approximately −57 and −54 dB on QT and QB, respectively (see Supplementary Material at [http://www.nature.com/npjqi] for additional data), lower than the direct on-chip cross-driving. The symmetric swapping of excitation under exchange is unlikely to explain the strong asymmetry in the amount of cross-excitation measured for the different qubits. Moreover, numerical simulations show that the observed effects are consistent with cross-driving alone (see Supplementary Material at [http://www.nature.com/npjqi] for additional data). This effect of cross-driving in the context of RB can be quantified using interleaved RB.39 In interleaved RB, the fidelity of an individual gate is estimated by interleaving repeated applications of that gate with a sequence of random Cliffords and comparing the performance with conventional RB. When using the VSM to implement individual qubit control, gates applied to one qubit should behave as an effective idling operation for the other. From this perspective, the sequential RB scheme can be viewed as interleaved RB for an idling operation. The idling fidelity can therefore be extracted by comparing the fidelities obtained for sequential RB with the fidelities for single-qubit RB. This yields an average idling fidelity for QB of 0.9986(5) (see Supplementary Material at [http://www.nature.com/npjqi] for additional data), consistent with the error due to additional T1 decay, confirming that cross-excitation effects do not dominate the error per Clifford.
The defining test of extensibility in our control architecture is to demonstrate the simultaneous, independent, single-qubit control over same-frequency qubits that is enabled by selective broadcasting using the VSM. We explore three paradigmatic schemes for implementing selective broadcasting of Cliffords on an arbitrary number of qubits n (Figure 3). In the most straightforward selective broadcasting scheme, the individual qubits are driven sequentially, with each pulse being directed to one qubit at a time. This results in a linear scaling of the average number of pulses per Clifford round (〈Np〉=1.875×n). By contrast, the second paradigm takes best advantage of the VSM’s capability to broadcast simultaneously to multiple qubits by compiling the constituent Clifford pulses to minimise Np for each Clifford combination in the sequence. However, compiling pulses comes at the cost of an exponentially increasing compilation time with the number of qubits before running the sequence.
Selective broadcasting schemes for simultaneous single-qubit control of multiple qubits. Main figure: Example of a single Clifford round for n=2 qubits targeting C2 (C13) in QT (QB) (Cj defined in Supplementary Material at [http://www.nature.com/npjqi]). In the sequential scheme, the pulses implementing C2 are directed to QT, after which the pulses implementing C13 are directed to QB. In the compiled scheme, the two Cliffords are realised concurrently using a pre-determined pulse sequence, with appropriate markers, which minimises the total number of pulses, Np (see Supplementary Material at [http://www.nature.com/npjqi] for additional data on the compilation algorithm). Finally, in the five-primitives scheme, a fixed sequence of five pulses is repeated in each round (Np=5). The targeted Cliffords are then applied simultaneously by selecting the appropriate subset of pulses for each qubit (see Supplementary Material at [http://www.nature.com/npjqi] for additional data on the five-primitives marker table). Top-right: scaling of the average pulses per multiqubit combination of Cliffords, 〈Np〉, versus qubit number n. The constant scaling achieved by the five-primitives scheme provides a dramatic improvement over the linear scaling of the sequential scheme. Although 〈Np〉 is always lowest for the compiled scheme, pre-compiling the optimal pulse and marker combinations is impractical for n≳5, and the improvement over the simpler five-primitives scheme is negligible by n~10.
This motivates our final broadcasting paradigm, where all Clifford gates can be implemented using the same fixed, ordered sequence of five pulse primitives (Figure 3). Independent Cliffords can be applied to all qubits, irrespective of n, by selectively directing the appropriate subset of pulses to each qubit, achieving a constant overhead in time for control of an arbitrary number of qubits. Although the number of pulse primitives must be at least five to produce the 24 unique Cliffords, the choice of the five pulses is not unique. We have chosen a combination of positive and negative rotations to partially null-out the effect of cross-driving on the undriven qubit (see Supplementary Material at [http://www.nature.com/npjqi] for additional data). We also alternate between two versions of the five pulse primitives, where in the second version they are in reverse order and opposite rotation to even further reduce cross-driving.
To demonstrate the full functionality of our control architecture, we implement all three selective broadcasting schemes and measure their performance using parallel single-qubit RB with independent Clifford sequences for each qubit. Figure 4 shows that the compiled scheme performs best, followed by the sequential and then 5-primitives schemes, consistent with the average number of pulses required for each (Figure 3). In all cases, the average fidelity per Clifford is still dominated by relaxation (Table 1). The results are completely consistent with the values obtained in the test for isolated single-qubit control.
Characterisation of sequential, compiled and five-primitives selective broadcasting schemes by RB. (a, b) Evolution of the average transmon populations for QT (a) and QB (b) as a function of the number of Clifford rounds. Curves are the best fits of single exponentials with offsets. (c, d) Expanded plots of second-excited-state leakage during RB.
Discussion
Our VSM allows efficient use of control equipment on same-frequency qubits. It enables high-precision single-qubit control of multiple qubits with a performance that surpasses the best-known surface-code fault-tolerance threshold for single-qubit gates of ~0.9940—42, and is mainly limited by relaxation. Although the measurements show a nonnegligible amount of leakage from the computational subspace after many pulses (Figure 2e,f), the corresponding leakage errors are outweighed by other gate errors. A significant amount of cross-excitation was measured in one qubit during the RB measurements (Figure 2h), which resulted primarily from on-chip cross-driving. In future experiments, this effect could be reduced by careful design of both the surface-code and physical chip layouts. In the first case, increasing the number of qubit frequencies used will result in larger lattice separations between same-frequency qubits. This will provide better effective isolation at the cost of increased design and hardware complexity. In the second case, circuit QED provides naturally good circuit isolation due to the superconducting ground plane, but optimising the on-chip coupling network to minimise spurious driving will still be one of the key problems in scaling up to larger systems. In addition, here we show that cross-driving effects can be reduced even at the control level. Specifically, as demonstrated here with the five-primitives pulse sequence (see Supplementary Material at [http://www.nature.com/npjqi] for additional data), we choose a sequence of control pulses in such a way that leakage pulses partially or completely cancel out. This technique is not limited to RB, but could also be used to minimise cross-driving in quantum algorithms. Furthermore, it is fully compatible with pulse-broadcasting methods, and allows straightforward scaling. This is not the case for compensation pulses, where the strength of each compensation pulse depends on the pulses applied to other qubits. By contrast with cross-driving, the measured cross-coupling (direct qubit–qubit quantum coupling) has no observable effect in the single-qubit RB measurements. Most likely, this is because rapid application of randomising Clifford pulses effectively decouples the cross-coupling dynamics. However, such a coupling may have a stronger effect in other contexts and may have to be addressed in future experiments.
We have introduced three selective broadcasting schemes for performing simultaneous, independent single-qubit RB on both qubits, in each case demonstrating performance that surpasses the fault-tolerance threshold for the surface code for both driven qubits. Selective broadcasting is not limited to transmon qubits; it can be applied to any other qubit system in which qubits can be sufficiently matched in frequency, and where a VSM can be realised. The naive sequential broadcasting approach still performs acceptably with two qubits, but scales poorly with increasing numbers of qubits. On the other hand, the compiled scheme by definition always minimises the length of the pulse sequence, but at the cost of exponentially increasing difficulty of the compilation step with the number of qubits. Moreover, our estimates show that the number of pulses per Clifford round rapidly asymptotes to a total of five pulses, thus only providing negligible gain in time and fidelity over the five-primitives scheme for even a handful of qubits. By contrast, the five-primitives scheme combines both scalability and simplicity of implementation (Figure 3), selecting the target Clifford by routing a subset of five primitive pulses using digital markers. It is the minimal set of pulses required for independent Clifford control for an arbitrary number of qubits with no additional overhead in the number of sequence pulses. On a technical level, marker-based selection of Clifford gates can be useful when fast feedback has to be applied on multiple qubits, as is often the case in quantum error correction protocols. Furthermore, by adding a sixth, non-Clifford gate to the five pulse primitives, this can be extended to achieve universal single-qubit control. We show that the fidelities are mainly limited by qubit relaxation for all broadcasting schemes, and are consistent with each other and with the single-qubit RB results once the average duration per Clifford round is taken into account. This confirms that selective pulse broadcasting does not decrease gate performance relative to that expected from the intrinsic pulse fidelities.
Owing to its small scale, our VSM prototype offers limited hardware savings. Although one microwave source is sufficient to control both QT and QB, full DRAG control still requires four AWG channels. However, no further channels will be required for controlling additional qubits, subject to the limitations of signal amplification and fan-out, which we estimate should enter at ~100 same-frequency qubits. Although our VSM is designed to be compatible with the full DRAG control required for weakly anharmonic transmon qubits, it is by no means limited to this case. In fact, our VSM already enables precision control of strongly anharmonic qubits such as flux and fluxonium qubits43,44 without any hardware modification and using only one input per frequency. In this case, there would already be savings in AWG channels at the scale of our prototype.
Combining the connectivity of our device, the VSM-based control and the fixed pulse overhead of the five-primitives broadcasting strategy, our experiment realises the simplest element of an extensible qubit control architecture. This design can be straightforwardly expanded to more same-frequency qubits without requiring any further microwave sources or arbitrary waveform generators. This experiment suggests that surface-code tiling with frequency reuse is a viable path towards large-scale quantum processors.
Materials and Methods
This section provides further details on the circuit quantum electrodynamics device and VSM, and describes the methods used to measure cross-coupling and cross-driving.
The use of control pulses for multiple qubits requires the qubits to be matched in frequency to avoid gate errors from off-resonant driving. Although QT and QB were designed to be identical, fabrication uncertainties resulted in a sweet-spot (maximum) frequency of 57 MHz higher than that of QB. With QB and QM kept at their respective sweet-spots (6.220 and 6.550 GHz, respectively), QT was then flux tuned to match QB with an accuracy of 50 kHz, determined using Ramsey measurements (see below). The coherence times at the operating point are provided in the Supplementary Material (see Supplementary Material at [http://www.nature.com/npjqi] for additional data).
The VSM was designed to accept multiple input pulses and selectively fan them out to multiple qubits with individual pulse tuning for each qubit (Figure 1). Each input signal is first split and then amplified back, before continuing on to a switch, phase shifter, tuneable attenuator and final amplifier. By ensuring that the line impedance does not depend on the state of the other switches, each VSM line can be controlled independently. Furthermore, the phase shifters are not implemented via delay lines to ensure the pulse timing is independent of the added phase.
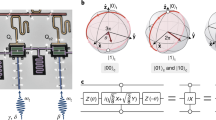
To characterise the cross-coupling between QT and QB, we measure the evolution of excited-state populations after a single excitation is injected at one of the qubits with a π pulse. To place a tight upper bound on the interaction strength J, the qubit frequencies must be matched as closely as possible. We achieve an accuracy of around 50 kHz using Ramsey experiments, limited by a combination of factors: the resolution of the flux tuning, the fitting resolution limit imposed by qubit T2 dephasing times, and also the frequency shifting induced by the qubit–qubit exchange interaction itself. The oscillation frequency in the single-excitation swap experiments (Figure 5a,b) gives a residual exchange interaction12 between QT and QB with strength J/2π≤36±1 kHz. The pulse length of 16 ns used throughout these experiments results in an average drive pulse Rabi frequency almost three orders of magnitude larger than this residual coupling, ensuring that our drive pulses act locally. In addition, the first data points in Figure 5a,b confirm that, immediately following a local π pulse on one qubit, there is no excitation measured in the other qubit. This shows that the measurements are diagonal in the computational basis. These are two important sanity checks for any architecture utilising same-frequency qubits.
Sources of spurious on-chip qubit interactions and cross-driving. (a, b) Cross-coupling: temporal evolution of a single excitation after initially exciting QT (a) or QB (b). Both qubits are measured simultaneously using multiplexed readout. The oscillations of population in both qubits are out of phase and have a common frequency. The sum of both populations shows approximately exponential decay with time constant 10.2(2) μs, which lies between the relaxation times of QT and QB. (c, d) Cross-driving: Rabi oscillations of QT (c) and QB (d) induced by pulses on the drive line of the other qubit. The pulse amplitude is normalised to the calibrated π-pulse amplitude required for the directly coupled qubit, the normalisation factor being the inverse of the cross-driving ratio rc.
To characterise the residual on-chip cross-driving, we disconnect the VSM and send driving pulses through the drive line for one of either QT or QB, and compare the amplitude required to implement a π pulse on each same-frequency qubit (Figure 5c,d). For this test, pulses are first amplified and then attenuated using a step attenuator to allow the large amplitude range required. The cross-driving on our chip is asymmetric, being stronger when QB is driven using the drive line of QT (−45 dB) than vice versa (−53 dB).
References
Monroe, C. & Kim, J. Scaling the ion trap quantum processor. Science 339, 1164–1169 (2013).
Awschalom, D. D., Bassett, L. C., Dzurak, A. S., Hu, E. L. & Petta, J. R. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 339, 1174–1179 (2013).
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Corcoles, A. D. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015).
Ristè, D. et al. Detecting bit-flip errors in a logical qubit using stabilizer measurements. Nat. Commun. 6, 6983 (2015).
Hornibrook, J. M. et al. Cryogenic control architecture for large-scale quantum computing. Phys. Rev. Appl. 3, 024010 (2015).
Knoernschild, C. et al. Independent individual addressing of multiple neutral atom qubits with a micromirror-based beam steering system. Appl. Phys. Lett. 97, 134101 (2010).
Weitenberg, C. et al. Single-spin addressing in an atomic mott insulator. Nature 471, 319–324 (2011).
Crain, S., Mount, E., Baek, S. & Kim, J. Individual addressing of trapped 171yb+ ion qubits using a microelectromechanical systems-based beam steering system. Appl. Phys. Lett. 105, 181115 (2014).
Xia, T. et al. Randomized benchmarking of single-qubit gates in a 2d array of neutral-atom qubits. Phys. Rev. Lett. 114, 100503 (2015).
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
DiVincenzo, D. P. Fault-tolerant architectures for superconducting qubits. Phys. Scr. 2009, 014020 (2009).
Helmer, F. et al. Cavity grid for scalable quantum computation with superconducting circuits. Europhys. Lett. 85, 50007 (2009).
Ghosh, J., Fowler, A. G. & Geller, M. R. Surface code with decoherence: an analysis of three superconducting architectures. Phys. Rev. A 86, 062318 (2012).
Gambetta, J. M. & Smolin, J. Frequency arrangement for surface code on a superconducting lattice. US Patent 9,111,230 filed 14 March 2013 and issued 18 August 2015.
Schutjens, R., Dagga, F. A., Egger, D. J. & Wilhelm, F. K. Single-qubit gates in frequency-crowded transmon systems. Phys. Rev. A 88, 052330 (2013).
Vesterinen, V., Saira, O.-P., Bruno, A. & DiCarlo, L. Mitigating information leakage in a crowded spectrum of weakly anharmonic qubits. Preprint at https://arxiv.org/abs/1405.0450 (2014).
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500 (2014).
Chow, J. M. et al. Universal quantum gate set approaching fault-tolerant thresholds with superconducting qubits. Phys. Rev. Lett. 109, 060501 (2012).
Bravyi, S. B. & Kitaev, A. Y. Quantum codes on a lattice with boundary. Preprint at http://arxiv.org/abs/quant-ph/9811052 (1998).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Chasseur, T. & Wilhelm, F. Complete randomized benchmarking protocol accounting for leakage errors. Phys. Rev. A 92, 042333 (2015).
Epstein, J. M., Cross, A. W., Magesan, E. & Gambetta, J. M. Investigating the limits of randomized benchmarking protocols. Phys. Rev. A 89, 062321 (2014).
Fragner, A. et al. Resolving vacuum fluctuations in an electrical circuit by measuring the Lamb shift. Science 322, 1357–1360 (2008).
Majer, J. et al. Coupling superconducting qubits via a cavity bus. Nature 449, 443 (2007).
DiCarlo, L. et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240 (2009).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Motzoi, F., Gambetta, J. M., Rebentrost, P. & Wilhelm, F. K. Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 103, 110501 (2009).
Chow, J. M. et al. Optimized driving of superconducting artificial atoms for improved single-qubit gates. Phys. Rev. A 82, 040305 (2010).
Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A 77, 012307 (2008).
Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett. 106, 180504 (2011).
Magesan, E., Gambetta, J. M. & Emerson, J. Characterizing quantum gates via randomized benchmarking. Phys. Rev. A 85, 042311 (2012).
Jerger, M. et al. Frequency division multiplexing readout and simultaneous manipulation of an array of flux qubits. Appl. Phys. Lett. 101, 042604 (2012).
Groen, J. P. et al. Partial-measurement backaction and nonclassical weak values in a superconducting circuit. Phys. Rev. Lett. 111, 090506 (2013).
Johnson, B. R. et al. Demonstration of robust quantum gate tomography via randomized benchmarking. New J. Phys. 17, 113019 (2015).
Magesan E. Private communication.
Ristè, D., Bultink, C. C., Lehnert, K. W. & DiCarlo, L. Feedback control of a solid-state qubit using high-fidelity projective measurement. Phys. Rev. Lett. 109, 240502 (2012).
Magesan, E. et al. Efficient measurement of quantum gate error by interleaved randomized benchmarking. Phys. Rev. Lett. 109, 080505 (2012).
Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504 (2007).
Fowler, A. G., Stephens, A. M. & Groszkowski, P. High-threshold universal quantum computation on the surface code. Phys. Rev. A 80, 052312 (2009).
Wang, D. S., Fowler, A. G. & Hollenberg, L. C. L. Surface code quantum computing with error rates over 1%. Phys. Rev. A 83, 020302 (2011).
Mooij, J. E. et al. Josephson persistent-current qubit. Science 285, 1036–1039 (1999).
Manucharyan, V. E., Koch, J., Glazman, L. I. & Devoret, M. H. Fluxonium: single cooper-pair circuit free of charge offsets. Science 326, 113–116 (2009).
Acknowledgements
We thank RN Schouten, W Vlothuizen and P Koobs de Hartog for experimental contributions and B Criger, T Chasseur and DJ Reilly for discussions. We acknowledge funding by the Dutch Organization for Fundamental Research on Matter (FOM), the Netherlands Organisation for Scientific Research (NWO/OCW and Vidi scheme), the EU FP7 project ScaleQIT, an ERC Synergy Grant and a Marie Curie Career Integration Grant (LDC).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplemental Information accompanies the paper on the npj Quantum Information website (http://www.nature.com/npjqi)
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Asaad, S., Dickel, C., Langford, N. et al. Independent, extensible control of same-frequency superconducting qubits by selective broadcasting. npj Quantum Inf 2, 16029 (2016). https://doi.org/10.1038/npjqi.2016.29
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2016.29
This article is cited by
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
Control System of Superconducting Quantum Computers
Journal of Superconductivity and Novel Magnetism (2022)
-
Variational preparation of finite-temperature states on a quantum computer
npj Quantum Information (2021)
-
A new class of efficient randomized benchmarking protocols
npj Quantum Information (2019)
-
Density-matrix simulation of small surface codes under current and projected experimental noise
npj Quantum Information (2017)