Programmable Heisenberg interactions between Floquet qubits

Abstract

The trade-off between robustness and tunability is a central challenge in the pursuit of quantum simulation and fault-tolerant quantum computation. In particular, quantum architectures are often designed to achieve high coherence at the expense of tunability. Many current qubit designs have fixed energy levels and consequently limited types of controllable interactions. Here by adiabatically transforming fixed-frequency superconducting circuits into modifiable Floquet qubits, we demonstrate an XXZ Heisenberg interaction with fully adjustable anisotropy. This interaction model can act as the primitive for an expressive set of quantum operations, but is also the basis for quantum simulations of spin systems. To illustrate the robustness and versatility of our Floquet protocol, we tailor the Heisenberg Hamiltonian and implement two-qubit iSWAP, CZ and SWAP gates with good estimated fidelities. In addition, we implement a Heisenberg interaction between higher energy levels and employ it to construct a three-qubit CCZ gate, also with a competitive fidelity. Our protocol applies to multiple fixed-frequency high-coherence platforms, providing a collection of interactions for high-performance quantum information processing. It also establishes the potential of the Floquet framework as a tool for exploring quantum electrodynamics and optimal control.

Main

The capability to coherently choreograph interactions between qubits is the foundation for the recent advances in quantum technologies. A quintessential example is the manipulation of the quantum Heisenberg model for the simulation of many-body quantum spin systems^1,2,3,4, which has led to the recent discoveries of intriguing physical phenomena such as discrete time crystal⁵, phantom spin-helix states⁶ and formation of photon bound states⁷. The Heisenberg interactions are also the primitives for expressive multi-qubit gates⁸ which play important roles in quantum algorithms⁹ and quantum error correction^10,11. Therefore, endowing quantum architectures with such archetypal interactions considerably extends their capabilities and performance.

The required tunability in solid-state quantum devices entails additional decoherence channels, demanding design overhead and increased operational complexity. For example, in the domain of superconducting circuits, the performance in flux-tunable devices is typically limited by unavoidable 1/f noise arising from the surrounding environment. Meanwhile, fixed-frequency platforms such as single-junction transmon^12,13 and fluxonium¹⁴ biased at the half-integer flux quantum¹⁵ have the best coherence times to date, but their native interactions are limited to the cross-resonance^16,17 and longitudinal couplings^18,19. Parametric longitudinal^20,21,22 and transverse interactions²³ can also be accomplished by introducing additional tunable couplers, but the performance could be undermined by the couplers’ coherence and spurious couplings.

In this Article, we present a reliable and hardware-efficient protocol to synthesize Floquet qubits^24,25,26 from statically coupled single-junction transmon qubits using time-periodic microwave drives, showing that the adiabatic mapping procedure can be hastened by exploiting a shortcuts-to-adiabaticity (STA) technique^27,28,29. Then, we implement an XXZ Heisenberg interaction between these Floquet qubits, described by the Hamiltonian

$$\frac{\hat{\mathcal{H}}_{\mathrm{XXZ}}}{\hbar} =\mathop{\sum}\limits_{i,\;j}{J}_{{{{\rm{XY}}}}}\left({\hat{\sigma }}_{{{{\rm{x}}}}}^{i}{\hat{\sigma }}_{{{{\rm{x}}}}}^{\,\,j}+{\hat{\sigma }}_{{{{\rm{y}}}}}^{i}{\hat{\sigma }}_{{{{\rm{y}}}}}^{\,\,j}\right)+{J}_{{{{\rm{ZZ}}}}}{\hat{\sigma }}_{{{{\rm{z}}}}}^{i}{\hat{\sigma }}_{{{{\rm{z}}}}}^{\,\,j}$$

(1)

and demonstrate that the transverse spin-exchange and longitudinal spin–spin interaction terms can be adjusted independently by tailoring the drive parameters.

To validate the robustness and practicality of the protocol, we characterize two-qubit iSWAP, CZ and SWAP gates which correspond to different anisotropy Δ = J_ZZ/J_XY values, achieving estimated fidelities of 99.32(3)%, 99.72(2)% and 98.93(5)%, respectively. In addition, we show that the Floquet-engineered interactions can be broadly applied to other levels in the system. Specifically, we explore the swapping between the qutrit states $\left\vert 11\right\rangle$ and $\left\vert 02\right\rangle$, then employ it to implement a three-qubit controlled-controlled-Z (CCZ) gate which is locally equivalent to the Toffoli gate³⁰, achieving an estimated fidelity of 96.18(5)%. Our work exemplifies the operational principles of Floquet qubits and illustrates their broad potential, thus opening promising pathways for future developments of the Floquet framework in enhancing the capabilities of fixed-frequency solid-state quantum platforms.

Synthesizing Floquet qubits

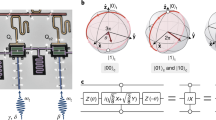
Figure 1a depicts the superconducting device used as a testbed in the experiment. It consists of single-junction transmon qubits¹² that are pair-wise coupled via mutual coplanar stripline resonators^31,32. Details of the quantum device and experimental setup are presented in Supplementary Notes 1 and 2. Although the frequencies of the qubits are fixed after fabrication, Floquet engineering has recently emerged as a powerful tool that allows the sculpting of effective Hamiltonians that are otherwise unavailable³³, thus promising an additional dimension to tune the system. Here, we synthesize Floquet qubits using detuned periodic microwave drives and tailor them to implement the Hamiltonian given by equation (1).

Fig. 1: Floquet qubit.

a, Experimental schematic depicting two single-junction transmon qubits Q₁ (red) and Q₂ (blue) coupled via a shared coplanar stripline resonator resulting in an effective static coupling³¹. Microwave pulses are applied to the transmission lines situated below the capacitor pads to sculpt the Floquet qubits and control single-qubit rotations. The Heisenberg interactions are programmed by tailoring pulses p₁, p₂ and p₃. b, Bloch-sphere representation of the adiabatic transformation from a bare qubit in the lab frame to a Floquet qubit in the rotating frame. c, Population in the excited state ${P}_{\left\vert 1\right\rangle }$ of Q₁, initially in $\left\vert 0\right\rangle$, when subjected to a microwave pulse with amplitude 100 MHz, detuning −40 MHz, ramp time τ_r and duration τ_g. Non-adiabaticity manifests as finite oscillations for short ramp time τ_r. d, Dependence of the maximum state leakage ${P}_{\left\vert 1\right\rangle }^{\max }$ on the pulse’s amplitude and ramp time τ_r. The drive is applied at the same frequency as in c. e, Dependence of ${P}_{\left\vert 1\right\rangle }^{\max }$ on the pulse’s ramp time τ_r and DRAG coefficient. The drive amplitude and frequency are the same as in c.

Source data

The mapping is described by Floquet formalism as follows. The Hamiltonian of a two-level spin-half system subjected to a periodic driving field with amplitude A, frequency ω_d and phase φ is given as

$$\frac{\hat{\mathcal{H}}_{\rm{q}}(t)}{\hslash}=-\frac{{\omega }_{{{{\rm{q}}}}}}{2}{\hat{\sigma }}_{{{{\rm{z}}}}}+A\cos ({\omega }_{{{{\rm{d}}}}}t+\varphi ){\hat{\sigma }}_{{{{\rm{x}}}}},$$

(2)

where ℏω_q is the energy gap of the two-level system, and ${\hat{\sigma }}_{{{{\rm{z}}}}}$ and ${\hat{\sigma }}_{{{{\rm{x}}}}}$ represent the Pauli operators. There exists no static eigenenergies and eigenstates of the system as solutions of the time-dependent Schrödinger equation ${\rm{i}}\hslash {\partial }_{t}\left\vert \psi (t)\right\rangle ={\hat{{{{\mathcal{H}}}}}}_{{{{\rm{q}}}}}(t)\left\vert \psi (t)\right\rangle$. However, due to the periodicity of ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{q}}}}}(t)$, the Schrödinger equation can be modified into the Floquet equation^34,35 $\left({\hat{{{{\mathcal{H}}}}}}_{{{{\rm{q}}}}}(t)-{\rm{i}}\hslash {\partial }_{t}\right){\left\vert {u}_{n}(t)\right\rangle }_{{{{\rm{F}}}}}=\hslash {\varepsilon }_{n}{\left\vert {u}_{n}(t)\right\rangle }_{{{{\rm{F}}}}}$, and static quasienergies ℏε_n can be found for time-periodic Floquet states ${\left\vert {u}_{n}(t)\right\rangle }_{{{{\rm{F}}}}}={\left\vert {u}_{n}(t+2\uppi /{\omega }_{\rm{d}})\right\rangle }_{{{{\rm{F}}}}}$. Here, the Floquet states are denoted with subscript F to distinguish them from the bare states in the lab frame. The Floquet and bare states are interconvertible following the relation

$${\left\vert {u}_{n}(t)\right\rangle }_{{{{\rm{F}}}}}={\rm{e}}^{{\rm{i}}{\varepsilon }_{n}t}\left\vert {\psi }_{n}(t)\right\rangle .$$

(3)

Interestingly, ${\rm{e}}^{{\rm{i}}k{\omega }_{{{{\rm{d}}}}}t}{\left\vert {u}_{n}(t)\right\rangle }_{{{{\rm{F}}}}}$ with integer k also satisfies the Floquet equation and has quasienergy ℏ(ε_n + kω_d), resulting in an infinite transition spectrum³⁵ ${\varepsilon }_{1}-{\varepsilon }_{0}=k{\omega }_{{{{\rm{d}}}}}\pm \sqrt{{A}^{2}+{({\omega }_{{{{\rm{d}}}}}-{\omega }_{{{{\rm{q}}}}})}^{2}}$, where the plus(minus) sign corresponds to red(blue)-detuned drive. In addition, the drive phase φ acts as a time translation operator on the Hamiltonian in equation (2), ${\left\vert {u}_{n}(t)\right\rangle }_{{{{\rm{F}}}}}\to {\left\vert {u}_{n}(t+\varphi /{\omega }_{{{{\rm{d}}}}})\right\rangle }_{{{{\rm{F}}}}}$. These show how the Floquet states and their quasienergies depend on the drive parameters A, φ and ω_d, which we can use to tailor the driven systems (see Supplementary Notes 3 and 4 for detailed Floquet formalism).

To prepare a Floquet qubit with the desired properties, we have to continuously map the undriven qubit to the Floquet basis, as shown in Fig. 1b. If the transformation is performed abruptly, finite tunnelling exists between the Floquet basis states, and the process becomes non-adiabatic. According to the Adiabatic Theorem³⁵, the tunnelling rate is proportional to dA/dt, that is, the target Floquet qubit corresponding to a larger drive amplitude must be transformed using a longer ramp time.

We experimentally explore this by irradiating qubit Q₁ initialized in $\left\vert 0\right\rangle$ using a cosine-ramp pulse with different pulse durations τ_g and ramp times τ_r. The drive amplitude is set to be 100 MHz in terms of on-resonant Rabi frequency, and the drive frequency is red-detuned by 40 MHz from Q₁’s transition frequency. As the qubit should remain in its instantaneous eigenstate under the adiabatic process, non-adiabatic effects manifest as finite excited state populations ${P}_{\left\vert 1\right\rangle }$ after the pulse, which oscillates with respect to the pulse duration due to the dynamical phase accumulation of the Floquet qubit (Fig. 1c). Evidently, shorter ramp times correspond to more severe non-adiabatic effects. In addition, the result in Fig. 1d confirms that a larger drive amplitude requires a longer ramp time to satisfy the adiabatic condition.

Interestingly, we find that using an STA technique known as derivative removal by adiabatic gate (DRAG)^28,29 helps reduce non-adiabatic effects substantially. As shown in Fig. 1e, the excited state leakage ${P}_{\vert 1 \rangle }^{\mathrm{max}}$ corresponding to a short-ramp pulse can be suppressed by adding a quadrature component to the pulse with amplitude A_Q = λ_DRAG × dA(t)/dt. In this case, τ_r can be reduced from 60 ns to 30 ns by employing a DRAG coefficient λ_DRAG = −0.7. This suggests that advanced optimal control techniques can be explored to further accelerate the mapping procedure. Importantly, our results below show that once adiabaticity is satisfied, the protocol is robust against adverse effects from the strong drives, including microwave crosstalk, calibration fluctuations and leakage to higher levels.

Tailoring Heisenberg interactions

Having established the general conditions for adiabatic mapping between undriven qubit states and Floquet states, we next generate the microwave pulses that establish the XXZ Heisenberg interaction in equation (1) between the Floquet qubits. The interaction Hamiltonian describing the coupling between Q₁ and Q₂ in Fig. 1a is ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{int}}}}}/\hslash =J{\hat{\sigma }}_{{{{\rm{x}}}}}^{(1)}{\hat{\sigma }}_{{{{\rm{x}}}}}^{(2)}$, where J is the static coupling strength, the superscripts are qubit indices, and the Pauli operators are defined in the undriven basis. Using the relation given by equation (3), this interaction can be described by a Floquet Hamiltonian:

$$\frac{\hat{\mathcal{H}}_{\rm{int,F}}}{\hbar} =J\mathop{\sum}\limits_{a,b,c,d}{c}_{ab}^{(1)}(t){c}_{cd}^{(2)}(t){\rm{e}}^{{\rm{i}}({\varepsilon }_{ab}^{(1)}+{\varepsilon }_{cd}^{(2)})t}{\hat{f}}_{ab}^{\,(1)}(t){\hat{f}}_{cd}^{\,(2)}(t),$$

(4)

where ${\varepsilon }_{ab}^{(k)}\equiv {\varepsilon }_{b}^{(k)}-{\varepsilon }_{a}^{(k)}$, ${c}_{ab}^{(k)}(t)=\left\langle {\psi }_{a}^{(k)}(t)| {\hat{\sigma }}_{{{{\rm{x}}}}}^{(k)}| {\psi }_{b}^{(k)}(t)\right\rangle$, ${\hat{f}}_{ab}^{\,(k)}(t)={\left\vert {u}_{a}^{(k)}(t)\right\rangle }_{{{{\rm{F}}}}} {\left\langle {u}_{b}^{(k)}(t)\right\vert }_{{{{\rm{F}}}}}$ for qubit Q_k and a, b, c, d ∈ {0, 1} for two qubits. The fast oscillation dynamics can be neglected by invoking the rotating wave approximation, leaving only the terms that follow energy conservation law, ${\varepsilon }_{ab}^{(1)}+{\varepsilon }_{cd}^{(2)}=0$ for abcd ∈ {0110, 1001, 0000, 0011, 1100, 1111}. Inspecting the reduced Hamiltonian then gives us insight on the types of interactions present between the qubits.

On one hand, the terms satisfying ${\varepsilon }_{01}^{(1)}={\varepsilon }_{01}^{(2)}$ correspond to the transverse XY spin-exchange interaction in equation (1) with ${J}_{{{{\rm{XY}}}}}=$$J{\langle {c}_{01}^{(1)}{c}_{10}^{(2)}\rangle }_{t}=J{\langle {c}_{10}^{(1)}{c}_{01}^{(2)}\rangle }_{t}$, where 〈…〉_t denotes the time-average value. This process follows the conventional wisdom that an XY exchange-type interaction between two coupled spins occurs when they are brought into resonance with each other. On the other hand, the rest of the reduced Hamiltonian produces the longitudinal ZZ spin–spin coupling in equation (1), ${J}_{{{{\rm{ZZ}}}}}=J{\langle {c}_{11}^{(1)}{c}_{11}^{(2)}+}$${{c}_{00}^{(1)}{c}_{00}^{(2)}-{c}_{00}^{(1)}{c}_{11}^{(2)}-{c}_{11}^{(1)}{c}_{00}^{(2)}\rangle }_{t}$. Consequently, we can program the transverse and longitudinal interactions independently by tailoring the quasienergies with periodic microwave drives.

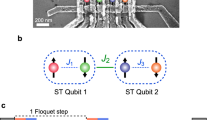
We validate this principle as follows. First, we achieve a pure transverse XY spin-exchange interaction corresponding to an XX Heisenberg model where the anisotropy is zero, Δ = J_ZZ/J_XY = 0. Given that Q₁’s frequency is lower than that of Q₂, their quasienergy differences ${\varepsilon }_{01}^{(k)}$ can be brought into resonance if Q₁(Q₂) is driven with red(blue)-detuned microwaves (Supplementary Note 5). After preparing the qubits in $\left\vert 10\right\rangle$, we apply two such pulses (p₁ and p₂ in Fig. 2a) with the same duration τ_g and amplitude A_XY at a detuning frequency of 40 MHz.

Fig. 2: Floquet-engineered XXZ Heisenberg interaction.

a, Energy diagram of qubits Q₁ and Q₂ and pulse schematics for spin-exchange XY and spin–spin ZZ interactions. b, Chevron pattern showing the dependence of ${P}_{\left\vert 01\right\rangle }$ on the amplitude A_XY and duration τ_g of pulses p₁ and p₂ for qubits initialized in $\left\vert 10\right\rangle$. The pulses are applied at frequencies 40 MHz red(blue)-detuned from Q₁₍₂₎’s $\left\vert 0\right\rangle \leftrightarrow \left\vert 1\right\rangle$ transition with DRAG coefficients λ_DRAG = −(+)0.6 and ramp time τ_r = 50 ns. c, Coherent oscillation between $\left\vert 10\right\rangle$ and $\left\vert 01\right\rangle$ for the optimal pulse amplitude A_XY/2π = 65.2 MHz highlighted by the red dashed line in b. d, Extracted longitudinal coupling angle Φ_ZZ between the qubits after p₁ and p₃ are applied at 40 MHz red-detuned from Q₁’s transition frequency. They are 200 ns long, with ramp time τ_r = 50 ns and DRAG coefficient λ_DRAG = −0.6. The amplitude of p₁ is fixed at A_XY/2π = 65.2 MHz, while the amplitude A_ZZ and phase φ of p₃ are varied to tune the ZZ coupling rate. e, Extracted longitudinal coupling angle Φ_ZZ between the qubits after being subjected to all three pulses. The amplitude A_XY of p₁ and p₂ is tuned to induce a full $\left\vert 10\right\rangle \leftrightarrow \left\vert 01\right\rangle$ swap, while the amplitude A_ZZ and phase φ of p₃ are varied to tune the ZZ rate during the swap.

Source data

We observe a coherent population transfer to state $\left\vert 01\right\rangle$ that forms a chevron pattern as a function of τ_g and A_XY, signifying a transverse coupling between the qubits (Fig. 2b). Notably, although the interaction occurs between the Floquet qubits in the dressed frame, the adiabatic connection ascertains the exchange between the bare qubit states after the reverse mapping, which bears resemblance to the latching mechanism in classical electronics. Indeed, at the optimal drive amplitude A_XY/2π = 65.2 MHz (Fig. 2c), $\left\vert 10\right\rangle$ and $\left\vert 01\right\rangle$ exhibit coherent oscillations at a rate of 3.2 MHz, which is limited by the static coupling constant J (Supplementary Note 5). The lack of fast oscillatory behaviour is a clear indication of the high mapping fidelity.

Next, we induce a pure longitudinal ZZ spin–spin coupling corresponding to an Ising interaction between the Floquet qubits. This can be accomplished by irradiating microwave drives p₁ on Q₁ and p₃ on Q₂ (Fig. 2a) at a frequency 40 MHz red-detuned from Q₁. The amplitude of p₁ is fixed at A_XY/2π = 65.2 MHz, while p₃ has parameterized amplitude A_ZZ and phase φ. For weak driving, A_XY,ZZ ≪ ω_q,d, the ZZ rate is given as ${J}_{{{{\rm{ZZ}}}}}\approx 2J{A}_{{{{\rm{XY}}}}}{A}_{{{{\rm{ZZ}}}}}\cos (\varphi )/\sqrt{({A}_{{{{\rm{XY}}}}}^{2}+{\delta }_{1}^{2})({A}_{{{{\rm{ZZ}}}}}^{2}+{\delta }_{2}^{2})}$, where δ_k is the detuning from Q_k’s frequency (Supplementary Note 5). Importantly, while the transverse coupling rate J_XY shown above is limited by the static coupling strength J, the longitudinal coupling rate J_ZZ can be tuned by two knobs, namely the drives’ amplitudes and phase difference. We characterize the interaction by first initializing the two qubits in the superposition state $(\left\vert 0\right\rangle +\left\vert 1\right\rangle )\otimes (\left\vert 0\right\rangle +\left\vert 1\right\rangle )/2$, applying the pulses as specified and then extracting the entangling phase ${\Phi}_{{{{\rm{ZZ}}}}}({\tau }_{{{{\rm{g}}}}})=\int\nolimits_{0}^{{\tau }_{{{{\rm{g}}}}}}{J}_{{{{\rm{ZZ}}}}}(t)\,{\rm{d}}t$ using tomographic reconstruction assisted by numerical optimization. As shown in Fig. 2d, this phase depends on p₃’s amplitude A_ZZ and phase φ, consistent with our description.

Leveraging the independent controls of the transverse and longitudinal interactions, we now tailor the interplay between them to adjust the anisotropy of the XXZ Heisenberg interaction model. To this end, we apply p₁ and p₂ pulses with their amplitude A_XY and duration τ_g tuned to induce a full $\left\vert 10\right\rangle \leftrightarrow \left\vert 01\right\rangle$ swap (Fig. 2c). Pulse p₃ is then jointly applied, albeit with parameterized amplitude A_ZZ and phase φ. Incorporating the swap condition into the tomography analysis, we extract the longitudinal entangling phase Φ_ZZ which depends on p₃’s parameters as shown in Fig. 2e. This demonstrates the versatility available in programming the anisotropy of the model given by equation (1). This demonstration only includes A_ZZ ≲ 20 MHz to alleviate the effect from p₃ on the swap condition, which stems from the large microwave crosstalk in the experimental device (Supplementary Note 2).

Benchmarking Heisenberg interactions

The programmable Heisenberg interaction endows quantum processors with an extensive quantum gate set and the capability to simulate many-body spin-half systems. Here we benchmark our Floquet-engineered Heisenberg interactions by characterizing a suite of representative two-qubit gates: the iSWAP, CZ and SWAP gates resulting from the XX Heisenberg model ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{XX}}}}}/{\hbar}={J}_{{{{\rm{XY}}}}}({\hat{\sigma }}_{{{{\rm{x}}}}}{\hat{\sigma }}_{{{{\rm{x}}}}}+{\hat{\sigma }}_{{{{\rm{y}}}}}{\hat{\sigma }}_{{{{\rm{y}}}}})$, Ising model ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{ZZ}}}}}/{\hbar}={J}_{{{{\rm{ZZ}}}}}{\hat{\sigma }}_{{{{\rm{z}}}}}{\hat{\sigma }}_{{{{\rm{z}}}}}$ and XXX Heisenberg model ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{XXX}}}}}/{\hbar}=J\left(\right.{\hat{\sigma}}_{{{{\rm{x}}}}}{\hat{\sigma }}_{{{{\rm{x}}}}}+{\hat{\sigma }}_{{{{\rm{y}}}}}{\hat{\sigma }}_{{{{\rm{y}}}}}+{\hat{\sigma }}_{{{{\rm{z}}}}}{\hat{\sigma }}_{{{{\rm{z}}}}}\left.\right)$, respectively. Accordingly, an iSWAP unitary arises naturally from a pure transverse XY interaction with the pulse duration τ_g corresponding to a full swap in Fig. 2c, implemented by applying p₁ and p₂. In practice, there is a dynamical ZZ coupling originating from microwave crosstalk, which can be tracked and compensated by simultaneously applying p₃ with appropriate amplitude and phase. Likewise, a CZ gate is realized when p₁ and p₃ are calibrated to bring up an entangling phase Φ_ZZ/2π = 0.25. Finally, we tailor all three pulses to sculpt an isotropic XXX Heisenberg interaction that leads to a SWAP gate at the correct gate time τ_g, at which both iSWAP and CZ conditions are satisfied. Our calibration steps are detailed in Supplementary Notes 6–8.

To quantify the gates’ performances without state preparation and measurement errors, we employ cycle benchmarking (CB)³⁶, which tailors all errors into stochastic Pauli channels via Pauli twirling and results in tight bounds on the estimated fidelity (Supplementary Note 9). Besides the dressed cycles that include the implemented gates, we also measure the reference cycle and extract its errors to estimate the relevant gate fidelities. Figure 3a shows the Pauli fidelity distribution histograms of both the reference and dressed cycles corresponding to the intended two-qubit gates. Comparing the dressed cycle data to the reference cycle result allows us to estimate the average gate fidelities of the implemented iSWAP, CZ and SWAP gates to be 99.32(3)%, 99.72(2)% and 98.93(5)%, respectively. We note that these gates are expandable to a continuous fSim gate set^8,37, which can be integrated into arbitrary quantum circuits compatible with fixed-frequency qubits by using more advanced circuit compilation tools³⁸ or efficient physical Z-gates.

Fig. 3: Characterization of two-qubit gates.

a, CB results showing the Pauli fidelity histogram for the Reference, iSWAP, CZ and SWAP cycles, with the solid vertical lines indicating the mean values. The corresponding two-qubit gate fidelities are estimated to be 99.32(3)%, 99.72(2)% and 98.93(5)%, respectively. b, Effective coherence time statistics of the Floquet qubit created by adiabatically driving Q₁ at a red-detuning of 40 MHz. Each curve shows the mean values of 20 different sweeps, and the shaded region represents the standard deviations. Inset: Excited state population at the end of the 355-μs-long $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$ measurement sequence.

Source data

Our analysis attributes the limitations of these results primarily to decoherence mechanisms (Supplementary Notes 10–12). Intriguingly, the Floquet qubits appear to exhibit coherence times deviating from those of the bare qubits, as shown in Fig. 3b. The measurements are performed using nominal energy relaxation and echo dephasing procedures on the bare Q₁, but with the addition of a microwave pulse applied 40 MHz red-detuned from its $\left\vert 0\right\rangle \leftrightarrow \left\vert 1\right\rangle$ transition during idle periods. The results are postselected to yield the populations of the desired states, and the experiment is repeated over twenty iterations to eliminate any potential outlier. While the dynamics remain the same at small drive amplitudes, T₁ tends to increase while ${T}_{2}^{E}$ tends to decrease at strong driving before non-adiabaticity sets in. Interestingly, we also discover a heating mechanism that enlarges the excited state population in the bare qubit at the end of the 355-μs-long $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$ measurement sequence, with ${P}_{\left\vert 1\right\rangle }^{{{{\rm{final}}}}}$ increasing with the driving amplitude (Fig. 3b, inset). We include additional details in Supplementary Note 13 and hope that future investigations can find efficient approaches to mitigate these effects, reminiscent of the recent progress in driven ultracold-atom systems³⁹.

Floquet qutrit and three-qubit gate

So far, the fundamental and universal importance of spin physics motivates our discussion to portray the implemented Floquet qubits as ideal spin-halfs. Nevertheless, many solid-state systems, including the transmon, naturally include multiple relevant energy levels. Making use of them expands the Hilbert space, allowing more information to be encoded, which leads to hardware-efficient execution of quantum algorithms^40,41 and hastens the development of fault-tolerant computation^42,43. We now show that the presented protocol can be tailored for multi-level systems, thereby paving pathways for quantum information processing using Floquet qudits.

Specifically, we leverage the techniques described so far to induce a transverse qutrit–qutrit interaction between the states $\left\vert 11\right\rangle$ and $\left\vert 02\right\rangle$. Although the cross-Kerr coupling has been explored⁴⁴, such an energy-exchange interaction is still absent in fixed-frequency qutrits. While this is a useful ternary gate itself, we presently show that integrating it into a sequence involving multiple qubits allows the implementation of a three-body CCZ gate³⁰, which plays an important role in quantum applications such as factorization^45,46 and quantum error correction^47,48. Notably, this scheme can be extended to implement an n-qubit gate⁴⁹. To this end, we add to the experiment Q₃, which is coupled to the right side of Q₂ in Fig. 1a and use Q₂ and Q₃ as control qubits (subscripted c), while Q₁ is designated as the target (subscripted t).

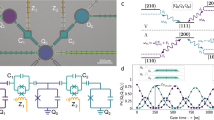
Figure 4a depicts the energy diagram of Q₂ and Q₃. Our approach to accomplish the interaction primarily involves applying a microwave pulse to Q₃ at a frequency red-detuned from its $\left\vert 1\right\rangle \leftrightarrow \left\vert 2\right\rangle$ transition to create a Floquet qutrit such that the control Floquet states ${\left\vert 11\right\rangle }_{{{{\rm{c}}}}}$ and ${\left\vert 02\right\rangle }_{{{{\rm{c}}}}}$ become degenerate. After initializing the control qubits in ${\left\vert 11\right\rangle }_{{{{\rm{c}}}}}$, we apply such a pulse with ramp time τ_r = 170 ns, DRAG coefficient λ_DRAG = −0.6 and varying amplitude A_XY and duration τ_g, which are tailored to ensure adiabaticity at a red-detuning of 22 MHz. The transverse interaction between ${\left\vert 11\right\rangle }_{{{{\rm{c}}}}}$ and ${\left\vert 02\right\rangle }_{{{{\rm{c}}}}}$ then manifests into an asymmetric chevron pattern with respect to A_XY and τ_g in Fig. 4b. Interestingly, we observe that the optimal swap condition occurs at a stronger amplitude relative to the symmetry point.

Fig. 4: Floquet qutrit and three-qubit CCZ gate.

a, Energy diagram of two coupled transmon circuits Q₂ and Q₃, with the subscript c denoting they are control qubits. A microwave drive with amplitude A_XY is applied at a frequency red-detuned from Q₃’s $\left\vert 1\right\rangle \leftrightarrow \left\vert 2\right\rangle$ transition to create a Floquet qutrit. b, Chevron pattern showing a coherent flip-flop between Q₂ and Q₃’s states ${\left\vert 11\right\rangle }_{{{{\rm{c}}}}}$ and ${\left\vert 02\right\rangle }_{{{{\rm{c}}}}}$, which depends on the amplitude A_XY and duration τ_g of the pulse. The red-detuning is 22 MHz, the ramp time is τ_r = 170 ns and the DRAG coefficient is λ_DRAG = −0.6. c, Gate sequence used to implement a three-qubit CCZ unitary, with Q₁ as the target qubit and Q₂, Q₃ as the control qubit pair. d, A conditionality measurement, using a Ramsey-like sequence {${{{{\rm{R}}}}}_{{{{\rm{Y}}}}}^{({{{\rm{t}}}})}(\frac{\uppi }{2})$, CCZ, ${{{{\rm{R}}}}}_{{{{\rm{Z}}}}}^{({{{\rm{t}}}})}(\phi )$, ${{{{\rm{R}}}}}_{{{{\rm{Y}}}}}^{({{{\rm{t}}}})}(\frac{\uppi }{2})$}, reveals the dependence of Q₁’s phase on the states of Q₂ and Q₃ under the CCZ gate implemented using the sequence in c, which is characteristic of a three-body entanglement. e, Truth table of the implemented Toffoli gate with a corresponding fidelity of 96.20(6)%. f, CB result showing the Pauli fidelity distributions of the three-qubit reference cycle and CCZ dressed cycle, with the solid vertical lines indicating the average values. The average gate fidelity is estimated to be 96.18(5)%.

Source data

A CCZ unitary can be implemented using the sequence given in Fig. 4c (Supplementary Note 14). The final CPhase gate on the control qubits is tuned to bring the effective operation on them to be ${\hat{\sigma }}_{{{{\rm{I}}}}}\otimes {\hat{\sigma }}_{{{{\rm{I}}}}}$ at the end of the sequence. After calibrating the individual gates, we verify the entanglement between the three qubits by extracting the Z-phase of the target qubit (Q₁) for different control states and observe a phase shift of approximately π for ${\left\vert 10\right\rangle }_{{{{\rm{c}}}}}$ (Fig. 4d), which evinces the CCZ effect. The sequence can be further sandwiched between single-qubit rotations on Q₁ to construct a Toffoli gate. The process can be straightforwardly validated by measuring the truth table^30,49, from which we extracted a fidelity of ${{{{\mathcal{F}}}}}_{{{{\rm{tt}}}}}={{{\rm{Tr}}}}({{{{\mathcal{U}}}}}_{\exp }{{{{\mathcal{U}}}}}_{{{{\rm{ideal}}}}}^{{\dagger} })/8=96.20(6) \%$ (Fig. 4e). Finally, we employ CB to benchmark the CCZ gate (Fig. 4f), achieving a fidelity of 96.18(5)%, with the main error resulting from decoherence (Supplementary Note 11).

Outlook

Our work embodies a transformative application of Floquet engineering in superconducting circuits where periodic drives are used to map static qubits to Floquet qubits with modifiable quasienergies, granting access to an unconventional tuning channel. We demonstrate the practicality and versatility of this approach by synthesizing Floquet qubits and qutrits, then realizing an XXZ Heisenberg interaction between them with fully tunable anisotropy. The robustness of the scheme against environmental noise, non-adiabaticity, leakage and calibration errors is reflected in the high gate fidelities, while overcoming the current limitations is straightforward. On one hand, the coherence times of the fixed-frequency transmon qubits in the experiment are relatively low, so we expect better performance in state-of-the-art devices. On the other hand, the coupling rate is primarily limited by the static coupling constant J, which can be increased substantially in future devices. In addition, the pulse shape used in this work is quite simple, so we believe that, in the future, advanced STA techniques can be employed to design shorter gates, further reducing errors from dephasing. Our preliminary assessment (Supplementary Note 15) shows the promising extensibility of the protocol to large-scale devices. We note that the experimental device is simply a testbed, and the full potential of this framework lies upon its adaptation to other synthetic fixed-frequency quantum architectures with better projected performance, such as fluxonium quantum processor with all-microwave control⁵⁰.

Having illustrated the useful properties of the Floquet qubits, we envision the following avenues to further develop and propel the concept to scale up fixed-frequency platforms. The protocol presented here involves transforming back to the static qubit, so normal operations such as readout and single-qubit gates can be employed without recalibration. In future applications, a Floquet qubit can, in principle, be permanently defined by applying a continuous periodic drive, streamlining the process and unlocking opportunities for control and readout of the Floquet qubit²⁵ (Supplementary Note 16). This approach also allows in situ tuning of the qubit frequencies, thus providing a practical solution for problems arising from two-level-system defects and spectral crowding. Alternatively, the ramp time can be reduced substantially if we operate in the diabatic regime, where the mapping is close to ideal despite finite transition between the Floquet states. We expect the potential development of optimal control within the Floquet framework to provide a reliable approach in this regime. Last but not least, the heating effect which correlates with the reduction in T₂ is reminiscent of a similar effect in cold-atom systems which has been successfully suppressed³⁹. This calls for deeper understanding of the quantum thermodynamics in driven solid-state systems and the development of new mitigation strategies.