« Prev Next »

What is Life History Evolution?
A female North Pacific Giant Octopus (Enteroctopus dofleini) lives three to four years; it lays thousands of eggs in a single bout and then dies. By contrast, a mature Coast Redwood Tree (Sequoia sempervirens) lives for many hundreds of years and produces millions of seeds each year (Figure 1). As these two examples illustrate, organisms differ dramatically in how they develop, the time they take to grow, when they become mature, how many offspring of a particular size they produce, and how long they live. Together, the age-, size-, or stage-specific patterns of development, growth, maturation, reproduction, survival, and lifespan define an organism's life cycle, its life history.

The principal aim of life history theory, a branch of evolutionary ecology, is to explain the remarkable diversity in life histories among species. But there is another, more compelling reason for why life history evolution is important: adaptation by natural selection is based on variation in Darwinian fitness among individuals, and since life history traits determine survival and reproduction they are the major components of fitness. The study of life history evolution is thus about understanding adaptation, the most fundamental issue in evolutionary biology.
Here we introduce the basics of life history theory and review what biologists have learned about life history evolution. For more in-depth coverage we refer to Stearns (1992), Roff (1992, 2002), Charlesworth (1994), and Flatt and Heyland (2011). Also see the Nature Education Knowledge articles by Shefferson (2010), Young (2010), and Fabian and Flatt (2011).
The Basics of Life History Theory
Life history theory seeks to explain how natural selection and other evolutionary forces shape organisms to optimize their survival and reproduction in the face of ecological challenges posed by the environment (Stearns 1992, Roff 1992, Stearns 2000), or as David Reznick has recently put it: "Life history theory predicts how natural selection should shape the way organisms parcel their resources into making babies" (Reznick 2010, p. 124). The theory does so by analyzing the evolution of fitness components, so-called life history traits, and how they interact: size at birth; growth pattern; age and size at maturity; number, size, and sex of offspring; age-, stage- or size-specific reproductive effort; age-, stage- or size-specific rates of survival; and lifespan.
The classical theory treats life history evolution as an optimization problem: given particular ecological factors (e.g., predators, nutrition) that affect an organism's probability of survival and reproduction, and given limiting constraints and trade-offs intrinsic to the organism, what are the optimal values and combinations of life history traits that maximize reproductive success? To find the solution to this problem we need to understand its "boundary conditions" (Stearns 2000): (1) how extrinsic, environmental factors affect survival and reproduction; and (2) how intrinsic connections among life history traits (trade-offs) and other constraints limit whether and how life history traits can evolve. Once these conditions have been understood and defined, life history models can be used to answer questions such as: How small or large should an organism grow? At what age and size should it mature? How many times should it reproduce? How many offspring should it produce and what size should they be? For how long should it reproduce and how long should it live?
Life history optimization problems are typically modeled by using the Euler-Lotka equation, which describes population growth rate (i.e., fitness) of a clonal genotype (or allele substitution) in continuous generation time as a function of its age at maturity, age at last reproduction, age-specific survival probability, and the expected age-specific number of offspring (Stearns 1992, Roff, 1992, Brommer 2000):
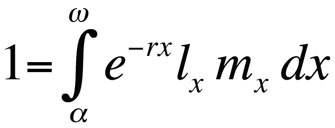
where α is the age at first reproduction, ω the age at last reproduction, lx the probability of surviving from birth to age class x, mx the expected number of offspring in age class x, and r the population growth rate or Malthusian parameter. The equation sums the probabilities of survival and reproduction over the entire lifetime of the individuals in the population and can then be solved for r. Note that in the context of life history theory r measures the growth rate or fitness of a clone or, in sexually reproducing organisms, the rate of spread of an allele that affects life history. Thus, the implicit assumption is that the modeled population consists of phenotypically and genetically identical individuals. If the population described by the Euler-Lotka equation is stationary (non-growing), r is zero and the equation becomes
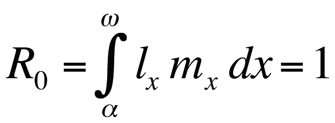
or, if generation time is discrete,
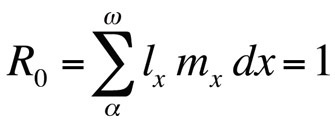
where R0 is the expected number of daughters per female per lifetime (net reproductive rate). This equation is simpler than the continuous-time version and can be used whenever r is zero or close to zero; for stable populations that do not change in size, R0 is the appropriate fitness measure (Stearns 1992, Roff 1992, Brommer 2000). Using this framework, one can ask what particular combination of life history traits maximizes fitness, or how much fitness is affected when one of the traits is changed. This approach has been used with great success to predict the evolution of life history traits.
Genetic Variation for Life History Traits
The evolution of life history traits by natural selection depends upon genetic variation on which selection can act to produce adaptations in response to the environment. The models mentioned above implicitly assume that life history evolution is not limited by a lack of genetic variation. Interestingly, however, the heritability (h2 = VA/VP = additive genetic variance divided by phenotypic variance), i.e. the proportion of phenotypic differences among individuals in a population that is explained by additive genetic differences among them, is usually small for life history traits. This low heritability could be caused by low amounts of additive genetic variance; yet, there exists ample genetic variation for life history traits in natural and laboratory populations. Consistent with the notion that fitness components harbor lots of genetic variation, many artificial selection experiments in the laboratory have successfully managed to cause evolutionary changes in life history traits in the predicted direction (Stearns 1992, Roff 1992, Houle 2001). One reason for the large VA of life history traits may be that they are highly complex, quantitative, polygenic traits influenced by many loci (Houle 1992).
But how can we reconcile the fact that VA is large while at the same time h2 is small? A likely reason for the low heritability of life history traits is that, although VA (the numerator) is large, VP (the denominator) is much larger than VA. Note that the phenotypic variance VP consists of VA, the additive genetic variance, plus a remainder, VR, that itself consists of all non-additive genetic sources of variation (i.e., due to dominance, epistasis, etc.) and phenotypic variation engendered by the environment (i.e., phenotypic plasticity, genotype by environment interactions; see below). Thus, life history traits probably have low heritability because they are influenced by many loci (which inflates both VA and VP) while at the same time harboring substantial amounts of residual variation VR, for example variation due to changes in the environment (which inflates VP but not VA) (Houle 1992, Houle 2001).
Moreover, although life history traits are under strong selection, which should exhaust genetic variance, several factors can maintain genetic variation for these traits, including mutation-selection balance, environmental heterogeneity and genotype by environment interactions, and negative genetic correlations (Stearns 1992, Roff 1992, Houle 2001). However, despite typically large amounts of life history variation, life history evolution is also subject to constraints.
Life History Trade-Offs and Other Constraints
Fitness would obviously be maximal if survival and reproduction would be maximal at all ages, stages, or sizes of an organism. In principle then, the basic problem of life history evolution is trivial: all life history traits should always evolve so as to maximize survival and reproduction and thus fitness (Houle 2001). This would very rapidly lead to the evolution of "Darwinian demons" (Law 1979) that would take over the world, i.e. organisms that start to reproduce as soon as they are born, produce an infinite number of offspring, and live forever. Such organisms, however, do not exist in the real world: Resources are finite, and life history traits are subject to intrinsic trade-offs and other types of constraints, so natural selection cannot maximize life history traits — and thus fitness — beyond certain limits. We call such limits evolutionary constraints (Stearns 1992, Houle 2001); as mentioned above, they represent the intrinsic "boundary condition" we must understand to predict life history evolution.
One of the most important types of constraint are life history trade-offs (Stearns 1992, Roff 1992, Flatt and Heyland 2011). A trade-off exists when an increase in one life history trait (improving fitness) is coupled to a decrease in another life history trait (reducing fitness), so that the fitness benefit through increasing trait 1 is balanced against a fitness cost through decreasing trait 2 (Figure 2A). (Note that trade-offs can also involve more than two traits.) At the genetic level, such trade-offs are thought to be caused by alleles with antagonistic pleiotropic effects or by linkage disequilibrium between loci.
Trade-offs are typically described by negative phenotypic or genetic correlations between fitness components among individuals in a population (Figure 2A). If the relationship is genetic, a negative genetic correlation is predicted to limit (i.e. to slow down or prevent) the evolution of the traits involved. Thus, a genetic trade-off exists in a population when an evolutionary change in a trait that increases fitness is linked to an evolutionary change in another trait that decreases fitness. The existence of genetic correlations can be established through quantitative genetic breeding designs or through correlated phenotypic responses to selection. For example, direct artificial selection for extended lifespan in genetically variable laboratory populations of fruit flies (Drosophila melanogaster) causes the evolution of increased adult lifespan (sometimes in 10 or fewer generations), but this evolutionary increase in longevity is coupled to decreased early reproduction (e.g., Zwaan et al. 1995). This suggests that lifespan and early reproduction are genetically negatively coupled, e.g. through antagonistic pleiotropic alleles (e.g., Flatt 2011, Fabian and Flatt 2011).
At the physiological level, trade-offs are caused by competitive allocation of limited resources to one life history trait versus the other within a single individual, for example when individuals with higher reproductive effort have a shorter lifespan or vice versa (Figure 2B). A helpful way to think resource allocation trade-offs is to imagine a life history as being a finite pie, with the different slices representing how an organism divides its resources among growth, storage, maintenance, survival, and reproduction (Reznick 2010; Figure 2C). The essential problem is this: given the ecological circumstances, and the fact that making one slice larger means making another one smaller, what is the best way to split the pie? Note that since resource allocation trade-offs might have a genetic basis, and since different genotypes may differ in aspects of resource allocation, the genetic and physiological views of trade-offs are not necessarily incompatible. However, physiological trade-offs at the individual level do not always translate into genetic (evolutionary) trade-offs at the population level. For instance, when the physiological (within-individual) trade-off is genetically fixed ("hard-wired") among all individuals within the population, all individuals will exhibit the same negative physiological relationship between two life history traits but the genetic correlation among individuals would be zero (Stearns 1989, Stearns 1992).
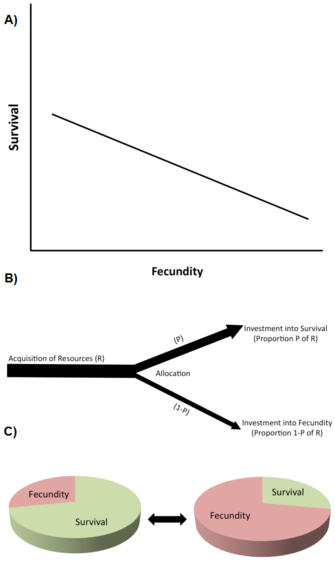
The book by Stearns (1992) lists 45 possible trade-offs among 10 major life history traits, and many more can be envisaged to exist. Those trade-offs that have received most attention include (1) current reproduction versus survival; (2) current versus future reproduction; (3) current reproduction versus parental growth; (4) current reproduction versus parental condition; and (5) number versus size of offspring.
Some of the best evidence for genetically based life history trade-offs comes from artificial selection and experimental evolution experiments carried out in Drosophila (see reviews in Stearns and Partridge 2001, Flatt and Schmidt 2009, Flatt 2011). In summary, many experiments have found: a negative correlation between early fecundity and adult lifespan; a positive correlation between developmental time and body size; a positive correlation between either developmental time or body size with early fecundity; and a negative correlation between early and late fecundity.
Other constraints on life histories that prevent natural selection from attaining a particular fitness optimum can involve biophysical, biochemical and structural factors, developmental properties of the organism, phylogenetic and historical contingencies, or simply a lack of genetic variation (Stearns 1992, Houle 2001).
Phenotypic Plasticity in Life History Traits
Genetic variation and constraints are not the only factors affecting the expression and evolution of life history traits. Another important issue is that life history variation is often strongly influenced by the environment (e.g., temperature, nutrition, predators,), a phenomenon called phenotypic plasticity, i.e. the ability of a single genotype (or clone) to produce different phenotypes across different environments (Stearns 1992, Roff 1997, Pigliucci 2001, DeWitt and Scheiner 2004). The plasticity of a specific genotype can be conceptually described by a mathematical function called a reaction norm, i.e. a line or curve that relates the phenotypes produced by this genotype to changes in the environment it experiences (Figure 3A).
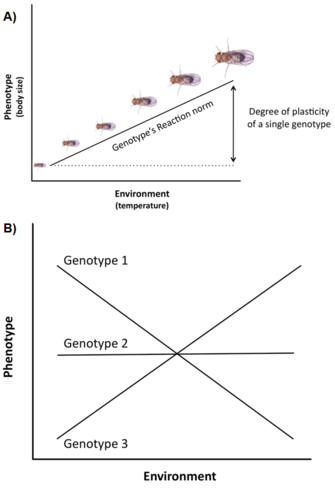
The importance of such plasticity in life history evolution is at least three-fold (Stearns and Koella 1986, Stearns et al. 1991, Stearns 1992, Nylin and Gotthard 1998, DeWitt and Scheiner 2004, Flatt 2005): (1) since plasticity modulates the phenotypic expression of genetic variation for single life history traits and of genetic correlations for pairs of traits, it affects the genetic response to selection across environments; (2) if there exists adaptive variation among genotypes for the plastic response, selection can produce an optimal reaction norm that maximizes fitness across environments; and (3) plasticity of a specific trait may homeostatically buffer the organism against environmentally-induced changes in other traits so that organismal performance and thus fitness is optimized.
Many life history traits (e.g., age at maturity, fecundity) exhibit a high degree of plasticity, and there is often significant genetic variation for plasticity in natural populations, i.e. genotypes have different reaction norms, a phenomenon called genotype by environment interaction (GxE) (Figure 3B). Moreover, not only single traits but also correlations between traits can be plastic, and different environments can change the slope and/or sign of the trait correlation (Stearns et al. 1991, Stearns 1992). In spadefoot toads (Scaphiophus couchii), for example, individuals that develop in ponds of short duration have a shorter larval period and a smaller body size at metamorphosis (with the traits being negatively correlated) than individuals that develop in ponds of long duration (with the traits being positively correlated) (Newman 1988, Stearns et al. 1991).
Having discussed the optimality modeling approach and the factors that influence the expression of life history traits, we turn now to discussing some major predictions for the evolution of life histories (for details see Stearns 1992, Roff 1992, Charlesworth 1994, Stearns 2000, Roff 2002).
Predictions for the Evolution of Life History Traits
At what age and size should an organism mature? A genotype's reproductive success depends strongly on its growth rate and — as a consequence of growth — on its age and size at maturity. To predict the optimal age and size at maturity we must understand the relative costs and benefits (in terms of mortality and reproduction) of either maturing early or late and of either growing large or staying small. The benefits of one "strategy" are the costs of the other, and vice versa. The benefits of maturing earlier and at a smaller size (i.e., the costs of maturing later and at larger size) include: (1) a higher probability of survival to maturity because of a shorter duration of the risky developmental and juvenile period, and (2) a shorter generation time which allows parents to produce offspring that are born earlier and that start to reproduce sooner. Thus, high juvenile mortality, for example, should favor the evolution of earlier maturity. Conversely, the benefits of maturing later and at a larger size (i.e., the costs of maturing earlier and at a smaller size) include: (1) longer growth which leads to larger size at maturity and thus increased fecundity (since fecundity often increases with size), (2) lower adult mortality (and thus potentially higher lifetime fecundity) due to a larger size (mortality due to predators is often lower for larger individuals), and (3) higher quality offspring (e.g., increased investment per offspring, better parental care) which improves survival of the offspring produced.
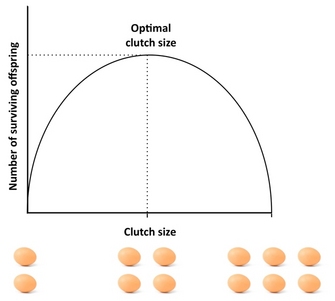
How many offspring should an organism produce? A good starting point to address this question is the "Lack clutch", a concept that goes back to the ornithologist David Lack (1947). Lack's basic insight was that birds should optimize their clutch size by maximizing the number of fledged (surviving) offspring. Deviations from this optimal clutch size would lower reproductive success: if parents produce too large a clutch, they may not be able to support and rear all their offspring, with some or all of them dying, whereas if they produce too small a clutch, the number of fledged offspring may be lower than what the parents could support (Figure 4). Although Lack was correct in his assertion that fitness is often maximized at intermediate investment, clutch sizes are typically smaller than what the Lack clutch predicts. This is because the concept ignores several factors that can reduce clutch size, including parental mortality, future reproduction, the rate of grandchildren production, and parent-offspring conflict. For example, the existence of trade-offs between current reproduction and parental survival, current and future reproduction, or the number and size of offspring can cause deviations from the Lack clutch, and models that take such factors into account usually yield a better fit with observed clutch size than the Lack clutch. For an excellent empirical study of optimal clutch size see the study by Daan et al. (1990) on European kestrels.
How often should an organism reproduce? Should it be semelparous (i.e., reproduce only once) or iteroparous (i.e., reproduce several times) (Figure 5; also see Young 2010)? Theory suggests that iteroparity and the evolution of increased reproductive lifespan are favored when adult survival is high and when adult fecundity or juvenile survival is low: high (or non-variable) adult survival increases the number of reproductive events per lifetime, and low (or variable) fecundity or juvenile survival cause fitness losses that select for increased compensatory reproductive effort. Conversely, semelparity and the evolution of decreased reproductive lifespan are favored when adult survival is low and juvenile survival is high. Thus, high (or non-variable) adult relative to juvenile survival favors iteroparity and lengthens reproductive lifespan while high (or variable) adult relative to juvenile mortality favors semelparity and shortens reproductive lifespan. Semelparous organisms typically have higher reproductive effort than iteroparous organisms.

The above considerations are aspects of a more general issue called the "general life history problem" or "reproductive effort model" (Schaffer 1983, Stearns 1992, Roff 1992, Charlesworth 1994): given that reproduction has both benefits (i.e., offspring production) and costs (e.g., decreased future reproduction, increased parental or offspring mortality), what is the optimal reproductive investment that maximizes fitness? Many theoretical and empirical studies have addressed this problem; some of the major conclusions from this work are (see Stearns 1992, Roff 1992, Charlesworth 1994): (1) reproductive effort often, but not always, increases with age because the cost of current reproduction in terms of future reproduction is expected to decrease with age (since the number of future reproductive events where costs may manifest themselves declines with age); (2) if reproductive effort yields decreasing returns or if mortality increases as the effort increases, intermediate reproductive investment and iteroparity are favored; otherwise, maximal reproductive effort and semelparity are favored; (3) if mortality increases in all age classes, reproductive effort increases early in life and age at maturity decreases; similarly, if adult mortality increases, age at maturity should decrease; and (4) if mortality increases after a particular age (or in one specific age class), reproductive effort increases before and decreases after that age. As particularly beautiful tests of such reproductive effort models we refer the reader to the field and laboratory experiments of David Reznick and colleagues on Trinidad guppies (e.g., Reznick et al. 1990).
How long should an organism live (also see Fabian and Flatt 2011)? The evolution of lifespan can be viewed as a balance between selection for increased reproductive lifespan (and thus potentially increased reproductive success) and aging (i.e., intrinsic age-dependent increase in mortality). The benefits of evolving a longer reproductive lifespan include (also see above): (1) a higher number of reproductive events (and thus offspring) per lifetime if extrinsic adult mortality is low, (2) sufficient time to reproductively compensate for offspring lost due to high juvenile mortality, and (3) decreased reproductive uncertainty due to high variation in juvenile mortality from one round of reproduction to the next, again by being able to compensate for lost offspring. These effects are counteracted by those that increase adult mortality (e.g., survival costs of reproduction; aging) relative to juvenile mortality. Thus, increases in the mean (and/or variance) of adult relative to juvenile mortality tend to favor a shorter reproductive lifespan and semelparity, whereas decreases in the mean (and/or variance) of adult relative to juvenile mortality tend to favor longer reproductive lifespan and iteroparity.
Today many of these predictions of life history theory are well supported by evidence; we shall end this article by giving an example of a particularly elegant experiment that has confirmed the major predictions of the "general life history problem".
An Example of an Empirical Test of the Theory
To test the basic tenets of life history theory, Stearns et al. (2000) used an outbred population of fruit flies (D. melanogaster) to establish two sets of replicate "experimental evolution" lines: three lines were exposed to a high adult mortality treatment (HAM; by randomly killing 90% of the flies twice per week) and three lines to a low adult mortality treatment (LAM; by killing 10% of the flies twice per week). After four years of experimental evolution under these conditions in the lab, Stearns and collaborators measured the life history phenotypes of all lines in both treatments to examine the flies' evolutionary responses to high versus low extrinsic mortality. The results of this long-term experiment were both clear-cut and intriguing, confirming the theoretical predictions: fruit flies that had evolved under HAM conditions developed more rapidly as larvae, eclosed earlier and at a smaller size as adults, had higher early peak fecundity, and showed a shorter lifespan than the LAM flies which evolved the opposite suite of adaptations. In other words, flies evolving in a highly dangerous environment responded evolutionarily by speeding up their development, decreasing their age and size at maturity, laying more eggs earlier, and living shorter: they adapted to high levels of random mortality by shifting their reproductive effort to earlier ages and by compressing their entire life history into a shorter lifespan. Thus, similar to the findings by Reznick et al. (1990) in guppies, these results confirm the major predictions of life history theory, in particular the major role of extrinsic adult mortality in shaping the evolution of growth, maturation, reproduction, and aging.
Summary
Here we have introduced the basics of life history theory. Life history theory attempts to understand how natural selection designs organisms to achieve reproductive success, given knowledge of how selective factors in the environment (i.e., extrinsic mortality) and factors intrinsic to the organism (i.e., trade-offs, constraints) affect survival and reproduction. By using a variety of theoretical and empirical methods, and in particular by applying optimality thinking, life history theorists have derived major predictions about the evolution of the major life history traits, including age and size at maturity, the number and size of offspring, age- or size-specific reproductive effort, reproductive lifespan, and aging. Based on these predictions, and by testing them in field and laboratory experiments, for example in flies, fish, or birds, life history biologists have provided us with some compelling answers to fundamental questions such as: How fast should an organism develop? At what age and size should it mature? How many offspring should it have and how large should they be? Should it reproduce once or more than once? And how long should it live? Through addressing these problems life history theory has made a major impact on our understanding of adaptation by natural selection, the most fundamental issue in all of evolutionary biology.References and Recommended Reading
Brommer, J.E. The evolution of fitness in life-history theory. Biological Reviews of the Cambridge Philosophical Society 75, 377-404 (2000).
Charlesworth, B. Evolution in Age-Structured Populations. Cambridge: Cambridge University Press (1994).
Daan, S. et al. Family planning in the kestrel (Falco tinnunculus): the ultimate control of covariation of laying date and clutch size. Behavior 114, 83-116 (1990).
DeWitt, T. J. & Scheiner, S. M. eds. Phenotypic Plasticity: Functional and Conceptual Approaches. Oxford: Oxford University Press (2004).
Fabian, D. & Flatt, T. The evolution of aging. Nature Education Knowledge, 2(11):9 (2011).
Flatt, T. The evolutionary genetics of canalization. Quarterly Review of Biology 80, 287-316 (2005).
———. Survival costs of reproduction in Drosophila. Experimental Gerontology 46, 369-375 (2011).
Flatt, T. & Heyland A. eds. Mechanisms of Life History Evolution. The Genetics and Physiology of Life History Traits and Trade-Offs. Oxford: Oxford University Press (2011).
Flatt, T. & Schmidt, P. S. Integrating evolutionary and molecular genetics of aging. Biochimica et Biophysica Acta 1790, 951-962 (2009).
Houle, D. Comparing evolvability and variability of quantitative traits. Genetics 130, 195-204 (1992).
———. "The character problem in life history evolution", in The Character Concept in Evolutionary Biology, 109-140, eds G. P. Wagner. Academic Press, 2001.
Lack, D. The significance of clutch size. Ibis 89, 302-352 (1947).
Law, R. Optimal life histories under age-specific predation. American Naturalist 114, 399-417 (1979).
Newman, R. A. Adaptive plasticity in development of Scaphiopus couchii tadpoles in desert ponds. Evolution 42, 774-783.
Nylin, S. & Gotthard, K. Plasticity in life-history traits. Annual Review of Entomology 43, 63-83 (1998).
Pigliucci, M. Phenotypic Plasticity: Beyond Nature and Nurture. Baltimore: The Johns Hopkins University Press (2001).
Reznick, D. N. et al. Experimentally induced life-history evolution in a natural population. Nature 346, 357-359 (1990).
Reznick, D. N. The Origin Then and Now. An Intepretative Guide to the Origin of Species. Princeton: Princeton University Press (2010).
Roff, D. A. The Evolution of Life Histories. Theory and Analysis. New York: Chapman and Hall, 1992.
———. Evolutionary Quantitative Genetics. New York: Chapman and Hall, 1997.
———. Life History Evolution. Sunderland: Sinauer Associates, Inc., 2002.
Schaffer, W. M. The application of optimal control theory to the general life history problem. American Naturalist 121, 418-431 (1983).
Shefferson, R. P. Why are life histories so variable? Nature Education Knowledge 1(12):1 (2010).
Stearns, S. C. The evolution of life histories. Oxford: Oxford University Press, 1992.
———. Trade-offs in life-history evolution. Functional Ecology 3, 259-268 (1989).
———. Life history evolution: successes, limitations, and prospects. Naturwissenschaften 87, 476-486 (2000).
Stearns, S. C. et al. The effects of phenotypic plasticity on genetic correlations. Trends in Ecology and Evolution 6, 122-126 (1991).
Stearns, S. C. et al. Experimental evolution of aging, growth, and reproduction in fruitflies, Proceedings of the National Academy of Sciences USA 97, 3309-3313 (2000).
Stearns, S. C. & Koella, J. C. The evolution of phenotypic plasticity in life-history traits - predictions of reaction norms for age and size at maturity. Evolution 40, 893-913 (1986).
Stearns, S. C. & Partridge, L. "The genetics of aging in Drosophila", in Handbook of the Biology of Aging, S. 5th ed., 353-368. Academic Press, 2001.
Young, T. P. Semelparity and Iteroparity. Nature Education Knowledge 1(9), 2 (2010).
Zwaan, B. et al. Direct selection on life span in Drosophila melanogaster. Evolution 49, 649-659 (1995).