
Nature Index introduces multilateral collaboration score
A new measure accounts for research collaboration within and between groups.
28 June 2018
EXPLAINER

The Nature Index has a new metric to gauge collaboration across multiple institutions in high-quality scientific research output.
The multilateral collaboration score (MCS) provides an indicator for an increasingly common characteristic of research collaboration: the involvement of not just one or two, but three or more principal institutions.
As the accompanying graph shows, 42% of articles published in journals tracked by the Nature Index in 2015-2017 were the result of collaboration between three or more principal institutions.
In a growing number of cases, research papers in journals tracked by the Nature Index have more than a thousand listed authors, putting the number of institutions collaborating on such papers into the hundreds.
The multilateral collaboration score goes beyond Nature Index’s existing metric of the bilateral collaboration score (CS), an indicator of collaborations between pairs only. The MCS can be calculated for a single institution or a group of multiple institutions. It is calculated using the fractional count (FC) by which Nature Index accounts for the share of authorship on each article, with the total FC on an article always amounting to one. If there are five collaborating authors from five different institutions on a given article, for example, each institution is allocated an equal share of the total FC, which in that case would be 0.2.
MCS takes into account the number of collaborating institutions on a given article, so it can be added across a number of institutions, with the total MCS of each article always amounting to one. To calculate an individual institution’s MCS on an article, each collaborating institution’s FC on the article is divided by one less than the total number of institutions (n) which collaborated on the article (i.e. n-1). The resulting values are summed for each pair of institutions to give the total MCS for that pair on an article. The MCS for an individual institution (A) is the sum of the values from each of its pairs (e.g. (A+B) + (A+C) + (A+D) etc.
For example, four institutions (n=4) collaborated on an article which appeared in Nature: “An absorption profile centred at 78 megahertz in the sky-averaged spectrum”. Their FCs were 0.667 for the Arizona State University (ASU), 0.200 for the Massachusetts Institute of Technology (MIT), 0.067 for the University of Colorado Boulder (CU-Boulder) and 0.067 for the Universidad Catolica de la Santisima Concepcion (UCSC Chile).
To calculate the MCS for ASU we first divide its FC by three (n-1), so 0.667/3 = 0.222. The same calculation is done for each institution; the values for each of the pairs are summed. So for ASU, the calculation is (ASU+MIT=0.289) + (ASU+CU-Boulder=0.244), + (ASU+ USCS Chile=0.244), which gives a total of 0.778, which is ASU’s MCS on this article.
Since the total MCS on an article always amounts to one, the combined MCS on the article for the three remaining institutions is the difference between 1 and ASU’s 0.778.
An individual institution’s total MCS is the sum of all its MCSs for each of the articles on which it has collaborated with two or more other institutions. The metric also allows the MCS for groups of institutions to be calculated, by summing their institutional MCS scores.
MCS can be calculated for a single institution with a group of institutions, for one group of institutions with another, or within one group of institutions.
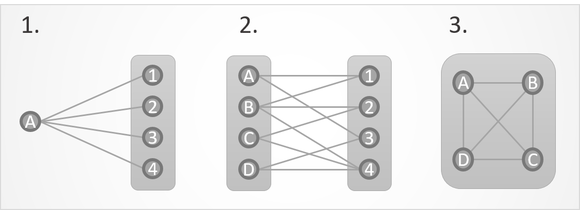
The first scenario can be used to rank institutions on the basis of the strength of their multilateral collaborations. The second scenario, one group of institutions to another, will be frequently used to show the strength of collaborations between groups, such as city to city, where each city’s score represents the summed MCSs for all of its institutions. In the third scenario, within one group of institutions, MCS for a group — for example, a city — tells you the strength of collaboration within the city, calculated by summing the MCSs for all intra-city collaborations between its institutions.
Data analysis by Aaron Ballagh and Bo Wu.
