An agglomerative hierarchical approach to visualization in Bayesian clustering problems

Abstract

Clustering problems (including the clustering of individuals into outcrossing populations, hybrid generations, full-sib families and selfing lines) have recently received much attention in population genetics. In these clustering problems, the parameter of interest is a partition of the set of sampled individuals—the sample partition. In a fully Bayesian approach to clustering problems of this type, our knowledge about the sample partition is represented by a probability distribution on the space of possible sample partitions. As the number of possible partitions grows very rapidly with the sample size, we cannot visualize this probability distribution in its entirety, unless the sample is very small. As a solution to this visualization problem, we recommend using an agglomerative hierarchical clustering algorithm, which we call the exact linkage algorithm. This algorithm is a special case of the maximin clustering algorithm that we introduced previously. The exact linkage algorithm is now implemented in our software package PartitionView. The exact linkage algorithm takes the posterior co-assignment probabilities as input and yields as output a rooted binary tree, or more generally, a forest of such trees. Each node of this forest defines a set of individuals, and the node height is the posterior co-assignment probability of this set. This provides a useful visual representation of the uncertainty associated with the assignment of individuals to categories. It is also a useful starting point for a more detailed exploration of the posterior distribution in terms of the co-assignment probabilities.

Introduction

In a clustering problem we have a collection of individuals (the sample), which must be classified into mutually exclusive categories. In general the number of categories represented in the sample, and the characteristics of these categories, are uncertain. Problems of this type have recently received much attention in population genetics, where the data available from the sampled individuals include their genotypes at a number of marker loci. (Other types of data, which may be available include the spatial positions of individuals, and observations of their behaviour.) Examples include the following. (i) Clustering individuals from an outcrossing species into putative populations (represented approximately as panmictic populations). These putative populations may correspond to subspecies, or even individual spawning grounds or breeding sites (for example, in phylopatric species of fish, amphibians or marine turtles). For Bayesian approaches to these problems, see Pritchard et al. (2000); Dawson and Belkhir (2001); Falush et al. (2003); Corander et al. (2003, 2004, 2006); Corander and Marttinen (2006); Pella and Masuda (2006); Huelsenbeck and Andolfatto (2007); Guillot et al. (2008). Methods are also available which make use of spatial position data in addition to genotype data from the sampled individuals (Guillot et al., 2005; François et al., 2006; Chen et al., 2007; Corander et al., 2008). (In the earlier work of Wasser et al. (2004), individuals were not classified into discrete populations.) (ii) The more general problem of clustering individuals from an outcrossing species into hybrid generations, including F1, F2 and B1 crosses, as well as parental populations has been addressed by Anderson and Thompson (2002). Falush et al. (2003) also allow for the possibility that the sample contains individuals of hybrid origin. (iii) Clustering individuals into (full-sib) families (Painter, 1997; Almudevar and Field, 1999; Thomas and Hill, 2000, 2002; Emery et al., 2001; Wang, 2004; Hadfield et al., 2006). Painter (1997); Thomas and Hill (2000); Smith et al. (2001) assumed that the separate full-sib families do not share any parents in common. Thomas and Hill (2002) and Wang (2004) imposed the weaker constraint that parents of only one sex are permitted to have multiple mates. Emery et al. (2001) imposed no constraints on the matings among parents. Hadfield et al. (2006) incorporated spatial information on the territories occupied by individuals. (iv) Clustering individuals from a partially selfing population into selfing lines (Wilson and Dawson, 2007), or individuals from a partially asexual population into clonal lineages.

In a clustering problem, the parameter of interest is a partition of the label set S of the sample. We refer to this parameter as the sample partition. A partition of a set S is a set of non-empty disjoint subsets of S, the union of which is the set S itself.

From a Bayesian point of view, inferences about the sample partition should be based on the (marginal) posterior distribution of the sample partition. An MCMC sampler can be used to generate a large sample of observations from the posterior distribution of the sample partition—or at least a distribution, which is an adequate approximation to this posterior distribution. This is the approach taken in many of the papers cited above. Here, we are concerned with the treatment of the output from the Markov chain sampler.

The visualization problem

Bayesian clustering problems of this type have certain features which have proved to be challenging. The number of ways of partitioning a set of n distinct elements into k non-empty disjoint (and unlabelled) subsets is equal to the Stirling number of the second kind, denoted by . These numbers grow very rapidly with n. The total number of ways of partitioning a set of n distinct elements into non-empty disjoint (and unlabelled) subsets, is given by the sum

This is the nth Bell number. (For further information see for example, Aigner (1979).) As these numbers grow very rapidly with n, it is only in cases where n is small, that a probability distribution over the space of partitions of the set can be visualized in its entirety. This is what we mean by a visualization problem. There need not be a problem if there are only a small number of partitions which have an appreciable share of the posterior probability—as these partitions can easily be identified and listed along with their individual posterior probabilities. However, if many of the individuals in the sample are difficult to classify, then there will be many plausible partitions, each one having an individually low posterior probability. Under these circumstances those regions where the probability is elevated will be difficult to identify.

In addition to this visualization problem, there is also a computational problem. The Monte Carlo method will not provide an accurate estimate of very low probabilities (because these will necessarily be based on a small number of observations). Therefore, in situations where there are a large number of plausible partitions, there is a need to collapse this marginal posterior distribution further, to obtain marginal posterior probabilities of more probable events.

Some authors, using Bayesian methodology, have avoided the visualization problem by considering only point estimation of the sample partition (Corander et al., 2003; Huelsenbeck and Andolfatto, 2007; Coulon et al., 2008). Corander et al. (2003) used a maximum a posteriori probability estimate. However, maximum a posteriori probability estimates are vulnerable to the computational problem which arises when there are many plausible partitions, each one having an individually low posterior probability.

The Bayesian framework provides us with a general strategy for overcoming visualization problems. We compute marginal distributions (possibly many different marginals), which can be visualized individually, each of which provides some information about the parameter of interest. We can also estimate the posterior probability that the sample partition satisfies a chosen condition. This is equivalent to the (marginal) posterior distribution of an indicator function corresponding to the chosen condition. We can compute these posterior probabilities for as many different conditions as we find helpful.

Dawson and Belkhir (2001) made use of the posterior co-assignment probabilities of sets of individuals. Let S denote the label set of the sample. The co-assignment probability of a set U⊆S is the probability that the set of individuals, U, all belong to the same category (or element of the partition). A co-assignment probability can also be interpreted as the probability that the sample partition satisfies a condition. In this case, the condition is that the chosen set U is a subset of (or is equal to) an element of the sample partition. Here, we denote the posterior co-assignment probability of the set U by Π(U).

The label-switching problem

In the past, Bayesian clustering methods have been beset by the so-called label switching problem described by Richardson and Green (1997). These are problems that can arise in Bayesian inference about any model having a set partition (such as a sample partition) as a parameter, when we try to compute marginal distributions for parameters, which depend upon an arbitrary labelling of the elements of the partition. The labelling of the elements is arbitrary whenever the prior and the likelihood function are both invariant under permutation of the component labels—in which case the posterior distribution is also invariant under permutation of the component labels. For example, one might be tempted to compute what we refer to here as the posterior assignment probability of individual i to a particular category α (conditional on there being K categories, say). This is the posterior probability that individual i belongs to category α, conditional on there being K categories. However, α is an arbitrary label, which does not refer to any fixed entity. A category is characterized by the individuals assigned to it, and by the value of some category-specific parameter, all of which are uncertain. In fact, Pritchard et al. (2000) recommended assigning individuals to discrete clusters using these posterior assignment probabilities, which they refer to as membership coefficients, and which are an output of their widely used software package (STRUCTURE).

In the case of STRUCTURE, this label-switching problem is obscured by the poor mixing of the Markov chain sampler. (According to Pritchard et al. (2000), their Markov chain samples in the vicinity of a single mode of the posterior distribution.) It is only as a consequence of poor mixing that a set of individuals, which have a high posterior co-assignment probability, also tend to remain associated with the same label over many iterations of the Markov chain sampler. In the model which underlies STRUCTURE, the parameter K is the number of potential populations. For each run of the Markov chain sampler, K is held fixed. The potential populations are labelled α=1,…,K. One of the outputs from a run of the Markov chain sampler is an n × K matrix of posterior assignment probabilities. This output is referred to as a Q-matrix. If the Markov chain sampler mixed well, then each of these assignment probabilities would be equal to 1/K, and so would be completely uninformative.

Recently (Jakobsson and Rosenberg, 2007) the software package CLUMPP has been developed to process the output from STRUCTURE. This program takes as its input the Q-matrices computed from r runs of the Markov chain sampler. It then searches for the sequence of r−1 permutations of the set {1,…,K} (and hence permutations of the columns of the Q-matrix), which maximizes a measure of similarity for the sequence of r Q-matrices. Once the required sequences of permutations have been found, it is applied to the sequence of Q-matrices. The resulting sequence of (column permuted) Q-matrices can then be passed as input to the visualization software package DISTRUCT (Rosenberg, 2004). It seems to us that CLUMPP does not address the label-switching problem. If the Markov chain sampler mixed well, then each of the Q-matrices (which CLUMPP takes as its input), would have every entry equal to 1/K, in which case the output from CLUMPP would be as uninformative as the input. If on the other hand the Markov chain sampler mixes poorly, then we cannot rely on it to make accurate estimates of posterior probabilities.

Label-switching problems can also arise in Bayesian inference about mixture models, whenever we try to compute marginal distributions for parameters which depend upon an arbitrary labelling of the component populations of the mixture. Richardson and Green (1997) drew attention to the label-switching problem in the context of their attempt to compute the marginal posterior distribution of component-specific parameters. For example, in the case of a population genetic model, where the components correspond to distinct panmictic populations, we might want to compute the marginal posterior distribution of the frequency of a particular allele type in each population. The solution to the label-switching problem offered by Richardson and Green (1997) was to rank the components of the partition with respect to the value of one of the component-specific parameters. It is then possible to compute the marginal posterior distribution for any component-specific parameter in the first component, the second component, and so on. Such an ordering of the components has been referred to as an identifiability constraint (Celeux et al., 2000; Hurn et al., 2003; Jasra et al., 2005). These are certainly well-defined marginals of the posterior distribution. However, there is no guarantee that any of these marginals will correspond to a unique component of the true mixture. We may also have to choose from a bewildering array of possible identifiability constraints. For example, in the case of a population genetic model, where the components correspond to distinct panmictic populations, we could choose to order the components with respect to the frequency of any allele type, at any locus, which is represented in the genotype data. An identifiability constraint of this type was used by Guillot et al. (2005).

When the number of potential components in the mixture is a constant K, the posterior distribution can be represented as a symmetric mixture of K! copies of a single joint distribution, each with a different permutation of the component labels. This observation is the starting point for an alternative approach proposed by Stephens (1997, 2000), where the aim is to assign each observation from the posterior distribution to one of the K! permutation. This is achieved by applying a k–means type clustering algorithm to the sample of observation from the posterior distribution, to assign each observation to one of the K! clusters. (For an alternative algorithm, see Celeux et al. (2000)) Jasra et al. (2005) referred to this method as a relabelling algorithm. This may prove to be a very difficult clustering problem when the K! components in the symmetric mixture overlap too much.

Jasra et al. (2005) favoured a third approach to the label-switching problem, originally advocated by Celeux et al. (2000) and Hurn et al. (2003). These authors proposed that the label-switching problem be solved within the framework of decision theory, by introducing a label-invariant loss function. The loss function is a function of parameter values of the model (the sample partition, and the component-specific parameters), and an action. (For an introduction to decision theory, see Berger (1985)) In Celeux et al. (2000) and Hurn et al. (2003), the action is simply a point estimate, of either the sample partition, or a sequence of component-specific parameters. (In principle, the action could also be the choice of a credible set, rather than the choice of a point estimate. However, in the case of the sample partition, this would take us back to the visualization problem.) Having introduced a loss function, we are in a position to compute the posterior expected loss for each possible action. In principle, we can search for the action that minimizes the posterior expected loss. However, this minimization procedure is computationally costly. Note that the choice of a loss function introduces further subjectivity, in addition to the subjectivity inherent in the choice of prior.

A solution

In contrast to Stephens (2000) and Jasra et al. (2005), we strongly recommend avoiding the label-switching problem by restricting attention to marginal distributions of only those parameters which are invariant under permutations of the labels of the categories. This point of view was expressed by Gilks (1997) in a contribution to the discussion of Richardson and Green (1997), from which we now quote.

‘I am not convinced by the authors’ desire to produce a unique labelling of the groups. It is unnecessary for valid Bayesian inference concerning identifiable quantities; … it is only the group members which lend meaning to the individual clusters.’

Unlike assignment probabilities, co-assignment probabilities are invariant under permutations of the labels of the categories. This was one reason why Dawson and Belkhir (2001, 2002) proposed using the posterior co-assignment probabilities as a basis for inferences about the sample partition. Furthermore, in situations where the posterior probabilities of individual partitions are too small (relative to Monte Carlo error) to be estimated reliably, the posterior co-assignment probabilities of many subsets of the label set can be estimated accurately, using a large sample of observations from the posterior distribution.

The availability of posterior co-assignment probabilities for sets of individuals suggests a solution to the visualization problem. If we have a rooted binary tree with n terminal nodes (external nodes, tips or leaves), each of which is labelled with a distinct element of the label set S of the sample, then each of the n−1 internal nodes of this tree specifies a subset (containing two or more elements) of the label set S. Included among these subsets is the set S itself, which is the set specified by the root node. By making the height of each node equal to the posterior co-assignment probability of the set of individuals defined by that node (the individuals whose labels occupy the terminal nodes that can be reached by ascending the tree from that node), we can present the posterior co-assignment probabilities of n−1 sets in a format which is easy to view and interpret.

Before proceeding, we need to clarify what is meant by a rooted binary tree, a terminal node and an internal node. A tree consists of nodes and edges (branches). (A tree is a graph.) It is possible to walk on a tree (stepping from one node to the next only when they are joined by an edge) from any node to every other node. (A tree is a connected graph.) When walking on a tree, it is impossible to return to the original node without travelling back along at least one of the same edges. (A tree is an acyclic-connected graph. This can be taken as the definition of a tree.) Every node of a tree is connected to at least one edge. A node which is connected to only one edge is called a terminal node (external node, tip or leaf). A node which is connected to more than one edge is called an internal node. In a rooted tree, one of the internal nodes is designated the root node. A rooted binary (bifurcating or fully resolved) tree is one in which the root node is connected to exactly two edges, and every other internal node is connected to exactly three edges.

We are now faced with the problem of choosing a rooted binary tree, and hence choosing which subsets of S are to be specified, together with their posterior co-assignment probabilities. Any hierarchical clustering algorithm will automatically pick out one particular hierarchy of sets, which can be represented in the form of a (rooted) binary tree. The computational time required for a divisive hierarchical clustering algorithm (where we begin by assigning all individuals to a single category) grows exponentially with the sample size n, because there are 2ⁿ⁻¹−1 distinct bipartitions of a set of n elements Edwards and Cavalli-Sforza, 1965). In contrast, the computational time required for an agglomerative hierarchical clustering algorithm (where we begin by assigning each individual to a separate category) is only of order n². For these computational reasons an agglomerative hierarchical clustering algorithm is preferable. But which agglomerative hierarchical clustering algorithm should we use? Dawson and Belkhir (2001) introduced the maximin agglomerative algorithm for this purpose. More recently, Corander et al. (2004) applied the complete linkage algorithm to the output from their MCMC sampler (the software package BAPS). The complete linkage algorithm is a special case of the maximin agglomerative algorithm.

Here, we recommend an agglomerative hierarchical clustering algorithm which we refer to as the exact linkage algorithm. The exact linkage algorithm is also a special case of the maximin agglomerative algorithm of Dawson and Belkhir (2001). In the next section, we describe the exact linkage algorithm.

We end this section by noting that, in general, the output from the exact linkage algorithm may be a rooted binary tree in which some internal nodes have height zero—represented co-assignment probabilities of zero. It is more natural to interpret a rooted binary tree having k nodes at height zero (1⩽k<n) as a rooted binary forest made up of k+1 separate trees. A forest is a graph in which every connected subgraph is a tree. In other words, a forest is composed of one or more trees.

The exact linkage algorithm

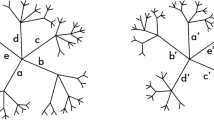
As with any agglomerative hierarchical clustering algorithm, the exact linkage algorithm begins with n terminal nodes, each of which is labelled with a distinct element of the label set S of the sample. (So the set of terminal nodes can be equated with the label set S.) At each subsequent iteration (t=1, 2, …), a new internal node is created, having two existing nodes (terminal or internal) as descendants. In this way, we build up a forest of rooted binary trees. (This rooted binary forest may include trivial trees consisting of a single terminal node.) This process of adding internal nodes can continue for a maximum of n−1 iterations (in which case we have, at the end of iteration n−1, a single-rooted binary tree having n terminal nodes and n−1 internal nodes). See Figure 1, where we illustrate the exact linkage algorithm with an example for a sample of five individuals.

Figure 1

The exact linkage algorithm. Here, we illustrate the exact linkage algorithm with an example for a sample of five individuals. At the initialization step (iteration t=0) we create five terminal nodes, labelled respectively 1, 2, 3, 4 and 5. This is followed by iterations t=1, 2, 3, 4. At each iteration t (⩾1) we begin with an update step. This is followed by an acceptance step at which we create a new internal node, labelled −t (where t is the iteration at which it is created). At the update step we update the set of proposed nodes. This updated set of proposed nodes is formed from all possible pairs of the root nodes available at the start of the present iteration. In this figure, every node (proposed node or accepted node) is positioned at a height equal to the co-assignment probability of the set defined by that node. The proposed nodes are arranged on the vertical axis to the right of the forest. Notice that it is always the highest proposed node, which is accepted. At iteration t=1 the proposed node (4, 5) is accepted and added to the tree, where it is labelled −1. At iteration t=2 the proposed node (1, 2) is accepted and added to the tree, where it is labelled −2. At iteration t=3 the proposed node (−1, 3) is accepted and added to the tree, where it is labelled −3. At iteration t=4 the proposed node (−3, −2) is accepted and added to the tree, where it is labelled −4.

Each internal node is labelled with an integer t (=1, 2, …, n−1), according to the iteration t at which it was created. Each node of this forest defines a set of individuals from the sample. A terminal node defines a set containing only one individual. Every internal node t, defines a set S(t)⊆S. This is the set of terminal nodes that can be reached by ascending the tree, starting from node t.

At any iteration t, a node is said to be a root node if it has not yet become the descendent of another node. Let R(t) denote the set of root nodes at the end of iteration t. At the end of iteration t, every root node in R(t) belongs to a distinct tree in the associated forest, and every tree in the forest has a unique root node which belongs to R(t). In the case of a trivial tree, consisting of a single terminal node, this terminal node is also the unique root node of the tree.

We now state the exact linkage algorithm.

The exact linkage algorithm

We begin with an initialization step.

(0) Set the iteration number to be t=0. Set the height of each terminal node to 1. Set R(0)=S (the set of terminal nodes).

To construct the internal nodes, at each subsequent iteration we repeat the following three steps.

• 1) Increase the iteration number by one (from t−1 to t), then construct a set Q(t) of proposed nodes. This is the set of the nodes which can be constructed by taking a pair (i,j) of (distinct) existing root nodes (i,j∈R(t−1), i≠j), and joining them together to create a new root node having these two nodes as its descendants.

• 2) Calculate the node height p(i,j) associated with each proposed node (i,j)∈Q(t).

• 3) Find the proposed node which is highest, and add this node to the forest. Label this new node t. So we have

Repeat steps 1–3 until either p(t)=0, or (at the end of iteration t=n−1) only one root node remains.

In the event of ties (multiple proposed nodes having the same height) occurring at step 3, we simply choose one of these highest nodes at random and accept it.

Notice that at each iteration the number of root nodes (and hence trees in the forest) is reduced by one. So, at the end of iteration t we have ∣R(t)∣=n−t root nodes. At the start of iteration t, the number of proposed nodes is

The node height p(i,j) of a proposed node (i,j) is a Monte Carlo estimate of the co-assignment probability Π(S(i,j)) of the set S(i,j)=S(i)∪S(j) defined by this proposed node. The Monte Carlo estimate is obtained from the sample of N observations of the sample partition. The sample is stored as an n × N array, where each line is an observation of the sample partition, represented as a vector of n integer values. Each position i in the vector of n integer values represents an individual (i∈S), and the integer value at position i is an arbitrary label α, indicating the element of the partition (a subset of S) to which that individual is assigned. To estimate the co-assignment probability Π(S(i,j)), we count the number of observations where the set S(i,j) is a subset of an element of the sample partition, and divide this count by the total number of observations N. We indicate this approximate relationship by writing

and

where S(t) is the set defined by the accepted node t.Notice that we can construct the set of proposed nodes Q(t) at step 1 of iteration t (⩾2), by updating the set of proposed nodes Q(t−1) from the previous iteration (t−1), as follows. Suppose that the most recent accepted node (labelled t−1) has descendants d₁ and d₂. First, delete the proposed node (d₁,d₂), along with all proposed nodes (d₁,j), (j,d₂), where j∈R(t−2) and j≠d₁,d₂. (The total number of nodes to be deleted is 2(n−t)+1.) Second, insert the nodes (t−1,j), where j∈R(t−2) and j≠t−1. (The total number of nodes to be inserted is n−t.) As a consequence, at step 2 of interaction t, we only need to compute the node heights of the n−t new proposed nodes created at step 1.

In Figure 1, steps 1 and 2 taken together, are referred to as the update step, because the proposed nodes are updated as described above. Step 3 is referred to as the acceptance step in Figure 1, because a proposed node is accepted and added to the forest.

It is possible to improve on this version of the exact linkage algorithm by ruling out certain proposed nodes right from the start. The version of the exact linkage algorithm which has now been implemented in the PartitionView software package, has been optimized along these lines.

The maximin agglomerative algorithm

As already mentioned, the exact linkage algorithm is a special case of the maximin agglomerative algorithm Dawson and Belkhir (2001). The maximin agglomerative algorithm is also described in Appendix A (see Supplementary information).

In the maximin agglomerative algorithm, clusters are constructed so as to maximize the minimum co-assignment probability of subsets of size d within clusters. This is why we have called this algorithm the maximin agglomerative algorithm. In fact, it is a generalization of the classical complete linkage (or furthest neighbour) algorithm (Sørensen, 1948; McQuitty, 1960; Defays, 1977)—to which it reduces in the case d=2.

The exact linkage algorithm includes a maximization step, but no minimization. So, the name maximin agglomerative algorithm is no longer appropriate. In the complete linkage algorithm the heights of nodes are upper bounds on the co-assignment probabilities for the sets they define, when these contain more than two individuals. This is in contrast to the exact linkage algorithm where the heights of nodes are exact (up to Monte Carlo sampling error) co-assignment probabilities for the sets they define (regardless of how many individuals they contain)—hence its name. An alternative more descriptive name for this algorithm is the most probable cluster agglomerative algorithm. This name reflects the fact that at each iteration of the algorithm, we accept that proposed node, which defines the cluster having the highest co-assignment probability, out of all the proposed nodes at the iteration in question.

As recognized in Dawson and Belkhir (2001), the tree or forest generated by the exact linkage algorithm captures more of the information from the posterior distribution than any other version of the maximin agglomerative algorithm. However, in our earlier work we implemented the maximin agglomerative algorithm, with dimension d=2, 3 or 4, for computational reasons. See Appendix B (Supplementary information) for details.

The exact linkage algorithm is implemented in PartitionView. The maximin agglomerative algorithm (with dimension d=2, 3 or 4) was implemented in the earlier companion programme, called Analyse.exe, which PartitionView.exe replaces. (Analyse.exe was an unfortunate choice of name (as it has already been used in population genetics, and no doubt elsewhere). It might be best to rename this programme posthumously as PartitionView0.exe.)

Interpretation of the forests generated by the exact linkage algorithm

As we descend the forest (from the terminal nodes towards the root node), passing successively through the nodes t=1, 2, …, n−1, the set S(t) defined by each node has a lower posterior co-assignment probability than the set defined by the preceding nodes. This brings us to the question of how to decide when a node t is sufficiently low that we can confidently reject the claim that all individuals in the set S(t) defined by this node belong to the same category. Perhaps, the most obvious method is for the user to choose a threshold value p for the probability of co-assignment. So, for every node t defining a set of individuals S(t) with co-assignment probability p(t)⩾p, we accept the co-assignment of all the individuals in the set S(t) defined by that node; while for nodes t having p(t)<p, we do not accept the corresponding co-assignments. Ideally, each user would choose a value for the threshold which corresponds to how averse they are to the risk of making false co-assignments. For example, a particularly cautious user might want to choose a threshold of P=0.9, or P=0.95, whereas a less cautious user might be content with a threshold of P=0.5. If we apply a rule of the above type, with any threshold p, to the sets defined by the nodes of a forest (with terminal nodes corresponding to the elements of the set S), then we can only accept the assignment of an individual i to a sequence of sets A, B, C, … (∣A∣<∣B∣<∣C∣<…<n) if these sets form a nested sequence (i∈A⊂B⊂C⊂…⊂S).

Examples

In this section, we illustrate the performance of the exact linkage algorithm for classifying individuals into categories, by applying it to the output from Markov chain samplers applied to simulated data sets—where the correct classification is known to us. The software package PartitionView (version 0 and now version 1.0) was originally developed as a companion programme to the MCMC sampler program Partition (Dawson and Belkhir, 2001). However, PartitionView can be used to process the output from a Monte Carlo sampler for any probability distribution which has, as a marginal, a probability distribution on the space of partitions of a set (with the obvious proviso that observations of the set partition can be recovered from the output of the Monte carlo sampler). To emphasize this fact, our first example is the classification of 100 individuals into selfing lines, on the basis of output from the Markov chain sampler program IMPPS (Wilson and Dawson, 2007). In this example, the true sample partition has a large number of small elements (many sets of size 1 or 2).

In our second example the simulated data set is a sample of 80 individuals drawn from two source populations (40 individuals from each population). The Markov chain sampler program HWLER Pella and Masuda (2006) was applied to this data set. We use this relatively simple example to illustrate how the rooted binary forests generated by the exact linkage algorithm may differ from those generated by the maximin agglomerative algorithm (with d=2, 3 and 4).

The rooted binary forest, or tree, generated by PartitionView is encoded in the ‘Newick 8:45’ format adopted by PHYLIP Felsenstein (2004). In the current version of PartitionView, a rooted binary forest consisting of multiple separate trees, is represented as a single-rooted tree, where the separate root nodes of the forest are joined together by a sequence of internal nodes which all have height zero. The root node of the resulting tree is also at height zero.

Example 1

Recently, Wilson and Dawson (2007) used the exact linkage algorithm (as implemented in PartitionView version 1.0) to process the output from the Markov chain sampler program IMPPS (Inference of Matrilineal Pedigrees under Partial Selfing). This is a Markov chain sampler for the joint posterior distribution of the pedigree of a sample from a partially selfing population, and the parameters of the population genetic model (including the selfing rate), given the genotypes of the sampled individuals at unlinked marker loci. The population genetic model is appropriate for a hermaphrodite annual species, allowing both selfing and outcrossing. Generations are discrete and non-overlapping, as is appropriate for an annual species. The local population or deme was founded in the recent past (T generations in the past), and the founders were drawn from an infinitely large unstructured source population. Throughout its existence, this deme has remained at a constant size of N diploid individuals. The N founders (the seed immigrants) are sampled independently from the source population. In the current version of IMPPS it is assumed that no seed immigration into the local deme has occurred since the founder generation. The efficient Markov chain Monte carlo strategy employed in the IMPPS program relies on the rather artificial assumption that, for every outcrossing event which occurs within the local deme, the pollen grain is drawn directly from the large source population.

The aspect of the pedigree that we are interested in here is the classification of individuals into selfing lines. Each selfing line is founded by an outcrossed ancestor: the most recent outcrossed ancestor (MROA) of the individuals belonging to that selfing line. The MROAs of a sample are the ancestors of the sample that we encounter if we trace the line of descent of each individual from the sample back up the pedigree until we encounter the first ancestor which is a product of outcrossing. If an individual in the sample is itself a product of outcrossing then that individual is an MROA, and we have no need to trace its ancestry back any further. The classification of individuals into selfing lines induces a partition of the label set of the sample. We refer to this sample partition as the selfing line partition. It is this partition which we want to infer from the genotype data.

The output from the IMPPS Markov chain sampler includes observations of the selfing line partition. From a large sample of such observations we can estimate the co-assignment probability of any set of individuals. Here, the relevant co-assignment probability is the posterior probability that all individuals in the set belong to the same selfing line (in other words, they share the same MROA).

A simulated data set was generated by a genealogical (reverse time) simulation of the model outlined above. The selfing rate was s=0.8, the local population was of size N=100, and age T=5 generations. The local population was exhaustively sampled (sample size n=100), and the individuals were genotyped at six polymorphic marker loci. This simulated data set was one of those analysed in Wilson and Dawson (2007), using the IMPPS Markov chain sampler. The true matrilineal pedigree of this exhaustive sample of n=100 individuals is represented in Figure 2. Outcrossing events are indicated by diamonds.

Figure 2

Example 1. The true matrilineal pedigree of the simulated data set. The true matrilineal pedigree of the exhaustive sample of all n=N=100 individuals from a single local population. Outcrossing events are indicated by diamonds. Those selfing lines which are represented in the sample by more than two individuals are colour-coded.

Every partition of a set S induces an integer partition of ∣S∣. The true selfing line partition in our example induces an integer partition of the sample size 100. This integer partition can be written as 1⁴⁰2¹⁴3²4¹5²6²—meaning that there are 40 sets of size 1, 14 sets of size 2 and so on, in the original set partition. This notation for an integer partition is referred to as the frequency representation of the integer partition.

We have colour-coded those true selfing lines, which are of size greater than two, and coloured each node of the forest according to the true selfing line of the set of individuals defined by the node. (All the branches in the clade defined by a node are similarly coloured according to the true selfing line of this set of individuals.) The true selfing lines are colour-coded as follows. The two distinct selfing lines of size 6 are designated the Red and the Orange line, respectively; the two distinct lines of size 5 are designated, the Green and the Blue lines, respectively; the selfing line of size 4 is the Violet line; and the two distinct lines of size 3 are the Purple and the Sienna line, respectively. The 14 selfing lines of size 2, and the 40 selfing lines of size 1, are assigned the colour black. Black is also used as the default colour for any internal nodes that define sets of individuals from multiple selfing lines.

A sample of 60 000 observations of the selfing line partition was generated by pooling three independent runs of the Markov chain sampler. Each run provided 20 000 observations, from the 20 000 iterations (without thinning) following a burn-in of 1000 iterations.

Figure 3 shows the rooted binary forest generated by applying the exact linkage algorithm to the pooled sample of 60 000 observations. To illustrate how successfully the true selfing lines have been identified, we have applied the same colour coding to this rooted binary forest as we applied to the true pedigree (in Figure 2).

Figure 3

Example 1. Output from the exact linkage algorithm. The rooted binary forest generated by applying the exact linkage algorithm to the output from the IMPPS Markov chain sampler (a pooled sample of 60 000 observations).

If we choose a threshold of P=0.75 (so that we accept the co-assignment of all the individuals in the set defined by any node t having p(t)⩾0.75), then we obtain a selfing line partition which induces an integer partition (of the sample size 100) having the frequency representation 1³⁸2¹⁴3²4¹5¹6²7¹.

The small number of errors in the inferred partition can be summarized as follows. The Blue line (of size 5) is erroneously fused with a set of size 2. In addition, one individual from a set of size 2 has been removed and placed erroneously with an individual from a set of size 1, and two sets of size 1 have been erroneously fused to form a set of size 2. The Red line (of size 6), the Orange line (of size 6), the Green line (of size 5), the Violet line (of size 4), the Purple line (of size 3) and the Sienna line (of size 3), are all present in the inferred partition, as are 12 out of the 14 selfing lines of size 2, and 37 out of the 40 selfing lines of size 1. Note that if we choose a lower threshold, of P=0.5 for example, only a few additional erroneous agglomerations of selfing lines are accepted.

Example 2

Our second example illustrates how the rooted binary forests generated by the exact linkage algorithm may differ from those generated by the maximin agglomerative algorithm (with d=2, 3 and 4). For this purpose we have chosen a simpler example. We reanalyse one data set (data set 4) out of the five simulated data sets reported in Dawson and Belkhir (2001). In our earlier publication, these five data sets were analysed by first using a Markov chain sampler (Partition) to generate a sample of observations from the posterior distribution of the sample partition, and then applying the maximin agglomerative algorithm (with d=2 and 3) to the output form this Markov chain sampler. These five data sets were reanalysed recently by Pella and Masuda (2006), who applied their Markov chain sampler (HWLER), followed by our maximin agglomerative algorithm (with d=2), and obtained rooted binary forests having more clearly defined clusters. Recall that the maximin agglomerative algorithm with d=2 is identical to the complete linkage algorithm (a classical distance-based method).

Data set 4 consists of the genotypes (at 10 unlinked marker loci) of 80 diploid individuals, sampled from a pair of populations (40 individuals from each population) which have diverged under random drift during a period of isolation following the fission of a common ancestral population. (For the details of the weak divergence scenario, see Dawson and Belkhir (2001).) For the true bipartition of the sample (the bipartition of the pooled sample induced by assigning each individual to its true population of origin), we have F_ST=0.065 (using the multi-locus estimator of Weir and Cockerham (1984)). Here, we designate the two populations Grey and Black, respectively. Pella and Masuda (2006) applied their HWLER program to data set 4, and generated a sample of 20 160 observations (with a period of five iterations) from the posterior distribution of the sample partition. They discarded the first 10 080 observations (half of the original sample) as burn-in. Here we have discarded the first 10 000 observations as burn-in, leaving a sample of 10 160 observations.

We applied the maximin agglomerative algorithm, with d=2, 3 and 4 (Figures 4, 5 and 6, respectively) to this sample, and used it to generate rooted binary forests. Using the PartitionView software, we also applied the exact linkage algorithm to this same sample, to generate another rooted binary forest (Figure 7).

Figure 4

Example 2. Output from the maximin agglomerative algorithm with d=2. The rooted binary forest generated by applying the maximin agglomerative algorithm, with d=2, to the output from the HWLER Markov chain sampler.

Figure 5

Example 2. Output from the maximin agglomerative algorithm with d=3. The rooted binary forest generated by applying the maximin agglomerative algorithm, with d=3, to the output from the HWLER Markov chain sampler.

Figure 6

Example 2. Output from the maximin agglomerative algorithm with d=4. The rooted binary forest generated by applying the maximin agglomerative algorithm, with d=4, to the output from the HWLER Markov chain sampler.

Figure 7

Example 2. Output from the exact linkage algorithm. The rooted binary forest generated by applying the exact linkage algorithm to the output from the HWLER Markov chain sampler.

In the analysis reported by Pella and Masuda (2006), using the maximin agglomerative algorithm with d=2, the rooted binary forest consisted of two separate trees, defining two well-supported clusters, corresponding to the two populations (Grey and Black respectively), with only one individual (a Grey individual, labelled 27 in the original analysis of Dawson and Belkhir (2001)) belonging to the wrong cluster. (Note that for this bipartition of the sample, we have F_ST=0.066 for the multi-locus estimator of Weir and Cockerham (1984)—a slight increase from the value obtained for the true bipartition.) We obtained similar results using the maximin agglomerative algorithm, with d=2, 3 and 4 and with the exact linkage algorithm (and burn-in=10 000).

The forests represented in Figures 5, 6 and 7, each consist of two separate trees, whereas the forest represented by Figure 4 consists of a single tree, but one whose root node is very close to zero. All these trees contain a node, which pairs the same Grey individual (labelled 27) with the same Black individual (labelled and 74 in the original analysis). As d is increased from 2 to 3, and then to 4, the height of the node which defines the cluster corresponding to the Grey population (excluding individual 23) falls, as does the height of the node which defines the cluster corresponding to the Black population (but also including individual 23). In the case of the forests generated by the maximin agglomerative algorithm, with d=4, and by the exact linkage algorithm, these two nodes are lower still, and there is a particularly sharp drop in node height when we reach the node where the pair of individuals 23 (Grey) and 74 (Black) are joined with the rest of the individuals from the second population. At least in the case of individual 23, the increased skepticism represented by this fall in node height, is a more accurate representation of the true situation. At the same time this forest indicates a greater reluctance to assign two Grey individuals (labelled 11 and 24) with the rest of the Grey population, and this is not so easily justified.

When we apply the maximin agglomerative algorithm, with different values for the dimension d, to the same sample of observations from a posterior distribution of partitions, we often obtain rooted binary forests having similar topologies (sharing many of the same internal nodes) as here. In such cases, we expect the heights of the internal nodes tend to fall as the dimension d is increased, as we can observe in Figures 4, 5, 6 and 7. In particular, the forests generated by the exact linkage algorithm (Figure 7) tend to have the lowest nodes—thus favouring more cautious co-assignment.

Discussion

We were not the first to use (posterior) co-assignment probabilities in the context of Bayesian clustering (Dawson and Belkhir, 2001). In a contribution to the discussion of Richardson and Green (1997), O'Hagan (1997) suggested computing pairwise posterior co-assignment probabilities. Painter (1997) recommended using posterior co-assignment probabilities in an early paper on Bayesian discovery of full-sib families. Emery et al. (2001) also used posterior co-assignment probabilities in Bayesian discovery of full-sib and half-sib families. However, Painter (1997) and Emery et al. (2001) only made use of pairwise co-assignment probabilities, and the visualization problem, which can arise with large samples of individuals was not addressed. In Dawson and Belkhir (2001) we offered a solution to the visualization problem. We also indicated how to make use of the co-assignment probabilities for sets of any size. However, in practice we only made use of co-assignment probabilities for sets of sizes 2, 3 and 4.

The exact linkage algorithm recommended here has two obvious advantages over classical hierarchical clustering algorithms. Firstly, the node heights in the resulting rooted binary forests have a direct Bayesian interpretation. This is not the case for the node heights which would result from applying various classical hierarchical clustering algorithms, for example, the average linkage algorithm ((Sokal and Michener (1958) and Sokal and Sneath (1963), pages 182–185) to the (symmetric) matrix of pairwise co-assignment probabilities (as the similarity matrix). Secondly, the exact linkage algorithm can make use of the additional information which the posterior distribution (of the sample partition) provides about the support for the co-assignment of sets of more than two individuals.

The PartitionView software package can now compute the posterior co-assignment probability of any set of individuals, regardless of whether or not it corresponds to a node of the rooted binary forest, so that the rooted binary forest can be used as a starting point for a more detailed exploration of the posterior distribution of the sample partition. We have also provided an R script for viewing, labelling and colouring the rooted binary forests in the output files (in ‘Newick 8:45’ format) generated by PartitonView.

The pairwise posterior co-assignment probabilities for all pairs of individuals are also provided in an output file. So any user who wants to use these probabilities as measures of similarity, and apply a classical hierarchical clustering algorithm (such as single linkage Florek et al. (1951); Sibson (1973), complete linkage Sørensen (1948); McQuitty (1960); Defays (1977), or average linkage Sokal and Michener (1958) and Sokal and Sneath (1963), pages 182–185) is free to do so.

PartitionView was originally designed to be a companion program to the Markov chain sampler program—Partition. (For more information about the Markov chain sampler implemented in the Partition software, see Dawson and Belkhir (2001).) Because the output file from Partition contains observations of the sample partition, users are free to design their own software for the visual representation of any chosen marginals of the posterior distribution of the sample partition. We would also like to make a plea to others who have developed (or may be planning to develop) their own software for sampling from the posterior distribution of the sample partition, to generate output files which contain complete observations of this type. This would mean that our visualization software (PartitionView) could be modified to process the output file. More generally, we recommend, as a general design principal for Bayesian inference software, that Monte Carlo samplers should provide output files which contain complete observations from the posterior distribution, and that the visualization software should be a separate module, which can take such a file as input.

PartitionView1.0 is freely available from the Partition web page: http://www.genetix.univ-montp2.fr/partition/partition.htm.