Abstract
We study the dynamics of the collision between two fermions in Hubbard model with on-site interaction strength U. The exact solution shows that the scattering matrix for two-wavepacket collision is separable into two independent parts, operating on spatial and spin degrees of freedom, respectively. The S-matrix for spin configuration is equivalent to that of Heisenberg-type pulsed interaction with the strength depending on U and relative group velocity vr. This can be applied to create distant EPR pair, through a collision process for two fermions with opposite spins in the case of |vr/U| = 1, without the need for temporal control and measurement process. Multiple collision process for many particles is also discussed.
Similar content being viewed by others
Introduction
Pairing is the origin of many fascinating phenomena in nature, ranging from superconductivity to quantum teleportation. Owing to the rapid advance of experimental techniques, it has been possible both to produce Cooper pairs of fermionic atoms and to observe the crossover between a Bose-Einstein condensate and a Bardeen-Cooper-Schrieffer superfluid1,2,3. The dynamic process of pair formation is of interest in both condensed matter physics and quantum information science. On one hand, the collective behavior of pairs gives rise to macroscopic properties in many-body physics. On the other hand, a single entangled pair is a promising quantum information resource for future quantum computation.
In recent years, the controlled setting of ultracold fermionic atoms in optical lattices is regarded as a promising route to enabled quantitative experimental tests of theories of strongly interacting fermions4,5,6,7. In particular, fermions trapped in optical lattices can directly simulate the physics of electrons in a crystalline solid, shedding light on novel physical phenomena in materials with strong electron correlations4,8,9. A major effort is devoted to simulate the Fermi-Hubbard model by using ultracold neutral atoms10,11,12. This approach offers experimental access to a clean and highly flexible Fermi-Hubbard model with a unique set of observables13 and therefore, motivate a large number of works on Mott insulator phase14,15 and transport properties16,17, stimulating further theoretical and experimental investigations on the dynamics of strongly interacting particles for the Fermi Hubbard model.
In this paper, we study the dynamics of the collision between two fermions with various spin configurations. The particle-particle interaction is described by Hubbard model, which operates spatial and spin degrees of freedom in a mixed manner. Based on the Bethe ansatz solution, the time evolution of two fermonic wave packets with identical size is analytically obtained. We find that the scattering matrix of the collision is separable into two independent parts, operating on spatial and spin degrees of freedom, respectively. The scattered two particles exhibit dual features. The spatial part behaves as classical particles, swapping the momenta, while the spin part obeys the isotropic Heisenberg-type exchange coupling. The coupling strength depends on the Hubbard on-site interaction and relative group velocity of two wavepackets. This finding can be applied to create distant EPR pair, through a collision process for two fermions with opposite spins without the need for temporal control and measurement process. Multiple collision process for many particles is also discussed.
Results
Fermi-Hubbard Model
A one-dimensional Hubbard Hamiltonian on an N-site ring reads

where  is the creation operator of the fermion at the site i with spin
is the creation operator of the fermion at the site i with spin  and U is the on-site interaction. The tunneling strength and the on-site interaction between fermions are denoted by
and U is the on-site interaction. The tunneling strength and the on-site interaction between fermions are denoted by  and U. For the sake of clarity and simplicity, we only consider odd-site system with
and U. For the sake of clarity and simplicity, we only consider odd-site system with  and periodic boundary condition
and periodic boundary condition  .
.
Now based on the symmetry analysis of the Hamiltonian (1) as shown in Methods section, we can construct the basis of the two-fermion invariant subspace as following

and

where K is the momentum vector, indexing the subspace. These bases are eigenvectors of the operators  ,
,  ,
,  and
and  . The corresponding definitions of the operators are detailed in Methods section. Straightforward algebra yields
. The corresponding definitions of the operators are detailed in Methods section. Straightforward algebra yields



and



while



and


Then there are four invariant subspaces with  ,
,  and
and  involved.
involved.
Dynamics of wavepacket collision
We now want to investigate the dynamics of two-wavepackets collision based on the two-particle solution, which is shown in Methods section. We begin with our investigation from the time evolution of an initial state

which represents two separable fermions a and b, with spin σ and  , respectively. Here
, respectively. Here

with  , b and
, b and  , is a wavepacket with a width
, is a wavepacket with a width  , a central position
, a central position  and a group velocity
and a group velocity  . We focus on the case
. We focus on the case  . The obtained result can be extended to other cases. In order to calculate the time evolution of state
. The obtained result can be extended to other cases. In order to calculate the time evolution of state  , two steps are necessary. At first, the projection of
, two steps are necessary. At first, the projection of  on the basis sets
on the basis sets  and
and  can be given by the decomposition.
can be given by the decomposition.

Secondly, introducing the transformation.



and using the identities


we have

with

where  is the normalized factor.
is the normalized factor.
We note that the component of state  on each invariant subspace indexed by K represents an incident wavepacket along the chain described by
on each invariant subspace indexed by K represents an incident wavepacket along the chain described by  that is presented in Eq. (59) of Methods. This wavepacket has width
that is presented in Eq. (59) of Methods. This wavepacket has width  , central position
, central position  and group velocity
and group velocity  . Accordingly, the time evolution of state
. Accordingly, the time evolution of state  can be derived by the dynamics of each sub wavepacket in each chain
can be derived by the dynamics of each sub wavepacket in each chain  , which eventually can be obtained from Eq. (60) of Methods section. According to the solution, the evolved state of
, which eventually can be obtained from Eq. (60) of Methods section. According to the solution, the evolved state of  can be expressed approximately in the form of
can be expressed approximately in the form of  , which represents a reflected wavepacket. Here
, which represents a reflected wavepacket. Here  is an overall phase, as a function of
is an overall phase, as a function of  , the position of the reflected wavepacket, being independent of U and the
, the position of the reflected wavepacket, being independent of U and the  is the reflection amplitude demonstrated in Eq. (61) of Methods. In addition, it is easy to check out that, in the case with
is the reflection amplitude demonstrated in Eq. (61) of Methods. In addition, it is easy to check out that, in the case with  , the initial state distribute mainly in the invariant subspace
, the initial state distribute mainly in the invariant subspace  , where the wavepacket moves with the group velocity
, where the wavepacket moves with the group velocity  . Then the state after collision has the approximate form
. Then the state after collision has the approximate form

which also represents two separable wavepackets at  and
and  respectively. Here Ω is the normalized factor and an overall phase is neglected. We would like to point out that the key point to achieve this interesting phenomenon is that the coordinates of the two particles can be decomposed into two independent parts in term of the center of mass coordinates and relative coordinate. We do not preclude that the initial two-particle state possessing the different shape may get to the same conclusion. However, the strict proof of this general condition is hardly obtained. For the sake of simplicity and clarity, we confine our disscussion to the case of two wavepackets
respectively. Here Ω is the normalized factor and an overall phase is neglected. We would like to point out that the key point to achieve this interesting phenomenon is that the coordinates of the two particles can be decomposed into two independent parts in term of the center of mass coordinates and relative coordinate. We do not preclude that the initial two-particle state possessing the different shape may get to the same conclusion. However, the strict proof of this general condition is hardly obtained. For the sake of simplicity and clarity, we confine our disscussion to the case of two wavepackets  and
and  with same shape.
with same shape.
Equivalent Heisenberg coupling
Now we try to express the two-fermion collision in a more compact form. We will employ an S-matrix to relate the asymptotic spin states of the incoming to outcoming particles. We denote an incident single-particle wavepacket as the form of  , where
, where  , R indicates the particle in the left and right of the collision zone, p the momentum and
, R indicates the particle in the left and right of the collision zone, p the momentum and  the spin degree of freedom. In this context, we give the asymptotic expression for the collision process as
the spin degree of freedom. In this context, we give the asymptotic expression for the collision process as

where the S-matrix

governs the spin part of the wave function. Here  denotes spin operator for the spins of particles at left or right,
denotes spin operator for the spins of particles at left or right,  , where
, where  and
and  represent the group velocity of the left and right wavepacket, respectively. Together with the scattering matrix
represent the group velocity of the left and right wavepacket, respectively. Together with the scattering matrix  for spatial degree of freedom
for spatial degree of freedom

we have a compact expression

to connect the initial and final states. In general the total scattering matrix has the form of exp , which is not separable into spatial and spin parts. Then Eq. (29) is only available for some specific initial states, e.g., spatially separable two-particle wavepackets with identical size. This may lead to some interesting phenomena.
, which is not separable into spatial and spin parts. Then Eq. (29) is only available for some specific initial states, e.g., spatially separable two-particle wavepackets with identical size. This may lead to some interesting phenomena.
It is interesting to note that the scattering matrix for spin is equivalent to the propagator

for a pulsed Heisenberg model with Hamiltonian

with  . Here
. Here  is time-ordered operator, which can be ignored since only the coupling strength
is time-ordered operator, which can be ignored since only the coupling strength  is time dependent. This observation accords with the fact that, in the large positive U case, the Hubbard model scales on the
is time dependent. This observation accords with the fact that, in the large positive U case, the Hubbard model scales on the  model18,19, which also includes the NN interaction term of isotropic Heisenberg type. Recently, we note that several perturbative techniques have been proposed to construct an effective spin Hamiltonian in the context of the one-dimensional interacting confined system20,21,22,23,24. Nevertheless, they confine their results to the strongly interaction regime. Here, we need to stress that the derivation of the Eq. (31) is obtained from the dynamic aspect and does not dependent on the approximation of large interaction strength U, which is different from that of those works.
model18,19, which also includes the NN interaction term of isotropic Heisenberg type. Recently, we note that several perturbative techniques have been proposed to construct an effective spin Hamiltonian in the context of the one-dimensional interacting confined system20,21,22,23,24. Nevertheless, they confine their results to the strongly interaction regime. Here, we need to stress that the derivation of the Eq. (31) is obtained from the dynamic aspect and does not dependent on the approximation of large interaction strength U, which is different from that of those works.
The aforementioned scattering matrix for spin also indicates that the effect of collision on two spins is equivalent to that of time evolution operation under the Hamiltonian  at an appropriate instant. In this sense, the collision process can be utilized to implement two-qubit gate. For two coupled-qubit system, the time evolution operator is simply given by
at an appropriate instant. In this sense, the collision process can be utilized to implement two-qubit gate. For two coupled-qubit system, the time evolution operator is simply given by

yielding

where  denotes qubit state. We can see that at instants
denotes qubit state. We can see that at instants  and π, the evolved states become
and π, the evolved states become


which indicates that  and
and  are entangling and swap operators, respectively. In practice, such protocols require exact time control of the operation.
are entangling and swap operators, respectively. In practice, such protocols require exact time control of the operation.
Comparing operator  and the S-matrix in Eq. (27), we find that two-qubit operations can be performed by the collision process, where U and relative group velocity
and the S-matrix in Eq. (27), we find that two-qubit operations can be performed by the collision process, where U and relative group velocity  are connected to the evolution time by the relation
are connected to the evolution time by the relation

Then we can implement entangling and swap gates for two flying qubits via dynamic process. To demonstrate the result, we consider several typical cases with  ,
,  and
and  , which correspond to the operations of swap, standby and entanglement, respectively. The collision processes are illustrated schematically in Fig. 1. The advantage of such a scheme is that the temporal control is replaced by pre-engineered on-state interaction U.
, which correspond to the operations of swap, standby and entanglement, respectively. The collision processes are illustrated schematically in Fig. 1. The advantage of such a scheme is that the temporal control is replaced by pre-engineered on-state interaction U.
In order to check the above conclusion, numerical simulation is performed. We define the initial and target states as


where  possess the same relative position but the exchanged momentum compared with the state
possess the same relative position but the exchanged momentum compared with the state  as in Eq. (37). On the other hand, we consider the evolved state
as in Eq. (37). On the other hand, we consider the evolved state  for the initial state being
for the initial state being  driven by the Hamiltonian (1) and caculate the fidelity
driven by the Hamiltonian (1) and caculate the fidelity  in Fig. 2. It is shown that when the state
in Fig. 2. It is shown that when the state  evolves to the same position with
evolves to the same position with  , the fidelity
, the fidelity  is almost to 1, which is in agreement with our previous theoretical analysis.
is almost to 1, which is in agreement with our previous theoretical analysis.
Plots of the fidelity  with the parameters Na = 20, Nb = 62, ka = −kb = π/2, in the system Eq. (1) with N = 81 and U = vr.
with the parameters Na = 20, Nb = 62, ka = −kb = π/2, in the system Eq. (1) with N = 81 and U = vr.
The red, blue and black lines represent the plots of fidelity  in the condition of
in the condition of  , 0.26 and 0.33, respectively. It shows that the fidelity is close 1, as α approaches to 0, which accords with the theoretical analysis in the text.
, 0.26 and 0.33, respectively. It shows that the fidelity is close 1, as α approaches to 0, which accords with the theoretical analysis in the text.
In ultracold atomic gas experiments, an extra harmonic potential is usually introduced to investigate the interaction between the atoms. To make closer connections with experiment, we will study how an trapping potential can effect on the two-particle collision process. The concerned Hamiltonian can be rewritten as

where  describes an additional (slowly varying) external trapping potential, e.g., a magnetic trap. The presence of the
describes an additional (slowly varying) external trapping potential, e.g., a magnetic trap. The presence of the  destroy the translation symmetry of the system, therefore one can hardly obtain the analytical result for two-particle collision. Based on this, we perform the numerical simulation to investigate the influence of the external field on the results obtained in a potential free system. In Fig. 3 , we plot the fidelity
destroy the translation symmetry of the system, therefore one can hardly obtain the analytical result for two-particle collision. Based on this, we perform the numerical simulation to investigate the influence of the external field on the results obtained in a potential free system. In Fig. 3 , we plot the fidelity  as a function of time t, where
as a function of time t, where  is driven by the Hamiltonian
is driven by the Hamiltonian  . The parameter
. The parameter  is chosen from 10−4 to 10−3 for a nearly realistic confinement15,25,26,27. It can be shown that the increase of the ratio of
is chosen from 10−4 to 10−3 for a nearly realistic confinement15,25,26,27. It can be shown that the increase of the ratio of  leads to decreasing of the maximum of fidelity. This can be explained as follow: When the strength of the trapping potential
leads to decreasing of the maximum of fidelity. This can be explained as follow: When the strength of the trapping potential  is much smaller than the hopping constant
is much smaller than the hopping constant  , the moving particle will not feel the variation of potential between the adjacent sites, especially at the center of trapping potential. If we consider the collision process at such region, the collision for the two particles only occurs at the neighbour sites due to the short-range interaction between the two particles. Thus, the effect of the confining harmonic potential can be neglected within the collision process.
, the moving particle will not feel the variation of potential between the adjacent sites, especially at the center of trapping potential. If we consider the collision process at such region, the collision for the two particles only occurs at the neighbour sites due to the short-range interaction between the two particles. Thus, the effect of the confining harmonic potential can be neglected within the collision process.
Plots of the fidelity  as a function of time t with parameters Na = 20, Nb = 62, ka = −kb = π/2, in the system Eq. (1) with N = 81 and U = vr.
as a function of time t with parameters Na = 20, Nb = 62, ka = −kb = π/2, in the system Eq. (1) with N = 81 and U = vr.
The blue, red, black and green lines represent the plots of fidelity  in the condition of
in the condition of  0.0005 0.001 and 0.002, respectively. It indicates that the increase of
0.0005 0.001 and 0.002, respectively. It indicates that the increase of  result in decreasing of the maximum of fidelity, which accords with the theoretical analysis in the text.
result in decreasing of the maximum of fidelity, which accords with the theoretical analysis in the text.
On the other hand, the Gaussian wavepacket is often employed to describe the moving particle in the lattice model. The presence of the trapping potential can change the shape and momentum of the moving wavepacket. When the strength of the trapping potential is much smaller than the hopping constant, if the time for the collision process is short enough, the trapping potential can be deemed as a homogeneous field to the involved particles and therefore can not effect on the collision process. For a given weak harmonic trapping potential, the wider of the wavepacket can lead to more time for finishing the collision process, in which the trapping potential can not be neglected. Nevertheless, one can not require the wavepacket to be narrow enough because it can make the two-particle state not to distribute mainly in the invariant subspace of center momentum  , thereby preventing the separation between the spatial and spin part of the two-particle collision. Based on this, the existence of the obtained results regarding the two-particle collision process is a tradeoff between the strength of the harmonic potential and the width of the wavepacket. To check this conclusion, the function
, thereby preventing the separation between the spatial and spin part of the two-particle collision. Based on this, the existence of the obtained results regarding the two-particle collision process is a tradeoff between the strength of the harmonic potential and the width of the wavepacket. To check this conclusion, the function  is introduced to characterize the variation of the maximum of fidelity
is introduced to characterize the variation of the maximum of fidelity  with respect to the width of the wavepacket
with respect to the width of the wavepacket  , which can be defined as
, which can be defined as

where  is the time that
is the time that  takes to reach the maximum value for a given α. In Fig. 4, we plot
takes to reach the maximum value for a given α. In Fig. 4, we plot  versus α, from which one can see that the function
versus α, from which one can see that the function  first increase then decrease as the variation of α. According to the above analysis, the decrease of width of the wavepacket can bring about two effects: On the one hand, the presence of the trapping potential can be approximately deemed as a homogeneous field due to the slight variation of trapping potential in effective collision process. This can enhance the
first increase then decrease as the variation of α. According to the above analysis, the decrease of width of the wavepacket can bring about two effects: On the one hand, the presence of the trapping potential can be approximately deemed as a homogeneous field due to the slight variation of trapping potential in effective collision process. This can enhance the  . On the other hand, the initial state will not distribute mainly in the invariant subspace
. On the other hand, the initial state will not distribute mainly in the invariant subspace  . Therefore, the spatial and spin part are not separable within the collision process, which can decrease the
. Therefore, the spatial and spin part are not separable within the collision process, which can decrease the  . As
. As  increase, the former effect is dominant. On the contrary, the latter effect is dominant as
increase, the former effect is dominant. On the contrary, the latter effect is dominant as  decrease. Moreover, the maximum of
decrease. Moreover, the maximum of  can be seen as a tradeoff between two such effects in this point of view.
can be seen as a tradeoff between two such effects in this point of view.
Plot of the function  with respect to α with parameters Na = 20, Nb = 62, ka = −kb = π/2, in the system Eq. (1) with N = 81 and U = vr.
with respect to α with parameters Na = 20, Nb = 62, ka = −kb = π/2, in the system Eq. (1) with N = 81 and U = vr.
The system is subjected to a weak trapping potential  in units of
in units of  . One can see that the maximum of fidelity
. One can see that the maximum of fidelity  first gets to 0.956 then decrease to 0.88 as the increase of α, which can be explained in the text.
first gets to 0.956 then decrease to 0.88 as the increase of α, which can be explained in the text.
Combining both aspects, we can conclude that if the strength of the external trapping potential is much smaller than the hopping constant and the width of the wavepacket is optimum, the results for collision process in our manuscript are still hold.
Multiple collision
We apply our result to many-body system. Considering the case that the initial state is consisted of many separable local particles with the same group velocity, termed as many-particle wavepacket train (MPWT), our result can be applicable if each collision time is exact known. In this paper, we only demonstrate this by a simple example. We consider the collision of two MPWTs with particle numbers M and N  . All the distances between two adjacent particles in two trains are identical. The initial state is
. All the distances between two adjacent particles in two trains are identical. The initial state is

where  and
and  denote the sequences of particles,
denote the sequences of particles,  and
and  denote the spin configurations in each trains. According to the above analysis, after collisions the final state has the form of
denote the spin configurations in each trains. According to the above analysis, after collisions the final state has the form of

where the spin configurations  and
and  are determined by the S-matrix, which is the time-ordered product of all two-particle S-matrices. During the collision process, the positions of particles in each train are always spaced by equal intervals. This makes it easier to determine the times of each collisions. Then the final state can be written as
are determined by the S-matrix, which is the time-ordered product of all two-particle S-matrices. During the collision process, the positions of particles in each train are always spaced by equal intervals. This makes it easier to determine the times of each collisions. Then the final state can be written as

where

and

where  and
and  are corresponding Pauli matrices. Applying the formula in Eq. (43) to the case with
are corresponding Pauli matrices. Applying the formula in Eq. (43) to the case with  ,
,  ,
,  ,
,  , we obtain
, we obtain

This conclusion is still true for the case with unequal-spaced  . For illustration, we sketch the case with
. For illustration, we sketch the case with  ,
,  ,
,  ,
,  ,
,  in Fig. 5(a). One can see that the spin part of the final state is the superposition of the combinations of the four spins.
in Fig. 5(a). One can see that the spin part of the final state is the superposition of the combinations of the four spins.
Schematic illustration of the collision between the two MPWTs.
(a) An incident single fermion comes from the left denoted as blue spin and collides with 3-fermion train, which comes from the right denoted as red spins. It can be seen that the single fermion keep the original momentum, but it entangles with the 3-fermion train at the end of the collision. The amplitudes of the four states are listed. It is shown that the final state is direct product between the states of single fermion and 3-fermion train when 
 with the corresponding parameter
with the corresponding parameter  , 0, respectively. (b) The collision between the two MPWTs come from the opposite direction with particle number
, 0, respectively. (b) The collision between the two MPWTs come from the opposite direction with particle number  . And the probability for the superposition of states is listed with
. And the probability for the superposition of states is listed with  .
.
Now we turn to investigate the entanglement between the single fermion and the MPWT with particle number N. As is well known, the generation and controllability of entanglement between distant quantum states have been at the heart of quantum information processing. Such as the applications in the emerging technologies of quantum computing and quantum cryptography, as well as to realize quantum teleportation experimentally28,29. Moreover, quantum entanglement is typically fragile to practical noise. Every external manipulation inevitably induces noise in the system. This suggests a scheme based on the above mentioned collision process for generating the entanglement between a single fermion and the N-fermion train without the need for the temporal control and measurement process. We note that although the incident single fermion keep the original momentum, it entangles with the N-fermion train after the collision, leading to a deterioration of its purity. To measure the entanglement between the single fermion and the N-fermion train, we calculate the reduced density matrix of the single spin

where

Thus the purity of the single fermion can be expressed as

where Tr denotes the trace on the single fermion. For the case of
denotes the trace on the single fermion. For the case of  , 1, we have
, 1, we have  , which requires
, which requires  and
and  , obtained from interaction parameter
, obtained from interaction parameter  and 0, respectively. It indicates that the single fermion state and N-fermion train state are not entangled. In contrast, the purity
and 0, respectively. It indicates that the single fermion state and N-fermion train state are not entangled. In contrast, the purity  at
at  when
when

It corresponds to a completely mixed state of the outgoing single fermion, or maximal entanglement between the single fermion state and N-fermion train. Together with Eq. (61), we have

which reduces to  for large N. This indicates that for large N, one needs to take a small U of order
for large N. This indicates that for large N, one needs to take a small U of order  to generate the maximal entanglement between the single fermion state and N-fermion train, or result in full decoherence of the single fermion.
to generate the maximal entanglement between the single fermion state and N-fermion train, or result in full decoherence of the single fermion.
In the case of two-train collision, the calculation can still be performed in the similar way. However, it is hard to get analytical result for arbitrary system. Here, we sketch the case with M = 2,  ,
,  ,
,  , in Fig. 5(b). The probability on each spin configuration is listed as illustration.
, in Fig. 5(b). The probability on each spin configuration is listed as illustration.
Discussion
Summarizing, we presented an analytical study for two-fermion dynamics in Hubbard model. We find that the scattering matrix of two-fermion collision is separable into two independent parts, operating on spatial and spin degrees of freedom, respectively, when two incident wavepackets have identical shapes. For two fermions with opposite spins, the collision process can create a distant EPR pair due to the resonance between the Hubbard interaction strength and the relative group velocity. The advantage of this scheme is without the need of temporal control and measurement process. Since it is now possible to simulate the Hubbard model via cold fermionic atoms in optical lattice, these results can be realized experimentally.
In conclusion, our finding is of both fundamental and practical interest, as it offers a concrete insight for the fundamental properties of particle paring in the context of the Hubbard model and provide a scheme to realize the distant EPR pair in the experiment.
Methods
Symmetry analysis
We analyze three symmetries of the Hamiltonian (1) as following, which is critical for achieving a two-particle solution. The first is particle-number conservation  , where
, where  , which ensures that one can solve the eigen problem in the invariant subspace with fixed
, which ensures that one can solve the eigen problem in the invariant subspace with fixed  , no matter U is real or complex. The second is the translational symmetry,
, no matter U is real or complex. The second is the translational symmetry,  , where
, where  is the shift operator defined as
is the shift operator defined as

with

This allows invariant subspace spanned by the eigenvector of operator  . Based on this fact, one can reduce the two-particle problem to a single-particle problem. The final is the SU(2) symmetry,
. Based on this fact, one can reduce the two-particle problem to a single-particle problem. The final is the SU(2) symmetry,  and
and  , where the spin operators are defined as
, where the spin operators are defined as


which satisfy the relation  .
.
Two-particle solutions
We present the detailed caculation for the two-particle solution in each invariant subspace. For the simplicity, we only focus on the solutions in subspaces  and
and  , since the one in subspace
, since the one in subspace  can be obtained directly from that in subspace
can be obtained directly from that in subspace  by operator
by operator  . A two-particle state can be written as
. A two-particle state can be written as

where the wave function  satisfies the Schrödinger equations
satisfies the Schrödinger equations

and

with the eigen energy  in the invariant subspace indexed by K. Here factor
in the invariant subspace indexed by K. Here factor  for
for  and
and  for
for  , respectively. As pointed in refs 30,31 in previous works, the eigen problem of two-particle matrix can be reduced to the that of single particle. We see that the solution of (58) is equivalent to that of the single-particle
, respectively. As pointed in refs 30,31 in previous works, the eigen problem of two-particle matrix can be reduced to the that of single particle. We see that the solution of (58) is equivalent to that of the single-particle  -site tight-binding chain system with nearest-neighbour (NN) hopping amplitude
-site tight-binding chain system with nearest-neighbour (NN) hopping amplitude  , on-site potentials U and
, on-site potentials U and  at 0th and
at 0th and  th sites, respectively. The solution of (57) corresponds to the same chain with infinite U. In this work, we only concern the scattering solution by the 0th end. In this sense,
th sites, respectively. The solution of (57) corresponds to the same chain with infinite U. In this work, we only concern the scattering solution by the 0th end. In this sense,  can be obtained from the equivalent Hamiltonian
can be obtained from the equivalent Hamiltonian

Based on the Bethe ansatz technique, the scattering solution can be expressed as

with eigen energy  ,
,  . Here the reflection amplitude
. Here the reflection amplitude

where


and  can be obtained from
can be obtained from  by taking
by taking  . We note that
. We note that  , which reveals a dynamic symmetry of the Hubbard model with respect to the sign of U.
, which reveals a dynamic symmetry of the Hubbard model with respect to the sign of U.
Additional Information
How to cite this article: Zhang, X. Z. and Song, Z. EPR pairing dynamics in Hubbard model with resonant U. Sci. Rep. 6, 18323; doi: 10.1038/srep18323 (2016).
References
Regal, C. A., Greiner, M. & Jin, D. S. Observation of Resonance Condensation of Fermionic Atom Pairs. Phys. Rev. Lett. 92, 040403 (2004).
Zwierlein, M. W., Stan, C. A., Schunck, C. H., Raupach, S. M. F., Kerman, A. J. & Ketterle, W. Condensation of Pairs of Fermionic Atoms near a Feshbach Resonance. Phys. Rev. Lett. 92, 120403 (2004).
Bourdel, T. et al. Experimental Study of the BEC-BCS Crossover Region in Lithium 6. Phys. Rev. Lett. 93, 050401 (2004).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885 (2008).
Zwerger, W., ed. The BCS-BEC crossover and the unitary Fermi gas. Vol. 836 (Springer, 2011).
Zwierlein, M. W. In Novel Superfluids Vol. 2, edited by Bennemann, K.-H. & Ketterson, J. B. (Oxford University Press, Oxford, 2014).
Bloch, I., Dalibard, J. & Nascimbène, S. Quantum simulations with ultracold quantum gases. Nature Phy. 8, 267 (2012).
Lewenstein, M. et al. Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond. Advances in Physics 56, 243 (2007).
Esslinger, T. Fermi-Hubbard Physics with Atoms in an Optical Lattice. Annu. Rev. Condens. Matter Phys. 1, 129 (2010).
Byrnes, T. et al. Quantum Simulator for the Hubbard Model with Long-Range Coulomb Interactions Using Surface Acoustic Waves. Phys. Rev. Lett. 99, 016405 (2007).
Byrnes, T. et al. Quantum simulation of Fermi-Hubbard models in semiconductor quantum-dot arrays. Phys. Rev. B 78, 075320 (2008).
Murmann, S. et al. Two Fermions in a Double Well: Exploring a Fundamental Building Block of the Hubbard Model. Phys. Rev. Lett. 114, 080402 (2015).
Köhl, M. et al. Fermionic Atoms in a Three Dimensional Optical Lattice: Observing Fermi Surfaces, Dynamics and Interactions. Phys. Rev. Lett. 94, 080403 (2005).
Jördens, R. et al. A Mott insulator of fermionic atoms in an optical lattice. Nature 455, 204 (2008).
Schneider, U. et al. Metallic and Insulating Phases of Repulsively Interacting Fermions in a 3D Optical Lattice. Science 322, 1520 (2008).
Strohmaier, N. et al. Interaction-Controlled Transport of an Ultracold Fermi Gas. Phys. Rev. Lett. 99, 220601 (2007).
Schneider, U. et al. Fermionic transport and out-of-equilibrium dynamics in a homogeneous Hubbard model with ultracold atoms. Nature Phys. 8, 213 (2012).
Spalek, J. t-J Model Then and Now: a Personal Perspective from the Pioneering Times. Acta Physica Polonica A 111, 409 (2007).
Auerbach, A. Interacting Electrons and Quantum Magnetism (Springer, New York, 1994).
Volosniev, A. G. et al. Strongly interacting confined quantum systems in one dimension. Nat. Commun. 5, 5300 (2014).
Deuretzbacher, F. et al. Quantum magnetism without lattices in strongly interacting one-dimensional spinor gases. Phys. Rev. A 90, 013611 (2014).
Volosniev, A. G. et al. Engineering the dynamics of effective spin-chain models for strongly interacting atomic gases. Phys. Rev. A 91, 023620 (2015).
Levinsen, J., Massignan, P. Bruun, G. M. & Parish, M. M. Strong-coupling ansatz for the one-dimensional Fermi gas in a harmonic potential. Science Advances 1, e1500197 (2015).
Yang, L., Guan, L. M. & Pu, H. Strongly interacting quantum gases in one-dimensional traps. Phys. Rev. A 91, 043634 (2015).
Helmes, R. W. et al. Mott Transition of Fermionic Atoms in a Three-Dimensional Optical Trap. Phys. Rev. Lett. 100, 056403 (2008).
Gorelik, E. V. et al. Néel Transition of Lattice Fermions in a Harmonic Trap: A Real-Space Dynamic Mean-Field Study. Phys. Rev. Lett. 105, 065301 (2010).
Fuchs, S. et al. Thermodynamics of the 3D Hubbard Model on Approaching the Néel Transition. Phys. Rev. Lett. 106, 030401 (2011).
Nielson, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambride University Press, 2002).
Horodecki, R. et al. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Jin, L., Chen, B. & Song, Z. Coherent shift of localized bound pairs in the Bose-Hubbard model. Phys. Rev. A 79, 032108 (2009).
Zhang, X. Z., Jin, L. & Song, Z. Self-sustained emission in semi-infinite non-Hermitian systems at the exceptional point. Phys. Rev. A 87, 042118 (2013).
Acknowledgements
This work is supported by the National Basic Research Program (973 Program) of China under Grant No. 2012CB921900 and the National Natural Science Foundation of China (Grants No. 11505126 and No. 11374163). X. Z. Zhang is also supported by PhD research startup foundation of Tianjin Normal University under Grant No. 52XB1415.
Author information
Authors and Affiliations
Contributions
X.Z.Z. did the derivations and revised the manuscript. Z.S. designed and supervised the project. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, X., Song, Z. EPR pairing dynamics in Hubbard model with resonant U. Sci Rep 6, 18323 (2016). https://doi.org/10.1038/srep18323
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep18323
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


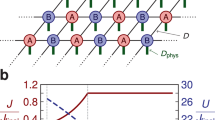

 , swap; (b)
, swap; (b)  , unchange; (c)
, unchange; (c)  , maximal entanglement.
, maximal entanglement.


