Introduction

State-of-art experimental platforms of cold atoms and trapped ions as analog quantum simulators have offered unique opportunities for studying far-from-equilibrium dynamics of isolated quantum many-body systems. Thanks to their high controllability and long coherence time, these platforms have already addressed a variety of intriguing phenomena that are in general difficult to simulate with classical computers, such as correlation spreading1,2,3 and relaxation4,5,6 after a quantum quench, many-body localization in a disorder potential7,8,9, and quantum scar states10,11. Nevertheless, accurate numerical methods using classical computers are highly demanded at the current stage of the studies of quantum many-body dynamics, since the classical computation still has complementary advantages over the quantum simulation in that it is free of noise and much more accessible owing to its wide dissemination. In this sense, it is important to cross-check the validity of quantum-simulation experiments and some numerical methods by comparing them with each other.

In particular, direct comparisons between experimental and numerical outputs have been made for dynamical spreading of two-point spatial correlations of the Bose-Hubbard model1,3,12,13,14,15, which can be realized experimentally with ultracold bosons in optical lattices16. The correlation spreading has attracted much theoretical interest12,13,14,15,17,18,19,20,21,22,23,24,25,26,27 in the sense that it is closely related to fundamental phenomena, including the propagation of quantum information and the thermalization. In one spatial dimension, quasi-exact numerical methods based on matrix product states (MPSs) have been used to validate the performance of the quantum simulators1,3,12. In two dimensions (2D), by contrast, accurate numerical simulations are challenging. Indeed, the comparisons with respect to a single-particle correlation have shown that a few types of the truncated Wigner approximation (TWA) fail to capture the real-time evolution accurately enough to extract the propagation velocity of the correlation3,14. Moreover, while the propagation velocities obtained by a two-particle irreducible strong-coupling (2PISC) approach quantitatively agree with the experimental value, and the approach is applicable to much weaker interaction than in the experiment, it does not necessarily provide the exact value of the correlation itself15.

In this paper, we present quantitative numerical analyses of the correlation-spreading dynamics of the 2D Bose-Hubbard model starting from a Mott insulating initial state with unit filling. To this end, we employ the tensor-network method based on the infinite projected entangled pair state (iPEPS)28,29,30,31,32,33,34,35 or the tensor product state36,37,38,39,40, which is an extension of MPS to 2D systems (see Fig. 1a). The iPEPS studies on real-time dynamics of isolated41,42,43,44,45,46,47,48,49 and open41,42,50,51,52 quantum systems in 2D have begun very recently. Previous simulations suggest that iPEPS can represent relatively low-entangled states in short-time dynamics for simple spin 1/2 systems41,42,43,44 and some itinerant electron systems46. This observation may be valid for real-time dynamics in Bose-Hubbard systems; however, little is known about it until now. We find that the single-particle correlation computed with iPEPS, as well as the estimated propagation velocity of the correlation front, agrees very well with the experimental result3, demonstrating that iPEPS can be useful for actual quantum-simulation experiments. We also conduct numerical simulations in a moderate interaction region, which has not been addressed by the previous experiments1,3. From the real-time evolution of the single-particle and density–density correlations, we show that the phase and group velocities approach each other when the interaction decreases.

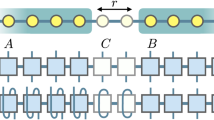
Fig. 1: Setup for numerical simulations of quench dynamics.
figure 1

a Schematic figure of infinite projected entangled pair state (iPEPS) with a two-site unit cell. Sublattice sites are represented by A and B. A rank-five tensor at each site is represented as a circle with four thin lines and one thick line. The former lines correspond to the virtual degrees of freedom with the bond dimension D, while the latter line corresponds to the physical degrees of freedom with the dimension of the local Hilbert space Dphys. The wave functions become more accurate as D increases. b Time dependence of the hopping J (a red solid line) and the onsite interaction U (a blue dashed line) with a finite-time quench. The parameter U/J is varied from ~99.4 to ~19.6 for −τQ < t < 0 with τQ being a finite quench time. In the case of a sudden quench, we discard the region −τQ < t < 0.

Full size image

Results

Model

We consider the Bose-Hubbard model on a square lattice53,54. The Hamiltonian is given as

$$\hat{H}\,=\,-J\mathop{\sum}\limits_{\langle ij\rangle }({\hat{a}}_{i}^{{{{\dagger}}} }{\hat{a}}_{j}\,+\,{\hat{a}}_{j}^{{{{\dagger}}} }{\hat{a}}_{i})\,+\,\frac{U}{2}\mathop{\sum}\limits_{i}{\hat{n}}_{i}({\hat{n}}_{i}\,-\,1)\,-\,\mu \mathop{\sum}\limits_{i}{\hat{n}}_{i},$$
(1)

where \({\hat{a}}_{i}^{{{{\dagger}}} }\) and \({\hat{a}}_{i}\) are the creation and annihilation operators at site i, \({\hat{n}}_{i}\,=\,{\hat{a}}_{i}^{{{{\dagger}}} }{\hat{a}}_{i}\) is the number operator, J is the strength of the hopping between nearest-neighbor sites, U is the strength of the onsite interaction, and μ is the chemical potential. The notation 〈ij〉 indicates that sites i and j are nearest neighbors. For simplicity, we ignore the effects of the trap potential and the Gaussian envelopes of optical lattice lasers, which do not affect short-time dynamics. We set the lattice spacing dlat to be unity. The ground state at the commensurate filling is the Mott insulating (superfluid) state for U ≫ J (U ≪ J). Hereafter, we will consider a sudden quench and a quench with a short time (see Fig. 1b and Supplementary Note 1 for details).

Quench starting from the Mott insulator: comparison with the exact diagonalization and the experiment

Let us first focus on the case of a sudden quench. We compare our results of iPEPS with those of the exact diagonalization (ED) method and obtain consistent results in a short time. In the ED simulations using the QuSpin library55,56, we choose the system sizes Lx × Ly up to 5 × 4 and use the periodic-periodic boundary condition. We examine to what extent the energy is conserved in the iPEPS simulations. The grand potential density \(\langle \hat{H}\rangle\) at T = 0 starting from the Mott insulator \({\otimes }_{i}\left|{n}_{i}\,=\,1\right\rangle\) should remain constant. They well converge for the bond dimensions D ≥ 6 and remain nearly constant up to t ~ 0.4ℏ/J (see Supplementary Note 2 for the time dependence of the grand potential density). We also investigate how the single-particle correlations converge with increasing bond dimensions. The equal-time single-particle correlation function at a distance r = (x, y) for the system size Ns is defined as

$${C}_{{{{{{{{\boldsymbol{r}}}}}}}}}^{{{{{{{{\rm{sp}}}}}}}}}(t)\,=\,\frac{1}{2{N}_{{{{{{{{\rm{s}}}}}}}}}}{\mathop{\sum }\limits_{i,j}}^{\prime}\langle {\hat{a}}_{i}^{{{{\dagger}}} }(t){\hat{a}}_{j}(t)\,+\,{\hat{a}}_{j}^{{{{\dagger}}} }(t){\hat{a}}_{i}(t)\rangle.$$
(2)

Here \(\mathop{\sum }\nolimits_{i,j}^{\prime}\) denotes the summation over (i, j) that satisfies ∣xj − xi∣ = x and ∣yj − yi∣ = y. In the iPEPS simulations, \(1/{N}_{{{{{{{{\rm{s}}}}}}}}}\,\times\, \mathop{\sum }\nolimits_{i,j}^{\prime}\) is replaced by \(1/2\,\times\, {\sum }_{i \,=\, A,B}\mathop{\sum }\nolimits_{j}^{\prime}\) with A and B being sublattice sites because of the translational invariance. As shown in Fig. 2, \({C}_{| {{{{{{{\boldsymbol{r}}}}}}}}| \,=\, 1}^{{{{{{{{\rm{sp}}}}}}}}}(t)\,:=\, [{C}_{{{{{{{{\boldsymbol{r}}}}}}}} \,=\, (1,0)}^{{{{{{{{\rm{sp}}}}}}}}}(t)\,+\,{C}_{{{{{{{{\boldsymbol{r}}}}}}}} \,=\, (0,1)}^{{{{{{{{\rm{sp}}}}}}}}}(t)]/2\) exhibits a peak at t ~ 0.15ℏ/J in both results, and they overlap in this short time. For t ≳ 0.15ℏ/J, the correlation functions of ED start to exhibit a significant finite-size effect, whereas those of iPEPS converge for D ≥ 6. We observe similar behavior for \({C}_{| {{{{{{{\boldsymbol{r}}}}}}}}| \,=\, \sqrt{2}}^{{{{{{{{\rm{sp}}}}}}}}}(t)\,:=\, {C}_{{{{{{{{\boldsymbol{r}}}}}}}} \,=\, (1,1)}^{{{{{{{{\rm{sp}}}}}}}}}(t)\). The iPEPS results are better simulated up to a longer time (see also Supplementary Note 3 for other interaction parameter regions).

Fig. 2: Single-particle correlation functions \({C}_{{{{{{{{\boldsymbol{r}}}}}}}}}^{{{{{{{{\rm{sp}}}}}}}}}(t)\) in the case of a sudden quench.
figure 2

Comparison is made between the infinite projected entangled pair state algorithm (iPEPS, blue lines with symbols) and the exact diagonalization method (ED, gray lines). The unit of time is taken as the inverse of the strength of the hopping J. U is the strength of the interaction. D is the bond dimension. Ns is the system size. The correlations at distances (a) ∣r∣ = 1 and (b) \(| {{{{{{{\boldsymbol{r}}}}}}}}| \,=\,\sqrt{2}\) are shown. Both results overlap in a short time.

Full size image

Next, we compare the correlations of iPEPS with those of the experiment3 for a finite quench time. In the experiment, a quench to the Mott insulating region has been investigated so far. Figure 3a–c show the time evolution of correlations at distances ∣r∣ = 1, 2, and 3, respectively. Qualitative behavior is essentially equivalent to the case of the sudden quench, although the correlation function shifts to an earlier time. For ∣r∣ = 1, both data show a peak at t ~ 0.12ℏ/Jfinal. Similarly, the first-peak times are consistent with each other for ∣r∣ = 2 and 3, and they become longer with increasing distances. When the energy is approximately conserved (namely, for t ≲ 0.4ℏ/Jfinal, see the time dependence of the grand potential density in Supplementary Note 4), the intensities of correlations also overlap very well. They are also consistent with those obtained by TWA3,13,14, while the iPEPS simulations can deal with a slightly longer time and capture the correlation peaks more clearly (see also Supplementary Note 5 for a detailed comparison with the TWA results). To see how well they match more quantitatively, we also compare the first-peak position of iPEPS with that of the experiment3 as shown in Fig. 3d. Both iPEPS and experimental results agree very well.

Fig. 3: Single-particle correlation functions \({C}_{{{{{{{{\boldsymbol{r}}}}}}}}}^{{{{{{{{\rm{sp}}}}}}}}}(t)\) in the case of a finite-time quench.
figure 3

Comparison is made between the infinite projected entangled pair state algorithm (iPEPS, blue lines with symbols) and the experiment (red circles with error bars). The unit of time is taken as the inverse of the strength of the hopping Jfinal after the quench. U is the strength of the interaction. D is the bond dimension. The correlations at distances (a) ∣r∣ = 1, (b) ∣r∣ = 2, and (c) ∣r∣ = 3 are shown. The error bars represent the standard error of five independent measurements3. d Comparison of the first-peak time between the iPEPS and experimental results. The error bars represent the fitting errors3. The iPEPS and experimental results agree within the experimental errors in all cases.

Full size image

Estimates of group and phase velocities in the moderate interaction region

Having confirmed the applicability of iPEPS simulations to real-time evolution of the Bose-Hubbard model, we study how information propagates by a sudden quench in the moderate interaction region. There are two kinds of velocity that are relevant to the correlation spreading. One is the group velocity vgr, which corresponds to the propagation of the envelope of the wave packet and is a suitable quantity to characterize the spreading of correlations. In non-relativistic quantum many-body systems, vgr is bounded above, and the upper bound is known as the Lieb-Robinson bound23,24,25,26,27,57,58. Notice that the Lieb-Robinson bound for the Bose-Hubbard model has not been rigorously derived with a few exceptions for limited situations18,23,24,25,26,27. The phase velocity vph is the other characteristic quantity, which corresponds to the propagation of the first peak of the wave packet, and does not have to obey the Lieb-Robinson bound.

Although the exact Lieb-Robinson bound is not known for the Bose-Hubbard model, there are some values that can be used as a guide. As discussed in previous studies1,3,12 in the weak interaction region, the single-particle dispersion up to constant is approximately given as \({\epsilon }_{U\,\ll\, J}({{{{{{{\boldsymbol{k}}}}}}}}) \,\sim\, -2J{\sum }_{\alpha }\cos {k}_{\alpha }\) (α = x, y in 2D), which is equivalent to the dispersion of free particles. The velocity of the correlation spreading would be well characterized by the group velocity of the single-particle excitation. The largest velocity of a single quasiparticle (along the horizontal or vertical direction α) is described by the maximal slope of the dispersion and is given by \(v\,=\,\mathop{\max}\nolimits_{{k}_{\alpha }}[d| {\epsilon }_{U\,\ll\, J}({{{{{{{\boldsymbol{k}}}}}}}})| /d{k}_{\alpha }]/\hslash \,=\,2J/\hslash\). Because both doublon and holon quasiparticles propagate with the group velocity v, the front of the correlation function moves at the speed of vfront, which should be smaller than \({v}_{\max }\,=\,2v\,=\,4J/\hslash\). Therefore, this speed \({v}_{\max }\) can be regarded as the Lieb-Robinson-bound-like value. Likewise, in the strong interaction region, the doublon and holon dispersions up to constant are approximately given as \({\epsilon }_{U\,\gg\, J}^{(d)}({{{{{{{\boldsymbol{k}}}}}}}}) \,\sim\, -4J\,{\sum }_{\alpha }\cos {k}_{\alpha }\) and \({\epsilon }_{U\,\gg\, J}^{(h)}(-{{{{{{{\boldsymbol{k}}}}}}}}) \sim -2J\,{\sum }_{\alpha }\cos {k}_{\alpha }\), respectively. Because the doublons and holons propagate with respective velocities 4J/ℏ and 2J/ℏ, vfront should be smaller than these two sum \({v}_{\max }\,=\,6J/\hslash\). Although we know the approximate limit values, the intermediate interaction region is yet to be explored.

To estimate the group velocity from the single-particle correlations, long-time simulations are required in general. However, it is challenging in the iPEPS simulations. To circumvent the difficulty, we estimate the group velocity by the density–density correlation. It is known that the propagation velocity of the first peak of this correlation agrees very well with the group velocity1,12. The equal-time density–density correlation function at a distance r = (x, y) for the system size Ns is defined as

$${C}_{{{{{{{{\boldsymbol{r}}}}}}}}}^{{{{{{{{\rm{dd}}}}}}}}}(t)\,=\,\frac{1}{{N}_{{{{{{{{\rm{s}}}}}}}}}}{\mathop{\sum }\limits_{i,j}}^{\prime}{\langle {\hat{n}}_{i}(t){\hat{n}}_{j}(t)\rangle }_{{{\rm{c}}}},$$
(3)

where 〈⋯〉c denotes a connected correlation function. In our simulations, \({\langle {\hat{n}}_{i}(t){\hat{n}}_{j}(t)\rangle }_{{{\rm{c}}}}\,=\,\langle {\hat{n}}_{i}(t){\hat{n}}_{j}(t)\rangle \,-\,1\) because \(\langle {\hat{n}}_{i}(t)\rangle \,=\,1\) for all sites and time steps. As in \({C}_{{{{{{{{\boldsymbol{r}}}}}}}}}^{{{{{{{{\rm{sp}}}}}}}}}(t)\), the summation is replaced by that within sublattice sites in the iPEPS simulations. The parity-parity correlation closely related to the density–density one can be measured in experiments by using the quantum-gas microscope techniques1.

We extract the propagation velocities from the first peak in both correlations for ∣r∣ = 1, 2, and 3. For simplicity, we consider the sudden quench hereafter. When the interaction becomes weaker, we have confirmed that the energy is conserved in a longer time frame; typically, t ≲ 0.9ℏ/J for U/J ~ 5 (see Supplementary Note 6 for the time dependence of the grand potential density in the weaker interaction region). All the correlation peaks for ∣r∣≤3 appear in this time frame (see Fig. 4). The first peak of the single-particle correlation appears at t ~ 0.35ℏ/J for ∣r∣ = 1, while it appears at t ~ 0.65ℏ/J for ∣r∣ = 3. By contrast, the first peak of the density–density correlation appears at t ~ 0.25ℏ/J for ∣r∣ = 1, while it appears at t ~ 0.7ℏ/J for ∣r∣ = 3. It takes a long time for propagation in the latter case. (See also the correlations for other interaction parameters given in Supplementary Note 7. Extraction of propagation velocities in the intermediate and strong interaction regions is summarized in Supplementary Notes 8, 9, respectively.) The first-peak time is almost a linear function of the distance, and the system exhibits the light-cone-like spreading of correlations (see the time dependence of distance summarized in Supplementary Note 8).

Fig. 4: Single particle and density–density correlation functions used to extract the propagation velocities.
figure 4

a Single-particle [\({C}_{{{{{{{{\boldsymbol{r}}}}}}}}}^{{{{{{{{\rm{sp}}}}}}}}}(t)\)] and (b) density–density [\({C}_{{{{{{{{\boldsymbol{r}}}}}}}}}^{{{{{{{{\rm{dd}}}}}}}}}(t)\)] correlation functions per bond at the interaction strength U/J = 5 for the bond dimension D = 8. The unit of time is taken as the inverse of the strength of the hopping J. The normalization factor at a distance r = (x, y) is given as Nbond = 2 for x ≠ y (∣r∣ = 1, 2, and 3), while it is Nbond = 4 for x = y (\(| {{{{{{{\boldsymbol{r}}}}}}}}| \,=\,\sqrt{2}\)). The black symbol corresponds to the first peak in the correlation function obtained by cubic spline interpolation of data points. The propagation velocities along the horizontal or vertical axis are extracted by the data at ∣r∣ = 1, 2, and 3. The velocity estimated from the density–density correlation functions is slower than that from the single-particle correlation functions.

Full size image

We summarize the interaction dependence of the group and phase velocities in Fig. 5. In the weak interaction region, the estimated group velocities are vgr ~ 4J/ℏ. They are similar to those obtained by the TWA at filling factor ν = 1013. They are also consistent with the group velocity vgr(U = 0) = 4J/ℏ of a single particle13. In the strong interaction region, the estimated group velocity vgr ~ (8 ± 2)J/ℏ at U/J = 19.6 coincides with that obtained by the 2PISC approach15 within the error bar of extrapolation. It is also comparable to the group velocity \({v}_{{{{{{{{\rm{gr}}}}}}}}}(U\gg J)\,=\,6J/\hslash \,\times\, [1\,+\,{{{{{{{\mathcal{O}}}}}}}}({J}^{2}/{U}^{2})]\) of a quasiparticle in the large U limit1,3,12. Similarly, the estimated phase velocity agrees very well with the results of the 2PISC approach15 and the experiment3. In the intermediate region, the estimated group velocity is closer to the single-particle group velocity in the superfluid region, whereas it is comparable to the 2PISC result near and above the critical point Uc/J ~ 16.759,60,61.

Fig. 5: Propagation velocities as functions of the ratio between the interaction (U) and hopping (J) strengths.
figure 5

The group (vgr, red circles) and phase (vph, blue squares) velocities are estimated from the density–density and single-particle correlation functions for the bond dimensions D = 8 and D = 9 using the infinite projected entangled pair state (iPEPS) algorithm. The data for D = 8 and D = 9 overlap within the error bars. The velocities and their error bars are obtained by extrapolation of the distance dependence of the peak time. The results obtained by the two-particle irreducible strong-coupling (2PISC) approach15 (triangles), the truncated Wigner approximation (TWA)13 (diamonds), and the experiment3 (a star) are shown. Both velocities gradually merge with decreasing interaction.

Full size image

In all parameter regions, no anomalies appear in the propagation velocities. As for the real-time dynamics after a sudden quench, there is no sign of the superfluid-Mott insulator quantum phase transition. This is because non-universal high-energy excitations come into play during the time evolution. The quantum phase transition at zero temperature does not have to affect the time-evolved states.

Both group and phase velocities gradually converge to the same value as U/J is decreased. This phenomenon can be understood in terms of the separation of the energy scales. When the interaction U is much stronger than the hopping J, the correlation function oscillates rapidly as a function of time12,22. The correlation function exhibits the envelope of the wave packet. The time scale of the period of oscillation is ~1/U, which determines the phase velocity vph ~ U. On the other hand, the time scale of the period of the envelope is ~1/J, which determines the group velocity vgr ~ J. Hence, the group and phase velocities differ as long as U ≫ J. When the interaction U becomes comparable to the hopping J, they start to coincide by slowing down the vibration. Note that this phenomenon occurs irrespective of the presence or absence of phase transitions.

Conclusions

We have studied real-time dynamics of the 2D Bose-Hubbard model after a sudden quench starting from the Mott insulator with unit filling. We have employed the 2D tensor-network method based on the iPEPSs, which are the 2D extension of the well-known MPSs in one dimension. Calculated single-particle correlation functions reproduce the recent experimental results very well. The iPEPS algorithm can simulate real-time dynamics long enough for extracting the propagation velocities from correlations. This fact suggests that, for the quench dynamics starting from the Mott insulator in the 2D Bose-Hubbard model, time-evolved states are not so highly entangled before and even slightly after the time at which the correlation front is reached. This finding raises questions about our understanding of how quantum states get entangled with real-time evolution.

We have also estimated the group and phase velocities in the moderate interaction region, in which the 2PISC approach and the TWA are not applicable. The estimated group velocities are continuously connected without singularity in the middle. Our findings would be useful in the future analog quantum simulation and in the future examination of the rigorous Lieb-Robinson bound of Bose-Hubbard systems. The ability of the tensor-network method that accurately calculates the real-time dynamics of 2D quantum many-body systems opens up the possibility of applying it to other quantum-simulation platforms, such as Rydberg atoms, trapped ions, and superconducting circuits.

Methods

Real-time evolution by infinite projected entangled pair states

We prepare iPEPS with a two-site unit cell (see Fig. 1a). The symbols D and Dphys denote the virtual bond dimension and the dimension of the local Hilbert space, respectively. The former improves the accuracy of the wave function, whereas the latter corresponds to the maximum particle number \({n}_{\max }\) as \({D}_{{{{{{{{\rm{phys}}}}}}}}}\,=\,{n}_{\max }\,+\,1\). Although \({n}_{\max }\) can take infinity in Bose-Hubbard systems, it is practically bounded above in the presence of interaction62,63. We can choose finite Dphys in the simulations of real-time dynamics. In the case of a sudden quench to the Mott insulating region (U/J > Uc/J ~ 16.759,60,61), we set the dimension of the local Hilbert space as Dphys = 3 because the number of particles deviates only slightly from unity62,63. For U/J < Uc/J, we choose Dphys = 5 so that the wave functions can further take into account the effect of particle fluctuations. When U is close to zero (at U/J = 2 in our simulations), we use slightly larger Dphys = 7 (see Supplementary Note 10 for the details of the choice of the dimensions of the local Hilbert space). The initial Mott insulating state \({\otimes }_{i}\left|{n}_{i}\,=\,1\right\rangle\) can be represented with the bond dimension D = 1. As for static properties, the Bose-Hubbard model was investigated by finite PEPS or iPEPS, and the phase transition between the Mott insulating and superfluid phases was reproduced64,65,66,67,68,69,70,71,72.

The wave function at each time \(\left|{{\Psi }}(t)\right\rangle \,=\,{e}^{-it\hat{H}/\hslash }\left|{{\Psi }}(0)\right\rangle\) is obtained by real-time evolving iPEPS41,42,43. The real-time evolution operator in a small time step dt can be approximated by the Suzuki-Trotter decomposition73,74,75 as \({e}^{-idt\hat{H}/\hslash } \,\sim\, {\prod }_{\langle ij\rangle }{e}^{-idt{\hat{H}}_{ij}/\hslash }\), where \({\hat{H}}_{ij}\,=\,-J({\hat{a}}_{i}^{{{{\dagger}}} }{\hat{a}}_{j}\,+\,{\hat{a}}_{j}^{{{{\dagger}}} }{\hat{a}}_{i})\,+\,U[{\hat{n}}_{i}({\hat{n}}_{i}\,-\,1)\,+\,{\hat{n}}_{j}({\hat{n}}_{j}\,-\,1)]/(2z)\,-\,\mu ({\hat{n}}_{i}\,+\,{\hat{n}}_{j})/z\) with the coordination number z = 4 is the local Hamiltonian satisfying \(\hat{H}\,=\,{\sum }_{\langle ij\rangle }{\hat{H}}_{ij}\). After applying the two-site gate \({e}^{-idt{\hat{H}}_{ij}/\hslash }\) to neighboring tensors, we approximate the local tensors by the singular value decomposition in such a way that the virtual bond dimension of iPEPS remains D. In the actual simulations, the second-order Suzuki-Trotter decomposition is used for this simple update algorithm32,76, and the tensor-network library TeNeS77,78,79 is adopted. The wave functions are optimized up to the bond dimension D = 9. Qualitative behavior of correlation functions is found to be nearly the same for D ≥ 6. When extracting the propagation velocities, we mainly use the data for D = 8 and D = 9 to ensure sufficient convergence of physical quantities. We do not preserve the U(1) symmetry during the calculation. Even without respecting the symmetry, we have numerically found that at these values of D, the number of particles is nearly conserved during the real-time evolution starting from the Mott insulator.

Physical quantities in the thermodynamic limit are calculated by the corner transfer matrix renormalization group method33,34,35,37,80,81,82,83,84,85,86. The bond dimension of the environment tensors is chosen as χ = 2D2 to ensure that physical quantities are well converged.

To compare our results obtained by iPEPS with the experiment3, we consider a quench with a short time τQ = 0.1 ms13,14 (see Fig. 1b). For −τQ < t < 0, both J and U are controlled. The wave function is updated as \(\left|{{\Psi }}(t\,+\,dt)\right\rangle \,\sim\, {e}^{-idt\hat{H}(t)/\hslash }\left|{{\Psi }}(t)\right\rangle\) with the time-dependent Hamiltonian \(\hat{H}(t)\) in this region. For t > 0, both parameters are fixed. We take Jfinal = J(t = 0) ~ 0.0612ℏ/τQ as the unit of energy. The discrete time step for the real-time evolution is set to be dt/(ℏ/Jfinal) = τQ/(ℏ/Jfinal)/15 ~ 0.00408 for all t. To compare the iPEPS results with the exact real-time dynamics in finite-size systems, we also consider a sudden parameter change and set the time step as dt/(ℏ/J) = 0.005. We have checked that the simulations with doubled and halved dt do not change the results significantly.