Universal scaling between wave speed and size enables nanoscale high-performance reservoir computing based on propagating spin-waves

Abstract

Physical implementation of neuromorphic computing using spintronics technology has attracted recent attention for the future energy-efficient AI at nanoscales. Reservoir computing (RC) is promising for realizing the neuromorphic computing device. By memorizing past input information and its nonlinear transformation, RC can handle sequential data and perform time-series forecasting and speech recognition. However, the current performance of spintronics RC is poor due to the lack of understanding of its mechanism. Here we demonstrate that nanoscale physical RC using propagating spin waves can achieve high computational power comparable with other state-of-art systems. We develop the theory with response functions to understand the mechanism of high performance. The theory clarifies that wave-based RC generates Volterra series of the input through delayed and nonlinear responses. The delay originates from wave propagation. We find that the scaling of system sizes with the propagation speed of spin waves plays a crucial role in achieving high performance.

Introduction

Non-local magnetization dynamics in a nanomagnet, spin-waves, can be used for processing information in an energy-efficient manner since spin-waves carry information in a magnetic material without Ohmic losses¹. The wavelength of the spin-wave can be down to the nanometer scale, and the spin-wave frequency becomes several GHz to THz frequency, which are promising properties for nanoscale and high-speed operation devices. Recently, neuromorphic computing using spintronics technology has attracted great attention for the development of future low-power consumption AI². Spin-waves can be created by various means such as magnetic field, spin-transfer torque, spin-orbit torque, voltage induced change in magnetic anisotropy and can be detected by the magnetoresistance effect³. Therefore, neuromorphic computing using spin waves may have a potential of realizable devices.

Reservoir computing (RC) is a promising neuromorphic computation framework. RC is a variant of recurrent neural networks (RNNs) and has a single layer, referred to as a reservoir, to transform an input signal into an output⁴. In contrast with the conventional RNNs, RC does not update the weights in the reservoir. Therefore, by replacing the reservoir of an artificial neural network with a physical system, for example, magnetization dynamics⁵, we may realize a neural network device to perform various tasks, such as time-series prediction^4,6, short-term memory^7,8, pattern recognition, and pattern generation. Several physical RC has been proposed: spintronic oscillators^5,9, optics¹⁰, photonics^11,12, memristor^13,14,15, field-programmable gate array¹⁶, fluids, soft robots, and others (see the following reviews for physical reservoir computing^17,18,19). Among these systems, spintronic RC has the advantage in its potential realization of nanoscale devices at high speed of GHz frequency with low power consumption, which may outperform conventional electric computers in future. So far, spintronic RC has been considered using spin-torque oscillators^5,9, magnetic skyrmion²⁰, and spin waves in garnet thin films^21,22,23,24.

One of the goals of neuromorphic computing is to realize integrated RC chip devices. To make a step forward in this direction, performance of a single RC unit must be studied and significantly more computational power per unit area might be required. For example, even for the prediction task of one-dimensional spatio-temporal chaos requires 10⁴−10⁵ nodes^6,10. Spatio-temporal chaos is an irregular dynamical phenomenon expressed by a deterministic equation. Its time series data is complex but still much simpler than the climate forecast. To increase the number of degrees of freedom N with keeping the total system size, the single RC unit (N~100 in this study) should be nanoscale²⁵ ideally ~100 nm or less. Also, high-speed operation at GHz frequency compatible with semiconductor devices might be desired.

Spintronics has been a promising technology for the development of nanoscale and high-speed operation nonvolatile memory devices. However, the current performance of spintronic RC demonstrated experimentally still remains poor compared with the Echo State Network (ESN)^7,8, idealized RC model implemented in conventional computers with random network and nodes updated by the tanh activation function. The biggest issue is a lack of our understanding of how to achieve high performance in the physical RC systems. It has been well studied that for the ESN, the memory capacity (MC) is bounded by N⁷. MC quantifies how many past steps RC can memorize. For the ESN with linear activation function, MC becomes N as long as each node is independent from other nodes. It has also been shown that the information processing capacity (IPC) of RC is bounded by N²⁶. Here, IPC captures the performance of RC in terms of the memory of past information and nonlinear transformation (see also Methods: Learning tasks). Besides MC and IPC, the computational capabilities of RC have been measured by the task of approximating the input-output relation of dynamical system models, such as the nonlinear autoregressive moving average (NARMA) model²⁷. The NARMA model describes noisy but correlated output time series from uniformly random input. Since the performance of MC and IPC is correlated with that of the NARMA task²⁸ (see also Methods: Relation of MC and IPC with learning performance and Supplementary Information Section I and II), it is natural to expect that the higher performance of RC is achieved under larger N.

To make N larger, the reservoir has to have a larger degree of freedom, either by connecting discrete independent units or by using continuum media. Using many units may be impractical because we need to make those units and connect them. The latter approach using continuum media is promising because spatial inhomogeneity may increase the number of degrees of freedom of the physical system. In this respect, wave-based computation in continuum media has attracting features. The dynamics in the continuum media have large, possibly infinite, degrees of freedom. In fact, several wave-based computations have been proposed^29,30.

The question is how to use the advantages of both wave-based computation and RC to achieve high-performance computing of time-series data. Even though the continuum media may have a large degree of freedom, in practice, we cannot measure all the information. Therefore, the actual N determining the performance of RC is set by the number of measurements of the physical system. There are two ways to increase N; by increasing the number of physical nodes, N_p, to measure the system (or the number of discrete units)³¹, and by increasing the number of virtual nodes, N_v^32,33. Increasing N_p is a natural direction to obtain more information from the continuum physical system. For spin wave-based RC, so far, higher performance has been achieved by using a large number of input and/or output nodes^23,24,34. However, in practice, it is difficult to increase the number of physical nodes, N_p, because it requires more wiring of multiple nodes. To make computational devices, fewer nodes are preferable in terms of cost and effort to make the devices. With these motivations in our mind, in this study, we propose spin-wave RC, in which we extract the information from the continuum media using a small number of physical nodes.

Along this direction, using N_v virtual nodes for the dynamics with delay was proposed to increase N in³². The idea of the virtual nodes is to use the time-multiplexing approach. By repeating the input N_v times at a certain time, we may treat reservoir states during the N_v steps as states in different virtual nodes. This idea was applied in optical fibers with a long delay line¹¹ and a network of oscillators with delay³³. Ideally, the virtual nodes enhance the number of degrees by N = N_pN_v. However, the increase of N = N_pN_v with N_v does not necessarily improve performance. In fact, RC based on STO (spin torque oscillator) struggle with insufficient performance both in experiments⁹ and simulations³⁵. On the other hand, for the photonic RC, the virtual nodes work effectively; even though it typically uses only one physical node (N_p = 1), the performance is high, for example, MC≈N_vN_p. Still, the photonic RC requires a large size of devices due to the long delay line^11,12. To use the virtual nodes as effectively as the physical nodes, we need to clarify the mechanism of high performance using the virtual nodes. Nevertheless, the mechanism of high performance remains elusive, and no unified understanding has been made.

In this work, we show nanoscale and high-speed RC based on spin wave propagation with a small number of inputs can achieve performance comparable with the ESN and other state-of-art RC systems. More importantly, by using a theoretical model, we clarify the mechanism of the high performance of spin wave RC. We show the scaling between wave speed and system size to make virtual nodes effective.

Results

Reservoir computing using wave propagation

The basic task of RC is to transform an input signal U_n to an output Y_n for the discrete step n = 1, 2,…, T at the time t_n. For example, for speech recognition, the input is an acoustic wave, and the output is a word corresponding to the sound. Each word is determined not only by the instantaneous input but also by the past history. Therefore, the output is, in general, a function of all the past input, ${Y}_{n}=g\left({\{{U}_{m}\}}_{m = 1}^{n}\right)$ as in Fig. 1a. The RC can also be used for time-series prediction by setting the output as Y_n = U_n+1⁴. In this case, the state at the next time step is predicted from all the past data; namely, the effect of delay is included. The performance of the input-output transformation g can be characterized by how much past information does g have, and how much nonlinear transformation does g perform. We will discuss that the former is expressed by MC³⁶, whereas the latter is measured by IPC²⁶ (see also Methods: Relation of MC and IPC with learning performance).

Fig. 1: Illustration of physical reservoir computing and reservoir based on propagating spin-wave network.

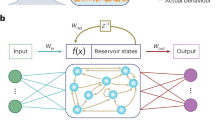
a Schematic illustration of output function prediction by using time-series data. Output signal Y is transformed by past information of input signal U. b Schematic illustration of reservoir computing with multiple physical nodes. The output signal at physical node A contains past input signals in other physical nodes, which are memorized by the reservoir. c Schematic illustration of reservoir computing based on propagating spin-wave. Propagating spin-wave in ferromagnetic thin film (m∥e_z) is excited by spin injector (input) through spin-transfer torque at multiple physical nodes with reference magnetic layer (m∥e_x) of magnetic tunnel junction. x-component of magnetization is detected by spin detector (output) through magnetoresistance effect using magnetic tunnel junction shown by a cylinder above the thin film at each physical node.

We propose physical computing based on a propagating wave (see Fig. 1b, c). Time series of an input signal U_n can be transformed into an output signal Y_n (Fig. 1a). As we will discuss in the next paragraph, this transformation requires large linear and nonlinear memories; for example, to predict Y_n, we need to memorize the information of U_n−2 and U_n−1 (see also Methods: Relation of MC and IPC with learning performance and Supplementary Information Section I). The input signal is injected in the first input node and propagates in the device to the output node spending a time τ₁ as in Fig. 1b. Then, the output may have past information at t_n−τ₁ corresponding to the step n−m₁. The output may receive the information from another input at different time t_n−τ₂. The sum of the two pieces of information is mixed and transformed as ${U}_{n-{m}_{1}}{U}_{n-{m}_{2}}$ either by nonlinear readout or by nonlinear dynamics of the reservoir (see next section: Learning with reservoir computing and Methods). We will demonstrate the wave propagation can indeed enhance MC and learning performance of the input-output relationship.

Before explaining our learning strategy described in next section Spin wave reservoir computing, we discuss how to achieve accurate learning of the input-output relationship ${Y}_{n}=g\left({\{{U}_{m}\}}_{m = 1}^{n}\right)$ from the data. Here, the output may be dependent on a whole sequence of the input ${\{{U}_{m}\}}_{m = 1}^{n}=\left({U}_{1},\ldots ,{U}_{n}\right)$. Even when both U_n and Y_n are one-variable time-series data, the input-output relationship g(⋅) may be T-variable polynomials, where T is the length of the time series. Formally, g(⋅) can be expanded in a polynomial series (Volterra series) such that $g\left({\{{U}_{m}\}}_{m = 1}^{n}\right)={\sum }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}{\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}{U}_{1}^{{k}_{1}}{U}_{2}^{{k}_{2}}\cdots {U}_{n}^{{k}_{n}}$ with the coefficients ${\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}$²⁷. Therefore, even for the linear input-output relationship, we need T coefficients in g(⋅), and as the degree of powers in the polynomials increases, the number of the coefficients increases exponentially. This observation implies that a large number of data is required to estimate the input-output relationship. Nevertheless, we may expect a dimensional reduction of g(⋅) due to its possible dependence on the time close to the current step, t_n, and on the lower powers. Still, our physical computers should have degrees of freedom N ≫ 1, if not exponentially large.

The reservoir computing framework is used to handle time-series data of the input U and the output Y⁷. In this framework, the input-output relationship is learned through the reservoir dynamics X(t), which in our case, is magnetization at the detectors. The reservoir state at a time t_n is driven by the input at the nth step corresponding to t_n as

$$\begin{array}{rc}X({t}_{n+1})\,=\,f\left(X({t}_{n}),{U}_{n}\right)\end{array}$$

(1)

with nonlinear (or possibly linear) function f(⋅). The output is approximated by the readout operator ψ(⋅) as

$$\begin{array}{rc}{\hat{Y}}_{n}\,=\,\psi \left(X({t}_{n})\right).\end{array}$$

(2)

Our study uses the nonlinear readout $\psi \left(X(t)\right)={W}_{1}X(t)+{W}_{2}{X}^{2}(t)$^6,37. The weight matrices W₁ and W₂ are estimated from the data of the reservoir dynamics X(t) and the true output Y_n, where X(t) is obtained by Eq. (1). With the nonlinear readout, the RC with linear dynamics can achieve nonlinear transformation, as Fig. 1b. We stress that the system also works with linear readout when the RC has nonlinear dynamics³⁷. We discuss this case in Supplementary Information Section V A. In this study, we focus on the second-order polynomial for the readout function. This is because we focus on the second-order IPC to quantify the performance of nonlinear transformation with delay (see Methods: Learning tasks: Information Processing Capacity (IPC)). In Supplementary Information Section I, we clarify that second-order nonlinearity is necessary to achieve high performance for the NARMA10 task. The effect of the order of the polynomials in the readout function is discussed in Supplementary Information Section V B.

Spin wave reservoir computing

The actual demonstration of the spin-wave reservoir computing is shown in Fig. 2 and each step is described in Learning with reservoir computing below. First, we demonstrate the spin-wave RC using the micromagnetic simulations (see Methods: Micromagnetic simulations). Next, to get an insight into the mechanism of learning, we discuss the theoretical model using a response function (see Methods: Theoretical analysis using response function).

Fig. 2: Schematic illustration of spin-wave reservoir computing using micromagnetic simulation and prediction of NARMA10 task.

Input signals U are transformed into the piece-wise constant input U(t), multiplied by binary mask ${{{{\mathcal{B}}}}}_{i}(t)$, and transformed into injected current $j(t)=2{j}_{c}{\tilde{U}}_{i}(t)$ with ${\tilde{U}}_{i}={{{{\mathcal{B}}}}}_{i}(t)U(t)$ for the ith physical node. Current is injected into each physical node with the cylindrical region to apply spin-transfer torque and to excite spin-wave. Higher damping regions in the edges of the rectangle are set to avoid reflection of spin-waves. The x-component of magnetization m_x at each physical and virtual node are collected and the extended state $\tilde{\tilde{{{{\bf{X}}}}}}$ is constructed from m_x and ${m}_{x}^{2}$. Output weights are trained by linear regression. The labels (1) to (6) correspond to step 1 to step 6 in Section Learning with reservoir computing, respectively.

Learning with reservoir computing

In this section, we describe each step of our spin-wave RC corresponding to each sub-figure in Fig. 2. Performance of spin-wave reservoir computing is evaluated by NARMA10 task (Fig. 2 (1,5,6)), MC and IPC (Fig. S2 in Supplementary Information Section III), and prediction of chaotic time-series data using Lorenz model (Fig. 5). Details of learning tasks are described in Methods: Learning tasks.

• step 1: preparing input and output time-series data

  Our goal using RC is to learn the functional g(⋅) in ${Y}_{n}=g\left({\{{U}_{m}\}}_{m = 1}^{n}\right)$ for the input time series U_n and the output time series Y_n (see Fig. 1a). At the first step, we prepare the ground-truth time series data for the input U_n and output Y_n for the time step n = 1,…,T. We assume both input and output are discrete time steps in time. In this study, we focus on the continuous value of the input and output, and therefore, ${U}_{n},{Y}_{n}\in {\mathbb{R}}$. To show the performance of our method does not rely on the continuous input, we also demonstrate the performance for the binary and senary inputs in Supplementary Information Section IV. The concrete form of the preparing data will be specified in each task discussed in Methods: Learning tasks.

• step 2: preprocessing the input and translating it into a physical input

  Next, we preprocess the input time series data so that we may drive the physical magnetic system and may perform reservoir computing. The preprocess has two parts: input weights and translation into physical input. First, the input time series U_n is multiplied by the input weight for each physical node. This is necessary because each physical node receives different parts of the input information. In the ESN, the input weights are typically taken from uniform or binary random distribution³⁸. In this study, we use the method of time multiplexing with N_v virtual nodes³². In this case, the input weights are more involved. Details of preprocessing inputs are described in Methods: Details of preprocessing input data

• step 3: driving the physical system

  Our RC architecture consists of the update of reservoir state variables X(t) as

  $$\begin{array}{rc}X(t+\Delta t)\,=\,f\left(X(t),U(t)\right)\end{array}$$

  (3)

  and the readout

  $$\begin{array}{rc}{\hat{Y}}_{n}\,=\,{{{\bf{W}}}}\cdot \tilde{\tilde{{{{\bf{X}}}}}}({t}_{n}).\end{array}$$

  (4)

  We approximate the functional g(⋅) by the weight W and the (extended) reservoir states $\tilde{\tilde{{{{\bf{X}}}}}}$.

  In our system, the reservoir state is magnetization at ith nanocontact (physical node) and at time t_n,k (virtual node). The magnetic system is driven by the injected DC current proportional to the input time series U, described in Methods: Micromagnetic simulations, with a pre-processing filter. From the resulting spatially inhomogeneous magnetization m(x, t), we measure the averaged magnetization at ith nanocontact m_i(t).

• step 4: measurement, readout, and post-processing

  We choose the x-component of magnetization m_x,i as a reservoir state, namely, ${X}_{n}={\{{m}_{x,i}({t}_{n,k})\}}_{i\in [1,{N}_{p}],k\in [1,{N}_{v}]}$. For the output transformation, we use $\psi ({m}_{i,x})={W}_{1,i}{m}_{i,x}+{W}_{2,i}{m}_{i,x}^{2}$. Therefore, the dimension of our reservoir is 2N_pN_v. The nonlinear output transformation can enhance the nonlinear transformation in reservoir⁶, and it was shown that even under the linear reservoir dynamics, RC can learn any nonlinearity^37,39. In Supplementary Information Section V A, we also discuss the linear readout, but including the z-component of magnetization ${{{\bf{X}}}}=\left({m}_{x},{m}_{z}\right)$. In this case, m_z plays a similar role to ${m}_{x}^{2}$.

  In our spin wave RC, the reservoir state is chosen as x-component of the magnetization

  $$\begin{array}{rc}{{{\bf{X}}}}&={\left({m}_{x,1}({t}_{n}),\ldots ,{m}_{x,i}({t}_{n}),\ldots ,{m}_{x,{N}_{p}}({t}_{n})\right)}^{T},\end{array}$$

  (5)

  for the indices for the physical nodes i = 1,2,…,N_p. Here, N_p is the number of physical nodes, and each m_x,i(t_n) is a T-dimensional row vector with n = 1, 2,…,T. We use a time-multiplex network of virtual nodes in RC³², and use N_v virtual nodes with time interval θ. The expanded reservoir state is expressed by N_pN_v × T matrix $\tilde{{{{\bf{X}}}}}$ as (see Fig. 2–(4))

  $$\begin{array}{l}\tilde{{{{\bf{X}}}}}\,=\,\left({m}_{x,1}({t}_{n,1}),{m}_{x,1}({t}_{n,2}),\ldots ,{m}_{x,1}({t}_{n,k}),\ldots ,{m}_{x,1}({t}_{n,{N}_{v}}),\right.\\\qquad\;\ldots ,{m}_{x,i}({t}_{n,1}),{m}_{x,i}({t}_{n,2}),\ldots ,{m}_{x,i}({t}_{n,k}),\ldots ,{m}_{x,i}({t}_{n,{N}_{v}}),\ldots ,\\\qquad\;{\left.{m}_{x,{N}_{p}}({t}_{n,1}),{m}_{x,{N}_{p}}({t}_{n,2}),\ldots ,{m}_{x,{N}_{p}}({t}_{n,k}),\ldots ,{m}_{x,{N}_{p}}({t}_{n,{N}_{v}})\right)}^{T},\end{array}$$

  (6)

  where t_n,k = ((n−1)N_v + (k−1))θ for the indices of the virtual nodes k = 1, 2,…,N_v. The total number of rows is N = N_pN_v. We use the nonlinear readout by augmenting the reservoir state as

  $$\tilde{\tilde{{{{\bf{X}}}}}}=\left(\begin{array}{c}\tilde{{{{\bf{X}}}}}\\ \tilde{{{{\bf{X}}}}}\circ \tilde{{{{\bf{X}}}}}\end{array}\right),$$

  (7)

  where $\tilde{{{{\bf{X}}}}}(t)\circ \tilde{{{{\bf{X}}}}}(t)$ is the Hadamard product of $\tilde{{{{\bf{X}}}}}(t)$, that is, component-wise product. Therefore, the dimension of the readout weights is N = 2N_pN_v. As discussed in Eq. (2), we focus on the readout function of the form $\psi \left(X(t)\right)={W}_{1}X(t)+{W}_{2}{X}^{2}(t)$. When additional nonlinear terms are included in the readout, we may add the rows of $\tilde{{{{\bf{X}}}}}\circ \tilde{{{{\bf{X}}}}}\cdots \circ \tilde{{{{\bf{X}}}}}$ in Eq. (7).

• step 5: training and optimization of the readout weight

  The weights in the readout are trained by reservoir variable X and the output Y to approximate the ground-truth output Y by the estimated one $\hat{{{{\bf{Y}}}}}$ as Eq. (4). The readout weight W is trained by the data of the output Y(t)

  $$\begin{array}{rc}{{{\bf{W}}}}\,=\,{{{\bf{Y}}}}\cdot {\tilde{\tilde{{{{\bf{X}}}}}}}^{{\dagger} }\end{array}$$

  (8)

  where X^† is pseudo-inverse of X.

  Unless otherwise stated, We use 1000 steps of the input time-series as burn-in. After these steps, we use 5000 steps for training and 5000 steps for test for the MC, IPC, and NARMA10 tasks.

• step 6: testing the trained RC

  Once we train the output wight W, we perform a test to estimate the approximated output $\hat{{{{\bf{Y}}}}}$ as

  $$\begin{array}{rc}\hat{{{{\bf{Y}}}}}\,=\,{{{\bf{W}}}}\cdot \tilde{\tilde{{{{\bf{X}}}}}}.\end{array}$$

  (9)

  By comparing the estimated output $\hat{{{{\bf{Y}}}}}$ and the ground-truth output Y, we may quantify the performance of the RC.

Performance of the tasks for MC, IPC, NARMA10, and prediction of chatoic time-series

Figure 3 shows the results of the three tasks. When the time scale of the virtual node θ is small and the damping α is small, the performance of spin wave RC is high. As Fig. 3a shows, we achieve MC ≈ 60 and IPC ≈ 60. Accordingly, we achieve a small error in the NARMA10 task, NRMSE ≈ 0.2 (Fig. 3c). These performances are comparable with state-of-the-art ESN with the number of nodes~100. When the damping is stronger, both MC and IPC become smaller. Because the NARMA10 task requires the memory with the delay steps ≈ 10 and the second order nonlinearity with the delay steps ≈ 10 (see Supplementary Information Section I), the NRMSE becomes larger when MC ≲ 10 and IPC ≲ 10²/2.

Fig. 3: Virtual node distance θ dependence of MC and IPC for.

a micromagnetics simulation and b response function method with different damping parameters α. MC and IPC normalized by the total number of dimensions N = 2N_vN_p are shown in the right axis. c Normalized root mean square error, NRMSE for NARMA10 task is plotted as a function of θ with different α.

In fact, when θ and α are small, MC ≈ N_pN_v and IPC ≈ N_pN_v. The result suggests that our spin-wave RC can use half of the degrees of freedom, respectively, for linear and nonlinear memories. Note that our system has N = 2N_vN_p. Around θ = 0.1 ns and α = 5.0 × 10⁻⁴, IPC exceeds N_vN_p = 64 whereas MC becomes smaller than N_vN_p. This is consistent with the trade-off between MC and IPC²⁶. The reason why IPC exceeds N_vN_p is as follows; even when we use the linear readout using only m_x, IPC becomes small but nonzero as shown in Supplementary Information Section V A. Therefore, m_x can perform nonlinear transformation because m_x exhibits oscillation with a finite amplitude. However, the nonlinear effect is too weak to have IPC ≈ N_pN_v, and m_x mainly performs linear memory.

The results of the micromagnetic simulations are semi-quantitatively reproduced by the theoretical model using the response function, as shown in Fig. 3b. This result suggests that the linear response function $G(t,{t}^{{\prime} })$ captures the essential feature of delay $t-{t}^{{\prime} }$ due to wave propagation. Similar to the results of micromagnetic simulations, our spin-wave RC shows IPC ≈ N_pN_v when θ and α are small. MC is slightly underestimated but still shows MC/N > 0.25, i.e. MC/(N_vN_p) > 0.5. When MC and IPC are computed using the response function, each of them is strictly bounded by N_vN_p because the linear part m_x can learn the linear memory (MC) whereas the nonlinear part ${m}_{x}^{2}$ can learn the nonlinear memory (IPC). In fact, IPC in Fig. 3b is bounded by N_pN_v = 64 in contrast with RC using micromagnetic simulations.

Propagating spin waves play a crucial role in high performance. We perform micromagnetic simulations with damping layers between nodes (Fig. 4a). The damping layers inhibit spin wave propagation. The result of Fig. 4b shows that the MC is substantially lower than that without damping, particularly when θ is small. The NARMA10 task shows a larger error (Fig. 4d). When θ is small, the suppression is less effective. This may be due to incomplete suppression of wave propagation. We also analyze the theoretical model with the response function by neglecting the interaction between two physical nodes, namely, G_ij = 0 for i ≠ j. In this case, information transmission between two physical nodes is not allowed. We obtain smaller MC and IPC than the system with wave propagation, supporting our claim (see Fig. 4c).

Fig. 4: Effect of the network connection on the performance of reservoir computing.

a Schematic illustration of the network of physical nodes connected through propagating spin-wave [left] and physical nodes with no connection [right]. b, c MC and IPC obtained using a connected network with 8 physical nodes [top] and physical nodes with no connection [bottom] calculated by b micromagnetics simulation and c response function method plotted as a function of virtual node distance θ. N_v = 8 virtual nodes are used. d Normalized root mean square error, NRMSE for NARMA10 task obtained by micromagnetics simulation is plotted as a function of θ with a connected network [top] and physical nodes with no connection [bottom]. MC and IPC normalized by the total number of dimensions N = 2N_vN_p are shown in the right axis.

Our spin wave RC also works for the prediction of time-series data. In the study of ref. ⁶, the functional relationship between the state at t + Δt and the states before t is learned by the ESN The schematics of this task are shown in Fig. 5c. The trained ESN can estimate the state at t + Δt from the past states from the estimated time series, and therefore, during the prediction step, it can predict the dynamics without the ground-truth time series data (Fig. 5c). In ref. ⁶, the prediction for the chaotic time-series data was demonstrated. Figure 5 shows the prediction using our spin wave RC for the Lorenz model. We can demonstrate that the RC shows short-time prediction (Fig. 5a) and, more importantly, reconstruct the chaotic attractor (Fig. 5b). Because the initial deviation exponentially grows in a chaotic system, we cannot reproduce the same time series in the prediction step. Nevertheless, we may reproduce the shape of the trajectory in the phase space.

Fig. 5: Prediction of time-series data for the Lorenz system using reservoir computing with micromagnetic simulations.

The parameters are θ = 0.4 ns and α = 5.0 × 10⁻⁴. a The ground truth (A₁(t), A₂(t), A₃(t)) and the estimated time series $(\hat{{A}_{1}}(t),\hat{{A}_{1}}(t),\hat{{A}_{3}}(t))$ are shown in blue and red, respectively. The training steps are during t < 0, whereas the prediction steps are during t > 0. b The attractor in the A₁A₃ plane for the ground truth and during the prediction steps. c Schematics of the training and prediction steps for this task. During the training step, RC estimates the time series of the next time step ${\hat{A}}_{i}(t+\Delta t)$ (i = 1, 2, 3) from the input time series A_i(t) (i = 1, 2, 3) by optimizing the readout weights so that the estimated ${\hat{A}}_{i}(t+\Delta t)$ approximates the ground truth A_i(t + Δt). During the prediction step after the training step, using the optimized readout weights, the estimated ${\hat{A}}_{i}(t)$ is transformed into the time series at the next step ${\hat{A}}_{i}(t+\Delta t)$, which is further used for the estimation at future time steps t + 2Δt,t + 3Δt,…. The ground truth time series is no longer used during the prediction step except at the initial time step.

Scaling of system size and wave speed

To clarify the mechanism of the high performance of our spin wave RC, we investigate MC and IPC of the system with different characteristic length scales/and different wave propagating speed v. We choose the characteristic length scale of our spin-wave RC system as the diameter 2R of the circle on which inputs are located (see Fig. 2-(3)), namely, l = 2R. Hereafter, we denote the characteristic length by l for general systems but interchangeably by l and R for our system. We use our theoretical model with the response function discussed in Methods: Theoretical analysis using response function to compute MC and IPC in the parameter space (v, R). This calculation can be done because the computational cost of our model using response function is much cheaper than numerical micromagnetic simulations. In this analysis, we assume that spin waves are dominated by the dipole interaction. This implies that the speed of the spin wave is constant. The power spectral density shown in Supplementary Information Section VIII A indicates that the amplitude of the spin waves is dominated by small wavenumbers k < 1/l₀. Nevertheless, the exchange interaction comes into play at 0 ≪ k < 1/l₀. The effect of the exchange interaction is that the speed of wave propagation exhibits distribution due to the wavenumber-dependent waves, which are faster than the waves of the dipole-only system. Accordingly, the average speed becomes faster. Although this effect modifies the evaluation of the spin-wave propagation speed, it does not change the scaling discussed in this section. We discuss the effect in Supplementary Information Section VII A.

Figure 6a, b shows that both MC and IPC have maximum when R ∝ v. The response function for the magnetization dynamics Eqs. (16) and (17) have a peak at some delay time as schematically shown in Fig. 6e (see also Section VII in Supplementary Information). Therefore, the response function plays the role of a filter such that the magnetization of the ith node m_i(t) at time t has the information of the input at time t−τ. The position of the peak is dependent on the distance between two nodes and the wave speed. As a result, m_i(t) may have the information of different delay times (see also Fig. 1c). The maximum delay time can be evaluated from the maximum time that spin wave propagation spends. This is nothing but the time for wave propagation between the furthest physical nodes. RC cannot memorize the information beyond this time scale of the delay. Together with the nonlinear readout, the spin-wave RC can memorize the past information and its nonlinear transformation.

Fig. 6: Scaling between characteristic size and propagating wave speed obtained by response function method.

The characteristic size l = 2R is quantified by the radius R of the circle on which inputs are located (see Fig. 2-(3)). a, c MC and b, d IPC as a function of the characteristic length scale between physical nodes R and the speed of wave propagation v with θ = 0.04 ns and α = 5.0 × 10⁻⁴. The results with the response function for the dipole interactions Eqs. (16) and (17) a, b and for the Gaussian function Eq. (19) c, d are shown. Open circle symbols in a–d corresponds to wave speed (v = 200 m⋅s⁻¹) and length (l = 2R = 500 nm) used in micromagnetic simulation. The damping time shown in a, b expresses the length scale obtained from the wave speed multiplied by the time scale of damping associated with α. e Schematic illustration of the response function and its relation to wave propagation between physical nodes. When the speed of the wave is too fast, all the response functions are overlapped (dense regime), while the response functions cannot cover the time windows when the speed of the wave is too slow (sparse regime).

To obtain a deeper understanding of the result, we perform the same analyses for the further simplified model, in which the response function is replaced by the Gaussian function Eq. (19) (see Methods). This functional form has the peak at t = R_ij/v and the width of the response function is w, where R_ij is the distance between ith and jth physical nodes (see Fig. 6e). Even in this simplified model, we obtain MC ≈ 40 and IPC ≈ 60, and also the maximum when l = 2R ∝ v (Fig. 6c, d). From this result, the origin of the optimal ratio between the length and speed becomes clearer; when l ≪ v, the response functions under different R_ij overlap so that different physical nodes cannot carry the information of different delay times. On the other hand, when l ≫ v, the characteristic delay time l/v exceeds the maximum delay time to compute MC and IPC, or exceeds the total length of the time series. Note that we set the maximum delay time as 100, which is much longer than the value necessary for the NARMA10 task.

We also analyse the results of micromagnetic simulations along the line with the scaling argument using the response function. As shown in insets of Fig. 7, MC becomes smaller when vτ₀ is larger under the fixed l, and when l is smaller l with fixed vτ₀. These trends of scaling obtained by micromagnetic simulations are comparable with the Gaussian model. However, the position of the peak deviates from the theoretical value. We speculate this is due to the finite system size, whose effect is not included in the theoretical model.

Fig. 7: Reports of reservoir computing using multiple nodes are plotted as a function of the length between nodes (l) and characteristic wave speed (v) times delay time (τ₀) for photonics systems (open symbols) and spintronics systems (solid symbols).

The size of symbols corresponds to MC, which is taken from literature^{12,23,34,41,42,43,45} and this work. The color scale represents MC evaluated by using the response function method. Inset figures show comparison between micromagnetic simulation and response function simulation using Gaussian model Eq. (19). Solid and open star symbols in the insets are vτ₀ evaluated by considering dipole interaction only (v = 200 m/s) and with modification of exchange interaction (v = 1000 m/s).

Reservoir computing scaling and performance in comparison with the literature

Our results suggest the universal scaling between the size of the system and the speed of the RC based on wave propagation. Figure 7 shows reports of reservoir computing in literature with multiple nodes plotted as a function of the length of nodes l and products of wave speed and delay time vτ₀ for both photonic and spintronic RC. MC and NRMSE for NARMA10 tasks using photonic and spintronic RC are reported in refs. ^{12,40,41,42,43,44,45} for photonic RC and refs. ^{9,23,34,35,46,47,48,49} for spintronic RC. Table 1 and 2 summarize the reports of MC for photonic and spintronic RC with different length scales, which are plotted in Fig. 7. We evaluate the characteristic length l in the reported systems by the longest distance between physical nodes for spintronic RC and the size of the feedback loop unit for photonic RC. Our system of the spin wave has a characteristic length l~500 nm and a speed of v~200 m s⁻¹. For the spintronic RC, the dipole interaction is considered for wave propagation in which speed is proportional to both saturation magnetization and thickness of the film⁵⁰ (see Supplementary Information Section VIII A). For the photonic RC, the characteristic speed is the speed of light, v~10⁸ m s⁻¹. Symbol size corresponds to MC taken from the literature (see Tables 1 and 2). Plots are roughly on a broad oblique line with a ratio l/(vτ₀)~1. Therefore, the photonic RC requires a larger system size, as long as the delay time of the input τ₀ = N_vθ is the same order (τ₀ = 0.3−3 ns in our spin wave RC). As can be seen in Fig. 6, if one wants to reduce the length of physical nodes, one must reduce wave speed or delay time; otherwise, the information is dense, and the reservoir cannot memorize many degrees of freedom (See Fig. 6e). Reducing delay time is challenging since the experimental demonstration of the photonic reservoirs has already used a short delay close to the instrumental limit. Also, reducing wave speed in photonics systems is challenging. On the other hand, the wave speed of propagating spin-wave is much lower than the speed of light and can be tuned by configuration, thickness and material parameters. If one reduces wave speed or delay time over the broad line in Fig. 7, information becomes sparse and cannot be used efficiently (See Fig. 6e). Therefore, there is an optimal condition for high-performance RC.

Table 1 Report of photonic RC with different length scales used in Fig. 7

Table 2 Report of spintronic RC with different length scales used in Fig. 7

The performance is comparable with other state-of-the-art techniques, which are summarized in Fig. 8. For example, for the spintronic RC, MC ≈ 30²³ and NRMSE ≈ 0.2³⁴ in the NARMA10 task are obtained using N_p ≈ 100 physical nodes. However, the spintronic RC with one physical node and 10¹−10² virtual nodes does not show high performance; MC is less than 10 (the bottom left points in Fig. 8). This fact suggests that the spintronic RC so far cannot use virtual nodes effectively, namely, MC ≪ N = N_pN_v. On the other hand, for the photonic RC, comparable performances are achieved using N_v ≈ 50 virtual nodes, but only one physical node. As we discussed, however, the photonic RC requires mm system sizes. Our system achieves comparable performances using ≲ 10 physical nodes, and the size is down to nanoscales keeping the 2−50 GHz computational speed. We also demonstrate that the spin wave RC can perform time-series prediction and reconstruction of an attractor for the chaotic data. This has not been done in spintronic RC.

Fig. 8: Reservoir computing performance compared with different systems.

a MC reported plotted as a function of physical nodes N_p. b Normalized root mean square error, NRMSE for NARMA10 task is plotted as a function of N_p. Open blue symbols are values reported using photonic RC while solid red symbols are values reported using spintronic RC. MC and NRMSE for NARMA10 task are taken from refs. ^{9,23,24,34,46,48,49} for spintronic RC and refs. ^{40,41,42,43,44} for photonic RC.

Discussion

Our results of micromagnetic simulations suggest that our system has a potential of physical implementation because all the parameters in this study are feasible using realistic materials. We found that RC performance such as MC can be increased by use of materials with low damping parameter. Thin films of Heusler ferromagnet with lower damping has been reported^51,52,53, considered as material system for spin-wave RC in this study. Nanoscale propagating spin waves in a ferromagnetic thin film excited by spin-transfer torque using nanometer electrical contacts have been observed^54,55,56. Patterning of multiple electrical nanocontacts into magnetic thin films was demonstrated in mutually synchronized spin-torque oscillators⁵⁶. In addition to the excitation of propagating spin-wave in a magnetic thin film, its non-local magnetization dynamics can be detected by tunnel magnetoresistance effect at each electrical contact⁵⁷, as schematically shown in Fig. 1c, which are widely used for the development of spintronics memory and spin-torque oscillators. The size of a magnetic tunnel junction can be 40nm in diameter, and therefore, it is compatible with our proposed system. In addition, virtual nodes are effectively used in our system by considering the speed of propagating spin-wave and distance of physical nodes; thus, high-performance reservoir computing can be achieved with the small number of physical nodes, contrary to many physical nodes used in previous reports. Spin wave can be excited by current pulse with typical time scale of GHz frequency, for example by Heusler ferromagnet alloys discussed above. This leads to the realization of fast and energy-efficient spin-wave RC. Energy consumption needed to process one time step calculated is an order of magnitude smaller than other physical RC such as memristor-based RC, which is mainly due to the fact that shorter input pulse can be used in spin-wave RC (see Supplementary Information Section IX). Therefore, spin-wave RC have potential to be used for future energy-efficient physical RC with spintronics read out network such as spin crossbar arrays^58,59.

There is an interesting connection between our study and the recently proposed next-generation RC^37,60, in which the linear ESN is identified with the NVAR (nonlinear vectorial autoregression) method to estimate a dynamical equation from data. Our theoretical analyses, shown in Eq. (15), clarify that the magnetization dynamics at physical and virtual nodes can be expressed by the Volterra series of the input, namely, a time delay of U_k with its polynomials (see Methods: Relation of MC and IPC with learning performance). On the other hand, the linear input-output relationship can be expressed with a delay as Y_n+1 = a_nU_n + a_n−1U_n−1 + …, or more generally, with the nonlinear readout or with higher-order response functions, as Y_n+1 = a_nU_n + a_n−1U_n−1 +…+ a_n,nU_nU_n + a_n,n−1U_nU_n−1+…. These input-output relations are nothing but Volterra series of the output as a function of the input with delay and nonlinearity²⁷. The coefficients of the expansion are associated with the response function. Therefore, the performance of RC falls into the independent components of the matrix of the response function, which can be evaluated by how much delay the response functions between two nodes cover without overlap. We should stress that the form of expansion is imposed neither in the response function nor in micromagnetic simulations. The structure is obtained from the analyses of the LLG equation. The results would be helpful to a potential design of the network of the physical nodes.

We should note that the polynomial basis of the input-output relation in this study originates from spin wave excitation around the stationary state m_z≈1. When the input data has a hierarchical structure, another basis may be more efficient than the polynomial expansion. Another setup of magnetic systems may lead to a different basis. We believe that our study shows simple but clear intuition of the mechanism of high-performance RC, that can lead to the exploration of another setup for more practical application of the physical RC.

Methods

Physical system of a magnetic device

We consider a magnetic device of a thin rectangular system with cylindrical injectors (see Fig. 1c). The size of the device is L × L × D. Under the uniform external magnetic field, the magnetization is along the z direction. Electric current translated from time series data is injected at the N_p injectors with the radius a and the same height D as the device. The spin-torque by the current drives magnetization m(x, t) and propagating spin-waves as schematically shown in Fig. 1c. The magnetization is detected at the same cylindrical nanocontacts as the injectors. The nanocontacts of the inputs and outputs are located on the circle with its radius R (see Fig. 2-(3)). The size of our system is L = 1000 nm and D = 4 nm. We set a = 20 nm unless otherwise stated. We set R = 250 nm in Performance of tasks for MC, IPC, NARMA10, and prediction of chaotic time-series section but R is varied in Scaling of system size and wave speed section as a characteristic length scale.

Details of preprocessing input data

In the time-multiplexing approach, the input time-series ${{{\bf{U}}}}=({U}_{1},{U}_{2},\ldots ,{U}_{T})\in {{\mathbb{R}}}^{T}$ is translated into piece-wise constant time-series $\tilde{U}(t)={U}_{n}$ with t = (n−1)N_vθ + s under k = 1,…,T and s = [0, N_vθ) (see Fig. 2–(1)). This means that the same input remains during the time period τ₀ = N_vθ. To use the advantage of physical and virtual nodes, the actual input j_i(t) at the ith physical node is U(t) multiplied by τ₀-periodic random binary filter ${{{{\mathcal{B}}}}}_{i}(t)$. Here, ${{{{\mathcal{B}}}}}_{i}(t)\in \{0,1\}$ is piece-wise constant during the time θ. At each physical node, we use different realizations of the binary filter as in Fig. 2-(2). The input masks play a role as the input weights for the ESN without virtual nodes. Because the different masks are used for the different physical nodes, each physical and virtual node may have different information about the input time series.

The masked input is further translated into the input for the physical system. Although numerical micromagnetic simulations are performed in discrete time steps, the physical system has continuous-time t. The injected current density j_i(t) at time t for the ith physical node is set as ${j}_{i}(t)=2{j}_{c}{\tilde{U}}_{i}(t)=2{j}_{c}{{{{\mathcal{B}}}}}_{i}(t)U(t)$ with j_c = 2 × 10⁻⁴/(πa²)A/m². Under a given input time series of the length T, we apply the constant current during the time θ, and then update the current at the next step. The same input current with different masks is injected for different virtual nodes. The total simulation time is, therefore, TθN_v.

Micromagnetic simulations

We analyze the magnetization dynamics of the Landau-Lifshitz-Gilbert (LLG) equation using the micromagnetic simulator mumax^3 61. The LLG equation for the magnetization M(x, t) yields

$$\begin{array}{l}{\partial }_{t}{{{\bf{M}}}}({{{\bf{x}}}},t)\,=\,-\frac{\gamma {\mu }_{0}}{1+{\alpha }^{2}}{{{\bf{M}}}}\times {{{{\bf{H}}}}}_{{{{\rm{eff}}}}}\\\qquad\qquad\qquad-\frac{\alpha \gamma {\mu }_{0}}{{M}_{s}(1+{\alpha }^{2})}{{{\bf{M}}}}\times \left({{{\bf{M}}}}\times {{{{\bf{H}}}}}_{{{{\rm{eff}}}}}\right)\\\qquad\qquad\qquad+\,\frac{\hslash P\gamma }{4{M}_{s}^{2}eD}J({{{\bf{x}}}},t){{{\bf{M}}}}\times \left({{{\bf{M}}}}\times {{{{\bf{m}}}}}_{{{{\rm{f}}}}}\right).\end{array}$$

(10)

In the micromagnetic simulations, we analyze Eq. (10) with the effective magnetic field H_eff = H_ext + H_demag + H_exch consists of the external field, demagnetization, and the exchange interaction. The concrete form of each term is

$${{{{\bf{H}}}}}_{{{{\rm{eff}}}}}={{{{\bf{H}}}}}_{{{{\rm{ext}}}}}+{{{{\bf{H}}}}}_{{{{\rm{demag}}}}}+{{{{\bf{H}}}}}_{{{{\rm{exch}}}}},$$

(11)

$${{{{\bf{H}}}}}_{{{{\rm{ext}}}}}={H}_{0}{{{{\bf{e}}}}}_{z}$$

(12)

$${{{{\bf{H}}}}}_{{{{\rm{ms}}}}}=-\frac{1}{4\pi }\int\nabla \nabla \frac{{\bf{M}}({\bf{x}}^{\prime})}{| {{{\bf{x}}}}-{{{{\bf{x}}}}}^{{\prime}}|}d{{{{\bf{x}}}}}^{{\prime}}$$

(13)

$${{{{\bf{H}}}}}_{{{{\rm{exch}}}}}=\frac{2{A}_{{{{\rm{ex}}}}}}{{\mu }_{0}{M}_{s}}\Delta {{{\bf{M}}}},$$

(14)

where H_ext is the external magnetic field, H_ms is the magnetostatic interaction, and H_exch is the exchange interaction with the exchange parameter A_ex. The spin waves are driven by Slonczewski spin-transfer torque⁶², which is described by the last term of Eq. (10). The driving term is proportional to the DC current, namely, J(x, t) = j_i(t) at the ith nanocontact and J(x, t) = 0 other regions.

Parameters in the micromagnetics simulations are chosen as follows: The number of mesh points is 200 in the x and y directions, and 1 in the z direction. We consider Co₂MnSi Heusler alloy ferromagnet, which has a low Gilbert damping and high spin polarization with the parameter A_ex = 23.5 pJ/m, M_s = 1000 kA/m, and α = 5 × 10^{−4 51,52,53,63,64}. Out-of-plane magnetic field μ₀H₀ = 1.5 T is applied so that magnetization is pointing out-of-plane. The spin-polarized current field is included by the Slonczewski model⁶² with polarization parameter P = 1 and spin torque asymmetry parameter λ = 1 with the reduced Planck constant ℏ and the charge of an electron e. The uniform fixed layer magnetization is m_f = e_x. We use absorbing boundary layers for spin waves to ensure the magnetization vanishes at the boundary of the system⁶⁵. We set the initial magnetization as m = e_z. The magnetization dynamics is updated by the fourth-order Runge-Kutta method (RK45) under adaptive time-stepping with the maximum error set to be 10⁻⁷.

The reference time scale in this system is t₀ = 1/γμ₀M_s ≈ 5 ps, where γ is the gyromagnetic ratio, μ₀ is permeability, and M_s is saturation magnetization. The reference length scale is the exchange length l₀ ≈ 5 nm. The relevant parameters are Gilbert damping α, the time scale of the input time series θ (see Section Learning with reservoir computing), and the characteristic length between the input nodes R.

Theoretical analysis using response function

To understand the mechanism of high performance of learning by spin wave propagation, we also consider a model using the response function of the spin wave dynamics. By linearizing the magnetization around m = (0, 0, 1) without inputs, we may express the linear response of the magnetization at the ith readout m_i = m_x,i + im_y,i to the input as

$$\begin{array}{l}{m}_{i}(t)\,=\,\mathop{\sum }\limits_{j=1}^{{N}_{p}}\int\,d{t}^{{\prime} }{G}_{ij}(t,{t}^{{\prime} }){U}^{(j)}({t}^{{\prime} }),\end{array}$$

(15)

where the response function G_ij for the same node is

$$\begin{array}{l}{G}_{ii}(t-\tau )\,=\,\frac{1}{2\pi }{e}^{-\tilde{h}(\alpha +i)(t-\tau )}\frac{-1+\sqrt{1+\frac{{a}^{2}}{{(d/4)}^{2}{(\alpha +i)}^{2}{(t-\tau )}^{2}}}}{\sqrt{1+\frac{{a}^{2}}{{(d/4)}^{2}{(\alpha +i)}^{2}{(t-\tau )}^{2}}}}\end{array}$$

(16)

and for different nodes,

$$\begin{array}{l}{G}_{ij}(t-\tau )\,=\,\frac{{a}^{2}}{2\pi }{e}^{-\tilde{h}(\alpha +i)(t-\tau )}\\\qquad\qquad\;\;\times \;\;\frac{1}{{(d/4)}^{2}{(\alpha +i)}^{2}{(t-\tau )}^{2}{\left(1+\frac{| {{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j}{| }^{2}}{{(d/4)}^{2}{(\alpha +i)}^{2}{(t-\tau )}^{2}}\right)}^{3/2}}.\end{array}$$

(17)

The detailed derivation of the response function is shown in Supplementary Information Section VII. Here, U^(j)(t) is the input time series at jth nanocontact. The response function has a self part G_ii, that is, input and readout nanocontacts are the same, and the propagation part G_ij, where the distance between the input and readout nanocontacts is ∣R_i−R_j∣. In Eqs. (16) and (17), we assume that the spin waves propagate only with the dipole interaction. We discuss the effect of the exchange interaction in Supplementary Information Section VII A. We should note that the analytic form of Eq. (17) is obtained under certain approximations. We discuss its validity in Supplementary Information Section VII A.

We use the quadratic nonlinear readout, which has a structure

$$\begin{array}{l}{m}_{i}^{2}(t)\,=\,\mathop{\sum }\limits_{{j}_{1}=1}^{{N}_{p}}\mathop{\sum }\limits_{{j}_{2}=1}^{{N}_{p}}\int\,d{t}_{1}\int\,d{t}_{2}\\\qquad\qquad{G}_{i{j}_{1}{j}_{2}}^{(2)}(t,{t}_{1},{t}_{2}){U}^{({j}_{1})}({t}_{1}){U}^{({j}_{2})}({t}_{2}).\end{array}$$

(18)

The response function of the nonlinear readout is ${G}_{i{j}_{1}{j}_{2}}^{(2)}(t,{t}_{1},{t}_{2})\propto {G}_{i{j}_{1}}(t,{t}_{1}){G}_{i{j}_{2}}(t,{t}_{2})$. The same structure as Eq. (18) appears when we use a second-order perturbation for the input (see Supplementary Information Section V A). In general, we may include the cubic and higher-order terms of the input. This expansion leads to the Volterra series of the output in terms of the input time series, and suggests how the spin wave RC works as shown in Methods: Relation of MC and IPC with learning performance (see also Supplementary Information Section II for more details). Once the magnetization at each nanocontact is computed, we may estimate MC and IPC.

We also use the following Gaussian function as a response function,

$$\begin{array}{l}{G}_{ij}(t)\,=\,\exp \left(-\frac{1}{2{w}^{2}}{\left(t-\frac{{R}_{ij}}{v}\right)}^{2}\right)\end{array}$$

(19)

where R_ij is the distance between ith and jth physical nodes. The Gaussian function Eq. (19) has its mean t = R_ij/v and variance w². Therefore, w is the width of the Gaussian function (see Fig. 6e). We set the width as w = 50 in the normalized time unit t₀. In Supplementary Information Section VII A, we introduce the skew normal distribution, which generalize Eq. (19) to include the effect of exchange interaction.

Learning tasks

NARMA task

The NARMA10 task is based on the discrete differential equation,

$$\begin{array}{l}{Y}_{n+1}\,=\,\alpha {Y}_{n}+\beta {Y}_{n}\mathop{\sum }\limits_{p=0}^{9}{Y}_{n-p}+\gamma {U}_{n}{U}_{n-9}+\delta .\end{array}$$

(20)

Here, U_n is an input taken from the uniform random distribution ${{{\mathcal{U}}}}(0,0.5)$, and Y_n is an output. We choose the parameter as α = 0.3, β = 0.05, γ = 1.5, and δ = 0.1. In RC, the input is U = (U₁, U₂,…,U_T) and the output Y = (Y₁, Y₂,…, Y_T). The goal of the NARMA10 task is to estimate the output time-series Y from the given input U. The training of RC is done by tuning the weights W so that the estimated output $\hat{Y}({t}_{n})$ is close to the true output Y_n in terms of squared norm $| \hat{Y}({t}_{n})-{Y}_{n}{| }^{2}$.

The performance of the NARMA10 task is measured by the deviation of the estimated time series $\hat{{{{\bf{Y}}}}}={{{\bf{W}}}}\cdot \tilde{\tilde{{{{\bf{X}}}}}}$ from the true output Y. The normalized root-mean-square error (NRMSE) is

$$\begin{array}{rc}{{{\rm{NRMSE}}}}&\equiv \sqrt{\frac{{\sum }_{n}{(\hat{Y}({t}_{n})-{Y}_{n})}^{2}}{{\sum }_{n}{Y}_{n}^{2}}}.\end{array}$$

(21)

Performance of the task is high when NRMSE≈0. In the ESN, it was reported that NRMSE ≈ 0.4 for N = 50 and NRMSE ≈ 0.2 for N = 200³¹. The number of node N = 200 was used for the speech recognition with ≈0.02 word error rate³¹, and time-series prediction of spatio-temporal chaos⁶. Therefore, NRMSE ≈ 0.2 is considered as reasonably high performance in practical application. We also stress that we use the same order of nodes (virtual and physical nodes) N = 128 to achieve NRMSE ≈ 0.2.

Memory capacity (MC)

MC is a measure of the short-term memory of RC. This was introduced in ref. ⁷. For the input U_n of random time series taken from the uniform distribution, the network is trained for the output Y_n = U_n−k. Here, U_n−k is normalized so that Y_n is in the range [–1,1]. The MC is computed from

$$\begin{array}{l}{{{{\rm{MC}}}}}_{k}\,=\,\displaystyle\frac{{\langle {U}_{n-k},{{{\bf{W}}}}\cdot {{{\bf{X}}}}({t}_{n})\rangle }^{2}}{\langle {U}_{n}^{2}\rangle \langle {({{{\bf{W}}}}\cdot {{{\bf{X}}}}({t}_{n}))}^{2}\rangle }.\end{array}$$

(22)

This quantity is decaying as the delay k increases, and MC is defined as

$$\begin{array}{l}{{{\rm{MC}}}}\,=\,\mathop{\sum }\limits_{k=1}^{{k}_{\max }}{{{{\rm{MC}}}}}_{k}.\end{array}$$

(23)

Here, ${k}_{\max }$ is a maximum delay, and in this study we set it as ${k}_{\max }=100$. The advantage of MC is that when the input is independent and identically distributed (i.i.d.), and the output function is linear, then MC is bounded by N, the number of internal nodes⁷.

We show the example of MC_k as a function of k and IPC_j as a function of k₁ and k₂ in Fig. S2a and b. When the delay k is short, MC_k ≈ 1 suggesting that the delayed input can be reconstructed by the input without the delay. When delay becomes longer reservoir does not have capacity to reconstruct delayed input, however, MC_k and IPC_j defined by Eqs. (22) and (25) have long tail small positive values, making overestimation of MC and IPC. To avoid the overestimation, we use the threshold value ε = 0.03727 below which we set MC_k = 0. The value of ε is set following the argument of ref. ²⁶. When the total number of readouts is N(=128) and the number of time steps to evaluate the capacity is T(=5000), the mean error of the capacity is estimated as N/T. We assume that the distribution of the error yields χ² distribution as (1/T)χ²(N). Then, we may set ε such that $\varepsilon =\tilde{N}/T$ where $\tilde{N}$ is taken from the χ² distribution and the probability of its realization is 10⁻⁴, namely, $P(\tilde{N} \sim {\chi }^{2}(N))=1{0}^{-4}$. In fact, Fig. S2a demonstrates that when the delay is longer, the capacity converges to N/T and fluctuates around the value. In this regime, we set MC_k = 0 and do not count for the calculation of MC. The same argument applies to the calculation of IPC.

Information processing capacity (IPC)

IPC is a nonlinear version of MC²⁶. In this task, the output is set as

$$\begin{array}{l}{Y}_{n}\,=\,\mathop{\prod}\limits_{k}{{{{\mathcal{P}}}}}_{{d}_{k}}({U}_{n-k})\end{array}$$

(24)

where d_k is non-negative integer, and ${{{{\mathcal{P}}}}}_{{d}_{k}}(x)$ is the Legendre polynomials of x order d_k. As MC, the input time series is uniform random noise ${U}_{n}\in {{{\mathcal{U}}}}(0,0.5)$ and then normalized so that Y_n is in the range [–1,1]. We may define

$$\begin{array}{l}{{{{\rm{IPC}}}}}_{{d}_{0},{d}_{1},\ldots ,{d}_{T-1}}\,=\,\displaystyle\frac{{\langle {Y}_{n},{{{\bf{W}}}}\cdot {{{\bf{X}}}}({t}_{n})\rangle }^{2}}{\langle {Y}_{n}^{2}\rangle \langle {({{{\bf{W}}}}\cdot {{{\bf{X}}}}({t}_{n}))}^{2}\rangle }.\end{array}$$

(25)

and then compute jth order IPC as We may define

$$\begin{array}{rc}{{{{\rm{IPC}}}}}_{j}&=\mathop{\sum}\limits_{{d}_{k}{{{\rm{s.t.}}}}j={\sum }_{k}{d}_{k}}{{{{\rm{IPC}}}}}_{{d}_{1},{d}_{2},\ldots ,{d}_{T}}.\end{array}$$

(26)

When j = 1, the IPC is, in fact, equivalent to MC, because ${{{{\mathcal{P}}}}}_{0}(x)=1$ and ${{{{\mathcal{P}}}}}_{1}(x)=x$. In this case, Y_n = U_n−k for d_i = 1 when i = k and d_i = 0 otherwise. Equation (26) takes the sum over all possible delay k, which is nothing but MC. When j > 1, IPC_j captures the nonlinear transformation and delays up of the jth polynomial order. For example, when j = 2, the output can be ${Y}_{n}={U}_{n-{k}_{1}}{U}_{n-{k}_{2}}$ or ${Y}_{n}={U}_{n-k}^{2}+{{{\rm{const.}}}}$ In this study, we focus on j = 2 because the second-order nonlinearity is essential for the NARMA10 task (see Supplementary Information Section I). In ref. ²⁶, IPC is defined by sum of IPC_j over j. In this study, we focus only on IPC₂, which plays a relevant role for the NARMA10 task (see Supplementary Information Section I). We denote IPC and IPC₂ interchangeably.

The example of IPC₂ as a function of the two delay times k₁ and k₂ is shown in Fig. S2b. When both k₁ and k₂ are small, the nonlinear transformation of the delayed input ${Y}_{n}={U}_{n-{k}_{1}}{U}_{n-{k}_{2}}$ can be reconstructed from U_n. As the two delays are longer, IPC₂ approaches the value N/T of systematic error. As we performed for the MC task, we define the same threshold ε, and do not count the capacity below the threshold in IPC₂.

Prediction of chaotic time-series data

Following ref. ⁶, we perform the prediction of time-series data from the Lorenz model. The model is a three-variable system of (A₁(t), A₂(t), A₃(t)) yielding the following equation

$$\frac{d{A}_{1}}{dt}=10({A}_{2}-{A}_{1})$$

(27)

$$\frac{d{A}_{2}}{dt}={A}_{1}(28-{A}_{3})-{A}_{2}$$

(28)

$$\frac{d{A}_{3}}{dt}={A}_{1}{A}_{2}-\frac{8}{3}{A}_{3}.$$

(29)

The parameters are chosen such that the model exhibits chaotic dynamics. Similar to the other tasks, we apply the different masks of binary noise for different physical nodes, ${{{{\mathcal{B}}}}}_{i}^{(l)}(t)\in \{-1,1\}$. Because the input time series is three-dimensional, we use three independent masks for A₁, A₂, and A₃, therefore, l ∈ {1, 2, 3}. The input for the ith physical node after the mask is given as ${{{{\mathcal{B}}}}}_{i}(t){\tilde{U}}_{i}(t)={{{{\mathcal{B}}}}}_{i}^{(1)}(t){A}_{1}(t)+{{{{\mathcal{B}}}}}_{i}^{(2)}(t){A}_{2}(t)+{{{{\mathcal{B}}}}}_{i}^{(3)}(t){A}_{3}(t)$. Then, the input is normalized so that its range becomes [0, 0.5], and applied as an input current. Once the input is prepared, we may compute magnetization dynamics for each physical and virtual node, as in the case of the NARMA10 task. We note that here we use the binary mask of {−1, 1} instead of {0, 1} used for other tasks. We found that the {0,1} does not work for the prediction of the Lorenz model, possibly because of the symmetry of the model.

The ground-truth data of the Lorenz time-series is prepared using the Runge-Kutta method with the time step Δt = 0.025. The time series is t ∈ [−60, 75], and t ∈ [−60, −50] is used for relaxation, $t\in \left(-50,0\right]$ for training, and $t\in \left(0,75\right]$ for prediction. During the training steps, we compute the output weight by taking the output as Y = (A₁(t + Δt), A₂(t + Δt), A₃(t + Δt)). After training, the RC learns the mapping (A₁(t), A₂(t), A₃(t)) → (A₁(t + Δt), A₂(t + Δt), A₃(t + Δt)). For the prediction steps, we no longer use the ground-truth input but the estimated data $(\hat{{A}_{1}}(t),\hat{{A}_{2}}(t),\hat{{A}_{3}}(t))$ as schematically shown in Fig. 5c. Using the fixed output weights computed in the training steps, the time evolution of the estimated time-series $(\hat{{A}_{1}}(t),\hat{{A}_{2}}(t),\hat{{A}_{3}}(t))$ is computed by the RC.

Relation of MC and IPC with learning performance

The relevance of MC and IPC is clear by considering the Volterra series of the input-output relation. The input-output relationship is generically expressed by the polynomial series expansion as

$$\begin{array}{l}{Y}_{n}\,=\,\mathop{\sum}\limits_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}{\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}{U}_{1}^{{k}_{1}}{U}_{2}^{{k}_{2}}\cdots {U}_{n}^{{k}_{n}}.\end{array}$$

(30)

Each term in the sum has k_n power of U_n. Instead of polynomial basis, we may use orthonormal basis such as the Legendre polynomials

$$\begin{array}{l}{Y}_{n}\,=\mathop{\sum}\limits_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}{\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}{{{{\mathcal{P}}}}}_{{k}_{1}}({U}_{1}){{{{\mathcal{P}}}}}_{{k}_{2}}({U}_{2})\cdots {{{{\mathcal{P}}}}}_{{k}_{n}}({U}_{n}).\end{array}$$

(31)

Each term in Eqs. (30) and (31) is characterized by the non-negative indices (k₁, k₂,…,k_n). Therefore, the terms corresponding to j = ∑_ik_i = 1 in Y_n have information on linear terms with time delay. Similarly, the terms corresponding to j = ∑_ik_i = 2 have information of second-order nonlinearity with time delay. In this view, the estimation of the output Y(t) is nothing but the estimation of the coefficients ${\beta }_{{k}_{1},{k}_{2},\ldots ,{k}_{n}}$.

Here, we show how the coefficients can be computed from the magnetization dynamics. In RC, the readout of the reservoir state at ith node (either physical or virtual node) can also be expanded as the Volterra series

$$\begin{array}{l}{\tilde{\tilde{X}}}^{(i)}({t}_{n})\,=\mathop{\sum}\limits_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}{\tilde{\tilde{\beta }}}_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}^{(i)}{U}_{1}^{{k}_{1}}{U}_{2}^{{k}_{2}}\cdots {U}_{n}^{{k}_{n}},\end{array}$$

(32)

where ${\tilde{\tilde{X}}}^{(i)}({t}_{n})$ is measured magnetization dynamics and U_n is the input that drives spin waves. At the linear and second-order in U_k, Eq. (32) is discrete expression of Eqs. (15) and (18). By comparing Eqs. (30) and (32), we may see that MC and IPC are essentially a reconstruction of ${\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}$ from ${\tilde{\tilde{\beta }}}_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}^{(i)}$ with i ∈ [1, N]. This can be done by regarding ${\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}$ as a T + T(T−1)/2+⋯-dimensional vector, and using the matrix M associated with the readout weights as

$$\begin{array}{l}{\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}\,=M\cdot \left(\begin{array}{r}{\tilde{\tilde{\beta }}}_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}^{(1)}\\ {\tilde{\tilde{\beta }}}_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}^{(2)}\\ \vdots \\ {\tilde{\tilde{\beta }}}_{{k}_{1},{k}_{2},\cdots \,,{k}_{n}}^{(N)}\end{array}\right).\end{array}$$

(33)

MC corresponds to the reconstruction of ${\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}$ for ∑_i k_i = 1, whereas the second-order IPC is the reconstruction of ${\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}$ for ∑_ik_i = 2. If all of the reservoir states are independent, we may reconstruct N components in ${\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}$. In realistic cases, the reservoir states are not independent, and therefore, we can estimate only <N components in ${\beta }_{{k}_{1},{k}_{2},\cdots ,{k}_{n}}$. For more details, readers may consult Supplementary Information Sections I and II.