Abstract
Although our every-day experience rejects it, the quantum Cheshire Cat suggests a potential spatial separation between different properties of a single particle in an interferometer. The first experiment with neutrons confirmed the quantum Cheshire Cat effect by using the path and spin degrees of freedom. The locations of each property are determined qualitatively through reactions to locally applied perturbations. Yet, no consensus on the interpretation has been reached. To clarify the origin of the effect, in the present experiment the energy degree of freedom is used as the third property; the three properties of neutrons appear to be separated in different paths in the interferometer. The analysis of the experiment suggests the strong involvement of the inner product between the state vectors, one evolved from the initial state through the perturbation and the other being the final state. The inner product results in amplitudes from two sub-beams which contribute to the intensity. The cross-term between amplitudes gives rise to the quantum Cheshire Cat.
Similar content being viewed by others
Introduction
Since the introduction of quantum mechanics, its theoretical framework has suggested counter-intuitive and paradoxical phenomena: entanglement1,2, Schrödinger’s cat3,4, and wave-particle duality5 are only three of the most popular ones. Their study provides us with a deeper understanding of nature and opportunities for new technology6,7,8,9. All the mentioned effects contradict our every-day ideas of physical reality. Although the different interpretations of quantum mechanics are equivalent in predicting measurement outcomes, their conflicting assumptions of the fundamental mechanisms vary greatly.
Another such effect concerns the location of a particle and its properties in an interferometer. Usually, a particle and its properties are considered as inseparable. In contrast, Aharonov et al.10 described intriguing interferometer experiments in which different properties of a physical entity appear to be spatially separated—localised in different paths/sub-beams of an interferometer. Aharonov et al. coined the term quantum Cheshire Cat (qCC) in tribute to the similar behaviour of the so-called Cheshire Cat in Lewis Carroll’s “Alice’s Adventures in Wonderland”11. In the novel, different parts of the Cheshire Cat can appear independently of each other.
Reference10 suggests applying an interaction in a particular sub-beam of an interferometer. If this generates conspicuous reactions of the detected intensity, the authors of Reference10 propose that the property associated with the interaction is localised in the manipulated sub-beam. The apparent separation of properties emerges in a pre- and post-selection procedure. In the interpretation of ref. 10, by applying an interaction in a path, a statement about the location of a property is deduced. To combine all deduced statements, the disturbance of the interactions needs to be small. This is achieved by choosing small interaction strengths such that the interactions are weak. Due to the small disturbances, the locations of the properties cannot be determined for a single neutron but only with the statistics of an ensemble. From the appearance of conspicuous reactions to each weak interaction when applied in a different path, the separation of properties is concluded. A possible combination of fundamental assumptions for this interpretation are the realistic separability of properties of a physical entity10 and a strictly linear reaction of the intensity to the interaction strengths12.
The first experimental realisation of a qCC was reported by Denkmayr et al.13 in a two-path neutron interferometer with the properties of particle and spin. While a particle is affected by an absorber, a neutron-spin interacts with magnetic fields. Implementing the absorption in one path affected the detected mean intensity and implementing a magnetic field in the other path affected the interference contrast, giving rise to the perception of a spatial separation between particle and spin.
A selection of other implementations of the Cheshire Cat effect and some discussions can be found in refs. 14,15,16,17,18,19,20,21,22. Possible experimental improvements were suggested, such as the simultaneous realisation of all weak measurements10, further consideration of not only the first-order but the second-order reactions to the midway interaction12, and the implementation of additional degrees of freedom as pointer systems17. The critique was expressed, for instance, questioning whether the observed effect is purely quantum mechanical14 and concerning the midway interaction strength20.
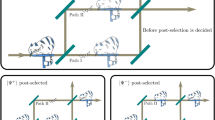
A generalised form of the qCC with arbitrarily many degrees of freedom and properties was proposed by Pan23. Here, we report on a three-path quantum Cheshire Cat in a neutron interferometric experiment24,25,26 by additionally using the energy as third property. The schematic of the three-path qCC is illustrated in Fig. 1. Each part of the cat corresponds to a property of the neutron. When directly attributing the location of properties to reactions to local manipulations, the associations are as follows: a direct-current (DC) spin rotation affects the spin, a radio-frequency (RF) rotation the energy, and absorption the particle. The reactions to the weak interactions are observed and weak values are determined for quantification. By means of this extended version we seek to demonstrate how the qCC emerges through the inner product of the involved state vectors and the cross-term of amplitudes from different interferometer paths. This will make the essence of the qCC evident.
The cat is separated into three different parts inside the interferometer. This is analogous to how the neutrons and their properties behave in the present experiment. The parts of the cat correspond to the neutron properties of spin (grin), particle (body) and energy (eyes). The reactions to the weak interactions applied during the experiment may lead to the perception that the properties of the neutron are separated.
Results
Scheme and theory
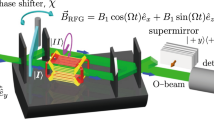
The experiment was carried out on the neutron interferometry station S18 at the high-flux reactor of the Institut Laue–Langevin (ILL) in Grenoble, France. The neutrons are monochromatised with a silicon perfect-crystal to a wavelength distribution peaked at λ0 = 1.92 Å and a relative wavelength uncertainty δλ/λ0 ≈ 2% equivalent to a relative energy uncertainty of δE/E0 ≈ 4%. Subsequently, magnetic prisms27 polarise the neutron’s spin to the upward +z-direction which defines the quantisation axis. We will use the symbols ↑ and ↓ to refer to up and down spin states, respectively, which correspond to the ± z-directions. The setup downstream of monochromator and polarisers is depicted in Fig. 2. The beam is split by the first two of four plates of a silicon perfect-crystal interferometer into the three separated sub-beams indexed by j ∈ {I, II, III}. Through recombination of all sub-beams, the O-beam in forward direction and the H-beam in the diffracted direction are produced. The phase drift between the sub-beam is limited to about 1 degree/hour through thermal isolation and air conditioning. A spin analysis is implemented in the O-beam by a polarising CoTi multilayer array, henceforth referred to as a supermirror. The intensity of the O-beam is recorded by a 3He counting tube. Inside the interferometer, two phase shifters (PS1 and PS2) control the phase relations between the three paths. Furthermore, if necessary, a weak spin or energy manipulation or a weak beam attenuation is applied in the interferometer.
An incoming neutron beam which is polarised in +z-direction (red arrows) is split into three paths inside a perfect-crystal interferometer. All sub-beams are recombined and the neutrons in the outgoing O-beam are detected. The experiment consists of three stages: first, the pre-selection or preparation stage (turquoise) where direct-current (DC) and radio-frequency (RF) spin manipulators flip the local spin vectors to the downward orientation (blue arrows) and produce three pairwise orthogonal sub-beams, cf. Section “Scheme and Theory” and Eq. (1). Second, the weak interaction stage (green) where one of three interactions, i.e. beam attenuation/absorption (abs) as well as DC and RF spin rotations, can be applied weakly in one of the three paths. Finally, the analysis or post-selection (orange) where the phase shifters (PS) 1 and 2 determine the phases χ1, χ2, cf. Eq. (2). At the recombination of the sub-beams and at the supermirror, respectively, the post-selection projects the incoming state onto a specific phase relation between the sub-beams in the O-beam and onto the up spin state. Since for the given pre- and post-selection of Eqs. (1) and (2) only the amplitude through path II is accepted by the post-selection, path II is referred to as the reference beam.
The experimental procedure is divided into the three stages of pre-selection, weak interaction, and post-selection. The pre-selection is realised by monochromator, polarising magnetic prisms, the beam splitters of the interferometer and two spin flippers in paths I and III. The spin flipper in path I induces a static DC spin flip and the one in path III an RF spin flip, where the frequency f of the oscillating field is 60 kHz (see the section “Adjustment Procedure for details of adjustment). The RF spin flip also changes the energy by ΔE = hf ≈ 0.25 neV, shifting the initial kinetic energy peaked at E0 ≈ 25 meV of the thermal neutrons to the new energy \({{{{{{{{\rm{E}}}}}}}}}^{{\prime} }={{{{{{{{\rm{E}}}}}}}}}_{0}-\Delta {{{{{{{\rm{E}}}}}}}}\), with ΔE/E0 ≈ 10−8. The combined effect of the aforementioned neutron optical components makes the separated sub-beams pairwise orthogonal when recombined: while the spin orientation is up in path II and down in paths I and III, the latter two are in different energy states. The two energy states exhibit time-dependent interference on the microsecond scale28. However, the detected counts are time-integrated and the given intensities are regarded as time averaged intensities such that the time-dependent interference is not observable. Time-independent, static interference is only observable if sub-beams with the same energy state are recombined29. Our model only needs to describe the observable effects and we assume the two energy states to be orthogonal to each other. Therefore, the two occupied energy levels and their respective two-level system behave like a pseudeospin system as applied earlier29,30,31,32. We will use the braket notation as an abbreviation to refer to the energy vectors as well as the path and spin vectors. The according triply entangled pre-selected initial state \(\left\vert {{{{{{{\rm{i}}}}}}}}\right\rangle\) is then written as
Therein, all states from different Hilbert spaces associated with a sub-beam are written together in a single ket for each path. The post-selection consists of PS1 and PS2 with their induced relative phases χ1 and χ2, the analysing crystal plates and the supermirror in the O-beam. The post-selection is represented by the inner product with the state \(\left\vert {{{{{{{\rm{f}}}}}}}}\right\rangle\) given by
which does not contain any energy terms, meaning no energy selection is employed in the post-selection. Therefore, all neutrons with up-spins and specific phase relations between the paths and arbitrary energy are selected to propagate towards the detector. We choose to attribute both phase shifts to the post-selection rather than the preparation; both approaches are equivalent. The post-selected intensity \({\left\vert \left\langle {{{{{{{\rm{f}}}}}}}}| {{{{{{{\rm{i}}}}}}}}\right\rangle \right\vert }^{2}\) only has a single non-zero contribution, coming from path II, while the components from the other paths in the initial state \(\left\vert {{{{{{{\rm{i}}}}}}}}\right\rangle\) are orthogonal to \(\left\vert {{{{{{{\rm{f}}}}}}}}\right\rangle\) such that their contributions to the post-selected intensity are zero. Consequently, given the pre-selection, only the component of the sub-beam through path II is post-selected. We will therefore refer to path II as the reference beam in our experiment. The other paths I and III can contribute to the post-selected intensity, however, when additional weak interactions are applied as described in the next paragraph. In contrast to the generalised proposal by Pan23 (see the section ”Discussion”), our post-selection is not energy selective. Nonetheless, our setup exhibits the same effects in the limit of small interaction strengths as clarified in the section “Discussion”.
In the weak interaction stage between pre- and post-selection, we apply a weak DC or RF spin rotation, or a beam attenuation. (For the reference measurements, all weak interactions are turned off.) The interaction strengths are tuned by the DC/RF spin rotation angles \({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}=\pi /9\,\hat{=}\,2{0}^{\circ }\), and the absorption coefficient \({{{{{{{\mathcal{A}}}}}}}}=0.1\) as realised by an Indium foil of 0.125 mm thickness. The absorption differs from the cases of DC/RF spin manipulations as it is not a unitary operation; the conceptual implications will be explained throughout the article. We apply only one interaction in one beam at a time. Any of the three interactions can be applied to any of the three paths, obtaining nine different situations. All interactions are weak and create only small disturbances on the initial state. By combining the results of each single situation, one can infer the locations of each property of the detected neutrons between pre- and post-selection in a realistic interpretation.
The relevant matrices for the spin and energy flips in the DC and RF cases are given by
and
respectively. The path projectors \({\hat{\Pi }}_{j}=\left\vert j\right\rangle \left\langle j\right\vert\) indicate in which path an operation or manipulation is conducted. Then the unitary operators for spin and energy rotations \({\hat{U}}_{j}^{{{{{{{{\rm{DC}}}}}}}}}\) and \({\hat{U}}_{j}^{{{{{{{{\rm{RF}}}}}}}}}\), with the rotation angle αrot around the x-axis in path j, while leaving the states in the other paths unchanged, can be expressed as (detailed calculation in Supplementary Note 1)
The x-direction is always defined by the beam direction in the respective section of the setup (see the section “Adjustment Procedure” for further explanation). Equation (5) indicates that the DC (RF) spin rotation reduces the amplitude of the original spin component (spin/energy component) in the corresponding path j from 1 to \(\cos ({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}/2)\) and creates a spin-flipped (spin/energy-flipped) component of amplitude \(-{{{{{{{\rm{i}}}}}}}}\sin ({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}/2)\). In the limit of small \({\alpha }_{{{{{{{{\rm{rot}}}}}}}}},\sin ({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}/2)\) is linear in αrot/2, while the change of the original component, \(1-\cos ({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}/2)\), is smaller, proportional to \({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}/8\).
The operator \({\hat{A}}_{j}^{{{{{{{{\rm{Abs}}}}}}}}}({{{{{{{\mathcal{A}}}}}}}})\) for a weak absorption is written as
It simply describes an attenuation in path j while all other paths are undisturbed.
To define post-selected states which are discriminated in their energy degrees of freedom, we introduce two ancillary states
and define the weak value33,34,35,36,37 for the hypothetical energy selection of \(\left\vert {{{{{{{{\rm{E}}}}}}}}}_{0}\right\rangle\) as
As we will see shortly, the weak values of the operators \({\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{{{{{{{{\rm{DC}}}}}}}}}{\hat{\Pi }}_{j},{\hat{\Pi }}_{j}\) and \({\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{{{{{{{{\rm{RF}}}}}}}}}{\hat{\Pi }}_{j}\), where j denotes the path, describe our results. The operator \({\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{{{{{{{{\rm{DC}}}}}}}}}{\hat{\Pi }}_{j}\) represents the x-component of the spin in path j, while the operator \({\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{{{{{{{{\rm{RF}}}}}}}}}{\hat{\Pi }}_{j}\) is the x-component of the energy observable in path j which is associated with flipping in the energy system. The calculation of their weak values is straightforward for the initial and final states given in Eqs. (1) and (2) and yields
The Kronecker delta δi,j yields the modulus of the respective weak value. Quantifying the location of properties in the realistic interpretation through the weak values, a modulus of an operator’s weak value of 1, which is one of the operator’s eigenvalues, is attributed to finding the corresponding property in the considered path. A modulus of the weak value of zero excludes finding the property in that path.
With these expressions, the time-averaged intensity I in the post-selected output port of the interferometer, with a weak DC spin rotation applied (DC case) in path j, is written as (details in Supplementary Note 1)
The second and third lines describe the intensity in terms of weak values and terms closely resembling them. The last line gives the expected intensity in terms of phase shifter orientation and chosen path number. An intensity oscillation with an amplitude of order αrot emerges under the condition of the Kronecker delta δj,I, which still gives the modulus of the respective weak value. This condition is met when the weak DC spin rotation is applied in path I. Then, part of the prepared down spin state, which is orthogonal to the reference state, is inverted to the up spin state, which is parallel to the reference state. The down-component is filtered out by the supermirror of the post-selection and the up-component is transmitted to the detector. Simultaneous to the emergence of the intensity oscillation, the mean intensity is increased by the additional parallel component with order \({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}\) as also pointed out in12. The same mean intensity increase is expected from a weak DC spin rotation in the RF-flipped path III because the same up spin component is created which is transmitted through the supermirror. No intensity oscillation due to the differing energies is observable, though, in our time-integrating detection mode. In contrast, by applying the weak DC spin rotation in path II, the portion of the reference beam accepted by the supermirror is decreased with order \({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}\). For small αrot, the first order term is dominant and the reactions to a weak DC spin rotation on the intensity in path I are conspicuous.
A similar result can be derived assuming a weak RF spin rotation (RF case) applied in path j:
The results in the DC and RF cases are similar up to the exchange of δj,I, δj,III, and χ1 in the DC case, respectively, for δj,III, δj,I, and χ2 in the RF case.
In the third case of an added weak absorber (absorber case), the intensity I is described as (details in Supplementary Note 1)
As a result, only an attenuation of the sub-beam in path II with its prepared up spin state will be registered after the post-selection at the detector in the O-beam.
Experimental data
The preparation is implemented by a DC flip in path I and an RF flip in path III. The measured interferograms (IFGs), depicted in Fig. 3, will be called preparational IFGs. The fit function for the time-averaged intensity of all IFGs is of the form
with the mean intensity offset I0 and an intensity oscillation with amplitude B, angular velocity ω, the phase shifter orientation χ, and the phase offset φ. The preparational IFGs characterise the orthogonality of the initial sub-states and are a reference for the quantitative data analysis. Phase shifts are implemented in all three paths, resulting in the three columns of Fig. 3. In addition, three different experimental settings for the initial state, used for different reference measurements as described in the section “Adjustment Procedure”, were realised, giving rise to the three rows in Fig. 3. The obtained contrast values, specified in Table 1, quantify the quality of the preparation. We will refer to the following 3 × 3 arrays of IFGs or numbers as matrices and to their diagonal, off-diagonal, and anti-diagonal elements as in a normal square matrix.
The blue dots indicate the intensities detected in the O-beam normalised by mean intensities plotted against phase shifts induced in the path specified at the bottom. The integration time per point is 90 s with a mean count rate of about 15/s. The blue statistical error bars indicate one standard deviation. The three rows of interferograms in the figure are obtained with different configurations for the preparation (prep) for the direct-current (DC), absorber (abs), and radio-frequency (RF) case as written to the left, which are used for different further reference measurements (see the section “Adjustment Procedure”for further explanation). Contrasts are extracted from sinusoidal fits plotted as solid blue lines. The low contrasts ≤4%, given in Table 1, imply a good preparational quality, i.e. a high degree of orthogonality between the sub-beams.
Finally, when separately applying one of the three weak interactions in one of the three sub-beams, the nine IFGs presented in Fig. 4 were recorded, which will be called weak-interaction IFGs. When comparing the weak-interaction IFGs of Fig. 4 with the preparational IFGs of Fig. 3, conspicuous reactions appear in the coloured diagonal elements of Fig. 4 where either significant intensity oscillations or a significant drop in count rate is produced. Weak values are extracted for all nine situations by comparing the measured IFGs of Figs. 3 and 4 with the predictions from Eqs. (10), (11), and (12) in the limit of small interaction strengths. The detailed data analysis is given in the section “Extraction of Weak Values”. The results are presented in Fig. 5 and Table 2 and approximate the ideal identity matrix given by Eq. (9).
In each row, a different weak interactions is applied, i.e., the direct-current (DC), absorber, and radio-frequency (RF) cases as labelled to the left. The blue dots indicate the intensities recorded in the O-beam, normalised by mean intensities of corresponding preparational interferograms of Fig. 3, plotted against phase shifts induced in the path specified at the bottom. The blue statistical error bars indicate one standard deviation, solid blue curves are fits. The most noticeable reactions compared to the preparational interferograms of Fig. 3 are found in the diagonal elements, coloured in light red. The off-diagonal elements (shown with white background) exhibit only inconspicuous reactions. The symbols in the upper right corners indicate different kinds of situations described in the section “Discussion”.
Graphical presentation of the weak values of the x spin component, path operator, and energy transition operator of each path as presented numerically in Table 2. The light red bars give the moduli of the relevant weak values extracted from interferograms in Figs. 3 and 4 for each path j. The black statistical error bars indicate one standard deviation. The green systematic error bars are estimated in the section “Extraction of Weak Values”. For the path weak values \({\left\langle {\hat{\Pi }}_{j}\right\rangle }_{{{{{{{{\rm{w}}}}}}}}}^{{{{{{{{{\rm{E}}}}}}}}}_{0}}\) of the absorber measurements, not the modulus but the weak value itself is given. Blue crosses indicate the ideal theoretical moduli of weak values which compose an identity matrix.
Discussion
To analyse the emergence of the qCC mathematically, we compare our experiment with the generalized N-path qCC described by Pan23. The generalised case considers N paths (indexed as j) and N − 1 properties of two level systems (indexed as p). The two basis vectors in each Hilbert space of a property will be denoted as 1 and 0. The state vector entering the interferometer is assumed as \(\left\vert 1,1,1,...\right\rangle\). The sub-states in each path are prepared to be mutually orthogonal by flipping the respective state vector of property p in path j = p + 1. (Roman numerals indicating paths will henceforth appear in equations together with Arabic numerals indicating properties.) The according pre-selection \(\left\vert {{{{{{{{\rm{i}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\) is denoted as
The according post-selected state \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\) which is dependent on the phases χj of the phase shifters in path j is chosen as
Please note that there is an analysis in the post-selection for each property p realised by a respective inner product with the post-selected state \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\). Similarly to the previous three-path consideration, the post-selected intensity \({\left\vert \left\langle {{{{{{{{\rm{f}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}| {{{{{{{{\rm{i}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle \right\vert }^{2}\) between pre- and post-selection has only a single non-zero contribution, coming from the component of path I, while the components from the other paths in the initial state \(\left\vert {{{{{{{{\rm{i}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\) are orthogonal to \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\) such that their contributions to the post-selected intensity are zero. This means that, given the pre-selection, only the component of the sub-beam through path I is post-selected. We will therefore refer to path I as the reference beam and all others as non-reference beams in the generalised case. The operator for a manipulation of property p in path j, while leaving the states in all other sub-beams unchanged, is given by (detailed calculation in Supplementary Note 1)
The weak values of the operators \({\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{p}{\hat{\Pi }}_{j}\) are written as
and the path weak values are written as
In addition to the N − 1 properties indexed as p, the “zeroth” property of the generalised case would be the particle behaviour in path I such that a beam attenuation only causes a linear reaction of the mean intensity in path I. This is analogous to Eq. (12) of the three-path consideration.
It follows in an exact calculation (details in Supplementary Note 1), without regarding the limit of small α, that the time-independent intensity behaves as
This expresses the intensity through the related measures of weak values, amplitudes, and experimental parameters. The first line states that the intensity is determined by the inner product between the post-selected state \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\) and the state unitarily rotated by \({\hat{O}}_{j}^{p}(\alpha )\) from the initial state \(\left\vert {{{{{{{{\rm{i}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\). The second line gives the intensity in terms of weak values for given interaction strength α. The weak values are multiplied with sine functions which depend on α. It follows by expanding the intensity for small α that the weak values appear in every order of α. Even though weak values were introduced as low order approximations33, they are the expansion coefficients in the Taylor series38,39 and describe the intensity for arbitrary interaction strengths α. In the third line, the intensity is expressed as the absolute squared of amplitudes from different paths; term 1 is the amplitude from the reference state in path I which is reduced by term 2 if the condition δj,1 = 1, or j = 1, is met. This means any weak interaction implemented in the reference beam will reduce its post-selected component through the inner product in the first line. Term 3 is the amplitude of a non-reference beam in path j which is produced if δj,p+1 = 1, or j = p + 1. The last line gives the intensity dependent on the experimental parameters of the interaction strength α and the phases χ1, χj. The intensity oscillation proportional to \(\sin ({\chi }_{1}-{\chi }_{j})\) is the cross-term between the amplitudes of terms 1 and 3 in the third line. The third and fourth terms in the last line are mean intensity changes which are conditioned through the Kronecker deltas δj,p+1 and δj,1. The data is analysed for second-order intensity changes in the section “Experimental Resources”.
We will go into detail now regarding the first line of Eq. (19) where the intensity is obtained by considering a rotation of the initial state \(\left\vert {{{{{{{{\rm{i}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\) and the inner product with the final state \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\). Therefore, the inner product in Hilbert space between the vectors of the post-selected state and the intermediate state before post-selection is essential. Any changes in the intensity compared to the preparational IFGs are a reaction to a weak interaction. As the weak interactions are unitary and the calculated intensity involves the inner product with \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{{{{{{{{\rm{N}}}}}}}}}\right\rangle\), the reactions are expressed by sinusoidal functions in the last line of Eq. (19). By regarding the parallel and orthogonal components to the post-selected state, we can identify three different kinds of situations:
The first kind of situation arises when a weak interaction is applied to a non-reference beam. Let us consider a perturbation rotating the sub-state of a non-reference beam and thereby generating a state component that is parallel to the post-selected state. This is equivalent to inverting a fraction of the sub-state from the orthogonal to the parallel component. Due to the behaviour given in Eqs. (5) and (16), in the limits of αrot and α becoming zero, the magnitude of the following reaction of the intensity is linear in the interaction strength α. We denote these situations where the intensity has a linear dependence on the interaction strength as sensitive. The large reaction is identified with the behaviour proportional to \(2\sin (\alpha /2)\) given in Eq. (19) for the exact calculation and, in the limit of αrot becoming zero, with the term proportional to αrot in Eqs. (10) and (11). At the same time, the parallel component causes an increased intensity proportional to \(+{\sin }^{2}(\alpha /2)\) in Eq. (19) and proportional to \(+{\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}\) in Eqs. (10) and (11).
The second kind of situation arises if any rotation is applied to the reference beam. Then the amplitude of the post-selected component is reduced. However, in comparison to the first kind of situation, it is only a small reaction proportional to \(-{\sin }^{2}(\alpha /2)\) in Eq. (19) and proportional to \(-{\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}\) in Eqs. (10) and (11). We denote these situations with a dependence of the intensity to the interaction strength of only quadratic of higher order as robust.
The third kind of situation concerns the states of the non-reference beams again, now in combination with unitary rotations which do not produce a post-selected component. Any reaction of the intensity is excluded by the Kronecker deltas and we conclude that in these situations the intensity is independent of the interaction strength. We denote these situations as indifferent to the respective unitary rotations.
To first order, the intensity dependencies on the weak interaction strengths are the same in the generalised and our experimental case. The large first order reactions are seen in the diagonal elements in the weak-interaction IFGs of Fig. 4, which are marked with asterisks (*) in the upper right corners of the graphs. In the same figure, second order reductions in the mean intensities compared to the preparational IFGs are expected to appear in the upper and lower IFGs of the middle column. The small reactions are due to the robustness of the reference beam with respect to rotations which is indicated with crosses ( × ). The differences between the general and our three-path case can be seen in the corner elements of the anti-diagonal in Fig. 4: in the generalised case, these elements should behave indifferently. However, without energy projection in our post-selection, we expect an increase in intensity proportional to \(+{\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}\). This is caused by the up spin components created by the weak interactions that produce additional counts without time-independent interference (explained in second paragraph of the section “Results”). Additionally, the left and right IFGs in the absorber case in Fig. 4 are indifferent in accordance with Eq. (12), as indicated with dashes (–). These situations do not involve rotations, however, and concern the location of the particle which is not explicitly regarded as a property by Pan.
Finally, we consider the weak values again. According to the considerations on the inner product between the state vectors, if the modulus of a weak value is zero, the intensity does not have a linear dependence on the interaction strength α. Then, the intensity is either robust or indifferent to the weak interaction in the considered path. If the modulus of a weak value is 1, it identifies a combination of path and weak interaction in which the intensity is sensitive to the weak interaction.
The sensitive behaviour is an interference effect emerging through the cross-term of amplitudes between the sub-beams I and j proportional to \(\sin ({\chi }_{1}-{\chi }_{j})\), cf. Eqs. (19) and (S.6) in Supplementary Note 1. The magnitude of the cross-term is linear in α for small interaction strengths. Therefore, the cross-term describes the conspicuous reactions of the intensity. Because the cross-term involves two paths, it offers an interpretation of delocalisation of properties in the interferometer40.
An alternative interpretation proposed by Aharonov et al.10 is inspired by realism and quantifies the location of a property in a path through the weak values. A weak value of 1 is attributed to finding the property in that path; a value of zero excludes finding the property in that path. We identify these values with the modulus of the weak values in the present experiment which is equivalent for phase shifter positions χ1 = χ2 = 0. According to the latter interpretation, with the present results of Fig. 5 and Table 2, the neutron’s x spin component is in path I, the particle in path II, and a third degree of freedom in path III which only reacts to a coupled spin-energy manipulation. This third degree of freedom is strongly connected to the neutron’s x component of the energy qubit in path III and we identify this as the energy degree of freedom; a spatial separation of the neutron’s properties inside the interferometer is observed.
But how is the interpretation of separated properties compatible with the pre-selected state \(\left\vert {{{{{{{\rm{i}}}}}}}}\right\rangle\) of Eq. (1) where a specific value for spin and energy is attributed to each sub-state? Initially, the neutron is distributed equally over all three paths, indicated by the expectation value \(\big\langle {{{{{{{\rm{i}}}}}}}}| {\hat{\Pi }}_{j}| {{{{{{{\rm{i}}}}}}}}\big\rangle =1/3\) for all paths. While we have so far considered only one particular final state, one could in principle also monitor all possible final states denoted by \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{m}\right\rangle\), where m is an index over all combinations of exit beam, spin state and energy state. This set of states is orthonormal and complete and we can express any expectation value as a weighted average over the weak values41,42. The expectation value of the path projector then reads
where pm denotes the probability for a given \(\left\vert {{{{{{{\rm{i}}}}}}}}\right\rangle\) of reaching the final state \(\left\vert {{{{{{{{\rm{f}}}}}}}}}_{m}\right\rangle\). Therefore, if we do not observe any intensity change when applying a weak beam attenuation in path I, it doesn’t exclude a non-zero component to the state vector in that path. But it means that the component only contributes to intensities in other exit channels. However, for all neutrons that did reach our final state we can retrospectively say that these neutrons never were in path I.
As for the spin degree of freedom (likewise for the energy), the expectation value of the joint operator \({\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{{{{{{{{\rm{DC}}}}}}}}}{\hat{\Pi }}_{j}\) yields the x-component of the spin in path j. For our initial state, this value becomes zero in all paths, \(\left\langle {{{{{{{\rm{i}}}}}}}}| {\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{{{{{{{{\rm{DC}}}}}}}}}{\hat{\Pi }}_{j}| {{{{{{{\rm{i}}}}}}}}\right\rangle =0\), because the spin in each path is prepared in the ± z directions and therefore has equal probabilities in ± x directions12. Nevertheless, the weak value associated with our post-selected final state \({\left\langle {\hat{\sigma }}_{{{{{{{{\rm{x}}}}}}}}}^{{{{{{{{\rm{DC}}}}}}}}}{\hat{\Pi }}_{{{{{{{{\rm{I}}}}}}}}}\right\rangle }_{{{{{{{{\rm{w}}}}}}}}}={{{{{{{{\rm{e}}}}}}}}}^{2{{{{{{{\rm{i}}}}}}}}{\chi }_{1}}\) does not become zero, cf. Eq. (9). The expectation value of zero results from the compensation by a similar weak value with opposite sign in another output port of the interferometer, which is in our setup the down spin component in the side exit of the front loop. (The front loop is encircled by sub-beams I and II.) The opposite sign results from the phase shift of π which always appears between the two output ports of an interferometer loop.
Only for weak beam attenuations, both considered interpretations agree that the weak values give the locations in the interferometer of the neutrons found in our output port \(\left\vert {{{{{{{\rm{f}}}}}}}}\right\rangle\). For the weak interactions with spin and energy, the interference effect allows for the conservative interpretation of a delocalisation of properties.
All weak interactions applied in our experiment cause similar reactions locally – in the respective path. But it is the inner product of the weakly manipulated state with the post-selected state which can generate a post-selected amplitude. In turn, this amplitude constitutes a cross-term in the intensity linear to the interaction strength. Only for distinct pairs of paths and weak interactions, the reactions are conspicious for a particular final state. We suggest to regard the conspicious reactions to give the effective locations. In context of the qCC, where each property is effectively located in a different path we suggest the term effective separation of properties. The further reaching interpretation of a physical separation of properties is not required to describe all observed phenomena. While we cannot decide between effective and physical separation with the present experiment, the realistically inspired interpretation of physically separated properties would need extraordinary evidence as verification. Therefore, at the present moment, we do not attribute physical reality to the interpretation of separated properties, neither for an ensemble of nor for single neutrons themselves.
Conclusion
A three-path quantum Cheshire Cat is demonstrated in neutron interferometry; the neutron, its spin and its energy appear to be in different paths of the interferometer. In the experiment, a state preparation (pre-selection) as well as a state filtration (post-selection) are implemented. Even though the post-selection is without energy discrimination, the quantum Cheshire Cat in the three-path interferometer emerges as predicted by the theory. The conspicuous reactions to the local weak interactions are used to infer the locations of the properties of the neutron. Intensity oscillations emerge when a weak spin or energy manipulation is applied, while the intensity is reduced for the weak beam attenuation applied. These reactions are observed only for a particular interaction for each path. Taking a realistic viewpoint, one may conclude that the neutrons propagate through the interferometer, with the particle, energy, and the spin’s x-component taking different paths.
However, the intensity is calculated through the inner product of the weakly manipulated state with the post-selected state and its absolute value squared. Only for distinct pairs of weak interactions and paths they are applied in, a certain component parallel to the reference state, i.e., the component originally remaining through the post-selection, is generated. The respective generated amplitude constitutes a cross-term between the amplitude of the weakly evolved sub-beam and the reference state. The cross-term gives rise to a conspicuous interference effect which in turn suggests the delocalisation of properties. This suggests the possible explanation of the effect not as physical but as effective separation of properties in the interferometer.
Methods
Adjustment Procedure
We defined the z-axis vertically and the x-axis by the local beam direction in each section of the interferometer. Alternatively, one could differentiate between the orientations of the coils by explicitly defining global x- and y-axes. This would add a phase shift to certain spin components. But since our analysis of the data does not require a detailed justification of the phase shift between preparational and weak interaction IFGs, we simply determined the phase shift from the fitting parameters (see the section “Extraction of Weak Values”).
Each pair of sub-beams constitutes an interference loop. They are referred to as front, rear and outer loop which are composed, respectively, of beams I and II, beams II and III, and beams I and III. To confirm the initial coherence of the sub-beams in the interferometer, IFGs of the interferometer empty of any local fields or absorbers were recorded which are depicted in Fig. 6. In the left case of Fig. 6 only PS1 was rotated and PS2 was oriented such that the rear loop passes on a maximum intensity in O-direction (see Fig. 2). Likewise, in the right case only PS2 was rotated and PS1 was oriented such that the front loop passes on a maximum intensity towards the last interferometer plate. In the middle case, both PS1 and PS2 are initially oriented such that a maximum intensity is acquired in O-direction. The IFG is then recorded by simultaneously rotating both PS1 and PS2 to induce a relative phase between the reference beam II and the other two sub-beams. Contrasts ≥ 50 % were reached which indicate the moderate level of coherence achievable with our interferometer in the respective loops. The specific values, given in the caption of Fig. 6, are used in the data analysis of the section “Extraction of Weak Values” to compare the observed contrasts when applying weak interactions.
The blue dots indicate the intensity detected in the O-beam normalised by mean intensity plotted against phase shift induced in the path specified at the bottom. The integration time per point is 30 s with a mean count rate of about 50/s. The blue statistical error bars indicate one standard deviation. Contrasts are extracted from the respective sinusoidal fits plotted as solid blue lines. The contrasts from left to right of 57(1) %, 53(3) %, and 50(2) % indicate the achievable level of coherence.
For both DC and RF coils, the currents for a spin flip have to be adjusted. These currents regulate the magnetic fields in x- and z-direction of each coil. The frequency for the RF coils was chosen to be 60 kHz. This corresponds to a resonant field of about 20 G = 2 mT local guide field strength. A global guide field of about 10 G was applied to allow for both RF and DC spin rotations: while this field was compensated to a net zero z-field in coils when applying DC rotations, it was approximately doubled to meet the flip condition for RF rotations. This combination minimises inhomogeneities in the fields of the miniature spin rotators43,44. To roughly adjust and determine the flip currents in both the DC as well as RF coils, only the respective sub-beam was used, while all others were blocked by beam stoppers. This composes a polarimetric setup and the intensity was measured with varied z-field and rotation currents. Estimates for guide field compensation (DC case) and amplification (RF case) were determined as well as for the currents/amplitudes Iflip for the x-fields of DC and RF flips. After that an interferometric method was used to ensure low initial contrasts: as spin flips produce an orthogonal state compared to the reference beam of path II, interferograms have minimal contrast at the flip conditions. When recording several interferograms with slightly varied currents I applied as described in the polarimetric case above, the resulting contrasts should have a sharper minimum due to the behaviour proportional to \(| \sin (I-{I}_{{{{{{{{\rm{flip}}}}}}}}})|\) which is locally proportional to I − Iflip. This has to be compared to the direct polarimetric approach with its cosine behaviour of the intensity which is locally proportional to \({(I-{I}_{{{{{{{{\rm{flip}}}}}}}}})}^{2}\) at its differentiable minimum.
A typical adjustment scan is depicted in Fig. 7 where the contrast is found the lowest at 1.5 A. To both sides of that value, the contrast is increasing at the lowest order linearly. A residual contrast of about 3% remains which is dominant in a small current interval at the minimum and which quantifies the overall spin manipulation efficiency of the setup. A principal source for reduced spin manipulation efficiencies ϵI, ϵIII in paths I and III are the field inhomogeneities over the beam cross-section. The systematic errors of the preparational contrast are estimated in the section “Extraction of Weak Values”.
The blue dots indicate the contrasts recorded with a radio-frequency (RF) spin flipper in operation and the current I for its local guide field amplification varied. The blue statistical error bars indicate one standard deviation, solid blue curve is the fit. Around the minimum at Iflip, the contrast has a local behaviour proportional to ∣I − Iflip∣ and therefore a sharper minimum than with a polarimetric approach via the intensity.
The efficiencies can be estimated by assuming a pure state but with components unaffected by the preparing DC and RF flippers. The component ϵI is spin flipped by the DC flipper in path I, while the remaining component stays in the reference state. Similarly, the component ϵIII is spin-energy flipped by the RF flipper in path III, while the remaining component stays in the reference state. The unaffected components are still coherent and interfere at recombination with the reference state from path II; a residual final contrast is observed. This reasoning can be extended to the weak measurement IFGs where the weak interactions modify the spin manipulation efficiencies to the values \({\epsilon }_{{{{{{{{\rm{I}}}}}}}}}^{{\prime} },{\epsilon }_{{{{{{{{\rm{III}}}}}}}}}^{{\prime} }\) and according contrast values for the off-diagonal elements of Fig. 4.
To meet the resonance condition for spin rotations, the external guide field is locally suppressed by a compensation field for the weak DC rotations, while it is locally increased for the weak RF rotations. All local fields create stray fields and switching them on and off induces field offsets and inhomogeneities in the adjacent coils which lower the efficiency of their spin manipulations. The offsets can be compensated with our devices but the inhomogeneities cannot.
Therefore, in the weak RF measurements, we chose to leave the local guide field amplification permanently turned on and compensate the field offset in the adjacent coils. Then only the RF-field is turned on and off rather than both the RF and z-fields. This technique lowers the efficiency of the manipulations through the inhomogeneities in the preparational cases but increases the overall efficiency when the weak interactions are applied. The technique cannot be applied in the DC case because it would create a zero-field region which induces depolarisation. Consequently, there are different preparational adjustments applied which ought to produce the same pre-selected state. This is the reason why there are multiple rows of preparational IFGs and their contrasts in Fig. 3 and Table 1.
The weak interaction IFGs were recorded in combination with the preparational IFGs in an alternating “on”/"off” scheme, i.e. by turning the weak interaction on and off, before moving the phase shifter to the next orientation. This measurement protocol ensures the comparability of phase and contrast of the “on” and “off” IFGs which is needed in the data analysis. The IFGs with absorbers were not recorded in an ‘on”/"off” scheme but right after each other while ensuring stable phase relations via the thermal control system.
Experimental Resources
For the given pre- and post-selection of Eqs. (1) and (2), the contrast of IFGs is ideally zero. As can be seen from Fig. 3 and Table 1, lower contrasts were achieved in the DC and absorber cases compared to the RF case. This is expected when implementing the technique described in the section “Adjustment Procedure”. On the other hand, the technique should increase the quality of the weak RF spin rotations. However, the weak value deviating the most from the theory is in the case of a weak RF interaction in path III where it is obtained as 0.75 compared to the prediction of 1, cf. Fig. 5, Table 2, and Eq. (9). As the coil for the preparational RF spin flip in path III is close to the coil inducing the weak RF rotation (see Fig. 2), their interaction in terms of electrical oscillating circuits could have induced unintended additional spin manipulations.
Again, the weak value for the RF case in path III deviates from the theory. The deviations of all the other weak values from their expectations are of the magnitude of their statistical errors. The errors are of the same magnitude for all elements as the decreased error of the amplitude for IFGs with low contrast is partly compensated by the increased error of the phase, see Eq. (23) in the data analysis below. Furthermore, we extract only the modulus of the weak values for spin and energy observables. Thus, these off-diagonal weak values cannot be distributed symetrically around zero.
The energy changes produced with the RF coils are coupled with spin flips in our experiment. This is in principle avoidable when using a combination of an RF and a DC spin flipper instead. The first one flips the energy and spin vector, while the second one flips the spin vector back to the initial orientation. This effectively produces an energy change without spin manipulation.
Since both spin and energy in our experiment are treated as two-level systems, four possible combinations exist which are orthogonal to each other. The keen reader might have noticed that one of them, the state \(\left\vert \uparrow ,{{{{{{{{\rm{E}}}}}}}}}^{{\prime} }\right\rangle\), was not mentioned, yet. This fourth state could only be produced by a combination of both a DC spin flip and an RF spin flip as described in the previous paragraph. This state has a particular character as it is expected to exhibit no conspicuous reaction to any single weak interaction – neither of DC nor RF spin rotations.
When applying the weak interactions in our experiment, changes in the mean intensities compared to the preparational IFGs are expected in seven of the nine situations, where the term situation now refers to a combination of a specific weak interaction applied in a specific path. For the weak beam attenuations, the intensity changes directly give the path weak values of Eqs. (9) and (12), Fig. 5, and Table 2. For the unitary spin/energy manipulations, the mean intensity changes correspond to the terms proportional to \(\pm {\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}\) in Eqs. (10) and (11). (In the exact calculation of Eq. (19), the mean intensity changes are represented by the terms proportional to \(\pm {\sin }^{2}(\alpha /2)\).) In our experiment, the intensities are expected to increase by \({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}/4\approx 3 \%\) when inducing weak unitary rotations in paths I or III, while a decrease of the same amount is expected for weak unitary rotations induced in path II. The measured intensity changes between the IFGs of Figs. 3 and 4 are given in Fig. 8 and Table 3. The theoretical prediction and the experimental results show reasonable agreement. Their comparison suffices to establish higher order reactions which demonstrate that the intensity changes in all three paths through the unitary weak interactions as described in12,13. But a higher statistical precision will be necessary to quantitatively confirm the theoretically predicted intensity changes.
Graphical presentation of relative changes between mean intensities Iweak of weak measurement interferograms (IFGs) in Fig. 4 normalised with mean intensities Iprep of preparational IFGs in Fig. 3 for each combination of weak interaction and path. Grey bars refer to an increase in intensity, pink ones to a decrease. The black statistical error bars indicate one standard deviation. Blue crosses indicate the values expected from theory. The normalised intensities are directly given in Table 3. In the absorber case (abs) described by Eq. (12), an intensity drop proportional to \({{{{{{{\mathcal{A}}}}}}}}\) of 10% is expected in path II. In the direct-current (DC) and radio-frequency (RF) cases described by Eqs. (10) and (11), intensity changes proportional to \({\alpha }_{{{{{{{{\rm{rot}}}}}}}}}^{2}\) of approximately ± 3% are expected.
Extraction of Weak Values
Parameters in this section with indices “empty”, “prep” and “weak” correspond to the three types of interferograms recorded, respectively, with either no elements in the interferometer, with the preparational DC and RF flip applied, and an additional weak interaction applied. To read out the signal generated by the weak interaction, we assume that, in the case of the weak interaction IFGs, the time-independent intensity oscillation of Eq. (13) is the sum of two independent oscillations:
Therein, the “signal” refers to the changes in the IFGs from the preparational case to the weak interaction case. The amplitude and phase of the signal can be retrieved by comparing interferograms of the sets consisting of an interferogram with only the preparation applied and an interferogram with an additional weak interaction applied. The signal amplitude Bsignal and its statistical error ΔBsignal follow from Eq. (21) as
and
The weak values are extracted by comparing experimental data with the theoretical prediction. By substituting the second last equality in Eq. (S.3) in Supplementary Note 1 into Eq. (21) and neglecting terms of order higher than αrot, we obtain
This includes the correction considering the maximum experimental contrast Cempty of the empty interferometer given through the fits in Fig. 6. The index j of the path where the rotation is implemented is omitted here. We can drop the oscillation proportional to Bprep already present in the preparational IFGs as it is an experimental imperfection and does not represent the behaviour described by weak values. It is however included through the error propagation of Eq. (23). Furthermore, we can insert \({\left\vert \left\langle {{{{{{{\rm{f}}}}}}}}| {{{{{{{\rm{i}}}}}}}}\right\rangle \right\vert }^{2}={I}_{0,{{{{{{{\rm{prep}}}}}}}}}\approx {I}_{0,{{{{{{{\rm{weak}}}}}}}}}\). In this context, it is important to discern between the phase \({\chi }^{{\prime} }\) of the wave function and the phase shifter position χ that are related via \({\chi }^{{\prime} }={\omega }_{{{{{{{{\rm{empty}}}}}}}}}\chi +const.\) such that \({\omega }_{{{{{{{{\rm{empty}}}}}}}}}\chi +{\varphi }_{{{{{{{{\rm{signal}}}}}}}}}={\chi }^{{\prime} }+{\varphi }_{{{{{{{{\rm{signal}}}}}}}}}^{{\prime} }\). It follows that
Since this relation must hold for all \({\chi }^{{\prime} }\), the imaginary part of the weak value must be sinusoidal as obtained in Eq. (9). Furthermore, the cosine function and the imaginary part of the weak value must have the same frequency and be in phase. The weak values of Eq. (9) all have constant moduli and we also assume this to hold for all extracted weak values. Thus we finally obtain in first order of αrot the measured modulus of the weak value
and its statistical error
The same steps lead to a similar result for the RF case. For the case of weak absorption, we measured the absorption coefficient of the Indium foil with a single interferometer path as
We substitute the second last line in Eq. (S.4) in Supplementary Note 1 into Eq. (21) such that
The index j of the path where the absorption is implemented is omitted again. Both oscillations can be neglected as they neither describe a reaction to the weak absorption nor change the mean intensity. With similar steps as for the DC case we calculate
with the effective absorption coefficient \({{{{{{{{\mathcal{A}}}}}}}}}_{{{{{{{{\rm{w}}}}}}}}}\) in the path of the interferometer where the absorber is inserted written as
The propagated statistical error of the path weak value is given by
An estimation of the upper boundaries of systematic errors is given in Table 4.
Data availability
The data that support the findings of this study are available at https://doi.org/10.5291/ILL-DATA.CRG-2880.
References
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Bell, J. S. On the Einstein-Podolsky-Rosen paradox. Physics (Long Island City, N.Y.) 1, 195–200 (1964).
Schrödinger, E. Die gegenwärtige situation in der Quantenmechanik. Naturwissenschaften 23, 807–812 (1935).
Schrödinger, E. Die gegenwärtige situation in der Quantenmechanik. Naturwissenschaften 23, 823–828 (1935).
De Broglie, L. Recherches sur la théorie des quanta. Ann. Phys. 10, 22–128 (1925). (French).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Ourjoumtsev, A., Tualle-Brouri, R., Laurat, J. & Grangier, P. Generating optical Schrödinger Kittens for quantum information processing. Science 312, 83–86 (2006).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge University Press, 2010).
Neamen, D.Semiconductor Physics and Devices: Basic Principles, 25–57. McGraw-Hill international edition (McGraw-Hill, 2012). https://books.google.at/books?id=7P9tzgAACAAJ.
Aharonov, Y., Popescu, S., Rohrlich, D. & Skrzypczyk, P. Quantum Cheshire Cats. New J. Phys. 15, 113015 (2013).
Carroll, L. Alice’s Adventures in Wonderland (MacMillan & Co., London, 1866).
Stuckey, W., Silberstein, M. & McDevitt, T. Concerning quadratic interaction in the quantum Cheshire Cat experiment. Int. J. Quantum Found. 2, 17 (2016).
Denkmayr, T. et al. Experimental observation of a quantum Cheshire Cat in matter-wave interferometry. Nat. Commun. 5, 4492 (2014).
Atherton, D. P., Ranjit, G., Geraci, A. A. & Weinstein, J. D. Observation of a classical Cheshire cat in an optical interferometer. Opt. Lett. 40, 879–881 (2015).
Ashby, J. M., Schwarz, P. D. & Schlosshauer, M. Observation of the quantum paradox of separation of a single photon from one of its properties. Phys. Rev. A 94, 012102 (2016).
Corrêa, R., Santos, M. F., Monken, C. H. & Saldanha, P. L. ‘Quantum Cheshire Cat’ as simple quantum interference. New J. of Phys. 17, 053042 (2015).
Duprey, Q., Kanjilal, S., Sinha, U., Home, D. & Matzkin, A. The Quantum Cheshire Cat effect: theoretical basis and observational implications. Ann. Phys. 391, 1–15 (2018).
Das, D. & Pati, A. K. Teleporting grin of a quantum Chesire Cat without cat. Preprint at https://arxiv.org/abs/1903.04152 (2019).
Liu, Z.-H. et al. Experimental exchange of grins between quantum Cheshire cats. Nat. Commun. 11, 3006 (2020).
Kim, Y. et al. Observing the quantum Cheshire cat effect with noninvasive weak measurement. npj Quantum Inform. 7, 13 (2021).
Sau, S., Ghoshal, A., Das, D. & Sen, U. Isolating noise and amplifying signal with quantum Cheshire cat. https://arxiv.org/abs/2203.00254 (2022).
Li, J.-K. et al. Experimental demonstration of separating the wave-particle duality of a single photon with the quantum Cheshire cat. Light Sci. Appl. 12, 18 (2023).
Pan, A. K. Disembodiment of arbitrary number of properties in quantum Cheshire cat experiment. Eur. Phys. J. D 74, 151 (2020).
Rauch, H. & Werner, S. A. Neutron Interferometry (Oxford University Press, 2000).
Klepp, J., Sponar, S. & Hasegawa, Y. Fundamental phenomena of quantum mechanics explored with neutron interferometers. Prog. Theor. Exp. Phys. 2014. https://doi.org/10.1093/ptep/ptu085 (2014).
Sponar, S., Sedmik, R. I. P., Pitschmann, M., Abele, H. & Hasegawa, Y. Tests of fundamental quantum mechanics and dark interactions with low-energy neutrons. Nat. Rev. Phys. 3, 309–327 (2021).
Badurek, G., Buchelt, R. J., Kroupa, G., Baron, M. & Villa, M. Permanent magnetic field-prism polarizer for perfect crystal neutron interferometers. Physica B 283, 389–392 (2000).
Badurek, G., Rauch, H. & Tuppinger, D. Neutron interferometric double-resonance experiment. Phys. Rev. A 34, 2600–2608 (1986).
Sponar, S. et al. Coherent energy manipulation in single-neutron interferometry. Phys. Rev. A 78, 061604 (2008).
Hasegawa, Y. et al. Engineering of triply entangled states in a single-neutron system. Phys. Rev. A 81, 032121 (2010).
Shen, J. et al. Unveiling contextual realities by microscopically entangling a neutron. Nat. Commun. 11, 930 (2020).
Lu, S. et al. Operator analysis of contextuality-witness measurements for multimode-entangled single-neutron interferometry. Phys. Rev. A 101, 042318 (2020).
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351–1354 (1988).
Duck, I. M., Stevenson, P. M. & Sudarshan, E. C. G. The sense in which a “weak measurement" of a spin-1/2 particle’s spin component yields a value 100. Phys. Rev. D 40, 2112–2117 (1989).
Watanabe, S. Symmetry of physical laws. Part III. Prediction and retrodiction. Rev. Mod. Phys. 27, 179–186 (1955).
Aharonov, Y., Bergmann, P. G. & Lebowitz, J. L. Time symmetry in the quantum process of measurement. Phys. Rev. 134, B1410–B1416 (1964).
Aharonov, Y. & Vaidman, L. The two-state vector formalism of quantum mechanics: an updated review. Preprint at https://arxiv.org/abs/quant-ph/0105101 (2007).
Cheon, T. & Poghosyan, S. Weak value expansion of quantum operators and its application in stochastic matrices. Preprint at https://arxiv.org/abs/1306.4767 (2013).
Dziewior, J. Weak Measurements 44–52 (Ludwig-Maximilians-Universität München, 2016). https://xqp.physik.uni-muenchen.de/publications/files/theses_master/master_dziewior.pdf.
Canton, S. E. et al. Direct observation of Young’s double-slit interferences in vibrationally resolved photoionization of diatomic molecules. Proc. Natl Acad. Sci. 108, 7302–7306 (2011).
Hosoya, A. & Shikano, Y. Strange weak values. J. Phys. A: Math. Theor. 43, 385307 (2010).
Hall, M. J. W., Pati, A. K. & Wu, J. Products of weak values: Uncertainty relations, complementarity, and incompatibility. Phys. Rev. A 93, 052118 (2016).
Geppert, H., Denkmayr, T., Sponar, S., Lemmel, H. & Hasegawa, Y. Improvement of the polarized neutron interferometer setup demonstrating violation of a Bell-like inequality. Nucl. Instrum. Methods Phys. Res. A 763, 417–423 (2014).
Danner, A., Demirel, B., Sponar, S. & Hasegawa, Y. Development and performance of a miniaturised spin rotator suitable for neutron interferometer experiments. J. Phys. Commun. 3, 035001 (2019).
Acknowledgements
The authors are grateful to Michael Jentschel for his courteous aid in the preparation of the water cooling system and the ILL for its continued hospitality. We thank Alok Kumar Pan and Andreas Dvorak for fruitful discussion, and Erwin Jericha for his critical response concerning the terminology of properties. This work was financed by Austrian science fund (FWF) Projects Nos. P 34105, P 30677, and P 27666. Y.H. is partly supported by KAKENHI Project No. 18H03466.
Author information
Authors and Affiliations
Contributions
A.D., R.W., and Y.H. conceived the experiment, A.D. and H.L. prepared it, A.D., N.G., H.L., and R.W. conducted it, A.D. and Y.H. analysed the data, A.D. wrote the paper with contributions from N.G., H.L., R.W., S.S., and Y.H.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests
Peer review
Peer review information
Communications Physics thanks Yutaka Shikano, Xiao-Ye Xu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Danner, A., Geerits, N., Lemmel, H. et al. Three-path quantum Cheshire cat observed in neutron interferometry. Commun Phys 7, 14 (2024). https://doi.org/10.1038/s42005-023-01494-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01494-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.