Abstract
Einstein’s theory of general relativity and quantum theory form the two major pillars of modern physics. However, certain inertial properties of a particle’s intrinsic spin are inconspicuous while the inertial properties of mass are well known. Here, by performing a neutron interferometric experiment, we observe phase shifts arising as a consequence of the spin’s coupling with the angular velocity of a rotating magnetic field. This coupling is a purely quantum mechanical extension of the Sagnac effect. The resulting phase shifts linearly depend on the frequency of the rotation of the magnetic field. Our results agree with the predictions derived from the Pauli–Schrödinger equation.
Similar content being viewed by others
Introduction
The principle of equivalence of inertial and gravitational masses is a corner stone of Einstein’s theory of general relativity.1 It follows from this principle that one cannot locally distinguish between inertial forces and pseudo-forces. Examples of pseudo-forces are the gravitational force, as experienced in the presence of a massive object, or Coriolis and centrifugal forces, which originate from circular motion of an observer in a non-inertial frame of reference. In terms of wave phenomena and in a rotating frame, the respective phase shifts are described by additional couplings compared to an inertial frame. The Sagnac effect2 refers to the observed phase shift induced between two counter-rotating light waves in a rotating interferometer. The phase shift is proportional to the scalar product of the rotation frequency and the area of the installed interferometer. This can also be written in the Hamiltonian \(\hat{H}^{\prime}\) as a coupling \(\sim \!{\overrightarrow{\Omega }}\cdot \overrightarrow{L}\) between the rotation vector \(\overrightarrow{\Omega }\) and the orbital angular momentum \(\overrightarrow{L}\) of the light wave around the center of rotation. The Sagnac effect for the de Broglie waves of neutrons was first demonstrated experimentally in the late 1970s.3 The orbital angular momentum in the coupling term of the Sagnac effect contains the mass which is usually the quantity associated with inertia.
In quantum theory the inertial properties of a particle are influenced not only by its inertial mass, but also by its spin. When solving Dirac’s equation in accelerated frames of reference in the non-relativistic regime, the Hamiltonian of a particle includes the term \(-\overrightarrow{\Omega }\cdot \overrightarrow{J}\),4 where \(\overrightarrow{\Omega }\) is the rotation vector of the frame and \(\overrightarrow{J}=\overrightarrow{L}+\overrightarrow{S}\) is the total angular momentum of the particle with the contribution \(\overrightarrow{S}\) of the spin angular momentum. The additional term \(\sim\!{\overrightarrow{\Omega}}\cdot \overrightarrow{S}\) is called spin-rotation coupling.
To measure the spin-rotation coupling, Mashhoon first published a proposal by S. A. Werner for an experiment involving a rotating neutron interferometer5 (in an arrangement insensitive to the Sagnac and gravity effects). In the further course, Mashhoon et al. suggested interferometer setups where longitudinally polarized neutrons pass through a rotating spin flipper6 which is in turn equivalent to a rotating magnetic field.7 The authors of Mashhoon et al.6 stated that “the phenomenon of spin-rotation coupling is of basic interest since it reveals the inertial properties of intrinsic spin.” For further theoretical contributions about spin-rotation coupling consider.8,9,10,11,12,13 One of them12 even doubted the existence of spin-rotation coupling for fermions. Recently, we reported on neutron polarimeter experiments14,15 whose measurement results can be attributed to the coupling of the neutron’s spin with the rotation of a magnetic field. However, the results of these experiments rely on the rotation of the polarization vector which can also be described with the semi-classical Bloch equations. Therefore, these previous results could in principle be reproduced with a classical magnetic moment.
In this letter, we present the results of the neutron interferometric experiment as suggested by Mashhoon and Kaiser.7 The relative phase between the partial wave functions of paths I and II in the interferometer is directly measured. By applying a direct measurement of the relative phase, instead of measuring the rotation of the polarization vector as in a polarimeter experiment, the purely quantum mechanical aspect of the spin-rotation coupling is demonstrated. This aspect is discussed in more detail in a later section.
Neutron interferometry16,17,18 is a technique to observe the interference effect of matter waves passing through a perfect silicon-crystal interferometer. It is an established, powerful tool to investigate fundamental quantum mechanical concepts with massive particles. Using neutron interferometry the 4π spinor symmetry of fermions,19,20 the spin-superposition law21,22 and the equivalence principle23,24 have been demonstrated.
Results
Theory
Let us consider an observer rotating relative to an inertial observer as discussed in Mashhoon.5 The wave function \(\psi ^{\prime} (\overrightarrow{r},t)\), with respect to the rotating frame of reference, is given by the wave function \(\psi (\overrightarrow{r},t)\) in the inertial frame as \(\psi ^{\prime} =\hat{U}\psi\). The unitary operator \(\hat{U}\) is given by \(\hat{U}=\exp ({\rm{i}}\ \overrightarrow{\Omega }\cdot \overrightarrow{J}t/\hslash )\), with \(\overrightarrow{J}\) being the total angular momentum, consisting of orbital and spin angular momentum. If the wave function \(\psi\) satisfies the Schrödinger equation \(\hat{H}\psi ={\rm{i}}\hslash \ \partial \psi /\partial t\), the wave function \(\psi ^{\prime}\) represents a solution of the Schrödinger equation \(\hat{H}^{\prime} \psi ^{\prime} ={\rm{i}}\hslash \ \partial \psi ^{\prime} /\partial t^{\prime}\) with \(\hat{H}^{\prime} =\hat{U}\hat{H}{\hat{U}}^{\dagger }-\overrightarrow{\Omega }\cdot \overrightarrow{J}\). A detailed comparison of the latter equations4,10 reveals the existence of a new effect associated with the coupling of intrinsic spin with rotation which is expressed by the Hamiltonian \(\delta {\hat{H}}_{{\rm{SR}}}^{\prime}=-\gamma \ \overrightarrow{\Omega }\cdot \overrightarrow{S}\) with the Lorentz factor \(\gamma\). As suggested by Mashhoon, the effect can indeed be derived as done before (e.g. Weinfurter and Badurek25) by solving the Pauli–Schrödinger equation in the lab frame for the interaction of the spin of a free neutron in a magnetic field with angular velocity \(\Omega\).
For a neutron propagating in +y-direction through an uniformly rotating magnetic field, which is expressed as \(\overrightarrow{B}(\Omega ,t)={B}_{1}{\left(\cos \left(\Omega t\right),0,\sin \left(\Omega t\right)\right)}^{T}\), a solution is given by
where \(\xi(t)\) generates the rotation of the initial spin state in the rotating frame \(\xi_{rot}(0)\) and is given as
with the vector \({\overrightarrow{\sigma }}_{{\rm{rot}}}\) comprising the Pauli matrices. The operator \({e}^{\frac{{\rm{i}}}{\hslash }\Omega {S}_{y}t}\) is the transformation from the rotating into the laboratory frame while the operator \({e}^{-\frac{{\rm{i}}}{2}{\overrightarrow{\alpha }}_{{\rm{rot}}}\cdot {\overrightarrow{\sigma }}_{{\rm{rot}}}}\) describes the spin evolution in the rotating frame with the operators acting accordingly. The magnitude of the rotation vector \({\overrightarrow{\alpha }}_{{\rm{rot}}}(t)={({\omega }_{1}t,\Omega t,0)}^{T}\) is given by
where the definition of the Larmor frequency \({\omega }_{1}=-\frac{2\mu }{\hslash }{B}_{1}\) is used and where \(\mu\) is the magnetic moment of the neutron. Both operators \(\hat{U}(\Omega )\) and \(\hat{U}({\overrightarrow{\alpha }}_{{\rm{rot}}})\) include a term \(\sim\!{\overrightarrow{\Omega}}\cdot \overrightarrow{S}\) while the operator \(\hat{U}({\overrightarrow{\alpha }}_{{\rm{rot}}})\) also includes the effect of the Larmor precession.
Experimental Setup
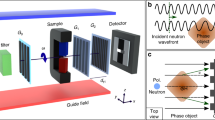
To directly confirm the consequences of spin-rotation coupling, the following experiment was carried out at the neutron interferometry station S18 at the high-flux reactor of the Institut Laue-Langevin (ILL) in Grenoble. The setup after the monochromator and polarizer is schematically illustrated in Fig. 1. The incoming beam, with initial polarization vector \(\overrightarrow{P}=\langle \overrightarrow{\sigma }\rangle\) parallel to the direction of flight (\({\hat{e}}_{y}\)), is coherently split at the first interferometer plate in two parts, the transmitted beam I and the reflected beam II. Both beams are reflected by plates three and two, respectively, and recombined at the fourth plate. The intensity of the +y-component of the polarization vector of the exit beam in forward direction (O-beam) is analyzed in the adjustment procedure (see Methods section for details) with a CoTi supermirror array, from now on called supermirror. The intensity transmitted by the supermirror is measured by the detector. The beam in the refracted direction (H-beam) is not used in the present experiment. In the interferometer a coil, henceforth called rotating field generator (RFG),15 is placed in path I. The field of the RFG is generated by a double coil arrangement for the x and z-direction which can be used to implement a static field or a field rotating about the beam axis in time with sinusoidally oscillating electric currents which are phase shifted by \(\pi/2\). To avoid unwanted thermal disturbance, the coil in the interferometer is water-cooled, resulting in a stabilized phase relation between both paths. The coil’s geometry is optimized to have no wire in the direct beam path thereby ensuring a high interferometric contrast. To induce a relative phase shift \(\chi\) between paths I and II, the phase shifter plate is used.
Monochromatized neutrons, with polarization vector parallel to the direction of propagation (+y), enter the interferometer. Inside the interferometer the rotating field generator (RFG) creates a magnetic field \({\overrightarrow{B}}_{{\rm{RFG}}}(\Omega ,t)\) in path I, rotating in a plane perpendicular to the neutron beam. After recombination at the last interferometer plate, the neutrons in forward direction (O-beam) are detected in a 3He counter tube. Spin directions are indicated with blue arrows, the magnetic field in violet. The phase shifter plate consists of a slab of sapphire and is rotated to record interferograms by inducing relative phase shifts \(\chi\) between the paths. A polarizing supermirror can be placed in the forward beam for spin analysis.
The RFG generates a rotating magnetic field \({\overrightarrow{B}}_{{\rm{RFG}}}\) around the y-axis. The incoming spin is parallel to the field rotation vector \(\overrightarrow{\Omega }\), i.e., orthogonal to the rotating magnetic field \({\overrightarrow{B}}_{{\rm{RFG}}}\), when entering the RFG.
Consider a cyclic evolution on the Bloch sphere of the initial spin state \(\xi (0)=\left|+y\right\rangle\) where \(\alpha {({t}_{1})}\) = 2π, with the time \({t}_{1}\) it takes for the neutron to fly through the region of the rotating magnetic field. Then the final spin state becomes \(\xi ({t}_{1})=-{e}^{i\Omega {t}_{1}/2}\left|+y\right\rangle\) which is solely dependent on the henceforth called Mashhoon Phase \(\Omega\, {t}_{1}/2\).
To adjust the case of \(\alpha (t_1)\) = 2π of cyclic evolution paths of the spin orientation in the RFG, the amplitude B1 of the rotating field is scanned with inserted supermirror. The cyclic paths are generated at a certain amplitude for each frequency \(f = \Omega / 2\pi\) from 0 kHz to 20 kHz. The necessary amplitudes decreased with increasing frequency as expected through (Equation 3). With adjusted amplitudes, the time evolutions of the spin states as presented in Fig. 2 are realized in the inertial frame.
The unit sphere in the inertial frame with the coordinates of the polar angle \(\vartheta\) and the azimuthal angle φ of polarization vectors \(\overrightarrow{P}(t)=\left\langle \xi (t)\right|\overrightarrow{\sigma }\left|\xi (t)\right\rangle\) with the spinor state \(\left|\xi \right\rangle =\cos (\vartheta /2)\left|\uparrow \right\rangle +{{\rm{e}}}^{{\rm{i}}\varphi }\sin (\vartheta /2)\left|\downarrow \right\rangle\) in the z-eigenbasis. The colored lines mark some experimentally realized cyclic time evolutions of the polarization vector induced in the RFG with a rotating magnetic field with different angular velocities \(\Omega\) from 2.5 kHz to 17.5 kHz and accordingly adjusted field amplitudes. The initial magnetic field is assumed in x-direction.
As path II will serve as a reference for the phase induced in path I, the spin orientations of both paths must be parallel at the last plate of the interferometer to guarantee maximum interference (see Methods section for details). At each phase shifter orientation, the counts per 20 s are recorded for different frequencies with the appropriate sinusoidal currents in the RFG. In the static case, \(\Omega\) = 0, the neutron spin rotates around the static B-field in x-direction by an angle of 2π, hence returning to its initial polarization vector.
Interferograms
For frequencies of the rotating field in the range from 0 kHz to 20 kHz and with removed supermirror, the interferograms depicted in Fig. 3a were recorded by changing the phase shifter orientation. With increasing frequency the interferograms are continuously shifted. The fitted phases of the interferograms relative to the static case are plotted in Fig. 3b. The expected phase \(\Omega t_1 /2\) is linearly dependent on the rotation frequency \(f\). This linear behavior complies with the measurement results. The time \(t_1\) inside the RFG is fixed. Deviations from the according linear fit are systematic due to misadjustment of the x and z-amplitudes of the rotating magnetic field inside the RFG.
Without supermirror: a A subset of interferograms recorded as intensity oscillations by rotating the phase shifter orientation, together with respective sinusoidal fit functions, for 2.5 kHz, 7.5 kHz, 12.5 kHz, and 17.5 kHz. With increasing frequency the interferograms are continuously shifted. Error bars indicate ±1 standard deviation. Gray dotted line is to guide the eye for the observed phase shift. b Linearly fitted phase of interferograms relative to the static case dependent on the rotation frequency of the magnetic field inside the RFG. Similar plots c and d recorded with supermirror inserted into the beam for additional spin analysis.
To demonstrate the independence of the effect from the polarization vector and therefore its purely quantum mechanical nature in the form of a phase shift, the experiment is also conducted with supermirror inserted in the O-beam; the results are plotted in Fig. 3c, d. The count rates with inserted supermirror are reduced because of the transmission T ≈ 0.4 of the additional neutron optical element. Nevertheless clear phase shifts because of spin-rotation coupling are visible here again. The slopes of the linear fits differ ~8% from each other. As the adjustment procedure is conducted with supermirror, we assume that removing the supermirror with its strong magnetic field had an unaccounted effect on the guide-field control (see methods section). In this case, all coils are misadjusted to some small extent.
Contrasts of interferograms with and without supermirror are plotted in Fig. 4. Without supermirror, the slight reduction in contrast is attributed mainly to the depolarization effect during the spin-rotation by the RFG. A small change of the contrast is also expected because of misalignment of the magnetic fields in the RFG. The negligible reduction in contrast compared to the empty interferometer confirms the coherent manipulation of the spin.
Discussion
Our setup is in principle also sensitive to the Sagnac phase caused by the rotation of the Earth. However, as the orientation of the interferometer is fixed during the measurements, the Sagnac phase is constant over the whole experiment and does not influence the relative phases presented here.
As the amplitude of the rotating field decreased with higher frequencies to adjust the case of \(a(t_1)=2\pi\), the phase shift in the interferograms is not due to a Zeeman effect.
One can also choose the inertial frame to express the Mashhoon phase shift by calculating the integrals of dynamical and geometric phases.26,27 But describing the effect in the rotating frame reveals the quantum mechanical analog to the Sagnac effect with its classical orbital angular momentum. Furthermore, the linear coupling is preferred due to simplicity. A valid interpretation of the results is an energy change for the rotating observer5 dependent on the orientation of spin and rotation vector.
The experimental procedure presented in this paper is equivalent to a symmetric situation where counter-rotating magnetic fields are present in both arms of the interferometer with frequencies \(\pm \Omega/2\).
A keen reader may point out that the effect due to spin-rotation coupling has long been observed (and utilized), for instance, in nuclear magnetic resonance (NMR) spectroscopy (e.g. Terenzi et al.28). It is true that the change of the direction of the spin-vector is known to be affected by the frequency of the used magnetic field; this effect is confirmed in our previous experiment with a neutron polarimeter14 and can be explained semi-classically with the Bloch equations in terms of rotations of the polarization vector. The orientation of the polarization vector can be measured with spin analysis.
Also the orientation of a classical magnetic moment evolves over time according to the Bloch equations. This is the classical analogon to the superposition of two perpendicular spin states as in neutron polarimetry. These spin states sum up to some spin vector represented by a respective polarization vector. The time evolutions of the superposing spin states are described by the Schrödinger equation which accounts for additional phase information. The classical and the quantum mechanical description are equivalent for our previous neutron polarimeter experiment.
In the present neutron interferometer experiment, the experimental results can only be described quantum mechanically as a phase shift is measured in neutron interferometry. The last interferometer plate is used to readout the phase information which has no analogy in the Bloch equations. This is the reason why spin analysis is possible but not necessary in the final measurements.
It is worth noting here that the present experiment confirms the phase shift due to spin-rotation coupling on a quantum system where intrinsic angular momentum is involved. Thus, the confirmed consequence is purely quantum mechanical in a sense that the phase shift on the wavefunction is induced by the interaction with a quantum mechanical degree of freedom.
More generally, a phase shift can also be induced under the condition that neither a classical force nor a classical torque acts on the neutrons;29,30 the phase shift on the spin-eigenstates may have more extended meaning than the change of the spin-vector. In this respect, the present experiment goes beyond the previous polarimeter experiment.14 Because the present experiment is sensitive to the phase shift, other quantum mechanical aspects can be implied more directly. Specifically, the intrinsic property of the neutron spin is indicated. This feature supports Mashhoon and Kaiser’s7 interpretation of an “inertia of intrinsic spin”.
Both Sagnac and Mashhoon effect can in turn be used to measure the rotation of a system without external reference from an inertial frame.31,32 As Mashhoon pointed out,5 “The Sagnac effect is proportional to the area of the interferometer, whereas the spin-rotation coupling phase shift is proportional to the length of the separate neutron paths.” More precisely, the Mashhoon phase shift is proportional to the time inside the interferometer and independent of the geometry itself, reflecting the intrinsic property of spin. Therefore, both paths can be chosen as close as experimentally convenient as in SESANS (Spin Echo Small Angle Neutron Scattering) setups33,34,35 with path separations of 10 μm. The ratio of Mashhoon to Sagnac phase shift is \(\sqrt{\pi }/(2k\sqrt{A})\) where \(k\) is the wave number of neutrons and A the area of the interferometer. In our setup with \(k\) ≈ 3.3 × 1010 m−1 and \(A\) ≈ 36 cm2, this ratio is of the order 10−10. To take full advantage of the Mashhoon effect, high frequencies are preferably used as applied in the kHz range in the present experiment. However, the Mashhoon effect can only be detected if the spin states in both paths are aligned differently while no rotation can be detected with parallel spin states or if both spin orientations are perpendicular to the axis of rotation.
Most recently, a theoretical contribution36 at the mergence of general relativity and quantum theory suggested a further neutron interferometer experiment on the Lense-Thirring effect37 “to complete nicely what we know at present about rotation in relativity”.
Conclusion
A neutron interferometer experiment was carried out to confirm the theoretical prediction of a spin-rotation coupling. The coupling in our experiment is established between the rotation of a magnetic field and the spin of the neutron. In contrast to previous neutron polarimeter experiments,14,15 the present interferometer experiment confirms the phase shift on the neutrons’ wavefunction which is a purely quantum mechanical effect and cannot be explained with the semi-classical Bloch equations. The observed linear dependence of the phase shift on the rotation frequency validates the spin-rotation coupling of neutrons as a purely quantum mechanical extension of the Sagnac effect.
Methods
Experimental setup
To understand the concept of the experiment, only the devices depicted in the setup of Fig. 1 are necessary. The full experimental setup is described in the following: a beam of monochromatized neutrons with a wavelength λ = 1.9 Å is split by a magnetic prism (not depicted) into two divergent, antiparallelly polarized sub-beams with spin states \(\left|\pm z\right\rangle\). Next, the neutrons enter a static magnetic guide field region (not depicted), generated by a coil in Helmholtz configuration that is placed between polarizer and analyzer and generates a field \({\overrightarrow{B}}_{0}=9\ {\rm{G}}\ {\hat{e}}_{z}\). For later use, we define \(| {\overrightarrow{B}}_{0}| ={B}_{0}\). The purpose of the guide field is to prevent depolarization because of magnetic stray fields, thereby upholding the degree of polarization of P ~ 0.99. Inside the guide field, a direct current spin rotator (DC1, not depicted) is placed in front of the interferometer and produces a local effective magnetic field in x-direction. In this x-field, the polarization vector is rotated due to Larmor precession by \(\pi/2\) from ±z to ±y, parallel to the flight direction of the neutrons. They traverse to a silicon perfect crystal interferometer which is aligned such that only the +y polarized sub-beam fulfills the Bragg condition of the lattice at the first plate of the interferometer. Consequently, the −y polarized sub-beam never reaches the detectors (in practice it is absorbed by a Cd-slab, not depicted).
In path I of the interferometer, the RFG generates a rotating magnetic field denoted as \({\overrightarrow{B}}_{{\rm{RFG}}}(\Omega ,t)={B}_{1}\cos (\Omega t){\hat{e}}_{x}+({B}_{1}\sin (\Omega t)-{B}_{0}){\hat{e}}_{z}\), rotating with angular velocity \(\Omega\) and amplitude B1 in a plane perpendicular to the neutron beam. This coil is the key element in the neutron optical setup and induces the spin-rotation coupling that shall be observed in the actual experiment. In path II, a coil of Helmholtz geometry38 (not depicted) produces a local z-field Bloc. This field locally increases the guide field strength and therefore the angle of Larmor precession (Larmor acceleration) which is used to align both spin orientations at the last plate by compensating differences in the Larmor precession angles (induced by the guide-field B0) acquired in the two paths. Finally another direct current spin rotator (DC2, not depicted) as well as a spin analyzer, which only transmits \(\left|+z\right\rangle\)-spins, are placed in front of the detector for the adjustment procedure which is described below.
Adjustment procedure
The coil DC1 is used to prepare the spin state \(\left|+y\right\rangle\) for the RFG while DC2 and analyzer are used to analyze the \(\left|+y\right\rangle\) spin component. As Larmor precession is induced inside the guide field pointing in z-direction between the coils, their distances need to be adjusted such that the input for the RFG and DC2 is a \(\left|+y\right\rangle\) spin state. To do this, path II is blocked with another Cadmium absorber, which is not depicted in Fig. 1. Coil DC1 rotates the polarization vector by \(\pi/2\) from \(\overrightarrow{z}\) to \(\overrightarrow{y}\) by Larmor precession about the static magnetic field inside the coil which is pointing in +x-direction. Another rotation of \(\pi/2\) about the same axis inside the RFG causes a minimum intensity in the case of a Larmor precession with an angle \(2\pi\) in the guide field in between DC1 and RFG with Larmor frequency \({\omega }_{0}=-\frac{2\mu }{\hslash }{B}_{0}\), where \(\mu\) is the magnetic moment of the neutron. The observed intensity oscillation is depicted in Fig. 5. The positions of DC1 and the RFG are fixed at the minimum intensity. The same procedure is repeated to adjust the position of DC2 relative to the RFG.
The RFG is supplied from now on with oscillating and \(\pi/2\) phase shifted currents for the x and z-fields to produce the rotating field while each DC coil produces a \(\pi/2\) rotation. For each frequency (0 kHz to 20 kHz), the amplitudes of both currents through the RFG are simultaneously increased from zero and its resulting minimum intensity until the same minimum intensity is produced again. This signifies the case of a cyclic rotation of the polarization vector inside the RFG.
As we want to investigate a Mashhoon phase shift in the interference between otherwise identical wave functions, both paths need to be recombined with aligned spin states. Therefore, the z-coil Bloc in path II is used, serving as Larmor accelerator. This coil is required since inside the RFG the z-field offset locally compensates the guide field, such that there is no static guide field present inside the RFG. To adjust the case of spin alignment, the absorber (not depicted) is switched to block path I while the \(\pi/2\)-rotations by both DC1 and DC2 are maintained. The current in the z-coil for the magnetic field Bloc in path II is scanned. The spins of both beams are aligned at the last plate with that current for the Larmor accelerator which produces a minimum intensity. The above setup procedure is necessary to adjust the currents and relative positions of DC1, DC2, the Larmor accelerator, and the RFG. For the actual measurements of the Mashhoon phase, the absorber, DC2, and the analyzer are removed, the latter two inserted again for the measurements with spin analysis. The prominent difference is a higher count rate without spin analysis due to fewer neutron optical components that have been inserted in the setup, mainly because of the transmission T ~ 0.4 of the supermirror for the +z-spin component (and T = 0 for −z).
Data availability
The data that support the findings of this study are available via https://doi.org/10.5291/ILL-DATA.CRG-2484.
References
Einstein, A. The Meaning of Relativity (Princeton University Press, 1923).
Sagnac, G. Sur la preuve de la réalité de l'éther lumineux par l’expérience de l’interférographe tournant. Comptes Rendus Acad. Sci. 157, 1410–1413 (1913).
Werner, S. A., Staudenmann, J. L. & Colella, R. Effect of earth’s rotation on the quantum mechanical phase of the neutron. Phys. Rev. Lett. 42, 1103–1106 (1979).
Hehl, F. W. & Ni, W.-T. Inertial effects of a Dirac particle. Phys. Rev. D. 42, 2045–2048 (1990).
Mashhoon, B. Neutron interferometry in a rotating frame of reference. Phys. Rev. Lett. 61, 2639–2642 (1988).
Mashhoon, B., Neutze, R., Hannam, M. & Stedman, G. E. Observable frequency shifts via spin-rotation coupling. Phys. Lett. A. 249, 161–166 (1998).
Mashhoon, B. & Kaiser, H. Inertia of intrinsic spin. Physica B. 385-386, 1381–1383 (2006).
Mashhoon, B. On the coupling of intrinsic spin with the rotation of the earth. Phys. Lett. A. 198, 9–13 (1995).
Soares, I. D. & Tiomno, J. The physics of the Sagnac-Mashhoon effects. Phys. Rev. D 54, 2808–2813 (1996).
Ryder, L. Relativistic treatment of inertial spin effects. J. Phys. A. 31, 2465–2469 (1998).
Ryder, L. Spin-rotation coupling and Fermi-Walker transport. Gen. Relativ. Gravit. 40, 1111–1115 (2008).
Arminjon, M. Should there be a spin-rotation coupling for a dirac particle? Int. J. Theor. Phys. 53, 1993–2013 (2014).
Stedman, G. E. Ring-laser tests of fundamental physics and geophysics. Rep. Prog. Phys. 60, 615–688 (1997).
Demirel, B., Sponar, S. & Hasegawa, Y. Measurement of the spin-rotation coupling in neutron polarimetry. New J. Phys. 17, 023065 (2015).
Danner, A., Demirel, B., Sponar, S., and Hasegawa, Y. Development and perfomance of a miniaturised spin rotator suitable for neutron interferometer experiments. J. Phys. Commun. 3, 035001 (2019).
Rauch, H., Treimer, W. & Bonse, U. Test of a single crystal neutron interferometer. Phys. Lett. A. 47, 369–371 (1974).
Rauch, H. and Werner, S. A. Neutron Interferometry (Oxford University Press, 2000).
Klepp, J., Sponar, S. & Hasegawa, Y. Fundamental phenomena of quantum mechanics explored with neutron interferometers. Prog. Theor. Exp. Phys. 2014, 082A01 (2014).
Rauch, H. et al. Verification of coherent spinor rotation of fermions. Phys. Lett. A. 54, 425–427 (1975).
Werner, S. A., Colella, R., Overhauser, A. W. & Eagen, C. F. Observation of the phase shift of a neutron due to precession in a magnetic field. Phys. Rev. Lett. 35, 1053–1055 (1975).
Badurek, G., Rauch, H. & Summhammer, J. Time-dependent superposition of spinors. Phys. Rev. Lett. 51, 1015–1018 (1983).
Summhammer, J., Badurek, G., Rauch, H., Kischko, U. & Zeilinger, A. Direct observation of fermion spin superposition by neutron interferometry. Phys. Rev. A. 27, 2523–2532 (1983).
Colella, R., Overhauser, A. W. & Werner, S. A. Observation of gravitationally induced quantum interference. Phys. Rev. Lett. 34, 1472–1474 (1975).
Bonse, U. & Wroblewski, T. Measurement of neutron quantum interference in noninertial frames. Phys. Rev. Lett. 51, 1401–1404 (1983).
Weinfurter, H. & Badurek, G. Measurement of Berry’s phase for noncyclic evolution. Phys. Rev. Lett. 64, 1318–1321 (1990).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A. 392, 45–57 (1984).
Aharonov, Y. & Anandan, J. Phase change during a cyclic quantum evolution. Phys. Rev. Lett. 58, 1593–1596 (1987).
Terenzi, C., Bouguet-Bonnet, S. & Canet, D. Direct 1H NMR evidence of spin-rotation coupling as a source of para→ortho-H2 conversion in diamagnetic solvents. J. Chem. Phys. 146, 154203 (2017).
Allman, B. E., Lee, W.-T., Motrunich, O. I. & Werner, S. A. Scalar Aharonov-Bohm effect with longitudinally polarized neutrons. Phys. Rev. A. 60, 4272–4284 (1999).
Lee, W.-T., Motrunich, O., Allman, B. E. & Werner, S. A. Observation of Scalar Aharonov-Bohm Effect with Longitudinally Polarized Neutrons. Phys. Rev. Lett. 80, 3165–3168 (1998).
Michelson, A. A. The effect of the Earth’s rotation on the velocity of light, I. Astrophys. J. 61, 137 (1925).
Michelson, A. A. & Gale, H. G. The effect of the Earth’s rotation on the velocity of light, II. Astrophys. J. 61, 140 (1925).
Rekveldt, M. Novel SANS instrument using Neutron Spin Echo. Nucl. Instrum. Methods Phys. Res. B. 114, 366–370 (1996).
Gähler, R., Golub, R., Habicht, K., Keller, T. & Felber, J. Space-time description of neutron spin echo spectrometry. Physica B. 229, 1–17 (1996).
Rekveldt, M. T. et al. Spin-echo small angle neutron scattering in Delft. Rev. Sci. Instrum. 76, 033901 (2005).
Papini, G. Gravitational qubits. Universe 5, 123 (2019).
Lense, J. & Thirring, H. Über den Einfluss der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z. 19, 156–163 (1918).
Geppert, H., Denkmayr, T., Sponar, S., Lemmel, H. & Hasegawa, Y. Improvement of the polarized neutron interferometer setup demonstrating violation of a Bell-like inequality. Nucl. Instrum. Methods Phys. Res. A. 763, 417–423 (2014).
Acknowledgements
We are grateful to Mario Pitschmann for helpful discussion. This work was financed by the Austrian Science Fund (FWF), Projects No. P27666-N20 and P30677-N36.
Author information
Authors and Affiliations
Contributions
A.D., B.D., S.S., and Y.H. conceived the experiment; A.D., B.D., W.K., H.L., and R.W. carried out the experiment; A.D., S.S., and Y.H. analyzed the data; all authors co-wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Danner, A., Demirel, B., Kersten, W. et al. Spin-rotation coupling observed in neutron interferometry. npj Quantum Inf 6, 23 (2020). https://doi.org/10.1038/s41534-020-0254-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-0254-8
This article is cited by
-
The Sagnac effect for spin-1/2 particles through local Wigner rotations
Quantum Information Processing (2022)
-
Tests of fundamental quantum mechanics and dark interactions with low-energy neutrons
Nature Reviews Physics (2021)
-
The Measurement Problem, an Ontological Solution
Foundations of Physics (2021)