Thermal-activated escape of the bistable magnetic states in 2D Fe₃GeTe₂ near the critical point

Abstract

Great effort has been made recently to investigate the phase transitions in two-dimensional (2D) magnets while leaving subtle quantification unsolved. Here, we demonstrate the thermal-activated escape in 2D Fe₃GeTe₂ ferromagnets near the critical point with a quantum magnetometry based on nitrogen-vacancy centers. We observe random switching between the two spin states with auto-correlation time described by the Arrhenius law, where a change of temperature by 0.8 K induces a change of lifetime by three orders of magnitude. Moreover, a large energy difference between the two spin states about 51.3 meV is achieved by a weak out-of-plane magnetic field of 1 G, yielding occupation probability described by Boltzmann’s law. Using these data, we identify all the parameters in the Ginzburg-Landau model. This work provides quantitative description of the phase transition in 2D magnets, which paves the way for investigating the critical fluctuation and even non-equilibrium phase transitions in these 2D materials.

Introduction

Phase transition and spontaneous symmetry breaking are the major theme in condensed matter physics. These physics at the mean-field level can be formulated using the Ginzburg-Landau (GL) theory for second-order phase transitions, in which the free energy in terms of the order parameters can be described by a double-well potential in the ordered phase. These transitions may also be observed in systems with reduced dimension. For instance, recently, the two-dimensional (2D) magnetism has been verified in van der Waals (vdWs) layered materials, including Fe₃GeTe₂ (ref. ¹), CrI₃ (ref. ²), Cr₂Ge₂Te₆ (ref. ³), and VSe₂ (ref. ⁴). Benefited from the vdWs layered structure, the significant anisotropy along the out-of-plane direction opens a finite spin wave excitation gap, which enables the withstanding of the predicted strong fluctuations in a 2D system from the Mermin-Wagner theorem^5,6,7. While the phase transitions and phase diagrams have been determined^1,2,3,8,9, their spin dynamics at finite temperatures near the critical points have not yet been quantitatively understood.

The nitrogen-vacancy (NV) centers¹⁰ in diamond can provide a non-perturbative and direct measurement of the magnetic field in these 2D magnets with a number of extraordinary advantages, including high spatial resolution^11,12,13, long coherence time¹⁴, wide temperature range (from low temperature to several hundreds Kelvin)^15,16, and high sensitivity^17,18. NV sensing techniques have been implemented successfully in imaging the magnetization in ultrathin vdW antiferromagnet CrI₃ and ferromagnet CrBr₃ and VI₃ (refs. ^13,19,20,21). Here, we demonstrate that the double-well energy landscape in finite 2D Fe₃GeTe₂ ferromagnets can be tuned by the temperature and external magnetic field using an NV magnetometer, which enables us to quantitatively determine the magnetization and its temporal fluctuations. We observe that when the temperature approaches the critical temperature (T_c) from below, random spin switching between the two spontaneous symmetry breaking states (denoted as |↑〉 and |↓〉) can be induced by thermal fluctuations. When these two states have the same energy, they are equally populated with the dwell time varying by three orders of magnitude upon changes in temperature of ~0.8 K. This behavior can be well described by the Arrhenius law. Furthermore, we show that the energy barrier of the two states can be tuned by a weak out-of-plane magnetic field, in which the occupation probability in these states can be described by the Boltzmann distribution law. A weak magnetic field of 1 G can yield a sizable energy difference of ~51.3 meV. These results are quantitatively consistent with the GL theory, in which all the parameters are determined. The tunability of this free energy landscape paves the way for investigation of the critical fluctuation, Kramers turnover and even non-equilibrium phase transition in these 2D materials^22,23,24.

Results and discussion

GL theory and quantum magnetometry based on color centers in diamond

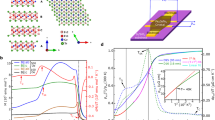
It is well known that magnets can be well described by the GL theory for continuous phase transition. There is no spontaneous magnetization at high temperature when $T > {T}_{{{{{{\rm{c}}}}}}}$ for the disordered phase; however, when $T < {T}_{{{{{{\rm{c}}}}}}}$, spontaneous magnetization takes place for the ordered phase, and the system will occupy only the state |↑〉 or ∣↓〉 (see Fig. 1a) even in a finite system. Near the critical point ($T < {T}_{{{{{{\rm{c}}}}}}}$), the total free energy can be described as $F=(-{a}_{2}\varDelta T{M}_{z}^{2}+{a}_{4}{M}_{z}^{4})A$, where $\Delta T={T}_{{{{{{\rm{c}}}}}}}-T$, ${a}_{2}$ and ${a}_{4}$ are two positive parameters, $A$ is the magnetic domain area (in unit of nm²) and ${M}_{z}$ is the order parameter for magnetic dipole moment density (in unit of μ_B nm^-2). In this free energy landscape, we have neglected the gradient of magnetization, which corresponds to the kinetic energy part in the GL model. Thus, the energy barrier height $\delta E={{Aa}}_{2}^{2}{\varDelta T}^{2}/{4a}_{4}$ is proportional to${\Delta T}^{2}$ and area A. For an infinite system, this energy barrier is much larger than ${K}_{{{{{{\rm{B}}}}}}}{T}_{{{{{{\rm{c}}}}}}}$, where ${K}_{{{{{{\rm{B}}}}}}}$ is the Boltzmann constant and spontaneous symmetry occurs, and the system will occupy only one of the states. However, in a finite system (independent of dimension) when the barrier height is comparable with the system temperature, one may expect thermal-activated escape between the two spin states (Fig. 1b)^23,25. Moreover, when an external magnetic field is applied, the two spin states will feel opposite splitting along the magnetization direction, with ${{{{{\rm{\delta }}}}}}{E}_{{{{{{\rm{m}}}}}}}=A{M}_{z}{B}_{z}$, where B_z is projection of the external magnetic field along the direction of magnetization. This leads to the energy difference $2{{{{{\rm{\delta }}}}}}{E}_{{{{{{\rm{m}}}}}}}$ between the |↑〉 and |↓〉 states (Fig. 1c). This picture motivates the possible tunability of the free energy landscape in a finite 2D magnets, and our central task in this work is to quantitatively describe the phase transition and thermal activation in 2D magnets near the critical point using the above free energy.

Fig. 1: The free energy landscape of the Ginzburg-Landau double-well model.

a Schematic of the Ginzburg-Landau (GL) double-well model with ${{{{{{\rm{Z}}}}}}}_{2}$ symmetry for a ferromagnet. b Schematic of the GL double-well model at different temperatures and zero external magnetic field. The dark and light purple lines indicate temperatures slightly below and above T_c, respectively. $\delta E$ is the energy barrier height. c Schematic of the GL double-well model at different external magnetic fields. The green and gray lines indicate with or without an external magnetic field, respectively. $2\delta {E}_{{{{{{\rm{m}}}}}}}$ is the energy gap between the |↑〉 and |↓〉 states. In these three figures, the red and blue arrows indicate the |↑〉 and |↓〉 states, respectively.

Our magnetometer employs a near-surface layer of magnetically sensitive NV centers in a bulk diamond with a polished (100) surface (Fig. 2a). The NV center exhibits a spin-1 triplet electronic ground state, and its Hamiltonian reads as $H=D({S}_{z}^{2}-2/3)+{\gamma }_{{{{{{\rm{e}}}}}}}{{{{{\bf{B}}}}}}\cdot {{{{{\bf{S}}}}}}$, where $D$ is the zero field splitting, ${\gamma }_{{{{{{\rm{e}}}}}}}=2.8$ MHz G⁻¹ is the electron spin gyromagnetic ratio, ${{{{{\bf{B}}}}}}$ is the magnetic field, which is constituted by a uniform external magnetic bias field ${{{{{{\bf{B}}}}}}}_{{{{{\rm{bias}}}}}}$ and a non-uniform field ${{{{{{\bf{B}}}}}}}_{{{{{{\rm{s}}}}}}}$ (~0 G to 2 G) generated by the sample, ${{{{{\bf{S}}}}}}$ is the vector electron spin operator and ${S}_{z}$ is its $z$ component^26,27 (see details in Supplementary Note I). In this study, we use B to denote the vector magnetic field (e.g., ${{{{{{\bf{B}}}}}}}_{{{{{\rm{bias}}}}}}$) and B to denote its projection onto the given axis (e.g., ${B}_{{{{{\rm{bias}}}}}}$). The NV spin is initialized and readout by a 532 nm linearly polarized laser²⁸, and its photoluminescence is collected by a single photon counting module. A continuous microwave field is applied to the NV center by a gold wire. When the microwave frequency resonates with the NV spin splitting ${f}_{\pm }=D\pm {\gamma }_{{{{{{\rm{e}}}}}}}({B}_{{{{{{\rm{s}}}}}}}+{B}_{{{{{\rm{bias}}}}}})$, the NV electron spin is driven from the |m_s = 0〉 to |m_s= ±1〉 states, resulting in weakened fluorescence (Fig. 2b). Here, ${B}_{{{{{{\rm{s}}}}}}}$ and ${B}_{{{{{\rm{bias}}}}}}$ are the projections of ${{{{{{\bf{B}}}}}}}_{{{{{{\rm{s}}}}}}}$ and ${{{{{{\bf{B}}}}}}}_{{{{{\rm{bias}}}}}}$ along the NV axis, respectively. Thus, ${B}_{{{{{{\rm{s}}}}}}}=\pm ({f}_{\pm }-D)/{\gamma }_{{{{{{\rm{e}}}}}}}-{B}_{{{{{\rm{bias}}}}}}$ is read out by the optically detected magnetic resonance (ODMR) spectrum¹⁰. Following this principle, imaging of the stray magnetic field from a given target is derived by the measurement of an ODMR spectrum at each pixel. We determine all the parameters in the GL model using this experimental technique.

Fig. 2: Quantum sensing of the 2D magnetism with NV centers in diamond.

a Schematic of the NV center-based magnetometer. The Fe₃GeTe₂ multilayer is transferred onto the diamond (100) surface and is encapsulated by two hBN flakes to avoid degradation and proximity-induced artifacts. The 532 nm laser, indicated by the green light cone, is focused perpendicular to the sample. The microwave is applied via a gold wire. Inset shows the specific structure and orientation of the NV center. b Energy level splitting of the NV center under an external magnetic field. The arrows indicate that the NV electron spin is driven, and f₋ (f₊) is the resonant frequency from the |m = 0〉 to |m_s = −1〉 (|m_s = +1〉) states. c Optical image of the Fe₃GeTe₂ multilayer (sample #1). The area marked by the blue dashed circle has a thickness >4.8 nm. Mapping of the stray magnetic field (d) and corresponding magnetization (e) from sample #1 measured at 165 K. f Dynamic mapping of the stray magnetic field via the three-point method. The out-of-plane component of the external bias magnetic field is set to zero (${B}_{{{{{\rm{bias}}}}}}^{z}=0$). The temperature is fixed at 171.0 K. The gray lines in each image represent the boundary of the sample. The four subfigures were taken sequentially in the order of the purple arrows.

Quantitative determination of magnetization

We studied ultrathin ferromagnetic Fe₃GeTe₂ that was mechanically exfoliated from a bulk crystal (the characterization of the Fe₃GeTe₂ single crystal is detailed in Supplementary Note II). The ultrathin Fe₃GeTe₂ was encapsulated with hexagonal boron nitride (hBN) on both sides to prevent degradation and proximity-induced artifacts²⁹, which was transferred onto the diamond in a glovebox filled with pure nitrogen. The thickness of the NV layer (~10 nm from the diamond surface), which is approximately a few nanometers, is much smaller than the distance between the Fe₃GeTe₂ multilayer and the NV layer (about 180 to 420 nm). Thus, as a good approximation, all the randomly distributed NV centers will feel the same magnetic field strength.

Figure 2c shows the optical image of the Fe₃GeTe₂ sample (#1) on the diamond substrate. The thickness of sample #1 was determined to be 4.8 nm via atomic force microscopy measurement (see details in Supplementary Note III). The ODMR imaging was performed under a bias field ${B}_{{{{{\rm{bias}}}}}}=123$ G with the direction parallel to the selected NV axis, which is approximately 54.7° with respect to the out-of-plane direction. This bias field is strong enough to polarize the Fe₃GeTe₂ multilayer completely (see the geometric configuration in Supplementary Fig. S1 and the magnetic hysteresis loop in Supplementary Note VII). Figure 2d shows the stray field imaging of sample #1 at $T=165$ K with a pixel size of ~300 nm. The magnetic signal from ultrathin Fe₃GeTe₂ is measured to be at the level of several Gauss (see details in Methods and Supplementary Section I). Since the directions of the NV axis and the sample magnetization are fixed, the quantified magnetization can be reconstructed from the stray magnetic field by using the reverse-propagation protocol^13,19,20,30, as detailed in Supplementary Note IV and Note V. The image of quantified magnetization is shown in Fig. 2e, where the magnetization ${M}_{z}$ is estimated to be 29.2 μ_B nm^-2. In considering the lattice constants of Fe₃GeTe₂ ($a=b=4$ Å)³¹, this value corresponds to a magnetic dipole moment of 0.22 μ_B for each Fe atom at 165 K, which is, as expected, smaller than the theoretical value of 1.2 μ_B -1.4 μ_B at zero temperature^8,31. Thus, this approach enables us to extract the local magnetization.

Magnetization fluctuation in a symmetric double-well potential

To efficiently measure the temporal magnetization fluctuations during the thermally activated escape process, we image in the following with a fast three-point sampling method³² (detailed in Methods and Supplementary Note VI) other than a full ODMR spectrum. The laser power used is ~300 μW, at which the measurement almost has a highest sensitivity, yet with negligible heating effect (see more details in Supplementary Note XIII). In our experiment, the stray field is represented by R, which is proportional to ${B}_{{{{{{\rm{s}}}}}}}$. With this fast technique, the magnetization fluctuations in Fe₃GeTe₂ were imaged at 171.0 K, which corresponds to $\Delta T=2.6$ K, as shown in Fig. 2f, with ${T}_{{{{{{\rm{c}}}}}}}=173.6$ K determined in Supplementary Fig. S6d. Here, the applied ${{{{{{\bf{B}}}}}}}_{{{{{\rm{bias}}}}}}$ was tuned into the in-plane direction with a lower field (see details in Supplementary Fig. S1) to mimic the out-of-plane zero-field condition for the Fe₃GeTe₂ multilayer. As shown in Fig. 2f, the stray field distributions clearly show random domains with positive (spin |↑〉) and negative (spin |↓〉) magnetic dipole moments, which are typical structures near the critical point. In addition, we find that these domains wiggled temporally. From the four subsequent measurements in Fig. 2f, we observed that the size and direction of the domains changed temporally on a time scale of tens of minutes. This change indicates that the magnetization in the Fe₃GeTe₂ multilayer cannot maintain its stable structure over a long time near the critical point due to the thermal fluctuation-induced escape process^23,25.

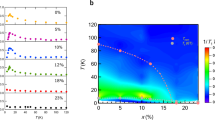
The field fluctuation in magnetic systems is a non-local effect that depends on the magnetic dipole moments in all domains from the sense of magnetic charges (see Supplementary Eq. S4-S5). To clearly show the two-level jump state in the Fe₃GeTe₂ multilayer, we chose another sample (#2) with only a single domain (see the details of sample #2 in Supplementary Note VIII). Fig. 3a shows the magnetization fluctuations via R(t) at different temperatures over 12 minutes of measurements at a fixed region (approximately 1 μm² in size) (see more details in Supplementary Note X). As expected, R(t) has only two discrete jumping states with either positive or negative values corresponding to the spin $| \!\! \uparrow \rangle$ or spin $| \!\! \downarrow \rangle$ states, respectively. For this kind of random two-state switch, we find that the time required for the spin switch is longer at lower temperatures, which originates from the larger barrier heights according to the GL double-well model (Fig. 1b). In Fe₃GeTe₂ (refs. ^1,8), only the short-range Heisenberg/Ising interactions are allowed. Thus, only the single spin switch by local thermal fluctuations is in principle favorable. Thermal-activated escape processes are characterized by the rare events; that is, they are phenomena that take place in a very long time scale compared to the dynamic time scale describing the local stability state, such as critical fluctuations.

Fig. 3: Detection of thermally activated escape in a finite system near T_c.

a Time traces of magnetization fluctuation from sample #2 at different temperatures under ${B}_{{{{{{\rm{bias}}}}}}}^{z}=0$. Here, ${t}_{\uparrow }$ ${{{{{\rm{and}}}}}}$ ${t}_{\downarrow }$ are the dwell times for spin |↑〉 and |↓〉 states, respectively. $\Delta T$ denotes ${T}_{{{{{{\rm{c}}}}}}}-T$. The red and blue arrows indicate the |↑〉 and |↓〉 states, respectively. b The normalized temporal autocorrelation function at different temperatures. c The temperature dependence of the correlation decay time. The round dots are the correlation decay times obtained by fitting an exponential function to the curves in (b). The squared dots are the averaged correlation decay times obtained from the histogram of the dwell times (see detailed plot in Supplementary Fig. S10). The dashed line is the fitting to the correlation decay time in (c) using Eq. 2 with a result of ${\tau }_{0}=13$ ms and $\alpha =31$ meV K⁻².

The switch between the two states resembles the jump of the nanoparticle trapped in a bistable optical potential^24,33 and folding dynamics of proteins³⁴ in Kramers theory by some stochastic processes. Following this treatment, we can study the temporal fluctuation separated by a finite time Δt by auto-correlation^23,25

$$C\left(\Delta t\right)=\left\langle R\left(t\right)R\left(t+\Delta t\right)\right\rangle -\left\langle R\left(t\right)\right\rangle \left\langle R(t+\Delta t)\right\rangle .$$

(1)

Figure 3b summarizes the temporal auto-correlation in sample #2 at different temperatures using the data in Supplementary Fig. S9. After normalization by C(0), it is described by ${e}^{-\Delta t/\tau }$, where τ is the correlation decay time. An interpretation of this behavior is given by Kramers turnover²⁵. It should be noted that for temperatures with $\Delta T > 2.00$ K, the magnetization fluctuation data cannot be fitted very well due to the limited cycles of spin switches within 12 minutes, while for $\Delta T < 1.22$ K, the jumping cannot be measured for the finite temporal resolution in our measurement. The fitted results of τ in a temperature range of 0.8 K are shown in Fig. 3c, in which τ drops by three orders of magnitude. This lifetime τ is closely related to the relaxation rate $\varGamma$ for a state initially in one of the local minima, which stochastically jumps to the other local minima under the influence of the thermal environment. In this way, $\varGamma$ is proportional to ${e}^{-{{{{{\rm{\delta }}}}}}E/({K}_{{{{{{\rm{B}}}}}}}T)}$. The lifetime is inversely proportional to this relaxation rate, yielding (see Fig. 1b).

$$\tau ={\tau }_{0}{e}^{\frac{\alpha {\Delta T}^{2}}{{K}_{{{{{{\rm{B}}}}}}}T}},$$

(2)

where $\alpha ={Aa}_{2}^{2}/{4a}_{4}$ and ${\tau }_{0}$ are two fitting parameters. At the critical point, the barrier width is zero, yielding a maximal relaxation rate and a minimal lifetime. The results in Fig. 3c exhibit an exponential decay function, from which we obtain ${\tau }_{0}=13$ ms and $\alpha =31$ meV K^-2. Although it cannot be detected in the current experiment, the short time of ${\tau }_{0}$ is quite physical and should exist as expected from the ultrafast switch betwee n two macroscopic states induced by the strong fluctuation. In Supplementary Fig. S10, we have also estimated the lifetime from the histogram of the dwell time for the two spin states following Cook and Kibble in a two-level model³⁵. This treatment also quantitatively yields the same lifetimes (see the squared data in Fig. 3c and more numerical data in Supplementary Fig. S9). We find that, roughly, these two spin states have almost the same lifetime, indicating that the two states have the same energy by the GL model with ${{{{{{\rm{Z}}}}}}}_{2}$ symmetry.

The above results are also useful for us to determine the two parameters ${a}_{2}$ and ${a}_{4}$ of the GL model quantitatively. Using the fitted value of $\alpha =31$ meV K^-2 and the measured M_z, we find that ${a}_{2}=2\alpha \Delta T/A{M}_{z}^{2}$ and ${a}_{4}=\alpha \Delta {T}^{2}/A{M}_{z}^{4}$. At $\Delta T=1.54$ K, the measured $R$ is $\pm 0.05$ for the two spin states, which equals to B_s=∓0.125 G. Thus, we estimate M_z to be ∓6μ_B nm^-2 (see estimation results in Supplementary Fig. S7). With all these results and $A\approx 1$ μm² (the area of sample #2), we have ${a}_{2}\approx 2.7\times {10}^{-6}\,{{{{{\rm{meV}}}}}}\,{{{{{{\rm{nm}}}}}}}^{2}\,{{{{{{\rm{K}}}}}}}^{-1}\,{\mu }_{{{{{{\rm{B}}}}}}}^{-2}$ and ${a}_{4}\approx 5.7\times {10}^{-8}\,{{{{{\rm{meV}}}}}}\,{{{{{{\rm{nm}}}}}}}^{6}\,{\mu }_{{{{{{\rm{B}}}}}}}^{-4}$. Together with the barrier height $\delta E={{Aa}}_{2}^{2}{\varDelta T}^{2}/{4a}_{4}$ = 74 meV. We can quantitatively characterize the GL model at each temperature point near T_c. For sample #3 (as mentioned later), using the experiments, we find ${a}_{2}\approx 5.0\times {10}^{-6}\,{{{{{\rm{meV}}}}}}\,{{{{{{\rm{nm}}}}}}}^{2}\,{{{{{{\rm{K}}}}}}}^{-1}\,{\mu }_{{{{{{\rm{B}}}}}}}^{-2}$ and ${a}_{4}\approx 3.4\times {10}^{-7}\,{{{{{\rm{meV}}}}}}\,{{{{{{\rm{nm}}}}}}}^{6}\,{\mu }_{{{{{{\rm{B}}}}}}}^{-4}$ at $\Delta T=1.70$ K, which are at the same order of magnitude as that in sample #2. The difference between these parameters arises from the different domain area A and thickness $h$. For sample #2, we have $A\approx 1$ μm² and $h=6$ layers; yet for sample #3, $A \sim 1-2$ μm² and $h=3-4$ layers; see Supplementary Section III. The difference between them can be qualitatively understood using ${a}_{2}\propto {h}^{-1}$, ${a}_{4}\propto {h}^{-3}$ and $\alpha \propto {Ah}$.

Magnetization fluctuation in a tilted double-well potential

The ${{{{{{\rm{Z}}}}}}}_{2}$ symmetry of the GL model can be broken by an out-of-plane magnetic field. Regarding its Ising-type interaction, the out-of-plane magnetic field drives the two states along opposite directions, yielding a tilted double-well model (Fig. 1c). From the GL double-well model in Fig. 1b and the experiments in Fig. 3a, we expect the occupation probability of the two spin states to satisfy the Boltzmann distribution. To this end, we define ${P}_{\uparrow }$ and ${P}_{\downarrow }$ as the probability in spin |↑〉 and spin |↓〉 states, respectively. We have the Boltzmann distribution law as (see Fig. 1c)

$${P}_{\downarrow }/{P}_{\uparrow }={e}^{\frac{2\delta {E}_{{{{{{\rm{m}}}}}}}}{{K}_{{{{{{\rm{B}}}}}}}T}}$$

(3)

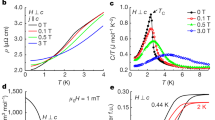
In Fig. 4, we have chosen an almost vanished out-of-plane magnetic field, such that the energy gap$2\delta {E}_{{{{{{\rm{m}}}}}}}\approx 0$. The in-plane magnetic field will not influence the magnetization for the leading Ising-type interaction. In this way, we expect $2\delta {E}_{{{{{{\rm{m}}}}}}}=2A{M}_{z}{B}_{{{{{{\rm{bias}}}}}}}^{z}$, where ${B}_{{{{{{\rm{bias}}}}}}}^{z}$ is the projection of ${{{{{{\bf{B}}}}}}}_{{{{{\rm{bias}}}}}}$ along the z-axis. We expect $\delta {E}_{{{{{{\rm{m}}}}}}}$ to be increased with the increasing of area A and sample thickness h, yet it can be reduced by $\Delta T$. We aim to show that this energy difference can be tuned by a weak out-of-plane magnetic field. We explore the magnetization fluctuations in sample #3 for different${B}_{{{{{{\rm{bias}}}}}}}^{z}$, and the results are presented in Fig. 4a (see the details of sample #3 in Supplementary Note III, Note IX and Fig. S11). Under different ${B}_{{{{{{\rm{bias}}}}}}}^{z}$, the probabilities of the Fe₃GeTe₂ multilayer being in the spin |↑〉 and spin |↓〉 states are different, exhibiting a clear tilted double-peak distribution at $R > 0$ and $R < 0$. The quantitative analysis of the probability ${P}_{\sigma }$ at these states and the average dwell time $\bar{{t}_{\sigma }}$ for these two states are shown in Figs. 4b and 4c, which exhibit a smooth crossover between the two states (see more details in Supplementary Fig. S12 and Fig. S14). Using the distribution in Eq. 3, we estimate $2\delta {E}_{{{{{{\rm{m}}}}}}}=51.3\,{{{{{\rm{meV}}}}}}\,{{{{{{\rm{G}}}}}}}^{-1}\times {B}_{{{{{{\rm{bias}}}}}}}^{z}-5.2\,{{{{{\rm{meV}}}}}}$, where the constant term may originate from the fact that the magnetization direction is not exactly parallel to the out-of-plane direction but has a slight angle (see ${P}_{\uparrow }$ and ${P}_{\downarrow }$ at different in-plane magnetic fields in Supplementary Fig. S13). Using $1{\mu }_{{{{{{\rm{B}}}}}}}=5.8\times {10}^{-6}$ meV G^-1, we estimate $A{M}_{z}\approx \pm 4.4\times {10}^{6}$ μ_B, which is close to our estimate from the magnetic field (see Methods). Thus, by changing the bias field by 1 G, an energy splitting of approximately 51.3 meV between the two states is realized, which is much larger than the critical temperature of ${K}_{{{{{{\rm{B}}}}}}}T=13.8$ meV, yielding the dwell of the state almost in only the lowest energy state. From this experiment, we see that the free energy landscape and the associated thermal escape rate in this system can be tuned by the temperature and in-plane magnetic field.

Fig. 4: Thermal-activated escape in a tilted double-well potential induced by an external magnetic field.

a Time traces of magnetization fluctuation in sample #3 at different ${B}_{{{{{{\rm{bias}}}}}}}^{z}$. The mean temperature is set to $\Delta T=1.30$ K. The figures in the right panel are the statistical histograms for the distributions of different spin states, in which the blue curves are curves fitted with two Gaussian functions. b ${P}_{\uparrow }$ and ${P}_{\downarrow }$ at different bias fields ${B}_{{{{{{\rm{bias}}}}}}}^{z}$. Here, ${P}_{\uparrow }={\int }_{0}^{+{\infty }}f(R){dR}/{\int }_{-{\infty }}^{+{\infty }}f(R){dR}$ and ${P}_{\downarrow }={\int }_{-{\infty }}^{0}f(R){dR}/{\int }_{-{\infty }}^{+{\infty }}f(R){dR}$ represent the occupation probability in the spin |↑〉 and |↓〉 states, respectively, where $f(R)$ is the probability distribution of R. The dots are experiment data and the lines are obtained from Eq. (3), taking $2\delta {E}_{m}=51.3\,{{{{{\rm{meV}}}}}}\,{{{{{{\rm{G}}}}}}}^{-1}\times {B}_{{{{{{\rm{bias}}}}}}}^{z}-5.2\,{{{{{\rm{meV}}}}}}$. c $\bar{{t}_{\uparrow }}$ and $\bar{{t}_{\downarrow }}$ at different bias fields ${B}_{{{{{{\rm{bias}}}}}}}^{z}$. Here, $\bar{{t}_{\uparrow }}$ and $\bar{{t}_{\downarrow }}$ are the averaged dwell times of all ${t}_{\uparrow }$ and ${t}_{\downarrow }$. The dots are experiment data and the lines are the exponential fitting to $\bar{{t}_{\uparrow }}$ and $\bar{{t}_{\downarrow }}$.

Spatial correlation in magnetization fluctuations

Finally, it is necessary to characterize the spatial magnetization correlation. Since NV centers measure the projection of ${{{{{{\bf{B}}}}}}}_{{{{{{\rm{s}}}}}}}$ in the ${{{{{{\bf{B}}}}}}}_{{{{{{\rm{bias}}}}}}}$-direction (see Supplementary Section I), we lack information about ${{{{{{\bf{B}}}}}}}_{{{{{{\rm{s}}}}}}}$ in the z-axis direction when ${B}_{{{{{{\rm{bias}}}}}}}^{z}=0$, which prevents the reconstructed magnetization. However, spatial magnetization correlation can be indirectly reflected by the analysis of magnetic field spatial correlation. The stray magnetic field of sample #4 with ${T}_{{{{{{\rm{c}}}}}}}\cong 165$ K and a spatial size of 12 ${{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}\times 10{{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}$ is prepared, and the results are presented in Fig. 5a. We characterize the two-site spatial correlation in the same way as Eq. (1) as^21,22

$$C\left({{{{{\bf{x}}}}}}-{{{{{\bf{y}}}}}}\right)=\left\langle R\left({{{{{\boldsymbol{x}}}}}}\right)R\left({{{{{\boldsymbol{y}}}}}}\right)\right\rangle -\left\langle R\left({{{{{\boldsymbol{x}}}}}}\right)\right\rangle \left\langle R\left({{{{{\boldsymbol{y}}}}}}\right)\right\rangle$$

(4)

where ${{{{{\bf{x}}}}}}$ and y are two points in the sample. We chose data with ΔT > 3 K for the spatial correlation analysis to ignore the temporal magnetization fluctuation during the measurement. Therefore, we focus on the stationary magnetization correlation. In Fig. 5b, we present the normalized and averaged spatial correlation along the y-axis. We expect the normalized magnetic correlation function to satisfy²²

$$C\left({{{{{\rm{r}}}}}}\right)={e}^{-\frac{r}{\xi }}\cos \left(\frac{{{{{{\rm{\pi }}}}}}r}{\lambda }\right)$$

(5)

where $r={{{{{\rm{|}}}}}}{{{{{\bf{x}}}}}}-{{{{{\bf{y|}}}}}}$, $\xi$ is the correlation decay length and $\lambda$ is the domain width. The results are presented in Fig. 5b, showing three major features: (I) When the separation is small ($r < \lambda$), the correlation function almost decays exponentially given by the first part of Eq. 5; (II) When $r > \lambda$, oscillation of the correlation function is observed due to the spatial distribution of finite domain walls; (III) $\xi$ and $\lambda$ are $\sim 1$ ${{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}$. The fitted results of $\xi$ and $\lambda$ are shown in Fig. 5c, in which the domain width increases with decreasing temperature and the correlation decay length does not exhibit temperature dependence (see more details in Supplementary Note XII). The variation in the domain width can be explained using dipole interactions and temperature-dependent uniaxial anisotropy³⁶. These observations demonstrate the potential application of our approach with diamond as a tool to qualitatively characterize the magnetization, phase transition and their critical behaviors in various 2D materials.

Fig. 5: Spatial magnetization fluctuations near T_c.

a The mapping of the stray magnetic field of sample #4 at different temperatures under ${B}_{{{{{{\rm{bias}}}}}}}^{z}=0$. The scale bar is 3 μm, and the sample is approximately 12 ${{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}\times 10{{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}$. b The normalized spatial magnetic field correlation along the y-axis. c The temperature dependence of the correlation decay length (gray dots) and domain width (red dots). The results are obtained by fitting with Eq. (5). The error bars are the standard deviation of the least-squares fit.

Conclusions

To conclude, we quantitatively investigate the landscape of the free energy and its bistability in a finite 2D ferromagnet Fe₃GeTe₂ and study the related thermally activated escape process using a non-perturbative NV magnetometer. Near the critical point, random switching between the two symmetry breaking states is observed, in which the autocorrelation time is described by the Arrhenius law. We show that by decreasing the temperature by approximately 0.8 K, this lifetime is decreased by three orders of magnitude when approaching the critical point, by which we show that the barrier height coefficient $\alpha =31$ meV K^-2. Moreover, since these two states have opposite spin polarizations, the degeneracy of these two states can be lifted by an out-of-plane magnetic field, giving rise to imbalanced random spin switching between the two bistable states. Using a Boltzmann distribution, we extract that energy difference to be approximately 51.3 meV G^-1; thus, a field of 1 G can induce an imbalance much greater than the temperature energy. These results are understood in terms of the GL model, in which all the parameters can be determined from the experimental data. Our work quantitatively characterizes the spontaneous thermally activated escape in a bistable 2D magnet, which helps us to gain much more insight into the critical behavior of ferromagnets near T_c. Finally, we demonstrate the ability of our approach for spatial magnetization correlation. In the theoretical analysis, we have assumed an empirical GL model, ignoring of the possible gradient term, and these results also call for a more deliberated understanding from the microscopic anisotropic Heisenberg models, taken all types of interacting into accounts. Our approach may open an exciting forefront for exploring the phase transition, Kramer turnover²⁵, and even critical fluctuation in various 2D materials, which has not yet been well understood.

Methods

Sample preparation

The NV centers adopted here were generated by implanting 16 keV ${{\!}^{14}{{{{{\rm{N}}}}}}}_{2}^{+}$ ions with a dose of 1 × 10¹³ cm⁻² into a [100]-faced ultra-pure single crystal diamond (Element six) followed by annealing at 1000 °C for 4 h. The Fe₃GeTe₂ single crystals were grown by the chemical vapor transport (CVT) method. High-purity Fe (99.95%), Ge (99.999%), and Te (99.999%) powders were mixed together in a stoichiometric molar ratio of 3:1:2. The temperatures of the source and growth zones were raised to 750 and 700 °C at a rate of 5 °C per min, respectively, and the temperatures were maintained for 7 days. Shiny black plate-like crystals were obtained after the furnace cooled naturally to room temperature. The diamond was placed in piranha solution (H₂SO₄:30%H₂O₂ = 7:3) and cooked at 120 °C for 2 h to remove surface impurities. A 25 μm diameter gold wire was soldered to the substrate glued with diamond to supply microwaves. The hBN flakes of 200–500 nm were mechanically exfoliated onto the diamond (following the optimum distance in ref. ²⁹) and within 100 μm of the gold wire. Fe₃GeTe₂ crystals were exfoliated onto polydimethylsiloxane (PDMS, Gel-Pak, WF-60-X4) for post-transfer in an inert gas glovebox with water and oxygen concentrations less than 1 ppm. The Fe₃GeTe₂ multilayer was identified by optical contrast and was transferred onto the diamond with encapsulation of hBN at both sides.

Low-temperature scanning confocal microscopy

The ODMR spectrum was obtained using a homemade scanning confocal microscope. The 532 nm laser was used as the excitation source and was guided into an objective lens with a numerical aperture of 0.50 (Olympus, LMPlanFL N/50×/0.50). The objective was placed under a three-axis (xyz) piezo-nanoscanning stage. The fluorescence photons from NV centers were also collected by the same objective with and were detected after 635 nm longpass filtering by a fiber-coupled single photon counter module (Excelitas, SPCM-AQRH-10-FC). The bias magnetic field was applied by a permanent magnet fixed to the three-axis translation stage. The samples were placed in a cryostat (Janis, ST-500) cooled by liquid nitrogen. The sample temperature control was realized by a temperature controller (Cryocon, Model 22C) and was calibrated by measuring the zero-field splitting parameter D (temperature dependent) of the fixed region NVs around the Fe₃GeTe₂.

Stray magnetic field measurement from the ODMR

The microwave was supplied by a microwave source (Rohde & Schwarz, SMIQ03B). After passing through a switch (Mini-Circuits, ZASWA-2-50DR+) and an amplifier (Mini-Circuits, ZHL-16 W-43+), resonant microwave fields were applied through the gold wire. Frequency switching and photon detection were synchronized by a pulse signal generator (SpinCore, PulseBlaster). With ${B}_{{{\mbox{bias}}}}$ applied along the selected NV-axis, the spin states |m_s = 0〉 and |m_s = ±1〉 exhibit Zeeman splitting. In the continuous wave ODMR measurement, the resonant microwave will drive the NV to make transitions between |m_s = 0〉 and |m_s = ±1〉, which is reflected in the fluorescence intensity. By performing a Lorentz fit to the ODMR spectrum, we obtained the peak position corresponding to the resonant frequency f₊. We can obtain ${B}_{{{{{{\rm{s}}}}}}}=({f}_{+}-D)/{\gamma }_{{{{{{\rm{e}}}}}}}-{B}_{{{{{\rm{bias}}}}}}$ with $D=2876.5$ MHz and ${B}_{{{{{\rm{bias}}}}}}=123$ G. By measuring the ODMR spectrum for each pixel, the corresponding imaging of B_s is obtained. In all the measurements, the power of the microwave was adjusted to maximize ODMR contrast but was maintained at a safe level to avoid additional heating effects.

Three-point sampling method

This method only measures the fluorescence changes at three preselected frequencies and thus can significantly improve the speed of magnetic detection. We choose three frequencies at ${f}_{1}={\omega }_{0}-w/2$, ${f}_{2}={\omega }_{0}+w/2$, and a far-off resonant frequency f₃, where w is the peak width and ω₀ is the peak position (in Fig. 3, $w\approx 14$ MHz). Then, the variation in magnetic field $\Delta {B}_{{{{{{\rm{s}}}}}}}$ is given by

$$\Delta {B}_{{{{{{\rm{s}}}}}}}=-\frac{{wR}}{2{\gamma }_{{{{{{\rm{e}}}}}}}}$$

where

$$R=\frac{{I}_{1}-{I}_{2}}{{I}_{1}+{I}_{2}-2{I}_{3}}$$

Here, I₁, I₂, and I₃ are the fluorescence intensities at f₁, f₂, and f₃, respectively. Thus, if $w=14$ MHz and $R=0.1$, we have a generated magnetic field of $\Delta {B}_{{{{{\rm{s}}}}}}=-0.25$ G. This measurement has been carefully compared with the full ODMR measurement, showing excellent accuracy. It works well when w is essentially constant and the peak shift ${{{{{\rm{|}}}}}}\delta {{{{{\rm{|}}}}}}\ll w$ satisfies ($\left|\delta \right| < 1$ MHz in Figs. 3 and 4. See ref. ³² for details of the derivation).

Theoretical sensitivity

In the three-point method, if the ODMR spectrum is of Lorentzian shape, when choosing the frequency at the resonance half-high ($f={\omega }_{0}\pm w/2$), the sensitivity is

$${\varepsilon }_{{{{{{\rm{tp}}}}}}}=\frac{4}{3\sqrt{3}}\frac{w}{C{\gamma }_{{{{{{\rm{e}}}}}}}\sqrt{{N}_{{{{{{\rm{p}}}}}}}}}$$

where w is the line width, C is the ODMR contrast and ${N}_{{{{{{\rm{p}}}}}}}$ is the photon-detection rate. In our system, there are ${N}_{{{{{{\rm{p}}}}}}}=1\times {10}^{6}$ count per second, $w=14$ MHz, and $C=0.1$; thus, ${\varepsilon }_{{{{{{\rm{tp}}}}}}}=0.038\,{{{{{\rm{G}}}}}}\,{{{{{{\rm{Hz}}}}}}}^{-1/2}$. When a 2D magnet with magnetization along the z-axis is attached to the diamond surface, the relationship between its projection of the stray magnetic field along the NV axis and the magnetization M_z is calculated using Supplementary Eq. (S16) as ${{{{{{\rm{d}}}}}}M}_{z}/{{{{{\rm{d}}}}}}{B}_{{{{\rm{s}}}}}\approx 22\,{\mu }_{{{{\rm{B}}}}}\,{{{{{\rm{n}}}}}}{{{{{{\rm{m}}}}}}}^{-2}\,{{{{{{\rm{G}}}}}}}^{-1}$. The 2D magnet is approximately 1 μm × 1 μm in size. The sensitivity is approximately $8\times {10}^{5}\,{\mu }_{{{{{\rm{B}}}}}}\,{{{{{{\rm{Hz}}}}}}}^{-1/2}$.

In our system, the most important factor limiting the sensitivity is the distance between the 2D magnet and the NV layer. If considering a single NV spin held in the tip of an atomic force microscope and whose distance from the 2D magnet is 20 nm, there are ${N}_{{{{\rm{p}}}}}=3\times {10}^{5}$ count per second, $w=10$ MHz, and $C=0.25$, thus ${\varepsilon }_{{{{{{\rm{tp}}}}}}}=0.020\,{{{{{\rm{G}}}}}}\,{{{{{{\rm{Hz}}}}}}}^{-1/2}$. Assuming that the monolayer Fe₃GeTe₂ has ${M}_{z}\approx 0.25\,{\mu }_{{{{{{\rm{B}}}}}}}\,{{{{{{\rm{nm}}}}}}}^{-2}$ at $\Delta T=0.2\,{{{{{\rm{K}}}}}}$ (estimated via Fig. S6d), at which point its stray magnetic field ${B}_{{{{\rm{s}}}}}\approx 0.25\,{{{{{\rm{G}}}}}}$, the correlation decay time is about 13 ms (estimated via Fig. 3c). The required sensitivity is about $0.028\,{{{{{\rm{G}}}}}}\,{{{{{{\rm{Hz}}}}}}}^{-1/2}$, which is close to the theoretical limit of ${\varepsilon }_{{{{{{\rm{tp}}}}}}}$. Thus, in principle, the temporal resolution can be increased to ten milliseconds. Furthermore, according to a recent report³⁷, the photon detection rate of single NV centers in diamond nanopillars can be up to ${N}_{{{{\rm{p}}}}} \sim 4\times {10}^{6}$ count per second, which implies that the minimum temporal resolution may be further increased.

Estimation of sample #3 magnetization

In Fig. 4a, we can see that $R$ is $\pm 0.045$ for the two spin states. Considering the line width $w=11$ MHz, it equals ${B}_{{{{{{\rm{s}}}}}}}=\mp 0.09$ G. Depending on the optical resolution and the thickness of the bottom hBN, we estimate ${M}_{z} \sim \mp 2.3\,{\mu }_{{{{{\rm{B}}}}}}\,{{{{{{\rm{nm}}}}}}}^{-2}$. For the domain area, since sample #3 is not a single domain, we cannot get it directly from the optical image. We cool down the temperature to 155 K (ΔT = 5.7 K) so as to suppress the magnetization fluctuations process and extract the domain area by the stray magnetic field of ~2 μm². Considering that the magnetic domain area decreases with increasing temperature (Fig. 4a is measured in ΔT = 1.3 K), we estimate that the magnetic domain area is ~1–2 μm². So, the total magnetization $A{M}_{z}$ is $\sim 2\times {10}^{6}-5\times {10}^{6}$ μ_B.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.