Introduction

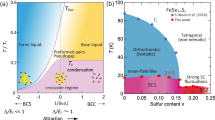
The study of the iron-based superconductor, FeSe, has resulted in various topics, such as the appearance of superconductivity in the electronic nematic phase without magnetism, Bardeen-Cooper-Schrieffer Bose-Einstein-condensation (BCS-BEC) crossover, and Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) superconductivity at very high magnetic fields1. FeSe has unique features among iron-based superconducting (SC) systems, such as the formation of Fermi surfaces with unconnected small hole and electron pockets with very small Fermi energies, and the absence of magnetism in the nematic phase where four-fold symmetry is broken on the FeSe plane. These features are maintained by isovalent substitution in FeSe1−xSx up to the nematic quantum critical point (QCP) (xc ≃ 0.17). In contrast to magnetism, the SC state spreads across a wide S-substitution regime2 and that developed in the nematic phase has a higher Tc (~9 K) than that in the tetragonal phase (x > xc) with four-fold symmetry (Tc ~ 4 K). According to recent angle-resolved-photo-emission-spectroscopy (ARPES) measurements for pure FeSe, the hole pocket near the zone center (Γ point) exhibits an ellipsoidal shape, and its SC gap has a two-fold symmetric character with possible nodal points3. This implies that s- and d-wave components are significantly mixed in the nematic phase. With increasing S-concentration levels, the nematic fluctuations are strongly enhanced, and the transport properties exhibit non-Fermi liquid behavior. Accompanied by such changes near the nematic QCP, a change in the SC-gap structure has been suggested based on the field dependence of the specific heat and thermal conductivity4. Moreover, a marked change in the SC gap has been observed in systematic scanning-tunneling-spectroscopy (STS) studies5,6. The SC-gap spectrum showed a small zero-energy conductance below xc, whereas it was significantly enhanced above xc.

Recently, Setty, et al. proposed a theoretical model for a system with spin-orbit coupling, multi-band structures, and time-reversal symmetry breaking (TRSB), and suggested that topologically protected nodal Fermi surfaces, referred to as Bogoliubov Fermi surfaces (BFSs), are induced in the SC state7,8. The appearance of the nonzero DOS in the specific heat and thermal conductance measurements in a heavily S-substituted regime can be explained by the formation of BFSs. TRSB required for BFSs was recently suggested from muon spin relaxation measurements9. The existence of BFSs is a significantly important topic because it is deeply associated with SC pairing symmetry. Furthermore, whether interband interactions exist between BFSs remains an open question. We investigated the formation of BFSs in the SC state and interband interactions from the perspective of low-energy magnetic fluctuations using 77Se-nuclear magnetic resonance (NMR) down to 100 mK. Deep in the SC state, we found the presence of spin fluctuations of Bogoliubov quasiparticles, which are associated with possible nesting properties between BFSs.

Results and discussion

Previous NMR measurements were performed mainly above Tc for pure bulk FeSe10,11,12,13,14,15,16,17,18 and S-substituted FeSe19,20,21,22,23,24. Studies have primarily focused on the relationship between superconductivity, nematicity, and magnetic order above Tc. We performed 77Se-NMR measurements in both the normal and SC states of FeSe1−xSx (0 ≤ x ≤ 0.23). A single crystal was used for each S-substitution level, and a magnetic field of 6.0 T was applied parallel to the FeSe plane to exclude the formation of vortices in the plane. Tc was determined from AC susceptibility measurements utilizing an NMR tank circuit. The susceptibility data are presented in detail in Supplementary Fig. 1 (see Supplementary Note 1); Tc for x ≤ 0.12 was approximately 9 K, whereas Tc for x = 0.18 was 3 K at 6.0 T. 77Se-NMR spectra for several S-substitution levels across xc ~ 0.17 are shown later. Similarly to pure FeSe10, the NMR spectra showed double peaks or edges below the nematic transition temperature, Tnem, which merged into one peak with increasing S substitution.

Figure 1a shows the evolution of the relaxation rate divided by temperature (1/T1T) with respect to S substitution, and Fig. 1b is a color plot of Fig. 1a. 1/T1T provides a measure of low-energy spin fluctuations. In general, 1/T1T is expressed as:

$$\frac{1}{{T}_{1}T} \sim \mathop{\sum}\limits_{{{{{{{{\bf{q}}}}}}}}}Im\chi ({{{{{{{\bf{q}}}}}}}})$$
(1)

where χ(q) is the wave-number (q)-dependent susceptibility. The T dependence of 1/T1T shown in Fig. 1a contrasts with that of the Knight shift which is discussed later. The Knight shift, which reflects the uniform susceptibility χ(0), monotonically decreases with decreasing temperature. The upturns of 1/T1T toward Tc originate from spin fluctuations with q ≠ 0. As shown in Fig. 1b, spin fluctuations develop remarkably in the nematic phase and are strongly suppressed in the tetragonal phase. Spin fluctuations are associated with the topological configuration of electron and hole pockets and interband couplings. Two-dimensional Fermi surfaces theoretically obtained in the tetragonal phase25 are schematically shown in Fig. 2b, c. The enhancement of χ(q) is expected at q ~ (π, 0) in the nematic phase, as well as in the tetragonal phase, owing to the interband coupling between electron and hole pockets, namely, q = (π, 0) nesting. However, the absence of a magnetic order implies that the nesting is not very strong. Such weak coupling is expected when orbital-selective coupling becomes important. The experimental results in Fig. 1a are almost consistent with those observed by another study19,22, wherein spin-fluctuation mediated pairing, that is, s±-wave pairing was suggested because Tc reached a maximum for significantly strong spin fluctuations (x ~ 0.1)19.

Fig. 1: 77Se relaxation rate (1/T1) divided by temperature (T) of FeSe1−xSx.
figure 1

a T dependence of 1/T1T at high temperatures. The magnetic field of 6.0 T was applied parallel to the FeSe plane. The data for 12%-S-substituted FeSe were already published20,23. b Color plot of 1/T1T. Tnem represents the nematic transition temperature, and Tc(6T) represents the superconducting (SC) transition temperature measured by means of the AC susceptibility at 6.0 T.

Full size image
Fig. 2: 1/T1T in the SC state and Bogoliubov Fermi surfaces (BFSs).
figure 2

a Temperature dependence of 1/T1T at low temperatures below Tc for several S-substitution levels. Arrows indicate Tc measured at 6.0 T. Error bars are estimated from those of T1. All data points contain the error bars, although many of the error bars are smaller than the data points. b Schematic diagram of two-dimensional Fermi surfaces obtained theoretically for the tetragonal phase together with contributions from three orbitals, dxy, dyz and dzx colored in blue, red, and green, respectively25. Sufficiently expanded BFSs expected below Tc are colored in purple7. Recently, quasiparticle excitations with a finite gap has been observed for the directions shown by the dotted curves29. c BFSs expanded from the nodal points of pure FeSe are colored in purple7.

Full size image

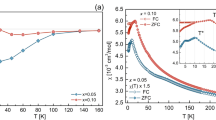
Figure 2a shows 1/T1T at temperatures below Tc for several S-substitution levels crossing xc ~ 0.17, which is the main results in this study. The decrease in 1/T1T below Tc is due to the opening of the SC gap. In conventional clean superconductors, 1/T1T should decrease to zero with decreasing temperature. However, 1/T1T for x = 0.05 and 0.10 became constant at low temperatures. With further substitution over xc, 1/T1T exhibited an upturn with decreasing temperature and the values became significantly larger than those for x = 0.05 and 0.10. Upturns of 1/T1T observed below and above Tc are very rare in SC systems. The low T behavior of 1/T1T = constant suggests a residual DOS. As a cause of the residual DOS, (1) the impurity effect, (2) the Volovik effect, and (3) the coexistence of SC and normal states may be possible. First, the behavior of 1/T1T = constant indicates an impurity effect in most cases. The impurity effect on 1/T1 has been studied theoretically at an early stage in the s±-wave scenario26.

For small impurity doping, the quasiparticle DOS is V-shaped as a function of energy, and the T dependence of 1/T1T shows a T2 dependence at temperatures below Tc. For fairly large impurity doping, the quasiparticle DOS has a finite value at zero energy, and 1/T1T exhibits a T-independent relation followed by a T2 dependence with decreasing temperature. At first, the impurity effect appears to explain the low T behavior of 1/T1T; however, this effect is excluded for the following reasons: (i) The upturn of 1/T1T for x = 0.18 is difficult to explain, and (ii) impurity doping levels should be remarkably different between x = 0.05 and 0.10 because the constant value of 1/T1T differs by approximately one order of magnitude. Therefore, Tc should be remarkably different between them. However, the value of Tc is almost the same between them. (iii) Furthermore, quantum oscillation measurements observed in a wide range of x covering the tetragonal phase indicates the relatively clean nature of the samples27. The Volovic effect can also induce an in-gap state similarly to the impurity effect. The DOS can be induced by an applied field owing to the Doppler shift of quasiparticle energy. The field dependence of 1/T1T has been theoretically investigated for s±- and d-wave cases28. This effect should result in almost the same 1/T1T values between x = 0.05 and 0.10, because the strength of the applied field is the same and the SC gap or Tc is almost the same between them. Therefore, this effect is excluded as well as the impurity effect. Another possibility is the coexistence of SC and normal states. The coexistence in real space implies that SC and normal metallic domains coexist. However, such a case can be excluded by the rather homogeneous spectra observed in the STS measurements5. Instead of the coexistence in real space, the coexistence in momentum space such as the formation of BFSs would be promising. BFSs that are expanded from the nodal points of pure FeSe and sufficiently expanded BFSs7 would play important roles for x < xc and x > xc, respectively, in view of the STS and specific-heat results4,5. The schematics of the former and latter are shown in Fig. 2c, b, respectively. In fact, BFSs should be much complicated because BFSs with two-fold symmetry have been suggested from recent ARPES measurments, although the measurements were performed for the tetragonal phase29.

For small x, BFSs expanded from the nodal points are small, and the nesting is hardly expected, as shown in Fig. 2c. Therefore, the enhancement of χ(q) or the upturn of 1/T1T is hardly expected, despite that such enhancement or upturn is caused in the normal state due to the nesting between original Fermi surfaces. In such a case, flip flop of a nuclear spin due to scattering by quasiparticles becomes a major relaxation process, like the Korringa relation in conventional metals. The Korringa relation, \(1/{T}_{1}T{K}_{{{{{{{{\rm{spin}}}}}}}}}^{2}=constant\), where Kspin is the spin part of the Knight shift K, is applied for conventional metals with free electrons or weakly interacting electrons. K is decomposed into Kspin and the orbital part Korb,

$$K={K}_{{{{{{{{\rm{spin}}}}}}}}}+{K}_{{{{{{{{\rm{orb}}}}}}}}},$$
(2)

where Kspin is proportional to the DOS and the uniform susceptibility χ(0). Kspin and Korb can be separated at high temperatures using the susceptibility data, χ(0). Korb is T-independent and is approximately 0.26% for x = 0.1223. For conventional superconductors, Kspin approaches zero as temperature is decreased owing to the SC gap. In case considered in this study, Kspin remains nonzero due to the DOS of BFSs. Therefore, 1/T1T can be expressed using the Korringa relation as follows despite of the SC state:

$$\frac{1}{{T}_{1}T{K}_{{{{{{{{\rm{spin}}}}}}}}}^{2}}=\frac{4\pi {k}_{{{{{{{{\rm{B}}}}}}}}}}{\hslash }{(\frac{{\gamma }_{{{{{{{{\rm{n}}}}}}}}}}{{\gamma }_{{{{{{{{\rm{e}}}}}}}}}})}^{2}K(\alpha )$$
(3)

where kB and ℏ are the Boltzman and Planck constants, respectively, γn(e) is the gyromagnetic ratio of 77Se (electron), and K(α) is a function of the Stoner enhancement factor α. The Stoner factor is expressed as α = Iχ(0) where I represents the interaction coupling. K(α) provides a measure of electron correlation. For ferromagnetic metals, K(α) < 1, whereas for antiferromagnetic metals, K(α) > 1. Further, for free electrons, α = 0 and K(α) = 1. A detailed expression of K(α) is provided in Supplementary Note 2. As 1/T1T for x = 0.10 is one order larger than that for x = 0.05, Kspin estimated using Eq. (2) is approximately three times larger than that for x = 0.05. We estimated residual Kspin from the experimental results of 1/T1T, assuming that the interaction between quasiparticles is negligibly small, that is, K(α) = 1. The value of Kspin is estimated to be 0.015% for x = 0.05. Subsequently, the ratio of Kspin between the SC and normal states is estimated to be 0.49, implying that the DOS of BFSs reaches almost half of the DOS observed in the normal state above Tc. In fact, certain quasiparticle correlations should exist (K(α) > 1), and the value mentioned above is overestimated. To obtain a more precise estimation, a further theoretical analysis of χ(q) is required.

The estimation for x = 0.05 and 0.10 is not applicable for x = 0.18, because the Korringa relationship breaks. The nesting between sufficiently expanded BFSs can cause the enhancement of χ(q). A drop just below Tc originates from the opening of the SC gap and a rise just above Tc originates from spin fluctuations, which are strongly suppressed in the tetragonal phase. Interestingly, the T dependence of 1/T1T below Tc is similar to that above Tc, although the magnitude of the upturn becomes one third across Tc. The T dependence of χ(q) at high temperatures originates from the nesting between original Fermi surfaces in the normal state. The reason why similar χ(q) is reestablished below Tc is that sufficiently expanded BFSs reflect original Fermi surfaces and a similar nesting becomes possible.

We have estimated Kspin from 1/T1T, however, it seems straightforward to estimate from K. Figure 3a shows the evolution of K with respect to S substitution. The results are almost consistent with those observed by another study19. In the nematic phase, two peaks appear reflecting two domains (the spectra of x = 0.05 and 0.12 in Fig. 3c). In Fig. 3a, only the average of the two peaks is plotted for temperatures below Tnem. The detailed shifts of each peak and their average are shown in Fig. 3b. Figure 3a certainly includes the information of χ(0) or Kspin. These quantities can be obtained from K − χ plots at high temperatures. This procedure is possible because both quantities are T-dependent at high temperatures (Fig. 3a). However, at very low temperatures below Tc, Kspin originating from the residual DOS and Korb can not be separated from each other because both quantities are T-independent. Thus, a theoretical investigation is needed to separate Kspin from Korb. Even if Korb is theoretically calculated, small residual Kspin( < 0.03) is estimated from the raw data, K(~0.28) by subtracting large Korb( ~ 0.25). This procedure can potentially contain a significant error. Furthermore, Korb may change below and above Tnem in the lightly S-substituted regime, which renders the estimation of residual Kspin much more challenging. The estimation of Kspin from 1/T1T is advantageous because the information on Korb is not needed.

Fig. 3: 77Se Knight shift (K) of FeSe1−xSx determined from nuclear magnetic resonance (NMR) spectra.
figure 3

a Temperature dependence of K at high temperatures. The shifts were measured at the field (6.0 T) parallel to the FeSe plane. In the nematic phase (x < 0.17), two peaks or edges appear as shown in Fig. 3c. We plotted the average of two peaks for K below Tnem. The data for 12%-S-substituted sample (x = 0.12) was cited from the previous works20,23. b K below Tnem for x = 0.05 and 0.12. Tnem and Tc represent the nematic and superconducting transition temperatures, respectively. Two peaks in Fig. 3c and their average are shown in both panels. Both panels are expansions of Fig. 3a. c 77Se-NMR spectra for x = 0.05, 0.12, and 0.18. Two peaks appearing for x = 0.05 and 0.12 merge into a single peak with increasing S-substitution level over xc (≥0.17).

Full size image

The low-T spin fluctuations above xc can be attributed to the interband couplings between BFSs. However, the question arises as to whether the disappearance of the nematic order or revival of four-fold symmetry on the FeSe planes is essential for the couplings between BFSs. To investigate this problem, 12%-S-substituted FeSe at approximately 1 GPa may provide a clue because the T dependence of 1/T1T is similar to that of 18%-S-substituted FeSe, that is, the suppression of spin fluctuations has been observed for 12%-S substitution at approximately 1 GPa20,23. Further investigations at very low temperatures and high pressures are required for S-substituted FeSe (x < xc).

Conclusion

In conclusion, we have observed anomalous spin fluctuations deep in the SC state for S-substituted FeSe over x > xc via 1/T1T measurements to 100 mK, which suggests the presence of Bogoliubov quasiparticles. The upturn of 1/T1T below Tc is similar to that above Tc, suggesting that χ(q) does not significantly change across Tc. Therefore, the upturn can be attributed to the enhancement of χ(q) due to the nesting between BFSs. This means that the expansion of BFSs is significantly large. The low-T spin fluctuations above xc contrast with those below xc arising from weekly interacting quasiparticles. The present NMR results highlight the novel SC state with BFSs, having excitations at zero energy.

Methods

We performed 77Se-NMR measurements at 6.0 T using a single crystal for each S-substitution level. Typical size is approximately 1.0 × 1.0 × 0.5 mm. We applied a magnetic field parallel to the FeSe planes to suppress the decrease in Tc and generation of vortecies. We performed pulsed-NMR measurements using a conventional spectrometer. NMR spectra were obtained by the Fast Fourier Transform (FFT) of a spin-echo signal. To detect a echo signal, we used 4-cycle pulse sequence. The relaxation time (T1) was measured by the saturation-recovery method, and the data points of the recovery curve were fitted by a single exponential function.