Introduction

Quantum spin liquids are strongly correlated many-body systems that exhibit remarkable properties such as emergent gauge fields, long-range entanglement, and fractionalized excitations1,2. However, even after 50 years from their original conception as resonating valence bond (RVB) states3, concrete realizations of these fascinating phases in magnetic insulator materials are few and far between. Today, advances in neutral-atom quantum simulators have unleashed the potential for realizing highly controllable, coherent quantum many-body systems, which are ideal testbeds for exploring quantum criticality4,5,6,7,8,9, probing quantum many-body dynamics10,11,12, and preparing exotic phases of quantum matter13,14. In particular, recent experiments on a 219-qubit programmable Rydberg quantum simulator15 have demonstrated the remarkable realization of a gapped topological phase known as the \({{\mathbb{Z}}}_{2}\) quantum spin liquid16,17,18,19.

The zoo of quantum spin liquids1,20,21, however, has many other species including, for instance, states where the invariant gauge group is U(1) instead of \({{\mathbb{Z}}}_{2}\). Such a U(1) quantum spin liquid is particularly interesting from the perspective of fundamental physics as it hosts an emergent gapless excitation, termed a photon in analogy to conventional electromagnetism22. Unfortunately, experimental efforts to realize such a phase in rare-earth pyrochlore materials23 are often complicated by competing microscopic interactions. On the theoretical side, standard parton mean-field constructions17,24 also do not guarantee the stability of the gapless state under monopole fluctuations25. These varied considerations highlight the importance of discovering robust candidates for studying the rich physics of U(1) gauge theories.

In this work, motivated by the recent experimental progress in trapping neutral atoms, we explore the possibility of finding such spin-liquid-like RVB states in finite-sized Rydberg arrays. We show that, on the honeycomb lattice, strong van der Waals interactions between Rydberg atoms lead to an effective blockade constraint26,27,28,29,30 that can be mapped to a trimer constraint on an underlying triangular lattice31. Related blockade-induced dimer constraints have played a central role in the recent proposals of gapped dimer-RVB \({{\mathbb{Z}}}_{2}\) spin liquids of Rydberg atoms on both the kagome32,33,34 and the ruby35 lattice. On the honeycomb lattice, however, the possibility for a trimer quantum spin liquid (TQSL) state arises owing to the correspondence with trimer instead of dimer coverings.

The emergent trimer constraint on the honeycomb lattice has previously been explored in the context of classical hard-core lattice gas models31,36,37 and ordered quantum correlated states in móire Mott insulators38. The quantum RVB state of trimers was first classified as a gapless liquid with an emergent U(1)  ×  U(1) local symmetry in Ref. 39, where a microscopic model for a Rydberg TQSL was also originally proposed. In this work, we focus on a similar system but crucially, in the presence of realistic long-ranged interactions, which are not only native to most quantum simulation platforms but also known to be particularly important vis-á-vis the stability of Rydberg spin liquids15. Specifically, we demonstrate the realization of a TQSL phase in honeycomb Rydberg arrays of finite size, for a range of experimentally relevant parameters, by carrying out detailed numerical studies. Here, and throughout the rest of this paper, we use “TQSL phase” to refer to a quantum phase defined by the coherent superposition of all possible trimer configurations for a given finite-sized lattice, in exact analogy to a dimer resonating valence bond phase. However, we do not address the prospects for the existence of such a TQSL phase in an infinite system, which lies beyond the scope of our calculations.

In order to explore the nature of the ground states, we turn to density-matrix renormalization group (DMRG)40,41 simulations and exact diagonalization (ED) of the so-called PXP model on finite-size clusters42. We find suggestive signatures of the TQSL phase on the finite-size clusters explored—including, for example, a high fidelity overlap with the perfect TQSL state—and demonstrate its robustness to real experimental conditions that include long-ranged interactions, relaxed boundary conditions, and experimental state preparation protocols. In addition, we find that the experimental protocol leads to an enhancement of TQSL fidelities compared to the ground state. Our understanding of the underlying mechanism thereof leads us to conjecture a universal fidelity enhancement for any state that is a superposition of configurations with the maximum allowed Rydberg excitations (subject to blockade constraints). Finally, we discuss the experimental signatures of the TQSL states and demonstrate that our proposal can be implemented and studied in today’s Rydberg atom quantum simulators.

Results

Trimer model mapping

We consider a system of Rydberg atoms arrayed on a honeycomb lattice with the distance between nearest-neighbor sites being a. This can be achieved experimentally by placing the neutral atoms in optical tweezers and arranging them using spatial light modulators, with currently attainable system sizes in excess of 200 atoms13. The atoms are driven between the ground (\(\left\vert g\right\rangle\)) and highly excited Rydberg states (\(\left\vert r\right\rangle\)) by a coherent laser drive with Rabi frequency Ω and detuning Δ, leading to the Hamiltonian

$$\frac{H}{\hslash }=\mathop{\sum}\limits_{i}\left(\frac{\Omega }{2}\left\vert {g}_{i}\right\rangle \left\langle {r}_{i}\right\vert +{{{{{{{\rm{h}}}}}}}}.{{{{{{{\rm{c}}}}}}}}.\right)-\mathop{\sum}\limits_{i}\Delta {n}_{i}+\mathop{\sum}\limits_{i < j}{V}_{ij}{n}_{i}{n}_{j},$$
(1)

where ℏ is the reduced Planck constant, i denotes the lattice sites, \({n}_{i}\equiv {\left\vert r\right\rangle }_{i}\left\langle r\right\vert\) counts the occupation of the excited states, and Vij are the van der Waals interactions between atoms in Rydberg states. The van der Waals interactions fall off with the distance between atoms, \({{{{{{{\mathcal{R}}}}}}}}\), as \(V({{{{{{{\mathcal{R}}}}}}}})={C}_{6}/{{{{{{{{\mathcal{R}}}}}}}}}^{6}\) and are central to the phenomenon of the Rydberg blockade that we utilize. More precisely, of the neighboring atoms lying within a distance Rb (the blockade radius), defined by V(Rb)  ≡  Ω, only one can be excited to the Rydberg state, leading to the blockade mechanism.

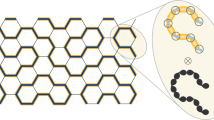
Choosing a blockade radius such that the k = 3 nearest neighbors of an atom on the honeycomb lattice are blockaded, the Rydberg blockade constraint becomes identical to a trimer constraint. The trimer in question is a covering of three edges forming a triangle within the triangular lattice built from the vertices placed at the centers of the honeycomb lattice. The constraint enforces that no edge or vertex is shared between trimers31. This trimer mapping is illustrated in Fig. 1a, where the blockaded neighbors of a central honeycomb atom are shown to match the corresponding forbidden triangular trimers. Thus, the space of maximally filled blockaded configurations—also referred to as the maximum independent set (MIS) subspace43,44—can be matched to trimer coverings of the dual triangular lattice. The number of covering configurations is found to scale exponentially with the total system size (area)37, despite the stiffness of individual trimer moves.

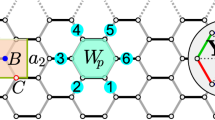
Fig. 1: Trimer quantum spin liquid (TQSL) on a honeycomb lattice of Rydberg atoms.
figure 1

a In the regime where three nearest-neighbor Rydberg atoms are within the blockade radius (k = 3 shell, shown in orange), the blockade-obeying configurations map exactly to the trimer coverings of the triangular lattice with vertices at the centers of the hexagons31. The number of trimer coverings on the triangular lattice grows exponentially with the system size37. b The TQSL is an equal superposition of exponentially many trimer coverings (one covering shown with filled triangles), and is characterized by a U(1) × U(1) local symmetry due to the tripartite nature of triangular lattice with respect to trimers39. For the tripartition and the trimer configuration shown, we assign two sets of electric fields directed from A to B and from B to C sublattices (arrows). The two U(1) degrees of freedom can be related to two conservation laws, as the independent fluxes are equal to the charges NA − NB and NB − NC enclosed by a closed loop. c Quantum phase diagram of Rydberg atoms on a 32 × 4 honeycomb lattice retaining three strongest interactions, as obtained by density matrix renormalization group (DMRG)46. The boundaries of the three ordered phases (Néel, columnar, and brick) are mapped out by entanglement entropy, energy susceptibility, and fidelity susceptibility peaks (full lines). In addition, a region with a large entanglement entropy is distinguished by fidelity and energy susceptibility (dashed lines) measurements in the regime where third-nearest neighbors are blockaded. The properties of this unordered phase agree with the expected properties of the TQSL state on a finite cylinder.

Full size image

While the classical trimer model is of interest in its own right as it was numerically found to avoid ordering for any density31, we are interested in a trimer model with quantum fluctuations that can be realized in Rydberg quantum simulators. The possibility for, to the best of our knowledge, novel physics in the quantum model arises by considering a trimer state that is an equal superposition of all of the exponentially many trimer covering configurations (TC):

$$\left\vert {{{{{{{\rm{TQSL}}}}}}}}\right\rangle =\frac{1}{\sqrt{{D}_{{{{{{{{\rm{MIS}}}}}}}}}}}\mathop{\sum}\limits_{{{{{{{{{\rm{TC}}}}}}}}}_{i}}\left\vert {{{{{{{{\rm{TC}}}}}}}}}_{i}\right\rangle ,$$
(2)

where DMIS denotes the dimension of the trimer covering subspace (i.e., the number of different trimer coverings), and the sum extends over all the trimer coverings TCi. Such a state was first proposed and classified by Ref. 39 as a gapless U(1)  ×  U(1) spin liquid. To see the emergence of the two local U(1) symmetries, one can tripartition the triangular lattice such that the trimers cover one site of each sublattice (A, B, C) and then assign electric fields on A–B and B–C trimer bonds, as shown in Fig. 1b 39. The total A–B (B–C) flux through a closed loop is then given by the difference between the number of A and B (B and C) sites enclosed by the loop, showing the presence of two independent U(1) symmetries (see Supplementary Note 1 for more details). The gaplessness of the TQSL state then follows from Polyakov’s results45 and was also confirmed numerically by Ref. 39.

While the abovementioned trimer mapping provides a general starting point, the nature of the quantum ground state of the microscopic model has to be carefully investigated to establish the existence of a quantum spin liquid phase, because other possibilities, including trivial disordered or valence bond solid (VBS) states, cannot be excluded a priori. Here, we do so by illustrating that certain ground states of the Hamiltonian (1) are in the TQSL phase—adiabatically connected to the perfect TQSL state on finite clusters.

DMRG phase diagram

We first explore the quantum phase diagram of the Rydberg Hamiltonian on the honeycomb lattice using DMRG on long cylinders of finite sizes46. We use bond dimensions of up to 1800 and retain the three strongest Rydberg interactions in Eq. (1), resulting in good convergence. The additional details of the numerical calculations are presented in the Methods section. We use the following quantities to map the boundaries of the different phases:

$${S}_{{{{{{{{\rm{vN}}}}}}}}} =-{{{{{{{\rm{Tr}}}}}}}}\,({\rho }_{0}\log {\rho }_{0}),\\ \chi =-\partial {E}_{0}^{2}/\partial {\Delta }^{2},\\ {{{{{{{\mathcal{F}}}}}}}} =2[1-| \left\langle \Psi (\Delta /\Omega )\right\vert \left\vert \Psi (\Delta /\Omega +\delta )\right\rangle | ]/{\delta }^{2},$$
(3)

where SvN is the von Neumann entanglement entropy (ρ0 being the reduced density matrix for half of the system), χ is the energy susceptibility (E0 being the ground state energy), and \({{{{{{{\mathcal{F}}}}}}}}\) is the fidelity susceptibility (\(\left\vert \Psi \right\rangle\) being the ground-state wavefunction). The phase diagram is presented in Fig. 1c.

Among the main features of the phase diagram are the presence of three ordered phases in three different blockade regimes. Intriguingly, an additional unordered region with a large entanglement entropy is apparent, clearly separated from the trivial disordered phase by a phase transition. The Rydberg density profile in all of the regions is presented in Fig. 2, while the static structure factors for the different phases are given in Supplementary Note 2. The first ordered phase appears in the nearest-neighbor (k  =  1) blockade regime, and it corresponds to the Néel phase with a staggered order within the honeycomb unit cell. The Néel state hosts a domain wall in the middle of the 32 × 4 honeycomb cluster employed here due to two different domains being preferred by the open boundaries on each end.

Fig. 2: Phases on the honeycomb lattice.
figure 2

Rydberg excitation density (〈ni〉, shaded from light to dark according to the colorbar) profiles at representative points of the DMRG (density matrix renormalization group) phase diagram from Fig. 1. While the columnar phase is defectless for this cluster, the Néel and brick phases host a domain wall in the middle of the lattice due to their incommensurability with the open boundary. The two ordered domains on each end of the system are indicated by red boxes, while the primitive unit cells for the ordered phases are delineated in blue. In contrast to the ordered phases, in the TQSL (trimer quantum spin liquid) region, a state with no density-wave order and bulk density close to the expected value of 1/6 is observed, on top of which, density oscillations spread inwards from the boundaries.

Full size image

The next-nearest-neighbor blockade (k = 2) leads to the stabilization of the columnar phase, characterized by the pattern of Rydberg excitations in Fig. 2. We note, however, that there exists an extensive classical string degeneracy in this k = 2 blockade regime (see Supplementary Note 5). From that classical manifold of states, the columnar pattern is stabilized by both third-neighbor Rydberg interactions and quantum fluctuations. Both of these effects prefer maximal distance between further-neighboring Rydberg excitations (see See Supplementary Information below), a condition satisfied by the columnar state. Incidentally, thermal fluctuations in the classical hard-core boson model on the honeycomb lattice lead to the same ordered phase in this regime31.

The final ordered phase, which we call the brick phase38, appears in the third-neighbor blockade regime (k = 3), with the Rydberg excitations patterned on the so-called brick lattice38 (see Fig. 2). Similar to the Néel state, open boundaries prefer different brick domains, leading to a domain wall in the middle of the cluster considered. The appearance of the brick ground state observed in our simulations is a consequence of quantum fluctuations breaking the exponential degeneracy of valid trimer coverings for the k = 3 blockaded classical model via an order-by-disorder mechanism47,48. The stabilization of the brick phase, in particular, can be understood by noting that the quantum fluctuations prefer maximally flippable configurations. The brick phase indeed satisfies the maximum flippability condition, as also observed in classical simulations of the hard trimer model relevant to twisted bilayer graphene38. Additional classical interactions on top of the hard trimer model were shown therein to favor maximal flippability and, in turn, also the brick state.

At intermediate detunings, however, an additional region emerges in the k = 3 blockade regime at fillings close to 1/6. This region shows no order and has a high entanglement entropy throughout. On changing the detuning at a fixed blockade radius, the fidelity and energy susceptibilities manifest a clear peak, as presented in Fig. 3, presumably stemming from a nonadiabatic change in the wavefunction compared to the trivial disordered phase. To probe the intrinsic (bulk) nature of the transition, we also calculate the energy susceptibility difference between 32 × 4 and 24 × 4 clusters (\({\chi }_{{}_{b}}\)), thus subtracting out the effects of four boundary columns of atoms at each end of the system. The energy susceptibility peak persists after such boundary subtraction with sizable magnitude, pointing to a putative transition in the bulk (inset of Fig. 3). We label this highly entangled region as TQSL in the phase diagram of Fig. 1 due to its separation from the trivial disordered phase and its appearance in the k = 3 regime with the density of ≈ 1/6 expected for a TQSL state. In addition, the gap is observed to decrease with system size in the TQSL phase, in contrast to the near-constant gap size in the trivial disordered phase (see Supplementary Note 2). The gap scaling and the enhanced susceptibility towards boundary-induced density oscillations (see Supplementary Note 2) are seemingly suggestive of a gapless state in the thermodynamic limit, broadly consistent with the expectations for a TQSL. We note, however, that the state is generically observed as gapped for finite clusters (since the discrete, allowed momenta need not coincide with the gapless point in momentum space) in the absence of twisted boundary conditions or flux insertion49,50,51. In the remainder of this paper, we focus on this intriguing TQSL regime identified by our DMRG simulations and present evidence for the existence of a true spin liquid ground state on finite clusters.

Fig. 3: Transition into the trimer quantum spin liquid (TQSL) regime.
figure 3

On going from the trivial disordered phase to larger Δ/Ω, clear peaks are visible in the fidelity (blue, evaluated from Eq. (3) for δ = 0.1 on a 32 × 4 cluster) and energy susceptibilities (orange) that are preserved upon boundary subtraction (between 32 × 4 and 24 × 4 clusters; inset). The second peak at a larger detuning arises from the transition into the (columnar) ordered phase.

Full size image

TQSL in the PXP model

In order to analyze the existence, characterization, and experimental feasibility of preparation of the TQSL state, we perform large-scale exact diagonalization calculations42. For these simulations, we employ a hard-constraint approximation to the full Rydberg Hamiltonian, known as the PXP model52, to enable us to reach large system sizes. The essence of this approximation is to eliminate states violating the Rydberg blockade from the Hilbert space. This is achieved by making the first k Rydberg interactions infinite and discarding the longer-range interactions while projecting the Rabi-oscillation term into the subspace of allowed configurations, leading to the Hamiltonian:

$$\frac{{H}_{{{{{{{{\rm{PXP}}}}}}}}}}{\hslash }=\frac{\Omega }{2}\mathop{\sum}\limits_{i}P{\sigma }_{i}^{x}P-\Delta \mathop{\sum}\limits_{i}{n}_{i},$$
(4)

where P is the projector onto the blockade subspace and \({\sigma }_{i}^{x}\equiv (\vert {g}_{i}\rangle \langle {r}_{i}\vert +{{{{{{{\rm{h}}}}}}}}.{{{{{{{\rm{c}}}}}}}}.)\). This allows us to explore the k = 3 blockade regime with ED42,53 on clusters of up to 60 sites with periodic boundary conditions in both directions, thus also better simulating the bulk of a large system. The PXP approximation has been effectively employed to understand a variety of phenomena in Rydberg systems, including quantum scars11,54,55, emergent lattice gauge theories56,57, and gapped spin liquids on the ruby lattice15,35.

We map out the ground-state phase diagram of the PXP model as a function of the tuning parameter, Δ/Ω. The phase boundaries are determined by considering the overlap of the ground state with the perfect TQSL state in Eq. (2) (equal superposition of all MIS states for the given cluster), \(| \left\langle \Psi \right\vert \left\vert {{{{{{{\rm{TQSL}}}}}}}}\right\rangle |\), the fidelity and energy susceptibilities, as well as changes in the low-lying energy spectrum of the model (see Supplementary Note 3). To explore the robustness of our predictions, we consider three different honeycomb cluster shapes with several system sizes and aspect ratios for each (see Supplementary Note 3). For all the shapes and sizes probed, we find a sizable TQSL region. The TQSL phase is identified by a high fidelity with respect to the perfect TQSL state as well as by explicitly checking that the ground state is predominantly near-equal weight and phase superposition of all trimer configurations (see Supplementary Note 3). An example for a particular cluster is shown in Fig. 4a, where the TQSL overlap and the fidelity susceptibility are plotted as a function of the detuning. Three regions, separated by fidelity susceptibility peaks, are observed: a trivial disordered phase for small detunings, a trimer RVB phase with a high TQSL overlap in the intermediate regime, and a phase with decreasing fidelity at high detunings pointing to the formation of a VBS state. In the majority of the other clusters explored, the VBS state is completely absent up to Δ/Ω = 5. This behavior, though driven by quantum fluctuations, is reminiscent of the effect of thermal fluctuations in the classical PXP-equivalent model at finite temperatures, which also lacks ordering for k = 3 at any density31. Furthermore, increasing the effective system size, as measured by the number of classically degenerate trimer coverings for a given cluster, leads to no drop in the TQSL fidelity in the spin liquid region, as shown in Fig. 4b. Lastly, examination of the structure of the ground states in the RVB phase reveals that they are predominantly equal-weight and equal-phase superposition of all trimer coverings (see Fig. 4c and Supplementary Note 3), strongly suggesting the TQSL nature of the state on the clusters explored.

Fig. 4: Trimer quantum spin liquid (TQSL) in the PXP model.
figure 4

A robust TQSL is detected in the PXP model42,53 with up to third-nearest neighbors blockaded. a Overlap of the ground state with the perfect TQSL state (blue circles) reveals three distinct regions in the 10  ×  6 shape 1 cluster with periodic boundary conditions (see Supplementary Note 3), namely, a trivial phase at small Δ/Ω, a trimer resonatning valence bond (RVB) region with high TQSL fidelity in the middle, and a VBS state with decreasing fidelity at high Δ/Ω. This is further confirmed by considering the fidelity susceptibility [orange squares, evaluated from Eq. (3) with δ = 0.05], wherein two clear peaks stemming from the trivial-TQSL and TQSL-valence bond solid (VBS) transitions appear. b The TQSL fidelity in the spin-liquid region is preserved upon increasing the effective system size, i.e., the number of trimer coverings [equivalent to the maximum independent set (MIS) degeneracy, DMIS], irrespective of cluster size or aspect ratio. The inset shows the different cluster shapes employed in simulations. The cluster from (a) is emphasized with a green triangle. c The spin-liquid nature of the state with high TQSL overlap is seen by considering the ground-state superposition structure for the typical 6 × 10 shape 3 cluster at Δ/Ω = 3.0, circled in (b). All MIS configurations have dominant almost-equal weights and equal phases (see Supplementary Note 3), while non-MIS configurations have an order-of-magnitude smaller weights.

Full size image

Dynamical preparation of TQSL states

We now explore the feasibility of preparing the TQSL state with an experimentally relevant quasi-adiabatic protocol, illustrated in Fig. 5a. The protocol, of total time T, consists of starting from an initial state where all atoms are in \(\left\vert g\right\rangle\) and increasing Ω to a desired value at a fixed large negative detuning in the first segment of duration 0.1T. This is followed by increasing Δ to its desired final value, and then finally, an Ω off ramp of length 0.1T at a fixed detuning. The pulses are then smoothed with a Gaussian kernel to eliminate short timescale effects.

Fig. 5: Adiabatic preparation of the trimer quantum spin liquid (TQSL).
figure 5

a We test the feasibility of preparing the TQSL state with an experimentally relevant adiabatic preparation protocol. The ramp-down time (Tdown = 0.9T) is denoted by a dashed gray line, the Rabi pulse with a blue line, and the detuning pulse with orange. b This results in prepared state fidelities that are several orders-of-magnitude better than the ground-state ones, as seen by plotting the prepared TQSL overlap as a function of the total preparation time (in units of 2π/Ω), rescaled by the system size (L = NxNy), for parameters representative of the TQSL phase. The blue dashed line shows the projection of \(\left\vert \Psi (0.9T)\right\rangle\) onto the MIS (maximum independent set) subspace. c TQSL overlap during the quasi-adiabatic sweep presented for the filled data points in (b), showing that the gain compared to the ground state stems mostly from the off-ramp part of the protocol, to the left of the gray dashed lines denoting Tdown. The off ramp effectively acts as a projector to the MIS subspace (see Supplementary Note 4) in a mechanism that is expected to be a general feature of Rydberg systems.

Full size image

The results for the TQSL overlap of the state at the end of the ramp as a function of the total time T are showcased in Fig. 5b. The obtained fidelities are, in most cases (see Supplementary Note 4), several orders of magnitude above the ground-state fidelity. It also appears that the fidelities can approach arbitrarily close to one with increasing T. The prepared fidelity depends only weakly on detuning within the TQSL phase, while it drops in the trivial and VBS phases (see Supplementary Note 4). This fidelity enhancement points to a role that the quasi-adiabatic preparation protocol might play in the preparation of spin liquid states in general and is consistent with the recent results reported in simulations of the \({{\mathbb{Z}}}_{2}\) spin liquid on the ruby lattice15,58.

Here, we are able to assign the origin of the fidelity enhancement to the off-ramp part of the pulse. As shown in Fig. 5c, the fidelity reached during the constant-Ω part of the pulse is of the order of the ground-state fidelity. In the off-ramp part (last 0.1T of time), a significant enhancement is seen. This is in agreement with the experimental observations on the ruby lattice (Private communication, Harvard atom array team.) and is shown to be valid for both honeycomb and ruby lattices (see Supplementary Note 4). We explain this off-ramp fidelity enhancement by a projection mechanism. First, we note that the time-dependent Hamiltonian during the off ramp can be thought of as a sequence of Hamiltonians with ever-increasing values of the ratio Δ/Ω. This leads to greater penalties for state admixtures with less than the maximum allowed number of Rydberg excitations (non-MIS configurations), thus leading to an effective projection to the MIS subspace. We test this hypothesis by comparing the TQSL overlap of the final prepared state to that of the state obtained by projecting \(\left\vert \Psi (0.9T)\right\rangle\) onto the MIS subspace. We find that while the fidelity of the projection is always higher than that of the prepared one, the two approach each other for long total preparation times (Fig. 5b and Supplementary Note 4). While such a mechanism appears to be connected to the PXP model’s details, we show in the next section that it applies more generally to Rydberg systems in a slightly modified form.

Robustness of the TQSL state

Given the theoretically expected RVB nature of the TQSL state, it is important to probe its robustness to perturbations stemming from the tails of the van der Waals interactions, which break the classical degeneracy of the trimer configurations. These (experimentally relevant) interaction tails discarded in the pure PXP model of Eq. (4) are always present in real atomic systems, so their inclusion is necessary in a realistic model. Note that the PXP approximation of the hard blockade was already relaxed completely in the DMRG studies above. Proceeding further, we now add the interaction tails up to \({{{{{{{\mathcal{R}}}}}}}}\,=\,3a\) to the PXP Hamiltonian of Eq. (4). The strength of the interaction tails is controlled by the dimensionless parameter Rb/a that we explore in the realistic range between 2 and \(\sqrt{7}\) for the k = 3 regime.

The resulting ground-state fidelities for several values of Rb/a are shown for a typical case in Fig. 6a, with additional clusters presented in Supplementary Note 3. Without tails, this cluster does not show a VBS phase up to Δ/Ω  =  5.0, thus presenting an extended TQSL region with the wavefunction character shown in Fig. 4c. Taking the tails into account, a sizable spin-liquid region, manifested as a high TQSL fidelity plateau, survives to large Rb/a at intermediate detunings. The size of the region and the maximum TQSL fidelity is reduced upon increasing the strength of the interaction tails. In addition, this region is now followed by the VBS plateau with fidelities independent of the interaction tails’ strengths.

Fig. 6: Effect of interaction tails.
figure 6

To probe the robustness of the TQSL (trimer quantum spin liquid), we add the interaction tails up to \({{{{{{{\mathcal{R}}}}}}}}=3a\) to the PXP Hamiltonian. a The ground-state overlap with the perfect TQSL state as a function of Δ/Ω for different interaction strengths (Rb/a) shows that the spin liquid survives the long-ranged interactions on the typical cluster with the large MIS (maximum independent set) degeneracy, though with a smaller parameter region for the TSQL phase and lower fidelities. b The adiabatic preparation protocol at parameters corresponding to the peak ground-state fidelity in the TQSL region, denoted by filled symbols in (a), still shows maximum preparation fidelities significantly above the ground-state ones. In contrast to the system without tails, an optimal total preparation time exists, showing the significance of semi-adiabatic effects. c The TQSL overlap during the adiabatic sweep continues to show a sizable gain during the off ramp, with an additional nonmonotonic feature. The behavior during the off ramp in the presence of interaction tails can still be explained by the universal off-ramp projection mechanism (see Supplementary Note 4).

Full size image

Next, we explore the quasi-adiabatic preparation protocol of Fig. 5a for the TQSL state in the presence of long-ranged interaction tails. The optimal TQSL overlap during the preparation protocol is shown in Fig. 6b for parameters corresponding to peaks of the ground-state fidelity in the TQSL phase [solid symbols in Fig. 6a]. We observe that the preparation fidelity—despite being lower than that for the pure PXP case and falling off with increasing Rb/a—still significantly outperforms the ground-state fidelity. Unlike the pure honeycomb PXP case, there now exists some optimal value of the total preparation time that is linear in the system size (see Supplementary Note 4), similar to the case of the pure PXP model on the ruby lattice58.

In order to gain further insight into the fidelity enhancement observed with dynamical state preparation, we also consider the fidelity as a function of the preparation time, as showcased in Fig. 6c. We find that in the first 0.9T segment of the protocol (denoted by gray dashed lines), the TQSL overlap from this dynamical preparation is similar to the one obtained from the ground state [see Fig. 6a]; however, the Ω off-ramp (the last 0.1T) leads to a significant fidelity enhancement over the ground state. Compared to the case without interaction tails, an additional upturn in \(1-| \left\langle \Psi (t)\right\vert \left\vert {{{{{{{\rm{TQSL}}}}}}}}\right\rangle |\) is consistently observed at the end of the ramp, leading us to consider the optimal protocol fidelity at intermediate times instead of the final prepared fidelity in Fig. 6b. This upturn can also be explained within the off-ramp projection mechanism. The semi-adiabatic protocol suppresses the destabilizing effect of the interaction tails for intermediate total preparation times, leading to a state before the off ramp (at 0.9T) that has equal MIS weights and phases, but still large admixtures of non-MIS configurations. Then, at the start of the off ramp, an effective projection to the k = 3 MIS subspace takes place. However, once Ω drops to a value such that the next shell becomes effectively blockaded, i.e., Vk+1(Rb/a) = Ω(t*), the projection to the MIS subspace for k  =  4 is the effective description of the off-ramp Hamiltonian evolution. Therefore, if one wishes to optimize for k = 3 ground states, the off ramp should be sharply cut off before t*. This picture is independent of the PXP-type approximations and generalizes well to the preparation of entangled quantum states or to the optimization algorithms44,59 arising from blockade physics in Rydberg atom simulators.

Discussion

Thus far, we have shown how a highly entangled TQSL phase can emerge in a honeycomb lattice of Rydberg atoms. Although its existence as a true thermodynamic phase in the infinite-system limit remains to be established, here, we have presented evidence for its emergence and robustness on finite-sized clusters. Exploring the experimentally accessible preparation protocols, we also uncovered an off-ramp fidelity enhancement mechanism potentially relevant to a broad range of quantum state preparation tasks in Rydberg platforms. We now turn to the question of the experimental characterization of the TQSL state.

The spin-liquid state that we report here is directly accessible in current-generation Rydberg atom simulators15,60 that can realize the relevant lattice geometry, achieve the necessary parameter regimes, and employ the quasi-adiabatic preparation protocol. From our simulations, the parameter range to search for the TQSL phase in experiments corresponds to Rb/a ≈ 2.0–2.4 and \({\Delta }_{\max }/{\Omega }_{\max }\approx 1.0\)–4.0. We consider 87Rb atoms and laser coupling a hyperfine ground state to a 70S1/2 Rydberg state; a realistic choice of \({\Omega }_{\max }=4.0\times 2\pi \,{{{{{{{\rm{MHz}}}}}}}}\) and C6 = 8.6 × 105 × 2π MHz μm6 leads to a honeycomb lattice constant of a ≈ 3.2–3.9 μm, therefore easily accommodating L > 200 atoms in a 100 × 100 μm array. The typical preparation times of ~ 3–5 μs correspond to T/L ~ 0.1, which, though currently less than optimal, should still lead to sizable TQSL fidelities and are comparable to the ones employed in the ruby-lattice experiments preparing a \({{\mathbb{Z}}}_{2}\) spin liquid phase15. Further improvements to experimental coherence times by increasing the laser power and moving to larger intermediate-state detunings can extend T/L to the optimal preparation time in experiments.

Two main experimental signatures would be sufficient to conclusively characterize the TQSL state. The first corresponds to testing its trimer character and the associated U(1)  ×  U(1) symmetry39 upon sampling the wavefunction in the experimentally accessible Z-basis. For each snapshot of the TQSL state, a corresponding trimer structure with fluxes can be assigned as presented in Fig. 1. One can then test for the U(1)  ×  U(1) conservation law by evaluating the flux enclosed by a closed loop (Φ) and comparing it to the theoretical expectations based on the occupation of different sublattices within the loop (NA,B,C). These operators are direct analogs of the closed Z-loops15 employed for detecting the \({{\mathbb{Z}}}_{2}\) topological phase on the ruby lattice. As an example, for A–B electric fields of the loop in Fig. 7a, ZAB = ΦAB − (NA − NB) is expected to be zero for a perfect (classical) trimer covering, and likewise for B–C. For a quantum TQSL state with additional number fluctuations (recall Ω ≠ 0), the value is no longer exactly zero, and the trivial and the TQSL phase are expected to be separated by a significant drop in 〈Z〉, as observed in our ED simulations and presented in Fig. 7b. In addition, we also sample the wavefunction in the TQSL region of the DMRG phase diagram of Fig. 1. In contrast to the trivial disordered and ordered columnar states surrounding it, the samples in the TQSL regime are found to be all unique and have predominantly trimer character. This trimer nature is demonstrated by evaluating 〈∣Z∣〉 in the TQSL region for the closed loop in Fig. 7a and averaging over all such loops in the bulk of the system, with the results shown in Fig. 7c.

Fig. 7: Experimental probes of the trimer quantum spin liquid (TQSL).
figure 7

Two experimental probes that together conclusively characterize a state as a TQSL are the measurements of Z- and X-loop operators. a The main experimental probe that distinguishes between trivial and TQSL phases entails checking the two U(1) conservation laws39 relating the electric field (arrows) flux with enclosed charges (number of different sublattice sites) along an arbitrary closed loop (example shown in blue). b Two Z-loop operators evaluated for the loop shown in blue in (a) for the 10 × 6 shape 1 cluster from Fig. 4a. The two U(1) conservation laws are violated in the trivial phase, but are approximately satisfied in both the TQSL and VBS (valence bond solid) phases. The second transition between the TQSL and the VBS present on this cluster is not distinguishable from Z-loop measurements alone, as both phases are of trimer character. c Expectation value of ∣Z∣, evaluated by sampling from DMRG ground state of 32 × 4 cylinder and averaging over the bulk of the system (discarding four rows of atom on each end of the system). The violations of the U(1) conservation laws are high in the trivial and columnar phase and low in the TQSL phase (denoted by dashed green lines extracted from energy susceptibility peaks in Fig. 3). Sampling errors are smaller than the marker size. d The X-loop experimental probe can be explicitly constructed for a given breathing move on the irregular honeycomb lattice of trimer domain walls shown here (see Supplementary Note 1). The X-loop operator is a product of σx operators needed to expand the loop. e An example of a simple breathing move is shown with configurations before and after the move differing only within the yellow shell around the perimeter of the loop, a general feature of any breathing move. The moves needed to expand the honeycomb, in this case, lead to the many-body X-loop operator that is a product of 24 individual honeycomb σx operators.

Full size image

The second experimental signature necessary for conclusive detection of the TQSL state concerns showing the resonance between different trimer configurations in superposition and can be performed using X-basis measurements. The relevant X-loop operators to be probed are those that flip between different trimer configurations; these can be found by considering the difference between two irregular breathing honeycomb lattices36,37,38,61 describing the underlying trimer configurations, as sketched in Fig. 7d, e. An X-loop operator is comprised of spin flips, \({\prod }_{i}{\sigma }_{i}^{x}\) in the vicinity of the loop’s perimeter. This operator corresponds to a particular breathing move and permutes within the classes of states in the MIS subspace. Thus, measuring the expectation value of different breathing operators, explicitly constructed from irregular honeycomb mappings, can distinguish between the TQSL and ordered trimer phases. The X-loop measurements would require a global basis rotation applied in the experimental protocol, akin to the measurements performed for the ruby lattice15,35. One possible approach is mapping the two states to a noninteracting hyperfine manifold and then employing single-qubit rotations62. Such X-loop operators are expected to decay exponentially with the perimeter of the loop X (due to the presence of nontrimer admixtures in the wavefunction) only in the TQSL phase, in complete analogy to the ruby-lattice X-loops15,35. The perimeter-law scaling is showcased for a breathing move in Fig. 7, where any difference between two loop-connected configurations is limited to the yellow-shaded region of two triangular layers around the loop’s perimeter. The additional prefactor for the X-loop’s intensity is related to the trimer subspace’s fractionalization into sectors described by topologically distinct irregular honeycomb lattices36. This prefactor is, in the worst case, proportional to the inverse of the number of topological classes, scaling as 1/L2 for system size L36. The constant nature of the prefactor for a given system size and shape still allows for probing the perimeter-law scaling of the X-loops, and thus, the TQSL phase.

Other useful probes of the TQSL phase may be more indirect. For instance, the TQSL should be featureless in the bulk, thus setting it apart from proximate ordered phases in measurements of the static structure factor. However, it should also be distinguishable from the trivial disordered state via energy susceptibility measurements that exhibit a peak at the trivial–TQSL transition (see Supplementary Note 2); note that the energy susceptibility can be experimentally extracted from the total density in the Z-basis, as χ = ∂〈n〉/∂Δ.

Our study opens up several research directions. Theoretically, it would be valuable to understand whether a U(1)  ×  U(1) spin liquid state can be stabilized in (2+1) dimensions by coupling the gauge field to gapless fermionic matter and to analytically demonstrate the irrelevance of perturbations (in the renormalization-group sense) about the spin-liquid fixed point25. Numerically, a question for future work would be to establish the TQSL as a stable phase of matter in the thermodynamic limit, perhaps using methods such as infinite DMRG63 or quantum Monte Carlo, which can provide new insights beyond exact diagonalization calculations that inevitably suffers from finite-size effects. Still, irregardless of the stability of the TQSL state in the thermodynamic limit, our results show that it should be possible to efficiently prepare the state on finite clusters with current experiments. Experimentally, the preparation and characterization of the TQSL state would pave a new path towards exploring its physics, including the robustness of the state, its gauge field dynamics, and the fractionalization of excitations. For example, in order to probe the excitations of the TQSL, Rydberg spectroscopy consisting of time-dependent correlator measurements can be employed using locally addressable Rydberg arrays62,64,65. Furthermore, it would be of interest to investigate the nature of the quantum critical points leading out of the TQSL phase as well as the associated nonequilibrium quantum many-body dynamics and potential dynamical phase transitions. More broadly, it would also be useful to explore further the prospect of preparing other many-body-blockade related emergent states, as proposed, e.g., in Ref. 28. Finally, the generic understanding of fidelity enhancements developed in this work can be of relevance to not only adapting the preparation protocols for obtaining strongly correlated states but also solving hard optimization problems66,67,68 on Rydberg atom simulators.

Methods

Exact diagonalization

Exact diagonalization simulations of the PXP Hamiltonian were performed using the Bloqade42 and Generic Tensor Networks53 packages with periodic boundary conditions on a torus. The Hamiltonians in the blockaded subspace were generated by Bloqade’s routines and diagonalized using the Lanczos scheme. The perfect TQSL state was generated by finding all MIS configurations and calculating the MIS degeneracy using Generic Tensor Networks. Three distinct shapes were explored with a variety of aspect ratios and system sizes of up to 60 sites. These cluster shapes are shown in Fig. 4b, which presents an example of a Nx = 4, Ny = 4 shape 1 cluster, a Nx = 6, Ny = 2 shape 2 cluster, and a Nx = 4, Ny = 3 shape 3 cluster.

State preparation

The quasi-adiabatic state preparation simulations of the PXP model without tails were executed using Bloqade’s42 ODE-solver-based routines with the same clusters and boundary conditions as reported for exact diagonalization and with the preparation protocol from Fig. 5a with a Gaussian kernel radius set at T/100. The time step used for simulating the dynamics was 5 × 10−4 (in units of 2π/Ω), leading to excellent convergence as manifested by a TQSL overlap changing by at most 10−7 upon further decreasing the time step to 10−4. The state preparation with tails was executed with Bloqade-generated Hamiltonians and pulses with Krylov-subspace-based evolution routines. The time step used for Trotterization was 10−3, which achieved a similar level of convergence as the ODE-solver-based methods. The two methods tested against each other for the Hamiltonian without tails have shown excellent agreement.

DMRG

The DMRG calculations were performed using the ITensor package46. The geometry studied here consisted of a long cylinder (with open boundary conditions along the shorter edge and periodic along the longer) shown in Fig. 8 for a Nx = 12, Ny = 4 system, with the phase diagram of Fig. 1 constructed for a 32 × 4 system. Phase diagrams for 24 × 4, 26 × 4, and 32 × 3 cylinders, as well as for a 32 × 4 system with the addition of interaction tails up to fifth-nearest neighbors (\({{{{{{{\mathcal{R}}}}}}}}\,=\,3a\)) were also fully reconstructed, with the phase boundaries qualitatively matching the ones for the 32 × 4 system, including the TQSL region. Other aspect ratios were employed for probing the properties of the TQSL regime, with Nx = 16–32 and Ny = 3–6. The sweep protocol employed was based on typically \({{{{{{{\mathcal{O}}}}}}}}(200)\) sweeps with bond dimensions in the range 400–1800, depending on the transverse system size (Ny, the number of unit cells in the transverse direction). Initially, many sweeps were performed at a relatively small bond dimension (<100), with the bond dimension being progressively increased in later stages. A gradually decreasing noise term was added until the final stages of the sweep to prevent the DMRG from being stuck in local minima. The protocol achieved good convergence with typical discarded weights below 10−10 and the relative change in the ground state energy after the final increase in the bond dimension being below 10−6.

Fig. 8: Cluster shape used in density matrix renormalization group (DMRG) simulations.
figure 8

DMRG was performed on cylindrical boundary conditions (OBC, open boundary conditions, along the Nx fold and PBC, periodic boundary conditions, along the Ny fold) with small transverse cylinder sizes (Ny).

Full size image

Note added

After the completion of this work, we became aware of a related work, Ref. 69, which, however, does not consider either the spin liquid phase or the stabilization of the solid phases.