Introduction

The ongoing search for exotic magnetic states in highly frustrated antiferromagnets1,2,3,4,5,6 has been extended to a new class of correlated materials with a two-dimensional honeycomb structure7,8,9,10 and its three-dimensional variants11. It is suggested that bond-dependent interactions could be realized in the spin–orbit coupled Mott insulators with the aforementioned lattice geometry12. In particular, the Kitaev honeycomb model exhibits a novel Kitaev quantum spin liquid (QSL), which hosts fractionalized Majorana fermions and flux excitations13. Realization of Kitaev interaction in real materials was first proposed in iridates14,15,16, and then turned toward α-RuCl3 in which Ru3+ ions are arranged in a honeycomb lattice and carry effective spin-1/2 particles7,9. Although α-RuCl3 displays long-range zigzag magnetic order at low temperature17,18,19,20,21,22, it is argued to be proximate to the Kitaev QSL owing to the broad continuum of magnetic excitations identified in Raman scattering23,24 and inelastic neutron scattering9,25,26,27.

In spite of massive research efforts, it has been challenging to determine exchange parameters of the proposed spin Hamiltonian for α-RuCl3 (see refs. 28,29 and references therein). However, there is a broad consensus on a sizable off-diagonal Γ interaction30,31, which is antiferromagnetic (AFM) and is potentially comparable to the celebrated Kitaev interaction26,32,33. Crucially, it is shown that the Γ interaction could help enhance the mass gap of Majorana fermions34 and is responsible for the strongly anisotropic responses to the magnetic field observed in α-RuCl3 provided that the Landé g-factor anisotropy is modest28,30,35. In contrast to the Kitaev model13, analytical solution of the honeycomb Γ model has not been found yet36. Previous classical studies have demonstrated that its ground state is a classical spin liquid37 followed by a flux-ordered spin liquid, which is stabilized in a finite temperature window38. Given the infinite classical ground-state degeneracy37, determining the precise quantum nature of Γ model is nontrivial, and existing numerical works have already led to conflicting results. Parallel works by exact diagonalization39 and density-matrix renormalization group (DMRG) study of a cylinder with a width of three unit cells40 both claim that the ground state is a nonmagnetic phase. A variational Monte Carlo simulation, on the other hand, suggests that it is a zigzag order41. Furthermore, a recent study proposes that it is a nematic paramagnet that spontaneously breaks the lattice rotational symmetry42.

In this work, we study a model which consists of the Γ term and of a staggered Heisenberg (\(\tilde{J}\)) interaction along the bonds, dubbed the bond-modulated\(\tilde{J}\)–Γ model (see Eq. 1). Depending on the sign of \(\tilde{J}\), it could either favor the zigzag order (\(\tilde{J}\,>\,0\)) or stripy order (\(\tilde{J}\,<\,0\)). If the ground state of Γ model is a zigzag ordered phase, then the zigzag order protruding from the pure Γ limit should compete with and survive up to a finite ferromagnetic \(\tilde{J}\) interaction. Otherwise, there will be an intermediate phase sandwiched between the two magnetically ordered states. Thus, this model works as a virtuous arena to clarify the debates by unfolding the competing states, although it is not a description of any particular material. By employing the DMRG method on both finite cylinders with circumferences of up to 10 sites and C3-symmetric hexagonal clusters43,44, we identify a disordered state in between. This phase manifests characters of a gapless QSL including a dense excitation spectrum, logarithmic entanglement entropy scaling, and short-range plaquette–plaquette correlation. The pure Γ limit belongs to this QSL and is separated from the zigzag order by a first-order transition.

Results

Model

The Hamiltonian of the bond-modulated \(\tilde{J}\)–Γ model reads

$${\mathcal{H}}=\tilde{J}\mathop{\sum}\limits_{\langle {i}{j} \rangle\parallel \gamma }{\eta }_{\gamma }{{\bf{S}}}_{{\rm{i}}}\cdot {{\bf{S}}}_{{\rm{j}}}+{{\Gamma }}\mathop{\sum}\limits_{\langle {i} {j} \rangle\parallel \gamma }({S}_{{\rm{i}}}^{\alpha }{S}_{{\rm{j}}}^{\beta }+{S}_{{\rm{i}}}^{\beta }{S}_{{\rm{j}}}^{\alpha }),$$
(1)

where \({S}_{{\rm{i}}}^{\gamma }\) (γ = x, y, z) is the γ-component of a spin-1/2 operator at site i, and α and β are the two other bonds on a honeycomb lattice. ηγ = 1 for the bond 〈ij〉γ along the horizontal direction and equals to −1 otherwise (see Fig. 1). \(\tilde{J}\) and Γ are parameterized using ϑ ∈ [0, π] so as to \(\tilde{J}=\cos \vartheta\) and \({{\Gamma }}=\sin \vartheta \,(\ge 0)\).

Fig. 1: Lattice geometry.
figure 1

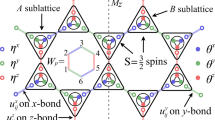
Illustration of an XC6 cylinder on a honeycomb lattice. ηγ is +1 (−1) for horizontal (zigzag) bonds. The insets are (left) the unit cell for the zigzag/stripy order with a1 = 3 and \({a}_{2}=\sqrt{3}\), (middle) the hexagonal plaquette operator \({\hat{W}}_{{\rm{p}}}\) with its six sites enumerated, and (right) the X (red), Y (green), and Z (blue) bonds.

Full size image

In what follows, we carry out a hierarchical study of Eq. (1) to provide multi-faceted evidences of the gapless QSL nature of Γ magnet. We start by mapping out the classical phase diagram via the parallel tempering Monte Carlo simulation45,46, and conclude that the ground state of Γ model sits exactly at the classical transition point on the verge of the zigzag phase. This makes sense because the zigzag ordering belongs to the macroscopic ground-state manifold of the classical Γ model37. Next, we show the energy reduction and sublattice magnetization within the linear spin-wave analysis (for a review, see ref. 47). Afterwards, we present a quantum phase diagram obtained by large-scale DMRG calculations on various distinct cluster geometries.

Classical phase diagram

Figure 2 shows the classical phase diagram of Eq. (1) obtained by Monte Carlo simulations45,46, coincide exactly with the subsequent results of energy optimization method (see "Methods” section). Due to the bond-modulated ηγ-term, the conventional zigzag and stripy orderings perpendicular to the Z bonds are induced when ϑ/π is 0 or 1, respectively. By introducing AFM Γ interaction, the ground state becomes more competitive, triggering the possibility of other magnetic orderings in the moderate interaction regime. The ground-state energy eg = Eg/(NS2) (Eg is the total energy) is shown in Fig. 2a, while selected spin configurations of the corresponding phases are depicted in Fig. 2b–d. In the phase diagram, the leftmost is the zigzag order with \({e}_{{\rm{g}}}^{{\rm{zz}}}=-(2{{\Gamma }}+3\tilde{J})/2\) and its magnetic moment direction is \({\bf{n}}\ [11\bar{1}]\). The rightmost is occupied by the stripy order with \({e}_{{\rm{g}}}^{{\rm{st}}}=-({{\Gamma }}-3\tilde{J})/2\). Its spins are perpendicular to \({\bf{n}}\,[11\bar{1}]\), but could vary freely in the plane spanned by \(\widetilde{{\bf{a}}}\,[112]\) and \(\widetilde{{\bf{b}}}\,[1\bar{1}0]\), showing an emergent continuous symmetry. Further, an extensive intermediate region appears in between. It is dominated by a so-called mixed phase in which the AFM order and two twining zigzag orders are degenerate with energy \({e}_{{\rm{g}}}^{{\rm{mixed}}}=-(2{{\Gamma }}-\tilde{J})/2\). Here, twining zigzag orders refer to the other two zigzag orders whose spin orientations are different from the one shown in Fig. 2b (for spin configurations, see Supplementary Note 1). The zigzag–mixed transition takes place exactly at \({\vartheta }_{{\rm{t,l}}}^{{\rm{cl}}}/\pi =0.5\), reflecting the classical spin liquid of the Γ model37. There is no direct transition between the mixed phase and the stripy phase expected to occur at \({\vartheta }_{{\rm{t,r}}}^{{\rm{cl}}}/\pi\) = \(1-\frac{1}{\pi }{\rm{atan}}\ 2\) ≈ 0.6476. Instead, a noncollinear phase (see Fig. 2d) with eg = \(-\sqrt{{\tilde{J}}^{2}+{{{\Gamma }}}^{2}/16}\) − \({{\Gamma }}/\sqrt{2}\) appears in a narrow window of ϑ/π that is less than 0.02, see inset of Fig. 2a.

Fig. 2: Classical phase diagram.
figure 2

a Monte Carlo simulations of classical energy eg under three XC clusters of 16 × 16 (red triangle), 24 × 24 (green square), and 32 × 32 (blue circle). The solid black line stands for the exact solution given by the energy optimization method. The classical phase diagram is then determined by kinks in energy curves. Inset: Zoom in of energy curves near \({\vartheta }_{{\rm{t,r}}}^{{\rm{cl}}}/\pi \approx 0.6476\). A noncollinear (NCL) phase appears in a narrow window of 0.6368 < ϑ/π < 0.6543. b, c Depict the zigzag order and stripy order, respectively. d A NCL phase with a unit cell of 4 × 2.

Full size image

Spin-wave theory

To understand the role played by quantum fluctuations and for the sake of comparison with the DMRG results later, we have performed the linear spin-wave calculation47 based on the quadratic Hamiltonian \(\bar{{\mathcal{H}}}={E}_{{\rm{g}}}[{S}^{2}\to S(S+1)]+\frac{S}{2}{\sum }_{{\boldsymbol{q}}}{\psi }_{{\boldsymbol{q}}}^{\dagger }{{\mathcal{M}}}_{{\boldsymbol{q}}}{\psi }_{{\boldsymbol{q}}}\), where \({\psi }_{{\boldsymbol{q}}}^{\dagger }=\left(\right.{a}_{{\boldsymbol{q}}}^{\dagger },{b}_{{\boldsymbol{q}}}^{\dagger },\cdots \ ,{a}_{-{\boldsymbol{q}}},{b}_{-{\boldsymbol{q}}},\cdots \left)\right.\) is the Nambu spinor, and \({{\mathcal{M}}}_{{\boldsymbol{q}}}\) is a 2 × 2 block matrix (see “Methods” section and Supplementary Note 2). There are four spin-wave dispersion branches ωqυ (υ = 1–4) for the four-sublattice (ns = 4) zigzag and stripy orderings. In the zigzag order, there exists a magnon gap Δ at M point in the Brillouin zone (see inset of Fig. 3a). When approaching Γ limit, \(\tilde{J}/{{\Gamma }}\ll 1\), the lowest magnon branch is softened and the gap vanishes as \({{\Delta }}/{{\Gamma }}\simeq \frac{\sqrt{30}}{3}\sqrt{\tilde{J}/{{\Gamma }}}\). Therefore, the zigzag order could only survive for AFM \(\tilde{J}\) (i.e., ϑ/π < 0.50), beyond which the magnon branch becomes imaginary and should be terminated by a transition.

Fig. 3: Spin-wave analysis of the stripy phase.
figure 3

a Four branches of the magnon spectra ωqυ in the stripy phase where ϑ/π = 0.75. The path along the symmetry directions in the momentum space is depicted in the inset. b Energy barrier δE between the stripy phases of different orientations in the classically allowed zone. Inset: Quantum energy correction ΔE(ϕ) vs angle ϕ suited at the \(\widetilde{{\bf{a}}}\)-\(\widetilde{{\bf{b}}}\) plane. The parameter is fixed to ϑ/π = 0.75, which is marked as a black hexagram in the main panel.

Full size image

The magnon spectra for the representative stripy order with ϑ/π = 0.75 are shown in Fig. 3a where the wave vector q is parameterized in units of (h, k) as q = \(\left(\right.\frac{2\pi }{{a}_{1}}h,\frac{2\pi }{{a}_{2}}k\left)\right.\)15. The spectra are symmetric with the middle of the Γ–M line, so the Γ and M points are equivalent. Due to the emergent continuous symmetry of the classical stripy order, the magnon spectra are gapless. In the presence of quantum fluctuations, however, the degeneracy is lifted via order-by-disorder mechanism48, selecting two of them that are either parallel or antiparallel to \(\widetilde{{\bf{b}}}\) axis (see inset of Fig. 3b). To illustrate it, we firstly define the quantum energy correction \({{\Delta }}E(\phi )=S{e}_{{\rm{g}}}^{{\rm{st}}}+\frac{S}{2{n}_{{\rm{s}}}}{\sum }_{\upsilon }\int \frac{{d}^{2}{\bf{q}}}{{(2\pi )}^{2}}{\omega }_{{\boldsymbol{q}}\upsilon }(\phi )\), where ϕ is the angle in the \(\widetilde{{\bf{a}}}\)-\(\widetilde{{\bf{b}}}\) plane49. For ϑ/π = 0.75, which is deep in the stripy order, we show ΔE(ϕ) vs. ϕ in the inset of Fig. 3b. The energy correction has its minima at ϕ = π/2 or 3π/2, corresponding to the two mostly favored configurations at the quantum level. The energy barrier δE, defined as the energy difference between ΔE(0) and ΔE(π/2), is approximately 0.0175. The main panel of Fig. 3b shows energy barrier at different ϑ/π in the stripy order. When ϑ/π = 1.00 the energy barrier is zero, consistent with the gapless Goldstone modes thereof. Beyond that, the energy barrier is finite, indicating that the stripy order should also be twofold degenerate in the quantum case.

Due to the magnon instabilities of zigzag and stripy orderings, they could only exist in their classically allowed regions. The corresponding phase transitions could be illuminated by their sublattice magnetization. It is observed that magnetization of the zigzag order is almost saturated when ϑ/π < 0.4. As ϑ/π approaches 0.5, it undergoes a considerable suppression and the lowest branch of the magnetization nearly vanishes at \({\vartheta }_{{\rm{t,l}}}^{{\rm{cl}}}/\pi =0.50\) (see Supplementary Fig. 5). The stripy order is more stable and its magnetization only has a small reduction at \({\vartheta }_{{\rm{t,r}}}^{{\rm{cl}}}/\pi \approx 0.6476\). However, spin-wave energy in the mixed phase, say AFM order, is overwhelmingly higher than its neighbors. It thus implies that the genuine phase in the intermediate region should be different from its classical counterpart, imposing restrictions on the applicability of the spin-wave analysis.

Intervening magnetically disordered state

As discussed, the spin-wave calculation fails in the intermediate regime, hence the quantum study is necessary. We have performed the standard DMRG computation on three XC clusters of 12 × 6 (n = 6), 16 × 8 (n = 8), and 20 × 10 (n = 10) and compute the ground-state energy eg = Eg/N which is shown in Fig. 4. The energy curves in the middle are very flat, while they have two sharp downwarping when away from the middle region, leading to two well-marked kinks that are signals of first-order transitions. These discontinuous phase transitions could also be advocated by the entanglement entropy, which has a trend to jump as the system size is increased (see Supplementary Figs. 9 and 11). Therefore, the DMRG result supports an intermediate region that impedes a direct transition between the zigzag and stripy phases50,51. For comparison, we also depict the spin-wave energy of the zigzag order (green belt) and stripy order (blue belt) in Fig. 4. It is clearly found that there is a further energy reduction of the zigzag order beyond the linear approximation, in accord with the dramatic suppression of magnetic order parameter which will be clarified later. Strikingly, as shown in the inset of Fig. 4, the energy eg of Γ model (ϑ/π = 0.5) exhibits a nonmonotonic scaling behavior52, indicative of a possible periodicity as revealed in the Kitaev model13. At each fixed circumference n, the energy is linearly decreasing with length Lx of the cylinder. By varying the circumference n from 4 to 10, the extrapolated energy has an oscillation in a window of −0.357 < eg < −0.352. Therefore, we estimate that the energy of Γ model is eg = −0.354(3) in the thermodynamic limit.

Fig. 4: Quantum ground-state energy.
figure 4

DMRG result of eg under three XC clusters where the circumferences n are 6 (red triangle), 8 (green diamond), and 10 (blue circle). The thick belts are the energy of the zigzag order (green belt) and stripy order (blue belt) obtained by the linear spin-wave theory (LSWT). Inset: Extrapolation of energy for Γ model. For each circumferences n the energy is linearly decreasing with 1/N and the special cases (Lx/Ly = 2) are marked by filled symbols. The extrapolated values fall in the purple band centered at −0.354(3).

Full size image

In order to unveil the nature of the intermediate region and to pin down the precise phase boundaries, we resort to the magnetic order parameter, which is defined as \({M}_{{\rm{N}}}({\bf{Q}})=\sqrt{{{\mathbb{S}}}_{{\rm{N}}}({\bf{Q}})/N}\) where \({{\mathbb{S}}}_{{\rm{N}}}({\bf{Q}})\) is the magnetic structure factor with Q being the ordering wavevector (see “Methods” section for definition). The zigzag phase has a peak at M point in the Brillouin zone, while the stripy phase possesses both peaks at M and \({\bf{M}}^{\prime}\) points. Crucially, magnetic structure factor of the intermediate region is diffuse with a soft peak. Figure 5a displays order parameters MN(Q) of the zigzag and stripy phases on four distinct XC clusters with a circumference ranging from 4 to 10. Akin to their spin-wave results, magnetization of the zigzag and stripy phases exhibits maxima at ϑ/π ≈ 0.25 and 0.75, respectively. This implies that these magnetic orderings are most stable, when Γ term is approximately of equal strength to the Heisenberg interaction. Away from these points, quantum fluctuations are enhanced so that the magnetic ordering in the intermediate region is dramatically suppressed, followed by an algebraically decay with the circumference n (see Fig. 5c, d). After a careful inspection of the finite-size effect, we conclude that the magnetization will disappear eventually as the best fitting gives M → 0.0 for Γ model (ϑ/π = 0.5).

Fig. 5: Magnetic order parameters and quantum phase diagram.
figure 5

a Magnetic order parameters M(Q) for the zigzag order (open symbols) and stripy order (filled symbols) with Q = M and/or \({\bf{M}}^{\prime}\) under four finite XC clusters. The thick gray line shows the magnetic order in the thermodynamic limit. b Quantum phase diagram of the bond-modulated \(\tilde{J}\)–Γ model. c, d Extrapolations of the maximal peaks \(\overline{M}\) throughout the reciprocal space. c Linearly extrapolation for Γ model with ϑ/π = 0.50. dϑ/π = 0.55 (red triangle), 0.60 (green diamond), and 0.65 (blue circle), respectively.

Full size image

The entire quantum phase diagram of Eq. (1) is presented in Fig. 5b. In addition to the conventional zigzag and stripy orderings, there is a disordered phase, which is later interpreted as a QSL, is stabilized in a large region between ϑt,l and ϑt,r with ϑt,l/π ≃ 0.50 and ϑt,r/π = 0.66(1). It should be noticed that even though the bond-modulated Heisenberg interaction has a strong tendency to favor the zigzag ordering, the ground state of Γ model remains disordered albeit the transition point ϑt,l is so close to π/2. A more elaborative study on hexagonal clusters of N = 24 and 32 suggests that ϑt,l/π = 0.498(1) (see Supplementary Fig. 12). For other less sensitive perturbations such as the third-nearest-neighbor Heisenberg (J3) interaction, the zigzag order could only exist for J3/Γ > 0.075 (see Supplementary Fig. 20). While for another off-diagonal \({{\Gamma }}^{\prime}\) interaction, the zigzag order is generated at \({{\Gamma }}^{\prime} /{{\Gamma }}<-0.015\)53. These, in turn, confirm the robust nonmagnetic character of Γ model notwithstanding the aggressive zigzag ordering.

Gapless excitation and entropy scaling

Next, we investigate the nature of the disordered phase by calculating the excitation gap and entanglement entropy. For this purpose, we target the first sixteen energy states on a 24-site hexagonal cluster by the DMRG method (see “Methods” section), and the first fifteen low-lying excitation gaps, Δυ = Eυ − Eg (υ = 1−15), is shown in Fig. 6a. It can be seen that Δ1 is vanishing small while Δ2 survives in the zigzag/stripy phases, indicative of the doubly degenerate ground states predicted by the semi-classical analysis. In the intermediate region, the ground state is unique and the density of state in the low-energy spectrum is higher than its neighbors. Such a collapse of excitation gaps could be interpreted as a sign of gapless spectrum54,55. To check the behavior of the lowest excitation gap as N is varied, we focus on four selected points at ϑ/π = 0.40, 0.50, 0.60, and 0.80, under hexagonal cluster of N = 18, 24, and 32. As can be seen from Table 1, the lowest excitation gap Δ2 of the zigzag phase (ϑ/π = 0.40) and stripy phase (ϑ/π = 0.80) is considerably large and slightly grows with the increasing of system size. For the intermediate phase, however, the lowest excitation gap Δ1 at ϑ/π = 0.50 and 0.60 declines quickly when N changes from 18 to 32, indicating that the excitation gap tends to close eventually.

Fig. 6: Excitation gaps.
figure 6

a The first fifteen excitation gaps Δυ with degeneracy for a N = 24 hexagonal cluster. The zigzag and stripy phases are doubly degenerate while the ground state of the QSL in the middle is unique. b The two lowest excitation gaps Δ1 (open symbols) and Δ2 (filled symbols) at three XC clusters where the circumferences n are 6 (red triangle), 8 (green diamond), and 10 (blue circle). The thick belt is the extrapolated bulk gap.

Full size image
Table 1 Lowest excitation gap on hexagonal clusters.
Full size table

We then turn to XC cylinders which enable us to calculate the excitation gaps on large system sizes. Above all, we calculate the first fifteen excitation gaps on a XC cluster of 8 × 4 and we find that there is unlikely a big ground-state degeneracy in the intermediate region since the gap increases gradually without abrupt change (see Supplementary Fig. 8). Therefore, we only present the two lowest excitation gaps on three larger XC clusters up to 200 sites (see Fig. 6b). The gaps in the middle are rather small, indicative of a gapless region. We also take a closer look of the gaps at ϑ/π = 0.50, where different YC clusters are also adopted. For either XC or YC cluster, Δ1,2 show a decreasing trend with the increasing of circumference n. In spite of the oscillation in value, they appear to vanish within a reasonable round-off, showing the gaplessness of the excitation spectrum in Γ model (see Supplementary Fig. 13). As a final consistency check for the gapless nature, we calculate the excitation gap on cylinder geometry of 2 × Lx × Ly (for geometry, see inset of Fig. 7b) with N = 2LxLy sites in total. Although the three-leg cylinder (Ly = 3) is gapped, excitation gap on cylinder of Ly = 4 decreases quickly with Lx and is expected to disappear as Lx → ∞ (see Supplementary Fig. 14). Such a strong size-dependent behavior of the excitation gap is typical of gapless systems.

Fig. 7: Entanglement entropy scaling.
figure 7

a Entanglement entropy \({\mathcal{S}}(l)\) of a consecutive segment of length l on a 2 × 16 × 4 cylinder in the Γ model. The solid symbols of the lowest branch represent the neat edge-cutting with l being a multiply of 8 (i.e., the number of the sites along each column). The bipartite entanglement entropy with l = N/2 is marked as a blue square. b Entanglement entropy scaling on three-leg cylinders (dashed line) and four-leg cylinders (solid line). The fitting constants are \((c,c^{\prime} )\approx (0.02,0.85)\) and \((c,c^{\prime} )\approx (2.92,1.09)\) for Ly = 3 and 4, respectively. The inset shows the bipartite partition of a four-leg cylinder with equal sites in the left and right halves.

Full size image

The entanglement entropy has appeared as a versatile tool in diagnosing quantum critical systems described by conformal field theory. In this regard, the von Neumann entanglement entropy is introduced and it is defined as \({\mathcal{S}}(l)=-{\rm{Tr}}(\rho {\mathrm{ln}}\,\rho )\) where ρ is the reduced density matrix of a subregion with length l56. Figure 7a shows the representative behavior of \({\mathcal{S}}(l)\) in the Γ model on a 2 × 16 × 4 cylinder, which contains eight sites along each column. When l is a multiply of 8, it corresponds to a neat edge-cutting where the two halves have smooth margins. The entanglement entropy is minimized and forms a lower branch as marked by solid symbols. Otherwise the subsystems will be more entangled, gaining extra entropy over the lower bound. Therefore, we shall fix l = N/2 to extract the central charge upon a series of finite cylinders. For such a critical system, it is recognized that the entanglement entropy scaling takes the form of \({{\mathcal{S}}}_{{\rm{vN}}}\equiv {\mathcal{S}}(N/2)=\frac{c}{6}{\mathrm{ln}}\,\left(\right.\frac{2{L}_{x}}{\pi }\left)\right.+c^{\prime}\) where c is the central charge and \(c^{\prime}\) is a non-universal constant56. In Fig. 7b, we shows the logarithmic fitting of \({{\mathcal{S}}}_{{\rm{vN}}}\) for cylinders of length Lx = 8, 16, 24, and 32. It is found that \({{\mathcal{S}}}_{{\rm{vN}}}\) obeys the formula well with the fitting constants \((c,c^{\prime} )\approx (2.92,1.09)\), showing that the central charge is close to 3. An alternative fitting of the lowest branch of the entropy on each cylinder also demonstrates that c ≃ 3 (see Supplementary Fig. 16). By contrast, for the three-leg cylinder the entropy is extremely insensitive to the length (see Fig. 7b), revealing a central charge of 0. The fact that the central charge depends highly on the width (Ly) of cylinders may imply the existence of spinon Fermi surface (SFS). In this scenario, the pockets of SFS might be detected by different cuts in the Brillouin zone, and thus the central charge could vary for different Ly. We note in passing that the central charge argument has also been used to explore the possible SFS in the field-induced gapless QSL in the Kitaev model57,58,59. Another possibility is a Dirac QSL6,60 with three Dirac Fermions around M points, which is potentially consistent with the central charge 3 on four-leg cylinders. Information of the central charge on wider cylinders should be helpful to distinguish between the two scenarios. Regardless of different QSL natures, the vanishing magnetization and excitation gap in the Γ model, together with the distinct central charges on cylinders of Ly = 3 (c = 0) and Ly = 4 (c = 3), manifest that its ground state is likely a gapless QSL.

Flux-like density and plaquette correlation

So far, we have confirmed that there is no magnetic ordering in the honeycomb Γ model, yet little is known about the lattice symmetry breaking. Very recently, there is a proposal of plaquette ordering stemming from a broken translational symmetry in the classical Γ model38. It is thus of interest to examine whether there is a plaquette ordering in the quantum situation. To this end, we study the hexagonal plaquette operator \({\hat{W}}_{{\rm{p}}}\) and its correlation. Actually, \({\hat{W}}_{{\rm{p}}}\) also has its own merit as it can capture the associated phase transitions33. The six-body plaquette operator is known as13

$${\hat{W}}_{{\rm{p}}}\,=\,{2}^{6}\mathop{\prod}\limits_{i\in p}{S}_{{\rm{i}}}^{\gamma }={2}^{6}{S}_{1}^{{\rm{x}}}{S}_{2}^{{\rm{y}}}{S}_{3}^{{\rm{z}}}{S}_{4}^{{\rm{x}}}{S}_{5}^{{\rm{y}}}{S}_{6}^{{\rm{z}}},$$
(2)

which is the product of spin operators on out-going bonds around a plaquette (see Fig. 1).

Figure 8 a shows the flux-like density \(\langle {\overline{W}}_{{\rm{p}}}\rangle ={\sum }_{{\rm{p}}}\langle {\hat{W}}_{{\rm{p}}}\rangle /{N}_{{\rm{p}}}\) where Np = N/2 is the number of hexagonal plaquette on clusters of N = 24 and 32. Starting from ϑ/π = 0.0, \(\langle {\overline{W}}_{{\rm{p}}}\rangle\) is zero, followed by a continuous decrease before arriving at the transition point, ϑ/π ≃ 0.50. Afterwards, it begins to increase and then surpasses the critical line to enter into the stripy phase where \(\langle {\overline{W}}_{{\rm{p}}}\rangle\, >\,0\). Recalling the quantum phase diagram shown in Fig. 5b, our result corroborates that the flux-like density could signal phase transitions. For Γ model we have \(\langle {\overline{W}}_{{\rm{p}}}\rangle =-0.25(2)\), which is about a quarter of that in the Kitaev model13. Based on the plaquette–plaquette correlation \(\langle {\hat{W}}_{{\rm{p}}}{\hat{W}}_{{\rm{q}}}\rangle\), we then introduce the plaquette order parameter \({{\mathcal{P}}}_{{{\rm{N}}}_{{\rm{p}}}}({\bf{Q}})\) via the plaquette structure factor \({{\mathcal{W}}}_{{{\rm{N}}}_{{\rm{p}}}}({\bf{Q}})\)38 (see “Methods” for definition). In Fig. 8b, we show that the QSL phase has a vigorous peak at Γ point in the reciprocal space but a weaker intensity at K point, signifying a perceptible plaquette correlation. Nevertheless, The fact that the strength of \({{\mathcal{P}}}_{{{\rm{N}}}_{{\rm{p}}}}({\bf{K}})\) goes down rapidly suggests that there is unlikely a plaquette ordering in the region, further corroborating a QSL without a broken symmetry.

Fig. 8: Flux-like density and plaquette correlation.
figure 8

a Flux-like density \(\langle {\overline{W}}_{{\rm{p}}}\rangle\) and b plaquette order parameter \({\mathcal{P}}({\bf{Q}})\) for N = 24 (red triangular) and 32 (blue circle). The inset exhibits the plaquette structure factor of Γ model, which has a relatively weak peak at K point (corner of the Brillouin zone) in the reciprocal space.

Full size image

Discussion

Ever since the seminal proposal of the Kitaev interaction in heavy 4d/5d transition metal oxides12, which triggers the thriving research direction of Kitaev materials, tremendous efforts have been devoted to realizing the Kitaev QSL in real materials, yet hampered by the ineluctable non-Kitaev terms such as the off-diagonal Γ interaction. Whereas the honeycomb Γ model has drawn enormous attention, its quantum nature is still under debate. To this end, we introduce a bond-modulated Heisenberg interaction to check its tendency towards probable magnetic orderings. For the magnetic phase diagram of the proposed bond-modulated \(\tilde{J}\)–Γ model, we find an intermediate region which is intervened between the zigzag and stripy phases. Though exhibiting magnetic order at the classical level, quantum fluctuations suppress such ordering since it acquires a large energy according to the spin-wave result. In the quantum case, it turns out to be disordered and is separated from its two neighbors by first-order transitions. By taking massive numerical efforts on the Γ model, we are able to confirm the following three subtle physical issues. (i) The low-energy spectrum is rather dense on a 24-site hexagonal cluster, and the lowest excitation gap goes down gradually with the expansion of cluster size. The empirical extrapolation on large cylinders up to 200 sites gives a vanishing energy gap, in line with the logarithmic behaviors of entanglement entropy. (ii) The zigzag magnetic ordering vanishes eventually, consistent with the suppression of magnetization of the zigzag order by spin-wave analysis. (iii) In the plaquette structure factor, there is a perceptible short-range plaquette correlation because of a subleading peak at K point. These findings strongly corroborate the ground state of Γ model is a gapless QSL rather than a zigzag order, despite the latter being close in energy.

We would like to mention that, due to the gapless nature and for the lack of continuous spin symmetry, it is exceedingly challenging to capture the fractionalized excitation in the proposed QSL. The flux insertion method, which pumps fractional particles from one edge to the other, is usually a promising way to elucidate the topological characters of the ground state. It is performed by adiabatically twisting boundary conditions of the Hamiltonian so that the U(1) symmetry is required. The discrete symmetries of the Γ model thus inherently hinder this trick. Actually, topological degeneracy is in general not well-defined for a gapless QSL, as different gauge sectors are closely connected due to gapless excitations. Nonetheless, the Kitaev QSL is special because flux \({\hat{W}}_{{\rm{p}}}\) is a conserved quantity, allowing for the identification of different flux sectors by the vison insertion55. Also of note is that a recent study suggests the existence of a nematicity due to the lattice rotational symmetry breaking42. We would like to stress that the symmetry of Γ model itself is discrete and the asymmetrical boundary condition could cause instability on the landscape of bond energy, making it hard to determine the nematicity in the thermodynamic limit. However, the pending lattice nematicity does not alter our proposal of the QSL, because it could be accompanied by a broken lattice symmetry as reported in other theoretical models61,62. Despite such challenges, our work emphasizes on the inspiring and intractable quantum nature of the Γ model. Notably, the dominating Γ region could be realized in α-RuCl3 under compression where the magnitude of Kitaev interaction is small53. In short, our results provide a significant guidance to further theoretical and experimental studies on honeycomb magnets.

Methods

Density matrix renormalization group

In order to check for finite-size effects, we have performed large-scale DMRG calculations43,44 on three kinds of cluster geometries. Firstly, the frequently used geometry is a Lx × Ly XCn cluster under cylindrical boundary condition (see Fig. 1). Here, X indicates the orientation of the cylinder, while n is the circumference of the cylinder. We consider even circumferences n (=Ly/a0) ranging from 4 to 10 lattice spacing a0, and use fixed ratio Lx/Ly = 2 unless stated explicitly otherwise. N = LxLy is the total number of spins. Secondly, we consider the honeycomb cylinder of 2 × Lx × Ly where Lx (Ly) is the number of unit cell along \({{\bf{e}}}_{1}=(\sqrt{3},0)\) (\({{\bf{e}}}_{2}=(1/2,\sqrt{3}/2)\)) direction (see the inset of Fig. 7). Due to the limitation of modern computational capability, we focus primarily on four-leg cylinders (Ly = 4). The maximal value of Lx is 32, and the total number of spins N = 2LxLy. Lastly, we also use the C3 symmetric hexagonal clusters with N = 24 and 32 sites under full periodic boundary conditions. In all cases, we keep up to m = 3000–5000 states and perform about 12 sweeps in the calculation, so as to ensure the truncation error is smaller than 10−6. When targeting the first few low-lying energy levels, we diagonalize a subspace of a sparse Hermitian matrix iteratively by Davidson algorithm, with the precision of each eigenvalue maintained at a desired standard. In addition, all the targeted states are used with an equal weight to construct the reduced density matrix.

The magnetic order parameter is defined by \({M}_{{\rm{N}}}({\bf{Q}})=\sqrt{{{\mathbb{S}}}_{{\rm{N}}}({\bf{Q}})/N}\) where \({{\mathbb{S}}}_{{\rm{N}}}({\bf{Q}})={\sum }_{\alpha \beta }{\delta }_{\alpha \beta }{{\mathbb{S}}}_{{\rm{N}}}^{\alpha \beta }({\bf{Q}})\) is the total static magnetic structure factor, with

$${{\mathbb{S}}}_{{\rm{N}}}^{\alpha \beta }({\bf{Q}})=\frac{1}{N}\mathop{\sum}\limits_{{\rm{ij}}}\langle {S}_{{\rm{i}}}^{\alpha }{S}_{{\rm{j}}}^{\beta }\rangle {e}^{{\rm{i}}{\bf{Q}}\cdot ({{\boldsymbol{R}}}_{{\rm{i}}}-{{\boldsymbol{R}}}_{{\rm{j}}})}.$$
(3)

Here, Ri is the position of spin and Q is the ordering wavevector. We also calculate the plaquette–plaquette correlation \(\langle {\hat{W}}_{{\rm{p}}}{\hat{W}}_{{\rm{q}}}\rangle\), where \({\hat{W}}_{{\rm{p}}}\) is the hexagon plaquette operator (see Eq. 2). Likewise, we define the static plaquette structure factor

$${{\mathcal{W}}}_{{{\rm{N}}}_{{\rm{p}}}}({\bf{Q}})=\frac{1}{{N}_{{\rm{p}}}}\mathop{\sum}\limits_{{\rm{pq}}}\langle {\hat{W}}_{{\rm{p}}}{\hat{W}}_{{\rm{q}}}\rangle {e}^{{\rm{i}}{\bf{Q}}\cdot ({{\boldsymbol{R}}}_{{\rm{p}}}-{{\boldsymbol{R}}}_{{\rm{q}}})},$$
(4)

where Rp is the central position of each plaquette, and Np = N/2 is the number of plaquette. To eliminate the strong finite-size effect due to the identity \(\left\langle \right.{({\hat{W}}_{{\rm{p}}})}^{2}\rangle\) = 1, we introduce the plaquette order parameter (see Supplementary Note 5)

$${{\mathcal{P}}}_{{{\rm{N}}}_{{\rm{p}}}}=\sqrt{\frac{{{\mathcal{W}}}_{{{\rm{N}}}_{{\rm{p}}}}({\bf{Q}})}{{N}_{{\rm{p}}}}}-\frac{1}{\sqrt{{N}_{{\rm{p}}}}}.$$
(5)

Simulation and energy optimization

We use the parallel tempering Monte Carlo simulation with the heat-bath algorithm to prevent the possible metastable state at low temperatures45,46. The simulation is carried out in a temperature range with a hundred of replicas. The heat-bath algorithm is performed at given temperature, followed by a so-called thermal replicas, where configuration swaps between different temperatures are allowed with a probability according to a detailed balance condition. The simulations are performed on three XC clusters of 16 × 16, 24 × 24, and 32 × 32, under toroidal boundary condition.

The resulting energy-optimized spin configuration is then served as the benchmark for the analytical calculation. The classical spin can be written as

$${{\boldsymbol{S}}}_{{\rm{i}}}=S\left(\sin {\theta }_{{\rm{i}}}\cos {\phi }_{{\rm{i}}},\sin {\theta }_{{\rm{i}}}\sin {\phi }_{{\rm{i}}},\cos {\theta }_{{\rm{i}}}\right),$$
(6)

where θi ∈ [0, π) and ϕi ∈ [0, 2π). Taking the zigzag (zz) order and stripy (st) order for instance, their classical energy are

$${e}_{{\rm{g}}}^{{{{\rm{zz}}}}}=-\frac{1}{2}\left(\right.3\tilde{J}+{{\mathcal{F}}}_{\max }(\theta ,\phi ){{\Gamma }}\left)\right.$$
(7)

and

$${e}_{{\rm{g}}}^{{\rm{st}}}=\frac{1}{2}\left(\right.3\tilde{J}+{{\mathcal{F}}}_{\min }(\theta ,\phi ){{\Gamma }}\left)\right.,$$
(8)

where the explicit form of the auxiliary function is

$${\mathcal{F}}(\theta ,\phi )={\sin }^{2}\theta \sin 2\phi -\sin 2\theta (\sin \phi +\cos \phi ).$$
(9)

Mathematically, the maximum of Eq. (9) is 2 with \((\theta ,\phi )=(\pi -{\rm{atan}}(\sqrt{2}),\pi /4)\) or \((\theta ,\phi )=({\rm{atan}}(\sqrt{2}),5\pi /4)\). This means that the classical energy of the zigzag phase is \({e}_{{\rm{g}}}^{{\rm{zz}}}=-(2{{\Gamma }}+3\tilde{J})/2\) with the classical magnetic direction \({\bf{n}}=[11\bar{1}]\). The mimimum of Eq. (9) is −1, and the energy of the stripy phase is \({e}_{{\rm{g}}}^{{\rm{st}}}=-({{\Gamma }}-3\tilde{J})/2\). Its moment direction is free to vary in a plane that is perpendicular to n, indicating an emergent continuous symmetry in the classical stripy phase. The analytical energy and spin configurations of the other magnetic phases are shown in Supplementary Note 1.

Linear spin-wave theory

We summarize the derivation of the spin wave spectra of the zigzag phase, which is one of the degenerate ground states of the classical Γ model. In the framework of linear spin-wave theory, the local spin operator \({{\bf{S}}}_{{\rm{i}}}=\left({S}_{{\rm{i}}}^{{\rm{x}}},{S}_{{\rm{i}}}^{{\rm{y}}},{S}_{{\rm{i}}}^{{\rm{z}}}\right)\) is represented by bosonic creation and annihilation operators ai and \({a}_{{\rm{i}}}^{\dagger }\). By virtue of the Holstein-Primakoff transformation, we have

$${\tilde{S}}_{{\rm{i}}}^{+}\simeq \sqrt{2S}{a}_{{\rm{i}}},\quad {\tilde{S}}_{{\rm{i}}}^{-}\simeq \sqrt{2S}{a}_{{\rm{i}}}^{\dagger },\quad {\tilde{S}}_{{\rm{i}}}^{{\rm{n}}}=S-{a}_{{\rm{i}}}^{\dagger }{a}_{{\rm{i}}}.$$
(10)

Here, \({\tilde{S}}_{{\rm{i}}}^{{\rm{n}}}\equiv ({\bf{S}}\cdot {\bf{n}})\) is the spin component along the classical ordered moment n and \({\tilde{S}}_{{\rm{i}}}^{\pm }\equiv ({{\bf{S}}}_{{\rm{i}}}\cdot {\bf{e}})\pm \imath [{{\bf{S}}}_{{\rm{i}}}\cdot ({\bf{n}}\times {\bf{e}})]\) are the ladder operators consisting of the orthogonal spin components, with e being an (arbitrary) unit vector perpendicular to n and satisfying the right-hand rule47. The spin operator is thus

$$\begin{array}{lll}{{\bf{S}}}_{\tau ,{\rm{i}}}\,=\,\sqrt{\frac{S}{2}}({a}_{{\rm{i}}}+{a}_{{\rm{i}}}^{\dagger }){\bf{e}}+\tau \sqrt{\frac{S}{2}}(-\imath {a}_{{\rm{i}}}+\imath {a}_{{\rm{i}}}^{\dagger })({\bf{n}}\times {\bf{e}}) +\,\tau (S-{a}_{{\rm{i}}}^{\dagger }{a}_{{\rm{i}}}){\bf{n}}\end{array}$$
(11)

where τ is introduced for classical spin which is either parallel (τ = +1) or antiparallel (τ = −1) to n. The γ-component of the spin \({S}_{\tau ,{\rm{i}}}^{\gamma }={{\bf{S}}}_{\tau ,{\rm{i}}}\cdot {{\bf{e}}}_{\gamma }\).

For the zigzag phase, we choose the following orthogonal axis, e = [112], \({\bf{n}}\times {\bf{e}}=[1\bar{1}0]\), and \({\bf{n}}=[11\bar{1}]\). Because of the four-sublattice (ns = 4) nature, the magnetic unit cell is taken as the rectangle of the area a1 × a2 with a1 = 3a0 and \({a}_{2}=\sqrt{3}{a}_{0}\), see Fig. 1. Within the magnetic unit cell, the wave vector q could be parameterized in units of (h, k) as q = \(\left(\right.\frac{2\pi }{{a}_{1}}h,\frac{2\pi }{{a}_{2}}k\left)\right.\)15. In this notation, M and \({\bf{M}}^{\prime}\) points in the Brillouin zone could be rewritten as (1, 0) and (0, 1), respectively. By introducing four flavors of Holstein–Primakoff bosons and using the Fourier transformation, we arrive at the following spin-wave Hamiltonian

$${{\mathcal{H}}}_{{\rm{SW}}}^{{\rm{zz}}}=-NS(S+1){e}_{{\rm{g}}}^{{\rm{zz}}}+\frac{S}{2}\mathop{\sum}\limits_{{\boldsymbol{q}}}{\hat{{\bf{x}}}}_{{\boldsymbol{q}}}^{\dagger }{\hat{{\bf{H}}}}_{{\boldsymbol{q}}}{\hat{{\bf{x}}}}_{{\boldsymbol{q}}}^{},$$
(12)

where \({\hat{{\bf{x}}}}_{{\boldsymbol{q}}}^{\dagger }=\left(\right.{a}_{{\boldsymbol{q}}}^{\dagger },{b}_{{\boldsymbol{q}}}^{\dagger },{c}_{{\boldsymbol{q}}}^{\dagger },{d}_{{\boldsymbol{q}}}^{\dagger },{a}_{{\boldsymbol{-q}}}^{},{b}_{{\boldsymbol{-q}}}^{},{c}_{{\boldsymbol{-q}}}^{},{d}_{{\boldsymbol{-q}}}^{}\left)\right.\) is a vector of length 2ns and \({\hat{{\bf{H}}}}_{{\boldsymbol{q}}}\) is a 2ns × 2ns matrix of the form

$${\hat{{\bf{H}}}}_{{\boldsymbol{q}}}=\left(\begin{array}{ll}{\hat{{{\Lambda }}}}_{{\boldsymbol{q}}}&{\hat{{{\Delta }}}}_{{\boldsymbol{q}}}\\ {\hat{{{\Delta }}}}_{{\boldsymbol{q}}}^{\dagger }&{\hat{{{\Lambda }}}}_{-{\boldsymbol{q}}}^{{\rm{T}}}\end{array}\right)$$
(13)

with

$${\hat{{{\Lambda }}}}_{{\boldsymbol{q}}}=\left(\begin{array}{*{20}{l}} A&{E}_{{\boldsymbol{q}}}&\circ &{B}_{{\boldsymbol{q}}}\\ {E}_{{\boldsymbol{q}}}^{* }&A&{B}_{{\boldsymbol{q}}}^{* }&\circ \\ \circ &{B}_{{\boldsymbol{q}}}&A&{E}_{{\boldsymbol{q}}}\\ {B}_{{\boldsymbol{q}}}^{* }&\circ &{E}_{{\boldsymbol{q}}}^{* }&A\\ \end{array}\right)$$
(14)

and

$${\hat{{{\Delta }}}}_{{\boldsymbol{q}}}=\left(\begin{array}{*{20}{l}} \circ &{C}_{{\boldsymbol{q}}}&\circ &{D}_{{\boldsymbol{q,+}}}\\ {C}_{{\boldsymbol{q}}}^{* }&\circ &{D}_{{\boldsymbol{q,+}}}^{* }&\circ \\ \circ &{D}_{{\boldsymbol{q,-}}}&\circ &{C}_{{\boldsymbol{q}}}\\ {D}_{{\boldsymbol{q,-}}}^{* }&\circ &{C}_{{\boldsymbol{q}}}^{* }&\circ \\ \end{array}\right).$$
(15)

The parameters in Eqs. (14) and (15) are given by

$$\left\{\begin{array}{l} A=3\tilde{J}+2{{\Gamma }}\\ {B}_{{\boldsymbol{q}}}=-2(\tilde{J}-{{\Gamma }}/3){\varrho }^{-1}\cos \pi k\\ {C}_{{\boldsymbol{q}}}=(\tilde{J}-{{\Gamma }}/3){\varrho }^{2}\\ {D}_{{\boldsymbol{q,\tau }}}=\frac{2{{\Gamma }}}{3}(\cos \pi k+\tau \sqrt{3}\sin \pi k){\varrho }^{-1}\\ {E}_{{\boldsymbol{q}}}=\frac{2{{\Gamma }}}{3}{\varrho }^{2}\end{array}\right.$$
(16)

where ϱ = eıπh/3. Since \({B}_{-{\boldsymbol{q}}}={B}_{{\boldsymbol{q}}}^{* }\), \({C}_{-{\boldsymbol{q}}}={C}_{{\boldsymbol{q}}}^{* }\), \({E}_{-{\boldsymbol{q}}}={E}_{{\boldsymbol{q}}}^{* }\), and \({D}_{-{\boldsymbol{q}},\tau }={D}_{{\boldsymbol{q,-\tau }}}^{* }\), we hence deduce that \({\hat{{{\Delta }}}}_{{\boldsymbol{q}}}^{\dagger }={\hat{{{\Delta }}}}_{{\boldsymbol{q}}}\) and \({\hat{{{\Lambda }}}}_{-{\boldsymbol{q}}}^{T}={\hat{{{\Lambda }}}}_{{\boldsymbol{q}}}^{\dagger }\).

The quadratic Hamiltonian Eq. (12) can be diagonalized via a bosonic Bogoliubov transformation T(q). To preserve the canonical commutation rules of the bosons, it should satisfy the orthogonality relations TΣT† = T†ΣT = Σ where Σ = diag(1, −1). The eigenvalues of \({{\Sigma }}{\hat{{\bf{H}}}}_{{\boldsymbol{q}}}\) give the magnon spectrum \({{\Omega }}({\boldsymbol{q}})={\rm{diag}}({\omega }_{{\boldsymbol{q,1}}},{\omega }_{{\boldsymbol{q,2}}},\cdots \ ,{\omega }_{{\boldsymbol{q}},{{\rm{n}}}_{{\rm{s}}}})\). The spin-wave dispersions of other magnetic orderings (including the mixed phase and the noncollinear phase) are shown in Supplementary Note 2.