Introduction

Topological insulators and superconductors are fascinating new states of matter1,2,3. The Kitaev topological superconductor model4 is an intriguing one-dimensional (1D) systems realizing topological insulators and superconductors. Especially, topological superconductors host Majorana edge states5,6,7,8, which are the key elements of a topological quantum computer9,10. The area of topological physics is expanded nowadays to photonic11,12,13,14,15,16, acoustic17,18,19,20,21, mechanical22,23,24,25,26,27,28,29 and electronic-circuit systems30,31,32,33,34,35,36,37. They are called artificial topological systems. There are several merits which are difficult to be achieved in inorganic crystals: 1) It is possible to make a fine tuning of the system, which is crucial for observing topological edge states. 2) It is possible to construct a few site systems. 3) It is possible to directly measure the site dependent information.

It is a nontrivial task to materialize the Kitaev topological superconductor model because it involves complex hoppings. It describes a p-wave topological superconductor, although the Majorana edge state itself can be generated in a s-wave superconductor with the aid of a topological insulator nanowire38,39. We note that there is no physical realization of the Kitaev topological superconductor model so far.

Electronic circuits present an ideal platform to realize various topological phases30,31,32,33,34,35,36,37,40,41,42,43,44,45,46. The emergence of topological edge states is observed by means of impedance resonance. However, experimental demonstrations have so far been restricted mainly to printed circuit boards with discrete components, except for a simulation of the Su-Schrieffer-Heeger model47 and an integrated-circuit realization of Floquet’s topological insulator48. The integrated-circuit realization is an important step toward industrial applications of topological electronics.

In order to generate Majorana-like states, it is necessary to simulate electron and hole bands in electronic circuits. Although there is a theoretical proposal with the use of chains of capacitors and inductors44,45, there is so far no experimental demonstration of this theoretical proposal.

Most of previous experiments were carried out based on patterned structures, where it is impossible to control the topological and trivial phases once the sample is manufactured. Actually, it is very hard to introduce switch structures in inorganic materials, photonic crystals and acoustic systems. On the other hand, transistors act as switches in electronic circuits and hence, there is a possibility to construct a switchable topological system based on electronic circuits.

In this paper, we perform an experimental demonstration of switchable topological integrated circuits, which are integrated-circuit realizations of topological systems, by taking the case of the Kitaev model. An integrated-circuit implementation enables us to realize high resonant frequency. In this paper, we realized a Kitaev chain implementation whose resonant frequency is as high as 13GHz. We explicitly observe the spatial profile of a topological edge state and determine its penetration length. The system may contain several topological and trivial segments simultaneously along a chain. In particular, we observe the signal of a Majorana-like state emerging at the interface of a topological segment and a trivial segment. It is topologically protected since it necessarily emerges between the topological and trivial segments. These two topologically different segments are interchangeable simply by switching between inductors and capacitors.

Results

Kitaev chain

The Kitaev chain model is the basic model of a topological superconductor. Our main result is its implementation in an integrated electronic circuit. To realize a Cooper pair it is necessary to incorporate an electron band and a hole band together with cross terms between these two bands into the circuit, as shown in Methods.

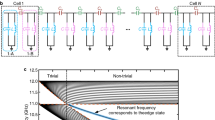
We first illustrate an electronic circuit for the Kitaev chain44,45 in Fig. 1a, b and c. The capacitor channel (indicated in red) corresponds to the electron band, while the inductor channel (in blue) corresponds to the hole band. The two main channels are crosslinked through Cx and Lx. Each node is connected to the ground via an inductor L0 or a capacitor C0 to realize a topological state or a trivial state, respectively, as shown in Fig. 1a, b. The topological phase is realized by the configuration shown in Fig. 1a, while the trivial phase is realized by the configuration shown in Fig. 1b.

Fig. 1: Kitaev chain.
figure 1

a–c The electronic-circuit representation of the Kitaev chain. a All-topological configuration where the topological edge state emerges at both the left and right edges of the chain. b All-trivial configuration that does not have a topological edge state. c The implemented state-configurable Kitaev chain circuit. d By using two single-pole double-throw (SPDT) switches with inverters in the unit cell, the connection of L0 and C0 can be swapped to change its topological/trivial state. The SPDT switch is realized by two Complementary Metal-Oxide-Semiconductor (CMOS) transmission gate switches. e A picture of an 16-unit cell integrated circuit for the Kitaev chain. f A picture of a unit cell. g A zoom of SPDT switches in f. Each SPDT switch is composed of an inverter and two transmission gates with n-type and p-type Metal-Oxide-Semiconductor field-effect transistors as in d.

Full size image

A single Kitaev chain may accommodate several segments which are either topological or trivial. A Majorana-like state emerges at an interface between the two phases. We introduce two single-pole double-throw (SPDT) switches in each unit cell as illustrated in Fig. 1c. The electric circuit for the SPDT switch is shown in Fig. 1d. The switching is done by swapping the connection of L0 and C0, by way of which the position of a Kitaev interface state is controlled. In the integrated circuits, the SPDT switch is simply implemented with an inverter and two Complementary Metal-Oxide-Semiconductor (CMOS) transmission gates, composed of n-type and p-type metal oxide semiconductor field-effect transistors as shown in Fig. 1f, g.

The Kitaev chain circuit shown in Fig. 1c is implemented onto the chip using 180 nm CMOS technology as shown in Fig. 1e. On a 5 mm × 5 mm chip, two 16-unit cell Kitaev chain circuits were integrated for two different target resonant frequencies, 7.3 GHz and 13.1 GHz. We show a zoom-in view of the unit cell layout in Fig. 1f, which shows that it includes 3 inductors L, Lx and L0, 3 capacitors C, Cx and C0, 2 SPDT switches, and a contact pad at each node for direct probing measurement with GSG (Ground, Signal, Ground) probes. A photo of the SPDT switches is shown in Fig. 1g. Two transmission gates and an inverter are integrated for each SPDT switch. The values for the capacitors and inductors are summarized in Table 1.

Table 1 Parameters used for the Kitaev chain.
Full size table

Topological edge states

Figure 2 a–c summarizes the impedance measurement results of the Kitaev chain designed for 13.1 GHz resonant frequency. Figure 2a, b shows the frequency dependence of the impedance measured from the left edge of the chain for topological setup and right edge of the chain for trivial setup, respectively. The solid and dashed lines show measurement and simulation results, respectively.

Fig. 2: Impedance measurements.
figure 2

a Frequency dependence of the impedance measured from the left edge of the electronic circuit with the characteristic frequency ωresonant = 13.1 GHz Kitaev chain for all-topological setup. b Frequency dependence of the impedance measured from the right edge of the electronic circuit with the characteristic frequency ωresonant = 13.1 GHz Kitaev chain for all-trivial setup. Solid and dashed lines show the measured and simulated results of the Kitaev chain, respectively. c The spatial profile of the impedance values for all-topological mode measured from both left and right edges at their measured resonant frequencies. d–f Similar results for the circuit with the characteristic frequency ωresonant = 7.3 GHz. The solid and dashed curves show measurement and simulation results, respectively.

Full size image

As we can see from the impedance peak of the leftmost edge in Fig. 2a, the measured resonant frequency is 13.08 GHz, while the resonant frequency directly calculated based on the on-chip L and C values in Table 1 is 17.2 GHz. This frequency shift is mainly caused by the parasitic inductance of the metal wires in the unit cell to connect the circuit elements as well as the parasitic capacitance introduced by the SPDT switches realized with transistors. Without considering the wires and transistors, the simulated resonant frequency is 16.4 GHz, which is closer to the theoretical value. Since the parasitic impact is inevitable on the integrated chip, we utilized a detailed electro-magnetic simulation to tune the actual resonant frequency. In addition, for both the topological and trivial setups, the measurement results show discrepancy from the simulation results mainly due to the imperfect transistor model. Especially, the peaking characteristics becomes less obvious in the topological setup. To verify the impact of the switch transistors, we have also designed and measured the Kitaev chain without switches as shown in Supplementary Fig. 1. When the chains are composed only of the passive components such as inductors and capacitors, the measurement results agree almost perfectly with the simulation results. See Supplementary Note 1 for more details, where measurement data is shown in Supplementary Fig. 2.

Figure 2b shows that no impedance peaks are observed at the resonant frequency in the trivial phase.

Figure 2c summarizes the two-point impedance values at their measured resonant frequencies when all the system is in the topological phase. The blue and red lines show the impedance measured from the left and the right edges, respectively. The leftmost (0-th) and rightmost (16-th) node impedance correspond to Z11 value of the 2 × 2 impedance matrix.

In the topological setup, the impedance peaks are observed at both the edges. The penetration length of the topological edge state is 0.860 unit cell for the left edge and 0.788 unit cell for the right edge. The discrepancy from the theoretical value 0.610 unit cell is mainly caused by the SPDT switches designed with transistors. See Supplementary Note 2 for details. A possible reason would be the hybridization effect of two topological edge states for a finite length chain. However, this is not the case. See Supplementary Note 3 and Supplementary Fig. 3.

We have also carried out a measurement for the Kitaev chain designed for 7.3 GHz, whose results are shown in Fig. 2d–f. As we can see from the impedance peak of the leftmost edge in Fig. 2d, the measured resonant frequency is 7.29 GHz, while the resonant frequency directly calculated based on the on-chip L and C values in Table 1 is 8.8 GHz. The simulated resonant frequency without wire is 8.6 GHz, which is much closer to the calculated value. Again, the shift in the resonant frequency is due to the effect of the parasitics which is inevitable on the integrated chip. For precise estimation of the actual resonant frequency including the impact of wirings, we utilized the EM simulation. In the topological setup, the impedance peaks are observed at both the edges. The penetration length of the topological edge state is 0.771 unit cell for the left edge and 0.916 unit cell for the right edge, while the theoretical value is 0.680 unit cell.

Topological interface states

We have so far observed the topological edge states. There is also a topological interface state between topological and trivial phases. It is possible to switch the topological and trivial phases for each segment. Figure 3 summarizes the 2-point impedance at the resonant frequency with 3 different switch configurations for the Kitaev chains with 7.3 GHz and 13.1 GHz designs. In Fig. 3a we divided the chain into 4 segments. The impedance peak that corresponds to the topological interface state emerges at the edges of the topological segments. When we move the left topological segment to the right by one unit, the location of the edge states moves accordingly as shown in Fig. 3b. Then if the two separated topological segments are combined into one segment as shown in Fig. 3c, we observe only two impedance peaks at the left and right edges of the single topological segments. This clearly demonstrates the movement of the topological interface state that emerges on the electronic-circuit realization of the Kitaev chain implemented onto the integrated circuit. We also observe the same behavior for two chains with different resonant frequencies, which proves that the topological interface state emerges independent of the designed resonant frequency.

Fig. 3: Topological interface states.
figure 3

Measurement results of the topological edge state locations depending on different Kitaev chain configurations. “n trivial (topological)" indicates that the trivial (topological) segment contains n unit cells. Blue (red) data points are for 7.3 GHz (13.1 GHz) chain. a The topological edge states emerge at 4th, 7th, 10th and 11th nodes. b The locations of the edge states move to the 5th, 8th, 10th and 11th nodes. c When two topological segments combine to one segment, the edge states emerge only at 5th and 12th nodes.

Full size image

Conclusion

We have materialized the Kitaev model in integrated circuits. The model has topological and trivial phases. It is possible to create several segments which are either topological or trivial in a single chain. Topological edge states emerge at both the edges of a topological segment, which are observable by mean of the impedance resonance.

We have demonstrated that the segment size can be as small as one unit cell because the penetration length can be made smaller than one unit cell: See Fig. 3b. Furthermore, we have equipped our integrated circuit with a switchable structure, which enables us to control the position of a topological interface state arbitrarily along a chain. Such a possibility is a great merit of topological electric circuits over other artificial topological systems, where an integrated topological pattern is printed once and for all.

We have observed that the resonant frequency is lower than the theoretical value estimated from \({\omega }_{{{{{{{{\rm{resonant}}}}}}}}}=1/\sqrt{LC}\). This is due to the parasitic inductance present in the wires. Details are shown in Supplementary Note 4 and Supplementary Fig. 4.

The integrated circuit has small inductance and capacitance, which leads to high frequency operation. Indeed, the characteristic frequency is 13GHz. It is much larger than the previous integrated circuit implementation48, where the characteristic frequency is 730 MHz. The size of the unit cell is 200μm and hence, largely integrated circuits are possible. The sample randomness is of the order of 1% in our sample. It is much smaller than that of commercially obtained inductors, where the randomness is of the order of 10%. The preciseness of circuit elements is beneficial for a sharp topological peak. Actually, particle-hole symmetry is slightly broken in our electric circuit due to the randomness. However, the topological peak is experimentally well observed because the topological peak is robust with 1% randomness as shown in Supplementary Fig. 5 in Supplementary Note 5. Mass production is possible in integrated circuits, which will benefit for future industrial applications of topological electronics.

In48, Floquet’s topological insulator is implemented onto the integrated circuit chip with 40 nm technology, which is applied to a wireless communication with a 4-element phased array antenna using 730 MHz carrier frequency. Since our 1-dimensional Kitaev chain enables the impedance switching by changing the position of the interface between topological and trivial segments, this structure can be applied as a high-frequency path selectors or switches based on impedance matching. Especially, our implementation achieves the resonant frequency more than 10 GHz and can be extended to higher frequency bands. Our results will be applicable to future 5G technology as in the case of the previous study48.

Methods

Measurements

A block diagram and a photo of the measurement setup are shown in Fig. 4. We observed the topological edge state based on two-point impedance measurement.

Fig. 4: Setup.
figure 4

a A microphotograph of the chip for the Kitaev chain, where A (B) shows the circuits for the 16-stage Kitaev model with 7.3 GHz (13.1 GHz). b A photo of the measurement setup c A block diagram of the measurement setup including power supply and serial-parallel interface (SPI) control signals.

Full size image

We observe two-point impedance with a vector network analyzer (VNA), Keysight N5222B. The chip measurement is done on the probe station, Formfactor Summit11000. A 2 × 2 Z-matrix is derived from the 2 × 2 S-parameter measured by the VNA. The chain configuration (the state of the SPDT switches) is controlled by the serial-parallel interface (SPI) integrated on the same chip, whose configuration data are written from an external PC.

Simulation is done with a circuit simulator, Cadence Spectre. The S-parameters of the passive components such as capacitors and inductors are extracted for circuit simulation with Cadence EMX, which is a planar 3D electromagnetic simulator based on the Fast Multipole Method (FMM) designed for high-frequency integrated circuits.

1D p-wave Kitaev topological superconductor model

The original Kitaev p-wave superconductor model is defined on the 1D lattice as

$$H = -\mu \mathop{\sum}\limits_{x}{c}_{x}^{{{{\dagger}}} }{c}_{x}-\frac{t}{2}\mathop{\sum}\limits_{x}\left({c}_{x}^{{{{\dagger}}} }{c}_{x+1}+{c}_{x+1}^{{{{\dagger}}} }{c}_{x}\right)\\ -\frac{1}{2}\mathop{\sum}\limits_{x}\left(\Delta {e}^{i\phi }{c}_{x}{c}_{x+1}+\Delta {e}^{-i\phi }{c}_{x+1}^{{{{\dagger}}} }{c}_{x}^{{{{\dagger}}} }\right),$$
(1)

where μ is the chemical potential, t > 0 is the nearest-neighbor hopping strength and Δ > 0 is the p-wave pairing amplitude of the superconductor.

By introducing the Nambu representation \({\Psi }_{k}^{{{{\dagger}}} }=({c}_{k}^{{{{\dagger}}} },{c}_{-k})\) and \({\Psi }_{k}={({c}_{k},{c}_{-k}^{{{{\dagger}}} })}^{T}\) one can write the Hamiltonian in the Bogoliubov-de Gennes form

$$H=\frac{1}{2}\mathop{\sum}\limits_{k}{\Psi }_{k}^{{{{\dagger}}} }H(k){\Psi }_{k},$$
(2)

with a 2 × 2 form Hamiltonian

$$H(k)=\frac{1}{2}\left(\begin{array}{cc}-t\cos k-\mu &i{\Delta }_{0}\sin k\\ -i{\Delta }_{0}\sin k&t\cos k+\mu \end{array}\right).$$
(3)

The zero-energy state of the Bogoliubov-de Gennes Hamiltonian is a Majorana state, and hence, there appear Majorana edge states in the topological phase of the Kitaev model.

Here, t, μ, σi and Δi represent the hopping amplitude, the chemical potential, the spin degree of freedom, and the superconducting gap parameter, respectively. It is well known that the system is topological for ∣μ∣ < ∣2t∣ and trivial for ∣μ∣ > ∣2t∣ irrespective of Δi provided Δi ≠ 0.

We then realize this p-wave Kitaev model by way of an electronic circuit. As shown in Fig. 1a, this circuit chain contains two main lines, one connected by a series of capacitors C implementing the electrons band, while another connected by a series of inductors L implementing the holes band, respectively. Pairing interaction between the two bands is simulated by bridging capacitors Cx and inductors Lx. Each electron node and each hole node is connected to the ground via a capacitor C0 and inductors L0, respectively. The hopping amplitudes t realized in the electrons band and holes band are opposite since the capacitors C contained in the electrons band contribute the terms iωC while the inductors L contained in the holes band contribute the terms 1/(iωL).

The circuit Laplacian is given by

$${J}_{ab}(\omega )=\left(\begin{array}{cc}{f}_{1}&{g}_{1}\\ {g}_{2}&{f}_{2}\end{array}\right),$$
(4)

where

$${f}_{1} = \, -2C\cos k+2C-{\left({\omega }^{2}{L}_{0}\right)}^{-1}\\ {f}_{2} = \, 2{\left({\omega }^{2}L\right)}^{-1}\cos k-2{\left({\omega }^{2}L\right)}^{-1}+{C}_{0}\\ {g}_{1} = \, -{C}_{x}{e}^{ik}+{\left({\omega }^{2}{L}_{x}\right)}^{-1}{e}^{-ik}\\ {g}_{2} = \, {\left({\omega }^{2}{L}_{x}\right)}^{-1}{e}^{ik}-{C}_{x}{e}^{-ik},$$
(5)

for topological phase and

$${f}_{1} = \, -2C\cos k+2C+{C}_{0}\\ {f}_{2} = \, 2{\left({\omega }^{2}L\right)}^{-1}\cos k-2{\left({\omega }^{2}L\right)}^{-1}-{\left({\omega }^{2}{L}_{0}\right)}^{-1}\\ {g}_{1} = \, -{C}_{x}{e}^{ik}+{\left({\omega }^{2}{L}_{x}\right)}^{-1}{e}^{-ik}\\ {g}_{2} = \, {\left({\omega }^{2}{L}_{x}\right)}^{-1}{e}^{ik}-{C}_{x}{e}^{-ik},$$
(6)

for trivial phase.

The essence to realize the 1D model in circuit form is to make the circuit Laplacian equal to the system Hamiltonian. Clearly, to make it possible, particle-hole symmetry (PHS) must be respected, which requires these three pairs of LC resonators shares the same resonant frequency, that is,

$${\omega }_{{{{{{{{\rm{resonant}}}}}}}}}\equiv 1/\sqrt{LC}=1/\sqrt{{L}_{0}{C}_{0}}=1/\sqrt{{L}_{x}{C}_{x}}.$$
(7)

Once PHS is respected, the relationship between circuit components and Hamiltonian parameters could be induced and expressed as follows:

$$\left\{\begin{array}{l}t=-C,\hfill \\ \mu =-2C+{C}_{0},\quad \\ {\Delta }_{0}=-{C}_{x}.\hfill \end{array}\right.$$
(8)

To make the 1D circuit chain topological, we set μ to 0 to meet the topological mode requirements of ∣μ∣ < ∣2t∣. This topological property is satisfied by the emergence of grounded capacitors C0 and inductors L0, since the system will be precisely located at the critical point between the topological and trivial states. Therefore, by exchanging the connections of C0 and L0, we could perform transitions between these two states.

Impedance resonance

The emergence of a topological edge states is observed via impedance resonance. The topological edge state is a zero-energy eigenstate of the Hamiltonian. It corresponds to the zero admittance, and hence, the emergence is observable by the divergence in the impedance.

The two-point impedance between the a and b nodes is given by32

$${Z}_{ab}\equiv {V}_{a}/{I}_{b}={G}_{ab},$$
(9)

where G is the Green function defined by the inverse of the Laplacian J, G ≡ J−1, Va is the voltage at site a and Ib is the current at site b.