Introduction

Since the discovery of topological insulators (TIs), tremendous effort has been devoted to the search for exotic topological phases of matter1,2,3,4,5,6,7,8,9,10. Recently, a novel class of exotic insulators with higher-order band topology, dubbed higher-order TIs (HOTIs), have been proposed11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26. The fascinating characteristic of HOTIs is that d-dimensional nth-order TIs have (d-n)-dimensional gapless boundary states11,12,13,14,15,16. For instance, two-dimensional (2D) second-order TIs with a quantized quadrupole moment, which is predicted by generalizing the fundamental relationship between the Berry phase and quantized polarization, support corner-localized modes lying in the middle of the energy gap17. Following the theoretical proposals of quadrupole TIs (QTIs), the topological corner states were observed experimentally in phononic18,19,20 and photonic21,22,23,24,25,26 systems.

The understanding of topological phases of matter has always been based on the topological band theory, which is defined in crystalline materials with long-range order and periodicity. To the best of our knowledge, topological phases are observed only in one-dimensional quasicrystals27. Although there are predictions of topological phases in 2D quasicrystals28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43, the experimental observations have never been reported.

Highly customizable electrical circuits have emerged as a new platform to engineer various topological states44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59. In this study, we report the realization of the 2D quasicrystalline QTIs in electrical circuits and observe the corner states experimentally. To realize the QTIs, we construct the Ammann–Beenker (AB) tiling circuits with two types (thin and fat) of rhombuses and we implement the nearest- and next-nearest-neighbor hoppings using lumped elements to realize rotational symmetry. Using impedance measurement, the corner states protected by quantized quadrupole moment are directly observed in the circuits. The robustness of topological corner states is also demonstrated. Our work provides the experimental evidence of topological phases in 2D quasicrystalline systems. We expect more topological states can be observed in circuits based on similar implementations.

Results

Quasicrystalline QTIs

We construct the QTI on an AB tiling quasicrystal by only considering nearest- and next-nearest-neighbor hoppings35. The tight-binding Hamiltonian is

$$H{\mathrm{ = }}A_0\mathop {\sum}\limits_j {c_j^\dagger \left( {{\Gamma}_2 + {\Gamma}_4} \right)c_j} + \frac{{A_1}}{2}\mathop {\sum}\limits_{j \ne k} {c_j^\dagger T\left( {\phi _{jk}} \right)c_k} ,$$
(1)

where

$$T\left( {\phi _{jk}} \right) = \left\{ \begin{array}{l}{\Gamma}_4 - i{\Gamma}_3{\mathrm{,}}\, - \pi /4 \le \phi _{jk} < \pi /4,\\ {\Gamma}_2 - i{\Gamma}_1{\mathrm{,}}\,\pi /4 \le \phi _{jk} < 3\pi /4,\\ {\Gamma}_4 + i{\Gamma}_3{\mathrm{,}}\,3\pi /4 \le \phi _{jk} < 5\pi /4,\\ {\Gamma}_2 + i{\Gamma}_1{\mathrm{,}}\,5\pi /4 \le \phi _{jk} < 7\pi /4,\end{array} \right.$$
(2)

and ϕjk indicates the polar angle of bond between site j and k with respect to the horizontal direction. Here, \(c_j^\dagger = \left( {c_{j1}^\dagger ,c_{j2}^\dagger ,c_{j3}^\dagger ,c_{j4}^\dagger } \right)\) is the creation operator in cell j. The first and second terms are the intracell and intercell hoppings with amplitudes A0 and A1, respectively. \({\Gamma}_4 = \tau _1\tau _0\) and \({\Gamma}_\upsilon = - \tau _2\tau _\nu \) with ν = 1,2,3. τ1,2,3 are the Pauli matrices and τ0 is the identity matrix. This model has a fourfold rotational symmetry \({\mathcal{C}}_{4}\) = UR, where \(U = \left( {\begin{array}{*{20}{c}} 0 & {i\tau _2} \\ {\tau _0} & 0 \end{array}} \right)\) and R is an orthogonal matrix permuting the sites of the tiling to rotate the whole system by π/4.

The rotational symmetry \({\mathcal{C}}_{4}\) results in a quantized quadrupole moment Qxy = 0,e/2. Thus, Qxy is a natural topological invariant, which can be calculated in real space60,61. By numerical calculations, we confirmed that the AB tiling quasicrystal has the non-trivial quadrupole moment Qxy = e/2 under the hopping ratio λ > 2.5(λ = A1/A0) (see Supplementary Note 1). The quantized quadrupole moment indicates the occurrence of the quadrupole insulator with protected corner states.

Realization in electrical circuits

The quasicrystalline lattice can be mapped to an electrical circuit. To realize quasicrystalline QTI, we design an electrical circuit depicted in Fig. 1a. The circuit is characterized by the Kirchhoff’s law

$$I_{pa} = \mathop{\sum}\limits_{qb} {J_{pa,qb}\left( \omega \right)V_{qb}\left( \omega \right)} ,$$
(3)

where \(I_{pa}\left( t \right) = I_{pa}\left( \omega \right)e^{i\omega t}\left[ {V_{qb}\left( t \right) = V_{qb}\left( \omega \right)e^{i\omega t}} \right]\) is the current (voltage) at site a(b) in cell p(q) and ω is the frequency of the circuit. The circuit Laplacian is \(J_{pa,qb}\left( \omega \right) = i\omega H_{pa,qb}\left( \omega \right)\), where

$$H_{pa,qb}\left( \omega \right) = C_{pa,qb} - \frac{1}{{\omega ^2}}W_{pa,qb},$$
(4)

with Cpa,qb being the capacitance between two sites and \(W_{pa,qb} = L_{pa,qb}^{ - 1}\) being the inverse inductivity between two sites. Here, the subscript g means the ground. Hpa,qb can be equivalent to the Hamiltonian of quasicrystal in Eq. (1) if the diagonal elements are zero at ω0. For the diagonal components with pa = qb, the grounded elements are chosen for satisfying \(C_{pa,pa} = - C_{pa,g} - \mathop {\sum}\nolimits_{q^{\prime}b^{\prime}} {C_{pa,q^{\prime}b^{\prime}}} \)and \(W_{pa,pa} = - L_{pa,g}^{ - 1} - \mathop {\sum}\nolimits_{q^{\prime}b^{\prime}} {L_{pa,q^{\prime}b^{\prime}}^{ - 1}} \).

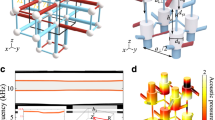
Fig. 1: Quasicrystalline quadrupole topological insulators in electrical circuits.
figure 1

a Schematic of the circuit with 69 unit cells. One unit cell consists of four sites labeled as 1, 2, 3, and 4 at the left-up corner. The colored sites are wired to grounded inductors and/or capacitors listed on the right. For example, the black hollow point 3 is connected to the ground by the capacitor–inductor pairs C1 and L1, and the yellow point 1 is connected to the ground by L4g. The sites in the same unit cell are wired by intracell inductors L1 (red dashed lines) and capacitors C1 (red solid lines), and the intercell elements between the unit cells are inductors L2 (gray dashed lines) and capacitors C2 (gray solid lines). b Photo of the fabricated circuit. The yellow and black elements are capacitors and inductors, respectively, and the wirings are indicated on overlay of the printed circuit board.

Full size image

As shown in Fig. 1a, the solid and dashed lines correspond to hoppings with positive and negative values, which can be realized by the capacitors and inductors, respectively. We choose capacitor C1 and inductor L1 for intracell hopping, and C2 and L2 for intercell hopping. The nearest-neighbor couplings between cells are introduced to stabilize the corner states in small size systems35. If these couplings are negleted, the exact AB tiling is restored and the physical results do not change qualitatively.

Under a suitable choice of the grounded elements, the tight-binding Hamiltonian of the QTI on a quasicrystalline lattice in Eq. (1) is mapped to the circuit Hamiltonian in Eq. (2). It is noteworthy that there exists a relation C2/C1 = L1/L2 = A1/A0.

The two-point impedance is:

$$Z_{ab} = \frac{{V_a - V_b}}{{I_{ab}}} = \mathop {\sum}\limits_n {\frac{{\left| {\psi _{n,a} - \psi _{n,b}} \right|^2}}{{j_n}}} $$
(5)

where Va(b) is the voltage on site a(b), Iab is the current between the two sites, and jn and \(\left| {\psi _n} \right\rangle \) are the eigenvalue and eigenstates of the matrix J(ω), respectively22. The two-point impedanace Zab diverges in the presence of zero-admittance modes (jn = 0) with \(\psi _{n,a} \ne \psi _{n,b}\). Hence, the corner states with zero-admittance can be observed by measuring the two-point impedance.

We consider the QTI on an AB tiling 2D quasicrystalline lattice. A circuit that realizes the QTIs is depicted in Fig. 1a. The unit cell of the circuit contains four sites denoted by labels 1, 2, 3, and 4. Each unit cell consists of three capacitors for positive coupling and one inductor for negative coupling, which can generate a synthetic magnetic π flux threading the unit-cell plaquette (equivalent to half the magnetic flux quantum, \(\left( {1/2} \right){\it{{\Phi}}}_0 = h/\left( {2e} \right)\), where h is the Planck constant). The existence of this non-zero flux opens the spectral gap for maintaining the corner-localized mid-gap modes. We use two pairs of capacitors and inductors (C1, L1) and (C2, L2), which have the same resonant frequency \(\omega _0{\mathrm{ = }}1/\sqrt {L_1C_1} = 1/\sqrt {L_2C_2} \), as the intracell and intercell wirings between the sites, respectively. The intracell and intercell elements are related by C2 = λC1 and L2 = L1/λ. The circuit is governed by the linear circuit theory with a circuit Laplacian J(ω)22. The circuit has a square-open boundary, which satisfies the global \({\mathcal{C}}_{4}\) symmetry at the resonant frequency ω0. Suitable grounded elements on the sites are chosen (site colors depicted in Fig. 1a indicate the values of the grounded capacitors and/or inductors) to sustain chiral symmetry at ω0, which pins the topological boundary modes in the middle of the bulk energy gap. The symmetry characteristic and quantized quadrupole moment of circuit indicate the occurrence of the QTI associated with topologically protected states localized on the corner sites. The edge states are gapped and merged with the bulk states. Hence, it is difficult to observe them experimentally (see Supplementary Note 2).

To realize the QTI experimentally, a circuit with 69 unit cells was fabricated as shown in Fig. 1b. The intracell elements with C1 = 10 nF and L1 = 1 mH result in a resonant frequency 50.3 kHz (parameters for other elements are given in “Methods”). Here we set the coupling ratio λ = 10, to get highly localized corner states, which can be observed by two-point impedance measurements between the corner/edge/bulk site and another bulk site using an impedance analyzer.

Figure 2 compares the experimental and theoretical results, which demonstrates the spectral and spatial localizations of the topological corner states. Figure 2a shows the spectrum of the circuit Laplacian J(ω) as a function of the normalized frequency ω/ω0. The isolated corner modes reside in the spectral gap of J(ω) at a fixed frequency ω0. The spatial distribution of the experimentally observed impedance of the corner states at ω0 is illustrated in Fig. 2b. The impedance is maximum at the four corner sites and exponentially decays at other sites. The comparison between the experimental and theoretical impedance spectra is shown in Fig. 2c, d, which demonstrate the spectral localization of the corner modes. The maximum measured impedance reaches 7 kΩ.

Fig. 2: Corner states on the circuit.
figure 2

a Spectra of the Laplacian J vs. the frequency that is normalized to the resonant frequency ω0. The isolated mode crossing in the gap corresponds to the topological corner states. b The experimental impedance distribution at the resonant frequency ω0 demonstrates the spatial localization of the corner states. c The experimental two-point impedances measured between the left-up corner/edge/bulk site and another bulk site. d The theoretical two-point impedances. Both the experimental and theoretical results demonstrate the spectral localization of the corner states.

Full size image

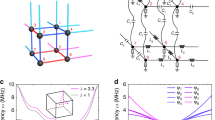
To justify the robustness of the corner states, we consider the effect of experimental element errors. The errors are generated in two ways: (i) random manufacturing variations in discrete elements and (ii) the deviation of the typical values of commercially available circuit components from the theoretical circuit parameters. Figure 3a shows the normalized eigenfrequencies ω/ω0 of the Laplacian J(ω) with element error ±5% and the number of the samples is 300. The eigenfrequencies of corner states (indicated by red circles) are located in the bandgap and far away from those of other states (indicated by blue circles). Experimentally, we construct a circuit with element error ±5% and measure the two-point impedances as a function of the normalized frequency ω/ω0. As shown in Fig. 3b, the corner states are spectrally localized with a deviation from ω0. Figure 3c–f shows the spatial impedance distributions at the frequencies of the four corner states. Compared with the spatial impedance distribution in Fig. 2b, although the maximum impedances are located at only one of the four corner sites, the topological corner states are still spatially localized. The spectral and spatial localizations imply the robustness of corner states on the circuit.

Fig. 3: Robustness of corner states on the circuit.
figure 3

a The normalized eigenfrequencies ω/ω0 of the circuit Laplacian J(ω) with element errors ±5% and the number of the samples is 300. The eigenfrequencies of the corner and bulk states are indicated by the red and blue circles. b The experimental two-point impedances measured between the left-up/left-down/right-up/right-down corner site and another bulk site. c–f The experimental impedance distributions at the frequencies of the left-up/left-down/right-up/right-down corner states.

Full size image

Discussion

The quadruple insulators were always realized on periodic systems with translational symmetry and the quadruple moments are well-defined in momentum space. Unlike the periodic structures, the quasi-periodic systems possess long-range order but do not have translational symmetry. Therefore, quasicrystalline insulators with a quantized quadrupole moment extend the concept of quadruple insulators defined in crystals. The realization of quadruple isolator in this work opens a way for the implementation of corner states in more quasi-periodic systems.

The circuit implementation of the 2D quasicrystalline QTIs confirms the existence and robustness of the corner states on the circuit. This work provides an experimental evidence for the first time to implement the topological phase in a 2D quasicrystalline system and extends the territory of topological phases beyond crystals to higher-dimensional aperiodic systems. The highly customizable circuit platform can also readily be applied to other 2D quasicrystals with different symmetries and to three-dimensional quasicrystalline structures62, which may realize more exotic topological states.

Methods

We choose the capacitors C1 = 10 nF, C2 = 100 nF, C1g = 100 nF, C2g = 200 nF, and the inductors L1 = 1000 μH, L2 = 100 μH with high Q factors (Q > 70 @ 50 kHz). The grounded elements are L1g = 83 μH, L2g = 100 μH, L3g = 45 μH, L4g = 31 μH, L5g = 23 μH, L6g = 500 μH, and L7g = 50 μH. After delicately choosing, the errors of the circuit elements are < ±1%. The intracell elements C1 and L1 result in a resonant frequency 50.3 kHz. Here we set the coupling ratio λ = 10 in order to get highly localized corner states and the two-point impedance measurement is carried out using an Impedance Analyzer 4192A LF.