Introduction

Bound states in the continuum (BICs) were originally proposed for electrons in a peculiar quantum mechanical potential by von Neumann and Wigner in 19291, and were later revealed to be a general phenomenon for both quantum and classical waves2,3. As for single-particle systems and their classical analogies, various mechanisms could be used to produce BICs. For example, the coupling of certain resonances to radiation modes could be forbidden by symmetry or separability, which are called symmetry-protected BICs or separable BICs4,5,6,7,8. In addition, it is also possible to suppress radiations into all channels by tuning a finite number of systematical parameters9,10,11,12,13,14,15,16,17,18. This suppression can always be interpreted as a result of the destructive interference of multiple radiating components. Moreover, instead of looking for the presence of BICs in a given system, we can also inversely design a system by engineering the potential, the hopping rate or the boundary shape of the system to construct BICs19,20,21. It is found that BICs proposed in classical-wave systems could have large quality-factors and extremely enhanced near-field concentrations. These superior properties give many important applications based on BICs, such as the ultralow threshold BIC-laser10,22,23. While, single-particle BICs are always fragile objects, which appear in artificial systems with specific designs. In this case, finding other robust ways to create BICs is of great significance.

On the other hand, except for the widely discussed single-particle system, many investigations have shown that the correlated few-body BICs can also exist in the two-boson Hubbard model by engineering the onsite interaction and impurity potential at bulk or boundary site24,25. In particular, two-boson bulk BICs could appear when the absolute value of impurity potential on the bulk site is larger than that of the Hubbard interaction, which is required to possess the same sign with the impurity potential on the bulk site24. As for the correlated two-boson model with a boundary impurity potential, it is shown that Tamm–Hubbard BICs require an infinitesimally-small value of the boundary impurity potential, which has the opposite sign with respect to the Hubbard interaction25. Different from most single-particle BICs that need specific designs in artificial systems, the two-boson BICs always exist in a wide range of interaction strengths and defective potentials. It can move into and out of the continuum continuously by tuning these parameters, making two-particle BICs become robust and tunable. Taken together, the currently proposed single- and few-body BICs are all based on the engineering of systematic symmetries, potential and material distributions, or particle-particle interactions. Exploring new mechanisms for the generation of BICs is still an important problem in the field of physics and material sciences.

In this work, we demonstrate both theoretically and experimentally that BICs can be purely induced by quantum statistics. Such a type of BICs can exist in anyonic systems with the statistical angle exceeding a threshold. Anyons are quantum quasi-particles with statistics intermediate between bosons and fermions26,27,28,29,30,31,32,33,34,35,36,37,38,39,40. The existence of anyons was predicted in the 1980s, and the strong experimental evidence of anyons has emerged recently33,34. It is widely known that anyons could play important roles in several areas of modern physics research, such as fractional quantum Hall systems35, spin liquids36 and topological quantum computations37. Meanwhile, some recent investigations have shown that quantum statistics could trigger the appearance of many interesting effects, such as anyonic Bloch oscillations38,39 and topological transitions40. Beyond these novel physical phenomena, here, we reveal that exotic BICs can also exist in non-interacting anyonic systems. Moreover, using the exact mapping of two anyons in the finite one-dimensional lattice to modes of the two-dimensional circuit, anyonic BICs are experimentally emulated. Our work opens the door to novel physics induced by the interplay between BICs and anyons.

Results

The theory of anyonic bound states in the continuum

We start by considering a pair of non-interacting anyons (marked by two letters of ‘m’ and ‘n’) hopping on a one-dimensional (1D) chain with open boundaries, as shown in Fig. 1a. In this case, the system can be described by the tight-binding lattice model as:

$$H=-J\mathop{\sum }\limits_{l=1}^{L-1}({\hat{a}}_{l}^{+}{\hat{a}}_{l+1}+{\hat{a}}_{l+1}^{+}{\hat{a}}_{l})$$
(1)

where \({\hat{a}}_{l}^{+}\) (\({\hat{a}}_{l}\)) is the creation (annihilation) operator of the anyon at the lth lattice site. L is the length of 1D lattice, and J is the single-particle hopping rate. In the following, we always set J = 1. The anyonic creation and annihilation operators obey commutation relations as \({{\hat{a}}_{k}^{+}{\hat{a}}_{l}-\hat{a}}_{l}^{+}{\hat{a}}_{k}{e}^{i\theta {{{{\mathrm{sgn}}}}}(\it l-\it k)}={\delta }_{{lk}}\) and \({{\hat{a}}_{l}{\hat{a}}_{k}-\hat{a}}_{k}{{\hat{a}}_{l}e}^{i\theta {{{{\mathrm{sgn}}}}}(\it l-\it k)}=0\), where \(\theta\) is the anyonic statistical angle and sgn(x) equals to −1, 0 and 1 for x < 0, x = 0 and x > 0, respectively. Based on the commutation relation, we note that two anyons on the same lattice site behave as ordinary bosons. In this case, anyons with \(\theta =\pi\) (always called as pseudofermions32) could be regard as bosons when they occupy the same site and ordinary fermions when they occupy different sites. The two-anyon solution can be expanded in Fock space as \(|\psi > =\frac{1}{\sqrt{2}}{\sum }_{n,m=1}^{L}{c}_{{nm}}{\hat{a}}_{n}^{+}{\hat{a}}_{m}^{+}|0 > \), where \(|0 > \) is the vacuum state and \({c}_{{nm}}\) is the probability amplitude with one anyon at site m and the other one at site n. Under the restriction of anyonic statistics, the equality of \({c}_{{mn}}={{e}^{i\theta {{{{\mathrm{sgn}}}}}(n-m)}c}_{{nm}}\) is satisfied. By solving the steady-state Schrödinger equation \({H|}\psi > =\varepsilon |\psi > \) of two anyons, the corresponding eigenequation with respect to \({c}_{{nm}}\) can be described by:

$$\varepsilon {c}_{{nm}}=-J[{{e}^{i\theta ({\delta }_{n,m}+{\delta }_{n,m-1})}c}_{n(m-1)}+{e}^{-i\theta ({\delta }_{n,m}+{\delta }_{n,m+1})}{c}_{n(m+1)}{+c}_{(n-1)m}+{c}_{(n+1)m}]$$
(2)
Fig. 1: Analytical results for the two-anyon bound states in the continuum (BICs).
figure 1

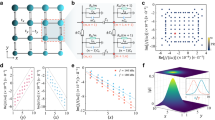
a The schematic diagram for the 1D lattice model possessing two anyons with the statistical angle marked by \(\theta\). b The scheme of the two-anyon Fock space. Solid lines and arrows represent real-valued hopping strengths and complex-valued hopping strengths, respectively. Two-anyon modes enclosed by black and blue dash blocks are presented in Fig. 1a. c and d The variations of \({Im}\left({k}_{n}\right)\) and \({Im}\left({{k}_{m}+k}_{n}\right)\) as functions of the anyonic statistical angle. Here, the two-anyon state is assumed in the form of \({c}_{n,m}={A}_{1}\exp \left(i{k}_{n}n+i{k}_{m}m\right)\) with n ≥ m. The purple (green) region corresponds to the range of statistical angle, where non-diverge BICs are supported (unsupported) in the two-anyon system. Here, km and kn are a pair of complex wave numbers related to two anyons.

Full size image

The mode coupling of two anyons determined by Eq. (2) can be illustrated in the 2D Fock space, as shown in Fig. 1b. The site located at (n, m) represents the two-anyon state of \({c}_{{nm}}\). In this case, the site enclosed by the black (blue) dash block corresponds to the state with the first (second) anyon locating at n = 3 (n = 4) and the second (first) anyon locating at m = 4 (m = 3), as presented in Fig. 1a. Solid lines and arrows represent real-valued hopping strengths (\(J\)) and complex-valued hopping strengths (Je±iθ), respectively. It is shown that anyonic statistics can only introduce complex couplings around diagonals (blue sites with n = m and n = m\(\pm 1\)). Away from diagonals (black sites with |n−m | >1), the mode couplings are real-valued.

The above eigenequation of two anyons can be solved analytically by assuming a Bethe-type ansatz of two-anyon state as \({c}_{{nm}}({k}_{n},\,{k}_{m},{A}_{i=1,..,8})\)24,25\(,\) which is in the form of a superposition with eight plane waves (see Supplementary Note 1 for details). Here, km and kn are a pair of complex wave numbers related to two anyons, and A1 to A8 are amplitudes of eight plane waves. We note that the eigenequation should be written in different forms with the considered lattice site locating at diagonals and off diagonals of the two-anyon Fock space. Hence, we handle these two cases separately to solve the two-anyon eigenequation.

At first, we substitute \({c}_{{nm}}({k}_{n},\,{k}_{m},{A}_{i=1,..,8})\) into the steady-state eigenequation away from diagonals. It is found that the eigen-energy of two distant anyons could be written as \(\varepsilon =-2{{\cos }}\left({k}_{m}\right)-2{{\cos }}({k}_{n})\). It manifests that energies of two-anyon scattering states are always ranging from −4 to 4. Then, we substitute \({c}_{{nm}}({k}_{n},\,{k}_{m},{A}_{i=1,..,8})\) into the steady-state eigenequation at diagonals. In this case, a set of linear equations related to A1 to A8 are obtained. These linear equations could be expressed in a matrix form as MijAj = 0 (i, j = 1,…,8), where M is an 8 by 8 matrix (see Supplementary Note 1 for details). Through the direct computation, we find that the determinant of matrix M satisfies det(M) = 0. This means that the two-anyon solution is admitted for any complex values of km and kn accompanied with suitable values of Aj (j = 1,…,8). The only limitation on km and kn is the non-diverge requirement of \({c}_{{nm}}\to 0\) with \(n,m\to \infty\).

Based on the solvability condition for the matrix equation MijAj = 0, we can assume the Bethe-type ansatz of two anyons in a simple form as \({c}_{{nm}}={A}_{1}\exp \left(i{k}_{n}n+i{k}_{m}m\right)\) with n ≥ m. Substituting this simplified two-anyon state into the steady-state eigenequation at diagonals, two complex wave-vectors kn and km can be expressed by the statistical angle θ as \({z}_{n}=-(-{e}^{i\theta }+{e}^{2i\theta }\pm \sqrt{-{e}^{i\theta }\,+\,3{e}^{2i\theta }\,-\,3{e}^{3i\theta }\,+\,{e}^{4i\theta }})/(\sqrt{1\,-\,{e}^{i\theta }}\sqrt{(-1\,+\,{e}^{i\theta }){e}^{i\theta }})\) and \({z}_{m}=\pm \sqrt{1-{e}^{i\theta }}/\sqrt{-{e}^{i\theta }+{e}^{2i\theta }}\) with \({z}_{n}=exp(-i{k}_{n})\) and \({z}_{m}=exp(-i{k}_{m})\) (see Supplementary Note 2 for details). We note that the assumed two-anyon state can be re-expressed as \({c}_{{nm}}={A}_{1}\exp [i{k}_{n}\left(n-m\right)+i({k}_{m}+{k}_{n})m]\) with n ≥ m. In this case, such a two-anyon state can meet the non-diverge requirement and become a perfect bound state if two wave-vectors satisfy relations of \({Im}\left({k}_{n}\right) > 0\) and \({Im}\left({{k}_{m}+k}_{n}\right) > 0\).

To get the required value of \(\theta\) for the appearance of two-anyon bound states, the variations of \({Im}\left({k}_{n}\right)\) and \({Im}\left({{k}_{m}+k}_{n}\right)\) as a function of the statistical angle \(\theta\) are calculated, as shown in Fig. 1c and d. We can see that a sudden change of \({Im}\left({{k}_{m}+k}_{n}\right)\) and \({Im}\left({k}_{n}\right)\) from negative (the green region) to positive (the purple region) appears when the statistical angle is beyond \(0.6\pi\). This indicates that the perfect bound state only appears when the value of statistical angle exceeds the threshold (\(\theta =0.6\pi\)). In addition, the effective on-site potential is uniform, and the absolute value of the coupling strength is also fixed to a constant in the mapped 2D lattice. Hence, eigen-energies of two-anyon bound states should always lie into the continued energy-spectrum of two-anyon scattering states, making perfect bound states of two anyons become anyonic BICs (see numerical demonstrations in the following).

An intuitive understanding for the existence of anyonic BICs with a threshold of \(\theta\) can be illustrated by the competition between statistics-induced localizations and free hoppings of anyons. Specifically, complex couplings induced by quantum statistics can generate a defective potential on corners of two-anyon Fock space. The larger the statistical angle is, the deeper the defective potential becomes. When the strength of defective potential can suppress the role of two-anyon free hoppings, localized two-anyon BICs appear.

To demonstrate the above analytical prediction of anyonic BICs, we numerically calculate the inverse participation ratio (IPR)41, which is defined by \({IPR}=\mathop{\sum}\nolimits_{m,n}|{{{{{{{\boldsymbol{C}}}}}}}_{{mn}}|}^{4}\), to qualify the localization of two-anyon eigenstates. As shown in Fig. 2a, the variation of IPRs of all two-anyon eigenmodes as a function of the statistical angle is calculated. The lattice length is set as L = 171. It is seen that a large ratio of two-anyon eigenstates (black dots) possess near-zero IPRs, corresponding to the extended two-anyon scattering states. There are also two types of anyonic eigenstates with relatively large IPRs, as marked by blue and red lines. But, these two types of two-anyon states show different behaviors with the change of \(\theta\). The mode marked by the blue line always exists at different values of \(\theta\). While, IPRs of two-anyon modes marked by the red line increase significantly when the value of \(\theta\) exceeds \(0.6\pi\) (as illustrated by the purple region). It indicates that this type of two-anyon states exhibit the enhanced localization with \(\theta\) exceeding a threshold.

Fig. 2: Numerical results for the demonstration of two-anyon bound states in the continuum (BICs).
figure 2

a The calculated inverse participation ratios of all two-anyon eigenstates with L = 171 at different anyonic statistical angles. Red and blue dash lines are used to mark two types of anyonic modes with large inverse participation ratios (IPRs). b and c The evolution of IPRs for two-anyon eigenmodes as a function of the lattice length with the statistical angles being \(0.8\pi\) and \(\pi\), respectively. d and e Numerical results on the variation of imaginary parts of eigen-energies as a function of the size for the lossless region, where the statistical angles are set as \(\theta =\pi\) and \(\theta =0.8\pi\), respectively. The inset of (d) plots the schematic diagram for the region with artificial losses.

Full size image

To justify whether these two types of localized anyonic modes are perfect bound states, we calculate the evolution of \({IPRs}\) as a function of the lattice length in Fig. 2b and c with the statistical angle being \(\theta =0.8\pi\) and \(\theta =\pi\), respectively. It is clearly shown that IPRs of two-anyon eigenstates marked by blue lines decrease significantly with the lattice size being increased, indicating that those states are leaky modes and could couple with two-anyon scattering states. While, IPRs of anyonic modes marked by red lines are saturated with increasing the lattice size, manifesting the perfect localization of these eigenmodes at both statistical angles. The splitting of eigenenergies of two-anyon bound states at \(\theta =0.8\pi\) is due to the finite size effect, where the two-anyon bound states at two corners (1, 1) and (L, L) are coupled with each other. In addition, following another numerical method on the demonstration of BICs42,43, we further calculate the scaling of imaginary part of two-anyon eigen-energies by changing the size of the lattice region with artificial losses. The artificial losses are introduced by adding the non-Hermitian on-site term (0.05i) to some lattice sites, which are inside the red area of the mapped 2D lattice model plotted in the inset of Fig. 2d. Here, the size of lossless region is marked by nl. Fig. 2d and 2e present numerical results on the variation of imaginary parts of two-anyon eigen-energies as a function of nl. Here, the statistical angles are set as \(\theta =\pi\) (in Fig. 2d) and \(\theta =0.8\pi\) (in Fig. 2e), respectively. The lattice length equals to L = 171. We can see that imaginary components of eigen-energies for anyonic BICs (corresponding to modes marked by red lines in Fig. 2a–c) approach to zero in an exponential scaling with increasing the size of the lossless region. This phenomenon further demonstrates the correctness of the existence of anyonic BICs.

Furthermore, as shown in Fig. 3a–e, we calculate eigenenergies of two anyons with \(\theta =\pi\), \(0.8\pi\), \(0.7\pi\), \(0.6\pi\) and \(0.5\pi\) (L = 171), respectively. Insets correspond to enlarged views of eigen-spectra (enclosed by red blocks) sustaining BIC-related two-anyon states. It is worth noting that the two-anyon eigen-spectra at different statistical angles are all chiral symmetric. In this case, the anyonic BICs should exist at a pair of positive and negative energies with equal absolute values, as marked by solid and dash blocks in Fig. 3a–e. Here, we focus on anyonic BICs with negative energies, and positive-energy counterparts possess identical properties. In Fig. 3f–j, we plot spatial distributions of BIC-related eigenmodes (enclosed by green circles in insets) at different statistical angles. It is clearly shown that two-anyon states are perfectly concentrated around two corners in the two-anyon Fock space with \(\theta > 0.6\pi\). The larger the statistical angle is, the stronger the localization of anyonic BICs becomes. In contrast, the two-anyon eigenstates are leaky modes with \(\theta \le 0.6\pi\). In addition, we can see that anyonic bound states are lying in the continuum of two-anyon scattering states with \(\theta > 0.6\pi\). These numerical results clearly verify that the two-anyon bound states are indeed anyonic BICs.

Fig. 3: Numerical results of eigen-spectra and spatial profiles of localized two-anyon states.
figure 3

a–e Calculated eigenenergies of the two-anyon model with \(\theta =\pi\), \(0.8\pi\), \(0.7\pi\), \(0.6\pi\) and \(0.5\pi\), respectively. Insets plot enlarged views of anyonic eigen-spectra sustaining eigenmodes related to bound states in the continuum (BICs) with negative energies. Chiral symmetric counterparts with positive energies are marked by red dash blocks. f–j Calculated spatial distributions of BIC-related eigenmodes with \(\theta =\pi\), \(0.8\pi\), \(0.7\pi\), \(0.6\pi\) and \(0.5\pi\), respectively. The mode index of two-anyon states (N) is in the range from 1 to L2 with L = 171. The color bars quantify the absolute value of probability amplitude.

Full size image

It is worthy to note that the physical origin for the formation of anyonic BICs is different from that of two-boson BICs24,25. To construct two-body BICs without single-body analogies, the effective two-body correlation is prerequisite. In theory, the most common two-body correlation is resulting from the Hubbard interaction, which could induce the formation of two-boson BICs. On the other hand, quantum statistics can also induce an effective correlation of two anyons, which is the origin for the formation of anyonic BICs in our system. In addition, we want to stress that the formation of anyonic BICs does not need the existence of the defective potential, but two-boson BICs induced by the Hubbard interaction must require a suitable value of the defective potential.

The requirement of the defective potential for two-boson boundary BICs can be analogized to Tamm surface states of truncated crystals, where the surface potential exceeding a threshold is required. In this case, the defective potential in two-boson systems could be regarded as the effective surface potential of the mapped 2D lattice. As for the two-anyon system, quantum statistics could induce effective defects at two corners in the mapped 2D lattice, which could trap two anyons to form anyonic BICs. Moreover, we can also understand this phenomenon from a mathematical viewpoint. Following the analytical method by assuming a Bethe-type ansatz of two-anyon state, the requirement on the existence of two-body BICs can be derived by expressing two wave numbers (\({k}_{n}\) and \({k}_{m}\)) with intrinsic parameters of the system, including the Hubbard interaction, the defective potential and the statistical angle. To separately express two wave numbers, two different equations related to \({k}_{m}\), \({k}_{n}\) must be constructed basing on the eigen-equation of the two-body system. As for the two-boson system without the defective potential, only one equation can be obtained by considering the eigenequation on the diagonal line (m = n)24,25. In this case, to get the other equation, the defective potential must be introduced. While, as for the case of two anyons, two equations can be directly obtained by considering anyonic eigenequations at m = n and m = n\(\pm\)1 (see Eq. 9 in Supplementary Materials). Hence, two wave numbers can be expressed by the statistical angle, making the statistical angle \({{{{{\rm{\theta }}}}}}\) solely determine the existence of anyonic BICs.

The experimental observation of our theoretically predicted anyonic BICs in real quantum systems is not an easy task. In the next part, we will construct 2D circuit networks to simulate the statistics-induced anyonic BICs

Experimental simulation of anyonic bound states in the continuum by 2D circuit networks

The 1D two-body Fock space possesses a rigorous correspondence to that of a single particle in the mapped 2D lattice. In this case, by mapping the low-dimensional few-body configuration space to the high-dimensional tight-binding lattice model, the few-body model can be effectively simulated by the single-particle system with high dimensions. In this case, the Fock space of two anyons (shown in Fig. 1b) can be regarded as a two-dimensional lattice model. Specifically, the probability amplitude for the 1D two-anyon model with one anyon at the site n and the other at the site m is directly mapped to the probability amplitude for the single particle locating at the site (n, m) of the 2D lattice. In details, lattice sites on the main diagonal (n = m), first two lateral diagonals (n = m\(\pm 1\)) and other sites (|n-m | >1) correspond to two anyons located at the same site, two nearest-neighbor sites and two distant sites, respectively. The hopping along a certain direction in the mapped 2D lattice represents the hopping of one anyon in the 1D lattice. In this case, the two-anyon eigenequation can be interpreted as an eigenvalue problem for the mapped 2D lattice, manifesting that the behavior of two anyons in the 1D lattice can be effectively simulated by a single particle in the mapped 2D lattice.

Based on the similarity between the circuit Laplacian and the lattice Hamiltonian44,45,46,47,48,49,50,51,52,53,54, electric circuits can be used as a flexible platform to implement the mapped 2D lattice with different statistical angles. To achieve the required complex coupling \(J{e}^{\pm i\theta }\) around diagonals, circuit pseudospins are needed to be constructed44,45. For this purpose, multiple circuit nodes are used to work as a single lattice site, and real and complex hopping rates can be realized by suitably braiding the connection pattern between two groups of circuit nodes, as shown in Fig. 4a. Left and right insets illustrate connection patterns for realizing real-valued and complex-valued coupling strengths, respectively. As for the case with \(\theta =0\), one circuit node can work as a single lattice site to fulfill the required real-valued coupling pattern. When the statistical angle equals to \(\theta =0.8\pi\) (\(\theta =\pi\)), five (two) circuit nodes, which are connected by capacitors \({C}_{{in}}\) (plotted in blue), are used to form an effective lattice site. In this case, to realize the real-valued hopping rate, capacitors \(C\) (plotted in red) are used to directly link adjacent nodes without a cross, as shown in the left inset. Differently, adjacent circuit nodes are crossly connected via \(C\) to achieve the hopping rate with a phase factor \({e}^{\pm i\theta }\) or \({e}^{\pm i0.8\theta }\), as presented in the right inset. In addition, each node is grounded by an inductor \({L}_{g}\). Through the appropriate setting of grounding and connecting, the circuit eigen-equation can be derived as:

$$({{f}_{0}}^{2}/{f}^{2}{-{v}_{\theta }{C}_{{in}}/C-4})V_{\downarrow ,(n,m)}=-{e}^{i\theta ({\delta }_{n,m}+{\delta }_{n,m-1})}{V}_{\downarrow ,n\left(m-1\right)}\\ -{e}^{-i\theta ({\delta }_{n,m}+{\delta }_{n,m+1})}{V}_{\downarrow ,n\left(m+1\right)}-{V}_{\downarrow ,\left(n-1\right)m}-{V}_{\downarrow ,\left(n+1\right)m}$$
(3)

where \(f\) is the eigenfrequency (\({f}_{0}=1/2\pi \sqrt{C{L}_{g}}\)) of the designed circuit. \({V}_{\downarrow ,(n,m)}\) represents the voltage of pseudospin at the circuit node (n, m), which obeys the statistics-dominated hopping rate. \({v}_{\theta }\) is an integer depending on the value of the statistical angle (\({v}_{0}=1{,v}_{0.8\pi }=3.618,{v}_{\pi }=2\)). Details for the derivation of circuit eigenequations are provided in Supplementary Note 3. It is shown that the eigen-equation of the designed electric circuit possesses the same form as Eq. (2). In particular, the probability amplitude for the 1D two-anyon model \({c}_{{nm}}\) is mapped to the voltage of pseudospin \({V}_{\downarrow ,(n,m)}\) at the circuit node (n, m). The eigenenergy (\(\varepsilon\)) of two anyons is directly related to the eigenfrequency (f) of the circuit as \(\varepsilon ={{f}_{0}}^{2}/{f}^{2}-v{C}_{{in}}/C-4\) with \(J=1\).

Fig. 4: The schematic diagram and simulation results of circuit simulators for anyonic bound states in the continuum (BICs).
figure 4

a The schematic diagram for the designed circuit simulator for two anyons. Left and right insets illustrate connection patterns for the realization of real-valued and complex-valued coupling strengths with \(\theta =0\), \(0.8\pi\), and \(\pi\), respectively. b The frequency-dependent impedance responses at the left-bottom corner (m = 1, n = 1) of designed electric circuits with different \(\theta\). Red and blue arrows mark two-anyon BICs and two-anyon leaky modes with large inverse participation ratios (IPRs). c and d The spatial impedance profiles at frequencies matched to eigenenergies of anyonic BICs with \(\theta =\pi\) and \(0.8\pi\), respectively. The color bars quantify the absolute value of simulated impedances.

Full size image

To analyze properties of anyonic BICs in the circuit simulator, we perform circuit simulations using the LTSpice software. Here, the value of \(C\), \({C}_{{in}}\) and \({L}_{g}\) are taken as 1 nF, 1 nF and 3.1 uH, respectively. The simulated 2D circuit networks contain \(171\times 171\) node groups (corresponding to the 1D two-anyon model with L = 171). We note that the impedance response is related to the local density of state of the corresponding quantum tight-binding model46,47. Hence, to test whether anyonic BICs exist at expected eigen-energies, we calculate frequency-dependent impedance responses of the corner node (m = 1, n = 1) at different values of \(\theta\), as presented in Fig. 4b. Here, the effective series resistance of inductance is set as 50\(m\Omega\). It is clearly shown that three significant impedance peaks appear with \({{{{{\rm{\theta }}}}}} > 0.6{{{{{\rm{\pi }}}}}}\). The frequencies of two peaks (as marked by red arrows) are matched to positive and negative eigenenergies of two-anyon BICs. We also note that the values (widths) of impedance peak decrease (increase) with the statistical angle changing from \({{{{{\rm{\pi }}}}}}\) to 2\({{{{{\rm{\pi }}}}}}/3\). This phenomenon is consistent with the theoretical prediction, where the localization strength of anyonic BICs is largest for two pseudofermions. And, central impedance peaks (marked by blue arrows) correspond to two-anyon leaky modes (marked by the blue line in Fig. 2a), which are not perfect bound states and could couple with two-anyon scattering states. In addition, spatial impedance distributions are further simulated at frequencies corresponding to negative eigenenergies of anyonic BICs with \({{{{{\rm{\theta }}}}}}={{{{{\rm{\pi }}}}}}\) (1.448 MHz) and \({{{{{\rm{\theta }}}}}}=0.8{{{{{\rm{\pi }}}}}}\) (1.224 MHz), as shown in Fig. 4c and d. We can see that impedance profiles are identical to that of anyonic BICs (shown in Fig. 3f and 3g), demonstrating the correctness of our designed anyonic circuit simulators.

To experimentally simulate the anyonic BICs, designed 2D circuit simulators with \(\theta =0\), \(\theta =0.8\pi\) and \(\theta =\pi\) are fabricated, where the corresponding parameters are the same to those used in Fig. 4. A photograph image of the circuit sample with \(\theta =\pi\) is presented in Fig. 5a. Here, four printed circuit boards (PCBs), where each one contains \(15\times 15\) node pairs, are applied for the circuit simulator. Enlarged views of the circuit around diagonals (enclosed by red block in Fig. 5a) and far away from diagonals (enclosed by the blue block in Fig. 5a) are plotted in Fig. 5b and c, respectively. It is shown that two circuit nodes connected by the capacitor \({C}_{{in}}\) (plotted in pink) are considered to form an effective lattice site. Voltages at these two nodes are defined by \({V}_{i,1}\) and \({V}_{i,2}\), which could be suitably formulated to construct a voltage pseudospin (\({V}_{\downarrow i}={V}_{i,1}-{V}_{i,2}\)) for realizing required site couplings. To simulate the real-valued hopping rate, two capacitors (\(C\)) labeled by orange symbols are used to directly link adjacent nodes without a cross. For the realization of the hopping rate with a direction-dependent phase factor (e±iπ), two pairs of adjacent nodes are connected crossly via the capacitor \(C\). Each node is grounded by an inductor \({L}_{g}\) in the back side of the PCB. In addition, the tolerance of the circuit element is <1% to avoid the detuning of circuit responses. Details of the sample fabrication are provided in Methods.

Fig. 5: Experimental results for simulating anyonic bound states in the continuum (BICs).
figure 5

a The Photograph image of fabricated circuit simulator with \(\theta =\pi\). The white dash line marks the diagonal of the circuit sample. Red and blue blocks enclose the diagonal and non-diagonal regions of the circuit. b and c Enlarged views of the fabricated circuit around and far away from the diagonal. Red and pink capacitors correspond to \(C\) and \({C}_{{in}}\). d The measured frequency-dependent impedance at the corner node (1,1) with \(\theta =\pi\), 0.8\(\pi\) and \(0\). e and f The measured impedance profiles for the two-pseudofermion circuit simulator at 1.448 MHz and the two-anyon circuit simulator with \(\theta =0.8\pi\) at 1.224 MHz. The color bars quantify the absolute value of measured impedances.

Full size image

As shown by the red line in Fig. 5d, we measure the frequency-dependent impedance response at the corner node (1,1) of the fabricated two-pseudofermion circuit simulator. We can see that two significant impedance peaks (marked by red arrows) appear at 0.992 MHz and 1.488 MHz, being consistent to the simulation result of anyonic BICs in Fig. 4b. The central peak (the blue arrow) at 1.167 MHz correspond to the two-anyon leaky mode with a large IPR marked by the blue line in Fig. 2a. The larger width of measured impedance peaks results from the loss effect in the fabricated circuit. To fit the strength of loss in the fabricated circuit, we calculate the frequency-dependent impedances with different series resistances of inductors (see Supplementary Note 4). We find that the effective series resistance of inductance in the fabricated circuit is ~150\(m\Omega\). In addition, the spatial impedance distribution of the circuit at 1.448 MHz is further measured, as shown in Fig. 5e. We can see that the concentrated impedance profile is in a good consistence with the anyonic BIC of two pseudofermions.

Then, we turn to the fabricated circuit with \({{{{{\rm{\theta }}}}}}=0.8{{{{{\rm{\pi }}}}}}\) (see Supplementary Fig. 2 for the photograph of the sample). Here, the fabricated circuit simulator also contains \(30\times 30\) node groups, which are large enough to ensure the exponential localization of anyonic BICs. The measured impedance spectrum of the circuit node (1,1) is shown in Fig. 5d. We can see that frequencies of two impedance peaks (0.914 MHz and 1.224 MHz marked by red arrows) are matched to the positive and negative energies of anyonic BICs with \({{{{{\rm{\theta }}}}}}=0.8{{{{{\rm{\pi }}}}}}\). The spatial distribution of measured impedance profile at 1.224 MHz is displayed in Fig. 5f, where a good consistence to the profile of the anyonic BIC is also observed. The central peak at 1.036 MHz (marked by the blue arrow) corresponds to the leaky two-anyon mode with a large IPR.

Finally, we measure the impedance response of the circuit simulator for two bosons. It is found that no large impedance peak appears, indicating that the strongly localized eigenstate does not exist for two bosons. These experimental results are consistent with the theoretical prediction, and clearly demonstrate the effectiveness on the simulation of statistics-induced anyonic BICs.

Conclusion

In conclusion, we discover a mechanism to generate BICs relying only on the quantum statistics. Based on analytical derivations and numerical calculations, we find that two-anyon BICs can perfectly concentrate on the boundary of the 1D lattice without the existence of any impurity potentials when the statistical angle of two non-interacting anyons is beyond a threshold. By mapping eigenstates of two anyons to modes of designed electric circuits, anyonic BICs are effectively simulated by measuring impedance responses in frequency and spatial domains. Specifically, we fabricate three electric circuit networks with \(\theta =0\), \(\theta =0.8\pi\) and \(\theta =\pi\), and find that the significant spatial localization of the impedance only appears in the circuit simulators with \(\theta =0.8\pi\) and \(\theta =\pi\), being consistent with the theoretical prediction that there is a threshold of \(\theta\) to trigger the formation of two-anyon BICs.

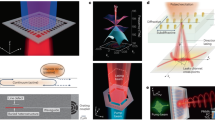
In addition, it is worth noting that our proposed anyonic BICs may also be realized in some quantum platforms32,33,34,55,56,57,58,59. For example, anyonic excitations can be created by bosons with occupation-dependent hopping amplitudes, which can be realized by assisted Raman tunneling32. Fig. 6a presents the schematic diagram for the realization of two-body anyonic BICs, where two 87Rb atoms locate in a tilted 1D optical lattice with open boundaries. The energy offset \(\triangle\) between neighboring sites is much larger than the lattice hopping J in the absence of tilting, making the direct hopping in the tilted lattice become ignored. Here, we consider two hyperfine states \(\left|A > =\right|F=1,{m}_{F}=-1 > \) and \(\left|B > =\right|F=2,{m}_{F}=-2 > \) of each 87Rb atom. In this case, four lasers L1,2,3,4 (L1, L4 and L2, L3 have the linear and circular polarizations, respectively) can be used to couple two states of 87Rb. As demonstrated by previous work59, we can assume in a very good approximation that the state \({{{{{\rm{|}}}}}}B > \) and \({|A} > \) are only coupled with L1, L4 and L2, L3, respectively, as shown in the inset of Fig. 6a.

Fig. 6: Realization of two-body anyonic bound states in the continuum (BICs) assisted by Raman tunneling.
figure 6

a The Raman scheme for the realization of two-anyon BICs by two 87Rb atoms. b–d Raman-assisted hoppings in the form of (A,0)\(\to\)(0,A), (A,A)\(\to\)(0,AB), and (AB,0)\(\to\)(A,A). Red and blue circles correspond to initial and final states of two atoms.

Full size image

We can use four lasers with frequencies being \({{{{{{\rm{\omega }}}}}}}_{1,2,3,4}\) to induce three types of Raman-assisted hoppings of two 87Rb atoms that are required to realize anyonic BICs. The first one is the transition (A,0)\(\to\)(0,A) with an energy shift \(\triangle E=-\triangle\), as shown in Fig. 6b. Such a transition can be induced by L2 and L3 with \({{{{{{\rm{\omega }}}}}}}_{2}-{{{{{{\rm{\omega }}}}}}}_{3}=-\triangle\). As shown in Fig. 6c, the second transition (A,A)\(\to\)(0,AB) with \(\triangle E=-\triangle +{U}_{{AB}}\) can be induced by L2 and L4 with \({\omega }_{2}-{\omega }_{4}=-\triangle +{U}_{{AB}}\). The third one (AB,0)\(\to\)(A,A) with \(\triangle E=-\triangle -{U}_{{AB}}\) shown Fig. 6d is induced by L1 and L3 with \({\omega }_{1}-{\omega }_{3}=-\triangle -{U}_{{AB}}\). \({U}_{{AB}}\) characterizes the interaction between \({|A} > \) and \({|B} > \) states of two atoms. It is worth noting that the undesired Raman processes of (A,0)\(\to\)(0,B), (A,A)\(\to\)(0,AA) and (AA,0)\(\to\)(A,A) can be kept out of resonance by setting \({U}_{{AA}}\gg W\) (the width of the Raman resonance). Under the above condition, the two-atom model with each atom having two states is reduced to a 1D single-component bosonic model. The on-site Fock states \({{{{{\rm{|}}}}}}0 > \), \({{{{{\rm{|}}}}}}1 > \) and \({{{{{\rm{|}}}}}}2 > \) correspond to \({{{{{\rm{|}}}}}}0 > \), \({{{{{\rm{|}}}}}}A > \) and \({{{{{\rm{|}}}}}}{AB} > \). By setting the Rabi frequency of the laser Lj to \({\Omega }_{{{{{{\rm{j}}}}}}}{{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}{\Phi }_{{{{{{\rm{j}}}}}}}}\) with \({\Phi }_{1}=-\Phi\), \({\Phi }_{2,3,4}=0\) and \(\left|{\Omega }\left|{\Omega }_{1}\right|\left|{\Omega }_{4}\right|/4=\left|{\Omega }_{2}\right|\left|{\Omega }_{3}\right|/3=\left|{\Omega }_{1}\right|\left|{\Omega }_{3}\right|/2\sqrt{3}=\left|{\Omega }_{2}\right|\left|{\Omega }_{4}\right|/2\sqrt{3}\,={\Omega }^{2}_{1}\right|\left|{\Omega }_{4}\right|/4\,=\left|{\Omega }_{2}\right|\left|{\Omega }_{3}\right|/3\,=\,\left|{\Omega }_{1}\right|\left|{\Omega }_{3}\right|/2\sqrt{3}=\left|{\Omega }_{2}\right|\left|{\Omega }_{4}\right|/2\sqrt{3}={\Omega }^{2}\) 59, we can obtain the effective Hamiltonian with occupation-dependent Peierls phase as \({H}_{{eff}}=-0.5{J\varOmega }^{2}/(\triangle \delta )\mathop{\sum}\limits_{j}({\hat{b}}_{j}^{+}{e}^{i\varPhi {\hat{n}}_{j}}{\hat{b}}_{j+1}+H.c.)\) with δ being the detuning from the single-photon transitions (\(\delta \gg {U}_{{AB}}, \triangle , \varOmega\)). \({b}_{j}^{+}\) (\({b}_{j}\)) are creation (annihilation) operators at site j, and \({\hat{n}}_{j}={\hat{b}}_{j}^{+}{\hat{b}}_{j}\). Based on the fractional version of a Jordan–Wigner transformation \({\hat{a}}_{j}={\hat{b}}_{j}{e}^{i\varPhi \mathop{\sum}\limits_{j=[1,j-1]}{n}_{j}}\), the effective Hamiltonian \({H}_{{eff}}\) is transformed to the two-anyon lattice model of Eq. (1) with \({\hat{a}}_{j}\) \(({\hat{a}}_{j}^{+})\) satisfying the anyonic statistics (\(\Phi\) is the anyonic statistical angle).

There are also many open questions related to anyonic BICs remained to be solved. For example, inspired by novel properties of three-boson states in Hubbard model60 and two-boson topological states in two dimensions61, it would be very interesting to investigate the 1D anyonic system with three or more anyons and two-anyon systems in two dimensions to see what novel phenomena related to anyonic BICs appear. And, following a recent experiment on the demonstration of nonlinearity-induced two-boson topological states with microwave qubits62, the study of influences by non-Hermitian, non-linear and topological effects on the anyonic BICs is also very interesting. These studies will shed more light on the novel physics of correlated BICs, and can also suggest a useful way to construct classical BICs in high dimensions.

Methods

Sample fabrications and circuit signal measurements

We exploit the 2D electric circuits by using PAD program software, where the PCB composition, stack-up layout, internal layer and grounding design are suitably engineered. Here, the well-designed 2D PCB possesses six layers, containing the top layer, the bottom layer, two mid-layers, and two internal planes, to suitably arrange circuit elements, linking wires and the ground setting. It is worth noting that the ground layer should be placed in the gap between any two layers to avoid the mutual inductance. Moreover, all PCB traces have a relatively large width (0.75 mm) to reduce the parasitic inductance, and the spacing between electronic devices is also large enough (0.3–0.5 mm) to avert spurious inductive coupling. The SMP connectors are welded on PCB nodes for the signal injection and detection. To ensure the realization of anyonic BICs in electric circuits, both the tolerance of circuit elements and series resistance of inductors should be as low as possible. For this purpose, we use a WK6500B impedance analyzer to select circuit elements with a high accuracy (the averaged disorder strength is <1%) and low losses.

Circuit simulations and numerical calculations

Our analytical theory on anyonic BICs is based on the Bethe-type ansatz of two-anyon eigenstates. Detailed derivations are given in Supplementary Materials. The matrix diagonalizations, which are used to calculate eigen-spectra and associated eigenmodes of two anyons, are completed in MATLAB interface. The numerical accuracy is high enough to ensure convergence. All circuit simulations are performed in LTSpice software.