Introduction

In two-dimensional honeycomb materials, such as graphene, silicene, and stanene1,2,3,4, topological phases determine the protected edge states in the nanoribbons. The quantum anomalous Hall effect (QAH) corresponds to chiral edge modes5,6, where the spin-up and spin-down modes flow along the same direction at the same upper or lower edges. The quantum spin Hall effect (QSH) corresponds to the helical edge states7. In this case, each edge contains a pair of counterpropagating spin-filtered states. While the spin-polarized QAH corresponds to the spin-polarized edge state, with only spin-up or spin-down modes flowing in opposite directions between the two edges8. These topological edge states can be applied in designing low-dissipation electronic devices9,10,11,12,13,14,15,16. Therefore, researchers are dedicated to finding more topological edge states.

Based on the modified Haldane model, Colomés and Franz17 proposed the antichiral edge state propagating in the same direction along two parallel boundaries. As required by the conservation of flow momentum, the number of states must remain equal for the entire system toward left and right. As a result, two counterpropagating bulk states appear, which belong to the strip bulk and are spatially separated from the edge states17,18. Some possible schemes19,20,21,22,23,24,25,26 have been proposed for realizing the antichiral edge states. For example, Hang et al. 25 constructed a circuit to realize a modified Haldane lattice with antichiral edge states, which has practical implications for theoretical applications. Based on the modified Haldane model, researchers proposed unipolar-bipolar filters27, valley polarization28, and topological phase transitions under uniaxial strain29 in a honeycomb lattice. Besides, although the antichiral edge states are bulk gapless, it is robust against disorder17. Thus, antichiral edge states have intriguing transport properties and potential applications in designing low-dissipation spintronic devices.

In previous studies, several methods have been used to manipulate topological edge states. Xu et al.30 proposed anisotropic chiral edge modes by applying circularly polarized light on silicene. Mannaï et al.29 investigated the effect of the strain on the antichiral edge modes. The results suggested that the strain may reverse the propagation direction of edge modes or eventually destroy them. In addition, studies on graphene demonstrated the effectiveness of side potentials in regulating the electronic structure31,32,33,34. Lu et al.35,36 investigated the effect of side potentials on the QSH state edges of silicene. Various spin- and valley-related polarized edge states were obtained by adjusting the side potentials and ribbon widths. However, the side potential on the antichiral edge states of zigzag honeycomb ribbons (zHNRs) was rarely studied.

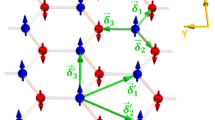
This study investigates the side potential-tunable antichiral edge states in zHNRs with a modified Haldane model. The schematic diagram of side potentials is shown in Fig. 1. The side potentials are composed of a potential field, staggered electric field, and exchange field applied on the boundaries of zHNRs. Five antichiral edge states are proposed by modulating the side potentials, which is important for designing the spin/charge switcher. Furthermore, an interpretation is proposed by calculating the spin-dependent energies in K’ and K valleys of the edge modes. A case study of Type-3 is conducted to illustrate the potential applications of induced antichiral edge states in the spin/charge switcher designs.

Fig. 1: Schematic plot of zigzag honeycomb nanoribbons with side potential.
figure 1

The side potentials include potential field U1,2, staggered potential field EZ1,2, and exchange field M1,2 along the boundaries. Ny is defined by the number of carbon atoms along the width direction, and W = 8 is the width of the side potentials.

Full size image

Results and Discussion

The Hamiltonian of the tight-binding model

The antichiral edge states can be obtained based on the modified Haldane model in zHNRs. Considering the side potentials U1,2, EZ1,2, and M1,2, the corresponding Hamiltonian of the tight-binding model can be described as:

$$H= -t\mathop{\sum}\limits_{\langle i,j\rangle \sigma }{c}_{i\sigma }^{{{\dagger}} }{c}_{j\sigma }+{t}_{2}\mathop{\sum}\limits_{\langle \langle i,j\rangle \rangle \sigma }{e}^{-i{\nu }_{ij}\phi }{c}_{i\sigma }^{{{\dagger}} }{c}_{j\sigma }\\ +\mathop{\sum }\limits_{i=1}^{W}\mathop{\sum}\limits_{\sigma }[{U}_{1}{c}_{i\sigma }^{{{\dagger}} }{c}_{i\sigma }+{E}_{Z1}{\mu }_{i}{c}_{i\sigma }^{{{\dagger}} }{c}_{i\sigma }+{M}_{1}{c}_{i\sigma }^{{{\dagger}} }{\sigma }_{\sigma \sigma }^{z}{c}_{i\sigma }] \\ +\mathop{\sum }\limits_{i={N}_{y}-W+1}^{{N}_{y}}\mathop{\sum}\limits_{\sigma }[{U}_{2}{c}_{i\sigma }^{{{\dagger}} }{c}_{i\sigma }+{E}_{Z2}{\mu }_{i}{c}_{i\sigma }^{{{\dagger}} }{c}_{i\sigma }+{M}_{2}{c}_{i\sigma }^{{{\dagger}} }{\sigma }_{\sigma \sigma }^{z}{c}_{i\sigma }]$$
(1)

where \({c}_{i\alpha }^{{{\dagger}} }\)(\({c}_{i\alpha }\)) is the electronic creation (annihilation) operator with the spin \(\sigma \,(\sigma =\uparrow \downarrow )\) at site i; \(\left\langle i,j\right\rangle\) and \(\left\langle \left\langle i,j\right\rangle \right\rangle\) run over all the nearest and the next-nearest-neighbor hopping sites. The first term describes the nearest-neighbor coupling of electrons with t = 2.7 eV. The second term denotes the modified Haldane model resulting in the antichiral edge state, which has been experimentally demonstrated25,26. The \({t}_{2}\) and \(\phi\) is set as 0.03 eV and \(-\pi /2\), respectively. For the modified Haldane model, \({v}_{ij}=1(-1)\) represents the counterclockwise (clockwise) hopping between sublattice A, while \({v}_{ij}=-1(1)\) represents that between sublattice B. The third and last terms are the side potentials, including the potential field U1,2, the staggered electric potential EZ1,2 with \({\mu }_{i}=\pm 1\) for A or B sublattice, and the exchange field M1,2. These side potentials are applied along the boundaries of the nanoribbon. \({\sigma }_{z}\) is the z component of the \(2\times 2\) Pauli matrix for the electron spin. The side potentials U and EZ can be induced by the gate voltages and the electrostatic potential effects of the substrate, such as SiC and hBN37. The M can be induced by the ferromagnetic insulators in the experiment. Experimentally, several groups have achieved local gate control of the electrostatic potential with nanoscale and hundreds of meV in nanoribbon-based devices38,39,40. A local exchange field with nanoscale on the 2D honeycomb lattices can be induced by the magnetic proximity effect with a magnetic insulator such as EuO41,42,43.

The low-energy effective Hamiltonian

In the continuum theory with the phase \(\phi =-\pi /2\), the low-energy Hamiltonian of the modified Haldane model with a uniformly applied external field (U, E, and M) in zHNRs can be expressed as28:

$${H}_{\eta }^{s}=\hslash {v}_{F}(\eta {\sigma }_{x}{k}_{x}+{\sigma }_{y}{k}_{y})+\eta {\lambda }_{MHM}{\sigma }_{0}+U{\sigma }_{0}+{E}_{Z}{\sigma }_{z}+sM{\sigma }_{0},$$
(2)

where \({v}_{F}\) is the Fermi velocity; \(\eta =+1(-1)\) represents the K (K’) valley. In the effective continuum model, this modified Haldane is given in the form of \(\eta {\lambda }_{MHM}{\sigma }_{0}\). For simplicity, \({t}_{2}\) in Eq. (1) is set as \({t}_{2}={\lambda }_{MHM}/3\sqrt{3}\)28. The \({\sigma }_{0}\)is the \(2\times 2\) identity matrix, the Pauli matrices \({\sigma }_{i}\)(i = x, y, z) represent the sublattice pseudospin, and s = 1(-1) represents the spin-up (down) mode. The corresponding energy dispersion is:

$${E}_{\eta ,s}=\eta {\lambda }_{MHM}+U+sM\pm \sqrt{{(h{v}_{F}k)}^{2}+{E}_{Z}^{2}}.$$
(3)

In the later discussion, Eq. (3) will be used to propose an interpretation for these edge states.

As shown in Fig. 1, the side potentials are applied along two boundaries of zHNRs with the same width of W = 8. Depending on the modulation requirements, the U, EZ, and M are applied separately or jointly along two boundaries of zHNRs.

The non-equilibrium Green’s function approach

For three-terminal devices, the transmission coefficients (Tij) from lead i to lead j is calculated by the non-equilibrium Green’s function formalism. In the spin-resolved case, it is expressed as follows44,45,46:

$${T}_{ij}^{\sigma }(E)=Tr[{{{{{{\boldsymbol{\Gamma }}}}}}}_{j}^{\sigma }(E){{{{{{\bf{G}}}}}}}^{R,\sigma }(E){{{{{{\boldsymbol{\Gamma }}}}}}}_{i}^{\sigma }(E){{{{{{\bf{G}}}}}}}^{A,\sigma }(E)].$$
(4)

where \({{{{{{\bf{G}}}}}}}^{R,\sigma }(E)\) and\({{{{{{\bf{G}}}}}}}^{A,\sigma }(E)\) are the retarded and advanced Green’s function with the spin \(\sigma\), respectively; \({{{{{{\boldsymbol{\Gamma }}}}}}}_{i}^{\sigma }(E)\,(i=1,2,3)\) is the spin-resolved linewidth function of lead i, indicating the coupling between the conductor region and lead i. The retarded (advanced) Green’s function is calculated as follows:

$${{{{{{\bf{G}}}}}}}^{R(A),\sigma }(E)={[{E}_{+(-)}{{{{{\bf{I}}}}}}-{{{{{{\bf{H}}}}}}}_{D}^{\sigma }-\mathop{\sum}\limits_{i}{{{{{{\boldsymbol{\Sigma }}}}}}_{i}^{R(A),\sigma }}(E)]^{-1}}.$$
(5)

where \({E}_{+}=E+i\eta ={[{E}_{-}]}^{\ast }\), with \(E\)and \(\eta\) representing the incoming electron energy and an infinitesimal positive number, respectively; \({{{{{\bf{I}}}}}}\)denotes the identity matrix; \({{{{{{\boldsymbol{\Sigma }}}}}}}_{i}^{R,\sigma }(E)={{{{\rm H}}}}_{D,i}{{{{{{\bf{g}}}}}}}_{i}^{R,\sigma }{{{{{{\bf{H}}}}}}}_{i,D}\) is the retarded self-energy matrix, with \({{{{\rm H}}}}_{D,i}\) and \({{{{{{\bf{H}}}}}}}_{i,D}\) representing the coupling matrix between the conductor and the lead i; \({{{{{{\bf{g}}}}}}}_{i}^{R,\sigma }\)is the retarded surface Green’s function of lead i, which can be calculated using the routine of Lopez-Sancho’s iterative method47. In section: Spin/charge current swither in the three-terminal device, the Hamiltonians of the conductor region are the same as Eq. (1), and the coupling between three leads and the conductor region is set as the first two terms of Eq. (1).

The local bond currents distribution

To investigate antichiral edge states in zHNRs and the electron transport details in the three-terminal device, the local bond currents were plotted in the lead and conductor region. The energy-dependent local bond current between sites i and j can be expressed as:48,49

$${J}_{ij}^{\sigma }(E)={H}_{ji}^{\sigma }{G}_{ij}^{ < ,\sigma }(E)-{G}_{ji}^{ < ,\sigma }(E){H}_{ij}^{\sigma }$$
(6)

where\({H}_{ij}^{\sigma }\) is the relevant matrix element of the conductor’s Hamiltonian; \({{{{{{\bf{G}}}}}}}^{ < ,\sigma }(E)\) is the lesser Green’s function in the energy domain, which can be expressed as:

$${{{{{{\bf{G}}}}}}}^{ < ,\sigma }(E)=-i{{{{{{\bf{G}}}}}}}^{R,\sigma }(E){{{{{{\boldsymbol{\Gamma }}}}}}}_{\alpha }^{\sigma }(E){{{{{{\bf{G}}}}}}}^{A,\sigma }(E)$$
(7)

Notably, Eq. (6) is related to the local bond current from the incidence of lead \(\alpha\).

In the following section, the impact of the side potentials on pristine antichiral edge states is studied. The transport property of the tunable antichiral edge states in the three-terminal device is also discussed. The widths of the upper and lower potentials are assumed to be the same (W = 8) for convenience, and the main conclusions are still valid when the W becomes different. The effectiveness is addressed in Supplementary Note 1. For a clear view of the band for the edge states, only a partial outline is displayed. In the following Figures, black, red, and blue curves (or arrows) highlight the band structures (or the edge states) for spin degeneracy, spin-up, and spin-down electrons, respectively. According to the different modulation requirements, the U, EZ, and M are applied separately or jointly along two boundaries of zHNRs. For example, if the value of the U is not displayed, U1 = U2 = 0. This law can also be applied to other cases.

Five possible antichiral edge states

As shown in Fig. 2, the original antichiral edge state is obtained based on the modified Haldane model17 in zHNRs. These edge states and counterpropagating associated bulk states are near the Fermi energy (zero energy), the range of which is defined by the black dashed line. Figure 2a shows the band structure, where the edge states propagate in the same direction on two parallel boundaries (Fig. 2a inset: the thin black arrows), and the gapless bulk states with counterpropagating modes (Fig. 2a inset: the thick black arrows). In addition, these edge states cross the Fermi energy (zero energy) represented by the black dot. According to Eq. (3), there are \(E=-{\lambda }_{MHM} \, < \, 0\) and \(E={\lambda }_{MHM} \, > \, 0\) for K’ and K valleys, respectively. Thus, the energy values in K’ and K valleys of the original edge states are of opposite signs. For the two-terminal system based on zHNRs, if both the leads and conductor are set to the modified Haldane model, the edge states can be obtained by calculating the local bond current distribution. Figure 2b shows the result of the local bond current distribution of the spin-up (down) edge states and spin degeneracy case, which is consistent with the edge state in Fig. 2a. In addition, the robustness of the antichiral edge states is investigated, and the results are presented in Supplementary Note 2.

Fig. 2: The band structure and local bond current distribution for pristine antichiral edge states.
figure 2

a The band structure. Inset: schematic diagram of corresponding edge states. b The local bond current distribution (E = 0.03 eV) for the pristine antichiral edge states. The black bands (arrows) denote the spin degeneracy case, and the red (blue) arrows indicate the spin-up (down) case. The other fixed parameters are: Ny = 40, W = 8, \({\lambda }_{MHM}=0.058t\) (relevant parameter of the modified Haldane model).

Full size image

Both edge states (spin-up and spin-down modes) are at the upper and lower boundaries of the zHNRs from pristine antichiral edge states. On this basis, five antichiral edge states can be proposed by removing the edge modes on the boundary of zHNRs. As shown in Fig. 3, Type-1 occurs when eliminating one of the edge states in the upper or lower boundaries. Type-2, Type-3, and Type-4 occur when two edge modes are removed from the boundary. For Type-2, the spin-up and spin-down edge states in the upper or lower boundaries are removed simultaneously. Type-3 and Type-4 are obtained by subtracting different and same spin edge states in the upper and lower boundaries, respectively. Similarly, Type-5 can be obtained when three edge modes are removed from the boundary of the nanoribbon. The counterpropagating bulk states of antichiral edges are marked by thick arrows, and the trivial bidirectional bulk states are not displayed18.

Fig. 3: Schematic diagram of the five possible antichiral edge states.
figure 3

The black arrows denote the spin degeneracy case, and the red (blue) arrows denote the spin-up (down) case. The thin and thick arrows represent the antichiral edge states and the counterpropagating bulk states, respectively.

Full size image

Five antichiral edge states have been proposed, and how to obtain these edge states by manipulating side potentials is described below.

Side potentials-tunable antichiral edge states

This section shows how to obtain the five antichiral edge states by modulating side potentials. As shown in Fig. 1, the side potentials are composed of potential field U, staggered potential field EZ, and exchange field M along the boundaries of zHNRs (W = 8). Each type has two or more cases, but only one case in each type is presented due to similarities.

As shown in Fig. 4a, the energy band of Type-1 reveals that the spin-up mode shifts to higher energy with the upper-edge eigenstate, which can be obtained with U1 = 0.2t and M1 = 0.2t. Three surviving edge states are present near the Fermi energy, and their range is defined by the black dashed line. The edge states and associated bulk states are marked by small black dots and green dots, respectively. From the local bond current distribution (illustration) and the probability distributions in Fig. 4b, c, it can be seen that the spin-up edge modes with positive velocity are only localized near the upper boundary of the ribbon. In contrast, the spin-down modes with positive velocity are localized on the upper and lower boundaries simultaneously. we have also discussed Fig. 4a in the presence of the intrinsic spin-orbit coupling (SOC) in the whole nanoribbons. The results show that the antichiral edge states can be induced as anisotropic and flat types. Afterward, anisotropic chiral edge states are induced with increasing SOC strength. These results are shown in Supplementary Note 3.

Fig. 4: The band structure, local bond current distribution and probability distribution for antichiral edge states.
figure 4

a The band structure of one case of Type-1 with U1 = 0.2t and M1 = 0.2t along the boundaries. Inset: local current distribution (E = 0.03 eV) and schematic diagram of corresponding edge states. b, c Corresponding probability distribution of edge states near the Fermi energy. d The band structure of zHNRs with the modified Haldane model under the external fields Ua = 0.2t and Ma = 0.2t. The black bands (arrows) denote the spin degeneracy case, and the red (blue) bands or arrows denote the spin-up (down) case. Other fixed parameters are the same as in Fig. 2.

Full size image

To further analyze the results obtained from Eq. (3), Ua = 0.2t and Ma = 0.2t are simultaneously applied to the entire zHNRs. As shown in Fig. 4d, the position of the spin-down edge states (defined by the black dashed line) has no change relative to the original edge states of the modified Haldane model, and the edge states cross the Fermi energy (zero energy). For the spin-up, however, the edge states are shifted to the higher energy, and the edge states no longer cross the Fermi energy (zero energy). This result can be illustrated by calculating the sign of energy values in K’ and K valleys. Due to the uniformity of the system, the corresponding energy in K’ and K Dirac points can be expressed as: \({E}_{K{{\hbox{'}}},s}=-{\lambda }_{MHM}+U+sM\), and \({E}_{K,s}={\lambda }_{MHM}+U+sM\). For the spin-up edge modes, \({E}_{K{{\hbox{'}}},\uparrow }=-{\lambda }_{MHM}+U+M=0.923{{{{{\rm{eV}}}}}}\) and \({E}_{K,\uparrow }={\lambda }_{MHM}+U+M=1.237{{{{{\rm{eV}}}}}}\). Thus, the energy values in K’ and K valleys of spin-up edge states share the same sign, indicating the edge states do not cross the Fermi energy (zero energy). For the spin-down edge modes, \({E}_{K{{\hbox{'}}},\downarrow }=-{\lambda }_{MHM}+U-M=-{\lambda }_{MHM} \, < \, 0\) and \({E}_{K,\downarrow }={\lambda }_{MHM}+U-M={\lambda }_{MHM} \, > \, 0\), suggesting no position change relative to the original edge states of the modified Haldane model.

Surprisingly, the approach used to understand the result of Fig. 4d is also suitable for analyzing the zHNRs applied on side potentials (Fig. 4a). Although it seems impossible to directly quantify the results obtained with side potentials applied on a finite width by Eq. (3), the qualitative analysis through Eq. (3) is effective, which will be explained later by numerical calculation. For the spin-up edge mode at the upper boundary of zHNRs, \({E}_{K{{\hbox{'}}},\uparrow }=-{\lambda }_{MHM}+{U}_{1}+{M}_{1} \, > \, 0\) and \({E}_{K,\uparrow }={\lambda }_{MHM}+{U}_{1}+{M}_{1} \, > \, 0\). Due to the non-uniformity of the system, \({E}_{K{{\hbox{'}}},\uparrow } < 0.923{{{{{\rm{eV}}}}}}\) and \({E}_{K,\uparrow } < 1.237{{{{{\rm{eV}}}}}}\). Thus, the energy values in K’ and K valleys of the spin-up edge state are the same sign that indicates the edge state does not cross the Fermi energy and is elevated to a trivial bulk state. For the spin-down mode at the upper edge, \({E}_{K{{\hbox{'}}},\downarrow }=-{\lambda }_{MHM}+{U}_{1}-{M}_{1} \, < \, 0\) and \({E}_{K,\downarrow }={\lambda }_{MHM}+{U}_{1}-{M}_{1} \, > \, 0\), which suggests that the position of the edge state has not changed from that of the original edge state. In addition, if the energy values in K’ and K valleys of the spin-down mode are the opposite sign, it indicates that the edge state crosses the Fermi energy (the edge mode stays near the Fermi energy). In other words, U1 need not be equal to M1. However, in our work, the specific case of U1 = M1 is considered to clearly show the result of Type-1. Because if U1 is not equal to M1, the simultaneous movement of the spin-up and spin-down energy bands may be dazzling. Similarly, the corresponding energy dispersion in K’ and K valleys of edge states at the lower boundary is expressed as \({E}_{K{{\hbox{'}}}} \, < \, 0\) and \({E}_{K} \, > \, 0\) since no side potentials are applied. Thus, at the lower edge, the edge modes are also unchanged: the two edge bands connecting K’ and K valleys across the Fermi level. In summary, the side potentials can shift one or more spin-polarized edge modes of the zHNRs out of the Femi energy region and retain other bands.

A natural question is how to understand that the qualitative analysis through Eq. (3) is valid in the system applying side potentials. Next, we will continue to use the result in Fig. 4a to show the effect of side potentials on the bands of edge states and the effectiveness of the qualitative analysis.

Figure 5a shows the band structure of the pristine antichiral edge state, with the illustration showing that no side potentials are applied to the nanoribbons. As the analysis in section: Five possible antichiral edge states, for K’ and K valleys, \(E=-{\lambda }_{MHM} \, < \, 0\) and \(E={\lambda }_{MHM} \, > \, 0\), respectively. Thus, the energy values in K’ and K valleys of pristine edge states are the opposite sign that indicates the edge state crosses the Fermi energy (zero energy).

Fig. 5: The variation of energy band structure with the potential width.
figure 5

a W = 0. b W = 4. c W = 8. d W = 16. e W = 20. f W = 40. The ribbon width Ny = 40 and is defined by the number of carbon atoms along the width direction. The fixed parameters are U1 = 0.2t and M1 = 0.2t.

Full size image

As shown in Fig. 5b, when potentials are applied on the upper boundary (W = 4 atoms), the band of the spin-up edge state in the upper boundary is greatly affected and shifts to higher energies. Thus, the side potentials can cause the spin-up edge state to exceed the Fermi energy. Moreover, \({E}_{K{{\hbox{'}}},\uparrow }\) and \({E}_{K,\uparrow }\) slightly increase as the edge-potential region extends to the middle of ribbons (Fig. 5b–e). Figure 5f shows the results of applying Ua = 0.2t and Ma = 0.2t simultaneously over the entire zHNRs, which has been analyzed in the result of Fig. 4d and will not be repeated here. The above findings show that the result in Figs. 4d, 5f can be obtained by increasing the width of potentials. In other words, the potentials uniformly applied on zHNRs can be divided into the upper boundary side potential, the middle potential and the lower boundary side potential. However, whether the edge state shifts and does not cross the Fermi energy depends on the side potential. We believe that the side potentials mainly affect the bands of the edge states. Therefore, although it seems impossible to directly quantify the results obtained with the potentials applied on a finite width by Eq. (3), the qualitative analysis through Eq. (3) is effective.

Type-2 is obtained by applying U1 = 0.2t or M1 = 0.2t, where the spin-up and spin-down modes are both removed from the upper boundary or lower boundary of zHNRs. The edge states near the Fermi energy and associated bulk states are marked by little black and green dots, respectively. The results of Fig. 6a, b correspond to U1 = 0.2t and M1 = 0.2t, respectively, and it is worth noting that their results are the same. The result of the local bond current distribution (illustration) shows that the spin-up and spin-down edge modes with positive velocities are localized near the lower boundary of the ribbon simultaneously.

Fig. 6: The band structure of one case of Type-2.
figure 6

a U1 = 0.2t. b M1 = 0.2t. Inset: local current distribution (E = 0.03 eV) and schematic diagram of corresponding edge states. The black bands (arrows) denote the spin degeneracy case, and the red (blue) bands denote the spin-up (down) case. Other fixed parameters are the same as in Fig. 2.

Full size image

The results of Fig. 6a, b can also be understood according to Eq. (3). When U1 is applied on zHNRs, the corresponding energy values in K′ and K valleys of the upper edge states (including spin-up and spin-down modes) are obtained and expressed as \({E}_{K{{\hbox{'}}}}=-{\lambda }_{MHM}+{U}_{1} \, > \, 0\) and \({E}_{K}={\lambda }_{MHM}+{U}_{1} \, > \, 0\), respectively. Thus, the energy values in K′ and K valleys of the upper edge states have the same sign that indicates these edge states do not cross the Fermi energy and are lifted. The corresponding energy values in K′ and K valleys of the lower edge states are expressed as \({E}_{K{{\hbox{'}}}}=-{\lambda }_{MHM} \, < \, 0\) and \({E}_{K}={\lambda }_{MHM} \, > \, 0\) since no side potentials are applied. Thus, the edge modes of the lower edge are also not changed. When M1 is independently applied on zHNRs, the corresponding energy values are expressed as \({E}_{K{{\hbox{'}}},s}=-{\lambda }_{MHM}+s{M}_{1}\) and \({E}_{K,s}={\lambda }_{MHM}+s{M}_{1}\). It can be obtained that \({E}_{K{{\hbox{'}}},\uparrow } \, > \, 0\), \({E}_{K,\uparrow } \, > \, 0\) and \({E}_{K{{\hbox{'}}},\downarrow } \, < \, 0\), \({E}_{K,\downarrow } \, < \, 0\). Thus, at the upper boundary, the energy in K′ and K valleys of spin-up (down) edge states have the same sign that indicates that the two edge states do not cross the Fermi energy and are shifted out of the Fermi energy range. For the edge modes originally existing at the lower boundary, \({E}_{K{{\hbox{'}}},\uparrow }={E}_{K{{\hbox{'}}},\downarrow }=-{\lambda }_{MHM} \, < \, 0\) and \({E}_{K,\uparrow }={E}_{K,\downarrow }={\lambda }_{MHM} \, > \, 0\); the position of the edge state has not changed from that of the original edge states. Thus, there exists a spin-degenerate edge current at the lower edge.

Similarly, Type-3 (Fig. 7a) can be obtained by applying M1 = 0.2t, M2 = 0.2t, and EZ = 0.2t simultaneously, Type-4 (Fig. 7b) can be obtained by applying U1 = 0.1t, U2 = −0.1t, M1 = −0.1t, and M2 = 0.1t simultaneously, and Type-5 (Fig. 7c) can be obtained by applying U1 = 0.2t, M2 = 0.2t, and EZ = 0.2t simultaneously. These results can also be understood according to the above analysis methods, which are not repeated here.

Fig. 7: The band structure of one case of Type-3, Type-4 and Type-5.
figure 7

a Type-3 with M1 = 0.2t, M2 = 0.2t, and EZ = 0.2t; b Type-4 with U1 = 0.1t, U2 = −0.1t, M1 = −0.1t, and M2 = 0.1t; c Type-4 with U1 = 0.2t, M2 = 0.2t, and EZ = 0.2t. Inset: local bond current distribution (E = 0.03 eV) and schematic diagram of corresponding edge states. The black arrow denotes the spin degeneracy case, and the red (blue) bands or arrows denote the spin-up (down) case. Other fixed parameters are the same as in Fig. 2.

Full size image

Spin/charge current switcher in the three-terminal device

By modulating side potentials, we obtain five types of antichiral edge states discussed above, where U, EZ and M were applied separately or jointly to the two boundaries of zHNRs depending on different modulation requirements. Next, we develop a spin/charge current switcher based on these edge states in a three-terminal system consisting of zHNRs. As shown in Fig. 8a, the three-terminal device includes Lead 1, Conductor, Lead 2 and Lead 3. The currents are incident from Lead 1 and finally transmitted into Lead 2 and Lead 3. Lead 1, Lead 2 and Lead 3 are set as pristine antichiral edge states, but the Conductor has the side potential-tunable antichiral edge mode. Five types of outputs can be achieved by the side potentials in the Conductor. Here, one case of Type-3 (Fig. 7a) is used as an example to discuss its output, and other cases are similar. Figure 8b, c show the results of transmission and local bond current, respectively. These results indicate that the spin-up and spin-down currents are separated and flow into the output leads when the edge state of the Conductor is set to Type-3 (Fig. 2), which corresponds to the result of Fig. 7a. The charge and spin currents can also be obtained when the edge state of the Conductor is set to Type-1. Thus, the above results show that the developed three-terminal device is a spin/charge switcher.

Fig. 8: Transmission spectra and local current distributions of the spin/charge current switcher.
figure 8

a Schematic of the three-terminal spin/charge current switcher. All leads are set as pristine antichiral edge states, and the Conductor is applied on side potential-tunable edge states. b Transmission spectrum of Type-3. c Corresponding local bond current distribution (E = 0.03 eV).

Full size image

Conclusions

In summary, based on the pristine antichiral edge states, we propose five antichiral edge states by considering permutation combinations. The pristine antichiral edge state has four edge modes, including two spin-up and two spin-down edge modes. Type-1 exists when one edge mode in the upper or lower boundary is eliminated. Type-2, Type-3, and Type-4 are obtained when two edge modes are removed from the boundary. Similarly, Type-5 is obtained when three edge modes are removed from the boundary of the nanoribbon. These antichiral edge states can be obtained by modulating the side potentials applied to the boundaries of zHNRs. The competition between \({\lambda }_{MHM}\),\(U\),\(M\), and \({E}_{Z}\), which leads to changes in the energy sign of K’ and K valleys of the edge states, can shift the spin-polarized edge modes out of the Fermi energy range, which disappears in the lower/upper edge-potential region. In addition, we also develop an excellent spin/charge switcher in the three-terminal device based on the side potential-tunable antichiral edge states. These results can be vital for future spintronic device designs. As a perspective of this work, we consider the effect of the side potentials on the Haldane model and obtain some preliminary results. In the next work, we plan to delve into this project.

Methods

All methods are included in the Results and Discussion section.