Drifting Faraday patterns under localised driving

Abstract

Physical systems undergoing spontaneous pattern formation are governed by intrinsic length scales that may compete with extrinsic ones, resulting in exceptional spatiotemporal behaviour. In this work, we report experimental and theoretical evidence that spatial nonuniformity sets Faraday-wave patterns in motion, which are noticeable in the zigzag and drift dynamics exhibited by their wave crests. We provide a minimal theoretical model that succeeds in characterising the growth of localised patterns under nonuniform parametric driving. Furthermore, the derivation accounts for symmetry-breaking nonlinear gradients that we show are the source of the drift mechanism, which comes into play right after the system has crossed a secondary bifurcation point. Numerical solutions of the governing equations match our experimental findings and theoretical predictions. Our results advance the understanding of pattern behaviour induced by nonuniformity in generic nonlinear extended systems far from equilibrium.

Introduction

Highly ordered replication of individual structures in patterns is generally related to the natural selection of an intrinsic length scale. This length is deeply rooted in the properties of the physical system supporting them, which can drastically differ. Patterns are frequently observed in nonequilibrium systems¹ and in very different contexts from the inanimate world, such as fluids, chemical reactions, magnetic textures, nonlinear optics, and granular layers^2,3,4,5. Often, most of the geometric and dynamic features of the patterns can be described by finding the link between the intrinsic length scale and the physical quantities in play. However, there is little understanding of how patterns may be affected if a second extrinsic length scale comes into play. This is a relevant question considering that systems are often driven into out-of-equilibrium states in limited regions of space, and the driving extent may compare to the intrinsic length scale of the system.

Standing gravity waves emerging on the free surface of a vertically vibrated fluid are one of the simplest examples of patterns in out-of-equilibrium systems. The vertical oscillation of the container has the effect of modulating the effective gravity. When the amplitude of such oscillations is above a certain threshold, one observes the spontaneous formation of a regular pattern of standing waves with a well-defined wavelength oscillating at half the driving frequency (parametric instability). These waves are known as Faraday patterns and were first reported in Faraday’s seminal experimental work on vertically vibrated fluid and granular layers^6,7. When the container is uniformly vibrated as a whole, Faraday patterns and localised structures support a rich assortment of spatiotemporal phenomena, such as pattern selection⁸, quasi-patterns⁹, alternating patterns¹⁰, supersquare patterns¹¹, oscillons¹², underlying streaming flows¹³, wavelength changing instabilities (Eckhaus instability)^14,15, turbulence generation^16,17, and complex dynamics of localised structures^18,19,20. However, the influence of nonuniform vertical vibration on the pattern dynamics²¹ remains a relevant open question that is puzzling due to the lack of suitable models.

In this work, we report the existence of drift instabilities in localised Faraday patterns induced at the surface of a fluid under a spatially nonuniform parametric drive. The counterintuitive effect of inducing a propagating phase in the system, even when the vertical vibration modulation is fixed in space, is an intriguing attribute and differs from other experimental realisations featuring special types of boundary conditions, such as annular channels^22,23,24. We show that such drift is entirely induced by the nonuniform nature of the vertical drive at the bottom of the fluid container and thus cannot be observed under uniform driving. We use the normal form theory to explain the observed drift through an amplitude equation for Faraday patterns under localised driving. We demonstrate that the evolution of the instabilities at the first order of nonlinearity is described by a quintic Complex Ginzburg-Landau equation with Weber-like and self-phase modulation terms in the form of nonlinear gradients. Such nonlinear gradients trigger drift instabilities through a spontaneous nonlinear symmetry breaking above a secondary bifurcation threshold.

Results

Drift instabilities in a vertically vibrated fluid

The experimental setup in Fig. 1a was suitably devised to study the spatiotemporal interactions of patterns under localised driving. Here, Faraday patterns, i.e., subharmonic standing waves induced by vertical vibrations, are sustained on the surface of a quasi-one-dimensional fluid of depth h = 20 mm in a container with a soft elastic bed. The free surface of the fluid is at y = 0 when at rest, and displacements of the surface from the equilibrium condition are described by the time-space dependent field η(x,  t) as shown in the Fig. 1d, e. The novelty of the setup is the way in which the system is forced. Instead of uniform vibrations, an array of linearly spaced pistons mechanically actuates on the soft bed (at y = − h), thus introducing localised vertical vibrations into the system. As detailed in the Methods, pistons are driven by a brushless motor through an array of rotating cams, which control the frequency and amplitude of oscillations of the set of pistons. For the bottom motion, we programmed a controlled oscillating Gaussian profile, $\exp \left(-{x}^{2}/2{\sigma }_{{{{{{{{\rm{i}}}}}}}}}^{2}\right)$, with a typical extrinsic length of injection L ~ 20 cm. The wavelength of the standing wave is related to L in a nontrivial way, but it is close to the uniform-forcing case, λ_n = L/nπ, where n is the number of visible antinodes on the stationary surface wave. The time-dependent part of the oscillatory drive is controlled in the laboratory by

$$\Gamma (t)={\Gamma }_{0}\cos (2\pi ft),$$

(1)

where f is the forcing frequency. The acceleration amplitude of the forcing Γ₀ can also be written as a function of the maximum bottom displacement a₀ and f.

Fig. 1: Experimental generation of localised Faraday patterns.

a Experimental setup for generating Faraday patterns in the surface of fluid under localised vertical vibrations. b Image received from the high-velocity camera. c Processed image with gamma manipulation, brightness manipulation and Gaussian filter. d Overlap of the processed image and detected free water surface η(x) at an arbitrary time t^*. e Spatiotemporal diagram of the free surface corresponding to a Faraday pattern η(x, t). f Modulus of $\tilde{\eta }(x,t)$ corresponding to the time envelope of the free surface oscillations.

To characterise the spatiotemporal patterns in our experiment, we recorded the fluid surface with a high-velocity camera (400 frames per second), as shown in Fig. 1b. The spatiotemporal data of the water level were obtained after several image-processing steps, including brightness and gamma corrections, resulting in a clear view of the liquid interface on the glass wall, as shown in Fig. 1c and d. Afterwards, a Gaussian filter with kernel size 3 × 3 pixels was applied. A Canny edge detector was used to find continuous edges in the image. For further analysis, the final data were stored as a discrete matrix η_ij representing the continuous water level η(x, t). A typical spatiotemporal diagram is shown in Fig. 1e. The temporal envelope of the pattern oscillations can be extracted by applying a Hilbert transform over time to the spatiotemporal data. Figure 1e shows a locally driven Faraday pattern for f = 14.8 Hz and Γ₀ = 0.613, and Fig. 1f is a spatiotemporal representation of the modulus of the Hilbert transform. The real part of the Hilbert transform relates to a stroboscopic view of the phenomenon at the frequency of the wave oscillation f/2.

At a fixed forcing frequency f = 14.8 Hz, a locally driven standing Faraday pattern with mode n = 6 forms above the threshold ${\Gamma }_{0}^{{{{{{{{\rm{f}}}}}}}}}=0.331$, as shown in Fig. 1e and f. By increasing the drive amplitude above ${\Gamma }_{0}^{{{{{{{{\rm{c}}}}}}}}}=0.613$, the pattern develops a zigzag motion, noticeable in the oscillations exhibited by the wave crests in the spatiotemporal diagrams of Fig. 2a. By further increasing the driving amplitude above Γ₀ = 0.691, we discovered drifting patterns and nonzero mean velocity in the system, as depicted in Fig. 2a. The drift superimposes with the zigzag motion and features the continuous annihilation and creation of modes at the opposite sides of the pattern. Such a drift of localised Faraday patterns is a nontrivial effect that has not been reported in the literature.

Fig. 2: Experiments of zigzag and drifting patterns.

a Typical behaviour of the drifting patterns in experiments with different drive amplitudes. b Measurements of the mean velocity 〈v〉 of the drifting patterns as a function of the drive amplitude Γ₀. The fit using Eq. (8) (without including noise effects) is shown as dashed lines, while the fit including noise is shown as a solid line. The inlet figure shows a power-law fit of the crest oscillation frequency as a function of the drive amplitude Γ₀. Error bars represent the mean of the standard deviation of measurements performed for the correspondent amplitude Γ₀ at the same frequency.

Both the drift velocity and zigzag frequency display a strong dependence on the drive amplitude. To characterise the dependence, we analysed the mean trajectory of the crests to compute the drift mean velocity as a function of Γ₀. Figure 2b shows the experimental measurements of the drift average velocity 〈v〉 for different values of Γ₀. Additionally, the frequencies of the zigzag motion were calculated and fitted to a power law, as shown in the inset of Fig. 2b. The curve fits the experimental observations for Γ₀ ≳ 0.676 well, especially when we consider the nonnegligible effect of unavoidable small additive noise, which is typical in experiments. Additive noise in bifurcations of emerging patterns²⁵ affects the most likely value of the mean drift velocity as follows:

$$\langle v\rangle =A\sqrt{\frac{1}{2}\left({\Delta }_{{{{{{{{\rm{D}}}}}}}}}+\sqrt{{\Delta }_{{{{{{{{\rm{D}}}}}}}}}^{2}+2\xi }\right)},$$

(2)

where Δ_D ≔ Γ₀ − Γ_c, Γ_c is the critical drive amplitude for the emergence of the drift velocity, and ξ is the noise intensity. Figure 2b shows the fitting curve using Eq. (2) in a solid red line, where the fitted parameter values are A = 2.463, Γ_c = 0.683, and ξ = 0.01. We observed agreement between the experimental measurements and the fit using Eq. (2).

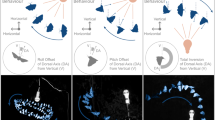
Figure 3 summarises our experimental results. In Fig. 3a, ${\Gamma }_{0}^{{{{{{{{\rm{f}}}}}}}}} \, < \, {\Gamma }_{0} \, < \, {\Gamma }_{0}^{{{{{{{{\rm{c}}}}}}}}}$, and the pattern is absolutely steady. Note that although the Gaussian driving profile in the bottom is centred around the origin, the maximum of the pattern is slightly shifted towards the negative values of x. Figure 3b, Γ₀ > Γ_c, illustrates a combination of a unidirectional drift with zigzag motion. A further increase in Γ₀ beyond the threshold of drift instability creates a complex convective state, as shown in Fig. 3c. In this latter case, the pattern dynamics exhibit convection towards both possible directions. We also noticed the emergence of branching phenomena, where a drifting maximum of the pattern breaks up into two crests momentarily travelling in opposite directions. We also observed intermittence in this regime: drift and branching ceased to occur for a short period of time, as evidenced in Fig. 3c for t ≳ 5 × 10⁵T. As explained below, the interplay of nonlinearities and the localised vertical drive plays a fundamental role in the underlying bifurcations behind these phenomena.

Fig. 3: Comparison between experiments and simulations of drifting patterns.

a–c Experimental evidence of the drift instability in a fluid subject to vertical and localised drive. The amplitude of the vertical drive is (a) Γ₀ = 0.56, (b) Γ₀ = 0.70, and (c) Γ₀ = 0.84. The detected level of the surface of the fluid is indicated by the colour scale. d–f Drift instability in the numerical simulations of the pdnlS equation (3) with μ = 0.45, α = 1, ν = 1.0, and σ_i = 16 for (d)γ₀ = 0.55, (e)γ₀ = 0.8375, and (f)γ₀ = 0.9000.

Modelling drift in localised Faraday patterns

It has been shown that pattern formation in the surface of a weakly viscous fluid in a trough with a large aspect ratio can be modelled by the parametrically driven nonlinear Schrödinger (pdnlS) equation³,

$${\partial }_{t}\psi =-(\mu +i\nu )\psi -i\alpha {\partial }_{xx}\psi -i{\left\vert \psi \right\vert }^{2}\psi +\gamma (x){\psi }^{* },$$

(3)

written here in dimensionless form. The pndlS model is simple yet can provide profound insights into the generic phenomenon of pattern formation in fluids and many extended nonequilibrium systems^{26,27,28,29,30,31}. In Eq. (3), pattern dynamics are described through a complex order parameter ψ that depends on space and time and is related to the displacement η of the free surface by $\eta (x,t)={{{{{{{\rm{Re}}}}}}}}\psi (x,t)\exp (i\pi ft)$. The parameter μ is the effective dissipation of the system, which accounts for both the fluid bulk viscosity and wave damping due to the friction with the walls³². The parameter α is related to a spatial coupling length, and the parameter $\nu =[{\left(f/{f}_{1}\right)}^{2}-1]/2$ is a small frequency detuning between the driving frequency and the natural frequency of the first transverse mode, ${f}_{1}={\left(2\pi \right)}^{-1}\sqrt{g\kappa \tanh \kappa }$, with κ = 2π/λ being the wavenumber of the fundamental mode³³.

Under uniform driving, the system destabilises when³ $\gamma \, > \, {\gamma }_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{h}}}}}}}}}=\mu$ through the spontaneous growth of a pattern for positive values of ν via a supercritical bifurcation^31,34 with leading eigenmodes of wavenumber ${\kappa }_{{{{{{{{\rm{c}}}}}}}}}=\pm \sqrt{\nu /\alpha }$. The effect of a localised profile in the vertical drive has been analysed²¹ by introducing the space-dependent Gaussian profile $\gamma (x)={\gamma }_{0}\exp \left(-{x}^{2}/2{\sigma }_{{{{{{{{\rm{i}}}}}}}}}^{2}\right)$, where σ_i gives the extension of the injection zone and γ₀ = Γ₀/4g is the dimensionless amplitude of the vertical drive. The linear stability analysis under a slightly localised Gaussian profile, i.e., ${\sigma }_{{{{{{{{\rm{i}}}}}}}}}\ll \sqrt{\alpha }$, shows that the envelope C₀ of the pattern has a discrete response given by the Gauss-Hermite polynomials²¹. Urra et al.²¹ showed that the threshold of the instability of the m-th Gauss-Hermite mode is given by

$${\gamma }_{0}^{(m)}=\mu +(2m+1)\frac{1}{{\sigma }_{{{{{{{{\rm{i}}}}}}}}}}\sqrt{\frac{\nu }{\alpha }},$$

(4)

and therefore, localised Faraday patterns appear at ${\gamma }_{0} \, > \, {\gamma }_{0}^{(0)}$ for m = 0.

In the lower panel of Fig. 3, we show the results from the numerical simulation of the pdnlS equation (3) for the given values of the parameters. Near the fundamental threshold of instability, the Faraday patterns are rather regular and highly ordered, as shown in Fig. 3d. The amplitude of the pattern increases with γ₀. However, at some value ${\gamma }_{{{{{{{{\rm{D}}}}}}}}}\in ({\gamma }_{0}^{(2)},{\gamma }_{0}^{(3)})$, a secondary instability emerges, and the pattern dynamics become complex for both the amplitude and phase. In Fig. 3d, we fixed γ₀ slightly below the secondary instability onset γ_D so the localised pattern is absolutely stable. Note that the maximum of the wave amplitude is shifted towards the left of the origin, as we observe in Fig. 3a. If γ₀ is slightly above the threshold γ_D, the unidirectional zigzag drift becomes evident, as shown in Fig. 3e. Experiments and simulations suggest the existence of a nonlinear symmetry-breaking mechanism in the system. Further increasing the drive amplitude γ₀, the system evolves towards a more complex state with a superposition of oscillations (suggesting an underlying Hopf instability), branching and drifting in both directions, as shown in Fig. 3f.

To provide a theoretical explanation of the observed behaviour, we characterised the dynamics of localised Faraday patterns near the fundamental threshold of instability through Eq. (3) using the method of normal forms (see Methods). Under this widely used formalism, a nonlinear system takes the “simplest”—or so-called normal—form preserving its essential features, i.e., dynamic behaviour, near a bifurcation point³⁵. To capture the dynamics close to the spatial instability, we introduced a bifurcation parameter $\delta ={\gamma }_{0}-{\gamma }_{0}^{(0)}$ and a small dimensionless parameter $\epsilon =\sqrt{\alpha }/{\sigma }_{{{{{{{{\rm{i}}}}}}}}}\ll 1$ characterising the length of the driving zone. With the condition ϵ ≪ 1 we assumed that the injection zone is large compared to the spatial coupling length, i.e., the system behaves as a weakly nonuniform system. We studied the behaviour of solutions around a Faraday pattern with critical wavenumber κ_c introducing a modulating complex amplitude function C(x, t)—an order parameter—, i.e.

$$\psi (x,t)=C(x,t){e}^{i{\kappa }_{{{{{{{{\rm{c}}}}}}}}}x}+c.c.+h.o.h.,$$

(5)

where h. o. h denotes the higher-order harmonics. Below the bifurcation point, ${\gamma }_{0} \, < \, {\gamma }_{0}^{(0)}$, one observes a stable uniform solution C = 0 (disordered phase). Such a uniform solution becomes unstable just above the bifurcation point, and C(x, t) has its own spatiotemporal dynamics modulating the underlying Faraday pattern (self-organised phase). At the leading order of nonlinearity, one obtains the following governing equation for the amplitude:

$${\partial }_{t}C=\frac{2\nu }{\alpha \mu }{\partial }_{xx}C+\left(\delta -\frac{\mu }{2{\sigma }_{{{{{{{{\rm{i}}}}}}}}}^{2}}{x}^{2}\right)C-i\frac{2}{\mu }\sqrt{\frac{\nu }{\alpha }}\left[3{\partial }_{x}\left({\left\vert C\right\vert }^{2}C\right)-2C{\partial }_{x}\left({\left\vert C\right\vert }^{2}\right)\right]-\frac{9}{2\mu }{\left\vert C\right\vert }^{4}C.$$

(6)

For nonextended systems, the homogeneous limit of Eq. (6) turns into the well-known normal form derived by Coullet et al.³⁴. The first two terms on the right-hand side of Eq. (6) are Weber-like terms that give the known linear limit of the nonuniform system²¹. At the modulational instability, the amplitude of the unstable Gauss-Hermite modes is saturated by the quintic nonlinearity given by the last term in Eq. (6).

Surprisingly, Eq. (6) displays unexpected terms proportional to ${\partial }_{x}\left({\left\vert C\right\vert }^{2}C\right)$ and $C{\partial }_{x}\left({\left\vert C\right\vert }^{2}\right)$. These are gradient-driven terms featuring self-phase modulation (SPM) effects in the slowly evolving modes of the localised Faraday patterns. Such terms are often introduced in the nonlinear Schrödinger equation to account for self-steepening effects and self-frequency shifting via stimulated Raman scattering^{36,37,38,39,40}. To our knowledge, this is the first time a complex quintic Ginzburg-Landau equation with Weber-like terms has been derived with these SPM terms appearing naturally from the weakly nonlinear analysis. We show below that such terms explain both the absolute and drift instabilities observed in our experiments of localised Faraday patterns.

In Fig. 4a, b, we compare the predictions of our normal form (6) and the pdnlS equation (3). In both cases, we numerically solved Eqs. (3) and (6) with no-flux boundary conditions. The initial conditions were given by small-amplitude random distributions of values in space for the real and imaginary parts of ψ and C. There is agreement between both models near the fundamental threshold of instability. Figure 4a and b confirm that the extension σ and the envelope profile of the Faraday pattern are well described by the normal form. Beyond the fundamental threshold, as one would expect, predictions from the normal form show some mismatch from the outcome of the pdnlS equation. Figure 4c shows the maximum amplitude of the Faraday pattern as a function of γ₀, and demonstrates that the normal form (6) describes the nature of the bifurcation of the pattern well, as explained in detail below.

Fig. 4: Comparison between theory and numerical simulations.

a, b Normalised amplitudes $| \tilde{\psi }|$ and ∣C∣ obtained numerically from Eq. (3) and Eq. (6), respectively, with μ = 0.45, ν = 1, α = 1, σ_i = 16, and (a)γ₀ = 0.67, (b)γ₀ = 0.8. c Normalised maximum amplitude of the saturated Faraday pattern, $| {C}_{\max }|$, as a function of γ₀, according to Eq. (7) (solid line) and the numerical solutions of pdnlS Eq. (3) (stars). Drift is observed above a critical value γ_D ≃ 0.837 indicated with a vertical dashed line.

The SPM terms in Eq. (6) are induced by nonlinear gradients, which reveal underlying complex phase dynamics. The gradient terms break the transverse reflection symmetry (x → − x) and dramatically affect the pattern selection in the system^41,42. Thus, the nonlinear gradients in Eq. (6) yield a nonlinear symmetry breaking where convection is characterised by an amplitude-dependent group velocity. In Fig. 5, we demonstrate examples of drift instabilities in the system obtained from numerical simulation of Eq. (6) for some given parameter values.

Fig. 5: Drift instabilities in the normal form.

Numerical results obtained from Eq. (6) with μ = 0.45, ν = 1, α = 1, and σ_i = 16. a–c A wave exhibiting absolute stability for γ₀ = 0.80. d–f Drift instability for γ₀ = 1.2. g–i A strongly nonlinear drift instability for γ₀ = 1.62.

In Fig. 5a, we show data for a run in which the system exhibited absolute stability with a pattern amplitude dominating over drifting and zigzag-like motion. In the absence of SPM terms, the localised Faraday pattern spontaneously grows centred around the Gaussian driving with width²¹ ${\sigma }_{{{{{{{{\rm{w}}}}}}}}}={\left(\sqrt{\nu/\alpha}{\,\sigma }_{{{{{{{{\rm{i}}}}}}}}}/\mu \right)}^{1/2}$. In Fig. 5a, we indicate with dashed lines the σ_w centred at the Gaussian driving for reference, evidencing the clear shift in ${{{{{{{\rm{Re}}}}}}}}(C)$ due to the SPM terms. The first frames of the simulation in Fig. 5b show that there is a transient drift towards the left as the pattern grows. However, the convection is too weak to overcome saturation, and the system rapidly becomes absolutely stable. Although the imaginary part of C displays a similar shift, the absolute value ∣C∣ exhibits no shift, and the phase lacks any spatiotemporal dynamics in this case, as shown in Fig. 5c.

Increasing the value of γ₀, we found for some value ${\gamma }_{{{{{{{{\rm{D}}}}}}}}}\in ({\gamma }_{0}^{(2)},{\gamma }_{0}^{(3)})$ that the propagation overcomes amplification and the system exhibits a nonlinear transition to drift instability. Figure 5d shows this scenario, in which a Faraday pattern displays a drift in the real part of its envelope. The real and imaginary parts of C exhibit the same drift, except for a phase factor. However, the absolute value ∣C∣ has no drift, as we show in Fig. 5e. Thus, the pattern drift is entirely due to the phase dynamics, as evidenced in Fig. 5f.

A further increase in γ₀ results in acceleration of the drift, as shown in Fig. 5g. The drifting wave also undergoes changes in both the frequency and wavelength. These observations confirm the nonlinear nature of the drift instability. Note that the drifting pattern becomes nonpropagating near the tails of the Gaussian drive, as highlighted in the inset of Fig. 5h. This pinning effect stems from the spatial nonuniformity of the vertical drive, which imposes smooth amplitude variations at the tails of the Gaussian drive and induces a boundary-like condition. When spatial variations in the pattern envelope become comparable to modulation amplitude, they could result in coupling between the slow scale of the envelope to the fast scale of the modulation of the underlying Faraday pattern, leading to pinning of the drifting wave⁴³. Moreover, the phase dynamics exhibit travelling waves inside the injection zone defined by the Gaussian drive, as evidenced in Fig. 5f and i. The mean velocity of such travelling waves decreases as γ₀ decreases.

Drift velocity characterisation

To gain further insight into the dynamic behaviour of the drifting localised patterns, we looked for an explicit expression for the average pattern velocity, 〈v〉. The key idea is that at the tails of the Gaussian driving, the normal form of Eq. (6) has an extra nonresonant term arising from the coupling between the slow-scale dynamics of C(x, t) and the fast scale of the modulation of the Faraday pattern. This effect has been observed in the pinning of patterns by a boundary-like condition⁴³. By calculating the normal form assuming that scale separation is no longer valid at the tails of the localised drive, we obtain the full amplitude equation,

$${\partial }_{t}C= \frac{2\nu }{\alpha \mu }{\partial }_{xx}C+\left(\delta -\frac{\mu }{2{\sigma }_{{{{{{{{\rm{i}}}}}}}}}^{2}}{x}^{2}\right)C-i\frac{2}{\mu }\sqrt{\frac{\nu }{\alpha }}\left[3{\partial }_{x}\left({\left\vert C\right\vert }^{2}C\right) -2C{\partial }_{x}\left({\left\vert C\right\vert }^{2}\right)\right] \\ -\frac{9}{2\mu }{\left\vert C\right\vert }^{4}C-\frac{3i}{2\sqrt{\nu }}{e}^{-i2{\kappa }_{{{{{{{{\rm{c}}}}}}}}}x}{C}^{2}{\partial }_{x}C,$$

(7)

where the last term proportional to $\exp (-i2{\kappa }_{{{{{{{{\rm{c}}}}}}}}}x)$ is nonresonant and has the form of a nonlinear gradient. Further calculations lead to a formula for the average velocity (see Methods)

$$\langle v\rangle =\sqrt{h-{h}_{{{{{{{{\rm{c}}}}}}}}}},$$

(8)

where h is a drift bifurcation parameter and h_c is a critical value. Thus, we conclude that for h close to h_c, the system exhibits a saddle-node bifurcation to drift instability with the pattern velocity increasing with the square root of h. In Fig. 2b, dashed lines indicate the fit of the velocity experimental measurements using Eq. (8). Note that neglecting noise effects on the bifurcation, we have ξ → 0 in Eq. (2), and we recover our theoretical prediction on Eq. (8), which is valid for the deterministic case.

Figure 6 shows the results from numerical simulations of the full normal form (7) for the given parameter values. Figure 6 shows that our full normal form captures the zigzag drifting and branching phenomena observed in the experiments. Figure 6a–c shows the real part of the order parameter C. The pattern in Fig. 6a exhibits a unidirectional drift with a zigzag-like motion for γ₀ = 0.3. Increasing the dimensionless drive amplitude to γ₀ = 0.37, we observe that the frequency of the zigzag-like motion increases, as shown in Fig. 6b, which is in agreement with our experimental observations in Fig. 2. The drift velocity also increases from Fig. 6a to Fig. 6b, as expected. Further increasing the value of γ₀, we observe the branching phenomenon shown in Fig. 6c. Figure 6d–f shows the corresponding dynamics of the real part of the complex field ψ, reconstructed from the numerical solutions of Eq. (7) through Eq. (5). The similarity between Fig. 6d, e and f with Fig. 3a–c, respectively, is noticeable.

Fig. 6: Zigzag drifting and branching phenomena.

Phenomena captured by the normal form with nonresonant terms. a–c Numerical simulations of Eq. (7) for ν = 0.25, μ = 0.15, and (a)γ₀ = 0.3, (b)γ₀ = 0.37, and (c)γ₀ = 0.38. d–f Real part of the complex field ψ reconstructed from (a), (b) and (c) through Eq. (5).

Self-phase modulation and nonlinear saturation

Here, we address the question of how drift instabilities impact our current understanding of the nonlinear saturation mechanism of localised patterns. This problem was first assessed in ref. ²¹ but without taking into account the SPM terms. Following previous calculations, we performed a multiple-scale analysis on Eq. (6) to investigate the role of the SPM terms. We found that SPM has no effect on the saturation of the fundamental mode close to the instability threshold. Assuming that the spatial and temporal scales of perturbations on the pattern amplitude are large, one obtains that the evolution of the amplitude D of the fundamental mode for ${\gamma }_{0} \sim {\gamma }_{0}^{(0)}$ is governed by

$$\frac{d}{dt}D=\delta D-\frac{9}{2\sqrt{3}\mu }{D}^{5},$$

(9)

in full agreement with previous results derived without the SPM terms. Equation (9) predicts the scaling law D ∝ δ^1/4, which has been previously verified in experiments²¹ and gives the signature of a supercritical bifurcation. Figure 4c shows the maximum stationary amplitude $| {C}_{\max }|$ of the Faraday wave as a function of γ₀: solid lines are predicted from Eq. (9), and symbols depict the results from the numerical simulations of the pdnlS Eq. (3). We conclude that the results of the multiple-scale analysis on the normal form (6) are in good agreement with both the numerical simulations of the pdnlS equation (3) and the Faraday-wave experiments.

Discussion

In ref. ²¹, we derived an amplitude equation describing the growth of nonlinear instabilities around the fundamental threshold ${\gamma }_{0}^{(0)}$, performing an appropriate expansion on the dispersion relation obtained from the WKBJ analysis. The resulting amplitude equation provides insight into how the nonlinear instability of the Gauss-Hermite modes gives rise to a saturated pattern. However, such an amplitude equation was not formally derived from the weakly nonlinear analysis.

Our findings unveil a connection between the drift instability of coherent structures and heterogeneity in general nonlinear systems far from equilibrium. In our system, such a connection is provided by the interplay between the wavelength of the Faraday pattern (an intrinsic length scale which depends mainly on the intrinsic and drive parameters of the system) and the spatial width σ_i of the Gaussian drive (an extrinsic length scale which is independent on the intrinsic parameters of the system and tunable). Indeed, the drift instabilities reported in this work are spontaneously induced by the spatial nonuniformity of the drive, i.e. a spatially featured non-drifting drive can generate drifting patterns. Under uniform drive, the amplitude of the Faraday pattern will be space-independent, and hence, the SPM terms causing the drift in Eq. (6) vanish. Note that only the nonuniform Weber-like term in Eq. (6) vanishes in the limit σ_i → ∞ (i.e., γ(x) → γ₀). However, although the SPM terms are not directly coupled to the Gaussian driving width σ_i, they are indirectly linked through the nonuniform profile of C(x, t) induced by the Gaussian drive. We believe this is the reason why such drift has not been reported in previous studies, which have been focused on uniformly accelerated systems. Recently, the role of spatial nonuniformity has often been identified as an important factor in nonlinear systems^{21,44,45,46,47}. Our theoretical insights on the underlying instabilities of localised patterns may be relevant in understanding other wandering localised structures observed in one and two-dimensional heterogeneous nonequilibrium systems. Moreover, drift instabilities in two dimensions open up possibilities for coherent structures arising from convection and multi-directed stream. It also remains the open question of how a spatial distribution of driving forces could interact with other self-driven drifting phenomena, such as those observed in walking droplets⁴⁸. Our findings open avenues of research, validating the use of SPM terms such as those naturally emerging in Eq. (6) to capture drift instabilities induced by nonuniform drives in different physical, chemical, and biological systems.

To summarise, we have shown that nonuniformity can trigger drift instabilities in the evolving amplitude of localised Faraday patterns. We performed an experimental study of Faraday waves on the free surface of a fluid under localised vertical driving. We show that above a secondary threshold of instability, the localised and nondrifting drive triggers drift instabilities in the surface patterns. We provide a theoretical explanation of the phenomenon based on a nonuniform version of the pdnlS equation as a simple model for parametric driven patterns. Under the assumption of a vertical drive modulated by a spatially spread Gaussian profile featured by an extrinsic length scale, we derived an evolution equation governing the slow dynamics of the pattern amplitude. The resulting normal form includes two unreported SPM terms that are linked to complex dynamics in the underlying patterns. We show that such terms trigger drift via nonlinear symmetry breaking induced by a nonlinear gradient. Numerical simulations of the pdnlS equation are also in agreement with both the theory and experimental data. These results extend our general understanding of nontrivial dynamical effects of nonuniformity in nonlinear extended parametric oscillators and how pattern selection can be dramatically affected by the nonuniform nature of the input of energy.

Methods

Experimental setup

We used a rectangular water basin, 15 mm long, 490 mm wide, and 100 mm deep, whose bottom centre consists of a rectangular soft elastomer made out of high-performance platinum cure liquid silicone Dragon Skin 10 medium 10A. The Gaussian drive, directly linked to $\gamma (x)={\gamma }_{0}\exp \left(-{x}^{2}/2{\sigma }_{{{{{{{{\rm{i}}}}}}}}}^{2}\right)$, is mechanically achieved in this waterproof soft zone through bottom vibrations. To control both the driving amplitude and frequency, we used a brushless servomotor with feedback (Model No. BLM-N23-50-1000-B) controlled with a DMC-40x0 motion controller from Galil Motion Control. The servomotor was coupled to a shaft to transmit the rotational motion to an evenly spaced array of 13 pistons (Δx = 16 mm), which were placed underneath the soft zone. Each piston holds linear bearings to maintain vertical motion and has a tiny roller in contact with a rotary cam fixed to the shaft, making the transmission of rotational oscillatory motion to linear oscillatory motion possible as shown in Fig. 7a. The key of the mechanism is the special design of the cams (see Fig. 7b) according to the specific formulae in Fig. 7c. The pistons are pushed with springs towards the cams to avoid detachment under peak accelerations. The setup resembles the mechanical transmission system of a music box, as shown in Fig. 1a, and allows to deform the bottom of the channel with a programmed spatial distribution.

Fig. 7: The cam-roller-spring-piston mechanism.

a Angular oscillatory motion displaces the piston to generate vertical oscillations. The special design of the cam (b) according to the formulae shown in the table (c), allows control of vertical displacement amplitude through angular amplitude in a range suitable for experiments (shaded region). The functions f and g smoothly close the cam edge, shown as the red curve in b.

For the experiment, the basin was filled up to 20 mm with a mixture of water and white ink for image detection purposes. For data acquisition, we used a Phantom VEO 440L camera controlled by PCC 3.5 software. The resolution of the images was 1280 × 252 pixels, and the acquisition time was approximately 94 s at 400 frames per second for every amplitude. Images were saved in greyscale to simplify the contour detection process.

Numerical methods

Numerical simulations of the pdnlS equation (3) and our normal form (6) were performed with no-flux boundary conditions (rigid impermeable wall) using a 401-point spatial grid with resolution dx = 0.25. We used finite differences of the second-order accuracy for the spatial derivatives, and time integration was achieved using a fourth-order Runge-Kutta scheme with time-step dt = 0.0001. To obtain the amplitude of the drifting localised Faraday patterns shown in Fig. 3, we first numerically obtained the pattern profile ψ(x, t) from the numerical simulation of Eq. (3). Then, the spatial complex amplitude C(x, t) was obtained from the Hilbert transform in space, $\widehat{\psi }(x,t)=(1/\pi )\int\nolimits_{-L/2}^{L/2}\,d\chi \,\psi (\chi ,t)/(x-\chi )$, which was computed at each time step of the numerical integration. When needed, the temporal complex amplitude is obtained via $\tilde{\psi }(x,t)=(1/\pi )\int\nolimits_{-T/2}^{T/2}\,d\tau \,\psi (\tau ,t)/(x-\tau )$. Both were obtained numerically with Matlabⓒ.

Normal forms

The theory of normal forms is a powerful method for the systematic construction of local, near-identity, and nonlinear transformations to simplify the equations describing the dynamics of complex nonlinear problems near a bifurcation point³⁵. We started by writing Eq. (3) in the form ∂_tΨ = LΨ + N, where Ψ ≔ (ψ_R, ψ_I), ψ ≔ ψ_R + iψ_I, L is a linear operator, and N is a nonlinear vector. We performed our transformations around a Faraday-pattern solution with critical wavenumber κ_c according to

$$\Psi =C(\eta ,t)\left(\begin{array}{c}1\\ 0\end{array}\right){e}^{i{\kappa }_{{{{{{{{\rm{c}}}}}}}}}x}+\mathop{\sum }\limits_{n=1}^{\infty }{{{{{{{{\bf{W}}}}}}}}}^{[n]}+c.c.,$$

(10)

where C(η, t) is a complex amplitude that varies as a function of η ≔ ϵ^1/2x, as described in the Results, and the vector functions ${{{{{{{{\bf{W}}}}}}}}}^{[n]}\in {{\mathbb{C}}}^{2},\,n\ge 1$ are higher-order corrections to be calculated. Assuming in Eq. (3) the scaling laws C ~ ϵ^1/4, δ ~ ϵ, ∂_t ~ ϵ and ∂_x ~ ϵ^1/2, one can expand the pdnlS equation at different orders of ϵ^1/4 and obtain a hierarchy of linear problems of the form

$${{{{{{{\mathcal{L}}}}}}}}{{{{{{{{\bf{W}}}}}}}}}^{[n]}={{{{{{{{\bf{b}}}}}}}}}_{n},$$

(11)

which can be solved for W^[n] only if b_n is in the image of the linear operator ${{{{{{{\mathcal{L}}}}}}}}$. According to the Fredholm alternative², at least one solution for W^[n] exists if $\exists !\left\vert {{{{{{{\bf{v}}}}}}}}\right\rangle \in \ker {{{{{{{{\mathcal{L}}}}}}}}}^{{{{\dagger}}} }$ such that 〈v∣b_n〉 = 0. Defining the inner product in the vector function space as

$$\langle {{{{{{{\bf{f}}}}}}}}| {{{{{{{\bf{g}}}}}}}}\rangle ={\kappa }_{{{{{{{{\rm{c}}}}}}}}}\int\nolimits_{{x}_{o}}^{{x}_{o}+1/{\kappa }_{{{{{{{{\rm{c}}}}}}}}}}dx{\left({{{{{{{{\bf{f}}}}}}}}}^{* }\right)}^{T}{{{{{{{\bf{g}}}}}}}},\quad \left\vert {{{{{{{\bf{f}}}}}}}}\right\rangle ,\left\vert {{{{{{{\bf{g}}}}}}}}\right\rangle \in {{\mathbb{C}}}^{2},$$

(12)

the Fredholm alternative yields a solvability condition to calculate W^[n] at each order of ϵ^1/4. Our normal form (6) is the solvability condition obtained at order ϵ^5/4.

Calculation of the drift velocity

We wrote our full normal form Eq. (7) in polar coordinates by setting $C=\rho \exp (i\theta )$. After removing the phase factor, the imaginary part reads

$${\partial }_{\tau }\theta =4{\partial }_{XX}\theta +\frac{8}{\rho }{\partial }_{X}\rho {\partial }_{X}\theta -4{\rho }^{2}\left(3{\partial }_{X}\rho +2| {\partial }_{X}\rho | \right)-\frac{3\mu }{\beta }\rho \left(\rho \sin \left[2\left(\beta X-\theta \right)\right]{\partial }_{X}\theta +\cos \left[2\left(\beta X-\theta \right)\right]{\partial }_{X}\rho \right),$$

(13)

with $\beta =\nu /\sqrt{\alpha }$, $X=x\sqrt{\nu /\alpha }$ and τ = 2μt. As depicted in Fig. 5f and i, the phase $\theta (x,t)=\arg (C)$ consists of two different superimposed dynamic behaviours: (i) a travelling wave with some phase velocity c = ω/k and (ii) a monotonically increasing one modulo 2π, such that $\arg (C)\in [-\pi ,\,\pi ]$ (following the conventional restriction of the inverse trigonometric functions to the principal branch). Based on this observation, we propose the ansatz $\theta (X,\,\tau )=\left[{\theta }_{c}(X-c\tau )+\chi (\tau )\right]\,{{{{{{\mathrm{mod}}}}}}}\,\,(2\pi )-\pi$, where θ_c and χ account for the travelling and increasing phase dynamics, respectively.

Close to the drift instability threshold, d〈θ〉_X/dt slowly evolves over time, and therefore, $\chi (\tau )\simeq {\langle \chi ({\tau }^{{\prime} })\rangle }_{\tau }$. Averaging Eq. (13) in both space and time, with ${\langle \theta (X,\tau )\rangle }_{X}={\sigma }_{{{{{{{{\rm{w}}}}}}}}}^{-1}\int\nolimits_{-{\sigma }_{{{{{{{{\rm{w}}}}}}}}}/2}^{{\sigma }_{{{{{{{{\rm{w}}}}}}}}}/2}dX\,\theta (X,\tau )$ and ${\langle \theta (X,{\tau }^{{\prime} })\rangle }_{\tau }=(\omega /T)\int\nolimits_{\tau }^{\tau +T}d{\tau }^{{\prime} }\,\theta (X,{\tau }^{{\prime} })$, one obtains

$$\frac{d\chi }{d\tau }=\frac{h}{2}-\frac{3\mu }{\beta }\left[{A}_{0}\cos (2\chi )-{B}_{0}\sin (2\chi )\right],$$

(14)

where ${A}_{0}={\left\langle \rho (\rho -1){\partial }_{X}{\theta }_{c}\sin \left[2\left(\beta X-{\theta }_{c}\right)\right]\right\rangle }_{X,\tau }$, ${B}_{0}={\left\langle \rho (\rho -1){\partial }_{X}{\theta }_{c}\cos \left[2\left(\beta X-{\theta }_{c}\right)\right]\right\rangle }_{X,\tau }$, and $h=-2{\langle {\partial }_{{\tau }^{{\prime} }}{\theta }_{c}\rangle }_{X,\tau }$. Finally, analytically solving Eq. (14), we obtain Eq. (8) with ${h}_{{{{{{{{\rm{c}}}}}}}}}={\left(6\mu /\beta \right)}^{2}({A}_{0}^{2}+{B}_{0}^{2})$.

Method of multiple scales

The method of multiple scales to study the effects of SPM in the Faraday pattern near the fundamental threshold of instability separates the time-scale dynamics of the different Gauss-Hermite modes controlling divergences in the perturbative developments⁴⁹. Just above the fundamental threshold of instability, the fundamental Gauss-Hermite mode, ${{{{{{{{\mathcal{G}}}}}}}}}_{0}$, dominates the amplitude dynamics of the Faraday pattern as higher-order modes decay²¹. As the bifurcation parameter is further increased, more Gauss-Hermite modes are excited. Each mode grows at its own growth rate or characteristic time. Assuming that the spatial and temporal scales of perturbations on the wave amplitude are large, the spatial derivative is rescaled by a small parameter ζ: ∂_x → ζ^1/2∂_x, and the time scales slowly evolve as T_i ≔ ζⁱt (with i = 1,  2,  …). Writing C as a perturbation series of the different time scales,

$$C(x,t):= \mathop{\sum }\limits_{k=1}^{\infty }{\zeta }^{k/4}{A}_{k}(x,{T}_{1},{T}_{2},\ldots ),$$

(15)

and using a similar expansion in the bifurcation parameter, δ = δ_o + ζδ₁ + ζ²δ₂ + …, results in a hierarchy of problems at each order of ζ^1/4, similar to Eq. (11) for A_k, k ≥ 1.

At order ζ^1/4, one obtains that A₁ is governed by the (time-independent) Weber equation²¹, whose general solution is given by a linear combination of the Gauss-Hermite modes with time-dependent coefficients D_n(T₁, …), n ≥ 0. In particular, the saturation of the fundamental Gauss-Hermite mode will be given by the time evolution of the first of such time-dependent coefficients, D_o(T₁, …).

At order ζ^5/4, in the analogous hierarchical equation (11), one obtains a vector b₅ that contains SPM terms. Given that the set of all Gauss-Hermite modes ${\{{{{{{{{{\mathcal{G}}}}}}}}}_{n}\}}_{n = 0}^{\infty }$ is a basis of the space, we write the functions A₂ and A₃ as the linear expansion

$${A}_{k}={D}_{o}^{(k)}({T}_{1}){{{{{{{{\mathcal{G}}}}}}}}}_{0}+\mathop{\sum }\limits_{n=1}^{\infty }{D}_{n}^{(k)}({T}_{1}){{{{{{{{\mathcal{G}}}}}}}}}_{n},\quad k=2,3.$$

(16)

However, near the threshold of instability of the fundamental mode, the modes ${{{{{{{{\mathcal{G}}}}}}}}}_{n}$ with n ≥ 2 are stable. Thus, the coefficients ${D}_{n}^{(k)}({T}_{1})$ for n ≥ 2 decay over time. Once the Faraday pattern has completely evolved, the maximum amplitude of the pattern is ${C}_{\max }\simeq {D}_{o}:= D$, and the functions A_k (k = 1, 2, 3) are even in space. Thus, using the Fredholm alternative, from symmetry arguments and the inner product (12), one obtains that the contribution of the self-phase modulation terms vanishes, and the solvability conditions lead to Eq. (7).