Introduction

It is widely believed that generic quantum systems isolated from their environments will evolve under their own dynamics until they reach an apparent equilibrium state that locally resembles the expectations of a thermal equilibrium state1,2. This expectation is seen as a stepping stone to reconcile predictions from statistical mechanics and those of basic quantum mechanics. One major exception to this rule is the case of low-dimensional quantum systems in the presence of random disorder. Non-interacting quantum systems in one dimension will entirely fail to thermalise due to any finite concentration of disorder3, and in recent decades it has been shown that interacting many-body systems appear to suffer the same fate4,5, leading to the phenomenon now known as many-body localisation (MBL)6,7,8,9,10,11,12. From a theoretical standpoint, MBL is now fairly well understood in terms of the emergence of an extensive number of conserved quantities known as (quasi-)local integrals of motion (LIOMs, also known as localised bits or l-bits) which can prevent many-body systems from reaching thermal equilibrium7,13. While phenomenological models based around the concept of l-bits have seen great success14,15, and there are several approaches that can map microscopic models onto effective l-bit models16,17,18,19,20,21,22,23,24,25,26, the l-bits themselves remain a strictly theoretical construct, inaccessible to any experimental probes. This is in contrast with the case of Anderson localised systems, where the exponentially localised l-bits can be straightforwardly related to the real-space decay of the single-particle states, which has been experimentally observed27.

In this work, we propose an experimentally feasible approach to measuring the actual real-space properties of local integrals of motion in many-body quantum systems using the entanglement negativity, a sensitive entanglement monotone that allows for the recovery of spatially resolved entanglement information. In this way, we accommodate the above missing link. Various quantities capturing correlations and entanglement, including the negativity, have been measured in recent experiments with ultra-cold bosons: ref. 28 has measured single-site and half chain number and configurational entanglement for a system subject to a quasi-periodic potential. These can be seen as a witness detecting the absence of thermalization, but they do not provide a length scale. The authors have also measured classical density-density correlations—akin to the proposal of ref. 29—showing exponentially decaying correlations, but this is a two-point classical measure, in contrast to the genuine entanglement between two half-regions considered here. Reference30 has studied a disordered system and has shown that the entanglement negativity can be directly measured. In a first experiment, the authors of the latter work prepared the system in a product state and measured the two-qubit entanglement of formation as they vary the separation between the qubits. While this setting is close in spirit to our approach, they have chosen a two-qubit setting, which is the only setting in which one can compute this quantity, so that the diagnostic time scale that allows observation of any spatial dependence is short. In a second experiment, the preservation of entanglement has been studied, departing from the approach taken here. Here, we demonstrate that the negativity itself gives direct access to a unique length scale that characterises the l-bits.

Results and discussion

Quasi-local operators

The question of whether many-body localisation is a well-defined stable phase in the thermodynamic limit remains unsettled, nevertheless systems showing MBL-like phenomenology for experimentally accessible times and system sizes appear to be well described by l-bit models, and their length scale is physically meaningful regardless of whether this description keeps holding for very long times and very large system sizes. Since the goal of the present work is to characterize the l-bits, we will now give precise definitions of what they are and the role they play in the dynamics.

Definition 1

(Quasi-local operators). An operator O on the lattice Λ is said to be quasi-local around a region R with localisation length ξ if for any region X ⊂ Λ containing R

$${\left\vert \left\vert O-\frac{1}{{2}^{| {X}^{c}| }}{{{{{{{{\rm{tr}}}}}}}}}_{{X}^{c}}(O)\otimes {{\mathbb{I}}}_{{X}^{C}c}\right\vert \right\vert }^{2}\le {\left\vert \left\vert O \right\vert \right\vert }^{2}\,K{e}^{-d(R,{X}^{c})/\xi }$$
(1)

where K > 0 is a universal constant, XC denotes the complement of X, \(d({X}^{c},R)={\min }_{x\in {X}^{c},r\in R}d(x,r)\) is the length of the shortest path from X to R, and ∥ ⋅ ∥ is the normalized 2-norm, \({\left\vert \left\vert O\right\vert \right\vert }^{2}={{{{{{{\rm{tr}}}}}}}}(O{O}^{{{{\dagger}}} })/{{{{{{{\rm{tr}}}}}}}}I\).

Intuitively, this definition says that most of the support of O is concentrated in and immediately around the region R, in the sense that if we truncate O to an operator only supported on a sphere centered at R, the resulting operator differs from O only by an error decaying exponentially in the radius of the sphere. Interestingly, the relatively loose sense of decay in 2-norm seems crucial, an insight that is often under-appreciated19,31. It is important to note that this is an abstract definition: it does not give operational advice on how to find those l-bits. What is more, even if they exist, they are by no means unique32. There could be “more local” l-bits than those given that still give rise to a complete set of l-bits. Either way, as is common, such l-bits serve as our definition for many-body localisation.

Definition 2

(Many-body localisation). A Hamiltonian

$$H=\mathop{\sum }\limits_{j=1}^{n}{\omega }_{j}^{(1)}{h}_{j}+\mathop{\sum }\limits_{j,k=1}^{n}{\omega }_{j,k}^{(2)}{h}_{j}{h}_{k}+\ldots$$
(2)

with real weights \(\{{\omega }_{j}^{(1)}\}\) and \(\{{\omega }_{j,k}^{(2)}\}\), is called many-body localised if it can be written as a sum of mutually commuting ([hj, hk] = 0 for all j, k) quasi-local terms hj, each centred around site j, and if \({\omega }_{{i}_{1},\ldots ,{i}_{n}}\le \omega {e}^{-| {i}_{1}-{i}_{n}| /\kappa }\) for some constant κ > 0, where i1 < i2 ⋯ < in.

In other words, a many-body localized Hamiltonian can be written as an effective model which is classical, in the sense that all Hamiltonian terms commute, and quasi-local, in the sense that the total coupling strength between two sites decays exponentially with distance.

Premise of the approach

When written in the basis that diagonalises the Hamiltonian, as in Eq. (2), these l-bits are strictly local objects, but in real-space they are quasi-local with exponentially decaying tails. In order to extract properties of l-bits from experiments, we shall consider the evolution of an arbitrary initial state under the following Hamiltonian dynamics as

$$\rho (t)={e}^{-it \, H}\rho {e}^{it \, H},$$
(3)

for times t ≥ 0. To simplify the notation, we will suppress the time argument for time t = 0. How can this time evolution be exploited to measure out real-space properties of the l-bits? Some intuition can be attained in the situation when the {hj} are strictly local. The terms that do not overlap do not contribute to the entanglement evolution at all. So in the end, it is the overlapping tails that will lead to entanglement growth.

Model

We will demonstrate our scheme numerically using the ‘standard model’ of MBL, namely the XXZ spin-1/2 chain with random on-site fields, while it should be clear that the approach taken would be applicable to any many-body localised model. Its Hamiltonian is given by

$$H={J}_{0}\mathop{\sum}\limits_{i}\left({S}_{i}^{x}{S}_{i+1}^{x}+{S}_{i}^{y}{S}_{i+1}^{y}+\Delta {S}_{i}^{z}{S}_{i+1}^{z}\right)+\mathop{\sum}\limits_{i}{h}_{i}{S}_{i}^{z},$$
(4)

with hi ∈ [ −d, d]. We shall set J0 = 1 as the unit of energy throughout, with Δ = 1.0 unless otherwise stated, and will use open boundary conditions. This model has been thoroughly studied and shown to exhibit a phase with anomalous thermalisation properties above a disorder strength of d ≳ 3.79, although recent work has suggested that the true phase transition in the thermodynamic limit could be at much larger values of d if it exists at all33,34,35,36,37.

The characteristic growth in time of the von Neumann entanglement entropy38,39 (or its correlation-based analogues29) mentioned above has been shown to be a good indicator of many-body localisation, able to distinguish it from single-particle Anderson localisation via the late-time logarithmic growth. Motivated by this, our aim in this work is to show that other entanglement measures which provide spatially-resolved information can not only distinguish many-body localisation from Anderson localisation, but can also allow direct quantitative measurement of the properties of many-body local integrals of motion.

Diagnostic entanglement quantity

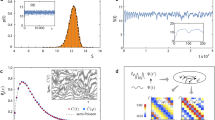
The main quantity of interest in this work is the logarithmic negativity, a measure of the entanglement between two subsystems of the spin chain, denoted A and B, separated by a distance r, which together with C constitutes the entire system (sketched in Fig. 1). It is defined as40,41,42,43

$${E}_{N}({\rho }_{A,B}(t)):= {\log }_{2}(\parallel {\rho }_{A,B}^{{T}_{A}}(t){\parallel }_{1}),$$
(5)

where \(\parallel O{\parallel }_{1}={{{{{{{\rm{tr}}}}}}}}| O|\) denotes the trace norm, \({\rho }_{A,B}(t)={{{{{{{{\rm{tr}}}}}}}}}_{\backslash \{A,B\}}[\rho (t)]\) is the time-dependent quantum state of subsystems A and B after tracing out all other lattice sites, and the superscript TA indicates the partial transpose with respect to subsystem A. This has been shown to be an entanglement monotone meaningfully quantifying entanglement42,43,44. In the following, we shall refer to this quantity simply as ‘negativity’. By contrast to the more commonly studied bi-partite von Neumann or Rènyi entanglement entropies which consider a single bi-partition between two connected subsystems, the entanglement negativity allows for a meaningful spatially resolved measure of mixed-state entanglement, as the two subsystems can be separated by an arbitrary distance r ≔ dist(A, B), a feature the von Neumann entropy cannot capture as a pure state entanglement measure. This measure can also be used to study the entanglement between subsystems of arbitrary size. However, for conceptual clarity, we shall mainly consider A and B to cover the entire chain except for a piece C with ∣C∣ = r + 1 separating A and B, as shown in Fig. 1. That said, the concept works as well for small regions A and B, as they are accessible in experiments and are discussed in the rigorous bounds. Numerical evidence is shown in Supplementary Note 5. The negativity has previously been investigated in the context of ground states of disordered spin chains45, quenches in random spin chains46, the many-body localisation transition47, and quench dynamics in the presence of a defect48. For clarity, in the following, we shall drop the explicit dependence of EN on the quantum state and instead use the notation EN(r, t) to represent the negativity associated to two subsystems separated by a distance r and a time t following a quench from an initial product state, emphasizing that this is indeed a spatially resolving entanglement measure.

Fig. 1: Division into subsystems and computation of negativity.
figure 1

a A sketch showing how a one-dimensional spin chain is partitioned into three subsystems. We are interested in computing the entanglement between subsystems A and B after subsystem C has been traced out, giving rise to a spatially-resolved entanglement measure. b Sketch of the initial quantum state in matrix product operator (MPO) form, made by taking the outer product of two matrix product state vectors. c Sketch of how the negativity is computed: the partial transpose of subsystem A corresponds to `twisting' the MPO legs while tracing out subsystem C corresponds to contracting the relevant MPO indices.

Full size image

A heuristic argument for why this quantity is relevant in our case can be given in the following manner. Reference13 has shown that the von Neumann entanglement entropy grows in time following a quench according to \({S}_{{{{{{{{\rm{ent}}}}}}}}}\propto \ln ({J}_{0}t/\hslash )\), once the system enters the late-time equilibration regime. If we wish to consider the entanglement negativity between two subsystems separated by a distance r, a reasonable starting assumption is that the negativity will vary in time according to the same \(\sim \ln (t)\) growth but will be exponentially suppressed in magnitude due to the spatial separation of the two subsystems, leading to an overall behaviour of \({E}_{N}\propto \exp (-r/\xi )\ln ({J}_{0}t/\hslash )\). We shall show that this ansatz is a good match for the numerical results. We also wish to emphasise that this logarithmic growth is characteristic of the interacting system and is entirely absent from Anderson-localised systems, meaning that the existence of this length scale is a distinct fingerprint of a many-body localised system.

Corroborating the reasoning with rigorous bounds

We see that Hamiltonians that are many-body localised in the sense of Definition 2 create entanglement at a rate that decays exponentially in the distance r = dist(A, B) between parts A and B, reflecting the exponential decay of the tails in quasi-local l-bits. In fact, not only this intuition can be made entirely rigorous, but, at the cost of slightly weakening the definition of quasi-locality, we are in the position to state precise upper bounds for the negativity for all times and distances.

Theorem 1

(Rigorous entanglement bounds). Let ρ be an initial product state. Let H be a many-body localised Hamiltonian as per Definition 2 with localisation length \(\xi \, < \, 1/(4\log (2))\) and \(2(1/\kappa -\log (2)) \, > \, 1/\xi\), consider three blocks A, C, B such that C divides A from B, with ∣C∣ = r + 1. The growth of the negativity of the state ρ(t) = e−itHρeitH restricted to the regions A, B is bounded as

$${E}_{N}(r,t)\le \min \{t\,O({e}^{-r/(2\xi )}),8\xi \,{\log }_{2}(t)-2r\}+O(1),$$
(6)

for times t ≥ er/(4ξ), while for t < er/(4ξ),

$${E}_{N}(r,t)\le t\,O({e}^{-r/(4\xi )}).$$
(7)

We hence find a short time behaviour signifying a linear growth in time, a cross-over regime governed by the correlation length, and a logarithmic growth for long times. These bounds—interesting in their own right and complementing and refining those of ref. 49—are perfectly compatible with the above numerical assessment. In Supplementary Note 8, we state details of the proof of the bound that makes extensive use of the precise form of the tails of the l-bits. Based on our numerical results, we expect that our assumptions on the localisation length and the definition of quasi-locality can be relaxed without affecting the result. We also note that the observed ξ − dependence of the late time decay of the entanglement with the size of C is not visible in this bound, though we expect that it can be refined to show this.

Numerical results

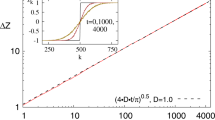
We first discuss qualitatively the results for the growth of the entanglement negativity with time for various different distances r, as shown in Fig. 2a) for a disorder strength d = 8.0 (deep in the localised phase), where we find that indeed the negativity grows logarithmically with time at late times. Results for further disorder strengths, system sizes, and subsystem sizes are available in Supplementary Notes 2, 3, 4 and 5. At short times, the negativity is dominated by diffusive transport on length scales shorter than the localisation length. At large distances r, the negativity remains close to zero until a time exponentially large in r, which can be used to define a ‘light cone’ that characterises the spreading of the entanglement negativity, shown in Fig. 2b. The three lines indicate when the negativity grows above a threshold ε ∈ {0.0001, 0.001, 0.005}, mapping out an approximately logarithmic light cone. As the negativity outside of this length cone is exponentially small, in the following analysis, we restrict ourselves to space-time coordinates (r, t), which are within the light cone. The existence of this light cone means that we gain only diminishing returns by going to larger system sizes: although we are able to separate the subsystems by a larger value of r, the evolution time required to obtain meaningful entanglement scales exponentially in r, which incurs a large computational cost for large systems and quickly becomes prohibitive.

Fig. 2: Behaviour of entanglement negativity in time and space.
figure 2

Results showing the growth of the negativity EN(r, t) with time for different distances r. Data is shown for a system size L = 24 and a disorder strength d = 8.0, averaged over Ns = 100 disorder realisations. a The dynamics of EN(r, t) following a quench from a Néel state, showing the logarithmic growth at late times. The circular markers are the raw data points, while the solid lines are a smoothed guide to the eye. The error bars indicate the standard error in the mean. We note that these error bars show agreement on average between the various disorder realizations, but they are not fully statistically independent errors, as would be expected in an experiment where each data point would come from a different run. b The full dynamics of EN(r, t), reflecting the logarithmic `light cone'. Each circle maps the point where the negativity grows beyond the corresponding threshold ε and the lines are linear fits. c By extracting the behaviour of \({E}_{N}(r,{t}^{* })\propto \exp (-r/\xi )\) at fixed times t* [dashed vertical lines in a, horizontal lines in b], we can extract a well-defined length scale ξ(t), which depends only weakly on time. The solid lines indicate the fits to the data points which are used to extract the l-bit length scale, demonstrating convergence at late times.

Full size image

In the late-time logarithmic growth regime, where the dynamics are dominated by the quasi-local nature of the l-bits, we extract the value of the negativity at a given time t* following the quench from an initial Néel state and plot it versus the subsystem separation r. We show this in Fig. 2c for several different choices of time t* [indicated by the dashed lines in Fig. 2a]. The data points form a straight line (on a logarithmic scale), and at late times the gradient of the line does not strongly change with the choice of time t*, appearing to saturate at a fixed value (although the y-axis offset will, of course, continue to increase in time). Further details are available in Ref. Under the assumption that the negativity decays exponentially with distance like \({E}_{N}(r,{t}^{* })\propto \exp (-r/\xi )\), we can perform a linear fit to the data shown in Fig. 2c and extract a well-defined length scale ξ which characterises the spatial extent of the l-bits. The results are shown in Fig. 3, where we find that the length scale ξ exhibits monotonic decay with increasing disorder strength, as expected. Note that no assumptions are involved other than the exponential decay of the negativity with distance at some fixed time t*: the resulting length scale is an emergent property of the many-body system. This assumption does not hold in the delocalised phase, where the entanglement does not enter a regime of logarithmic growth. We can further compare the length scale extracted from our procedure with the l-bit decay lengths computed using the established numerically exact method of ref. 19, using the definition of quasi-locality from Eq. (1). We find excellent agreement between the entanglement-based length scale and the l-bit localisation length obtained independently from this method, confirming that the length scale probed by the negativity is the localisation length of the l-bits.

Fig. 3: Extracted l-bit length scale.
figure 3

The characteristic l-bit length scale ξ extracted from the entanglement negativity at time t* = 500, shown in blue for L = 24 with Ns ∈ [50, 100] disorder realisations and various values of the disorder strength d. Error bars indicate the fit error and are roughly the same size as the plot markers. Orange lines mark the localisation length obtained through exact diagonalisation following ref. 19. For further details on calculating the localisation length using exact diagonalisation, see Supplementary Note 7. The black line indicates the localisation length of the corresponding Anderson-localised system, obtained by directly diagonalising the Hamiltonian in the non-interacting limit (Δ = 0), for a system of size L = 128 with Ns = 10000.

Full size image

For comparison, we also indicate the corresponding localisation length of an Anderson localised system, here obtained by directly diagonalising the Hamiltonian with Δ = 0 (following a Jordan-Wigner transform into the fermionic representation). We compute the eigenvectors of the Hamiltonian in the non-interacting setting, which decay in real space as \(\exp (-r/\xi )\)50, average over disorder realisations and extract the localisation length ξ from a least-squares fit. The length scale extracted from the TEBD data behaves in a qualitatively similar manner to the single-particle localisation length but is always larger, confirming that we are not measuring single-particle properties but are indeed extracting a genuinely many-body feature of the system. In the delocalised phase, our assumed form of the negativity is no longer valid, and as such, the method cannot extract a reliable length scale.

We also note that the entanglement negativity is not the only entanglement measure which may be used in this way: any spatially-resolved entanglement probe should behave similarly. In Supplementary Note 6, we demonstrate that the mutual information also gives consistent results.

Conclusion

In this work, we have outlined an experimentally feasible procedure for measuring local integrals of motion based on their contribution to the slow growth of the negativity at long times following a quench from an arbitrary initial state. We have demonstrated that the length scale which we obtain from this procedure, which characterises the l-bits, is in good agreement with that obtained using other theoretical methods in the literature. The crucial advantage is that our scheme is experimentally tractable, unlike other purely theoretical/numerical methods, which cannot be verified in real experiments. It would be extremely interesting to apply this method to other scenarios where many-body localisation is believed to exist, such as in disorder-free systems and two-dimensional models, in order to see if well-defined length scales based on the spreading of entanglement may still be extracted in these situations. This work paves the way for the application of spatially-resolved entanglement probes to phenomena in quantum simulation beyond many-body localisation, where such methods may be able to provide valuable insight into emergent length scales associated with other types of quasi-particles.

Methods

We compute the negativity using time-dependent matrix product state simulations – an instance of a tensor network method51—implemented in the Quimb package52 using the time-evolving block decimation (TEBD) algorithm to perform the evolution53,54, with the system initially prepared in a Néel state. We use system size L = 24 with a maximum bond dimension of χ = 192. We perform the time evolution using a maximum time step dt = 0.05, at each step discarding singular values smaller than ϵ = 10−10. We have checked that the results are well-converged. Detailed benchmarks are shown in Supplementary Note 1. Our TEBD results are compared against l-bit length scales obtained using exact diagonalisation, following ref. 19.

The negativity can be computed straightforwardly from a matrix product state (MPS) representation55. The state vector can be turned into a matrix product operator (MPO) (sketched in Fig. 1) representing the quantum state by considering vectors and dual vectors represented as MPS. The partial transpose can be computed by ‘twisting’ the legs of the MPO tensors, while the partial trace over subsystem C can be performed by contracting the free indices of the MPO tensors in this subsystem. At long times, the negativity should saturate at a value controlled by the size of the subsystems, and at any time t < ts (where ts is the saturation time), the negativity should satisfy the hierarchy EN(r1, t) < EN(r2, t) for any two distances r1 > r2.