Light-wave control of correlated materials using quantum magnetism during time-periodic modulation of coherent transport

Abstract

Light–wave quantum electronics utilizes the oscillating carrier wave to control electronic properties with intense laser pulses. Without direct light–spin interactions, however, magnetic properties can only be indirectly affected by the light electric field, mostly at later times. A grand challenge is how to establish a universal principle for quantum control of charge and spin fluctuations, which can allow for faster-than-THz clock rates. Using quantum kinetic equations for the density matrix describing non–equilibrium states of Hubbard quasiparticles, here we show that time–periodic modulation of electronic hopping during few cycles of carrier–wave oscillations can dynamically steer an antiferromagnetic insulating state into a metalic state with transient magnetization. While nonlinearities associated with quasi-stationary Floquet states have been achieved before, magneto–electronics based on quasiparticle acceleration by time–periodic multi–cycle fields and quantum femtosecond/attosecond magnetism via strongly–coupled charge–spin quantum excitations represents an alternative way of controlling magnetic moments in sync with quantum transport.

Introduction

The advent of intense phase-coherent mid-infrared (MIR), terahertz (THz), and attosecond laser pulses with well-characterized temporal profiles opened a promising direction for achieving coherent control of quantum materials during sub-oscillation-cycle timescales^{1,2,3,4,5,6,7,8,9}. During a single cycle of coherence oscillations, quasi-stationary states (e.g., Floquet) have not yet been reached and relaxation is reduced. In quantum materials, emergent phenomena arise from strong couplings between electronic, spin, and lattice degrees of freedom^10,11,12,13. Adiabatic tuning of such microscopic interactions, by applying, for example, high pressure and magnetic or electric fields, is an established method for controlling the phase diagram of quantum materials. However, such static perturbations affect simultaneously different materials properties, which acts against the desirable quantum control and selectivity. Ultra-short laser fields, on the other hand, provide nonequilibrium means of manipulating structural and electronic properties. Of main interest for this paper is that nonlinear ultrafast processes initiated by coherent photoexcitation can dynamically steer quantum materials to nonequilibrium states that may not be accessible via quasi-equilibrium pathways^{3,5,6,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40}. Unlike for photoexcitation at high optical frequencies, where relaxation of high-energy photocarriers masks the quantum dynamics due to strong coupling to the bath, multicycle driving of quantum systems by intense THz or MIR laser fields can achieve nonadiabatic quantum tuning^{1,3,4,6,25,41,42,43,44,45,46,47}. For example, THz/MIR laser electric fields can act as an oscillating force that accelerates electrons in controllable trajectories during cycles of carrier-wave oscillations^{1,3,4,25,41,42}, or be used to control the phase of the many-electron wavefunction^3,25,48,49. In this way, coherent electronic transport can drive quantum systems into metastable or pre-thermalized phases^{3,21,24,25,50,51} and control phase transitions⁹. At the same time, in the absence of a direct light–spin interaction, magnetic properties can only be affected indirectly by the laser electric field. Recent experiments, however, have revealed femtosecond quantum magnetism^5,33, attosecond coherent magnetism², and femtosecond spin–orbit torque coherent dynamics^43,52,53,54, among other ultrafast light-induced spin effects^55,56. Such experimental results suggest that magnetic properties can be manipulated during oscillations of a time-periodic driving electric field^2,55,57. Given the currently available multicycle intense laser pulses, a better understanding of driven electron spin dynamics during non-dissipative sub-cycle timescales is needed.

Here, we investigate theoretically the hypothesis that light-wave-periodic modulation of electronic hopping between atomic sites occupied by noncollinear local spins can be used to coherently control magnetic states and phase transitions prior to the establishment of quasi-stationary states^1,2,5,9,25. Our focus is on the role of quantum fluctuations of a highly responsive background of local spins that interact strongly with itinerant electron spins. We investigate, in particular, the role of strong electron–magnon couplings^{5,33,58,59,60,61} during light-driven coherent hopping of electrons. By introducing Hubbard operators⁶² to describe electron quasi-particles strongly coupled to the local spins, we treat spin quantum fluctuations in the limit of strong (infinite) on-site magnetic exchange interaction. By deriving quantum kinetic equations of motion for the density matrix of such Hubbard quasi-particles, we develop a generally applicable model for describing the transient quantum state that evolves in time from a noncollinear spin state driven by a few-cycle bias laser field. The latter dynamics is determined by strongly coupled charge and spin quantum excitations driven by ultrafast modulation in time of interatomic electronic hopping amplitudes. Rather than adopting a quasi-stationary Floquet picture, here we calculate the nonadiabatic time evolution of the quantum state during cycles of oscillation (i.e., prior to the development of quasi-stationary states) for short relaxation times typical in many materials. We truncate the density matrix hierarchy introduced by strong local correlations by using a generalized mean-field approximation. The latter constrains the electronic motion to the lowest Hubbard band^62,63. By obtaining the light-driven spin and charge coherent local populations and intersite coherences and by using them to calculate the total energy as a function of lattice displacements Q_i, we find three main nonequilibrium effects: (i) a more homogeneous spatial electronic distribution develops due to light-driven quantum transport assisted by quantum canting of an antiferromagnetic (AFM) local spin background; (ii) a transient magnetization develops simultaneously with coherent electronic transport as a result of light-induced modulation of the AFM-ordered core spin background; and (iii) a light-induced change in the total energy minimum towards undistorted lattice, Q_i = 0, develops during few cycles of oscillations. Our model may be used to implement coherent control experimentally, for example, by tailoring the laser field temporal profile to obtain the desired current determined by intersite electronic coherences^3,25,64.

Results

To demonstrate our proposed light-wave control scheme, we describe the sub-oscillation-cycle coherent nonlinear response of an AFM insulating state to time-periodic modulation of the electronic hopping amplitudes during few oscillation cycles. For this, we consider a general model that describes local correlated configurations on a lattice. We assume that such multielectron/multiatom configurations on different sites are coupled by coherent hopping of an electron that interacts strongly with the local spins while conserving total spin. We calculate the coherent time evolution in response to such hopping amplitude time modulation. While numerical results were obtained by using as an example a complex charge-exchange (CE)-type AFM (CE-AFM) unit cell relevant to the quantum femtosecond magnetism experiments of refs. ^5,33, our proposed paradigm of light-wave quantum control presents a more general strategy for tailoring quantum materials properties during coherence oscillations⁶.

Model

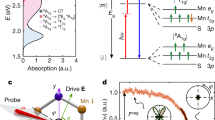
The proposed paradigm of light-wave control applies to a general Hamiltonian H(t) = H_local + H_hop(t) that can be split into two parts: local interactions, H_local, and electronic hopping, H_hop(t) (see “Methods”). We assume ultra-short modulation of H_hop(t) from equilibrium, with few cycles of time oscillations during the ~100 fs duration of the laser pulse. For example, such carrier-wave time modulation can arise from the direct coupling of the electromagnetic vector potential, which for tight-binding Hamiltonians is described by the standard Peierls substitution (see “Methods” and Supplementary Note 1). Similar few-cycle time modulation can also arise from lattice coherence oscillations⁶ and THz dynamical symmetry breaking^3,25,65. The strong spin interactions of interest (see “Methods” and Supplementary note 1) are part of H_local and include a local ferromagnetic (FM) interaction, −J_H∑_iS_i⋅s_i, between the itinerant electron spin-1/2 (s_i) and the localized electron spin −S (core spins S_i). To break the symmetry and introduce a preferred magnetization direction during time evolution, we include a weak magnetic field. To separate the quasi-equilibrium spin directions from quantum spin dynamics, we work in the local coordinate systems with z-axis along the directions defined by (classical) spin canting angles θ_i. We solve quantum kinetic equations of motion (see Supplementary Note 1) to calculate the spin deviations from θ_i driven by H_hop(t) (“Methods”). To describe the strong local (on-site) correlations, we consider a basis of N_e electron ($\left|im\right\rangle$) and N_e + 1 electron ($\left|i\alpha M\right\rangle$) eigenstates of H_local at each lattice site i (“Methods”). We assume that these local configurations are eigenstates of the core spin S_i and the total spin J_i = S_i + s_i, respectively. α labels the different N_e + 1-electron local configurations (e.g., different multiatom and orbital configurations, different Hubbard bands, etc.). Coherent electronic hopping from site i to site j results in N_e + 1 → N_e transitions at site i and N_e → N_e + 1 transitions at site j between the above local configurations (as illustrated in Fig. 1a). To describe the strong local coupling of the spin and charge excitations, we introduce composite fermion quasi-particles created by Hubbard operators⁶². The latter create transitions $\left|im\right\rangle \to \left|i\alpha M\right\rangle$ with excitation energies ${\varepsilon }_{\alpha \sigma }^{Q\theta }(i)=-{J}_{\mathrm{H}}S-\sigma {\mu }_{\mathrm{B}}{B}_{\mathrm{ext}}\,\cos\, {\theta }_{i}-{E}_{\alpha }^{\mathrm{JT}}{Q}_{i}$, where σ = ±1 (“Methods”). We assume an AFM spin configuration here, θ_i = 0, π. ${E}_{\alpha }^{\mathrm{JT}}$ describes to linear order the dependence of the quasi-particle energy on the coherent lattice displacement Q_i. We also assume two local configurations α per site, which are split in energy due to, for example, Jahn–Teller (JT) electron–lattice coupling, Q_i ≠ 0. For example, in the case of the CE-type AFM charge-ordered (CO) and orbital-ordered (OO) phase whose femtosecond magnetic response was studied experimentally in insulating Pr_0.7Ca_0.3MnO₃ (PCMO) manganites^5,33, α may correspond to the different e_g orbitals that diagonalize H_local, for example, x² − y²/3z² − r², 3x² − r²/y² − r², or 3y² − r²/x² − r² on different sites⁶⁶. More generally, the unit cell of manganites consists of Mn + O local configurations (α) analogous to the Cu + O configurations in the cuprates⁶⁷, which are split in energy by JT and strong Coulomb local interactions⁶⁷ and justify the use of generalized tight-binding models such as the one considered here⁶². In our model, Q_i = Q_B (bridge sites) or Q_i = 0 (corner sites) leads to an energy gap between the electronic configurations on neigboring sites on the same plane. We derive quantum kinetic equations for the density matrix ρ that describes local populations and intersite coherences of the local electronic configurations (see “Methods” and Supplementary note 1). We then solve these equations of motion to describe the adiabatic and nonadiabatic time evolution of the quantum state driven by time modulation of intersite coherent hopping amplitudes.

Fig. 1: Time evolution of an antiferromagnetic state driven by time-periodic ultra-short modulation of the intersite hopping amplitudes V(t).

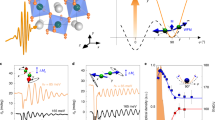
a Schematic of the antiferromagnetic configuration used in our numerical calculation. The complex unit cell consists of zig-zag ferromagnetic chains with interchanging corners (red circle) and bridge (blue circle) lattice sites. Neighboring chains are antiferromagnetically coupled in the plane and stacked in antiferromagnetically coupled identical planes along the z-axis. Red arrows indicate the electronic hopping between antiferromagnetic sites that triggers the spin quantum dynamics of main interest. Time evolution is induced by both adiabatic (b) and nonadiabatic (c) time modulation of the electronic hopping amplitudes V(t). The V(t) temporal profile in c results from a few-cycle electric field pulse with Rabi energy d_R = eEa = 100 meV and duration t_p = 100 fs. The latter drives nonthermal populations of different spin and charge local configurations at the “bridge” (Q_B ≠ 0, d, e, h, and i) and “corner” (Q_C = 0, f, g, j, and k) lattice sites. d–g, h–k show the time-dependent populations driven by adiabatic (b) and nonadiabatic (c) coherent hopping modulation, respectively. Vertical lines in h indicate the time delay in the development of different spin state populations during the nonadiabatic light-wave-driven time evolution.

Adiabatic dynamics-equilibrium state

The numerical results here were obtained for the tight-binding parameters and three-dimensional CE/AFM CO/OO unit cell of ref. ⁶⁶, sketched in Fig. 1a. Such complex unit cell applies to the quantum femtosecond magnetism experiments of ref. ⁵ and consists of AFM-coupled zig-zag chains with FM-ordered spins on four alternating full (bridge) and empty (corner) lattice sites per chain (CO, “Methods”). These chains are located in identical x–y planes that are AFM coupled along the z-direction. We obtained reasonable numerical convergence of the time evolution for a 4 × 4 × 4 lattice. While the proposed control mechanism during light-wave oscillations applies to any AFM unit cell, the CE/CO/OO unit cell⁶⁶ used here demonstrates that convergence is obtained for large unit cells, where ab initio calculations of the time dependence are computationally demanding. We first solve the density matrix equations of motion for intersite hopping amplitudes that increase adiabatically in time, from zero to their static values:

$${V}_{\alpha \beta }(t)={t}_{\alpha \beta }(i-j)\frac{t}{T}\,,\,0\le t\le T$$

(1)

and V_αβ(t) = t_αβ for t ≥ T, as shown in Fig. 1b, c. The static values t_αβ reflect the microscopic atomic configurations and can be extracted for specific materials by, for example, fitting to ab initio calculations. Figures 1 and S1 show the time evolution of the above eigenstate of H_local to a stationary state with given hopping amplitudes t_αβ ≠ 0 and quantum spin canting. As seen in Fig. 1, the bridge site, Fig. 1d, e, and the corner site populations, Fig. 1f, g, have reached stationary values within numerical accuracy at t = T. This is clearly illustrated in Fig. S2, where we let the system develop for longer times, t > T, after the hopping amplitudes have reached their static values.

Electron hopping from a full bridge to an empty corner site creates M = S + 1/2 → m = S quasi-hole excitations at the bridge sites (Fig. 1d) and m = S → M = S + 1/2 quasi-electron excitations at the corner sites (Fig. 1g). This (M = 2, m = 3/2) → (m = 3/2, M = 2) charge transfer process does not change the core spin (Fig. 1e, f) and is the only one allowed in the classical limit S → ∞, J_H → ∞ for θ_i = 0, π. There, hopping between AFM sites can only occur via thermodynamic fluctuations of the classical canting angles θ_i^66,68. Here, the stationary solution of the density matrix equations of motion demonstrates that small populations of M = S − 1/2 = 1 and m = S − 1 = 1/2 canted spin configurations emerge during intersite charge excitations for frozen θ_i = 0, π. The above spin populations arise from coherent electronic hopping (quantum transport) with simultaneous quantum canting of the core spins S_i. The latter spin canting originates from the off-diagonal interaction ${J}_{\mathrm{H}}{S}_{i}^{-}\cdot {s}_{i}^{+}$. Such quantum spin fluctuations away from the local z-axis distort the AFM core spin background already in the equilibrium state. Figure S1 shows the spin distortion from the AFM configuration for the full range of magnetic fields and lattice displacements. Figure S1 also demonstrates that, in equilibrium, the energy landscape and equilibrium lattice displacement Q_B are only slightly changed by the electronic hopping and spin fluctuations. This is not the case, however, in the light-driven nonequilibrium quantum state discussed next.

Light-driven nonequilibrium state

We now present the main results of this paper, obtained by calculating the time evolution of a stationary state driven by multicycle time modulation of the equilibrium hopping amplitudes (Fig. 1c). Here, we consider ultra-short timescales: pulse duration t_p = 100 fs, intersite coherence dephasing time T₂ ~ 20 fs < t_p, and charge/spin coherent population lifetime T₁ ~ 200 fs > t_p. Dephasing times T₂ ~ 10 fs are typical in metals^69,70, while T₂ ~ 15 fs has been measured in La_0.5Sr_1.5MnO₄ manganites⁷¹. For the insulating AFM manganite studied in ref. ³³, we measured T₁ ~ 500 fs. Important is that T₁ exceeds a cycle of oscillation, so that dissipation is suppressed during the timescales that steer the time evolution. We compare in Fig. 1h–k the spin-resolved populations of all different local configurations at the bridge (panels h and i) and corner (panels j and k) lattice sites as a function of time for fixed Q_B. At the bridge sites, the m = 3/2 local spin population (Fig. 1h) increases with a simultaneous decrease of the M = S + 1/2 = 2 majority population from its ground state value (Fig. 1i). In addition, light-induced core spin populations with m < 3/2 develop at the bridge sites (Fig. 1h), which indicates quantum canting of the local magnetic moments from their equilibrium values. A remarkable time delay in the development of the different spin populations is seen in Fig. 1h (vertical lines), which signifies a non-instantaneous time evolution of the core spins during oscillation cycles. The population of M < 2 states (Fig. 1i) comes from electronic hopping back to the bridge sites. Such back-and-forth electronic coherent motion is expected from Rabi oscillations between the local electronic configurations at different sites, which are driven by the strong light field used here.

Quantum spin canting is stronger on the corner sites, which become populated during light-induced hopping of electrons from bridge sites. This is seen in Fig. 1j, k, which shows a significant population of m < 3/2 and M < 2 spin configurations on the corner sites. Quantum spin canting, in turn, enhances electronic delocalization, by allowing hopping between AFM sites that is prohibited in the classical limit S → ∞, J_H → ∞. The complex CE-AFM unit cell of Fig. 1a serves to highlight that such effects can occur in layered quantum materials with AFM-coupled planes. In particular, light-driven in-plane electronic transport from the populated bridge to empty corner sites allows for subsequent interplane hopping to empty sites in the neighboring AFM-coupled planes, which have identical lattice configurations and thus no energy barrier due to Q_B. Our results demonstrate the possibility for light-induced time-dependent modulation of angular momenta S_i that are coupled to itinerant spins s_i via local interactions ∝s_i⋅S_i, for example, spin–orbit or magnetic exchange. In this way, light-wave oscillations can transiently modulate spin texture.

The calculated time-dependent effects are controlled by the Rabi energy d_R(t) = eaE(t), where a is the lattice constant, e is the electron charge, and $E(t)=E{e}^{-{t}^{2}/{t}_{\mathrm{p}}^{2}}\sin ({\omega }_{\mathrm{p}}t)$ is the light-wave field with frequency ω_p (see “Methods” and Supplementary Note 1). The role of the intense multicycle electric field is to drive electron transitions between neighboring site local configurations, which are separated by an energy barrier controlled by the local lattice displacements Q_i(t). Such electronic quantum transport is driven when the Rabi energy d_R and/or the frequency ω_p approach the intersite energy barrier^7,8,72,73,74. Since corresponding experiments require both intense fields and electronic coherence, it is favorable to use very short pulses with few cycles of oscillation, for example, MIR or THz multicycle fields (Fig. 1c). In this way, the important dynamics occur during the oscillation cycles, where Rabi flopping between neighboring sites has been demonstrated^2,7,8.

We now show that nonadiabatic time evolution during few cycles of oscillations dynamically steers a stationary state of H_local + H_hop to a nonequilibrium quantum state. The latter quantum state is characterized by a nonthermal density matrix ρ(Q_B, t), which describes the spin-resolved populations of the local configurations, as well as the coherences between all possible pairs of lattice sites (i, j) (see Supplementary Note 1). Here, we demonstrate that the nonequilibrium quantum state is controlled by varying the multicycle electric field in Fig. 2a. Figure 2 shows the calculated core spin dynamics, S_z(t), at the bridge sites (Q_B ≠ 0) (Fig. 2b) and the corner sites (Q_C = 0) (Fig. 2c) for the equilibrium values of Q_B. Similar time-dependent results were obtained for all other lattice displacements, which determines ρ(Q_B, t) in the two-dimensional parameter space (Q_B, t). Due to the difference in the local correlations between the bridge and corner sites (Fig. 1c, b), the light-wave field drives a femtosecond spatially dependent core spin time modulation S_i(t). The latter develops due to the off-diagonal interaction ${J}_{\mathrm{H}}{{\mathrm{s}}}_{i}^{\pm }\cdot {{\mathrm{S}}}_{i}^{\mp }$ (quantum fluctuations), as the itinerant electron spin, s_i, and charge, f_i, transfers between the bridge and corner sites (Fig. 2d, e). ${{\mathrm{s}}}_{i}^{z}(t)\ne \frac{{f}_{i}(t)}{2}$ due to the quantum spin fluctuations ${{\Delta }}{s}_{i}^{z}(t)$ (“Methods”), which drive the system away from the equilibrium AFM order^75,76. The coherent itinerant spin and charge distributions calculated here arise from second-order (or higher) nonlinear processes (see equations of motion in the Supplementary Note 1) and thus display time oscillations with a frequency ~2ω_p (Fig. 2d, e). Such oscillations, also shown in Fig. S3, are averaged out for high optical frequencies, where the rotating wave approximation applies, and present experimental signatures for coherent dynamics. With increasing d_R, S_z(t) decreases from its equilibrium value at both bridge and corner sites (Fig. 2b, c), respectively, as the charge imbalance gives way to a more uniform charge distribution (Fig. 2d). The difference in such light-induced canting of S_i(t) between the bridge (Fig. 2b) and the corner (Fig. 2c) sites results in the emergence of femtosecond magnetization with increasing field. The latter develops in sync with coherent electronic hopping⁸ controlled by the values of Rabi energy d_R and frequency ℏω_p with respect to the intersite energy gap determined by Q_B(t).

Fig. 2: Nonadiabatic charge and spin dynamics driven by few-cycle electric fields.

a The electric fields used in the simulations to obtain ultrafast time modulation of the intersite electronic hopping amplitudes. b, c Bridge and corner site local spin dynamics, S_z(t). d, e Itinerant electron charge and spin dynamics at the bridge and corner sites.

The above light-driven charge and spin redistribution among sites with different lattice displacements prepares a nonequilibrium “initial condition” that “suddenly” changes the energy landscape and thus induces lattice forces during multicycle field oscillations. The initial condition for such lattice dynamics (Fig. 2d) displays almost homogeneous charge distribution throughout the system, with a simultaneous development of net magnetization via quantum spin canting. This new electronic configuration changes the total energy landscape E(Q_B, t) = 〈H_local〉 + 〈H_hop(t)〉 + $\frac{1}{2}k{Q}_{\mathrm{B}}^{2}$, where k characterizes the lattice elastic energy. Figure 3 shows that the light-driven modulation of coherent electronic hopping results in a new global minimum of E(Q_B, t) as a function of the lattice displacement Q_B, which develops non-instantaneously as the Rabi energy d_R = eEa increases above a threshold value. This is expected when d_R approaches the intersite energy barrier controlled by Q_B^6,7,8, seen in Fig. 3. Here, we identify three regimes of Q_B dependence, determined by the population of the different local configurations α. The Q_B > 0 region includes displacements around equilibrium, Q_B ≈ 0.75. This shape of E(Q_B) is determined by the low-energy bridge site populated configurations favored by the JT interaction. These populations lead to a linear Q_B dependence of the Hamiltonian. The latter lowers the local energy 〈H_local〉 for Q_B > 0, but raises it for Q_B < 0⁶⁶. For Q_B ~ 0, our numerical results, obtained via time propagation, are less accurate due to the diminished energy barrier between neighboring sites. In this regime, the energy bands calculated in ref. ³³ lead to metallic behavior. Our time-dependent calculation in Fig. 3 shows that such metastable Q_B ~ 0 state can be accessed as the global minimum changes with increasing Rabi energy d_R, from Q_B > 0 to Q_B ~ 0, during few cycles of oscillation. More specifically, below threshold (d_R = 50 meV in Fig. 3a), the total energy minimum remains at a finite coherent lattice displacement ${Q}_{\mathrm{B}}<{Q}_{\mathrm{B}}^{\mathrm{eq}}$. The main effect is then the softening of the phonon mode, as well as a non-parabolic dependence of E(Q_B) with increasing d_R. This is evident for d_R = 100 meV after three cycles of oscillations (Fig. 3b). Note that phonon modes with a period ~100 fs comparable to the pulse duration can be realized in quantum and semiconductor materials³¹ and therefore the lattice can respond to the light-wave oscillations. Above threshold, d_R = 400 meV, Fig. 3c shows that a new total energy global minimum at Q_B ~ 0 develops in time, where the energy bands indicate a metallic phase not realized in equilibrium³³. The non-instantaneous transition between Q_B > 0 (insulating) and Q_B ~ 0 (metallic) states³³ occurs via a series of intermediate nonequilibrium states and new local minima (Fig. 3c). It is driven by coherent displacements Q_B(t) (not calculated here), which develop rapidly due to the strong time-dependent forces $-\frac{{\mathrm{d}}E({Q}_{\mathrm{B}},t)}{{\mathrm{d}}{Q}_{\mathrm{B}}}$ ²¹.

Fig. 3: Light-wave-driven phase transitions above electric field threshold.

The total energy landscape is shown as a function of lattice displacement Q_B, obtained by using the calculated nonthermal populations and coherences at characteristic time instances during the oscillation cycles. We compare low (a), intermediate (b), and high (c) Rabi energies d_R = eEa. The highlighted area around Q_B ~ 0 indicates the parameter regime where the time propagation simulations are less accurate, due to the near degenerate energy levels between neighboring sites. For such a small Q_B, band calculations³³ indicate a metallic behavior that is not realized in equilibrium. Furthermore, the multiple total energy local minima that develop in c for large Rabi energy d_R indicate the nonequilibrium nature of the phase transition.

Discussion

We have shown that light-driven itinerant electron spin and charge quantum excitations that interact strongly with an AFM local spin background can destabilize an equilibrium AFM insulating state with lattice displacements Q_i ≠ 0 towards a metallic transient state with Q_i ~ 0 and finite magnetization. Based on these results, we can envision in sync quantum THz tuning and coherent control of electronic and magnetic properties of quantum materials by tunable multicycle THz/MIR electric fields. For example, recent results in topological quantum materials indicate that a metastable phase with unique topological switching dynamics assisted by phonons emerges during cycles of lattice coherence oscillations, driven by a few-cycle THz electric field above threshold^6,35. Also, coherent control of structural phase transitions⁹ has been suggested. Importantly, the ability to experimentally control coherent electronic transport on sub-cycle timescales sets the stage for attosecond magnetism², quantum femtosecond magnetism^{5,52,55,57,77,78,79,80}, and light-wave quantum electronics^{1,3,4,25,41,42} before the system reaches a steady state. Our results suggest a microscopic mechanism of quantum femtosecond/attosecond magnetism^2,5,77,78 driven by the light electric field and spin quantum fluctuations. In weakly correlated magnetic systems, it has been debated whether femtosecond magnetization arises from adiabatic processes associated with electron, spin, and phonon populations, or from coherent processes associated with angular momenta interacting with photoexcited electrons^55,77. Here, we propose a different mechanism, based on the strong coupling of electric quantum transport with local moment quantum fluctuations. Understanding the time evolution of a quantum state by simultaneous light-wave control of electronic, magnetic, and lattice properties prior to heating is important for THz magneto-electronics and coherent spintronics, as well for designing quantum materials properties far from equilibrium, leading, for example, to a light-induced switch that twists both spins and the crystal lattice³⁵.

Methods

Local configurations and conservation of total spin

To describe the strong coupling of spin and charge excitations, we consider composite fermion quasi-particles created by Hubbard operators⁶². These operators describe transitions between the multielectron/multiatom local configurations that diagonalize the local (atomic) Hamiltonian H_local in the system of interest. Examples include Zhang–Rice singlet Cu + O configurations in the cuprates, or Mn + O configurations in manganese oxides⁶⁷ (Fig. 1c). Our model considers a general local basis of eigenstates of H_local, with N_e or N_e + 1 electrons at each lattice site i. Coherent hopping of itinerant electrons from site i to site j results in N_e + 1 → N_e transitions at site i and N_e → N_e + 1 transitions at site j between these local states. The N_e localized (core) electrons on each site i are modeled in terms of core local spins S_i⁶⁶. We include in our basis all such spin eigenstates $\left|im\right\rangle$, with S_z = m = −S, …, S (we take S = 3/2, ℏ = 1). Hopping of itinerant electrons, with spin s_i, populates N_e + 1-electron local configurations $\left|i\alpha M\right\rangle$. To ensure spin conservation during such electronic hopping, the latter configurations are chosen as eigenstates of the total spin J_i = S_i + s_i. Assuming strong Hund’s rule interaction, we only retain the low-energy local configurations with J = S + 1/2 (lower Hubbard band), but keep all J_z = M= −J, …, J configurations. The energy eigenvalues of $\left|i\alpha M\right\rangle$ for local Hamiltonian H_local are denoted as ${E}_{i}^{Q}(\alpha M)$. The energy splitting between different configurations α depends on the local lattice displacement, Q_i, at the given i. Such energy splitting for Q_i ≠ 0 can arise, for example, from JT electron–lattice local coupling^66,68. α can also label Hubbard bands due to local Coulomb interactions, as well as multiorbital and multiatom local eigenstates. For our numerical calculations here, we consider a lattice consisting of “bridge” (Q_B ≠ 0) and “corner” (Q_C = 0) sites (Fig. 1c)^66,68, which interchange inside the x–y plane. Along the z-axis, we consider identical stacked planes with AFM spins. While we used the CE-AFM unit cell of Fig. 1c, relevant to the quantum femtosecond magnetism experiment of ref. ⁵, and the tight-binding parameters of ref. ⁶⁶, our proposed light-wave oscillation control paradigm applies to any unit cell with noncollinear spins.

We describe the spins by introducing local coordinate systems on each site i, whose z-axis aligns with the classical spin canting angle θ_i dictated by thermodynamics. For the AFM state considered here, θ_i = 0 or θ_i = π in equilibrium, determined by the free energy rather than by quantum dynamics. M = S + 1/2 and m = S correspond to spins pointing along θ_i. To capture attosecond and femtosecond light-driven quantum spin dynamics away from the quasi-equilibrium spin configuration, we include in our basis all spin quantum numbers M and m and calculate their populations during nonadiabatic/coherent time evolution. The atomic eigenstates of the total spin J_i with J = S + 1/2 are expressed as

$$\left|i\alpha M\right\rangle = \;\sqrt{\frac{S+M+\frac{1}{2}}{2S+1}}\,\left|i\alpha ;\uparrow M-\frac{1}{2}\right\rangle \\ +\sqrt{\frac{S-M+\frac{1}{2}}{2S+1}}\,\,\left|i\alpha ;\downarrow M+\frac{1}{2}\right\rangle ,$$

(2)

where M = −J, …, J. These total spin eigenstates diagonalize the on-site magnetic exchange interaction J_HS_i⋅s_i. The above equation introduces the Glebsch–Gordan coefficients

$${F}_{\sigma }(M)=\sqrt{\frac{S+\frac{1}{2}+\sigma M}{2S+1}}.$$

(3)

By neglecting the upper Hubbard band consisting of J = S − 1/2 configurations, here we do not include spin dynamics on timescales of the order of the inverse magnetic exchange energy ~ℏ/J_H → 0, so we consider the strong coupling limit J_H → ∞. We focus on spin quantum fluctuations due to electron–magnon coupling driven by the off-diagonal on-site magnetic interaction ${J}_{\mathrm{H}}{S}_{i}^{\pm }\cdot {s}_{i}^{\mp }$. The latter interaction excites magnons during the itinerant electron motion.

In models that treat the core spins S_i as classical variables^66,68, the itinerant electrons are assumed to move on top of an adiabatically decoupled local spin background. For strong coupling, all spins are FM-locked, pointing along θ_i at all times^66,68. In this approximation, M = S + 1/2 and m = S are the only allowed spin configurations in the local coordinate systems. Any spin dynamics is then described by classical variables θ_i(t). Within the mean-field approximation, local spin precession on the timescale of the inverse magnetic exchange energy ∝ℏ/J_H can be driven by photoelectrons via femtosecond spin–torque^79,80 or femtosecond spin–orbit torque^52,53,54. Here we take the limit J_H → ∞. Our emphasis is on spin quantum fluctuations, where the spin direction deviates from θ_i(t) during electronic motion due to strong electron–magnon coupling^58,59,60,61. For example, electrons accelerated by a light-wave electric field can hop from site to site by simultaneously exciting low-energy magnon excitations, which leads to coherent populations of all M and m configurations, constrained by total spin conservation and by phase space blocking of the high-energy J = S − 1/2 configurations. Spin quantum fluctuations thus allow the electrons to hop on sites with antiparallel spins by forming local states with J = S + 1/2 but M < S − 1/2, which is possible via ${J}_{\mathrm{H}}{S}_{i}^{\pm }\cdot {s}_{i}^{\mp }$ (see Eq. (2)).

Lattice density matrix

The nonequilibrium quantum state is described by a real-space density matrix defined on a lattice. The latter consists of two parts. The populations (diagonal matrix elements) and on-site coherences, defined on the basis of multielectron/multiatom configurations that describe the local physics, are given by

$${\rho }_{i}(m)=\langle | im\rangle \langle im| \rangle ,\;{\rho }_{i}^{\alpha \beta }(M)=\langle | i\alpha M\rangle \langle i\beta M| \rangle .$$

(4)

The above on-site density matrix describes all local properties at site i, including charge and spin ultrafast dynamics⁸¹. The core spin component S_z(i)³³, measured with respect to θ_i, is obtained as

$${S}_{z}(i)=\mathop{\sum }\limits_{m=-S}^{S}m\ {\rho }_{i}(m)+\mathop{\sum }\limits_{M=-S-\frac{1}{2}}^{S+\frac{1}{2}}M\ \frac{S}{S+\frac{1}{2}}\ \mathop{\sum }\limits _{\alpha }{\rho }_{i}^{\alpha \alpha }(M).$$

(5)

Similarly, the z-component of the itinerant electron spin is obtained as³³

$${s}_{z}^{\alpha }(i)=\frac{1}{2S+1}\mathop{\sum }\limits_{M=-S-\frac{1}{2}}^{S+\frac{1}{2}}M\ {\rho }_{i}^{\alpha \alpha }(M).$$

(6)

In the classical limit, S → ∞, the only populated configurations have m = S or M = S + 1/2. The spatially dependent electron charge populations of configurations α are given by

$${f}_{i}^{\alpha }=\mathop{\sum }\limits_{M}{\rho }_{i}^{\alpha \alpha }(M).$$

(7)

Quantum transport leads to time-dependent fluctuations in ${f}_{i}^{\alpha }$, which also changes the itinerant electron spin classical values, $\frac{{f}_{i}^{\alpha }}{2}$^2,78. Here we consider, in addition to the charge fluctuations during quantum transport, the spin quantum fluctuations ΔS_z(i) = S − S_z(i) and ${{\Delta }}{s}_{z}^{\alpha }(i)=\frac{{f}_{i}^{\alpha }}{2}-{s}_{z}^{\alpha }(i)$. The latter result from nonthermal/coherent populations of local configurations with M ≤ S − 1/2 and m ≤ S − 1 during electronic quantum transport. In particular, such nonthermal spin-resolved populations lead to time-dependent core spin modulation S_i(t) of main interest here.

The coherences (off-diagonal density matrix elements) between the local configurations at different lattice sites i and j describe the quantum transport⁸² in a deformable quantum spin background. For this, we introduce composite fermion local excitations⁶², with spin σ/2 measured with respect to the local z-axis along θ_i. These quasi-particles are created by the Hubbard operators

$${\hat{e}}_{\alpha \sigma }^{\dagger }(iM)=\left|i\alpha M\right\rangle \left\langle i,M-\frac{\sigma }{2}\right|,$$

(8)

where σ = ±1 (ℏ = 1). The above Hubbard operators change the local charge via N_e → N_e + 1 transitions between correlated local states. They obey noncanonical anti-commutation relations^33,62. M = S + 1/2 corresponds to maximally polarized core and itinerant spins FM-aligned along θ_i. In this case, σ = ↑. For quasi-particle excitations with σ = ↓, configurations with M ≤ S − 1/2 must also be populated, Eq. (2).

We introduce the following quasi-particle intersite coherences:

$${\rho }_{ji}^{\bar{\sigma }\sigma }(\beta ;\alpha M)=\langle {\hat{e}}_{\beta \bar{\sigma }}^{\dagger }(j)\ {\hat{e}}_{\alpha \sigma }(iM)\rangle ,$$

(9)

where ${\hat{e}}_{\beta \sigma }^{\dagger }(j)={\sum }_{M}{F}_{\sigma }(M){\hat{e}}_{\beta \sigma }^{\dagger }(jM).$ These coherences describe the time-dependent changes in the local populations and on-site density matrix, ∂_tρ_i (see Supplementary Note 1). They determine the electronic current defined by the continuity equation. We calculate the time evolution of the above density matrix, with both lattice- and off-diagonal elements, by solving quantum kinetic equations of motion derived using the Hamiltonian discussed next (see Supplementary Note 1).

Model Hamiltonian

We split the Hamiltonian H(t) into local (atomic limit of independent lattice sites) and intersite coherent hopping parts, where the latter includes the coupling of the light-wave electric field: H(t) = H_local + H_hop(t). The spin interactions here are part of H_local, described by

$${H}_{\mathrm{mag}}= \; -\!{J}_{\mathrm{H}}\mathop{\sum }\limits_{i}{{\bf{S}}}_{i}\cdot {{\bf{s}}}_{i}\\ -g{\mu }_{\mathrm{B}}{B}_{\mathrm{ext}}\mathop{\sum }\limits_{i}{S}_{i}^{z}-2{\mu }_{\mathrm{B}}{B}_{\mathrm{ext}}\mathop{\sum }\limits _{i}{s}_{i}^{z}.$$

(10)

The first term is the strong FM interaction between the itinerant and core spins (Hund’s rule). The last two terms describe the coupling of a magnetic field B_ext, whose role in our calculation is to break the symmetry during the time evolution and thus allow for magnetic states. μ_B = $\frac{e\hslash }{2m}$ is the Bohr magneton and g = 2. To separate the quantum canting dynamics, we work in the local coordinate systems, whose z-axis point at an angle θ_i with respect to the laboratory (global) z-axis. We assume for simplicity that such spin canting is entirely within the x–z plane and transform from global (${{\bf{S}}}_{i}^{\prime}$) to local (S_i) spin coordinates as follows:

$${S}_{z}^{\prime}={S}_{i}^{z}\,\cos\,{\theta }_{i}-{S}_{i}^{x}\,\sin\,{\theta }_{i},\;{S}_{y}^{\prime}={S}_{i}^{y},\;{S}_{x}^{\prime}={S}_{i}^{z}\,\sin \,{\theta }_{i}+{S}_{i}^{x}\,\cos\,{\theta }_{i}.$$

(11)

Using the above transformation, we obtain in terms of local coordinates

$${H}_{\mathrm{mag}} = \; -{J}_{\mathrm{H}}\mathop{\sum }\limits _{i}{{\bf{S}}}_{i}\cdot {{\bf{s}}}_{i}\\ -g{\mu }_{\mathrm{B}}{B}_{\mathrm{ext}}\mathop{\sum }\limits _{i}\left({S}_{i}^{z}\,\cos\, {\theta }_{i}-{S}_{i}^{x}\,\sin\, {\theta }_{i}\right)\\ -2{\mu }_{\mathrm{B}}{B}_{\mathrm{ext}}\mathop{\sum }\limits _{i}\left({s}_{i}^{z}\,\cos \,{\theta }_{i}-{s}_{i}^{x}\,\sin \,{\theta }_{i}\right).$$

(12)

Here, we consider an AFM reference state with θ_i = 0, π. In the chosen basis of local configurations, the local Hamiltonian is expressed as

$${H}_{\mathrm{local}}[{Q}_{i},{\theta }_{i}]= \;\mathop{\sum }\limits _{i}\mathop{\sum }\limits _{\alpha M}{E}_{i}^{Q}(\alpha M)\ \left|i\alpha M\right\rangle \left\langle i\alpha M\right|\\ +\mathop{\sum }\limits_{i}\mathop{\sum }\limits _{m}{E}_{i}^{Q}(m)\ \left|im\right\rangle \left\langle im\right|.$$

(13)

Off-diagonal terms can also be included, but are not considered here. The Hubbard quasi-particle, Eq. (8), excitation energies are given by

$${\varepsilon }_{\alpha \sigma }^{Q}(iM)={E}_{i}^{Q}(\alpha M)-{E}_{i}^{Q}\left(M-\frac{\sigma }{2}\,\right).$$

(14)

They depend on the local lattice displacements Q_i, treated as classical variables here. Using

$$\left\langle i\alpha M\right|{S}_{i}^{z}\left|i\alpha M\right\rangle =M-\frac{M}{2S+1}$$

(15)

to calculate the magnetic energy contribution, we obtain

$${\varepsilon }_{\alpha \sigma }^{Q\theta }(i)=-{J}_{\mathrm{H}}S-\sigma {\mu }_{\mathrm{B}}{B}_{\mathrm{ext}}\,\cos \,{\theta }_{i}-{E}_{\alpha }^{\mathrm{JT}}{Q}_{i},$$

(16)

where σ = ±1. ${E}_{\alpha }^{\mathrm{JT}}$ describes the lattice dependence of the quasi-particle energies for different local configurations α, expanded to O(Q). An M dependence of the quasi-particle energy can also be included in the calculation, not considered here.

H_hop(t) describes the coherent hopping of the above quasi-particle excitations and conserves the total spin for any local canting angles θ_i. After transforming to the local coordinate system at each site i,

$${H}_{\mathrm{hop}}(t)= -\!\mathop{\sum}\limits _{ij}\mathop{\sum}\limits _{\sigma }\mathop{\sum}\limits _{\alpha \beta }{V}_{\alpha \beta }(i-j)\left[\cos \,\frac{{\theta }_{ij}}{2}\ {\hat{e}}_{\alpha \sigma }^{\dagger }(i)\ {\hat{e}}_{\beta \sigma }(j)\right.\\ \;\left.+\;\sigma \, \sin \,\frac{{\theta }_{ij}}{2}\ {\hat{e}}_{\alpha \sigma }^{\dagger }(i)\ {\hat{e}}_{\beta -\sigma }(j)\right],$$

(17)

where θ_ij = θ_i − θ_j. The hopping amplitudes, ${V}_{\alpha {\alpha }^{\prime}}={t}_{\alpha {\alpha }^{\prime}}+{{\Delta }}{V}_{\alpha {\alpha }^{\prime}}(t)$, have both static (${t}_{\alpha {\alpha }^{\prime}}$) and transiently modulated (${{\Delta }}{V}_{\alpha {\alpha }^{\prime}}$) contributions, where the latter arise from the coupling of the light-wave electric field and/or from phonon oscillating coherence. For example, the Peierls expression of the hopping amplitude between sites r_i and r_j in terms of the laser vector potential A(t) gives

$${V}_{\alpha {\alpha }^{\prime}}(j-i)={t}_{\alpha {\alpha }^{\prime}}(j-i)\exp [-ie{\bf{A}}(t) ({r}_{j}-{r}_{i})/\hslash c].$$

(18)

Since the details of the short-lived time-periodic, multicycle modulation of the hopping amplitudes are not crucial for the transient state results obtained here, we expand in terms of A for simplicity and consider the linear term that drives quantum transport and electronic current:

$${{\Delta }}{V}_{\alpha {\alpha }^{\prime}}(i-j)\approx \frac{{d}_{\mathrm{R}}(t)}{\hslash {\omega }_{p}}{t}_{\alpha {\alpha }^{\prime}}(i-j).$$

(19)

A more complete derivation of light-wave quantum transport may be found in ref. ⁶⁵. For σ = 1, the first term of Eq. (17) recovers the double exchange Hamiltonian^66,68. This is the only allowed term if we assume FM-locked itinerant and core spins at all times, but vanishes for AFM spins, θ_ij = ±π, considered here. The rest of the terms in H_hop describe intersite quasi-particle hopping accompanied by local spin excitations^33,67 induced by electron–magnon coupling^58,59,60. The latter permits electronic hopping between AFM sites even in the limit J_H → ∞ (Fig. 1c).

By using the above general Hamiltonian, we derived a closed system of quantum kinetic equations of motion for ρ_i(m), ${\rho }_{i}^{\alpha \beta }(M)$, and ${\rho }_{ji}^{\bar{\sigma }\sigma }(\beta ;\alpha M)$ for all lattice sites, which are presented in Supplementary Note 1. We thus describe the time-evolved quantum state on a three-dimensional lattice with periodic boundary conditions. We obtained reasonable convergence for a 4 × 4 × 4 lattice with two configurations per site. As discussed in Supplementary Note 1, by introducing Hubbard operators, we obtain exact equations for ∂_tρ_i that do not explicitly depend on the local interactions. In particular, ∂_tρ_i couples to intersite coherences of the form $\langle {\hat{e}}_{\alpha \sigma }^{\dagger }(i)\ {\hat{e}}_{\beta \sigma }(j)\rangle$ and $\langle {\hat{e}}_{\alpha \sigma }^{\dagger }(i)\ {\hat{e}}_{\beta -\sigma }(j)\rangle$, where i ≠ j. We thus satisfy charge and spin conservation in an exact way.