Abstract
Many scientific phenomena are linked to wave problems. This paper presents an effective and suitable technique for generating approximation solutions to multi-dimensional problems associated with wave propagation. We adopt a new iterative strategy to reduce the numerical work with minimum time efficiency compared to existing techniques such as the variational iteration method (VIM) and homotopy analysis method (HAM) have some limitations and constraints within the development of recurrence relation. To overcome this drawback, we present a Sawi integral transform (\(\mathbb {S}\)T) for constructing a suitable recurrence relation. This recurrence relation is solved to determine the coefficients of the homotopy perturbation strategy (HPS) that leads to the convergence series of the precise solution. This strategy derives the results in algebraic form that are independent of any discretization. To demonstrate the performance of this scheme, several mathematical frameworks and visual depictions are shown.
Similar content being viewed by others
Introduction
Several notable advances in computational approaches have been developed for engineering and scientific applications, including geometrical description, flexible artificial materials, and acoustic wave propagation1,2,3. Partial differential equations (PDEs) have a significant impact on many scientific and engineering fields, including electronics, hydrodynamics, computational motion, physical biology, the engineering of chemicals, dietary fiber, mechanics, material dynamics, and geometrical optics4,5,6,7. Numerous researchers have investigated different methods to derive the analytical results for such PDEs. Utilizing a meshfree approach named the Radial basis function pseudo spectral (RBF-PS) method, researchers numerically examined the solutions for both integer and fractional KdV type equations on a finite domain with periodic boundary conditions8,9. Although the computations associated with these approaches are fairly straightforward and certain variables are based on the assumption of a variety of limitations. As a result, many scientists are looking for new techniques to overcome these restrictions. Numerous scientists and other researchers have offered several methods for assessing the analytical findings10,11,12. Several academics and scientists have used HPS13,14 to solve complicated physical problems. When employing this method, the solution series converges relatively quickly in most cases. The authors15,16 used HPS to the oscillation challenges in nonlinearity and demonstrated its effectiveness in providing analytical findings.
The wave problem is a partial differential equation for a scalar function offering wave propagation in the motion of fluids. Wazwaz17 used the VIM to study linear and nonlinear problems. Ghasemi et al.18 computed the effective results for two-dimensional nonlinear differential problem using HPS. Keskin and Oturanc19 proposed a new method for the analytical results of wave problems. Dehghan et al.20 applied HAM to derive the approximation results for PDEs. Ullah et al.21 proposed a homotopy optimum technique to generate algebraic findings for wave challenges. Thorwe and Bhalekar22 used Laplace transform method to obtain approximation solution of partial integro-differential equations. Adwan et al.23 presented analytical findings for multidimensional wave challenges and validated the proposed technique. The HPS was applied for the approximate solutions of wave equations by Jleli et al.24. The researchers in25 proposed the finite element technique and separated the wave system to derive their approximate solution. These approaches include a lot of limitations and assumptions during the estimation of problems.
The current study aims to use a new iterative technique for multi-dimension challenges by combining \(\mathbb {S}\)T and HPS. In the present work, we eliminate these drawbacks and constraints by offering a novel iterative method for these multi-dimensional wave issues. An iteration series with approximate findings that are close to the precise outcomes is produced by this new strategy. This technique performs more effectively and produces more appealing outcomes for the present challenges. The following is a description of this work: the concept of Sawi integral transform is given in “Fundamental concepts”. In “Formulation of new iterative strategy”, we build our new strategy to achieve the multi-dimension model findings. The convergence theorem has been laid out in “Convergence of new iterative strategy”. In “Numerical applications”, a few numerical examples are examined to demonstrate the power of new technique and we offer the conclusion at the end of “Conclusion remarks and future work”.
Fundamental concepts
In this portion, we give few fundamental features of \(\mathbb {S}\)T that are helpful in the development of our new strategy.
Sawi transform
Definition 2.1
Let \(\vartheta \) be a function of \(\eta \ge 0\). Then, \(\mathbb {S}\)T is26,27
in which \(\mathbb {S}\) represents the symbol of \(\mathbb {S}\)T. Now
where \(Q(\theta )\) shows the function of \(\vartheta (\eta )\). The \(\mathbb {S}\)T of \(\vartheta (\eta )\) for \(\eta \ge 0\) exist if \(\vartheta (\eta )\) tends to exponentially ordered and piecewise continuous. The existence of \(\mathbb {S}\)T for \(\vartheta (\eta )\) is basically predicated on the two requirements mentioned.
Proposition 1
Now, we define the basic propositions of \(\mathbb {S}\)T. Therefore, let \(\mathbb {S}\{\vartheta _{1}(\eta )\}=Q_{1}(\theta )\) and \(\mathbb {S}\{\vartheta _{2}(\eta )\}=Q_{2}(\theta )\)28,29, thus
Proposition 2
Now, for the differential characteristics of \(\mathbb {S}\)T, we consider \(\mathbb {S}\{\vartheta (\eta )\}=Q(\theta )\), the differential characteristics are defined as30
Formulation of new iterative strategy
This section examines the approximate solutions of 1D, 2D, and 3D wave problems by using new iterative strategy (NIS). This approach can be used to solve differential equations based on initial conditions. We stated that the construction of this approach does not depend on integrating and other suppositions. Let a differential equation like that
subjected to initial conditions
where \(f(\vartheta )\) denotes the nonlinear element, \(f(x_{1},\eta )\) is known component of arbitrary constants \(a_{1}\) and \(a_{2}\), and \(\vartheta (x_{1},\eta )\) is a uniform function. Moreover, we may express Eq. (4) like this:
A function of a real variable can be transformed into an expression of a complex variable using an integral transformation known as the Sawi transform in mathematics. This transformation has several uses in the fields of science and technology because it serves as a tool to deal with differential problems.
Apply \(\mathbb {S}\)T on Eq. (6), we get
Using the formula as defined in Eq. (3), it yields
Thus, \(Q(\theta )\) is derived as
On inverse \(\mathbb {S}\)T on Eq. (7), we get
Use the condition (5), we obtain
This Eq. (8) is known as the development of NIS of Eq. (4).
Let HPS be introduced as
where as the nonlinear variable \(f(\vartheta )\) is stated as
Hence, we are able to generate \(H_{n}'s\) polynomial as
Use Eqs. (9)–(11) in Eq. (8) and evaluate the similar components of p, it yields
Following this procedure, which results in
Hence, Eq. (12) provides a closed-form approximation to the differential problem.
Convergence of new iterative strategy
Theorem 4.1
Let \([a,b]\times [0,T]\) be the rectangular interval on which the Banach space \(B\equiv C([a,b]\times [0,T])\) is defined. Then Eq. (12) \(\vartheta (x_{1},\eta )=\sum _{i=0}^{\infty }\vartheta _{i}(x_{1},\eta )\) is convergent series, if \(\vartheta _{0}\in B\) is bounded and \(\left\| \vartheta _{i+1}\right\| \le \left\| \vartheta _{i}\right\| , \forall \vartheta _{i} \in B\), and for \(0<\delta <1\).
Proof
Taking the series \(\left\{ F_r\right\} \) as a partial sum of Eq. (12), we obtain
Next, we establish that \(\left\{ F_r\right\} _{r=0}^{\infty }\) is a Cauchy sequence in B in order to validate this theorem. Therefore,
Hence, for any pair \(r, n \in N\), where \(r>n\), we have
where \(\beta =\frac{\left( 1-\delta ^{r-n}\right) }{(1-\delta )} \delta ^{n+1}\). Since \(\vartheta _0(x_{1}, \eta )\) is bounded, therefore \(\left\| \vartheta _0(x_{1}, \eta )\right\| <\infty \). As n grows and \(n \rightarrow \infty \) leads to \(\beta \rightarrow 0\) for \(0<\delta <1\), so
Consequently, \(\left\{ F_r\right\} _{r=0}^{\infty }\) in B is a Cauchy sequence. It follows that the series solution of Eq. (12) is convergent. \(\square \)
Theorem 4.2
If \(\sum _{k=0}^n \vartheta _k(x_{1}, \eta )\) represents the approximate series solution of Eq. (4), then maximal absolute error can be determined by
in which \(\delta \) is a digit which means \(\dfrac{\left\| \vartheta _{i+1}\right\| }{\left\| \vartheta _i\right\| } \le \delta \).
Proof
Using Eq. (15) from Theorem (4.1), we obtain
Here, \(\left\{ F_r\right\} _{r=0}^{\infty } \rightarrow \vartheta (x_{1}, \eta )\) as \(r \rightarrow \infty \) and from Eq. (13), we get \(F_n=\sum _{k=0}^n \vartheta _k(x_{1}, \eta )\),
Now, \((1-\delta ^{r-n})<1\), since \(0<\delta <1\)
\(\square \)
Hence, the proof.
Numerical applications
We provide some numerical tests for showing the precision and reliability of NIS. We can observe that, as compared to other approaches, this method is substantially easier to apply in obtaining the convergence series. We illustrate the physical nature of the resulting plot distribution with graphical structures. Furthermore, a visual depiction of the error distribution demonstrated the near correspondence between the NIS outcomes and the precise results. We can compute the absolute error estimates by evaluating the exact solutions with the NIS values.
Example 1
Consider the one dimensional wave equation
subjected to initial
and boundary conditions
Apply \(\mathbb {S}\)T on Eq. (21), we get
Using the formula as defined in Eq. (3), it yields
Thus, \(Q(\theta )\) reveals as
On inverse \(\mathbb {S}\)T, we have
Thus HPS yields such as
By assessing comparable components of p, we arrive at
Likewise, we can consider the approximation series in such a way that
which can approaches to
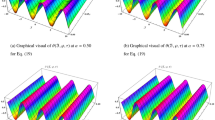
Figure 1 shows periodic soliton waves in two diagrams: Fig. 1a 3D surface plot for analytical results of \(\vartheta (x_{1},\eta )\) and Fig. 1b shows 3D surface plot for precise results of \(\vartheta (x_{1}, \eta )\) for one-dimensional wave equation at \(-10\le x_{1} \le 10\) and \(0\le \eta \le 0.01\). The effective agreement among analytical and the precise results at \(0\le x_{1} \le 5\) along \(\eta =0.1\) is shown in Fig. 2, which further validates the strong agreement of NIS for example (5.1). We can precisely propagate any surface to reflect the pertinent natural physical processes, according to this technique. The error distribution among analytical and precise results for \(\vartheta (x_{1}, \eta )\) along \(x_{1}\)-space at different values is shown in Table 1. This contraction demonstrates the effectiveness of proposed technique in finding the closed-form results for the wave problems.
Example 2
Consider the two-dimensional wave equation
subjected to initial
and boundary conditions
Apply \(\mathbb {S}\)T on Eq. (27), we get
Using the formula as defined in Eq. (3), it yields
Thus, \(Q(\theta )\) reveals as
On inverse \(\mathbb {S}\)T, we have
Thus HPS yields such as
By assessing comparable components of p, we arrive at
Likewise, we can consider the approximation series in such a way that
which can approaches to
Figure 3 shows periodic soliton waves in two diagrams: Fig. 3a: 3D surface plot for analytical results and Fig. 3b: 3D surface plot for precise results of \(\vartheta (x_{1},y_{1},\eta )\) for two-dimensional wave equation at \(-5\le x_{1} \le 5\), \(0\le \eta \le 0.01\) along \(y_{1}=0.5\). The effective agreement among analytical and the precise results at \(0\le x_{1} \le 5\), \(y_{1}=0.1\) along \(\eta =0.1\) is shown in Fig. 4, which further validates the strong agreement of NIS for example (5.2). We can precisely propagate any surface to reflect the pertinent natural physical processes, according to this technique. The error distribution among analytical and precise results for \(\vartheta (x_{1},y_{1},\eta )\) along \(x_{1}\)-space at different values is shown in Table 2. This contraction demonstrates the effectiveness of proposed technique in finding the closed-form results for the wave problems.
Example 3
Consider the three-dimensional wave equation
subjected to initial
and boundary conditions
Apply \(\mathbb {S}\)T on Eq. (33), we get
Using the formula as defined in Eq. (3), it yields
Thus, \(Q(\theta )\) reveals as
On inverse \(\mathbb {S}\)T, we have
Thus HPS yields such as
By assessing comparable components of p, we arrive at
Likewise, we can consider the approximation series in such a way that
which can approaches to
Figure 5 shows two diagrams: Fig. 5a: 3D surface plot for analytical results and Fig. 5b: 3D surface plot for precise results of \(\vartheta (x_{1},y_{1},z_{1},\eta )\) for two-dimensional wave equation at \(5\le x_{1} \le 10\) and \(0\le \eta \le 0.01\) with \(y_{1}=0.5\) and \(z_{1}=0.5\). The effective agreement among analytical and the precise results at \(0\le x_{1} \le 10\), \(y_{1}=0.5\), \(z_{1}=0.5\) along \(\eta =0.5\) is shown in Fig. 6, which further validates the strong agreement of NIS for example (5.3). We can precisely propagate any surface to reflect the pertinent natural physical processes, according to this technique. The error distribution among analytical and precise results for \(\vartheta (x_{1},y_{1},z_{1},\eta )\) along \(x_{1}\)-space at different values is shown in Table 3. This contraction demonstrates the effectiveness of proposed technique in finding the closed-form results for the wave problems.
Conclusion remarks and future work
In this article, we successfully applied the new iterative strategy for the approximate results of multi-dimensional wave problems. This technique uses the recurrence relation to produce the findings of the analysis. The findings obtained from numerical examples show that our technique is simple to implement and has a greater rate of convergence than existing approaches. The Sawi integral transform has the ability to control the global error, which makes it a suitable method for solving problems with rapidly changing solutions. The method is relatively easy to implement, especially for problems with periodic solutions. The 3D figures in the illustrated problems show the periodic soliton waves in the deep well. The physical behavior of the problems is depicted by the 3D graphical representations, and the visual inaccuracy between the exact outcomes and the produced results is represented by the 2D plot distribution. This method requires accurate initial guesses for the solution, which can be challenging in some cases. In terms of its effectiveness and efficiency, the Sawi integral transform is a relatively new method and has not been widely studied or compared to other numerical methods for solving PDEs. However, in the cases where it has been applied, it has shown promising results, with relatively high accuracy and efficiency compared to other methods. This composition of Sawi transform and the homotopy perturbation strategy gives the solution of multi-dimensional problems which is very useful in wave propagation. This novel iterative technique can also be used to solve other physical chemistry, engineering, and medical research challenges, such as calculating the growth rate of tumors, calculating the total quantity of infecting cells, calculating the amount of viral particles in blood during HIV-1 diseases, analyzing the impact of humidity on skew plate vibration, and calculating the amount of chemicals involved in chemical chain reactions in the future.
Data availibility
This article includes all of the data from this study.
References
Khan, W. A. Numerical simulation of Chun–Hui He’s iteration method with applications in engineering. Int. J. Numer. Methods Heat Fluid Flow 32(3), 944–955 (2021).
Gepreel, K. A. & Al-Thobaiti, A. Exact solutions of nonlinear partial fractional differential equations using fractional sub-equation method. Indian J. Phys. 88(3), 293–300 (2014).
Althobaiti, A., Althobaiti, S., El-Rashidy, K. & Seadawy, A. R. Exact solutions for the nonlinear extended KdV equation in a stratified shear flow using modified exponential rational method. Results Phys. 29, 104723 (2021).
Jan, H. U., Uddin, M., Abdeljawad, T. & Zamir, M. Numerical study of high order nonlinear dispersive PDEs using different RBF approaches. Appl. Numer. Math. 182, 356–369 (2022).
Cakmak, M. & Alkan, S. A numerical method for solving a class of systems of nonlinear Pantograph differential equations. Alex. Eng. J. 61(4), 2651–2661 (2022).
Yu, J., Lu, L., Meng, X. & Karniadakis, G. E. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput. Methods Appl. Mech. Eng. 393, 114823 (2022).
Momani, S. & Odibat, Z. Analytical approach to linear fractional partial differential equations arising in fluid mechanics. Phys. Lett. A 355(4–5), 271–279 (2006).
Jan, H. U. et al. On the approximation of eventual periodicity of linearized KdV type equations using RBF-PS method. Appl. Appl. Math. 17(2), 571–580 (2022).
Uddin, M., Jan, H. U. & Usman, M. RBF-PS method for approximation and eventual periodicity of fractional and integer type KdV equations. Partial Differ. Equ. Appl. Math. 5, 100288 (2022).
Uddin, M. et al. On the solution of fractional order kdv equation and its periodicity on bounded domain using radial basis functions. Math. Probl. Eng. 20, 22 (2022).
Raslan, K., Ali, K. K. & Shallal, M. A. The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations. Chaos, Solitons Fractals 103, 404–409 (2017).
Rezazadeh, H. et al. Optical soliton solutions of the generalized non-autonomous nonlinear schrödinger equations by the new Kudryashov’s method. Results Phys. 24, 104179 (2021).
Biazar, J. & Ghazvini, H. Convergence of the homotopy perturbation method for partial differential equations. Nonlinear Anal. Real World Appl. 10(5), 2633–2640 (2009).
Mohyud-Din, S. T. & Noor, M. A. Homotopy perturbation method for solving partial differential equations. Z. Nat. A 64(3–4), 157–170 (2009).
He, J.-H., El-Dib, Y. O. & Mady, A. A. Homotopy perturbation method for the fractal toda oscillator. Fractal Fract. 5(3), 93 (2021).
Nadeem, M., He, J.-H. & Islam, A. The homotopy perturbation method for fractional differential equations: Part 1 Mohand transform. Int. J. Numer. Methods Heat Fluid Flow 31(11), 3490–3504 (2021).
Wazwaz, A.-M. The variational iteration method: A reliable analytic tool for solving linear and nonlinear wave equations. Comput. Math. Appl. 54(7–8), 926–932 (2007).
Ghasemi, M., Kajani, M. T. & Davari, A. Numerical solution of two-dimensional nonlinear differential equation by homotopy perturbation method. Appl. Math. Comput. 189(1), 341–345 (2007).
Keskin, Y. & Oturanc, G. Reduced differential transform method for solving linear and nonlinear wave equations. Iran. J. Sci. Technol. Trans. A Sci. 34(2), 133–142 (2010).
Dehghan, M., Manafian, J. & Saadatmandi, A. The solution of the linear fractional partial differential equations using the homotopy analysis method. Z. Nat. A 65(11), 935 (2010).
Ullah, H. et al. Approximate solution of two-dimensional nonlinear wave equation by optimal homotopy asymptotic method. Math. Probl. Eng. 20, 15 (2015).
Thorwe, J. & Bhalekar, S. Solving partial integro-differential equations using Laplace transform method. Am. J. Comput. Appl. Math. 2(3), 101–104 (2012).
Adwan, M., Al-Jawary, M., Tibaut, J. & Ravnik, J. Analytic and numerical solutions for linear and nonlinear multidimensional wave equations. Arab J. Basic Appl. Sci. 27(1), 166–182 (2020).
Jleli, M., Kumar, S., Kumar, R. & Samet, B. Analytical approach for time fractional wave equations in the sense of Yang–Abdel–Aty–Cattani via the homotopy perturbation transform method. Alex. Eng. J. 59(5), 2859–2863 (2020).
Mullen, R. & Belytschko, T. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation. Int. J. Numer. Meth. Eng. 18(1), 11–29 (1982).
Singh, G. P. & Aggarwal, S. Sawi transform for population growth and decay problems. Int. J. Latest Technol. Eng. Manage. Appl. Sci. 8(8), 157–162 (2019).
Higazy, M., Aggarwal, S. & Nofal, T. A. Sawi decomposition method for volterra integral equation with application. J. Math. 2020, 1–13 (2020).
Mahgoub, M. M. A. The new integral transform “Sawi Transform’’. Adv. Theor. Appl. Math. 14(1), 81–87 (2019).
Higazy, M. & Aggarwal, S. Sawi transformation for system of ordinary differential equations with application. Ain Shams Eng. J. 12(3), 3173–3182 (2021).
Jafari, H. A new general integral transform for solving integral equations. J. Adv. Res. 32, 133–138 (2021).
Acknowledgements
This research was supported by the Chunhui Project of the Chinese Ministry of Education (202201245).
Author information
Authors and Affiliations
Contributions
J.L.: methodology, writing-original draft. M.N.: investigation, M.S.O.: software. Y.A.: supervision, funding project. This paper has been read and approved by all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, J., Nadeem, M., Osman, M.S. et al. Study of multi-dimensional problems arising in wave propagation using a hybrid scheme. Sci Rep 14, 5839 (2024). https://doi.org/10.1038/s41598-024-56477-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-56477-5
Keywords
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.