Application of Yang homotopy perturbation transform approach for solving multi-dimensional diffusion problems with time-fractional derivatives

Abstract

In this paper, we aim to present a powerful approach for the approximate results of multi-dimensional diffusion problems with time-fractional derivatives. The fractional order is considered in the view of the Caputo fractional derivative. In this analysis, we develop the idea of the Yang homotopy perturbation transform method (YHPTM), which is the combination of the Yang transform (YT) and the homotopy perturbation method (HPM). This robust scheme generates the solution in a series form that converges to the exact results after a few iterations. We show the graphical visuals in two-dimensional and three-dimensional to provide the accuracy of our developed scheme. Furthermore, we compute the graphical error to demonstrate the close-form analytical solution in the comparison of the exact solution. The obtained findings are promising and suitable for the solution of multi-dimensional diffusion problems with time-fractional derivatives. The main advantage is that our developed scheme does not require assumptions or restrictions on variables that ruin the actual problem. This scheme plays a significant role in finding the solution and overcoming the restriction of variables that may cause difficulty in modeling the problem.

Introduction

The study of fractional calculus is becoming more interesting in various branches of mathematical problems including integral and derivatives of fractional order. The phenomena of fractional order problems have a great attraction in other branches of science and engineering such as as astronomy, optical fiber, biomechanics, chemical reactions, heat transform, and fluid flows^1,2. In recent years, numerous researchers have introduced the analytical and numerical approaches to obtain their approximate solutions. Malan and Lewis³ utilized edge-based finite volume method to model heat and mass transfer in heterogeneous porous materials. Arafa and Hagag⁴ presented q-Homotopy analysis transform method for the analytic solution of fractional coupled Ramani problem. El-Sayed et al.⁵ developed the idea of Adomian’s decomposition method for the approximate solution of the reaction-diffusion model of fractional order. It is still challengeable task to obtain the exact solution of these fractional problems. Most of the fractional system do not have the exact solutions due to the difficulty of fractional order. To investigate their approximate solutions, various authors presented their schemes that obtain the results very close to the exact solution such as Fractional Temimi–Ansari method⁶, Differential transform scheme⁷, Haar wavelet operational matrix⁸, Natural transform⁹, Sumudu residual power series method¹⁰, Finite difference approach¹¹, High-order finite element scheme¹², Local fractional Sumudu transform¹³, Sub-equation method¹⁴.

This work is concerned with the time fractional multi-dimensional diffusion equation^15,16:

$$\begin{aligned} D^{\alpha }_{\tau }\vartheta =\nabla . (D(\vartheta (r,\tau ),r)\nabla \vartheta (r,\tau )), \qquad 0<\alpha \le 1 \end{aligned}$$

(1)

where $D^{\alpha }_{\tau }=\dfrac{\partial ^{\alpha }}{\partial \tau ^{\alpha }}$ stands for the Caputo fractional derivative, $\vartheta (r,\tau )$ and $D\vartheta (r,\tau )$ represent the density of the diffusing material and the diffusion coefficient for $\vartheta$ at the point $r = (x, y, z)$ and time $\tau$ respectively. If the diffusion coefficient is free from density (i.e. $D\vartheta (r,\tau )=\sigma ^{2}$ is a constant), then problem (1) tends to the fractional order multi-dimensional heat equation, such that $D^{\alpha }_{\tau }\vartheta =\sigma ^{2}\nabla ^{2}\vartheta$. In case of $\alpha =1$, the problem (1) reduces to the classical multi-dimensional diffusion equation.

Recently, Yang¹⁷ proposed the idea of Yang transform for the first time and showed that this scheme is straightforward for deriving the results of a steady heat transfer equation. The idea of homotopy perturbation method (HPM) was constructed by He in 2004 and showed that this scheme is suitable for different types of problems¹⁸. Later, many researchers extend this study and combined HPM to obtain the approximate solution of some more fractional differential problems. Liu¹⁹ et al. combined Yang transform with HPM to derive the analytical results of time-fractional Klein–Gordon problems. Yasmin²⁰ combined Yang transform with the Adomian decomposition approach to present the analysis of the Whitham–Broer–Kaup problem with time-fractional order. The Yang transform with HPM performed excellent results in finding a solution of fractional order KdV and Burger problem²¹. The study of HPM²² has becoming more and more interesting and numerous researchers have showed the combination of HPM with an other operator produces faster rate of convergence^23,24. Akbarzade and Langari²⁵ showed that HPM is more reliable tool than variational iteration scheme in finding the approximate results of three dimensional heat problems. Kumar et al.¹⁶ applied the modification of HPM whereas Prakash and Kumar²⁶ suggested the application of fractional variational iteration scheme to present the analytical view of multi-dimensional diffusion problems. Researchers showed that combination of these transformation with the HPM provide the excellent results than the traditional HPM. Since various analytical and numerical schemes are presented by experts in the literature. In the most of schemes, authors have faced some difficulties and limitations due to the heavy calculations in the iteration series. The use of integration in variational iteration scheme and convolution theorem Laplace transform make the solution complicated and may occur some assumption and restrictions on variables that is the main drawback of these schemes^27,28. To overcome, this drawback, we propose the idea of YHPTM for the approximate solution of multi-dimensional diffusion problems with time-fractional derivatives.

In this work, we combine the YT with HPM to develop a novel scheme that is expressed by YHPTM. We consider a few problems to test the accuracy and performance of this proposed scheme. We note that our developed scheme produces results very close to the exact results after a few iterations and some graphical visuals are also provided to show its performance with graphical errors. We begin this article as; we present the idea of Yang transform in “Concept of Yang transform” including its definitions. We develop the idea of YHPTM for the solution of fractional problems and provide its convergence analysis in “Formulation of YHPTM” and “Convergence and error analysis” respectively. In “Applications”, we illustrate some examples to test the compactness and authenticity of our proposed scheme. We conclude our study in the last section “Conclusion”.

Concept of Yang transform

In this segment, we define the concept of YT with its basic properties.

Definition 2.1

The Caputo fractional derivative is defined as^29,30

$$\begin{aligned} D^{\alpha }_{\tau }\vartheta (\Im ,\tau )=\frac{1}{\Gamma (k-\alpha )}\int _{0}^{\tau }(\tau -q)^{k-\alpha -1}\vartheta ^{k}(\Im ,q)\ dq, \qquad k-1 < \alpha \le k. \end{aligned}$$

Definition 2.2

The YT is stated as^17,19

$$\begin{aligned} Y[\vartheta (\tau )]=R(\xi )=\int _{0}^{\infty } e^{-\dfrac{\tau }{\xi }} \vartheta (\tau ) d \tau {,} \end{aligned}$$

whereas ${\mathcal {Y}}^{-1}[R(\xi )]=\vartheta (\tau )$ is known as the inverse of YT.

Definition 2.3

The YT of a fractional derivative is given as^17,19

$$\begin{aligned} Y[\vartheta ^{\alpha }(\tau )]=\frac{R(\xi )}{\xi ^{\alpha }}-\sum _{k=0}^{n-1}\frac{\vartheta ^{k}(0)}{\xi ^{\alpha -k-1}},\qquad n-1 < \alpha \le n. \end{aligned}$$

Proposition

The differential properties of YT for a function $\vartheta (\tau )$ are defined as¹⁹

$$\begin{aligned} \begin{aligned} Y[\vartheta '(\tau )]&=\frac{R(\xi )}{\xi }-\vartheta (0),\\ Y[\vartheta ''(\tau )]&=\frac{R(\xi )}{\xi ^{2}}-\frac{\vartheta (0)}{\xi }-\vartheta '(0). \end{aligned} \end{aligned}$$

Formulation of YHPTM

In this section, we construct the idea of YHPTM which is used to derive the approximate results of multi-dimensional diffusion problems with time-fractional derivatives. This scheme does not require the restriction of variables and any hypothesis. Let’s assume the following differential problem of time-fractional order as

$$\begin{aligned} D^{\alpha }_{\tau }\vartheta (\Im ,\tau )=L_{1}\vartheta (\Im ,\tau )+L_{2}\vartheta (\Im ,\tau )+h(\Im ,\tau ), \end{aligned}$$

(2)

with initial condition

$$\begin{aligned} \vartheta (\Im ,0)=k(\Im ). \end{aligned}$$

(3)

Operating YT on Eq. (2) such as

$$\begin{aligned} Y[D^{\alpha }_{\tau }\vartheta (\Im ,\tau )]=Y[L_{1}\vartheta (\Im ,\tau )+L_{2}\vartheta (\Im ,\tau )+h(\Im ,\tau )]. \end{aligned}$$

This implies

$$\begin{aligned} \frac{1}{\xi ^{\alpha }}\Big [R(\xi )-\xi \vartheta (0)\Big ]=Y[L_{1}\vartheta (\Im ,\tau )+L_{2}\vartheta (\Im ,\tau )+h(\Im ,\tau )]. \end{aligned}$$

Hence $R(\xi )$ is evaluated such as

$$\begin{aligned} R[\xi ]=\xi \vartheta (0)+\xi ^{\alpha } Y\Big [L_{1}\vartheta (\Im ,\tau )+L_{2}\vartheta (\Im ,\tau )+h(\Im ,\tau )\Big ]. \end{aligned}$$

(4)

Operating inverse YT on Eq. (4), it yields

$$\begin{aligned} \vartheta (\Im ,\tau )=G(\Im ,\tau )+Y^{-1}\Bigg [\xi ^{\alpha } \wp \Big \{L_{1}\vartheta (\Im ,\tau )+L_{2}\vartheta (\Im ,\tau )\Big \}\Bigg ], \end{aligned}$$

(5)

where

$$\begin{aligned} G(\Im ,\tau )=Y^{-1}\Big [\xi \vartheta (0)+\xi ^{\alpha }Y[h(\Im ,\tau )]\Big ]. \end{aligned}$$

Now, HPM is defined as

$$\begin{aligned} \vartheta (\Im ,\tau )=\sum _{i=0}^{\infty }p^{i}\vartheta _{i}(\Im ,\tau ), \end{aligned}$$

(6)

and

$$\begin{aligned} L_{2}\vartheta (\Im ,\tau )=\sum _{i=0}^{\infty }p^{i}H_{i}(\vartheta ){,} \end{aligned}$$

(7)

where $H_{n}$ polynomials are expressed as;

$$\begin{aligned} H_{n}(\vartheta _{0},\vartheta _{1},\ldots , \vartheta _{n})=\frac{1}{n!}\frac{\partial ^{n}}{\partial p^{n}}\Bigg (L_{2}\Big (\sum _{i=0}^{\infty } p^{i}\vartheta _{i}\Big )\Bigg )_{p=0}, \ \ \ \ n=0,1,2,\ldots {.} \end{aligned}$$

Use Eqs. (6) and (7) in Eq. (5), it yields

$$\begin{aligned} \sum _{i=0}^{\infty }p^{i}\vartheta _{i}(\Im ,\tau )=G(\Im ,\tau )+Y^{-1}\Bigg [\xi ^{\alpha } Y\Big \{L_{1}\sum _{i=0}^{\infty }p^{i}\vartheta _{i}(\Im ,\tau )+\sum _{i=0}^{\infty }p^{i}H_{i}(\vartheta )\Big \}\Bigg ]. \end{aligned}$$

(8)

Comparing the coefficient of p, we obtain

$$\begin{aligned} p^{0}&:\vartheta _{0}(\Im ,\tau )=G(\Im ,\tau ),\\ p^{1}&:\vartheta _{1}(\Im ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\vartheta _{0}(\Im ,\tau )+H_{0}(\vartheta )\bigg \}\Bigg ],\\ p^{2}&:\vartheta _{2}(\Im ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\vartheta _{1}(\Im ,\tau )+H_{1}(\vartheta )\bigg \}\Bigg ],\\ p^{3}&:\vartheta _{3}(\Im ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\vartheta _{2}(\Im ,\tau )+H_{2}(\vartheta )\bigg \}\Bigg ],\\&\vdots , \end{aligned}$$

similarly, it can be continued to the following series

$$\begin{aligned} \vartheta (\Im ,\tau )=\vartheta _{0}+\vartheta _{1}+\vartheta _{2}+\cdots =\sum _{i=0}^{\infty }\vartheta _{i}(\Im ,\tau ). \end{aligned}$$

(9)

Equation (9) represents the approximate solution of the fractional problem (2).

Convergence and error analysis

The following theorems are built on the idea of the proposed scheme and provided to show the convergence and error analysis of the problem (2)

Theorem 4.1

Let $\vartheta (\Im , \tau )$ be the exact results of Eq. (2) and consider $\vartheta (\Im , \tau ), \vartheta _n(\Im , \tau ) \in H$ and $\sigma \in (0,1)$, where $\textrm{H}$ represents the Hilbert space. Then, the derived results $\sum _{i=0}^{\infty } \vartheta _i(\Im , \tau )$ can converge $\vartheta (\Im , \tau )$ in case of $\vartheta _i(\Im , \tau ) \le \vartheta _{i-1}(\Im , \tau ) \forall i>A$, thus, for any $\omega>0 \exists A>0$, there is $\left\| \vartheta _{i+n}(\Im , \tau )\right\| \le \beta , \forall m, n \in N$.

Proof

Let a sequence such as $\sum _{i=0}^{\infty } \vartheta _i(\Im , \tau )$. Then

$$\begin{aligned} \begin{aligned} \vartheta _0(\Im , \tau )&=\vartheta _0(\Im , \tau ), \\ \vartheta _1(\Im , \tau )&=\vartheta _0(\Im , \tau )+\vartheta _1(\Im , \tau ), \\ \vartheta _2(\Im , {\mathfrak {I}})&=\vartheta _0(\Im , \tau )+\vartheta _1(\Im , \tau )+\vartheta _2(\Im , {\mathfrak {I}}), \\ \vartheta _3(\Im , {\mathfrak {I}})&=\vartheta _0(\Im , \tau )+\vartheta _1(\Im , \tau )+\vartheta _2(\Im , \tau )+\vartheta _3(\Im , \tau ), \\&\vdots \\ \vartheta _i(\Im , \tau )&=\vartheta _0(\Im , \tau )+\vartheta _1(\Im , \tau )+\vartheta _2(\Im , \tau )+\cdots +\vartheta _i(\Im , \tau ), \end{aligned} \end{aligned}$$

(10)

To achieve the valuable solution, we must show that $\vartheta _i(\Im , \tau )$ defines a “Cauchy sequence”. Moreover, consider

$$\begin{aligned} \begin{aligned} \left\| \vartheta _{i+1}(\Im , {\mathfrak {I}})-\vartheta _i(\Im , {\mathfrak {I}})\right\|&=\left\| \vartheta _{i+1}(\Im , {\mathfrak {I}})\right\| \le \sigma \left\| \vartheta _i(\Im , {\mathfrak {I}})\right\| \le \sigma ^2\left\| \vartheta _{i-1}(\Im , {\mathfrak {I}})\right\| \le \sigma ^3\left\| \vartheta _{i-2}(\Im , {\mathfrak {I}})\right\| \ldots \\&\le \sigma _{i+1}\left\| \vartheta _0(\Im , {\mathfrak {I}})\right\| . \end{aligned} \end{aligned}$$

(11)

For $i, n \in N$, it yields

$$\begin{aligned} \begin{aligned} \left\| \vartheta _i(\Im , \tau )-\vartheta _n(\Im , {\mathfrak {I}})\right\| =&\left\| \vartheta _{i+n}(\Im , \tau )\right\| =\Vert \vartheta _i(\Im , \tau )-\vartheta _{i-1}(\Im , \tau )+\left( \vartheta _{i-1}(\Im , \tau )-\vartheta _{i-2}(\Im , \tau )\right) \\&+\left( \vartheta _{i-2}(\Im , \tau )-\vartheta _{i-3}(\Im , \tau )\right) +\cdots +\left( \vartheta _{n+1}(\Im , \tau )-\vartheta _n(\Im , \tau )\right) \Vert , \\ \le&\left\| \vartheta _i(\Im , \tau )-\vartheta _{i-1}(\Im , \tau )\right\| +\left\| \left( \vartheta _{i-1}(\Im , {\mathfrak {I}})-\vartheta _{i-2}(\Im , {\mathfrak {I}})\right) \right\| \\&+\left\| \left( \vartheta _{i-2}(\Im , \tau )-\vartheta _{i-3}(\Im , \tau )\right) \right\| +\cdots +\Vert \left( \vartheta _{n+1}(\Im , \tau )-\vartheta _n(\Im , \tau ) \Vert \right. , \\ \le&\sigma ^i\left\| \vartheta _0(\Im , {\mathfrak {I}})\right\| +\sigma ^{i-1}\left\| \vartheta _0(\Im , \tau )\right\| +\cdots +\sigma ^{i+1}\left\| \vartheta _0(\Im , {\mathfrak {I}})\right\| , \\ =&\left\| \vartheta _0(\Im , \tau )\right\| \left( \sigma ^i+\sigma ^{i-1}+\sigma ^{i+1}\right) , \\ =&\left\| \vartheta _0(\Im , \tau )\right\| \frac{1-\sigma ^{i-n}}{1-\sigma ^{i+1}} \sigma ^{n+1}. \end{aligned} \end{aligned}$$

(12)

As $0<\sigma <1$, and $\vartheta _0(\Im , \tau )$ is bounded, then consider $\beta =1-\sigma /\left( 1-\sigma _{i-n}\right) \sigma ^{n+1}\left\| \vartheta _0(\Im , \tau )\right\|$, and thus, $\left\{ \vartheta _i(\Im , \tau )\right\} _{i=0}^{\infty }$ tends to “Cauchy sequence” in H. Hence, the sequence $\left\{ \vartheta _i(\Im , \tau )\right\} _{i=0}^{\infty }$ is convergent with the $\lim _{i\rightarrow \infty } \vartheta _i(\Im , \tau )=\vartheta (\Im , \tau )$ for $\exists \vartheta (\Im , \tau ) \in {\mathcal {H}}$. This ends the proof. $\square$

Theorem 4.2

Let $\sum _{h=0}^k \vartheta _h(\Im , \tau )$ is finite and $\vartheta (\Im , \tau )$ shows the derived series results. Consider $\sigma >0$ such as $\left\| \vartheta _{h+1}(\Im , \tau )\right\| \le \left\| \vartheta _h(\Im , {\mathfrak {I}})\right\|$, then the following relation produces the maximum absolute error.

$$\begin{aligned} \left\| \vartheta (\Im , \tau )-\sum _{h=0}^k \vartheta _h(\Im , \tau )\right\| <\frac{\sigma ^{k+1}}{1-\sigma }\left\| \vartheta _0(\Im , \tau )\right\| . \end{aligned}$$

(13)

Proof

Since $\sum _{h=0}^k \vartheta _h(\Im , \tau )$ is finite, this implies that $\sum _{h=0}^k \vartheta _h(\Im , \tau )<\infty$. Consider

$$\begin{aligned} \begin{aligned} \left\| \vartheta (\Im , \tau )-\sum _{h=0}^k \vartheta _h(\Im , {\mathfrak {I}})\right\|&=\left\| \sum _{h=k+1}^{\infty } \vartheta _h(\Im , \tau )\right\| , \\&\le \sum _{h=k+1}^{\infty }\left\| \vartheta _h(\Im , \tau )\right\| , \\&\le \sum _{h=k+1}^{\infty } \sigma ^h\left\| \vartheta _0(\Im , \tau )\right\| , \\&\le \sigma ^{k+1}\left( 1+\sigma +\sigma ^2+\cdots \right) \left\| \vartheta _0(\Im , \tau )\right\| , \\&\le \frac{\sigma ^{k+1}}{1-\sigma }\left\| \vartheta _0(\Im , \tau )\right\| . \end{aligned} \end{aligned}$$

(14)

This ends the proof. $\square$

Applications

We illustrate four applications of multi-dimensional diffusion problems with time-fractional derivatives. We consider two-dimensional and three-dimensional heat flow problems in the sense of Caputo fractional derivative. These examples exhibit the performance and capability of the presented scheme. Graphical results and absolute errors show that YHPTM is a very promising tool for solving fractional differential problems. MATHEMATICA 11 software is used for numerical computations during the calculation phase and construction of figures.

Example 1

Let us consider the two-dimensional homogeneous time-fractional heat flow problem

$$\begin{aligned} \frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}=\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}-\vartheta , \end{aligned}$$

(15)

with the initial condition

$$\begin{aligned} \vartheta (\Im ,\wp ,0)=\sin \Im \cos \wp . \end{aligned}$$

(16)

Applying the YT on Eq. (15), we get

$$\begin{aligned} Y\Big [\frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}-\vartheta \Big ]. \end{aligned}$$

The application of YT in fractional form yields

$$\begin{aligned} \frac{1}{\xi ^{\alpha }}\Big [R(\xi )-\xi \vartheta (0)\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}-\vartheta \Big ]. \end{aligned}$$

Thus, $R(\xi )$ is obtained as

$$\begin{aligned} R[\xi ]=\xi \vartheta (0)+\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}-\vartheta \Big ]. \end{aligned}$$

(17)

Using inverse YT on Eq. (17), we get

$$\begin{aligned} \vartheta (\Im ,\wp ,\tau )=\vartheta (\Im ,\wp ,0)+Y^{-1}\Big [\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}-\vartheta \Big ]. \end{aligned}$$

(18)

Implementing the idea of of HPM to derive the He’s iterations

$$\begin{aligned} \sum _{i=0}^{\infty }p^{i}\vartheta (\Im ,\wp ,\tau )=\vartheta (\Im ,\wp ,0)+Y^{-1}\Big [\xi ^{\alpha } Y\Big [\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \Im ^{2}}+\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \wp ^{2}}-\sum _{i=0}^{\infty }p^{i}\vartheta _{i}\Big ]. \end{aligned}$$

Relating the similar components of p, we get

$$\begin{aligned} p^{0}&:\vartheta _{0}(\Im ,\wp ,\tau )=\vartheta (\Im ,\wp ,0)=\sin \Im \cos \wp ,\\ p^{1}&:\vartheta _{1}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{0}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{0}}{\partial \wp ^{2}}-\vartheta _{0}\bigg \}\Bigg ]=-3 \sin \Im \cos \wp \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)},\\ p^{2}&:\vartheta _{2}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{1}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{1}}{\partial \wp ^{2}}-\vartheta _{1}\bigg \}\Bigg ]=3^{2} \sin \Im \cos \wp \frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)},\\ p^{3}&:\vartheta _{3}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{2}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{2}}{\partial \wp ^{2}}-\vartheta _{2}\bigg \}\Bigg ]=-3^{3} \sin \Im \cos \wp \frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)},\\ p^{4}&:\vartheta _{4}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{3}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \wp ^{2}}-\vartheta _{3}\bigg \}\Bigg ]=3^{4} \sin \Im \cos \wp \frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)},\\&\vdots . \end{aligned}$$

Similarly, it can be continued to the following series

$$\begin{aligned} \begin{aligned} \vartheta (\Im ,\wp ,\tau )&=\vartheta _{0}(\Im ,\wp ,\tau )+\vartheta _{1}(\Im ,\wp ,\tau )+\vartheta _{2}(\Im ,\wp ,\tau )+\vartheta _{3}(\Im ,\wp ,\tau )+\vartheta _{4}(\Im ,\wp ,\tau )+\cdots ,\\&=\sin \Im \cos \wp \Big (1-3\frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}+3^{2}\frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}-3^{3}\frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}+3^{4}\frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}+\cdots \Big )+\cdots . \end{aligned} \end{aligned}$$

(19)

which can be closed form

$$\begin{aligned} \vartheta (\Im ,\wp ,\tau )=e^{-3\tau }\sin \Im \cos \wp . \end{aligned}$$

(20)

Figure 1

The three-dimensional surfaces solution of $\vartheta (\Im ,\wp ,\tau )$.

Figure 2

The two-dimensional graphical visual of $\vartheta (\Im ,\wp ,\tau )$ at multiple values of $\alpha$.

Table 1 Absolute error between the obtained results and the exact solution at $\wp =0.5$ and $\tau =0.001$.

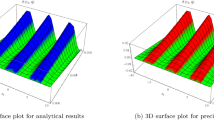
In Fig. 1, we provide the graphical visuals of approximate series solution of Eq. (19) and the exact solution of Eq. (20) at $-10 \le \Im \le 10$ and $0 \le \tau \le 0.1$. These visuals indicate that when we increase the value of fractional order $\alpha$, our graphical results approach to the exact graph significantly. We plotted the graphical error in two-dimensional visuals in Fig. 2 at $\alpha = 0.25, 0.50, 0.75, 1$. This shows comparison yields that YHPTM is fast and convenient approach. Table 1 presents the absolute errors between the approximate solution and the exact solution of three-dimensional heat flow problem. This table shows that when $\alpha =1$, our obtained values are very close to the exact solution than the values of $\alpha =0.50$ and the value of absolute error decreases precisely.

Example 2

Consider the following time-fractional heat flow problem in a inhomogeneous two-dimensional form

$$\begin{aligned} \frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}=\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\sin \wp , \end{aligned}$$

(21)

with the initial condition

$$\begin{aligned} \vartheta (\Im ,\wp ,0)=\sin \Im \sin \wp +\sin \wp . \end{aligned}$$

(22)

Applying the YT on Eq. (21), we get

$$\begin{aligned} Y\Big [\frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\sin \wp \Big ]. \end{aligned}$$

The application of YT in fractional form yields

$$\begin{aligned} \frac{1}{\xi ^{\alpha }}\Big [R(\xi )-\xi \vartheta (0)\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\sin \wp \Big ]. \end{aligned}$$

Thus $R(\xi )$ is obtained as

$$\begin{aligned} R[\xi ]=\xi \vartheta (0)+\xi ^{\alpha +1} \sin \wp +\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}\Big ]. \end{aligned}$$

(23)

Using inverse YT on Eq. (23), we get

$$\begin{aligned} \vartheta (\Im ,\wp ,\tau )=\vartheta (\Im ,\wp ,0)+\sin \wp \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)} +Y^{-1}\Big [\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}\Big ]. \end{aligned}$$

(24)

Implementing the idea of HPM to derive the He’s iterations

$$\begin{aligned} \sum _{i=0}^{\infty }p^{i}\vartheta (\Im ,\wp ,\tau )=\vartheta (\Im ,\wp ,0)+\sin \wp \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}+Y^{-1}\Big [\xi ^{\alpha } Y\Big [\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \Im ^{2}}+\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \wp ^{2}}\Big ]. \end{aligned}$$

Relating the similar components of p, we get

$$\begin{aligned} p^{0}&:\vartheta _{0}(\Im ,\wp ,\tau )=\vartheta (\Im ,\wp ,0)=\sin \Im \sin \wp +\sin \wp +\sin \wp \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)},\\ p^{1}&:\vartheta _{1}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{0}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{0}}{\partial \wp ^{2}}\bigg \}\Bigg ]=-2\sin \Im \sin \wp \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}-\sin \wp \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}-\sin \wp \frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)},\\ p^{2}&:\vartheta _{2}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{1}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{1}}{\partial \wp ^{2}}\bigg \}\Bigg ]=2^{2}\sin \Im \sin \wp \frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}+\sin \wp \frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}+\sin \wp \frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)},\\ p^{3}&:\vartheta _{3}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{2}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{2}}{\partial \wp ^{2}}\bigg \}\Bigg ]=-2^{3}\sin \Im \sin \wp \frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}-\sin \wp \frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}-\sin \wp \frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)},\\ p^{4}&:\vartheta _{4}(\Im ,\wp ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{3}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \wp ^{2}}\bigg \}\Bigg ]=-2^{4}\sin \Im \sin \wp \frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}-\sin \wp \frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}-\sin \wp \frac{\tau ^{5\alpha }}{\Gamma (5\alpha +1)},\\&\vdots . \end{aligned}$$

Similarly, it can be continued to the following series

$$\begin{aligned} \begin{aligned} \vartheta (\Im ,\wp ,\tau )&=\vartheta _{0}(\Im ,\wp ,\tau )+\vartheta _{1}(\Im ,\wp ,\tau )+\vartheta _{2}(\Im ,\wp ,\tau )+\vartheta _{3}(\Im ,\wp ,\tau )+\vartheta _{4}(\Im ,\wp ,\tau )+\cdots ,\\&=\sin \wp +\sin \Im \sin \wp \Big (1-2\frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}+2^{2}\frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}-2^{3}\frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}+2^{4}\frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}+\cdots \Big )+{\cdots ,} \end{aligned} \end{aligned}$$

(25)

which can be closed form

$$\begin{aligned} \vartheta (\Im ,\wp ,\tau )=\sin \wp +e^{-2\tau }\sin \Im \sin \wp . \end{aligned}$$

(26)

Figure 3

The three-dimensional surfaces solution of $\vartheta (\Im ,\wp ,\tau )$.

Figure 4

The two-dimensional graphical visual of $\vartheta (\Im ,\wp ,\tau )$ at multiple values of $\alpha$.

Table 2 Absolute error between the obtained results and the exact solution at $\wp =0.5$ and $\tau =0.005$.

In Fig. 3, we provide the graphical visuals of approximate series solution of Eq. (25) and the exact solution of Eq. (26) at $-1 \le \Im \le 1$ and $0 \le \tau \le 0.5$. These visuals indicate that when we increase the value of fractional order $\alpha$, our graphical results approach to the exact graph significantly. We plotted the graphical error in two-dimensional visuals in Fig. 4 at $\alpha = 0.25, 0.50, 0.75, 1$. This shows comparison yields that YHPTM is fast and convenient approach. Table 2 presents the absolute errors between the approximate solution and the exact solution of three-dimensional heat flow problem. This table shows that when $\alpha =1$, our obtained values are very close to the exact solution than the values of $\alpha =0.50$ and the value of absolute error decreases precisely.

Example 3

Consider the following time-fractional heat flow problem in a three-dimensional homogeneous form

$$\begin{aligned} \frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}=\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}-2\vartheta , \end{aligned}$$

(27)

with the initial condition

$$\begin{aligned} \vartheta (\Im ,\wp ,\varpi ,0)=\sin \Im \sin \wp \sin \varpi . \end{aligned}$$

(28)

Applying the YT on Eq. (27), we get

$$\begin{aligned} Y\Big [\frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}-2\vartheta \Big ]. \end{aligned}$$

Using the properties functions of YT , we obtain

$$\begin{aligned} \frac{1}{\xi ^{\alpha }}\Big [R(\xi )-\xi \vartheta (0)\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}-2\vartheta \Big ]. \end{aligned}$$

Thus $R(\xi )$ is obtained as

$$\begin{aligned} R[\xi ]=\xi \vartheta (0)+\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}-2\vartheta \Big ]. \end{aligned}$$

(29)

Using inverse YT on Eq. (29), we get

$$\begin{aligned} \vartheta (\Im ,\wp ,\varpi ,\tau )=\vartheta (\Im ,\wp ,0)+Y^{-1}\Big [\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}-2\vartheta \Big ]. \end{aligned}$$

(30)

Implementing the idea of HPM to derive the He’s iterations

$$\begin{aligned} \sum _{i=0}^{\infty }p^{i}\vartheta _{i}(\Im ,\wp ,\varpi ,\tau )=\vartheta (\Im ,\wp ,\varpi ,0)+Y^{-1}\Big [\xi ^{\alpha } Y\Big [\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \Im ^{2}}+\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \wp ^{2}}+\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \varpi ^{2}}-2\sum _{i=0}^{\infty }p^{i}\vartheta _{i}\Big ]. \end{aligned}$$

Relating the similar components of p, we get

$$\begin{aligned} p^{0}&:\vartheta _{0}(\Im ,\wp ,\varpi ,\tau )=\vartheta (\Im ,\wp ,\varpi ,0)=\sin \Im \sin \wp \sin \varpi ,\\ p^{1}&:\vartheta _{1}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{0}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{0}}{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \varpi ^{2}}-2\vartheta _{0}\bigg \}\Bigg ]=-5\sin \Im \sin \wp \sin \varpi \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)},\\ p^{2}&:\vartheta _{2}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{1}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{1}}{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \varpi ^{2}}-2\vartheta _{1}\bigg \}\Bigg ]=5^{2}\sin \Im \sin \wp \sin \varpi \frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)},\\ p^{3}&:\vartheta _{3}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{2}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{2}}{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \varpi ^{2}}-2\vartheta _{2}\bigg \}\Bigg ]=-5^{3}\sin \Im \sin \wp \sin \varpi \frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)},\\ p^{4}&:\vartheta _{4}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{3}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \varpi ^{2}}-2\vartheta _{3}\bigg \}\Bigg ]=5^{4}\sin \Im \sin \wp \sin \varpi \frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)},\\&\vdots . \end{aligned}$$

Similarly, it can be continued to the following series

$$\begin{aligned} \begin{aligned} \vartheta (\Im ,\wp ,\varpi ,\tau )&=\vartheta _{0}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{1}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{2}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{3}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{4}(\Im ,\wp ,\varpi ,\tau )+\cdots ,\\&=\sin \Im \sin \wp \sin \varpi \Big (1-5\frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}+5^{2}\frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}-5^{3}\frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}+5^{4}\frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}+\cdots \Big )+\cdots {,} \end{aligned} \end{aligned}$$

(31)

which can be closed form

$$\begin{aligned} \vartheta (\Im ,\wp ,\varpi ,\tau )=e^{-5\tau }\sin \Im \sin \wp \sin \varpi . \end{aligned}$$

(32)

Figure 5

The three-dimensional surfaces solution of $\vartheta (\Im ,\wp ,\varpi ,\tau )$.

Figure 6

The two-dimensional graphical visual of $\vartheta (\Im ,\wp ,\varpi ,\tau )$ at multiple values of $\alpha$.

Table 3 Absolute error between the obtained results and the exact solution at $\wp =\varpi =0.5$ and $\tau =0.001$.

In Fig. 5, we provide the graphical visuals of approximate series solution of Eq. (31) and the exact solution of Eq. (32) $-3 \le \Im \le 3$ and $0 \le \tau \le 0.1$. These visuals indicate that when we increase the value of fractional order $\alpha$, our graphical results approach to the exact graph significantly. We plotted the graphical error in two-dimensional visuals in Fig. 6 at $\alpha = 0.25, 0.50, 0.75, 1$. This shows comparison yields that YHPTM is fast and convenient approach. Table 3 presents the absolute errors between the approximate solution and the exact solution of three-dimensional heat flow problem. This table shows that when $\alpha =1$, our obtained values are very close to the exact solution than the values of $\alpha =0.50$ and the value of absolute error decreases precisely.

Example 4

Consider the following time-fractional heat flow problem in a three-dimensional inhomogeneous form

$$\begin{aligned} \frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}=\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}+\sin \varpi , \end{aligned}$$

(33)

with the initial condition

$$\begin{aligned} \vartheta (\Im ,\wp ,\varpi ,0)=\sin (\Im +\wp )+\sin \varpi . \end{aligned}$$

(34)

The application of YT in fractional form yields

$$\begin{aligned} Y\Big [\frac{\partial ^{\alpha } \vartheta }{\partial \tau ^{\alpha }}\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}+\sin \varpi \Big ]. \end{aligned}$$

Using the properties functions of YT, we obtain

$$\begin{aligned} \frac{1}{\xi ^{\alpha }}\Big [R(\xi )-\xi \vartheta (0)\Big ]=Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}+\sin \varpi \Big ]. \end{aligned}$$

Thus $R(\xi )$ is obtained as

$$\begin{aligned} R[\xi ]=\xi \vartheta (0)+\xi ^{\alpha } \wp [\sin \varpi ]+\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}\Big ]. \end{aligned}$$

(35)

Using inverse YT on Eq. (35), we get

$$\begin{aligned} \vartheta (\Im ,\wp ,\varpi ,\tau )=\vartheta (\Im ,\wp ,\varpi ,0)+\sin \varpi \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}+Y^{-1}\Big [\xi ^{\alpha } Y\Big [\frac{\partial ^{2}\vartheta }{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta }{\partial \varpi ^{2}}\Big ]. \end{aligned}$$

(36)

Implementing the idea of HPM to derive the He’s iterations

$$\begin{aligned} \sum _{i=0}^{\infty }p^{i}\vartheta (\Im ,\wp ,\varpi ,\tau )=\vartheta (\Im ,\wp ,\varpi ,0)+\sin \varpi \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}+Y^{-1}\Big [\xi ^{\alpha } Y\Big [\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \Im ^{2}}+\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \wp ^{2}}+\sum _{i=0}^{\infty }p^{i}\frac{\partial ^{2}\vartheta _{i}}{\partial \varpi ^{2}}\Big ]. \end{aligned}$$

Relating the similar components of p, we get

$$\begin{aligned} p^{0}&:\vartheta _{0}(\Im ,\wp ,\varpi ,\tau )=\vartheta (\Im ,\wp ,0)=\sin (\Im +\wp )+\sin \varpi +\sin \varpi \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)},\\ p^{1}&:\vartheta _{1}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{0}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{0}}{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta _{0}}{\partial \varpi ^{2}}\bigg \}\Bigg ]=-2 \sin (\Im +\wp )\frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}-\sin \varpi \frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}-\sin \varpi \frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)},\\ p^{2}&:\vartheta _{2}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{1}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{1}}{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta _{0}}{\partial \varpi ^{2}}\bigg \}\Bigg ]=2^{2} \sin (\Im +\wp )\frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}+\sin \varpi \frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}+\sin \varpi \frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)},\\ p^{3}&:\vartheta _{3}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{2}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{2}}{\partial \wp ^{2}}\bigg \}+\frac{\partial ^{2}\vartheta _{0}}{\partial \varpi ^{2}}\Bigg ]=-2^{3} \sin (\Im +\wp )\frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}-\sin \varpi \frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}-\sin \varpi \frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)},\\ p^{4}&:\vartheta _{4}(\Im ,\wp ,\varpi ,\tau )=Y^{-1}\Bigg [\xi ^{\alpha } Y\bigg \{\frac{\partial ^{2}\vartheta _{3}}{\partial \Im ^{2}}+\frac{\partial ^{2}\vartheta _{3}}{\partial \wp ^{2}}+\frac{\partial ^{2}\vartheta _{0}}{\partial \varpi ^{2}}\bigg \}\Bigg ]=2^{4} \sin (\Im +\wp )\frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}+\sin \varpi \frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}+\sin \varpi \frac{\tau ^{5\alpha }}{\Gamma (5\alpha +1)},\\&\vdots . \end{aligned}$$

Similarly, it can be continued to the following series

$$\begin{aligned} \begin{aligned} \vartheta (\Im ,\wp ,\varpi ,\tau )&=\vartheta _{0}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{1}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{2}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{3}(\Im ,\wp ,\varpi ,\tau )+\vartheta _{4}(\Im ,\wp ,\varpi ,\tau )+\cdots ,\\&=\sin \varpi +\sin (\Im +\wp ) \left( 1-2\frac{\tau ^{\alpha }}{\Gamma (\alpha +1)}+2^{2}\frac{\tau ^{2\alpha }}{\Gamma (2\alpha +1)}-2^{3}\frac{\tau ^{3\alpha }}{\Gamma (3\alpha +1)}+2^{4}\frac{\tau ^{4\alpha }}{\Gamma (4\alpha +1)}+\cdots \right) + {\cdots ,} \end{aligned} \end{aligned}$$

(37)

which can be closed form

$$\begin{aligned} \vartheta (\Im ,\wp ,\varpi ,\tau )=\sin \varpi +e^{-2\tau }\sin (\Im +\wp ). \end{aligned}$$

(38)

Figure 7

The three-dimensional surfaces solution of $\vartheta (\Im ,\wp ,\varpi ,\tau )$.

Figure 8

The two-dimensional graphical visual of $\vartheta (\Im ,\wp ,\varpi ,\tau )$ at multiple values of $\alpha$.

Table 4 Absolute error between the obtained results and the exact solution at $\wp =\varpi =0.5$ and $\tau =0.005$.

In Fig. 7, we provide the graphical visuals of approximate series solution of Eq. (37) and the exact solution of Eq. (38) $-1 \le \Im \le 1$ and $0 \le \tau \le 0.5$. These visuals indicate that when we increase the value of fractional order $\alpha$, our graphical results approach to the exact graph significantly. We plotted the graphical error in two-dimensional visuals in Fig. 8 at $\alpha = 0.25, 0.50, 0.75, 1$. This shows comparison yields that YHPTM is fast and convenient approach. Table 4 presents the absolute errors between the approximate solution and the exact solution of three-dimensional heat flow problem. This table shows that when $\alpha =1$, our obtained values are very close to the exact solution than the values of $\alpha =0.50$ and the value of absolute error decreases precisely.

Conclusion

In this study, we successfully developed the YHPTM approach for obtaining the approximate solution of the two-dimensional and three-dimensional heat flow problems. Since the equations involving fractional order are quite difficult to solve directly, we introduce the idea of YT to dissolve the fractional order of the problem. The scheme of YT is limited and unable to generate the series solution, therefore, we implement HPM to derive the successive iterations from the classical equation that leads the results to the exact solution very easily. We consider four test problems to show the efficiency and effectiveness of this proposed scheme. It has been found that our derived results demonstrate a great confirmation of compromise with the exact solution. We also analyzed the efficiency of our proposed scheme in two-dimensional and three-dimensional through graphical structures. The obtained results are efficient and significant, demonstrating that YHPTM is accurate and authentic for fractional problems. It is expected to consider this scheme for fractional problems in the sense of Atangana–Baleanu derivatives and other partial differential equations involving fractal theory and fractional calculus in our future work.