Introduction

The two-speed transmission system is a variable speed system with two speed outputs, which is widely used in the fields of helicopter, tank, loader, automobile and so on. A two-speed transmission system is added in the main subtraction of the helicopter, which can realize helicopter cruise and hover (start and stop) and achieve the lowest fuel consumption. The typical structure of two-speed transmission system consists of friction clutch, overrunning clutch and planetary gear transmission system1,2,3. The performance and service life of the two-speed transmission system directly affect the performance and service life of the helicopter and other equipment. The study of nonlinear characteristics of two-speed transmission system can guide the optimal design and manufacture of transmission system.

At present, the friction clutch and the planetary gear transmission system have been widely used, and the research on the nonlinear characteristics of the coupling transmission system between the friction clutch and the planetary gear has been a hotspot. Han4 established a nonlinear dynamics model considering time-varying meshing stiffness, tooth side clearance and static transmission error, and solved it by using numerical integration method, and analyzed the dynamics characteristics of the system through global bifurcation diagram. Li5 studied the meshing characteristics of planetary gear train when the position of the planetary frame changes under variable loads. Wang6 established a torsional dynamics model of planetary gear transmission system considering friction, time-varying meshing stiffness, meshing damping and clearance, solved the system vibration equation by Runge–Kutta method, and analyzed the bifurcation and chaos characteristics of the system through bifurcation diagrams and phase diagrams. Luo7 established a dynamic model including time-varying meshing stiffness, sliding friction and torque, and studied the influence of sliding friction on the dynamic characteristics of planetary gear mechanisms. For the 3K-ii planetary gear system, Sang8 established a torsional vibration dynamic model of the system by using the lumped parameter method, and analyzed the influence of tooth root crack on the system. Ryali9 studied the load distribution and dynamic characteristics of planetary gear system under internal and external excitation. Xu10 established a new gear tooth modification model according to the characteristics of tooth top modification and tooth profile modification of planetary gear train. Ling11 analyzed the motion and various nonlinear dynamics characteristics of planetary gear system by using global bifurcation diagram, FFT spectrum, Poincare diagram, phase diagram and maximum Lyapunov index. Li12 established the reliability prediction model of helicopter planetary gear train under partial load. Xiang13 identified the influence of system motion on the change of backlash by using global bifurcation diagram, maximum Lyapunov index (LLE), FFT spectrum, Poincare diagram, phase diagram and time series.

The research on nonlinear characteristics of planetary gear transmission system mainly focuses on modeling methods, solving methods, stability judgment and other aspects. The models mainly include pure torsional model and bending-torsional coupling model, and the time-varying meshing stiffness, tooth clearance and comprehensive meshing error are usually considered in the modeling. The nonlinear dynamics of planetary gear transmission system can be solved by analytical method and numerical method.

The dynamics of friction clutch is mainly studied by modeling and analyzing the clutch independently or simplifying other mechanical structures. The analysis and solution methods are mainly numerical iteration, concentrated parameters and finite element method. Li14 analyzed the self-excited vibration characteristics of clutch and discussed the influence of clutch related physical parameters on its performance based on the established 4-DOF nonlinear multi-body dynamics model and Karnopp friction model. Bao15,16 established the transient thermal analysis model of friction clutch and the motion coupling model in the engagement process, and studied the influence of the groove shape of the friction disc on the transient temperature field in the clutch engagement process and the influence of relevant parameters on the speed and transmission torque of clutch engagement. Wang17 proposes an improved model for calculating the meshing stiffness of a helical gear system caused by a gear crack, which takes into account the transverse and axial effects of the gear tooth stiffness and the gear foundation stiffness. The results show that the meshing stiffness of the gear is greatly reduced by the existence of cracks. The time domain vibration response of cracked gear is sudden, and the frequency spectrum shows that the more serious the crack, the more abundant the side frequency component and the higher the amplitude. Wang18 proposed an improved meshing stiffness calculation model for helical gear pairs, which fully considered not only the tooth stiffness of axial gear and the foundation stiffness of axial gear, but also the transverse gear tooth stiffness and foundation stiffness affected by surface roughness under elastohydrodynamic lubrication. The results show that compared with the traditional method, the improved meshing stiffness calculation model can obtain the meshing stiffness under actual lubrication conditions, but the traditional method ignores the axial meshing force and the friction force acting on the gear teeth and gear base.

Compared with the single clutch or planetary gear, the dynamic characteristics of the coupling system composed of friction clutch and planetary gear are more complex. Although this kind of system is widely used, the nonlinear characteristics of friction clutch-planetary gear system are rarely studied. Aleksandar19 established a simulation model of friction clutch and planetary gear train, and conducted a simulation analysis on the transition process of planetary gear train in the shift process. Michel Bauer20 established a friction clutch-planetary gear train model suitable for hybrid power and conducted a simulation study on its shifting characteristics. Wang21 established a planetary gear torsional vibration model considering clutch friction torque and other factors, and studied the influence of clutch friction torque and planetary gear meshing stiffness on system vibration. Chen22 established a nonlinear dynamics model of two-stage gear transmission system with overrunning clutch, numerically solved the model with Runge–Kutta method, and studied the influence of gear modulus and clutch torsional stiffness on dynamic characteristics of the system.

Through the above analysis, it can be seen that although there have been some studies on the nonlinear characteristics of planetary gear and friction clutch, there are still few studies on the coupling system combined with them, and the influence of the dynamic friction coefficient of friction clutch on the stability of the coupling system is not clear in the research process. Therefore, this paper intends to establish pure torsional nonlinear dynamic differential equations considering the number of planetary wheels, gear clearance and clutch dynamic load by using the lumped-parameter method, and then solve the dimensionless differential equations by using the four-order Runge–Kutta method with variable step size. The influence of dynamic friction coefficient of friction clutch on nonlinear dynamic characteristics of two-speed transmission system is analyzed qualitatively. The research results can provide reference for the optimization design and manufacturing of the subsequent system.

High-gear in-gear dynamics model of a two-speed transmission system

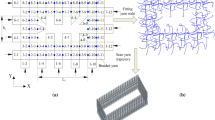
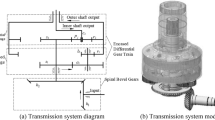
The structure schematic diagram of the two-speed transmission system is shown in Fig. 1. When the friction clutch is released, the planetary frame is connected with the overrunning clutch in the locked state. The power goes through the sun wheel in turn, the middle two planetary wheels, and then the inner gear ring output. At this time, it corresponds to the low gear state. When the friction clutch is engaged, the overrunning clutch is in the overrunning state, and the planetary frame can rotate freely at this time. The power also goes through the sun wheel, the middle two planetary wheels, and the inner gear ring output, which corresponds to the high gear state at this time. In this paper, the nonlinear characteristics of two-speed transmission system are studied for high speed in gear. Its dynamic model is shown in Fig. 2.

Figure 1
figure 1

A two-speed drivetrain: (a) Schematic with (1) The sun wheel, (2) The first stage planetary wheel, (3) The planetary shelf, (4) Input axis, (5) Overrunning clutch, (6) The first Second planetary wheel, (7) Inner gear ring, (8) Friction clutch, and (9) Output shaft; (b) 3D model.

Full size image
Figure 2
figure 2

High-speed gear dynamics model of two-speed transmission system.

Full size image

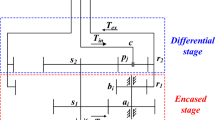
In the Fig. 2, Rbs is the radius of the solar wheel base circle; Rbp1 is the radius of the base circle of the first stage planetary gear. Rbp2 is the radius of the base circle of the second planetary gear. Rbr1 is the radius of the base circle of the inner gear ring; TD is the driving torque; TL is the load moment; JC is the moment of inertia of the planetary frame; θc is the torsional deformation of the planetary frame; JC1is the moment of inertia of the friction clutch input end; θc1 is the torsional deformation of the input end of the friction clutch; JC2 is the rotational inertia of the output end of the friction clutch; θc2 is the torsional deformation of the output end of the friction clutch; Jo is the moment of inertia of the load of the two-speed transmission system; θo is the torsional deformation of the load shaft of the two-speed transmission system. Ksp1 is the time-varying meshing stiffness of the solar wheel and the first stage planetary wheel; Csp1 is the meshing damping of the sun wheel and the first stage planetary wheel; Kp1p2 is the time-varying meshing stiffness of the second stage planetary gear and the first stage planetary gear. Cp1p2 is the meshing damping between the second stage planetary wheel and the first stage planetary wheel; Kp2r1 is the time-varying meshing stiffness between the inner gear ring and the second stage planetary gear. Cp2r1 is the meshing damping of the inner gear ring and the second stage planetary gear.

A mathematical model of a two-speed transmission system in high gear

As shown in Fig. 2, Ksp1(t)is the time-varying meshing stiffness of the solar wheel and the first stage planetary gear pair. Its value can be regarded as a rectangular wave, as shown in Eqs. (1)–(4):

$$k_{sp1} (t) = k_{sp1} (t + 2\pi /\omega ) = k_{sp1} + \sum\limits_{r = 1}^{R} {k_{sp1r} \cos (r\omega_{e} t{ - }\varphi_{r} )} ,$$
(1)
$${{k_{sp1} }}/ {{k_{tp} }} = \epsilon_{sp1} ,$$
(2)
$${{k_{\text{sp1r}} }}/{{k_{tp} }} = {{\sqrt {2 - 2\cos (2\pi r(\epsilon_{sp1} - 1))} }} / {(\pi r)},$$
(3)
$$\varphi_{{\text{sp}}1r} = a\tan ({{(1 - \cos (2\pi r(\epsilon_{sp1} - 1)))}} / {(\sin (2\pi r(\epsilon_{sp1} - 1)))}),$$
(4)
$$\left\{\begin{array}{c}{J}_{S}{\ddot{\theta }}_{S}+\sum_{i=1}^{N}({C}_{sp1i}({R}_{bs}{\dot{\theta }}_{s}-{R}_{bp1i}{\dot{\theta }}_{p1i}-{R}_{bc}{\dot{\theta }}_{c}-{\dot{e}}_{sp1i}\left(t\right)){R}_{bs}+{K}_{sp1i}({R}_{bs}{\theta }_{s}\\ -{R}_{bp1i}{\theta }_{p1i}-{R}_{bc}{\theta }_{c}-{e}_{sp1i}(t)){R}_{bs})={T}_{s}\\ {J}_{p1i}{\ddot{\theta }}_{p1i}+\frac{{R}_{bp1i}}{{R}_{bc}}{J}_{p1i}{\ddot{\theta }}_{c}-{C}_{sp1i}({R}_{bs}{\dot{\theta }}_{s}-{R}_{bp1i}{\dot{\theta }}_{p1i}-{R}_{bc}{\dot{\theta }}_{c}-{\dot{e}}_{sp1i}\left(t\right)){R}_{p1i}\\ -{K}_{sp1i}(({R}_{bs}{\theta }_{s}-{R}_{bp1i}{\theta }_{p1i}-{R}_{bc}{\theta }_{c}-{e}_{sp1i}(t)){R}_{p1i}\\ +{K}_{p1ip2i}({R}_{bp1i}{\theta }_{p1i}+{R}_{p2i}{\theta }_{p2i}-{e}_{p1ip2i}\left(t\right)){R}_{p1i}+{C}_{p1ip2i}({R}_{p1i}{\dot{\theta }}_{p1i}\\ +{R}_{bp2i}{\dot{\theta }}_{p2i}-{\dot{e}}_{p1ip2i}\left(t\right)){R}_{p1i}=0\\ {J}_{p2i}{\ddot{\theta }}_{p2i}+\frac{{r}_{bp2i}}{{r}_{bc}}{J}_{p2i}{\ddot{\theta }}_{c}-{C}_{p1ip2i}({R}_{bp1i}{\dot{\theta }}_{p1i}+{R}_{bp2i}{\dot{\theta }}_{p2i}-{\dot{e}}_{p1ip2i}\left(t\right)){R}_{p2i}\\ -{K}_{p1ip2i}(({R}_{bp1i}{\theta }_{p1i}+{R}_{bp2i}{\theta }_{p2i}-{e}_{p1ip2i}\left(t\right)){R}_{p2i}+{C}_{p2ir1}({R}_{br1}{\dot{\theta }}_{r1}\\ -{R}_{bp2i}{\dot{\theta }}_{p2i}-{R}_{bc}{\dot{\theta }}_{c}-{\dot{e}}_{p2ir1}\left(t\right)){R}_{p2i}+{K}_{p2ir1}({R}_{br1}{\theta }_{r1}-{R}_{bp2i}{\theta }_{p2i}\\ -{R}_{bc}{\theta }_{c}-{e}_{p2ir1}\left(t\right)){R}_{p2i}=0\\ {J}_{r1}{\ddot{\theta }}_{r1}+\sum_{i=1}^{N}\left({C}_{p2ir1}({R}_{br1}{\dot{\theta }}_{r1}-{R}_{bp2i}{\dot{\theta }}_{p2i}-{R}_{bc}{\dot{\theta }}_{c}-{\dot{e}}_{p2ir1}\left(t\right)){R}_{r1}\right){R}_{r1}+{K}_{p2ir1}({R}_{br1}{\theta }_{r1 } \\ -{R}_{bp2i}{\theta }_{p2i}-{R}_{bc}{\theta }_{c}-{e}_{p2ir1}\left(t\right)){R}_{r1})={T}_{r1}\\ \left({J}_{c}+{NJ}_{p1i}+{NJ}_{p2i}\right){\ddot{\theta }}_{c}+\sum_{i=1}^{N}(\frac{{r}_{bc}}{{r}_{bp1i}}{J}_{p1i}{\ddot{\theta }}_{p1i}+\frac{{r}_{bc}}{{r}_{p2i}}{J}_{p2i}{\ddot{\theta }}_{p2i})\\ -\sum_{i=1}^{N}({K}_{sp1i}{\theta }_{sp1i}({R}_{bs}{\theta }_{s}-{R}_{bp1i}{\theta }_{p1i}-{R}_{bc}{\theta }_{c}-{e}_{sp1i}(t){R}_{bs}\\ +{K}_{p2ir1}({R}_{br1}{\theta }_{r1}-{R}_{bp2i}{\theta }_{p2i}-{R}_{bc}{\theta }_{c}-{e}_{p2ir1}\left(t\right)){R}_{bs})\\ -\sum_{i=1}^{N}({C}_{sp1i}({R}_{bs}{\dot{\theta }}_{s}-{R}_{bp1i}{\dot{\theta }}_{p1i}-{R}_{bc}{\dot{\theta }}_{c}-{\dot{e}}_{sp1i}\left(t\right)){R}_{bs}\\ +{C}_{p2ir1}({R}_{br1}{\dot{\theta }}_{r1}-{R}_{bp2i}{\dot{\theta }}_{p2i}-{R}_{bc}{\dot{\theta }}_{c}-{\dot{e}}_{p2ir1}\left(t\right)){R}_{bs})\\ +{C}_{c1}\left({\dot{\theta }}_{c}-{\dot{\theta }}_{c1}\right)+{K}_{c1}\left({\theta }_{c}-{\theta }_{c1}\right)=0\\ {J}_{c1}{\ddot{\theta }}_{c1}-{C}_{c1}\left({\dot{\theta }}_{c}-{\dot{\theta }}_{c1}\right)-{K}_{c1}\left({\theta }_{c}-{\theta }_{c1}\right)=-{T}_{cl}\\ {J}_{c2}{\ddot{\theta }}_{c2}+{C}_{c2}\left({\dot{\theta }}_{c2}-{\dot{\theta }}_{O}\right)+{K}_{c2}\left({\theta }_{c2}-{\theta }_{O}\right)={T}_{cl}\\ {J}_{O}{\ddot{\theta }}_{O}-{C}_{c2}\left({\dot{\theta }}_{c2}-{\dot{\theta }}_{O}\right)-{K}_{c2}\left({\theta }_{c2}-{\theta }_{O}\right)={T}_{L}\end{array}\right. ,$$
(5)

where, Ksp1 is the average value of time-varying meshing stiffness; Ksp1r is the amplitude of the RTH harmonic; ϕsp1r is the phase Angle of the RTH harmonic; εsp1 is the coincidence degree between the solar gear and the first planetary gear; The first five harmonics can be taken to get a more accurate accuracy, so R = 5.

Assuming that all the gears are unmodified involute spur gears, and ignoring the bending deformation of the input and output shafts, the pure torsional nonlinear mathematical model of the two-speed transmission system as shown in Eq. (5) can be derived by using the concentrated parameter method and Newton's law.

Where θs, θp1i, θp2i and θr1 are respectively the torsional vibration displacements of the sun wheel, the i planetary wheel of the first stage, the i planetary wheel of the second stage and the inner gear ring (i = 1, 2, N). Differentiation concerning time; Input torque Ts(t) is the fluctuation value, which can be expressed as Ts(t) = Tsm + TsaT(t), where Tsm is the mean of the torque, TsaT(t) is the instantaneous fluctuation value, and can be expressed as TsaT(t) = TsaTsin(ωaTt + ϕaT); esp1i(t) is the static transmission error between the sun wheel and the first stage i planetary wheel, and is related to the manufacture and assembly of gears. It can be regarded as esp1i(t) = êsin(ωet + ϕe). Tc1 is the friction torque of the inner gear ring and the planetary frame, which is related to the pressure applied by the friction clutch, the number of friction plates and the friction coefficient of the friction plates, as shown in Eq. (6), where Ro is the radius of the outer circle of the friction plate, and Ri is the radius of the inner circle of the friction plate. TL(t) is the load torque applied on the output shaft of the driveline.

$${T}_{cl}=n{\int }_{{R}_{i}}^{{R}_{o}}dT=\frac{2}{3}\mu n{F}_{n}\left(\frac{{R}_{o}^{3}-{R}_{i}^{3}}{{R}_{o}^{2}-{R}_{i}^{2}}\right)$$
(6)

Suppose \({\text{x}}_{\text{s}}={\text{R}}_{\text{bs}}\theta_{\text{s}}\), \({\text{x}}_{\text{p1i}}={\text{R}}_{\text{bp1i}}\theta_{\text{p1i}}\), \({\text{x}}_{\text{p2i}}={\text{R}}_{\text{bp2i}}\theta_{\text{p2i}}\), \({\text{x}}_{\text{r1}}={\text{R}}_{\text{br1}}\theta_{\text{r1}}\), \({\text{x}}_{\text{c1}}={\text{R}}_{\text{bc}}\theta_{\text{c1}}\), \({\text{x}}_{\text{c2}}={\text{R}}_{\text{bc}}\theta_{\text{c2}}\), \({\text{x}}_{\text{o}}={\text{R}}_{\text{o}}\theta_{\text{o}}\), \({\text{x}}_{\text{c}}={\text{R}}_{\text{bc}}\theta_{\text{c}}\), where \({x}_{s}\), \({x}_{p1i}\), \({x}_{p2i}\), \({x}_{r1}\), \({x}_{c1}\), \({x}_{c2}\), \({x}_{o}\) are the equivalent linear displacements of the solar wheel, the planetary wheel 1, the planetary wheel 2, the inner gear ring, the input end of the friction clutch, the output end of the friction clutch, and the output shaft, respectively. By defining new variables \({\text{X}}_{\text{sp1i}}={\text{x}}_{\text{s}}-{\text{x}}_{\text{p1i}}-{\text{x}}_{\text{c}}-{\text{e}}_{\text{sp1i}}\left({\text{t}}\right)\), \({\text{X}}_{\text{r1p2i}}={\text{x}}_{\text{r1}}-{\text{x}}_{\text{p2i}}-{\text{x}}_{\text{c}}-{\text{e}}_{\text{r1p2i}}\left({\text{t}}\right)\), \({\text{X}}_{\text{p1ip2i}}={\text{x}}_{\text{p1i}}+{\text{x}}_{\text{p2i}}-{\text{e}}_{\text{p1ip2i}}\left({\text{t}}\right)\), \({\text{X}}_{\text{cc1}}={\text{x}}_{\text{c}}-{\text{x}}_{\text{c1}}\), \({\text{X}}_{\text{cl}}={\text{x}}_{\text{c1}}-{\text{x}}_{\text{c2}}\), \({\text{X}}_{\text{c2o}}={\text{x}}_{\text{c2}}-{\text{x}}_{\text{o}}\), \({\text{X}}_{\text{c1}}={\text{x}}_{\text{c1}}\), \({\text{X}}_{\text{c2}}={\text{x}}_{\text{c2}}\), \({\text{X}}_{\text{o}}={\text{x}}_{\text{o}}\).

The dimensionless time scale \({\tau}=t{aa}_{n}\) and the displacement scale \({b}_{c}\) are defined. \({\text{aa}}_{\text{n}}=\sqrt{{\text{K}}_{\text{sp1i}}{(}{\text{r}}_{\text{bs}}^{2}/{\text{J}}_{\text{bs}}+{\text{R}}_{\text{p1i}}^{2}/{\text{J}}_{\text{p1i}}{)}}\), \({\text{X}}_{\text{sp1i}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{\text{1i}}{\tau}\), \({\text{X}}_{\text{r1p2i}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{\text{2i}}{\tau}\), \({\text{X}}_{\text{p1ip2i}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{\text{3i}}{\tau}\), \({\text{X}}_{\text{cc1}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{4}{\tau}\), \({\text{X}}_{\text{cl}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{5}{\tau}\), \({\text{X}}_{\text{c2o}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{6}{\tau}\), \({\text{X}}_{\text{c1}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{7}{\tau}\), \({\text{X}}_{\text{c2}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{8}{\tau}\), \({\text{X}}_{\text{o}}\text{(t)=}{\text{b}}_{\text{c}}{{\text{q}}}_{9}{\tau}\).

$$\left[\begin{array}{ccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\ddot{q}}_{1i}\\ {\ddot{q}}_{2i}\\ {\ddot{q}}_{3i}\end{array}\\ \begin{array}{c}{\ddot{q}}_{4}\\ {\ddot{q}}_{5}\\ {\ddot{q}}_{6}\end{array}\\ \begin{array}{c}{\ddot{q}}_{7}\\ {\ddot{q}}_{8}\\ {\ddot{q}}_{9}\end{array}\end{array}\right]+\left[\begin{array}{ccccccccc}{\epsilon }_{11i}& 0& {\epsilon }_{13i}& 0& 0& 0& 0& 0& 0\\ 0& {\epsilon }_{22i}& {\epsilon }_{23i}& 0& 0& 0& 0& 0& 0\\ {\epsilon }_{31i}& {\epsilon }_{32i}& {\epsilon }_{33i}& {\epsilon }_{34i}& 0& 0& 0& 0& 0\\ 0& {\epsilon }_{42}& 0& {\epsilon }_{44}& 0& 0& 0& 0& 0\\ 0& 0& 0& {\epsilon }_{54}& 0& 0& 0& {\epsilon }_{58}& {\epsilon }_{59}\\ 0& 0& 0& 0& 0& 0& 0& {\epsilon }_{68}& {\epsilon }_{69}\\ 0& 0& 0& {\epsilon }_{74}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& {\epsilon }_{88}& {\epsilon }_{89}\\ 0& 0& 0& 0& 0& 0& 0& {\epsilon }_{98}& {\epsilon }_{99}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\dot{q}}_{1i}\\ {\dot{q}}_{2i}\\ {\dot{q}}_{3i}\end{array}\\ \begin{array}{c}{\dot{q}}_{4}\\ {\dot{q}}_{5}\\ {\dot{q}}_{6}\end{array}\\ \begin{array}{c}{\dot{q}}_{7}\\ {\dot{q}}_{8}\\ {\dot{q}}_{9}\end{array}\end{array}\right]+\left[\begin{array}{ccccccccc}{k}_{11i}& 0& {k}_{13i}& 0& 0& 0& 0& 0& 0\\ 0& {k}_{22i}& {k}_{23i}& 0& 0& 0& 0& 0& 0\\ {k}_{31i}& {k}_{32i}& {k}_{33i}& {k}_{34i}& 0& 0& 0& 0& 0\\ 0& {k}_{42}& 0& {k}_{44}& 0& 0& 0& 0& 0\\ 0& 0& 0& {k}_{54}& 0& 0& 0& {k}_{58}& {k}_{59}\\ 0& 0& 0& 0& 0& 0& 0& {k}_{68}& {k}_{69}\\ 0& 0& 0& {k}_{74}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& {k}_{88}& {k}_{89}\\ 0& 0& 0& 0& 0& 0& 0& {k}_{98}& {k}_{99}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{q}_{1i}\\ {q}_{2i}\\ {q}_{3i}\end{array}\\ \begin{array}{c}{q}_{4}\\ {q}_{5}\\ {q}_{6}\end{array}\\ \begin{array}{c}{q}_{7}\\ {q}_{8}\\ {q}_{9}\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{P}_{S}-{\ddot{e}}_{sp1i}\left(t\right)\\ {P}_{r1}-{\ddot{e}}_{r1p1i}\left(t\right)\\ -{\ddot{e}}_{p1ip2i}\left(t\right)\end{array}\\ -\begin{array}{c}{P}_{1}\\ {P}_{1}-{P}_{2}\\ {P}_{2}+{P}_{3}\end{array}\\ \begin{array}{c}-{P}_{1}\\ {P}_{2}\\ {P}_{3}\end{array}\end{array}\right]$$
(7)

where:

\({\epsilon }_{11i}=\sum_{i=1}^{N}\frac{{C}_{sp1i}}{{m}_{S}{\omega }_{n}}+\frac{{C}_{sp1i}}{{m}_{p1i}{\omega }_{n}}\), \({\epsilon }_{13i}=-\frac{{C}_{p1ip2i}}{{m}_{p1i}{\omega }_{n}}\), \({\epsilon }_{22i}=\sum_{i=1}^{N}\frac{{C}_{p2ir1}}{{m}_{r1}{\omega }_{n}}-\frac{{C}_{p2ir1}}{{m}_{p2i}{\omega }_{n}}\), \({\epsilon }_{23i}=\frac{{C}_{p1ip2i}}{{m}_{p2i}{\omega }_{n}}\), \({\epsilon }_{31i}=-\frac{{C}_{sp1i}}{{m}_{p1i}{\omega }_{n}}\), \({\epsilon }_{32i}=\sum_{i=1}^{N}\frac{4{C}_{p2ir1}}{{m}_{c}{\omega }_{n}}+\frac{{C}_{p2ir1}}{{m}_{p2i}{\omega }_{n}}\), \({\epsilon }_{33i}=\frac{{C}_{p1ip2i}}{{m}_{p1i}{\omega }_{n}}-\frac{{C}_{p1ip2i}}{{m}_{p2i}{\omega }_{n}}\), \({\epsilon }_{34i}=-\frac{2{C}_{c1}}{{m}_{c}{R}_{bc}^{2}{\omega }_{n}}\), \({\epsilon }_{42}=-\sum_{i=1}^{N}\frac{2{C}_{p2ir1}}{{m}_{c}{\omega }_{n}}\), \({\epsilon }_{44}=\frac{{C}_{c1}}{{R}_{bc}^{2}{m}_{c}{\omega }_{n}}+\frac{{C}_{c1}}{{R}_{bc}^{2}{m}_{c1}{\omega }_{n}}\), \({\epsilon }_{54}=-\frac{{C}_{c1}}{{R}_{bc}^{2}{m}_{c1}{\omega }_{n}}\), \({\epsilon }_{58}=-\frac{{C}_{c2}}{{R}_{bc}^{2}{m}_{c2}{\omega }_{n}}\), \({\epsilon }_{59}=\frac{{C}_{c2}}{{R}_{bc}{{R}_{O}m}_{c2}{\omega }_{n}}\), \({\epsilon }_{68}=\frac{{C}_{c2}}{{R}_{bc}^{2}{m}_{c2}{\omega }_{n}}+\frac{{C}_{c2}}{{R}_{bc}^{2}{m}_{O}{\omega }_{n}}\), \({\epsilon }_{69}=-\frac{{C}_{c2}}{{R}_{bc}{{R}_{O}m}_{c2}{\omega }_{n}}-\frac{{C}_{c2}}{{R}_{bc}{{R}_{O}m}_{O}{\omega }_{n}}\), \({\epsilon }_{88}=\frac{{C}_{c2}}{{R}_{bc}^{2}{m}_{c2}{\omega }_{n}}\), \({\epsilon }_{89}=-\frac{{C}_{c2}}{{R}_{bc}{{R}_{O}m}_{c2}{\omega }_{n}}\), \({\epsilon }_{98}=-\frac{{C}_{c2}}{{R}_{bc}^{2}{m}_{O}{\omega }_{n}}\), \({\epsilon }_{99}=\frac{{C}_{c2}}{{R}_{bc}{{R}_{O}m}_{O}{\omega }_{n}}\), \({k}_{11i}=\sum_{i=1}^{N}\frac{{K}_{sp1i}}{{m}_{S}{{\omega }_{n}}^{2}}+\frac{{K}_{sp1i}}{{m}_{p1i}{{\omega }_{n}}^{2}}\), \({k}_{13i}=-\frac{{K}_{p1ip2i}}{{m}_{p1i}{{\omega }_{n}}^{2}}\), \({k}_{22i}=\sum_{i=1}^{N}\frac{{K}_{p2ir1}}{{m}_{r1}{{\omega }_{n}}^{2}}-\frac{{K}_{p2ir1}}{{m}_{p2i}{{\omega }_{n}}^{2}}\), \({k}_{23i}=\frac{{K}_{p1ip2i}}{{m}_{p2i}{{\omega }_{n}}^{2}}\), \({k}_{31i}=-{K}_{12i}=\frac{{K}_{sp1i}}{{m}_{p1i}{{\omega }_{n}}^{2}}\), \({k}_{32i}=\frac{{K}_{p2ir1}}{{m}_{p2i}{{\omega }_{n}}^{2}}+\sum_{i=1}^{N}\frac{4{K}_{p2ir1}}{{m}_{c}{{\omega }_{n}}^{2}}\), \({k}_{33i}=\frac{{K}_{p1ip2i}}{{m}_{p1i}{{\omega }_{n}}^{2}}-\frac{{K}_{p1ip2i}}{{m}_{p2i}{{\omega }_{n}}^{2}}\), \({k}_{34i}=-\frac{2{K}_{c1}}{{m}_{c}{R}_{bc}^{2}{{\omega }_{n}}^{2}}\), \({k}_{42}=-\sum_{i=1}^{N}\frac{2{K}_{p2ir1}}{{m}_{c}{{\omega }_{n}}^{2}}\), \({k}_{44}=\frac{{K}_{c1}}{{R}_{bc}^{2}{m}_{c}{{\omega }_{n}}^{2}}+\frac{{K}_{c1}}{{R}_{bc}^{2}{m}_{c1}{{\omega }_{n}}^{2}}\), \({k}_{54}=-\frac{{K}_{c1}}{{R}_{bc}^{2}{m}_{c1}{{\omega }_{n}}^{2}}\), \({k}_{58}=-\frac{{K}_{c2}}{{R}_{bc}^{2}{m}_{c2}{{\omega }_{n}}^{2}}\),\({k}_{59}=\frac{{K}_{c2}}{{R}_{bc}{{R}_{O}m}_{c2}{{\omega }_{n}}^{2}}\), \({k}_{68}=\frac{{K}_{c2}}{{R}_{bc}^{2}{m}_{c2}{{\omega }_{n}}^{2}}+\frac{{K}_{c2}}{{R}_{bc}^{2}{m}_{O}{{\omega }_{n}}^{2}}\), \({k}_{69}=-\frac{{K}_{c2}}{{R}_{bc}{{R}_{O}m}_{c2}{{\omega }_{n}}^{2}}-\frac{{K}_{c2}}{{R}_{bc}{{R}_{O}m}_{O}{{\omega }_{n}}^{2}}\), \({k}_{88}=\frac{{K}_{c2}}{{R}_{bc}^{2}{m}_{c2}{{\omega }_{n}}^{2}}\), \({k}_{89}=-\frac{{K}_{c2}}{{R}_{bc}{{R}_{O}m}_{c2}{{\omega }_{n}}^{2}}\), \({k}_{98}=\frac{{K}_{c2}}{{R}_{bc}^{2}{m}_{O}{{\omega }_{n}}^{2}}\), \({k}_{99}=-\frac{{K}_{c2}}{{R}_{bc}{{R}_{O}m}_{O}{{\omega }_{n}}^{2}}\), \({P}_{S}=\frac{{F}_{S}}{{m}_{S}{b}_{c}{\omega }_{n}^{2}}\), \({P}_{r1}=\frac{{F}_{r1}}{{m}_{r1}{b}_{c}{\omega }_{n}^{2}}\), \({P}_{1}=\frac{{F}_{cl}}{{m}_{c1}{b}_{c}{\omega }_{n}^{2}}\), \({P}_{2}=\frac{{F}_{cl}}{{m}_{c2}{b}_{c}{\omega }_{n}^{2}}\), \({P}_{3}=\frac{{F}_{L}}{{m}_{O}{b}_{c}{\omega }_{n}^{2}}\).

Including \({m}_{s}=\frac{{J}_{s}}{{{r}_{bs}}^{2}}\), \({m}_{p1i}=\frac{{J}_{p1i}}{{{r}_{bp1i}}^{2}}\), \({m}_{p2i}=\frac{{J}_{p2i}}{{{r}_{bp2i}}^{2}}\), \({m}_{r}=\frac{{J}_{r}}{{{r}_{br}}^{2}}\), \({m}_{c}=\frac{{J}_{c}}{{{r}_{bc}}^{2}}\).

Parameter study

The basic parameters of the two-speed transmission system are shown in Table 1. The Runge–Kutta method with fourth-order variable step size is used to solve the equation set 7. The initial values of all displacements are 0, and the initial values of all velocities are 0.01, and the solution interval is [0, 600t].

Table 1 Two-speed transmission system parameters.
Full size table

The influence of excitation frequency

Figure 3 shows the dimensionless torsional vibration bifurcation diagram of the inner gear ring drawn with the excitation frequency of ωh as the control variable in the high speed mode of the two-speed transmission system. It can be seen from the Fig. 3 that there is an obvious jump phenomenon at ωh = 0.65 and at ωh = 0.87 of the inner gear ring. When 0.65 ≤  ωh ≤ 0.87, the inner gear ring moves in a single periodic motion, and the vibration increases with the increase of the excitation frequency. When the excitation frequency is in the low frequency band (ωh ≤ 0.65 and 0.87 ≤ ωh ≤ 1.02) and the high frequency band (ωh ≥ 2.0), the torsional vibration is a relatively stable single periodic motion, which is not affected by the excitation frequency. When the excitation frequency is in the range of 1.04 ≤ ωh ≤ 1.25, 1.41 ≤ ωh ≤ 1.87, the inner gear ring enters the chaotic region. When the excitation frequency is within 1.27 ≤ ωh ≤ 1.4, the motion of the system is a double cycle motion. In the range of 1.88 ≤ ωh ≤ 1.98, the movement of the system changes from double period to single period. Figure 4 shows the time domain diagram, phase diagram and Poincare cross section diagram of the system at the excitation frequency point ωh = 0.7633, 1.6196, 1.9332 and 2.2588, which respectively correspond to quasi-periodic, chaotic, double cycle and haploid periodic motions.

Figure 3
figure 3

Global bifurcation diagram of torsional vibration of internal gear ring varying with excitation frequency ωh.

Full size image
Figure 4
figure 4

Time domain diagram, phase diagram and Poincare cross section diagram corresponding to different excitation frequency points of inner gear ring: (a) ωh = 0.7633, (b) ωh = 1.6196, (c) ωh = 1.9332, (d) ωh = 2.2588.

Full size image

Influence law of dynamic friction coefficient of friction clutch

Figure 5 shows the influence of dynamic friction coefficient of friction clutch on bifurcation characteristics of internal gear ring. As can be seen from the figure, with the increase of the dynamic friction coefficient, the oscillation value of the system in the unstable region can be effectively suppressed. From Fig. 5a–c, it can be seen that the system experienced quasi-periodic motion and haploperiodic motion in the whole excitation frequency range. In the low frequency band ωh ≤ 0.5, the motion of the system fluctuates up and down in a small range, and enters a quasi-periodic motion in the range of 0.5 ≤ωh ≤ 0.6, and then appears an obvious jump phenomenon. When the excitation frequency ωh ≥ 1.0, the dynamic friction coefficient of the friction clutch has almost no effect on the bifurcation characteristics of the system. With the increase of the excitation frequency, the system keeps a single periodic motion. As can be seen from Fig. 5d–g, the bifurcation structure, motion form and chaotic response region of the system are significantly changed when the dynamic friction coefficient is small. In the range of low frequency band (ωh ≤ 0.65), with the reduction of friction coefficient, the fluctuation caused by the system movement is effectively alleviated. As the excitation frequency increases, it can be seen from the Fig. 5 that there is an obvious jump phenomenon, but the peak of the jump can be reduced by reducing the friction coefficient. When the excitation frequency ωh ≥ 0.9, the system experienced a single periodic motion, chaotic motion, and double periodic motion. When the excitation frequency is 0.9 ≤ ωh ≤ 1.5, the movement of the system enters into chaotic motion from single-fold periodic motion and then into double periodic motion. In this frequency range, with the decrease of friction coefficient, the area of chaotic response of the system gradually widens and the single-fold periodic motion is reduced. This shows that the reduction of the dynamic friction coefficient of the friction clutch makes the motion response of the system more complex in the excitation frequency of 0.9 ≤ ωh ≤ 1.5. In the range of high frequency band (ωh ≥ 2.0), the dynamic friction coefficient of friction clutch has almost no effect on the bifurcation structure and motion form of the system, and the system keeps the single-fold periodic motion.

Figure 5
figure 5

Influence of dynamic friction coefficient of friction clutch on bifurcation characteristics of internal gear ring. (a) μ = 0.17, (b) μ = 0.16, (c) μ = 0.15, (d) μ = 0.14, (e) μ = 0.13, (f) μ = 0.12, (g) μ = 0.11.

Full size image

Conclusion

The dynamic differential equation of pure torsional nonlinear dynamic load is established by lumped parameter method, and the parameters of planetary wheel number, backlash and clutch dynamic load are considered in the modeling process, and the equations are dimensionless. Then the fourth order Runge–Kutta method with variable step size is used to solve the dimensionless differential equation, and the phase diagram and Poincare diagram in the high-speed gear file are obtained. By changing the friction coefficient of the friction clutch, the influence of parameter change on the nonlinear dynamic characteristics of the system is analyzed, and the following conclusions are obtained:

  1. (1)

    With the increase of excitation frequency, the system went through a single period, a quasi period, chaos, a double period, and then the second period turned into chaotic motion, and then the second period turned into a double period and a single period motion, and the path to the chaos was found out. To make the system have good dynamic characteristics, the excitation frequency of the system should be guaranteed to be small or large.

  2. (2)

    In the low-frequency band (ωh ≤ 0.9), the friction coefficient of the friction clutch can be reduced to reduce the vibration amplitude; In the middle-frequency band (0.9 ≤ ωh ≤ 1.9), reducing the friction coefficient will make the system tend to be unstable vibration. In the high-frequency band (1.9 ≤ ωh ≤ 2.5), it is a single-times periodic motion, which is not affected by the friction coefficient. In order to make the system have good stability and reduce the vibration of the system during operation, when the system is in the low-frequency stage, it is more appropriate to select a smaller value for the friction coefficient of the friction clutch; When the system is in the intermediate frequency stage, it is more appropriate to take a larger value for the friction coefficient of the friction clutch; When the system is in the high-frequency phase, the friction coefficient can be optionally selected because the coefficient of friction has little effect on the stability of the system.

Limitations and deficiencies

  1. (1)

    This paper adopts the lumped parameter method in modeling and the Runge–Kutta method in solving differential equations, which is a commonly used modeling and solving method for system dynamics. However, the lumped parameter method is a simplified modeling method, which usually regards the shaft as a point mass or a rigid connection, and has certain limitations in capturing the deflection and deformation of the shaft.

  2. (2)

    In future studies, under the condition that the amount of calculation is appropriate, if the accuracy is required to be high, the potential energy method or Timoshenko theory can be considered for modeling, which will make the results more accurate.