Introduction

Coaxial rigid rotor is an important technology for helicopters to achieve high-speed flight, but the characteristics of constant velocity reverse rotation of internal and external rotor shaft bring challenges to the structure and parameter design of the transmission system. There are currently four configurations which are cylindrical gear meshing1,2,3, bevel gear meshing4,5,6,7, face gear meshing8,9and encased differential planetary gear meshing10 respectively that can realize coaxial reversal output by searching for published papers and patents at home and abroad. Encased differential planetary gear train is a composite transmission configuration that couples star gear train and planetary gear train, which has the advantages of excellent bearing capacity and compact structure and has been widely used in ship engineering. However, due to the influence of the structure and the load distribution of the internal and external rotor shaft, the encased differential planetary gear train has problems such as nonuniform power distribution of the encased and differential stage system, power flow cycle and so on, resulting in its load sharing characteristics are more complex than that of star gear train or planetary gear train. In order to improve the load sharing performance of the system, it is necessary to study the load sharing structural parameters of the encased differential planetary gear train.

The transmission shaft and aeronautical gear in the helicopter main gearbox are generally connected by splines, and when the splines have radial clearance, the floating of the gear can be realized to improve the load sharing performance, which has attracted the attention of some scholars. Dong et al.11,12,13 carried out the research on the load sharing characteristics of floating spline clearance on planetary gear train, power split transmission and face gear transmission system respectively. The results show that gear floating can obviously improve the load-sharing performance. Shen et al.14 analyzed the influence of the internal and external spline clearance on the load sharing characteristics of the planetary gear train, but ignored the continuity of the spline support reaction force. Guo Fang et al.15 analyzed the effect of floating spline structure on the performance and stability of the star gear train. From the above research, it can be concluded that the floating spline structure is of great help to improve the load sharing performance of star gear train and planetary gear train, thus it can be applied to encased differential planetary gear train to enhance its load sharing performance.

The dynamic behavior of encased differential planetary gear systems have also attracted the attention of many researchers. Tan et al.16 conducted experimental research on encased differential planetary gearboxes with three load sharing methods: sun gear floating, flexible pin shaft and flexible inner ring gear, and explored the characteristics of encased differential planetary transmission load sharing performance with multiple load sharing measures. Hu et al.17 investigates the effect of random error on the dynamic load sharing characteristics of encased differential planetary gear train. Mo et al.18 established the nonlinear dynamic mode of encased differential planetary gear train and analyzed the effect of load torque on dynamic behavior. Zhu et al.19 established pure torsional freedom vibration equation of encased differential planetary train and used the multi-scale method to derive the stability conditions of summation resonance frequencies caused by the meshing stiffness fluctuations for this train. Shi et al.20 built a coupled dynamic model of a coaxial counter-rotating epicyclic transmission system based on the gear system dynamics and Lagrange equation, and the displacement response, speed response and the load distributions were achieved by the numerical analysis method. Kuznetsova et al.21 constructed the dynamic model of encased differential planetary gear train used in drilling technology and the influence of the parameters of the system on the eigenfrequencies of the oscillations is estimated. Sun et al.22 established a torsional-lateral dynamic model of encased differential planetary gear train and predicted the dynamic characteristics of the system.

Although scholars have carried out deep research on the dynamic behavior of encased differential planetary gear trains, there is little literature on the analysis of the load sharing behavior of encased differential planetary gear trains. Moreover, most of the research objects are single output configurations, and there is no problem of the influence of internal and external output shaft loads on the load sharing characteristics of the system, so it is necessary to conduct research on the load sharing characteristics of encased differential planetary gear trains for coaxial-counter rotating configurations. In this paper, a dynamic model with floating splines is established to analyze the effects of input torque, spline clearance, spline shaft stiffness and friction coefficient on the load sharing characteristics of the system, and provide guidance and reference for the design of floating spline structure.

The dynamic load-sharing model of encased differential planetary gear train

Basic structure of encased differential planetary gear train

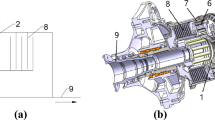
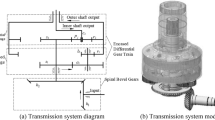
The encased differential planetary gear train consists of an encased stage star gear train and a differential stage planetary gear train, and the diagram is shown in Fig. 123. The encased star gear train is composed of sun gear s1, star gear ai, bi(i = 1, 2, …, M) and inner ring gear r1, and the differential stage planetary gear train is composed of sun gear s2, planetary gear pj(j = 1, 2,…, N) and inner ring gear r2. The star gear system is a fixed-axis system in which the carrier remains stationary, and the ring gear serves as the output. This configuration is utilized in the literature24. On the other hand, the traditional planetary gear system is a rotating system where the ring gear remains fixed, and the carrier serves as the output. This configuration is used in the literature25. This paper employs a differential planetary gear system, where both the ring gear r2 and the carrier c can rotate. However, the speeds of the sun gear s2 and the ring gear r2 can be controlled by the sun gear s1, thus achieving closed-loop motion functionality. The power transmission of the system can be divided into two paths, one is output by r1 through the encased stage system, and the other is output by r2 through the differential stage system. The constant velocity reverse output of the internal and external rotor shafts can be realized through structural parameter design.

Figure 1
figure 1

Motion diagram of encased differential planetary gear train.

Full size image

The motion equations of the encased stage and differential stage system can be denoted by Eqs. (1), (2), respectively.

$$\omega_{r1} = - \frac{{z_{s1} z_{b1} }}{{z_{r1} z_{a1} }} \cdot \omega_{s1}$$
(1)
$$\frac{{\omega_{s2} - \omega_{c} }}{{\omega_{r2} - \omega_{c} }} = - \frac{{z_{r2} }}{{z_{s2} }}$$
(2)

where ωi(i = s1, s2, a1, b1, r1, r2) represent angular velocity corresponding to gear; zi(i = s1, s2, a1, b1, r1, r2) represent the teeth number corresponding to gear.

Furthermore, since the sun gears s1 and s2 are connected, and the ring gears r1 and r2 are connected, it follows that

$$\left\{ \begin{gathered} \omega_{s1} = \omega_{s2} \hfill \\ \omega_{r1} = \omega_{r2} \hfill \\ \end{gathered} \right.$$
(3)

By simultaneously solving Eqs. (1)–(3). Eq. (4) can be obtained.

$$\left\{ \begin{gathered} \omega_{r2} = - \frac{{z_{s1} z_{b1} }}{{z_{r1} z_{a1} }}\omega_{s1} \hfill \\ \omega_{c} = \frac{{z_{s2} z_{r1} z_{a1} - z_{r2} z_{s1} z_{b1} }}{{z_{r1} z_{a1} (z_{s2} + z_{r2} )}}\omega_{s1} \hfill \\ \end{gathered} \right.$$
(4)

To achieve the counter-rotating output of the carrier c and the ring gear r2, it is necessary to satisfy the condition of Eq. (5).

$$\omega_{c} = - \omega_{r2}$$
(5)

By simultaneously solving Eqs. (4), (5), the meshing conditions required to achieve the counter-rotating output of the encased differential planetary gear system can be obtained which can refer to Eq. (6).

$$\frac{{z_{s2} z_{r1} z_{a1} - z_{r2} z_{s1} z_{b1} }}{{z_{s1} z_{b1} (z_{s2} + z_{r2} )}}{ = }1$$
(6)

Time varying meshing stiffness

Since the coincidence of gears is generally not an integer, there is a situation of alternating meshing of single and double teeth, resulting in time varying meshing stiffness, which is calculated according to the method from literature25, as shown in Eq. (7).

$$k_{m} (t) = k_{m}^{a} + 2k_{m}^{v} \sum\limits_{n = 1}^{\infty } {(a_{n} \cos n\omega t + b_{n} \sin n\omega t)}$$
(7)

where \({\text{k}}_{\text{m}}^{\text{a}}\) represents the comprehensive meshing stiffness of the gear pair m, \(2{\text{k}}_{\text{m}}^{\text{v}}\) is the stiffness fluctuation value, an, bn are the Fourier transform coefficient, ω is the meshing period of the gear pair. The calculation of stiffness parameter values can be referred to Eqs. (8)–(11).

$$a_{n} = \frac{{sin(2n\pi \varepsilon_{m} )}}{n\pi }$$
(8)
$$b_{n} = \frac{{2[sin(n\pi \varepsilon_{m} )]^{2} }}{n\pi }$$
(9)
$$k_{m}^{a} = (\varepsilon_{m} - 1)k_{m}^{\max } + (2 - \varepsilon_{m} )k_{m}^{\min }$$
(10)
$$2k_{m}^{v} = k_{m}^{\max } - k_{m}^{\min }$$
(11)

where \({\text{k}}_{\text{m}}^{\text{min}}\) denotes the single contact stiffness, \({\text{k}}_{\text{m}}^{\text{max}}\) denotes the comprehensive meshing stiffness, εm denotes the contact ratio of the gear pair, which can be referred to Eq. (12)–(14).

$$\begin{aligned} q = & 0.04723 + \frac{0.15551}{{z_{n1} }} + \frac{0.25791}{{z_{n2} }} - 0.00635x_{1} - 0.11654\frac{{x_{1} }}{{z_{n1} }} \mp 0.00193x_{2} \\ & \quad - 0.24188\frac{{x_{2} }}{{z_{n2} }} + 0.00529x_{1}^{2} + 0.00182x_{2}^{2} \\ \end{aligned}$$
(12)
$$k_{m}^{min} = C_{M} C_{R} C_{B} cos\beta /q$$
(13)
$$k_{m}^{max} = (0.75\varepsilon + 0.25)k_{m}^{min}$$
(14)

where zni, xi(i = 1, 2) represents the tooth number and modification coefficient of gear(i = 1 for pinion gear, i = 2 for bull gear), “−” and “ + ” are used for external meshing and internal meshing in the symbol “\(\mp\)” respectively. CM denotes the theoretical correction coefficient which is generally 0.8, CR is the structural coefficient of the billet which is generally 1, CB is the basic tooth profile coefficient which is generally 1, β is the helix angle of the gear, ε is the contact ratio of gear pair.

The meshing damping26 of the gear pair can be expressed as

$$c_{m} = 2\xi_{m} \sqrt {\frac{{I_{m1} \cdot I_{m2} }}{{I_{m1} \cdot r_{bm2}^{2} + I_{m2} \cdot r_{bm1}^{2} }}k_{m}^{a} }$$
(15)

where ξm is the meshing damping ratio of the gear, the value ranges from 0.03 to 0.17, Im is the moment of inertia (1 corresponds to the pinion gear, 2 corresponds to the bull gear), and rm is the radius of the base circle of the gear.

Equivalent meshing error

The equivalent meshing error of the gear mainly includes manufacturing error and installation error. There are many types of manufacturing error, such as eccentricity error and tooth profile error, and this article mainly focuses on eccentricity error. Installation error refers to the error caused by the actual installation position of the gear deviating from its theoretical installation position during the installation process, and the error size is constant. Taking the planetary gear train as an example, Fig. 2 is a schematic diagram of the manufacturing error and installation error of the sun gear and the planetary gear. In the figure, the actual centroid position and the actual installation position are placed at the same point Os', Op', and the ideal centroid position and the ideal installation position are placed at the same point Os, Op.

Figure 2
figure 2

Schematic diagram of manufacturing error and installation error of the sun gear and the planetary gear.

Full size image

The manufacturing and installation errors of the external meshing pair are shown as Eq. (16).

$$\left\{ \begin{gathered} e_{Esi} = E_{s} sin[(\omega_{s} - \omega_{c} )t + \beta_{s} + \alpha_{w} - \varphi_{i} ] \hfill \\ e_{Asi} = A_{s} sin[ - \omega_{c} t + \gamma_{s} + \alpha_{w} - \varphi_{i} ] \hfill \\ e_{Espi} = E_{p} sin[(\omega_{p} - \omega_{c} ) + \beta_{pi} + \alpha_{w} ] \hfill \\ e_{Aspi} = A_{p} sin(\gamma_{pi} + \alpha_{w} ) \hfill \\ \end{gathered} \right.$$
(16)

where E, A are the manufacturing error amplitude and the installation error amplitude respectively. ωs, ωc are the angular velocity of the sun gear and the planetary carrier, respectively, and when the system is a fixed shaft gear train, ωc = 0. αw is meshing angle of the external meshing gear pair, φi is the position angle of the ith planetary gear relative to the initial position, which can be expressed as φi = 2π(i − 1)/Np + φ0, φ0 is the initial position angle, Np is the number of planetary gear. βs and γs are the initial phase of manufacturing and installation errors of the sun gear, respectively. βpi and γpi are the initial phase of manufacturing and installation errors of the planet gears.

The manufacturing and installation errors of the internal meshing pair are shown as Eq. (17).

$$\left\{ \begin{gathered} e_{Eri} = E_{r} sin[ - \omega_{c} t + \beta_{r} - \alpha_{n} - \varphi_{i} ] \hfill \\ e_{Ari} = A_{r} sin[ - \omega_{c} t + \gamma_{r} - \alpha_{n} - \varphi_{i} ] \hfill \\ e_{Erpi} = E_{p} sin[(\omega_{p} - \omega_{c} )t + \beta_{pi} - \alpha_{n} ] \hfill \\ e_{Arpi} = A_{p} sin(\gamma_{pi} - \alpha_{n} ) \hfill \\ \end{gathered} \right.$$
(17)

where αn is the meshing angle of the inner meshing pair, βr, γr are the initial phases of manufacturing error and the installation error of the internal ring gear respectively.

The equivalent meshing error27 of the gear pair is

$$\left\{ \begin{gathered} e_{spi} = e_{Esi} + e_{Asi} + e_{Espi} + e_{Aspi} \hfill \\ e_{rpi} = e_{Eri} + e_{Ari} + e_{Erpi} + e_{Erpi} \hfill \\ \end{gathered} \right.$$
(18)

Dynamic model of encased differential planetary gear train

The encased differential planetary gear system has (15 + 6 M + 3N) degrees of freedom, and its generalized coordinates are as follow.

$$\begin{gathered} {\text{X}} = \left( {x_{{{\text{r1}}}} ,y_{{{\text{r1}}}} ,\phi_{{{\text{r1}}}} ,x_{{{\text{s1}}}} ,y_{{{\text{s1}}}} ,\phi_{{{\text{s1}}}} ,\zeta_{{{\text{ai}}}} ,\eta_{{{\text{ai}}}} ,\phi_{{{\text{ai}}}} ,\zeta_{{{\text{bi}}}} ,\eta_{{{\text{bi}}}} ,\phi_{{{\text{bi}}}} ,x_{{{\text{r2}}}} ,y_{{{\text{r2}}}} ,\phi_{{{\text{r2}}}} ,x_{{{\text{s2}}}} ,y_{{{\text{s2}}}} ,\phi_{{{\text{s2}}}} ,x_{{\text{c}}} ,y_{{\text{c}}} ,\phi_{{\text{c}}} ,\zeta_{{{\text{pj}}}} ,\eta_{{{\text{pj}}}} ,\phi_{{{\text{pj}}}} } \right)^{T} \hfill \\ \quad \quad \left( {i = {1},{2}, \ldots ,M,\;j = {1},{2}, \ldots ,N} \right) \hfill \\ \end{gathered}$$

where r1, s1, ai, bi represent the internal gear, sun gear, first stage star gear, and second stage star gear of the encased stage system. r2, s2, c, pj represent the internal gear, sun gear, carrier, and planet gear of the differential stage system. M and N represent the number of star gear and planet gear, which are both taken 3 in this paper. x, y, φ represent the horizontal displacement, vertical displacement, and torsional displacement of the components. ξ, η are the radial and tangential displacements of the star gear or planet gear.

The relative meshing displacement of the star gear train or planetary gear train meshing pair along the direction of the meshing line can be expressed as

$$\delta_{mn} = V_{mn} q_{mn} - e_{mn} (t)$$
(19)

where Vmn represents the meshing vector, with the external meshing shown in Eq. (20), and the internal meshing shown in Eq. (21). qmn represents the degree of freedom involved in meshing, as shown in Eq. (22). emn represents the equivalent meshing error of the meshing pair mn. When the system is star gear train, m = s1, r1, n = ai、bi(i = 1, 2,…, M). When the system is planetary gear system, m = s2, r2, n = pj(j = 1, 2,…, N).

$$V_{mn} = \left[ {\begin{array}{*{20}l} {sin\psi_{mn} } \hfill & {\quad cos\psi_{mn} } \hfill & {\quad r_{bm} } \hfill & {\quad - sin\psi_{mn} } \hfill & {\quad - cos\psi_{mn} } \hfill & {\quad - r_{bm} } \hfill \\ \end{array} } \right]$$
(20)
$$V_{mn} = \left[ {\begin{array}{*{20}c} { - sin\psi_{mn} } & {\quad cos\psi_{mn} } & {\quad - r_{bm} } & {\quad sin\psi_{mn} } & {\quad - cos\psi_{mn} } & {\quad r_{bm} } \\ \end{array} } \right]$$
(21)
$$q_{mn} = \left[ {\begin{array}{*{20}c} {x_{m} } & {\quad y_{m} } & {\quad \phi_{m} } & {\quad \zeta_{n} } & {\quad \eta_{n} } & {\quad \phi_{n} } \\ \end{array} } \right]^{T}$$
(22)

when the meshing form is external meshing, ψmn = αm-φi, the meshing form is internal meshing, ψmn = αm + φi. αm represents the pressure angle of component m.

Figures 3 and 4 show the dynamic model of the encased star gear train and the differential planetary gear train respectively. The Lagrange equation is used to derive the dynamic equation, and the derivation process can be referred to literature28, which is no longer mentioned in this article. The overall dynamic matrix is

$$M\left\{ {\ddot{x}} \right\} + \left( {C + \omega_{c} G} \right)\left\{ {\dot{x}} \right\} + \left( {K_{b} + K_{m} - \omega_{c}^{2} K_{\omega } } \right)\left\{ x \right\} = Q$$

where M is the mass matrix, C is the damping matrix, G is the gyroscopic matrix, Kb is the support stiffness matrix, Km is the meshing stiffness matrix, Kω is the centrifugal stiffness matrix, Q is the excitation vector.

Figure 3
figure 3

Dynamic model of encased star gear train.

Full size image
Figure 4
figure 4

Dynamic model of differential planetary gear train.

Full size image

Calculation model of load sharing coefficient

Due to manufacturing error, installation errors and etc., the load distribution between the star gear or planetary gear is not equal. The LSC(load sharing coefficient) is usually used to describe the load distribution between the central member (sun gear, ring gear) and the planetary gear or star gear. The smaller the LSC, the better the load sharing performance of the system. The load sharing factor can be obtained from Eq. (23)–(24)29.

$$\left\{ \begin{gathered} b_{s1a} = {{max(M \cdot F_{s1aj} (t)} \mathord{\left/ {\vphantom {{max(M \cdot F_{s1aj} (t)} {\sum\limits_{j = 1}^{M} {F_{s1aj} (t))} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{M} {F_{s1aj} (t))} }} \, (j = 1,2,...,M{)} \hfill \\ b_{r1b} = {{max(M \cdot F_{r1bj} (t)} \mathord{\left/ {\vphantom {{max(M \cdot F_{r1bj} (t)} {\sum\limits_{j = 1}^{M} {F_{r1bj} (t)){ (}j = 1,2,...,M{)}} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{M} {F_{r1bj} (t)){ (}j = 1,2,...,M{)}} }} \hfill \\ b_{s2p} = {{max(N \cdot F_{s2pj} (t)} \mathord{\left/ {\vphantom {{max(N \cdot F_{s2pj} (t)} {\sum\limits_{j = 1}^{N} {F_{s2pj} (t))} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{N} {F_{s2pj} (t))} }} \, (j = 1,2,...,N{)} \hfill \\ b_{r2p} = {{max(N \cdot F_{r2pj} (t)} \mathord{\left/ {\vphantom {{max(N \cdot F_{r2pj} (t)} {\sum\limits_{j = 1}^{N} {F_{r2pj} (t))} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{N} {F_{r2pj} (t))} }} \, (j = 1,2,...,N{)} \hfill \\ \end{gathered} \right.$$
(23)
$$\left\{ \begin{gathered} LSC_{s1a} = \left| {b_{s1a} - 1} \right|_{max} + 1 \hfill \\ LSC_{r1b} = \left| {b_{r1b} - 1} \right|_{max} + 1 \hfill \\ LSC_{s2p} = \left| {b_{s2p} - 1} \right|_{max} + 1 \hfill \\ LSC_{r2p} = \left| {b_{r2p} - 1} \right|_{max} + 1 \hfill \\ \end{gathered} \right.$$
(24)

where LSCs1a, LSCr1b, LSCs2p, and LSCr2p are the maximum LSCs of the sun gear-star gear pair, inner ring gear-star gear pair, sun gear-planetary gear pair and inner ring gear-planetary gear pair in a meshing cycle respectively. Fi(i = s1a, r1b, s2p, r2p) refers to the dynamic meshing force of ith gear pair .

Load sharing structure floating spline

The floating spline structure is generally placed in the position of the sun gear of the encased stage system or differential stage system. When the force acting on the sun gear is unbalanced, sun gear can generate radial micro-displacements to balance the load due to the existence of radial clearance of spline connection. However, the sun gear cannot float freely resulting from the constraints of the spline shaft. The clearance between internal and external spline are shown in Fig. 5.

$$F_{m} = \tau \cdot F_{n}$$
(25)

where \(\tau = \tau_{0} \cdot sgn(v_{s} )\), \(\tau_{0}\) is the coefficient of friction, which is taken 0.1 in this paper, vs is the relative slip velocity, sgn(vs > 0) = 1, Fn is the positive pressure of the spline contact surface.

Figure 5
figure 5

The schematic diagram of clearance between internal and external spline.

Full size image

The reaction force of the spline shaft acting on the sun gear is shown in Fig. 630. When 0 ≤ Rs < R1, the internal and external spline do not generate relative slip, and the supporting reaction force is provided by the bending deformation of the spline shaft. When R1 ≤ Rs < R2, the relative slip of the internal and external spline occurs, and the supporting reaction force is provided by spline friction force. When Rs ≥ R2, the radial clearance of the internal and external spline is eliminated, and the supporting reaction force is supported by the bending deformation of the spline shaft again. Where Rs is the floating amount of the sun gear, and R1 and R2 are the floating amount of the sun gear which undergoes the state of generating and exiting slip respectively, which can be calculated by Eq. (26)–(28).

$$R_{s} = \sqrt {x_{s}^{2} + y_{s}^{2} }$$
(26)
$$R_{1} = {{F_{m} } \mathord{\left/ {\vphantom {{F_{m} } {k_{s} }}} \right. \kern-0pt} {k_{s} }}$$
(27)
$$R_{2} = R_{1} + b_{spline}$$
(28)

where ks is the bending stiffness of the splined shaft, bspline is the radial clearance of floating spline, mm, xs and ys are the vibration displacements of the sun gear in the x and y directions respectively.

Figure 6
figure 6

Schematic diagram of sun gear supporting reaction force with floating spline structure.

Full size image

The function of supporting reaction force of sun gear with floating spline structure can be expressed as

$$F_{sx} = \left\{ \begin{gathered} k_{s} R_{s} cos\varphi { 0} \le R_{s} < R_{1} \hfill \\ F_{m} cos\varphi \, R_{1} \le R_{s} < R_{2} \hfill \\ k_{s} (R_{s} - b_{spline} )cos\varphi \, R_{s} \ge R_{2} \hfill \\ \end{gathered} \right.$$
(29)
$$F_{sy} = \left\{ \begin{gathered} k_{s} R_{s} sin\varphi { 0} \le R_{s} < R_{1} \hfill \\ F_{m} sin\varphi \, R_{1} \le R_{s} < R_{2} \hfill \\ k_{s} (R_{s} - b_{spline} )sin\varphi \, R_{s} \ge R_{2} \hfill \\ \end{gathered} \right.$$
(30)

where φ is the direction angle of the [xs, ys] vector.

The analysis of the load-sharing characteristics about the encased differential planetary gear train

Dynamic parameter of the encased differential planetary train

In order to conduct the dynamic analysis of encased differential planetary train, structural and dynamic parameters are needed. Table 1 shows the structural parameters of the encased differential planetary gear train, Table 2 shows the dynamic parameters of the encased differential planetary gear train31, Table 3 shows the error parameters of the encased differential planetary gear train, and the gear error is given according to the four-level machining accuracy32. This paper assumes that the output speed of the internal and external rotor shaft is 230 r/min, and the input speed of the system can be obtained according to the transmission ratio conversion and its value is 1295 r/min and the input torque is 1600 Nm.

Table 1 Structural parameters of encased differential planetary gear train.
Full size table
Table 2 Dynamic parameters of encased differential planetary gear train.
Full size table
Table 3 Error parameters of encased differential planetary gear trains.
Full size table

The effect of input torque on load sharing performance of encased differential planetary gear system

The input torque is a crucial parameter influencing the load-sharing characteristics of the system. However, due to the particularity of the encased differential planetary gear train structure, the torque distribution among system components differs from that of traditional planetary gear train, further impacting the load sharing behavior of the system. Therefore, it is necessary to conduct research on the torque distribution of components in the encased differential planetary gear train, followed by studying the influence of input torque on the load sharing performance of the system.

Figure 7 illustrates the torque diagram of differential planetary gear train. Here, ωi and Ti represent the angular velocity and torque of component i(i = s2, c, r2) respectively. According to literature33, the equilibrium relationship between torques can be obtained, as shown in Eq. (31).

$$\frac{{T_{s2} }}{1} = \frac{{T_{r2} }}{{ - i_{{s_{2} r_{2} }}^{c} }} = \frac{{T_{c} }}{{i_{{s_{2} r_{2} }}^{c} - 1}}$$
(31)
Figure 7
figure 7

Torque diagram of differential planetary gear train.

Full size image

Assuming that the load torque ratio of the internal and external rotor shafts is α which can be calculated by Eq. (32).

$$\alpha = - \frac{{T_{in} }}{{T_{ex} }}$$
(32)

where Tin denotes the internal rotor shaft torque which can be expressed as Tin = Tc, Tex denotes the external rotor shaft torque which can be expressed as Tex = Tr1 + Tr2, “−“ indicates that the output torque of the internal and external rotor shaft is in opposite direction. Therefore, Eq. (32) can be rewritten as

$$\alpha = - \frac{{T_{c} }}{{T_{r1} + T_{r2} }}$$
(33)

By simultaneously solving Eqs. (31) and (33), Eq. (34) can be obtained.

$$\left\{ \begin{gathered} T_{r1} = \frac{{(\alpha - 1)i_{{s_{2} r_{2} }}^{c} + 1}}{{\alpha (i_{{s_{2} r_{2} }}^{c} - 1)}}T_{c} \hfill \\ T_{r2} = \frac{{i_{{s_{2} r_{2} }}^{c} }}{{1 - i_{{s_{2} r_{2} }}^{c} }}T_{c} \hfill \\ T_{s2} = \frac{1}{{i_{{s_{2} r_{2} }}^{c} - 1}}T_{c} \hfill \\ \end{gathered} \right.$$
(34)

where \(i_{s2r2}^{c}\) is the conversion transmission ratio of the differential stage system.

Since the encased stage system is a fixed-shaft gear train, the torque Ts1 of the sun gear s1 can be expressed as

$$T_{s1} = T_{r1} \cdot \frac{{z_{s1} z_{b} }}{{z_{r1} z_{a} }}$$
(35)

And the torque ratio of the central components of the encased stage system to the differential stage system can be calculated by Eq. (36), (37).

$$\frac{{T_{s1} }}{{T_{s2} }} = \frac{{(\alpha - 1)i_{{s_{2} r_{2} }}^{c} + 1}}{\alpha } \cdot \frac{{z_{s1} z_{b} }}{{z_{r1} z_{a} }}$$
(36)
$$\frac{{T_{r1} }}{{T_{r2} }} = - \frac{{(\alpha - 1)i_{{s_{2} r_{2} }}^{c} + 1}}{{\alpha \cdot i_{{s_{2} r_{2} }}^{c} }}$$
(37)

The effect of α on the torque ratio of the central components of the encased stage system to the differential stage system is shown in Fig. 8. It can be found that input torque of sun gear of encased stage and differential stage is equal when α = 0.4171. And the input torque of inner ring gear of encased stage and differential stage is equal when α = 0.7158. With the value of α increases to 1, Ts1/Ts2 = 0.1774, Tr1/Tr2 = 0.4314, which indicates that the input torque of central component of encased stage system is much smaller than that of differential stage system. Ts1/Ts2 = 0.1774, Tr1/Tr2 = 0.4314 when α = 1.432, which indicates the input power is all concentrated in the differential stage system, and the encased stage system does not bear the load. When the value of α is greater than 1.432, Ts1/Ts2 < 0 and Tr1/Tr2 < 0, the power flow cycle is generated inside the system, which reduces the transmission efficiency of the system in a large extent, so this situation needs to be avoided in practical applications.

Figure 8
figure 8

The effect of α on the torque ratio of the central components of the encased stage system to the differential stage system.

Full size image

Assuming that the load torques of the internal and external rotor shaft are equal, the variation law of the LSC of the meshing pair of the encased differential planetary gear train with the increase of input torque can be obtained, as shown in Fig. 9. It can be found that with the increase of input torque, the LSC of all gear pairs shows a decreasing trend, and the increase of torque inhibits the decline rate of LSC. Moreover, LSC of the encased stage gear pair is greater than that of the differential stage gear pair, and the difference of LSC gradually decreases with the increase of the input torque. When the input torque increases from 1000 to 5000Nm, the LSC of the encased stage system decreases by 51.2%, from 2.774 to 1.355, where the LSC of the encased stage system can be obtained by the mean value of LSCs1a and LSCr1b, the calculation of LSC about the differential stage system is the same. Similarly, the LSC of the differential stage system decreases by 17.2%, from 1.279 to 1.059. It can be seen from Fig. 8 that torque of differential stage system is much greater than that of encased stage system when the load torque of internal and external rotor shaft is equal. This is because when the error amplitude of component is constant, the error displacement excitation projected into the direction of the meshing line is also constant, resulting in the stable error excitation load of the gear pair which can be found from Eq. (10). The meshing force of the gear pair increases as the input torque increases, which results in the influence of load distribution caused by error excitation become less, and system can achieve better load sharing performance. In summary, the load sharing performance of the differential stage system is much better than that of the closed stage system, but this gap will gradually decrease as the input torque increases. Therefore, it can be found that with the main goal of improving the load sharing performance of the encased stage system, the overall improvement of the encased differential planetary gear system is more obvious.

Figure 9
figure 9

Schematic diagram of LSCs of gear pair of encased differential planetary gear train with the change of input torque.

Full size image

The effect of floating spline clearance on load sharing performance of encased differential planetary system

The influence of floating spline clearance of sun gear on the load sharing characteristics of encased differential planetary gear train is studied in this section, in which the bending stiffness of the spline shaft of the encased and differential sun gear is 3.5 × 108 N/m, and the friction coefficient of the spline is 0.1. Figure 10 shows the time domain variation curve of the LSCs of gear pair s1a under different floating spline clearances. It can be found that LSC exhibits time variant and reaches peak at t = 0.7611 s whose value is 2.06 when bs1 = 0 μm, bs2 = 0 μm, that is, there is no radial clearance between the internal and external spline of the sun gear. When bs1 = 20 μm, bs2 = 0 μm, LSCs are significantly reduced, and the maximum value of LSC is reduced to 1.709, while the vibration shows instability in partial time interval. This is because when the internal and external spline are in a relative slip state, the sun gear can adjust the radial deformation adaptively to improve the load sharing performance, but the change of friction direction and the impact caused by the small radial clearance affect the stability of the system vibration. The load sharing performance of the system is improved in a step further and the maximum value of LSC is also reduced to 1.416 when bs1 = 50 μm, bs2 = 0 μm. Furthermore, the system returned to a stable condition, which result from the spline clearance is large enough to avoid the shock of the internal and external spline.

Figure 10
figure 10

Schematic diagram of the change of LSC of gear pair s1a under different floating spline clearance.

Full size image

Figures 11 and 12 show the effect of the spline radial clearance of the encased stage sun gear s1 and the differential stage sun gear s2 on the LSC of the system respectively. It can be found that the load sharing performance of the encased stage system is improved, while the load sharing performance of the differential stage system is almost unchanged when bs1 increases. When bs1 exceeds 40 μm, bs1 has no significant effect on the load sharing performance of the encased stage system. In addition, LSCs1a > LSCr1b when bs1 is less than 30 μm, and LSCs1a < LSCr1 when bs1 is bigger than 30 μm conversely. It indicates that bs1 has a greater influence on the gear pair s1a than r1b. Moreover, the load sharing performance of both the encased stage and the differential stage system is improved a bit when the spline radial clearance of the sun gear s2 of the differential stage system increases. On the one hand, the floating spline of the sun gear of the differential stage system has little effect on the load sharing performance of the encased stage system, and on the other hand, the load sharing performance of the differential stage system is good enough. It can be concluded that adjusting the spline clearance of the encased stage sun gear s1 can improve the load sharing performance of the encased differential planetary gear train more effectively under the same condition through comparison.

Figure 11
figure 11

Effect of floating spline clearance of encased stage sun gear s1 on LSC.

Full size image
Figure 12
figure 12

Effect of floating spline clearance of differential stage sun gear s2 on LSC.

Full size image

The effect of spline shaft stiffness on load sharing performance of encased differential planetary system

The influence of spline shaft stiffness on the load sharing characteristics of encased differential planetary gear train is explored in this section, in which the spline clearance of the sun gear of the encased and differential stage system is 0 μm, and the friction coefficient of the spline is 0.1. Figure 13 shows the time domain variation curve of the LSCs of gear pair s1a under different spline shaft stiffness. It can be found that the load sharing performance of gear pair s1a is improved significantly when the spline shaft stiffness is in a condition where ks2 remains unchanged and ks1 decreases. Because the smaller the spline shaft stiffness, the larger flexibility the sun gear supporting, making it easier for the sun gear to generate floating deformation to improve the load sharing performance. Figures 14 and 15 show the effect of the spline shaft stiffness of the encased stage sun gear s1 and the differential stage sun gear s2 on the LSC of the system respectively. It can be found that with the increase of ks1, LSC of the encased stage system is increasing, while the increase rate is decreasing, and LSC of the differential stage system is almost unchanged. Furthermore, as the increase of ks2, LSCs of both the encased stage system and the differential stage system increases, while the increase amplitude is small. Therefore, the load sharing performance of the encased differential planetary gear train can be more effectively improved by reducing the spline shaft stiffness of the encased stage sun gear s1.

Figure 13
figure 13

Schematic diagram of the change of LSCs of gear pair s1a under different spline shaft stiffness.

Full size image
Figure 14
figure 14

Effect of spline shaft stiffness of encased stage sun gear s1 on LSC.

Full size image
Figure 15
figure 15

Effect of spline shaft stiffness of differential stage sun gear s2 on LSC.

Full size image

The effect of friction coefficient on load sharing performance of encased differential planetary system

The influence of friction coefficient on the load sharing characteristics of encased differential planetary gear train is studied in this section, in which the spline clearance of the sun gear of the encased stage system is 50 μm, and the spline shaft stiffness is 3.5 × 108N/m. Meanwhile, the spline clearance of the sun gear of the differential stage system is 0 μm, and the spline shaft stiffness is 3.5 × 108 N/m. Figure 16 shows the time domain variation curve of the LSCs of gear pair s1a under different friction coefficient. It can be found that the load sharing performance of gear pair s1a is improved with the increase of friction coefficient. This is due to rising of friction coefficient increase R1 and R2 which can be deduced by Eqs. (21), (22). The maximum floating amount of the sun is also increased further, so the load sharing performance of the system is improved. Figure 17 shows the effect of the friction coefficient on the LSC of the system. It can be concluded that with the increase of friction coefficient, LSCs of the encased stage system is gradually decreasing, and LSCs of the differential stage system is almost unchanged.

Figure 16
figure 16

Schematic diagram of the change of LSC of gear pair s1a under different friction coefficient.

Full size image
Figure 17
figure 17

Effect of friction coefficient on LSC.

Full size image

The coupling effect of sun gear spline shaft stiffness and radial clearance of the encased stage system on load sharing characteristics

The coupling effect of spline shaft stiffness and radial clearance of the encased stage system on the load sharing performance of the system is studied in this section, in which the spline shaft stiffness of the differential stage sun gear is 3.5 × 108 N/m, the spline clearance is 0 μm, and friction coefficient takes 0.1. Figures 18, 19, 20, 21 show the coupling effect of the spline shaft stiffness and radial clearance of the encased stage sun gear s1 on the LSCs1a, LSCr1b, LSCs2p and LSCr2p of the system respectively. It can be found that the larger spline shaft stiffness is, the more obvious the influence of radial clearance on the encased stage system. Conversely, the smaller the spline radial clearance, the more obvious the effect of spline shaft stiffness on the encased stage system. In addition, the parameters of the floating spline of the encased stage sun gear have little effect on the load sharing performance of the differential stage system.

Figure 18
figure 18

Effect of spline shaft stiffness and radial clearance of encased stage sun gear s1 on LSCs1a.

Full size image
Figure 19
figure 19

Effect of spline shaft stiffness and radial clearance of encased stage sun gear s1 on LSCr1b.

Full size image
Figure 20
figure 20

Effect of spline shaft stiffness and radial clearance of encased stage sun gear s1 on LSCs2p.

Full size image
Figure 21
figure 21

Effect of spline shaft stiffness and radial clearance of encased stage sun gear s1 on LSCr2p.

Full size image

Conclusion

In this paper, the dynamic model of encased differential planetary gear train with floating spline is established with the consideration of the influence of time-varying mesh stiffness, manufacture error and installation error. The input torque, spline radial clearance, spline shaft stiffness and friction coefficient on the load sharing performance of the encased differential planetary gear system are studied, then the following conclusions are obtained:

  1. (1)

    The torque distribution of encased stage system and differential stage system are affected by the internal and external rotor shaft load torque ratio α. As α increases, both Ts1/Ts2 and Tr1/Tr2 exhibit a decreasing trend, but the rate of decrease for Tr1/Tr2 is faster, and the power transferred to the encased stage system decreases. When α exceeds 1.432, the system generates power flow cycle.

  2. (2)

    With the increase of input torque, the LSC of all gear pairs shows a decreasing trend, and the increase of torque inhibits the decline rate of LSC. In addition, the LSC of the encased stage gear pair is greater than that of the differential stage gear pair when load torque of the internal and external rotor shaft is same. While with the increase of the load torque, the difference of LSC is decreasing.

  3. (3)

    As the floating spline clearance of the encased stage sun gear s1 increases, LSC of the encased stage system increases, while LSC of the differential stage system remains almost unchanged. When the floating spline clearance of the sun gear s2 in the differential stage increases, both LSC of the encased stage and the differential stage systems are slightly raised. Under the same conditions, adjusting the floating spline clearance of the encased stage sun gear s1 can more effectively improve the load-sharing performance of the system.

  4. (4)

    With the increase of spline shaft stiffness ks1, LSC of the encased stage system is increasing, while the increase rate is decreasing, and LSC of the differential stage system is almost unchanged. In addition, as the increase of ks2, LSCs of both the encased stage system and the differential stage system increases, while the increase amplitude is small.

  5. (5)

    As the friction coefficient increases, LSCs of the encased stage system gradually decrease, while those of the differential stage system remain almost unchanged.