Abstract
An important measure of the development of quantum computing platforms has been the simulation of increasingly complex physical systems. Before fault-tolerant quantum computing, robust error-mitigation strategies were necessary to continue this growth. Here, we validate recently introduced error-mitigation strategies that exploit the expectation that the ideal output of a quantum algorithm would be a pure state. We consider the task of simulating electron systems in the seniority-zero subspace where all electrons are paired with their opposite spin. This affords a computational stepping stone to a fully correlated model. We compare the performance of error mitigations on the basis of doubling quantum resources in time or in space on up to 20 qubits of a superconducting qubit quantum processor. We observe a reduction of error by one to two orders of magnitude below less sophisticated techniques such as postselection. We study how the gain from error mitigation scales with the system size and observe a polynomial suppression of error with increased resources. Extrapolation of our results indicates that substantial hardware improvements will be required for classically intractable variational chemistry simulations.
Similar content being viewed by others
Main
The prospect of accurately simulating ground states of quantum systems on quantum hardware has motivated substantial theory and hardware developments over the last decade. With fault-tolerant quantum computing in its infancy1 and many years from promised applications2,3,4,5,6, attention has focused on algorithms requiring only short-depth quantum circuits, such as the variational quantum eigensolver (VQE)7,8. Theoretical developments in ansatz design8,9,10,11,12,13 and measurement optimization14,15,16,17,18 have enabled small to midscale VQE experiments11,19,20,21,22,23,24,25,26. A key target of variational quantum algorithms has been the electronic structure problem in chemistry8,11,19,20,21,22,23,27. Such simulations are challenging to implement on quantum hardware due to a long-range two-body fermionic Hamiltonian and stringent accuracy requirements. This makes it unclear whether a beyond-classical simulation of chemistry can be achieved without fault tolerance. Determining the requirements for such a simulation is a critical open problem.
The electronic structure problem can be expressed in models of varying complexity and realism. Quantum simulations of chemistry in the Hartree–Fock (mean-field) approximation were implemented for system sizes up to 12 qubits in ref. 23, and to our knowledge, this study retains the record for the largest VQE calculation of a chemical ground state on quantum hardware. As a next step, one can consider working in the seniority-zero subspace of the entire Hilbert space, which assumes all electrons come in spin-up or spin-down pairs12,28,29,30,31,32,33. This has the advantage of projecting a local fermionic problem onto a local qubit problem12. The S0 ground state is not a priori classically efficiently simulatable12 (although good approximate methods are known to exist for many problems33,34,35). This makes it a good stepping stone beyond Hartree–Fock towards the full electronic structure problem.
Recent quantum experiments have relied on error-mitigation techniques36, which are not scalable like error correction1,37 but promise to substantially shrink experimental errors. Popular methods are based on postselection38,39, rescaling24,40,41, purification23,42,43,44 and probabilistic cancellation40,45. Various schemes and combinations of error-mitigation techniques have been implemented in practice20,22,23,24,25,26,46. However, many of these methods do not promise to remove bias to the level of accuracy needed for useful simulation of chemistry, or remain untested beyond few-qubit experiments. Shifting from non-interacting fermions to correlated electronic structure, one loses two error-mitigation advantages that were crucial to the success of ref. 23: efficient density-matrix purification by means of McWeeny iteration47, and low-cost gradient estimation.
In this work, we compare the performance of three different error-mitigation techniques—postselection, echo verification (EV) and virtual distillation (VD)—on the problem of preparing ground states in the seniority-zero space, using up to 20 qubits of a superconducting quantum processor. Using either EV or postselected VD, we are able to accurately reproduce the ground-state energy and order parameter for an N = 10–qubit simulation of the Richardson–Gaudin (RG) model, improving over unmitigated estimates by one to two orders of magnitude. This demonstrates an improvement over classical pair coupled-cluster doubles (pCCD) and the non-interacting Bardeen–Cooper–Schrieffer (BCS) theory, neither of which are qualitatively correct over the entire range of coupling values considered. We study the scaling of the mean absolute error in energy and the order parameter with the system size and observe that EV and VD suppress errors by a factor Nα for values of α between 0.8 and 2.5. EV was further able to greatly mitigate error of six- and ten-qubit simulations of the ring opening of cyclobutene (CB). Although the stringent error requirements (<0.05 Hartree) to differentiate between mean-field and the exact solution could only be achieved for the six-qubit case, this still represents the largest VQE simulation of electronic structure for chemistry that we are aware of so far. From these data, we are able to estimate the minimum requirements for a beyond-classical quantum simulation of similar form: a 25× decrease in hardware error rates (from those observed in this work), a limit of O(N) depth for future variational ansatzes and the need to pre-optimize ansatzes classically without intermediate calls to a device. Even if this list of requirements is achieved, meeting the high level of accuracy required for the electronic structure problem will pose a serious challenge, as chemical accuracy is around 60× less than our mean accuracy for the ten-qubit CB problem.
The RG model
We first prepare approximate ground states of the RG model on ten sites at half-filling across a range of coupling strengths g. This model is chosen as a well-known benchmark with well-understood exact and approximate solutions. We work in the seniority-zero space (where all electrons are paired with their opposite spin) and use a unitary pair coupled cluster doubles (UpCCD) variational ansatz12 with parameters optimized in noiseless simulation. In Fig. 1a, we estimate the prepared states’ energy using various error-mitigation techniques: postselection, EV and postselected virtual distillation (PS-VD). We compare these results to exact diagonalization in the S0 subspace (also known as double occupied configuration interaction) and classical pCCD and BCS solutions. We see that using EV or PS-VD, we are able to reproduce the entire energy curve to high accuracy, which neither pCCD nor the non-interacting BCS theory can achieve. The experimental error in the result is the sum of the UpCCD model error and the experimental error. To disambiguate the effects of UpCCD model error, in Fig. 1b we plot the error between our experimental data and the UpCCD ground-state energy. The observed gain from error mitigating some estimate y can be quantified by the suppression factor
We summarize this across our experimental data in Table 1. For the energy (y = E), we find PS-VQE consistently achieves ηE ≈ 2, whereas EV achieves \({\bar{\eta }}_{E}=85\) and \(\max ({\eta }_{E})=460\) and VD achieves \({\bar{\eta }}_{E}=60\) and \(\max ({\eta }_{E})=140\). The residual error following EV or PS-VD fluctuates on a scale larger than statistical error bars, which we attribute to device drift.
a, Energy as a function of the coupling parameter g, estimated using various error-mitigation techniques (markers) and compared to classical models (lines). The classical pCCD results do not converge below a critical value, resulting in their cut-off. b, Log plot of experimental energy error (ignoring the model error from the UpCCD approximation). c, Many-body order parameter for the RG Hamiltonian (see text), again compared to classical models. d, Experimental error in estimating the superconducting order parameter versus the target state in the UpCCD approximation (again ignoring model error). Error bars show 1 standard deviation uncertainty from sampling noise, estimated by propagating variance (raw VQE, PS-VQE) or bootstrapping (EV, PS-VD); see Supplementary Information Section III for details. a.u., arbitrary units.
The RG Hamiltonian has a well-known phase transition in the attractive regime (g ≤ 0) in the thermodynamic limit, which appears in the BCS state at finite N but is not present in the true ground state due to finite size effects48,49,50. This gives us a second physically relevant target to simulate and a qualitative feature (the cusp at g = 0) to resolve. The traditional order parameter for the BCS state, \({{{\varDelta }}}_{\mathrm{BCS}}=\frac{1}{2N}{\sum }_{j}(\langle {a}_{j\uparrow }{a}_{j\downarrow }\rangle +\langle {a}_{j\downarrow }^{{\dagger} }{a}_{j\uparrow }^{{\dagger} }\rangle )\), is zero on the RG Hamiltonian ground state due to number conservation. However, \({{\varDelta }}=\frac{1}{N}{\sum }_{j,\sigma }\sqrt{\langle {n}_{j\sigma }^{2}\rangle -{\langle {n}_{j\sigma }\rangle }^{2}}\) satisfies Δ = ΔBCS for the BCS ground state of the Hamiltonian, giving a many-body-order parameter49. In Fig. 1c, we plot experimental estimates of Δ across the range of g values considered. In the absence of error mitigation, although the order parameter dips around g = 0, the true cusp is not reproduced. Both EV and PS-VD clearly improve over the BCS approximation for g > 0.5, with EV particularly able to reproduce the cusp at g = 0. We measure the performance of the error-mitigation techniques by plotting the error in Δ against the noise-free UpCCD result in Fig. 1d. The suppression (equation (1), y = Δ) from EV and PS-VD during order-parameter estimation is slightly less than for energy estimation: for EV, we find \({\bar{\eta }}_{{{\Delta }}}=32\) and \(\max ({\eta }_{{{\Delta }}})=56\); and for PS-VD, we find \({\bar{\eta }}_{{{\Delta }}}=18\) and \(\max ({\eta }_{{{\Delta }}})=51\).
We now study the scaling of the studied error-mitigation techniques for the RG model over system sizes N = 4, 6, 8, 10. In Fig. 2a, we plot the absolute error in the energy estimates, averaged across all points in Fig. 1, and repeat this for different system sizes N. (Plots equivalent to Fig. 1 for different system sizes can be found in Supplementary Information Section VI.D.) We observe that the energy error scales sublinearly after applying EV or VD, demonstrating an asymptotic difference from raw VQE or PS-VQE of a factor of ~N2. We similarly observe an ~N−N2 gap between EV/VD and VQE/PS-VQE in the order-parameter error (Fig. 2b); the difference in the suppression factor is not statistically significant. Next, we extract various fidelity metrics from the experimental data in Fig. 2c, which approximate the (inverse) increased variance of our error-mitigated estimators36. The data for PS-VQE (red plus), EV (green square) and PS-VD (yellow triangle) directly correspond to the circuit overhead required by different error-mitigation techniques. These fidelity metrics allow us to estimate the required number of experiment repetitions to reduce statistical noise in the energy estimation to <0.1 a.u.(arbitrary units) in Fig. 2d, assuming ten-qubit fidelity is maintained. We observe a substantial gap between the experimental and theoretical sampling cost of EV (green squares). We attribute this to known overheads of EV that are not in the theoretical model (Supplementary Information Section IV.A).
a, Experimental energy error (versus the UpCCD ground state) averaged over all points studied of the RG model. Error bars show sample standard deviation and lines a power-law fit. b, Experimental error in order parameter (versus the UpCCD ground state) averaged over all points studied of the RG model. Error bars and lines same as a. c, Different fidelity metrics for PS-VQE, EV, PS-VD and Loschmidt (LS) echo (see legend) averaged over all points studied of the RG model. d, Number of shots required for convergence at g = −0.9. Crosses and pluses give simulated estimations with two types of term grouping (see text for details) using observed fidelities of a ten-qubit experiment from c. Other symbols give experimental shots used.
CB ring opening
We further validated scalable error-mitigation protocols by simulating the conrotatory ring opening pathway for CB in an active space of six orbital and six electrons and ten orbitals and ten electrons corresponding to a six- and ten-qubit simulation of the electronic structure Hamiltonian. The mechanism of this ring opening is described by the Woodward–Hoffmann rules for pericyclic ring openings corresponding to the in-phase combination of the two carbon 2p orbitals when brought together to form the four-member carbon ring. Similar to the RG model, this was chosen as a well-known benchmark system with well-understood chemistry.
The geometries along the reaction path are determined from a nudged elastic-band calculation using density functional theory (B3LYP) to evaluate forces. The final structures use a minimal basis set (STO-3G) to generate the active-space Hamiltonians to project into the seniority-zero sector. The Woodward–Hoffmann rules are a type of molecular orbital theory, and thus we expect this reaction to be qualitatively described in mean-field theory. This is verified numerically for our seniority-zero model where the largest configuration interaction coefficient has an average value of 0.974(9) for six orbitals and 0.973(9) for ten orbitals, indicating a single-reference system. As such, our unitary pCCDs ansatz targets the dynamic correlation corrections to the mean field.
The average PS-VQE absolute error is 0.058 ± 0.006 and 0.395 ± 0.023 Hartree, and the mean suppression factor is \({\bar{\eta }}_{E}=5.0\) and 2.9 for the six- and ten-orbital systems, respectively. The average echo-verified absolute error is 0.011 ± 0.005 and 0.064 ± 0.035 Hartree and the mean suppression factor (equation (1)) is \({\bar{\eta }}_{E}=54\) and 38 for the six- and ten-orbital system respectively. Although there is notable improvement in energy across the reaction pathway for the ten-orbital system, the magnitude of the errors is larger than the 0.037 Hartree energy difference between CB and 1,3-butadiene. Furthermore, a visual inspection of Fig. 3 indicates high parallelity errors in the ten-orbital system. Given that the error bars on EV are smaller than the parallelity error (point scatter), we attribute the main source of error to device drift.
Comparison of raw VQE (purple, ‘R’), PS-VQE (yellow, ‘PS’) and EV (green, ‘EV’) on an optimized unitary pair coupled-cluster ansatz. Darker (lighter) points correspond to six-qubit (6Q) (ten-qubit (10Q)) simulations. Error bars denote 1 s.d. calculated by either propagating error (VQE) or bootstrapping (EV). From left to right, the reaction path corresponds to the ring opening reaction. For the ten-orbital case, the unitary pair coupled-cluster ansatz (evaluated in simulation) has less than 1.8 × 10−4 energy difference from exact diagonalization in the seniority-zero space. The blue curves correspond to the exact diagonalization of the seniority-zero active space Hamiltonian spanning ten orbitals (broad, lighter-blue line) and six orbitals (narrow, darker-blue line). The red curve is the RHF mean-field energy. Some of the data are plotted on a discontinuous and different scale to preserve the visual scale of the reaction energy along the reaction coordinate.
Discussion and outlook
Many of the features of our experimental data can be understood physically. The similar performance of EV and PS-VD can be understood following the equivalence of the two techniques shown in refs. 46,51, which treat EV as purification of two states separated in time. However, this equivalence is broken by the further circuitry of the two techniques: EV requires Greenberger-Horne-Zeilinger (GHZ) state preparation, whereas VD requires bell-basis measurements and more routing. This doubles the susceptibility of the VD fidelity to measurement noise, to which we attribute the gap between this and the EV fidelity in Fig. 2c. Despite the fidelity gap, we observe PS-VD has a substantially smaller sampling cost than EV, which comes from known measurement bottlenecks52 and overhead to reduce on-chip magnetic field fluctuations (Supplementary Information Section II.D). We can attribute the gap in performance between VD with and without postselection to this further measurement circuitry (Supplementary Information Section VI.A): we suggest that the bell-basis measurements used are not robust to noise that does not conserve particle number and that the primary effect of postselection is to mitigate this noise source. The performance improvement of EV/VD over postselection is expected from numerical predictions in refs. 42,44 and analytic results of ref. 53 (although we show in Supplementary Information Section VI.B that this cannot be guaranteed). Finally, we can explain the qualitative feature in Fig. 1 around g = 0, where the energy error drops but the order parameter error increases. This comes from two coincidental effects: Δ is more sensitive to error around Δ = 0, but at this point the energy becomes less dependent on off-diagonal terms, reducing its sensitivity to phase noise.
We now consider how the required number of experiment repetitions (shots) scales to classically intractable simulations, using the data in Fig. 2d. Taking a 50-qubit experiment as a proxy lower bound for a beyond-classical quantum computation, and assuming the ability to freely weight our shot distribution, we estimate that at least 108 or 109 shots would be required when using VD or EV, respectively. This is executable on current hardware in a wall-clock time of >1 hour or >10 hours, respectively. Including the difference between experiment and theory at ten qubits raises the cost of EV to 5 × 1010 shots, which would require several days to achieve. These numbers do not include the large multiplicative cost of variational optimization. Furthermore, the requirements for accurate electronic structure simulations may be lower than the 0.1 a.u. requirement considered here. Methods to pre-optimize variational ansatzes classically and applications of VQE to problems simpler than electronic structure may thus be necessary for beyond-classical VQE experiments.
Next, we consider what device fidelity would be required to scale to a beyond-classical experiment. To maintain circuit fidelity F over a depth 3N/2, fully parallel circuit as N scales from 10 to 50 requires all error rates to drop by a factor of 25 (~N2). As any reduction in F incurs a poly(F−1) sampling cost42,44, and as F scales exponentially in the error rate, and as F ≈ 10% for PS-VD (Fig. 2d), we see little room for negotiation on this 25× lower bound. To achieve a 25× decrease in error rate would require a 50-qubit device with fidelities on all two-qubit gates ≤3 × 10−4. This analysis likely precludes a large number of ansatzes with depth much greater than linear. For instance, successfully implementing a 50-qubit VQE with ansatz depth 3N2/2 with EV or VD would require error rates to drop ~1,000×. However, the sublinear scaling in the energy error following the application of EV or VD (Fig. 2a) indicates that a 25× decrease in error rate would be sufficient to deal with the bias in the resulting experiment; the dominant cost of error-mitigated quantum experiments comes from the sampling and fidelity requirements. Confirming this point in studies on other systems is a key target for future work.
We have observed that EV and VD suppress errors by one to two orders of magnitude on a range of quantum simulation problems using up to 20 superconducting qubits. We further observe that the error-suppression performance of these mitigation techniques increases with the number of qubits. This allows us to conclude that variance, not bias, will be the limiting factor in purification-based error-mitigation techniques going forward. As our error-mitigation protocols target expectation values themselves and are blind to the outer loops combining these to estimate energies or order parameters, we expect these results to hold for a wider range of problems than the VQE examples studied here. Any algorithm using circuits with similar structure, such as time evolution on spin chains, or brick-wall parameterized quantum circuits for quantum machine learning, should see similar gains in performance. Testing whether this extends to more generic circuits (for example, higher-dimensional or sparse circuits, or primitive circuits for fault tolerance54) is a clear target for future work.
Methods
Simulating the seniority-zero subspace
The seniority of a Slater determinant is the number of unpaired electrons; thus, the seniority-zero (S0) sector of Hilbert space for an N-electron system in M orbitals is the space of \({M}\choose {N/2}\) determinants leaving no electrons unpaired given a particular pairing of the spin orbitals. Seniority is not a global symmetry of the electronic structure Hamiltonian, and it is basis dependent; it has been used as a way to classify determinant subspaces to generate better approximations for solving the Schrödinger equation28,29,31,32 and as a starting point for modelling strong correlations from electron-pair states55.
Supported by the S0 subspace, there exists a set of operators satisfying the su(2) algebra constructed from pairs of fermion ladder operators and the spatial orbital number operator56
where p, q and α, β are orbital and spin indices, respectively, and δ is the Kronecker delta function. These operators form a basis for Hamiltonians projected into the S0 subspace. The equivalence to an su(2) algebra means seniority-zero models resemble Heisenberg spin −1/2 models, which are easily expressed as Pauli operators.
In this work, we focus on two Hamiltonians to validate purification-based error-mitigation strategies. The first is the RG or pairing model
with εp the single-particle energy for site p, and g the coupling strength. At small N this corresponds to a single strength all-to-all coupling of fermion pairs. In this Article, we work at half-filling by adding a chemical potential μ to the single-particle energies:
This is a model for a small superconducting grain when g < 0 (refs. 48,49,50), but with a g-dependent Debye frequency49. The second model is the electronic structure Hamiltonian (Helec) projected into the S0 subspace:
where h and V are the one- and two-body term coefficients. The all-to-all connected Heisenberg spin Hamiltonian is not known to be classically solvable in general, but good approximate methods exist. This is especially true for the RG model, which is often integrable35, well-approximated by density-matrix renormalization group34 and pair coupled-cluster techniques in the repulsive regime and solvable by quantum Monte Carlo in the attractive regime (where it has no sign problem). Pair coupled-cluster theory is also known to work well for the electronic structure problem in the S0 subspace29,57,58,59 while full configuration interaction quantum Monte Carlo shows a reduced sign problem60. As such, although we have strong evidence that the quantum circuits used in this text are not classically simulatable (Supplementary Information Section II.A), we do not believe directly scaling S0 simulations represents the easiest path to a quantum advantage in chemistry; this is instead a stepping stone between a mean-field solution and the full electronic structure problem.
The unitary pair coupled-cluster ansatz and energy estimation
In this work, we use a Trotterized UpCCD ansatz12 compiled into a set of qubits in a ladder geometry with nearest-neighbour coupling. The ladder ansatz (instead of a generic ring) allows us to efficiently measure terms in the Hamiltonian corresponding qubits that are not physically adjacent after encoding with a minimal number of SWAP operations. When mapped from fermions to qubits, the UpCCD ansatz has the form
where each \(\text{G}{\text{S}}_{ij}(\theta)\) is a Givens SWAP gate corresponding to the product of a Givens rotation gate by an angle θ on a pair labelled by qubits i and j followed by a SWAP operation12
The GS gate corresponds to a coherent partial pair excitation (by the angle ϕ) followed by a pair SWAP. Given several layers Nℓ in equation (6) and total number of qubits N, there are a total of NℓN/2 free parameters in the ansatz. To minimize the amount of time qubits are idle, we order the spatial orbitals such that the Fermi vacuum is \(\left\vert 0101\ldots 01\right\rangle\)—for example, the restricted Hartree–Fock state—corresponding to an interleaved list of occupied and virtual orbital labels in ascending energy order. The Hamiltonian qubit ordering is then chosen such that when all θ = 0, the Hartree–Fock state for each model is returned. The alternating SWAP gate arrangement allows us to couple each occupied pair with each unoccupied pair once in depth N/2 (Supplementary Information Section II.C). Thus, in this work, we set Nℓ = N/2 for all systems. Each GS(θ) gate is compiled into a product of three controlled-Z (CZ) gates interleaved with tunable single-qubit microwave gates (Extended Data Fig. 1, top; see Supplementary Information Section II.B for decompositions).
To perform energy estimation on our two S0 models, expectation values with respect to nearest-neighbour and non-nearest-neighbour qubits are required. The expectation value 〈XiXj + YiYj〉 is estimated by performing a number-preserving diagonalization16,23 mapping the expectation value to the difference of 〈Zi〉 and 〈Zj〉. The ladder geometry allows us to measure all non-nearest-neighbour pairs across the rungs of the ladder in a similar fashion at the further cost of at most one SWAP operation. The full measurement protocol is detailed further in Supplementary Information Section II.C. All-to-all coupling is achieved in N circuits, bringing the total number of different circuits to measure the Hamiltonian’s expectation value to N + 1. Strategies with fewer circuits exist, but they do not allow for postselection on particle number.
EV and VD
EV, introduced in ref. 44, is an error-mitigation technique that uses two copies of a quantum state \(\left\vert \psi \right\rangle\) reflected in time (preparation ↔ unpreparation) to estimate 〈ψ∣O∣ψ〉 for a unitary O (refs. 46,52). EV can be implemented without control gates, given a known reference eigenstate \(\left\vert \phi \right\rangle\) of O orthogonal to \(\left\vert \psi \right\rangle\) (here \(\left\vert \phi \right\rangle =\left\vert 00\ldots \right\rangle\)). To implement (control-free) EV, we act O on a prepared superposition of \(\left\vert \psi \right\rangle\) and \(\left\vert \phi \right\rangle\), generated by acting our UpCCD ansatz on the cat state \(\left\vert 00\ldots 0\right\rangle +\left\vert 0101\ldots 01\right\rangle\). Then, we estimate the expectation value of \(\left\vert \phi \right\rangle \left\langle \psi \right\vert\) (the term \(\left\vert \phi \right\rangle \left\langle \psi \right\vert\) is not Hermitian but may be written as a sum of the Hermitian operators \(\left\vert \phi \right\rangle \left\langle \psi \right\vert +\left\vert \psi \right\rangle \left\langle \phi \right\vert\) and \(i\left\vert \phi \right\rangle \left\langle \psi \right\vert -i\left\vert \psi \right\rangle \left\langle \phi \right\vert\)) on the resulting state \(\left\vert {{\varPsi }}\right\rangle =O\frac{1}{\sqrt{2}}(\left\vert \psi \right\rangle +\left\vert \phi \right\rangle )\). The estimation is performed by inverting the preparation unitary. In total, adding control-free EV to a variational circuit requires doubling the circuit depth and adding circuitry to prepare and unprepare GHZ states. This will reduce the fidelity of the final circuit from F to < F2. As experiment runtime scales inversely with circuit fidelity, this will cost us slightly in the experiment.
To estimate expectation values by means of EV, we use the fact that
where \(O\left\vert \phi \right\rangle ={\mathrm{e}}^{\mathrm{i}\phi }\left\vert \phi \right\rangle\). The expectation value 〈ψ∣O∣ψ〉 can be recovered from equation (10) as the other terms are known. The largest effect of noise on the echo-verified estimator (equation (10)) is to dampen 〈Ψ∣ϕ〉〈ψ∣Ψ〉 → F〈Ψ∣ϕ〉〈ψ∣Ψ〉 (ref. 44). We can estimate F independently by removing O from the circuit, which yields a Loschmidt echo of the preparation unitary61. This is achieved in practice by removing a virtual Z rotation (Extended Data Fig. 1, bottom), making the estimated Loschmidt fidelity an accurate estimate of F. Further EV implementation details can be found in Supplementary Information Section II.D.
VD42,43 is an error-mitigation technique that uses collective measurements of k copies of a state ρ to estimate expectation values with respect to \({\rho }^{k}/{{{\rm{Tr}}}}[{\rho }^{k}]\), where Tr is the trace. VD schemes are based on the observation that the cyclic shift operator S(k) is easily diagonalized and therefore can be measured, which yields, for example, for k = 2,
with \({O}_{s}=\frac{1}{2}(I\otimes O+O\otimes I)\), and I is the identity. S(2) can be simultaneously diagonalized with Os when O = Zi by a GS(π/4) rotation between pairs of identified qubits on the two registers. For two N/2 × 2 ladders on a square lattice geometry, this requires one round of SWAP gates to shift identified qubits next to each other. Operators O ≠ Zi are measured by rotating to Zi (Section 4.2) and following the above procedure. The VD circuit is only six two-qubit gates deeper than PS-VQE. However, as we double the number of qubits used, we more than double the total circuit size and reduce the total circuit fidelity again from F to <F2.
As the GS(π/4) gate is number-conserving, VD can be combined with postselection: the global excitation number ∑j(Zj ⊗ I + I ⊗ Zj) is a good symmetry. This requires that the state before measurement also conserve number. This is true when estimating 〈XiXj + YiYj〉 but not when estimating 〈ZiZj〉: when mapping ZiZj → Zi, one can only preserve the parity of the total number of excitations. In the main text of this work, we present results showing VD with postselection only (PS-VD). We compare VD with and without postselection in Supplementary Information Section VI.A.
Data availability
Raw and processed experimental data can be found at https://doi.org/10.5281/zenodo.7225821.
Code availability
Code to generate quantum circuits and process raw data is available in ReCirq: https://github.com/quantumlib/ReCirq.
References
Acharya, R. et al. Suppressing quantum errors by scaling a surface code logical qubit. Nature 614, 676–681 (2023).
von Burg, V. et al. Quantum computing enhanced computational catalysis. Phys. Rev. Res. 3, 033055 (2021).
Lee, J. et al. Even more efficient quantum computations of chemistry through tensor hypercontraction. PRX Quantum 2, 030305 (2021).
Gidney, C. & Ekerå, M. How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. Quantum 5, 433 (2021).
Campbell, E. T. Early fault-tolerant simulations of the Hubbard model. Quant. Sci. Technol. 7, 015007 (2021).
Berry, D. W. et al. Quantifying quantum advantage in topological data analysis. Preprint at https://arxiv.org/abs/2209.13581 (2022).
Peruzzo, A. et al. A variational eigenvalue solver on a quantum processor. Nat. Commun. 5, 4213 (2014).
McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 23023 (2016).
Wecker, D., Hastings, M. B. & Troyer, M. Progress towards practical quantum variational algorithms. Phys. Rev. A 92, 042303 (2015).
Grimsley, H. R., Economou, S. E., Barnes, E. & Mayhall, N. J. An adaptive variational algorithm for exact molecular simulations on a quantum computer. Nat. Commun. 10, 3007 (2019).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Elfving, V. E., Millaruelo, M., Gámez, J. A. & Gogolin, C. Simulating quantum chemistry in the seniority-zero space on qubit-based quantum computers. Phys. Rev. A 103, 032605 (2021).
Lee, J., Huggins, W. J., Head-Gordon, M. & Whaley, K. B. Generalized unitary coupled cluster wave functions for quantum computation. J. Chem. Theory Comput. 15, 311 (2018).
Huggins, W. J. et al. Efficient and noise resilient measurements for quantum chemistry on near-term quantum computers. npj Quantum Inf. 7, 23 (2021).
Cotler, J. & Wilczek, F. Quantum overlapping tomography. Phys. Rev. Lett. 124, 100401 (2020).
Bonet-Monroig, X., Babbush, R. & O’Brien, T. E. Nearly optimal measurement scheduling for partial tomography of quantum states. Phys. Rev. X 10, 031064 (2020).
Verteletskyi, V., Yen, T.-C. & Izmaylov, A. F. Measurement optimization in the variational quantum eigensolver using a minimum clique cover. J. Chem. Phys. 152, 124114 (2020).
Huang, H.-Y., Kueng, R. & Preskill, J. Predicting many properties of a quantum system from very few measurements. Nat. Phys. 16, 1050–1057 (2020).
O’Malley, P. J. J. et al. Scalable quantum simulation of molecular energies. Phys. Rev. X 6, 31007 (2016).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491–495 (2019).
Hempel, C. et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 8, 031022 (2018).
Sagastizabal, R. et al. Error mitigation by symmetry verification on a variational quantum eigensolver. Phys. Rev. A 100, 010302 (2019).
Arute, F. et al. Hartree-Fock on a superconducting qubit quantum computer. Science 369, 1084–1089 (2020).
Stanisic, S. et al. Observing ground-state properties of the Fermi-Hubbard model using a scalable algorithm on a quantum computer. Nat. Comm. 13, 5743 (2022).
Kim, Y. et al. Scalable error mitigation for noisy quantum circuits produces competitive expectation values. Nat. Phys. 19, 752–759 (2023).
van den Berg, E., Minev, Z. K., Kandala, A. & Temme, K. Probabilistic error cancellation with sparse Pauli-Lindblad models on noisy quantum processors. Nat. Phys. 19, 1116–1121 (2023).
Motta, M. et al. Quantum chemistry simulation of ground- and excited-state properties of the sulfonium cation on a superconducting quantum processor. Chem. Sci. 14, 2915–2927 (2023).
Limacher, P. A. et al. A new mean-field method suitable for strongly correlated electrons: computationally facile antisymmetric products of nonorthogonal geminals. J. Chem. Theory Comput. 9, 1394 (2013).
Boguslawski, K. et al. Efficient description of strongly correlated electrons with mean-field cost. Phys. Rev. B 89, 201106 (2014).
Johnson, P. A. et al. Richardson-Gaudin mean-field for strong correlation in quantum chemistry. J. Chem. Phys. 153, 104110 (2020).
Gunst, K., Van Neck, D., Limacher, P. A. & De Baerdemacker, S. The seniority quantum number in tensor network states. SciPost Chem. 1, 001 (2021).
Kossoski, F., Damour, Y. & Loos, P.-F. Hierarchy configuration interaction: combining seniority number and excitation degree. J. Phys. Chem. Lett. 13, 4342–4349 (2022).
Fecteau, C.-E. et al. Near-exact treatment of seniority-zero ground and excited states with a Richardson-Gaudin mean field. J. Chem. Phys. 156, 194103 (2022).
Dukelsky, J., Roman, J. M. & Sierra, G. Comment on ‘polynomial-time simulation of pairing models on a quantum computer’. Phys. Rev. Lett. 90, 249803 (2003).
Dukelsky, J. Integrable Richardson-Gaudin models in mesoscopic physics. J. Phys. Conf. Ser. 338, 012023 (2012).
Cai, Z. et al. Quantum error mitigation. Rev. Mod. Phys. (in the press).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
McArdle, S., Yuan, X. & Benjamin, S. Error-mitigated digital quantum simulation. Phys. Rev. Lett. 122, 180501 (2019).
Bonet-Monroig, X., Sagastizabal, R., Singh, M. & O’Brien, T. Low-cost error mitigation by symmetry verification. Phys. Rev. A 98, 062339 (2018).
Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119, 180509 (2017).
Li, Y. & Benjamin, S. C. Efficient variational quantum simulator incorporating active error minimization. Phys. Rev. X 7, 021050 (2017).
Huggins, W. J. et al. Virtual distillation for quantum error mitigation. Phys. Rev. X 11, 041036 (2021).
Koczor, B. Exponential error suppression for near-term quantum devices. Phys. Rev. X 11, 031057 (2021).
O’Brien, T. E. et al. Error mitigation via verified phase estimation. PRX Quantum 2, 020317 (2021).
Endo, S., Benjamin, S. C. & Li, Y. Practical quantum error mitigation for near-future applications. Phys. Rev. X 8, 031027 (2018).
Huo, M. & Li, Y. Dual-state purification for practical error mitigation. Phys. Rev. A 105, 022427 (2022).
McWeeny, R. Some recent advances in density matrix theory. Rev. Mod. Phys. 35, 668 (1963).
von Delft, J., Zaikin, A., Golubev, D. & Tichy, W. Parity-affected superconductivity in ultrasmall metallic grains. Phys. Rev. Lett. 77, 3189 (1996).
Braun, F. & von Delft, J. Superconductivity in ultrasmall metallic grains. Phys. Rev. B 59, 9527 (1999).
Dukelsky, J. & Sierra, G. The crossover from the bulk to the few-electron limit in ultrasmall metallic grains. Phys. Rev. B 61, 12302 (1999).
Cai, Z. Resource-efficient purification-based quantum error mitigation. Preprint at https://arxiv.org/abs/2107.07279 (2021).
Polla, S., Anselmetti, G.-L. R. & O’Brien, T. E. Optimizing the information extracted by a single qubit measurement. Phys. Rev. A, 108, 012403 (2023).
Koczor, B. The dominant eigenvector of a noisy quantum state. New. J. Phys. 23, 123047 (2021).
Pivetaeu, C., Sutter, D., Bravyi, S., Gambetta, J. M. & Temme, K. Error mitigation for universal gates on encoded qubits. Phys. Rev. Lett. 127, 200505 (2021).
Surján, P. R., Szabados, Á., Jeszenszki, P. & Zoboki, T. Strongly orthogonal geminals: size-extensive and variational reference states. J. Math. Chem. 50, 534–551 (2012).
Ring, P. & Schuck, P. The Nuclear Many-Body Problem (Springer Science & Business Media, 2004).
Henderson, T. M., Bulik, I. W., Stein, T. & Scuseria, G. E. Seniority-based coupled cluster theory. J. Chem. Phys. 141, 244104 (2014).
Stein, T., Henderson, T. M. & Scuseria, G. E. Seniority zero pair coupled cluster doubles theory. J. Chem. Phys. 140, 214113 (2014).
Vu, N. & Eugene DePrince, A. Size-extensive seniority-zero energy functionals derived from configuration interaction with double excitations. J. Chem. Phys. 152, 244103 (2020).
Shepherd, J. J., Henderson, T. M. & Scuseria, G. E. Using full configuration interaction quantum Monte Carlo in a seniority zero space to investigate the correlation energy equivalence of pair coupled cluster doubles and doubly occupied configuration interaction. J. Chem. Phys. 144, 094112 (2016).
Mi, X. et al. Information scrambling in quantum circuits. Science 374, 1479–1483 (2021).
Acknowledgements
Some discussion and collaboration on this project occurred while using facilities at the Kavli Institute for Theoretical Physics, supported in part by the National Science Foundation under grant no. NSF PHY-1748958.
Author information
Authors and Affiliations
Contributions
T.E.O. calibrated the device and ran the experiments. V.E.E., G.A. and C.G. designed the UpCCD ansatz. V.E.E., G.A. and T.E.O. designed the scheduling of the ansatz onto a 2 × N grid. F.G. and C.G. designed the conjugate model gradient descent algorithm and preoptimized ansatz parameters for the ansatz. N.C.R. wrote the pair coupled-cluster code, preoptimized ansatz parameters and performed the classical chemistry calculations for the CB model. T.E.O., W.J.H., S.P., K.K. and R.B. designed and optimized the error-mitigation and EV measurement strategies. O.O. and C.G. developed the BQP completeness proof for the UpCCD ansatz. T.E.O., N.C.R., C.G., F.G., V.E.E. and R.B. wrote the paper. T.E.O., C.G., R.B. and N.C. led and coordinated the project. All authors contributed to revising the manuscript and writing the Supplementary Information. All authors contributed to the experimental and theoretical infrastructure to enable the experiment.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
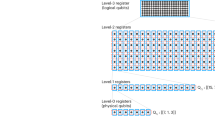
Extended Data Fig. 1 The UpCCD ansatz and its compilation to a 2D superconducting transmon grid.
(top) Decomposition of the gates used in this experiment to CZ and single-qubit gates. See Supplementary Information Section II.B for details. (second from top, left) 2 × 5 grid with couplers in a square lattice geometry, showing couplers used during the ansatz (ring coupler, purple) and those used only during measurement (cross-coupler, red). (second from top, right) 2+1D circuit cartoon of a combined ansatz and measurement on a 2 × 5 transmon qubit array. (third from top) Cartoon of error-mitigation techniques used in this experiment. Different circuit pieces are described in the legend. (bottom) an example 8-qubit echo verification circuit to measure the expectation value of (X1X7 + Y1Y7 + Z1 + Z7)/2. Shaded gates at the top and bottom of the qubit array wrap around the 2 × 4 ring.
Supplementary information
Supplementary Information
Supplementary Figs. 1–8 and discussion.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
O’Brien, T.E., Anselmetti, G., Gkritsis, F. et al. Purification-based quantum error mitigation of pair-correlated electron simulations. Nat. Phys. 19, 1787–1792 (2023). https://doi.org/10.1038/s41567-023-02240-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-023-02240-y