Introduction

Computing molecular properties and processes relies on solving the Schrödinger equation to find the many-electron wave function. An exact solution to this problem formally scales exponentially with the number of electrons. Therefore, current high-accuracy algorithms with polynomial scaling, including coupled-cluster and many-body perturbation theory, fail when the electronic entanglement and correlation cannot be easily approximated1. These situations often arise in open-shell systems with strong spin coupling, such as stretched molecular bonds and transition metal complexes2. For this reason, universally accurate simulations of complex processes, such as metalloenzyme catalysis and high-temperature superconductivity, remain difficult3. Gate-based quantum computation has the potential to overcome this challenge by representing the electronic wave function using polynomially scaling quantum resources, providing a route for solving strongly correlated electronic structure problems4.

Current and near-term quantum devices are impaired by noise and are limited to shallow quantum circuits5. The most promising near-term approaches optimise the parameters of an ansatz for the quantum state, and algorithms such as the variational quantum eigensolver6 (VQE) are expected to outperform classical computational methods with modest quantum resources. However, the best ansatz for strongly correlated wave functions is far from clear, raising the question of how near-term quantum computing can usefully address unsolved electronic structure problems in chemistry. These questions are further complicated by the lack of numerical insight into the mathematical limits of different ansätze, such as how the accuracy scales with the number of operators or circuit depth.

We present a method for discovering highly compact ansätze by combining products of spin symmetry-preserving fermionic operators with a global optimisation algorithm, the Discretely Optimised Variational Quantum Eigensolver (DISCO-VQE), which optimises both the discrete sequence of operators and their continuous variational parameters. Numerical simulations demonstrate that accurate wave functions for strongly correlated electronic systems can be parametrised with efficient quantum circuits. These advances facilitate the design of high-accuracy quantum ansätze for solving challenging electronic structure problems on quantum devices, which will provide a deeper theoretical understanding of how these mathematical approximations encode strong electron correlation.

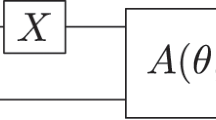
Ansatz-based approaches apply a unitary transformation \(\hat{U}\) to an initial state \(\left\vert {{{\Phi }}}_{0}\right\rangle\) in the form of a quantum circuit, constructed through a series of parametrised building blocks as \(\hat{U}={\hat{U}}_{1}({\theta }_{1})\cdots {\hat{U}}_{N}({\theta }_{N})\). The parameters θi are optimised on a classical computer by extremising an objective function, such as the electronic energy, which is evaluated using the quantum computer. This product structure defines a family of wave functions that we term unitary product states (UPS), and encompasses every quantum computational chemistry ansatz that has been proposed to date.

The ideal unitary product state should satisfy:

  • Universality — describe any electronic eigenstate;

  • Practicality — minimise circuit depth with few entangling gates;

  • Symmetry — preserve good quantum numbers for operators that commute with the Hamiltonian.

Currently, the most popular ansätze use either hardware-efficient unitary operators constructed from qubit operations that minimise the depth of a specific quantum circuit7, or physically-motivated fermionic unitary operations8 based on the second-quantised representation of electronic systems1. Second-quantised fermionic operators conserve particle number and Pauli antisymmetry, ensuring that truncated approximations predict accurate properties beyond the energy, and providing suitable initial states for fault-tolerant quantum phase estimation, where efficiency depends on the initial overlap with exact states. However, fermionic operators require multiple gate operations that lead to deep quantum circuits, creating a trade-off between symmetry-preservation and gate efficiency8.

Initial developments based on fermionic operators included the unitary coupled cluster approach6,8 (UCC), inspired by the success of coupled cluster theory for classical computing9. The UCC unitary transformation is an exponential of a sum of anti-Hermitian fermionic operators, usually restricted to one- and two-body excitations8. However, since fermionic operators generally do not commute, representing this unitary transformation as a quantum circuit requires a Trotter approximation, which is only exact in the infinite limit: \({{{{\rm{e}}}}}^{\hat{A}+\hat{B}}=\mathop{\lim }\limits_{m\to \infty }{({{{{\rm{e}}}}}^{\hat{A}/m}{{{{\rm{e}}}}}^{\hat{B}/m})}^{m}\). Instead, focus has shifted to a particular UPS form called disentangled UCC10. While it has been shown theoretically that exact states can be represented using a suitably-ordered infinite product of one- and two-body fermionic operators10, finite expansions are sensitive to the operator order, fail for strong correlation11,12, and do not conserve the \(\langle {\hat{S}}^{2} \rangle \) quantum number13. In our view, refering to these states as UCC is no longer appropriate since the connection to the many-body cluster operator is not retained in practice. The ADAPT-VQE optimisation algorithm14, and its extensions15,16,17,18, iteratively build a UPS from a pool of operators, selecting the operator with the largest energy improvement at each step. Although promising, variants of ADAPT-VQE that use qubit operators may not converge to the exact ground state19, and current qubit and fermionic implementations are not guaranteed to conserve spin symmetry17,20. Furthermore, as we show in this work, the ADAPT-VQE optimisation strategy will generally not identify the best representation with the fewest number of operators from a given pool.

Here we describe an approach that fulfils the ansatz requirements using a symmetry-preserving unitary product state (s-UPS) that conserves Pauli antisymmetry, particle number symmetry, and the \(\langle {\hat{S}}_{z} \rangle\) and \(\langle {\hat{S}}^{2}\rangle\) quantum numbers using a fermionic operator pool. We prove that this ansatz is universal and demonstrate that it is gate-efficient. Identifying the appropriate choice of the operators is system-dependent and challenging. We solve this problem by introducing the DISCO-VQE algorithm, which simultaneously optimises the operator sequence and their variational parameters. Our approach discovers the most accurate s-UPS representation with a minimal number of parameters, demonstrating that high-accuracy gate-efficient quantum circuits can be achieved, and providing a practical route for designing highly accurate ansätze in the future.

Results

Symmetry-preserving unitary product states

Fermionic unitary operators correspond to an exponential of anti-Hermitian second-quantised operators \({\hat{\kappa }}_{pq\ldots }^{rs\ldots }={a}_{r}^{{\dagger} }{a}_{s}^{{\dagger} }\cdots {a}_{q}^{\phantom{{\dagger} }}{a}_{p}^{\phantom{{\dagger} }}-{a}_{p}^{{\dagger} }{a}_{q}^{{\dagger} }\cdots {a}_{s}^{\phantom{{\dagger} }}{a}_{r}^{\phantom{{\dagger} }}\). These operators ensure Pauli antisymmetry, conserve particle number, and can be mapped onto qubit operators using fermion-to-qubit encodings21,22. We define a symmetry-preserving unitary product state (s-UPS) of length M as

$$\left\vert {{\Psi }}({{{\bf{t}}}},{{{\boldsymbol{\mu }}}})\right\rangle =\mathop{\prod }\limits_{i=1}^{M}{{{{\rm{e}}}}}^{{t}_{i}{\hat{\kappa }}_{{\mu }_{i}}}\left\vert {{{\Phi }}}_{0}\right\rangle ,$$
(1)

where \(\left\vert {{{\Phi }}}_{0}\right\rangle\) is an arbitrary initial state, and only spin-adapted generalised one-body and paired two-body operators are allowed, that is \({\hat{\kappa }}_{{\mu }_{i}}\in \{{\hat{\kappa }}_{p}^{q}+{\hat{\kappa }}_{\bar{p}}^{\bar{q}},{\hat{\kappa }}_{p\bar{p}}^{q\bar{q}}\}\). The indices p, q (where p < q) denote arbitrary spin orbitals and the absence (presence) of an overbar indicates a high-spin (low-spin) orbital. Individual operators may appear multiple times with different amplitudes, defined by the continuous coordinates t = (t1, …, tM). Because the \({\hat{\kappa }}_{{\mu }_{i}}\) need not commute, the ansatz depends on the sequence of operators, denoted by the ordered indices μ = (μ1, …, μM).

Using generalised fermionic operators, where p and q represent arbitrary spin orbitals, removes any dependence on the separation of occupied or virtual orbitals in a mean-field reference. In contrast to many-body perturbation theory, these operators represent Lie algebra generators23 for unitary transformations in the D-dimensional Hilbert space and can rotate any initial state into any exact state. Universality of the generalised (unpaired) one- and two-body fermionic operators has been proved by realising that their nested commutators can generate the full Lie algebra10. Since a product of unitary operators corresponds to an exponential of a sum of operators and their commutators, \({{{{\rm{e}}}}}^{\hat{A}}{{{{\rm{e}}}}}^{\hat{B}}={{{{\rm{e}}}}}^{\hat{A}+\hat{B}+\frac{1}{2}[\hat{A},\hat{B}]+...}\), combining enough operators in a suitable order can represent any unitary transformation in the Hilbert space24. The universality of the s-UPS ansatz can be proved using the additional observation that generalised two-body operators can be expressed as nested commutators of one-body and paired two-body operators, as we show in the Supplementary Methods and illustrate diagrammatically in Supplementary Figure 1. This proof requires the reference state to have at least one pair of doubly occupied and doubly unoccupied orbitals. We postulate that M≤(D − 1) will allow any initial state to be rotated into an exact state without redundant parameters, and provide numerical examples that support this hypothesis. In practice, we expect sufficient accuracy with smaller M values.

Since these elementary operators are spin-adapted (the commutators \([{\hat{S}}^{2},\hat{\kappa }]\) and \([{\hat{S}}_{z},\hat{\kappa }]\) vanish), the s-UPS ansatz conserves the spin symmetry of the initial state for every truncation M, avoiding spin-constrained optimisation13 or spin projection17. In contrast, spin-adapted unpaired two-body operators require the exponentiation of a sum of non-commuting operators, and their application in a quantum circuit requires a Trotter approximation, which destroys the spin adaptation13. Furthermore, paired two-body operators \({\hat{\kappa }}_{p\bar{p}}^{q\bar{q}}\) can be implemented with a constant number of two-qubit controlled-NOT (CNOT) gates, while the CNOT count for unpaired two-body operators grows linearly with the number of orbitals (see Supplementary Methods).

The s-UPS ansatz can be viewed as a generalisation of the quantum-number-preserving (QNP) approach25 and the swap-network k-UpGGCSD framework26, where spin-adapted orbital rotation gates (generalised spin-adapted one-body operators) and pair exchange gates (paired two-body operators) between nearest-neighbour qubits are used to define low-depth quantum circuits with local connectivity. Since we include operators connecting any pair of orbitals, and allow a variable operator ordering, we expect greater accuracy with fewer parameters. Furthermore, while universality of the QNP ansatz was only postulated and demonstrated numerically25, our fermionic representation has allowed a rigorous proof.

Discretely optimised variational quantum eigensolver

Fixed operator orderings are typically poor approximations to the optimal unitary product state and very little is understood about what constitutes a good ordering14,27. Without a priori information, the optimal operator ordering can be approached as a coupled discrete and continuous optimisation problem for the continuous operator amplitudes t and the discrete ordered operator set μ. Exploiting the variational principle, the optimal s-UPS representation can be identified by minimising the energy

$$E({{{\bf{t}}}},{{{\boldsymbol{\mu }}}})=\left\langle {{{\Phi }}}_{0}\right\vert \left(\mathop{\prod }\limits_{i=M}^{1}{{{{\rm{e}}}}}^{-{t}_{i}{\hat{\kappa }}_{{\mu }_{i}}}\right)\hat{H}\left(\mathop{\prod }\limits_{i=1}^{M}{{{{\rm{e}}}}}^{{t}_{i}{\hat{\kappa }}_{{\mu }_{i}}}\right){{{\Phi }}}_{0}.$$
(2)

The nonlinearity of E(t, μ) with respect to t creates local minima that hinder global optimisation12,28. Previous discrete optimisation strategies include mapping the problem to a probabilistic framework29, genetic algorithms30,31, or an iterative gate-by-gate optimisation algorithm32. However, stochastic approaches are not guaranteed to find the global minimum, while the gate-by-gate approach cannot escape local discrete minima, and the strong interdependence of the operators means that crossover steps in genetic algorithms are less likely to lower the energy30.

Instead, we have developed the Discretely Optimised Variational Quantum Eigensolver (DISCO-VQE), which facilitates global optimisation by taking steps in both the continuous and discrete spaces for the s-UPS ansatz. For a given μ, we define a local discrete neighbourhood as the operator sequences connected by:

  • cyclically permuting the ordered set;

  • mutating one operator into another from the pool;

  • swapping the position of two operators.

Following the generalised basin-hopping (GBH) approach33,34,35, we define a biminimum34 as a configuration (t, μ) that is a minimum in the continuous parameters and lies lower in energy than neighbouring minima after a step in the discrete space, including relaxation of the continuous parameters. DISCO-VQE alternates between a series of basin-hopping36,37 steps that explore the continuous energy landscape for a fixed set of operators, and discrete steps in the space of operator orderings (Fig. 1). After each round of basin-hopping steps we identify the lowest-energy configuration that can be reached by cyclically permuting the operators and reoptimisation of the continuous coordinates. Similarly, we identify the lowest energy mutation and pair swap for each operator and accept this step if it lowers the energy. By testing mutations and pair swaps for every operator individually, DISCO-VQE can completely change the discrete parameters in each macrocycle and, in principle, the optimal operator sequence could be discovered after one macro iteration. In practice, the combined space of continuous and discrete parameters exhibits many local biminima and uphill moves are required to escape these traps. The full algorithm is detailed in the Supplementary Methods.

Fig. 1: DISCO-VQE optimises the continuous coordinates t and the discrete space of operator orders μ.
figure 1

This generalised basin-hopping approach identifies the best s-UPS wave function using cyclic permutations, mutations, and pair swaps of the unitary operators.

Full size image

To avoid a bias towards any particular region of the discrete space, the search is initialised with identity operators that represent the initial state \(\left\vert {{{\Phi }}}_{0}\right\rangle\). In the future, the use of informed guesses based on intuition into the best operator order may improve the optimisation efficiency.

Analysis of computational scaling

Obtaining high-accuracy wave functions using adaptive algorithms, such as DISCO-VQE and ADAPT-VQE, increases the computational cost relative to a fixed ansatz approach. For M operators chosen from a pool of size N, the computational scaling of DISCO-VQE is determined by the cost of the operator mutations and pair swaps. One cycle of operator mutations tests whether the energy is lowered when each of the M operators is replaced with another operator from the pool, giving a scaling of \({{{\mathcal{O}}}}(MN)\). Similarly, one cycle of pair swaps considers every possible way to interchange the current operators, with a scaling of \({{{\mathcal{O}}}}({M}^{2})\). The overall scaling of the discrete search is therefore \({{{\mathcal{O}}}}(\max ({M}^{2},MN))\), allowing the combinatorial space of operator sequences to be searched with polynomial scaling in M and N.

Global optimisation allows highly accurate wave functions to be discovered with smaller operator pools and fewer variational parameters than methods such as ADAPT-VQE. To avoid stagnation, the standard fermionic ADAPT-VQE implementation14 must consider all unpaired two-body operators with a pool that scales as \(N \sim {{{\mathcal{O}}}}({n}_{\text{q}}^{4})\), where nq is the number of qubits. The discrete gradients needed to iteratively grow the ansatz scale as \({{{\mathcal{O}}}}(N)\), giving fermionic ADAPT-VQE an overall scaling of \({{{\mathcal{O}}}}({n}_{\text{q}}^{4})\). In contrast, our spin-adapted one-body and paired two-body operator pool scales as \(N \sim {{{\mathcal{O}}}}({n}_{\text{q}}^{2})\). Assuming that chemical accuracy can be achieved with M≤N, which is true for the examples we consider, the overall scaling of DISCO-VQE becomes \({{{\mathcal{O}}}}(M{n}_{\text{q}}^{2})\), which is at worst the same as fermionic ADAPT-VQE with unpaired two-body operators. Further reductions may be achieved with additional restrictions, such as constraining the operators to act between nearest-neighbour qubits to give \(N \sim {{{\mathcal{O}}}}({n}_{\text{q}})\). The current state of knowledge does not provide a prediction for how the number of operators M required to achieve a given accuracy will scale with the system size.

The computational cost of DISCO-VQE scales linearly with the number of basin-hopping steps in the continuous space and the number of discrete macrocycles, which are primarily determined by the amount of computing resources available. In this work, our aim is to calibrate the best achievable accuracy, so we use a large number of cycles, as detailed in the Supplementary Methods. However, any number of basin-hopping steps must always be at least as accurate as the current best optimisation with the same initial guess, while the reoptimisation in the discrete search means that the continuous space can still be explored without any basin-hopping steps (Supplementary Figure 2). Furthermore, because DISCO-VQE starts by selecting mutations for the initial empty set of operators, which is essentially the same as the ADAPT-VQE procedure, even a single discrete macrocycle will ensure that DISCO-VQE is at least as accurate as ADAPT-VQE with the same operator pool (Supplementary Figure 2). Consequently, even for a single macrocycle, DISCO-VQE will always match or exceed the accuracy of current state-of-the-art VQE calculations.

Exact wave functions using DISCO-VQE

The universality of the s-UPS ansatz means that wave functions with an arbitrarily small energy error can be obtained using a finite number of spin-adapted one-body and paired two-body unitary operators. DISCO-VQE calculations on linear and tetrahedral H4 show that chemical accuracy (1.59 mEh) requires only nine and five operators, respectively (Fig. 2a–b). Furthermore, exact ground states can be identified using thirteen or eight operators, respectively, compared to a Hilbert space of 36 configurations. These results support our postulate that exact s-UPS representations require a finite number of operators M that is less than the Hilbert space size, in contrast to previous theoretical work that could only demonstrate universality in the limit M → ∞10.

Fig. 2: DISCO-VQE produces exact wave functions using global optimisation.
figure 2

The panels illustrate the convergence of DISCO-VQE and ADAPT-VQE with respect to the number of operators for (a) linear H4, R(H − H) = 0.90 Å, and (b) tetrahedral H4, R(H − H) = 1.98 Å, using the STO-3G basis set45. (c) DISCO-VQE identifies the exact wave function throughout the linear H4 binding curve, while ADAPT-VQE and random ordered sets of thirteen operators exhibit a large variation in accuracy. DISCO-VQE surpasses the accuracy of ADAPT-VQE using only six operators, while chemically accurate binding curves require ten operators (Supplementary Figure 5). Computational details for the DISCO-VQE and ADAPT-VQE calculations are provided in the Supplementary Discussion.

Full size image

Practical electronic structure calculations generally require consistent accuracy for every relevant geometry of a molecule. DISCO-VQE achieves this goal for linear H4 by identifying exact wave functions with thirteen operators at all geometries (Fig. 2c). Fixing the ansatz to the ordering identified at equilibrium gives near-exact energies across the full binding curve (Supplementary Figure 4), demonstrating that accurate and transferable fixed ansätze can be defined. The operator sequence and optimised parameters for this fixed ansatz are included in Supplementary Table 1, providing a high-accuracy quantum circuit for use in practical VQE experiments. In comparison, random fixed ansätze are relatively accurate near equilibrium, but exhibit a large energy variation towards dissociation (Fig. 2c). Furthermore, optimisation using ADAPT-VQE with the paired operator pool accurately describes equilibrium and dissociation, but gives appreciable errors at intermediate geometries, where electron correlation is most challenging (Fig. 2c).

Global optimisation of the continuous coordinates and discrete operator ordering is essential for realising the universality of the s-UPS ansatz. The improved algorithmic optimisation provided by DISCO-VQE is clear from comparison with ADAPT-VQE calculations using the same pool of operators. By adding one operator at a time, ADAPT-VQE performs a local optimisation, which may not converge to the exact ground-state wave function, as demonstrated in Fig. 2a–b. DISCO-VQE can escape these local minima and implements global optimisation for any sequence of operators.

Stagnation of the ADAPT-VQE optimisation was previously described in ref. 19 and arises from combining the gradient-based selection criterion with particular operator pools. The restriction to paired two-body operators means that the ADAPT-VQE gradient14 no longer coincides with the residual of the Anti-Hermitian Contracted Schrodinger Equation38 and converged solutions are not necessarily eigenstates39. A near-exact ADAPT-VQE result for linear H4 can be obtained by including unpaired two-body operators (Fig. 2a), although DISCO-VQE is still more accurate with fewer operators, and truncated wave functions exhibit spin contamination (Supplementary Figure 3).

Applicability to open-shell molecules

High-spin molecules are an important target for quantum algorithms because conserving open-shell spin symmetry in standard methods, such as coupled-cluster theory, introduces significant computational complexity40. Rubin et al. have recently shown that ADAPT-VQE using the full unpaired operator pool struggles to converge to the high-spin triplet ground state of O2 using the restricted open-shell HF (ROHF) reference state, while starting from a more accurate ROHF-CCSD state introduces spin contamination20. These issues arise from a plateau in the energy with respect to the number of operators (Fig. 3a), which causes the magnitude of the discrete gradient to temporarily fall below the convergence threshold used in ref. 20 (Fig. 3b: top panel). Adding more operators eventually causes the energy to decrease, although 32 operators are ultimately required to reach chemical accuracy.

Fig. 3: The s-UPS ansatz accurately predicts the high-spin triplet state of O2 (STO-3G) while preserving the \(\langle {\hat{S}}^{2}\rangle\) quantum number.
figure 3

Two core molecular orbitals are frozen and the bond length is R(O-O) = 2.55 Å. a DISCO-VQE optimisation achieves chemical accuracy with only nine operators from the ROHF reference state, while ADAPT-VQE with the paired operator pool fails to converge to the correct state. b ADAPT-VQE using the full unpaired operator pool can become spin contaminated and exhibits a plateau in the energy with respect to the number of operators, which creates a minimum in the magnitude of the ADAPT-VQE discrete gradient. Computational details for DISCO-VQE and ADAPT-VQE calculations are provided in the Supplementary Discussion.

Full size image

In contrast, the s-UPS ansatz provides a chemically accurate representation of the O2 ground state using only nine operators from a Hilbert space of 448 configurations. This highly accurate open-shell s-UPS approximation is achieved despite only including spin-adapted one-body and paired two-body operators in the pool, with no modifications to the DISCO-VQE procedure. As for the H4 results, the importance of global optimisation in the discrete space is demonstrated by the stagnation of ADAPT-VQE calculations using the paired operator pool. Furthermore, enforcing spin symmetry at the operator level ensures that every s-UPS truncation preserves the \(\langle {\hat{S}}^{2}\rangle =2\) property of the ROHF reference state, guaranteeing a spin-pure representation (Fig. 3b: bottom panel). Hence, universal wave functions for any spin state can be achieved using the s-UPS approach.

Accuracy of truncated approximations

Practical quantum computations on large molecules will still require truncated wave function approximations. Global optimisation using DISCO-VQE provides the most accurate s-UPS for a given number of operators, while conserving spin symmetry at every truncation. For example, DISCO-VQE calculations on linear H6, with a Hilbert space of 400 configurations, achieve chemical accuracy with 30 operators (Fig. 4a) while ADAPT-VQE optimisation stagnates between 14 and 40 operators (Fig. 4a). DISCO-VQE requires 10 operators to surpass the accuracy of ADAPT-VQE using the paired operator pool (Fig. 4b) and improves the energy using fewer parameters compared to previous fermionic operator methods (Fig. 4c). Hence, DISCO-VQE provides the most accurate result with a specified number of fermionic operators in linear H6.

Fig. 4: DISCO-VQE provides the most accurate s-UPS wave function for a given number of operators.
figure 4

a DISCO-VQE with 30 operators provides chemically accurate energies for the linear H6 binding curve (STO-3G). This number of operators matches the size of the operator pool. b Comparison of DISCO-VQE errors and the previous state-of-the-art methods across the full binding curve. ADAPT-VQE calculations use the same paired operator pool. The un-Trotterised 1-UpCCGSD and 2-UpCCGSD results are taken from ref. 12. The non-parallelity error (NPE) is the difference between the maximum and minimum error in the energy. Boxes illustrate the upper and lower quartiles, and whiskers represent the maximum and minimum values. c DISCO-VQE produces highly accurate energies at R(H − H) = 2.0 Å with fewer continuous parameters than previous algorithms. The k-uCJ results are taken from ref. 46. The accuracy of the 2-UpCCGSD12 or 2-uCJ46 approaches is surpassed with 30 operators, while ADAPT-VQE with the full unpaired operator pool required at least 78 operators to obtain comparable results14. Computational details for the DISCO-VQE and ADAPT-VQE calculations are provided in the Supplementary Discussion.

Full size image

Symmetrically stretched H2O and N2 dissociation represent strongly correlated molecular tests for wave function approximations, with Hilbert space dimensions of 441 and 400, respectively, when the four lowest molecular orbitals of N2 are frozen. DISCO-VQE calculations with a truncated s-UPS ansatz produce highly accurate energies across the H2O binding curve (Fig. 5a). In contrast, ADAPT-VQE optimisation using the paired operator pool fails to identify chemically accurate wave functions at any bond length (Fig. 5a), while previous studies that include unpaired two-body operators are much less accurate than our approach41. The un-Trotterised k-UpCCGSD ansatz required 126 variational parameters to reach an accuracy of 0.07 mEh27, while Trotterised calculations with over 250 operators have residual errors of 0.02–200 mEh42. Our global optimisation strategy significantly increases the accuracy with fewer operators than the previous algorithms.

Fig. 5: Wave functions built using DISCO-VQE accurately describe the potential energy surface for strongly correlated molecules.
figure 5

The number of operators in these DISCO-VQE calculations is chosen to match the size of the operator pool in the STO-3G basis set, with (a) 42 operators for the symmetric stretch of H2O and (b) 30 operators for the dissociation of N2. The four lowest energy molecular orbitals are frozen in N2. Un-Trotterised k-UpCCGSD results for N2 are taken from ref. 27. Computational details for the DISCO-VQE and ADAPT-VQE calculations are provided in the Supplementary Discussion.

Full size image

DISCO-VQE achieves chemical accuracy at nearly every N2 bond length using 30 operators, giving a very accurate binding curve (Fig. 5b). In comparison, UPS representations built from randomly ordered sets that include all two-body operators have errors of 16–64 mEh12, demonstrating the importance of global optimisation that treats both the discrete operator space and the continuous space of operator amplitudes. The parameter reduction is highlighted by comparing to the un-Trotterised k-UpCCGSD results, which require over 180 parameters to obtain a better mean-average error27 (Supplementary Table 2). In contrast, ADAPT-VQE optimisation with the paired operator pool does not produce a smooth binding curve (Fig. 5b), while including unpaired two-body operators breaks the total spin symmetry for truncated approximations17. The s-UPS ansatz conserves the initial \(\langle {\hat{S}}^{2}\rangle\) value at every truncation, and DISCO-VQE global optimisation achieves a highly accurate and operator-efficient description of this strongly correlated electronic system.

Maximising the efficiency of quantum circuits

Applications on near-term quantum devices must balance accuracy against the number of two-qubit CNOT gates in the quantum circuit, which contribute the largest source of hardware noise. This challenge has motivated hardware-efficient ansätze where the operator pool requires few CNOT gates, such as qubit-ADAPT-VQE15 and qubit-excitation-based (QEB) ADAPT-VQE18. However, these methods can break fermionic antisymmetry, particle number, or spin symmetry, giving unphysical electronic states.

Despite employing fermionic operators, DISCO-VQE achieves chemical accuracy for linear H6 using less than a third of the CNOT gates required for hardware-efficient ansätze (Fig. 6). These favourable CNOT counts are achieved by removing redundancies from the quantum circuit using discrete optimisation and through the CNOT efficiency of paired two-body operators. Therefore, efficient quantum circuits can be achieved using symmetry-preserving fermionic operators without relying on a hardware-efficient ansatz.

Fig. 6: DISCO-VQE identifies accurate and efficient quantum circuits with significantly fewer CNOT gates than the previous state-of-the-art.
figure 6

Calculations correspond to linear H6 at R(H − H) = 1.5 Å. Data for the qubit-ADAPT-VQE and QEB-ADAPT-VQE methods are taken from ref. 18. CNOT counts are evaluated using the efficient circuit design introduced in ref. 47.

Full size image

Balancing weak and strong electron correlation

Balancing weak and strong electron correlation is essential for quantum chemistry, but has proved difficult to achieve in practice. Many-body perturbation techniques can be quantitatively accurate for weak correlation, but fail for strong correlation where the molecular orbital picture breaks down. The accuracy of the DISCO-VQE results across the H6, H2O, and N2 potential energy surfaces demonstrate that the s-UPS ansatz can quantitatively describe both correlation regimes.

The strongly correlated half-filled Hubbard lattice represents a challenging condensed matter physics problem for many-body approximations43. The correlation strength is determined by the balance of the on-site repulsion U and the one-electron adjacent site hopping term t. DISCO-VQE calculations with a truncated s-UPS wave function provide excellent accuracy in both the weak (U ≪ t) and strong (U ≫ t) correlation limits (Fig. 7a) using a consistent number of operators and parameters. ADAPT-VQE optimisation with the paired operator pool provides an accurate representation of weak correlation, but is less accurate than DISCO-VQE as the correlation strength increases. The converged ADAPT-VQE wave functions include significantly more operators than DISCO-VQE for intermediate correlation (U/t ≈ 10), but are less accurate (Fig. 7c). We see that global optimisation using DISCO-VQE is essential for obtaining quantitatively accurate s-UPS wave functions for both weak and strong correlation with a consistent quantum circuit cost.

Fig. 7: DISCO-VQE captures the correct physics for a strongly correlated two-dimensional Hubbard lattice (4 × 2) using 56 operators.
figure 7

The corresponding Hilbert space contains 4900 configurations, and the number of operators is chosen to match the size of the operator pool. The DISCO-VQE energy (a) is very accurate in both the weak correlation (U ≪ t) and strong correlation (U ≫ t) regimes. Similarly, DISCO-VQE accurately predicts the double occupancy (b), which becomes exact in the weak and strong correlation limits. Analogous ADAPT-VQE calculations using the paired operator pool require seven times more operators at intermediate correlation but give less accurate results (c). Computational details for DISCO-VQE and ADAPT-VQE calculations are provided in the Supplementary Discussion.

Full size image

Physical properties beyond the energy are also important for understanding quantum phase behaviour. The strongly correlated half-filled Hubbard model is characterised by an antiferromagnetic phase, where the electrons are unpaired and localised on individual sites. The double occupancy \(\left\langle {\hat{n}}_{p}{\hat{n}}_{\bar{p}}\right\rangle\) measures the probability of simultaneously finding two electrons on the same site, which tends to zero for U/t → ∞ and 0.25 for U/t → 0. Truncated s-UPS representations identified using DISCO-VQE accurately predict this change across different U/t values (Fig. 7b) and exhibit the correct limits. Hence both the wave function and the energy can be accurately predicted, providing a physically complete description of strong electron correlation.

Finally, the 1/8-filling fraction is more challenging for standard quantum Monte Carlo techniques due to the fermionic sign problem44. DISCO-VQE calculations for the 4 × 2 lattice achieve exact wave functions using only seven operators (Fig. 8). This number is significantly lower than the 56 operators used for the inexact half-filled result, suggesting that the performance of the s-UPS ansatz for a fixed number of operators is primarily related to the size of the relevant number- and \(\langle \hat{S}_z \rangle\)–preserving Hilbert space sector, which is 64-dimensional in this case. These results provide further evidence for the applicability of our approach across various different electron correlation regimes.

Fig. 8: DISCO-VQE identifies a numerically exact representation of the 1/8-filled 2-dimensional Hubbard model.
figure 8

Only seven operators are required to obtain an exact result for the 4 × 2 lattice, demonstrating the applicability across various different electron correlation regimes.

Full size image

Discussion

We have shown that an arbitrary electronic state can be parametrised with the s-UPS ansatz built from spin-adapted one-body and paired two-body fermionic operators. This ansatz conserves fermionic antisymmetry, particle number, and the \(\langle {\hat{S}}^{2}\rangle\) and \(\langle {\hat{S}}_{z}\rangle\) quantum numbers without constrained optimisation or spin projection, and can parametrise any spin state. The flexibility and accuracy of these wave functions comes from identifying the best sequence of unitary operators. The DISCO-VQE algorithm can universally address this challenge by performing a coupled discrete and continuous global optimisation of the wave function. Numerical simulations demonstrate that chemically accurate energies can be achieved for weakly and strongly correlated molecules using significantly fewer operators and CNOT gates than previous techniques.

The s-UPS ansatz offers key advantages for practical quantum algorithms: it can parametrise arbitrarily accurate wave functions; preserves the Hamiltonian spin symmetries at every truncation; and provides low CNOT counts suitable for noisy quantum hardware. Conserving physical symmetries is essential for subsequent fault-tolerant quantum phase estimation, where efficiency depends on the overlap of the initial and exact states. Furthermore, formulating generalised fermionic operators as Lie algebra generators for unitary rotations moves beyond the many-body unitary coupled cluster framework and embraces the natural capabilities of qubit rotations in quantum computation, bridging the gap between fermionic operators and hardware-efficient approaches such as the quantum-number-preserving ansatz25. These advances enable quantitative, physically accurate, and gate-efficient quantum circuits for simulating strongly correlated chemistry using near-term quantum computers.

We have not explicitly considered spatial symmetry in the present calculations, meaning that the spatial symmetry of the initial state may not be preserved as the unitary operators are applied sequentially. For point groups with non-degenerate irreducible representations, conservation of spatial symmetry can be trivially enforced by restricting the one-body operators to act between orbitals with the same spatial symmetry, while paired two-body operators automatically conserve symmetry. However, the effect of this restriction on the convergence of DISCO-VQE is beyond the scope of the current work, and we leave this question for future investigations.

The success of many proposed quantum algorithms relies on the accuracy of the initial state, which must be prepared at a polynomial cost. Whether this accuracy is achievable using current UPS ansätze remains an open question and depends on: how the ansatz expressibility grows with the number of operators and parameters; whether strong correlation can be parametrised with low circuit depth; and how the number of operators scales with the system size for a given level accuracy. Definitive answers to these questions will require further work. Here we have shown that global optimisation using DISCO-VQE provides reliable lower bounds on the minimum number of operators and circuit depth required for a given operator pool, providing insights into ansatz design. Our results clearly demonstrate how a combination of theory and numerical simulations can produce high-accuracy ansätze to treat strong correlation on quantum devices.