Introduction

The Dirac equation, which describes the wavefunction for a spin-1/2 particle in the framework of relativistic quantum mechanics, represents a cornerstone of modern physics. Over the past century, this equation has been producing enduring profound influences on a wide variety of fields of modern science and technology, ranging from atomic physics to quantum electrodynamics1, and from material engineering2,3,4,5 to medical imaging6.

Despite the fundamental importance of the Dirac equation, the physics underlying its dynamical solution has not been fully understood owing to the associated elusive phenomena, exemplified by Zitterbewegung (ZB)7, the oscillatory motion of a particle, as a result of the interference between the positive and negative energy components. For a free electron, the predicted ZB has an amplitude on the order of the Compton wavelength, ℏ/mc ~ 10−12 m, and thus cannot be unambiguously observed due to the restriction of the Heisenberg uncertainty principle. Although whether or not ZB really exists in relativistic quantum mechanics is still an open question8,9,10,11, enduring efforts have been made to its simulations with different quantum systems, including circuit quantum electrodynamics11, ion traps12,13, ultracold atoms14,15,16,17, semiconductor quantum wells18,19,20,21,22,23, graphene24,25,26,27,28,29,30,31,32,33, and moiré excitons34. These investigations have shed new light on ZB, which itself, however, is not a unique character of Dirac particles as similar phenomena can also appear in some classical wave systems35,36,37,38,39,40. This leads us to consider whether the ZB associated with Dirac particles has a deeper quantum origin that can manifest itself even without ZB. Answering this question is critical for understanding the dynamical behaviors of Dirac particles at a more fundamental level, but a deep exploration is still lacking.

Results

Theoretical predictions

We here present an investigation on this important issue, and unveil a universal quantum interference behavior in the position-momentum space. The nonclassicality of this behavior is manifested by the negativity of the phase space quasiprobability distribution–Wigner function (WF), as well as by the quantum correlation between the spatial and internal degrees of freedom. These quantum signatures distinguish the ZB of the Dirac particle, obtained by integrating the WF over the momentum, from the trembling motion of classical wavepackets, and more importantly, can express themselves even in the absence of any negative component. We demonstrate this unique interference pattern with a circuit, where the spinorial characteristic of a Dirac particle is encoded in the two lowest energy levels of a superconducting Xmon qubit41,42,43, while the position and momentum are mapped to the quadratures of the photonic field. The measured WFs and entanglement entropy agree well with theoretical predictions. Furthermore, we simulate the Klein tunneling44,45 in a linear potential field and observe mesoscopic superpositions of two separated wavepackets in phase space.

We focus on the simplest case that the motion of a Dirac particle is confined to one dimension (1D), for which the Hamiltonian reduces to

$${H}_{{{{\rm{D}}}}}=c{\sigma }_{y}\hat{p}+m{c}^{2}{\sigma }_{z}.$$
(1)

Here c denotes the light speed in the vacuum, \(\hat{p}\) represents the momentum operator of the particle with a rest mass of m, and σy and σz are the Pauli operators that endow the Dirac particle a spinor characteristic, manifested by a two-component wavefunction, where the spatial position and momentum are correlated with the degree of freedom defined in an “internal space", which will be referred to as pseudospin for simplicity. Unlike the Schrödinger equation, the Dirac equation is linear in both the time- and space-derivatives, satisfying the Lorentz-covariance, and includes the spin degree of freedom at the ab initio level by describing the wave function in terms of a spinor. These features have led to remarkable accomplishments, including predictions of the spin-1/2 feature of electrons and the existence of anti-particles indicated by the negative-energy component accompanying the positive one, and introduction of the spin-orbit interaction that led to a more refined fine structure description of the spectrum. These predictions are based on stationary solutions of the Dirac equation and show excellent agreements with experiments. As the Hamiltonian commutes with the momentum operator, it is illuminating to uncover the physics in the momentum representation, where the momentum operator \(\hat{p}\) can be taken as a parameter p. For a specific value of p, HD has two eigenvalues \(\pm {E}_{p}=\pm \sqrt{{p}^{2}{c}^{2}+{m}^{2}{c}^{4}}\), with the corresponding eigenstates \(\left\vert {\phi }_{+}(p)\right\rangle ={\left(\cos {\phi }_{p},{{{\rm{i}}}}\sin {\phi }_{p}\right)}^{T}\) and \(\left\vert {\phi }_{-}(p)\right\rangle ={\left({{{\rm{i}}}}\sin {\phi }_{p},\cos {\phi }_{p}\right)}^{T}\), where \(\tan (2{\phi }_{p})=\frac{p}{mc}\). Suppose that the system is initially in the product state

$$\left\vert \psi (0)\right\rangle =\int{{{\rm{d}}}}p\,{\xi }_{p}\left\vert p\right\rangle \left\vert X\right\rangle ,$$
(2)

where \(\left\vert \pm X\right\rangle =\frac{1}{\sqrt{2}}{\left(1,\pm 1\right)}^{T}\) and ξp denotes the wave function in the momentum representation. Under the Dirac Hamiltonian, the system evolves as

$$\left\vert \psi (t)\right\rangle =\int{{{\rm{d}}}}p\,\left\vert p\right\rangle {\xi }_{p}(\cos {\varphi }_{t}\left\vert X\right\rangle -{{{\rm{i}}}}{{{{\rm{e}}}}}^{-2{{{\rm{i}}}}{\phi }_{p}}\sin {\varphi }_{t}\left\vert -X\right\rangle ),$$
(3)

where φt = Ept/ℏ. This directly yields the average position evolution,

$$\begin{array}{l}\left\langle x(t)\right\rangle \,=\,\left\langle x(0)\right\rangle +\left\langle v(0)\right\rangle t\\ \qquad\qquad+\,\hslash \int{{{\rm{d}}}}p\,{\left\vert {\xi }_{p}\right\vert }^{2}{x}_{p}(1-\cos 2{\varphi }_{t}),\end{array}$$
(4)

where xp = dϕp/dp, \(\left\langle x(0)\right\rangle\) represents the average value of the initial position, and \(\left\langle v(0)\right\rangle\) denotes the initial mean velocity. The ZB, manifested by the last term, is observable only in the intermediate regime where mc is comparable with p.

In the non-relativistic regime \(\left\vert p\right\vert \ll mc\), the ZB amplitude A ≃ λc/2, where λc = ℏ/mc is the Compton wavelength, which sets the lower bound for the uncertainty of the position, and consequently, the ZB cannot be observed. In the far-relativistic regime \(\left\vert p\right\vert \gg mc\), \(A\ll \hslash /2\left\langle p\right\rangle \ll \delta x\), where δx = ℏ/2δp is the limitation of precision attainable for any position measurement imposed by the Heisenberg uncertainty relation.

As we have noted, ZB itself does not manifest quantum effects, but is closely related to quantum entanglement between the internal and spatial degrees of freedom, produced by their coupling. Under the time evolution, the populations of two states \(\left\vert \pm X\right\rangle\) become increasingly balanced, and the entropy tends to 1. Due to this entanglement, the spatial quantum interference appears when the WF is correlated with the projection of the pseudospin along some basis, e.g., \(\{\left\vert \pm B\right\rangle \}\). The WFs associated to \(\left\vert \pm B\right\rangle\) are respectively

$${{{{\mathcal{W}}}}}_{\pm }(x,p)=\frac{1}{\pi \hslash }\int{{{\rm{d}}}}v\,{\phi }_{\pm }^{* }(p+v){\phi }_{\pm }(p-v){e}^{-2{{{\rm{i}}}}vx/\hslash },$$
(5)

where \({\phi }_{\pm }(p)={\xi }_{p}\left\langle \pm B\right\vert (\cos {\varphi }_{t}\left\vert X\right\rangle -{{{\rm{i}}}}{{{{\rm{e}}}}}^{-2{{{\rm{i}}}}{\phi }_{p}}\sin {\varphi }_{t}\left\vert -X\right\rangle )\). During the evolution, the wavepacket is continually deformed under the competition between the momentum-dependent and static energy terms in the Dirac Hamiltonian, which leads to a nonlinear dependence of the energy on the momentum. This nonlinear process evolves an initial Gaussian wavepacket to a non-Gaussian one, manifesting pseudospin-dependent quantum interference signatures. The ZB phenomenon appears as the integral of the weighted mixture of the two WFs over the momentum, which reflects the classical probability distribution, but does not manifest the underlying quantum nature. It should be noted that the presence of ZB is challenged by the claim that the positive and negative components could not be assigned to a single particle8, however, recent experimental evidence indicates nature does not prohibit the existence of a quantum superposition of a particle with its antiparticle46. We further note that even when the particle remains in the positive branch, there still exists phase space quantum interference, though ZB disappears.

Device and experimental scheme

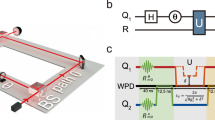
The simulation is performed with a superconducting qubit of angular frequency ω0 that encodes the internal state of the simulated spinor, whose position and momentum are mapped onto the two quadratures of the microwave field stored in a bus resonator, defined as \(\hat{x}=\frac{1}{\sqrt{2}}({a}^{{\dagger} }+a)\) and \(\hat{p}=\frac{{{{\rm{i}}}}}{\sqrt{2}}({a}^{{\dagger} }-a)\), where a† and a denote the creation and annihilation operators for the photonic field of angular frequency ωr. If we take ℏ = 1, \(\hat{x}\) and \(\hat{p}\) satisfy the same commutation relation as the position and momentum operators. The qubit is subjected to two longitudinal parametric modulations with amplitudes εj and angular frequencies νj (j = 1, 2), and a transverse continuous microwave driving with an amplitude Ω (Fig. 1a). With the choice ωr = ω0 + 2ν1, the resonator is coupled to the qubit at the second upper sideband of the first modulation with the effective strength η = λJ2(μ)/247, where Jn(μ) is the nth Bessel function of the first kind, with μ = ε1/ν1. When Ω ≫ 2η, the transverse drive effectively transforms the rotating-wave interaction into an equal combination of rotating- and counter-rotating-wave interactions, simulating the coupling between the internal and external degrees of freedom of the spinor. Then the resulting effective Hamiltonian reduces to the form of Eq. (1), with the correspondences \({\sigma }_{y}={{{\rm{i}}}}\left\vert g\right\rangle \langle e| -{{{\rm{i}}}}| e\rangle \left\langle g\right\vert\), \({\sigma }_{z}=\left\vert e\right\rangle \langle e| -| g\rangle \left\langle g\right\vert\), \({c}^{* }=\sqrt{2}\eta\) and m*c*2 = ε2/4, where c* and m* denote the effective light speed and mass of the Dirac particle in the simulation, respectively (see Supplementary Note 1).

Fig. 1: Diagram and pulse for simulating 1D Dirac particles.
figure 1

a Analog of the Dirac particle in a circuit. The internal and external degrees of freedom of the Dirac particle are respectively encoded in a superconducting qubit and the field mode in a microwave resonator, whose quadratures behave like the position (x) and momentum (p) of the particle. b Engineering of the Dirac Hamiltonian. The coupling between the internal and external states of the spinor is simulated by transversely driving the qubit with continuous microwave, and longitudinally modulating it with two alternating current (AC) fluxes. The first parametric modulation controls the qubit-resonator interaction at the second upper sideband, which together with the transverse driving, effectively realizes the momentum term. The second parametric modulation serves for adjusting the effective mass of the simulated particle. c Pictorial representation of the system’s initial state. The qubit’s state \(\left\vert X\right\rangle\) is represented by its Bloch vector, while the resonator’s coherent state \(\left\vert {{{\rm{i}}}}\sqrt{2}\right\rangle\) is characterized by its WF.

Full size image

Before the experiment, both the resonator and the spinor qubit are initialized to their ground states. The experiment starts with the application of a pulse to the resonator, translating its state along the p-axis in phase space by an amount of p0 = 2, and thus transforming the initial vacuum state to the coherent state \(\left\vert {{{\rm{i}}}}\sqrt{2}\right\rangle\). Then a π/2 rotation is performed on the test qubit, transforming it from \(\left\vert g\right\rangle\) to \(\left\vert X\right\rangle\) at the operating frequency ω0/(2π) = 5.26 GHz. The initial qubit-resonator state is pictorially shown in Fig. 1b. After this initial state preparation, two parametric modulations with frequencies ν1/(2π) = 160 MHz and ν2/(2π) = 33.4 MHz are applied to the qubit. These modulations, together with the transverse microwave driving at the frequency ω0, couple the qubit to the bus resonator with a fixed frequency of ωr/(2π) = 5.584 GHz, effectively realizing the Dirac Hamiltonian in the rotating frame. The ratio between the effective momentum and mass of the Dirac particle is controlled by adjusting the modulation amplitudes ε1 and/or ε2. Detailed system parameters are shown in the Supplementary Table 1.

ZB interference behaviors

We investigate the interference behaviors with the choice of effective spinor frequency \(\omega ={m}^{* }{c}^{* }=\sqrt{2}\eta {p}_{0}\), with \({c}^{* }=\sqrt{2}\eta\), which ensures that the Dirac particle described by the Dirac equation HD has an initial momentum of p0. After a preset evolution time, both the parametric modulations and microwave driving are switched off. This is followed by Wigner tomography, realized by performing a phase space displacement, \(D(\gamma )={{{{\rm{e}}}}}^{\gamma {a}^{{\dagger} }-{\gamma }^{* }a}\), to the resonator and then tuning an ancilla qubit on resonance with the resonator. The photon number population of the displaced resonator field, \({{{{\mathcal{P}}}}}_{n}(\gamma )\), inferred from the measured Rabi oscillation signals, directly yields the WF, \({{{\mathcal{W}}}}(x,p)=\frac{1}{\pi }{\sum }_{n}{(-1)}^{n}{{{{\mathcal{P}}}}}_{n}(\gamma )\)47,48, where \(x=\sqrt{2}{{{\rm{Re}}}}\gamma\) and \(p=\sqrt{2}{{{\rm{Im}}}}\gamma\). The nonclassical features of the simulated Dirac particle can be revealed by the WFs of the resonator conditional on the detection of the qubit state. The WFs correlated with the measurement outcomes \(\left\vert g\right\rangle\) and \(\left\vert e\right\rangle\) are presented in the upper panels of Fig. 2a, b, and the result irrespective of the test qubit’s state is displayed in Fig. 2c, all measured after an evolution time 330 ns. As expected, during the evolution the initial Gaussian wavepacket is split into two parts, propagating towards opposite directions. The WF associated with each qubit state displays a region of negativity that is a purely quantum-mechanical effect. This result can be interpreted as follows. Under the Dirac Hamiltonian, each component accumulates a phase that nonlinearly depends on the “momentum" and “mass" as \(\sqrt{{p}^{2}+{({m}^{* }{c}^{* })}^{2}}{c}^{* }t\). Such a process corresponds to a non-Gaussian operation, turning a Gaussian state to a non-Gaussian state. The two rods sprouting from the bulk of the distorted wavepacket interfere with each other, resulting in a negative quasiprobability distribution in the region between them. The lower panels show the probability distribution \({{{\mathcal{P}}}}(x)\) with respect to the quadrature x, obtained by integrating \({{{\mathcal{W}}}}(x,p)\) over p.

Fig. 2: Observation of phase space quantum interference.
figure 2

WFs correlated with the basis states \(\left\vert g\right\rangle\) (a) and \(\left\vert e\right\rangle\) (b) of the test qubit; (c) WF irrespective of the test qubit’s state, all measured after an evolution time of 330 ns. Probability distributions \({{{\mathcal{P}}}}(x)\) with respect to the quadrature x, shown in the lower panels, are obtained by integrating the WF \({{{\mathcal{W}}}}(x,p)\) over p. d Entropy evolution of the test qubit. This entropy is directly obtained from the density matrix of the qubit, measured irrespective of the resonator’s state. Symbols “exp." and “sim." represent the experimental and corresponding simulated data, respectively. e Evolution of the average value of the resonator’s quadrature \(\left\langle x\right\rangle\). The value at each point is extracted from the measured WF.

Full size image

Another important feature associated with the simulated particle is the production of quantum entanglement between its internal and external degrees of freedom. To quantitatively characterize the behavior, we present the von Neumann entropy of the test qubit, \({{{\mathcal{S}}}}=-{{{\rm{tr}}}}({\rho }_{q}{\log }_{2}{\rho }_{q})\), measured for different evolution time t in Fig. 2d, where ρq denotes the reduced density operator of this qubit. The measured results (red circles) agree with the numerical simulation (blue curve), where the small fluctuations are due to the fast Rabi oscillations. ZB is manifested in the time-evolving mean position, which is related to \({{{\mathcal{P}}}}(x)\) by \(\langle x\rangle ={{{\rm{tr}}}}(\rho x)\), where ρ is the corresponding density matrix deduced by the measured WF data (see Supplementary Note 5). This evolution, inferred from the measured WF, is presented in Fig. 2e, which coincides with the simulation (green curve), confirming that ZB has a deeper root that is of pure quantum characteristic. We notice that the numerical simulation curves of Fig. 2d, e both have high frequency vibrations. The high-frequency signals mainly come from the first parametric modulation with frequency 2π × 160 MHz, whose Jacobi-Anger expansion will produce two major frequency components of 2π × 160 MHz and 2π × 320 MHz around the dynamically resonant frequency (see Supplementary Note 1).

Although ZB appears only when the system is in a superposition of positive and negative components, phase space quantum interference is actually a universal inherent characteristic of Dirac particles, which can manifest itself even without negative components. This point can be illustrated with the representative example, where the momentum has a Gaussian distribution, centered at p0 with the spread δp. When restricted to the positive branch, the system state can be written as

$$\left\vert \psi (t)\right\rangle =\int{{{\rm{d}}}}p\,{{{{\rm{e}}}}}^{{{{\rm{i}}}}{\theta }_{p}(t)}{\xi }_{p}\left\vert p\right\rangle \left\vert {\phi }_{+}(p)\right\rangle ,$$
(6)

where \({\xi }_{p}={(\delta p\sqrt{2\pi })}^{-1/2}{{{{\rm{e}}}}}^{-{(p-{p}_{0})}^{2}/{(2\delta p)}^{2}}\). This implies that the internal degrees freedom is necessarily entangled with the momentum except for a plane wave with δp → 0. As it is experimentally difficult to prepare such an entangled state, we reveal the associated quantum feature by numerical simulation. The entanglement entropy as a function of δp is shown in Fig. 3a, which is independent of the evolution time. We here have set ℏ = c = 1 and m = p0 = 1. Unlike the entropy, the phase space interference pattern is time-dependent. To clearly reveal such an interference behavior, we assume that δp = 1, and θp(0) = 0. The unconditional WFs, for different evolution times under the ideal Dirac Hamiltonian, are shown in Fig. 3b. Unexpectedly, the WF displays a time-evolving quantum interference pattern, even without correlating the result with the internal state. We note that the phase space quantum interference effects were previously predicted for some special states with both positive and negative components11, but the presence of such effects without ZB has not been revealed. The WFs correlated with \(\left\vert g\right\rangle\) and \(\left\vert e\right\rangle\), together with the evolutions of mean position and entanglement entropy, are displayed in the Supplementary Note 3.

Fig. 3: Quantum characteristics in the positive branch.
figure 3

a Entanglement entropy versus the momentum spread. b WF evolution with a momentum spread δp = 1. In the numerical simulations, the Dirac particle is supposed to have a mass of m = 1 and a Gaussian momentum distribution with a mean value of p0 = 1. For simplicity, we here take the natural unit with ℏ = c = 1.

Full size image

Klein tunneling

Pushing one step further, we simulate Klein tunneling in a linear potential field40,44. It was first noted by Klein that a relativistic electron may exhibit a counter-intuitive behavior when confronted with a semi-infinite step potential with V = 0 and V0 for x < 0 and x ≥ 0, respectively. This occurs in the regime V0 > E + mc2, for which the electron can propagate through the barrier without damping, where it is transformed into a positron, where E denotes the initial kinetic energy. In our setup, it is not easy to engineer the step-shaped potential. However, a linear potential can be added to the Dirac Hamiltonian in situ by applying a continuous microwave to the resonator, given by \(V=\sqrt{2}\,\epsilon x\), where ϵ is the amplitude of the drive, and set to be 2π × 0.39 MHz in our experiment. For simplicity, the simulation is performed for the choice ε2 = 0. Figure 4a, b showcase the WFs of the resonator correlated with the states \(\left\vert g\right\rangle\) and \(\left\vert e\right\rangle\) of the spinor qubit, respectively, and Fig. 4c presents the result irrespective of the qubit’s state, all measured after an evolving time t = 288 ns. As expected, the linear potential drags the phase space evolution down along the p-axis by an amount \(\sqrt{2}\epsilon t\), but does not affect the motion along the x-axis. The resulting cat-like state was previously predicted to exist as a solution of a relativistic spin-1/2 charged particle in an external magnetic field49, but has not been characterized in previous simulations50,51. To illustrate this phenomenon more clearly, we display the time evolutions of the measured \(\left\langle x\right\rangle\) and \(\left\langle p\right\rangle\) in Fig. 4d, e, respectively, where the dots and diamonds respectively denote the results for wavepackets along the positive and negative directions of the x-axis. The measured results imply that the two wavepackets have the same momentum at each moment, but move along the opposite directions. This can be explained as follows. For x > 0, the momentum of the Dirac particle is given by p2 = (E − V)2 − m2 (c = 1), with the group velocity vg = dE/dp = p/(E − V)45. When the massless particle moves from left to right with E < V, p is assigned with its negative solution, so that vg is positive.

Fig. 4: Simulation of Klein’s tunneling.
figure 4

The potential is simulated by applying a drive to the resonator with the strength ϵ = 2π × 0.39 MHz. The simulation is performed without the second parametric modulation so that the system dynamics are analogous to a massless particle penetrating a linear potential. a Measured WF of the resonator conditional on the detection of the spinorial state \(\left\vert g\right\rangle\). b Resonator’s WF correlated with the detection of \(\left\vert e\right\rangle\). c Unconditional WF. These WFs are reconstructed for the system evolving from the initial ground state \(\left\vert g,0\right\rangle\) for a time 288 ns. d, e Evolutions of the measured \(\left\langle x\right\rangle\) and \(\left\langle p\right\rangle\). The dots and diamonds denote the measured values for wavepackets along the positive and negative directions of the x-axis, and the triangles correspond to the results without discrimination between the moving directions.

Full size image

Discussion

We have performed an investigation on the dynamical evolution of the Dirac particle, showing that the competition between its dynamic and static energies leads to a time-evolving phase space quasi-probability distribution, which underlies its spatial motion. The quantum interference signatures appear in the phase space spanned by position and momentum, but disappear when the momentum is traced out. We demonstrate this discovery with numerical simulations and with a circuit experiment, where a superconducting qubit represents the internal degree of freedom, which is coupled to the microwave field in a resonator that encodes the spatial degree of freedom. The measured negativities of the WFs and entanglement entropy distinguish the ZB of the Dirac particle from that exhibited by the classical systems. In addition to fundamental interest, the demonstrated nonclassicality can serve as a resource for quantum-enhanced sensing52.