Introduction

Quantum coherence not only represents one of the most striking features of quantum mechanics, but also serves as a resource for quantum information processing1,2,3. A quantum mechanical object can simultaneously follow different paths in either ordinary space or in Hilbert space spanned by state vectors. Interference occurs when these paths are recombined and no path information is available. It is impossible to obtain the particle’s path information without at the same time destroying the coherence between the paths and the resulting interference pattern; that is, any effort to determine which path the particle takes would involve coupling the particle to the which-path detector (WPD) and hence correlate their states. In the recoiling-slit gedanken experiment introduced by Einstein and Bohr4, though the loss of the interference pattern is usually attributed to the position-momentum uncertainty relation, it can also be explained in terms of the entanglement between the photon and the two-slit apparatus induced by the path-dependent recoil5. In the gedanken experiment proposed by Scully et al.6,7, where two high-quality micromaser cavities, each on one path of an atomic beam passing through a two-slit assembly, act as the WPD, the atomic path is marked by the photon the atom deposits in the corresponding cavity. In this case, the loss of the interference pattern of the atoms has no relation with the position-momentum uncertainty relation; instead, the entanglement between the atomic path and the photonic state of two cavities leads to the loss of the quantum coherence between the atomic paths, and hence destroys the interference. The disappearance of interference due to the introduction of a WPD has been demonstrated in different experiments5,6,7,8,9,10,11,12,13,14,15, which cannot be explained by Heisenberg’s uncertainty relation in any form.

In contrast to the case that the WPD states correlated with the two paths of the interfering particles are completely distinguishable, the duality relation is much more subtle in the intermediate regime16,17,18, where only partial which-path information is available, so that the coherence between the paths is not completely lost and interference fringes with a reduced visibility are retained. In ref. 18, Englert performed a detailed analysis on this case by introducing a WPD, whose states associated with the interfering paths are not orthogonal. He showed that, for a given amount of which-path information stored in the WPD, quantified by the distinguishability, D, the fringe visibility, V, is limited by an inequality D2 + V2 ≤ 1, which corresponds to a quantitative description of the wave-particle duality. For an imbalanced two-way interferometer without WPD, the inequality becomes P2 + V2 ≤ 1, where P represents the path predictability. Recently, Bagan et al. generalized this result to the case with multiple interfering paths, deriving the relation between the coherence among these paths and the amount of path information19. The reduction of fringe visibility due to a partial acquisition of which-path information has been observed in the optical system20, cavity QED5,21, and superconducting circuit platform15. In the atomic interference experiment reported in Ref. 11, where the internal degree of freedom of an atom acts as the WPD for its spatial paths, the relation for the path information and fringe visibility was verified in the intermediate regime. In this experimental demonstration, the system-WPD entanglement plays a critical role for enforcing the complementarity principle, though it was not quantified in the experiment.

In recent years, the quantitative triality relation among the visibility, predictability, and entanglement was detailedly investigated in composite systems that are in a pure state22,23,24,25,26,27,28,29,30, and was confirmed in classical optical interference experiments31,32, as well as in single-photon experiments33,34. An experimental investigation involving two entangled superconducting qubits has also been reported35, but where no interference experiment was performed. Here we investigate the relation among the fringe visibility of an interfering qubit, its quantum entanglement with a WPD, and the original coherence. We show that the system-WPD entanglement measured by concurrence and the available fringe visibility obey the equality \({E}^{2}+{V}^{2}={C}_{0}^{2}\), where C0 is the original coherence of the interfering system, which serves as a resource for producing entanglement and interference pattern. Our equality quantitatively characterizes the entanglement-interference complementarity in terms of the resource theory of coherence, in contrast with previous investigations. Due to the inevitable environmentally induced decoherence effects, it is experimentally challenging to prepare a real quantum system in a perfect pure state, so that investigation of a duality relation with a non-unity coherence resource is of experimental relevance. We experimentally investigate this relation with a superconducting Ramsey interferometer, where a resonator serves as the WPD for a qubit in its quantum state space. The entanglement between the WPD and the qubit is controlled via their effective interaction time, achieved by the qubit’s frequency tunability. The values of C0 and V are measured independently, with the experimental results well agreeing with theoretical predictions and revealing that coherence serves as a resource for both entanglement and interference. Unlike the photonic experiments33,34, the present interference experiment is performed in a deterministic way, which pushes forward the experimental exploration of the entanglement-interference complementarity.

Results

Theoretical predictions

Let us illustrate the underlying physics with a Mach-Zehnder interferometer, with the diagram shown in Fig. 1a, where the interfering system, initially traveling along path 0, passes through a beam-splitter (BS) which splits the path 0 into two paths 0 and 1. When traveling along path 1, the system is subsequently subjected to a phase shift θ and coupled to a WPD, which undergoes a unitary transformation, denoted as U. The second BS recombines the two paths. It is convenient to denote these two paths as the basis states \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\), respectively. With this notation, the system can be described as a qubit, and the effect of each BS corresponds to the Hadamard transformation \(\left\{\left\vert 0\right\rangle \to \left(\left\vert 0\right\rangle -{{{\rm{i}}}}\left\vert 1\right\rangle \right)/\sqrt{2};\left\vert 1\right\rangle \to \left(\left\vert 1\right\rangle -{{{\rm{i}}}}\left\vert 0\right\rangle \right)/\sqrt{2}\right\}\). When the WPD is initially in a pure state \(\left\vert {W}_{0}\right\rangle\), the qubit-WPD state after their coupling is

$$\left\vert \psi \right\rangle =\frac{1}{\sqrt{2}}\left(\left\vert 0\right\rangle \left\vert {W}_{0}\right\rangle -{{{{\rm{ie}}}}}^{{{{\rm{i}}}}\theta }\left\vert 1\right\rangle U\left\vert {W}_{0}\right\rangle \right).$$
(1)

After the second Hadamard transformation, the probability of detecting the qubit in the state \(\left\vert 1\right\rangle\) is

$${P}_{1}=\frac{1}{2}\left[1+{V}_{0}\cos \left(\theta +\phi \right)\right],$$
(2)

where \({V}_{0}=\left\vert \left\langle {W}_{0}\right\vert U\left\vert {W}_{0}\right\rangle \right\vert\) and \(\phi =\arg \left(\left\langle {W}_{0}\right\vert U\left\vert {W}_{0}\right\rangle \right)\). This θ-dependent probability manifests the interference behavior, with the fringe visibility reduced to V0 due to the qubit-WPD entanglement. When the WPD lies in a multi-dimensional Hilbert space, we map it to the two-dimensional space {\(\left\vert {W}_{0}\right\rangle ,\left\vert {W}_{1}\right\rangle\)} so that the qubit-WPD entanglement can be measured with concurrence36, where

$$\left\vert {W}_{1}\right\rangle =\sqrt{\frac{1}{1-{V}_{0}^{2}}}\left(U\left\vert {W}_{0}\right\rangle -{V}_{0}{{{{\rm{e}}}}}^{{{{\rm{i}}}}\phi }\left\vert {W}_{0}\right\rangle \right)$$
(3)

is orthogonal to \(\left\vert {W}_{0}\right\rangle\). With this mapping, the joint qubit-WPD state can be considered as a two-qubit entangled state. The concurrence for measuring the amount of the qubit-WPD entanglement is \(E=\sqrt{1-{V}_{0}^{2}}\). This concurrence is equivalent to the distinguishability, D, which measures the path information stored in the WPD, and is defined as

$$D=\frac{1}{2}{{{{\rm{Tr}}}}}_{{{{\rm{w}}}}}\left\vert {\rho }_{{{{\rm{w}}}},0}-{\rho }_{{{{\rm{w}}}},1}\right\vert ,$$
(4)

where \({\rho }_{{{{\rm{w}}}},0}=\left\langle 0\right\vert \rho \left\vert 0\right\rangle /{{{{\rm{tr}}}}}_{{{{\rm{w}}}}}\left(\left\langle 0\right\vert \rho \left\vert 0\right\rangle \right)\) and \({\rho }_{{{{\rm{w}}}},1}=\left\langle 1\right\vert \rho \left\vert 1\right\rangle /{{{{\rm{tr}}}}}_{{{{\rm{w}}}}}\left(\left\langle 1\right\vert \rho \left\vert 1\right\rangle \right)\) respectively denote the density operators of the WPD associated with the interfering qubit’s \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) states after their coupling, with \(\rho =\left\vert \psi \right\rangle \left\langle \psi \right\vert\) denoting the density operator for the joint qubit-WPD state, and the tracing is over the WPD’s degree of freedom.

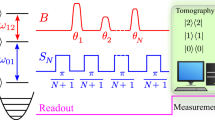
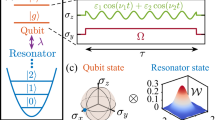
Fig. 1: Interferometer and pulse sequence.
figure 1

a Diagram of the two-way interferometer supplemented by a WPD. A quantum system is evolved to a superposition of taking paths 0 and 1 by the first beam-splitter (BS). Then it is subjected to an adjustable relative phase shift (θ), and coupled to the WPD which undergoes a unitary transformation, U, conditional on the system’s path 1. After recombination of the two paths by the second BS, the system is detected. b Logic diagram of the on-chip Ramsey interferometer. A superconducting Xmon qubit, Q1, acts as the interfering qubit, whose quantum state is split and recombined by two Hadamard transformations (H), in between which the which-path information in the quantum state space is controllably encoded on the photonic field of a resonator, R. A second Xmon qubit Q2 is used for preparing and detecting the state of the resonator. c Pulse sequence. The interference experiment with which-path information acquisition consists of three parts: Preparation of the resonator’s initial state \(\left\vert {W}_{0}\right\rangle\) with Q2; Ramsey interference supplemented with the WPD, realized by sandwiching the Q1-resonator interaction between two π/2 pulses, \({R}_{\pi /2}^{\theta }\) and \({R}_{\pi /2}^{x}\); State readout.

Full size image

We note that E = D holds only when the two paths of the interfering system are completely coherent. When the coherence between the two paths is partially lost before the qubit-WPD coupling, the corresponding qubit’s state is described by the density operator

$${\rho }_{{{{\rm{q}}}},0}=\frac{1}{2}\left[\left\vert 0\right\rangle \left\langle 0\right\vert +\left\vert 1\right\rangle \left\langle 1\right\vert +{{{\rm{i}}}}{C}_{0}\left({{{{\rm{e}}}}}^{-{{{\rm{i}}}}\theta }\left\vert 0\right\rangle \left\langle 1\right\vert -{{{{\rm{e}}}}}^{{{{\rm{i}}}}\theta }\left\vert 1\right\rangle \left\langle 0\right\vert \right)\right],$$
(5)

where C0 is the coherence between the two paths, defined as the sum of the moduli of the off-diagonal elements1.

After the qubit-resonator coupling and the subsequent Hadamard transformation, the probability of detecting the qubit in the state \(\left\vert 1\right\rangle\) is

$${P}_{1}^{{\prime} }=\frac{1}{2}\left[1+V\cos \left(\theta +\phi \right)\right],$$
(6)

where V = C0V0 is the fringe visibility. This visibility and the qubit-WPD entanglement satisfy the equality (see Supplementary Note 2)

$${E}^{2}+{V}^{2}={C}_{0}^{2}.$$
(7)

This implies that both the qubit-WPD concurrence and the fringe visibility are reduced by a factor of C0 due to the decoherence between the paths before the qubit-WPD coupling. In distinct contrast, the distinguishability, \(D=\sqrt{1-{V}_{0}^{2}}\), is not affected by the decoherence, and consequently, \({D}^{2}+{V}^{2} > {C}_{0}^{2}\) unless C0 = 1. The results can be interpreted as follows. The conditional unitary evolution arising from the qubit-WPD coupling corresponds to an incoherent operation, which cannot produce entanglement when the qubit is in an incoherent state before this operation3. Both the interference and the qubit-WPD entanglement originate from the original coherence of the interfering qubit; this coherence, as a resource, can be either converted to entanglement or used for interference. For a given coherence resource, the more the amount of entanglement, the weaker the interference effect. In contrast, the distinguishability does not depend on the coherence resource; instead, it is determined by the distance between the WPD states associated with the two paths. For example, even for C0 = 0, D can reach 1 as long as the two WPD states are orthogonal. The equality of Eq. (7) also holds for the unbalanced interferometer, where the two paths are not equally populated before coupling to the WPD (see Supplementary Note 1). We note that this equality represents a more general triality relation, which reduces to the previously proposed triality equality22,23,24,25,26,27,28,29,30 when the interfering qubit is initially a pure state so that \({C}_{0}^{2}=1-{P}^{2}\), where P denotes the predictability.

Device and experimental scheme

These theoretical predictions can be demonstrated on different platforms with controlled natural or artificial atoms37,38, among which circuit quantum electrodynamics systems represent a typical example owing to the available strong coupling between superconducting qubits and microwave photons39,40. The experiment is implemented with a circuit Ramsey interferometer, with the logic diagram of the process sketched in Fig. 1b. The device involves 5 frequency-tunable Xmon qubits41,42,43,44, one of which (Q1) acts as the interfering qubit, whose two lowest levels, denoted as \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\), correspond to two interfering paths in the Hilbert space. Such a Ramsey interferometer is analogous to the Mach-Zehnder interferometer, where the BSs are replaced by two Hadamard transformations (H). The photonic field stored in a bus resonator, R, is used to acquire the which-path information of Q1 before the recombination of the two interfering paths. A second qubit Q2 serves as the ancilla for preparing and reading out the state of the resonator. In our experiment, the tunable phase shift θ between the two interfering paths is incorporated into the first microwave pulse. The experimental parameters are detailed in Table 1.

Table 1 Experimental parameters.
Full size table

To enable the resonator to act as the WPD, before coupling to Q1 it is prepared in the coherent superposition containing 0 and 1 photon: \(\left\vert {W}_{0}\right\rangle =(\left\vert {0}_{{{{\rm{r}}}}}\right\rangle -\left\vert {1}_{{{{\rm{r}}}}}\right\rangle )/\sqrt{2}\). The resonator’s conditional unitary evolution, U, is realized by tuning the frequency associated with Q1’s transition \(\left\vert 1\right\rangle \leftrightarrow \left\vert 2\right\rangle\), \({\omega }_{12}\), close to the resonator’s frequency, where \(\left\vert 2\right\rangle\) represents the second excited state of Q1. After an interaction time τ = π/Ω, the resonator undergoes an evolution, \(U={{{{\rm{e}}}}}^{{{{\rm{i}}}}\beta \left\vert {1}_{{{{\rm{r}}}}}\right\rangle \left\langle {1}_{{{{\rm{r}}}}}\right\vert }\), conditional on Q1’s state \(\left\vert 1\right\rangle\), where β = π[1 − δ/(2Ω)], with \(\Omega =\sqrt{2{g}_{1}^{2}+{\delta }^{2}/4}\) and δ = ω12 − ωr45,46. This conditional dynamics correlates the two paths (the qubit being in \(\left\vert 0\right\rangle\) or \(\left\vert 1\right\rangle\)) produced by the first π/2 pulse (\({R}_{\pi /2}^{\theta }\)) with the resonator’s states \(\left\vert {W}_{0}\right\rangle\) and \(U\left\vert {W}_{0}\right\rangle\), respectively. After the second π/2 pulse \({R}_{\pi /2}^{x}\), the probability of detecting the qubit in \(\left\vert 1\right\rangle\) state is given by Eq. (2), which corresponds to a θ-dependent Ramsey interference signal, with the fringe visibility \({V}_{0}=\cos (\beta /2)\).

Measurement of the entanglement-interference relation for a unity source coherence

The interference experiment starts by simultaneously driving the ancilla qubit Q2 from the ground state \(\left\vert {0}_{{{{\rm{a}}}}}\right\rangle\) to the superposition state \((\left\vert {0}_{{{{\rm{a}}}}}\right\rangle -{{{\rm{i}}}}\left\vert {1}_{{{{\rm{a}}}}}\right\rangle )/\sqrt{2}\) with a π/2 pulse \({R}_{\pi /2}^{x}\), and applying a π/2 pulse \({R}_{\pi /2}^{\theta }\) to Q1 (Fig. 1c), which produces a π/2 rotation around the axis with an angle θ to x-axis on the equatorial plane of the Bloch sphere. Then Q2 is tuned on-resonance with the resonator initially in the vacuum state \(\left\vert {0}_{{{{\rm{r}}}}}\right\rangle\) for a time 12.5 ns, which realizes a swapping operation, mapping the ancilla state to the resonator, preparing it in the superposition of the zero- and one-photon states required for storing the which-path information of the interfering qubit. After preparation of the WPD’s state \(\left\vert {W}_{0}\right\rangle ,{Q}_{2}\) is biased back to its idle frequency. Subsequently, Q1’s transition \(\left\vert 1\right\rangle \leftrightarrow \left\vert 2\right\rangle\) is tuned close to the resonator’s frequency to realize the conditional evolution U, resulting in entanglement between Q1 and the resonator. Following this conditional dynamics, Q1 is tuned back to its idle frequency, where the second π/2 pulse \({R}_{\pi /2}^{x}\) is applied. The Ramsey signals, defined as the probability for measuring Q1 in \(\left\vert 1\right\rangle\) state as a function of θ, for conditional phase shifts β = π/4, π/2, 3π/4, and π are displayed in Fig. 2a, b, c, d, respectively. As expected, the fringe visibility decreases as β increases for 0 ≤ β ≤ π, as a result of the increasing entanglement between Q1 and the resonator. The extracted fringe visibility as a function of β is denoted by diamonds in Fig. 2e, which is in well agreement with the numerical simulation (blue dashed line). We note that the qubit has a slight probability of being populated in the \(\left\vert 2\right\rangle\)-state after the conditional phase shift, as a consequence of experimental imperfections. In the experiment, the maximal residual population of this state is measured to be 0.022, which only changes the Ramsey fringe visibility by about 1.29%.

Fig. 2: Measured entanglement-interference relation for a unity source coherence.
figure 2

The Ramsey interference is revealed by the probability of measuring the test qubit in the state \(\left\vert 1\right\rangle\) as a function of θ for different conditional phase shift β: a π/4; b π/2; c 3π/4; d π. The corresponding fringes visibilities are 0.8853, 0.6473, 0.3184, and 0.0311, respectively. e Measured fringe visibility V (diamonds), Q1-Q2 concurrence E (dots), and distinguishability D (triangles) as a function of the conditional phase shift β of the resonator. E is measured after mapping the resonator’s state back to Q2. The results are obtained with the pulse sequences shown in the Supplementary Fig. 5. Squares denote the quantity \(\sqrt{{E}^{2}+{V}^{2}}\). The dashed lines correspond to numerical results. The error bars are the standard deviation of the measurements. For some data points, the error bar is smaller than the marker.

Full size image

To quantitatively investigate the change of entanglement between Q1 and the resonator accompanying the decrease of the fringe visibility, we map the state of the resonator back to Q2 for joint state tomography. This is achieved by tuning Q2 on resonance with the resonator for a time of 12.5 ns after the resonator’s interaction with Q1, and then biasing back it to its idle frequency. Then the joint Q1-Q2 density matrix is measured by quantum state tomography (see Supplementary Note 10). The resulting Q1-Q2 concurrence as a function of β is represented by dots in Fig. 2e, which agrees with the simulation (green dashed line). As expected, the higher the concurrence, the lower the fringe contrast. The source coherence C0 is measured through quantum state tomography on Q1 right after the first π/2 pulse \({R}_{\pi /2}^{\theta }\); preparation of the WPD state \(\left\vert {W}_{0}\right\rangle\), coupling Q1 to the WPD, and subsequent WPD-Q2 state mapping are unnecessary for measuring C0. The quantity \(\sqrt{{E}^{2}+{V}^{2}}\) as a function of β is also displayed in Fig. 2e (squares), which well coincides with the measured C0. The slight difference between the measured values of these quantities mainly results from energy relaxation and dephasing of the qubits and photon loss of the resonator.

We further reveal the relation between the distinguishability of the two paths and the entanglement between the interfering qubit and the WPD for the fully coherent qubit state. This is achieved by extracting the density matrices ρw,0 and ρw,1 of the WPD associated with the interfering qubit’s \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) states after their coupling, obtained by projecting the measured Q1-Q2 density matrix ρ to Q1’s basis states \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\), which are displayed in Supplementary Note 3. The resulting distinguishability D, as a function of the conditional phase β, is denoted by the triangles of Fig. 2e, which coincides with the Q1-Q2 concurrence (green dots) very well, verifying the WPD acquires the which-path information by entangling its state with the interfering qubit.

Measurement of entanglement-interference relations for different source coherences

To further confirm the quantitative relation among the system’s original coherence C0, fringe visibility V, and the system-WPD entanglement E for partially coherent qubit states, we adjust the temporal orders of the π/2 pulse (\({R}_{\pi /2}^{\theta }\)) of the Ramsey interferometer and the preparation of the WPD’s superposition state \(\left\vert {W}_{0}\right\rangle\), and delay this preparation procedure for a time t after \({R}_{\pi /2}^{\theta }\). Due to the energy relaxation and dephasing during this delay, the density operator of Q1 is given by Eq. (5), with \({C}_{0}\simeq {{{{\rm{e}}}}}^{-t/2{T}_{1}-t/{T}_{\varphi }}\). The conditional phase shift of the resonator induced by coupling to Q1 is set to β = π/2. The measured fringe visibility V (diamonds), Q1-Q2 concurrence E (dots), the system’s original coherence C0 (stars), and the distinguishability D (triangles), as functions of the delay t, are displayed in Fig. 3. As expected, both V and E decrease as the delay increases. In addition to the decoherence of the test qubit, the concurrence is affected by thermal excitations of the ancilla and the resonator during the delay, which accounts for the result that the measured concurrence decays faster than the visibility, so that the measured \(\sqrt{{E}^{2}+{V}^{2}}\) (squares) is smaller than C0. On the other hand, measured D (triangles) almost does not change with the delay, which implies that it is independent of the source coherence.

Fig. 3: Measured entanglement-interference relations for different source coherences.
figure 3

The diamonds, dots, stars, and triangles denote the fringe visibility, concurrence, source coherence, and distinguishability, respectively. The results are obtained with the preparation of the WPD’s superposition state \(\left\vert {W}_{0}\right\rangle\) delayed by a preset time. The conditional phase shift of the resonator induced by coupling to Q1 is β = π/2. Squares denote evolution of the quantity \(\sqrt{{E}^{2}+{V}^{2}}\). The error bars represent the standard deviation of the measurements. For some data points, the error bar is smaller than the corresponding symbol.

Full size image

Discussion

We have derived an equality relating the fringe visibility of an interfering system and its entanglement with a WPD inside an interferometer to the original coherence. The result reveals, for a given amount of coherence resource, the available fringe visibility is determined by the system-WPD entanglement: the stronger the system’s entanglement with the WPD, the lower the available fringe visibility. We perform an experimental test of this relation in a superconducting circuit, in which a resonator is prepared in a superposition of zero- and one-photon states and acts as the WPD for a superconducting Xmon qubit. The measured results agree well with the theoretical predictions, confirming the entanglement-interference complementarity.