Introduction

Quantum computing1 holds the promise of revolutionizing the field of machine learning (ML)2,3,4. Powered by quantum Fourier transform and amplitude amplification, potential exponential speed-up has been envisaged for high-dimensional and big-data ML tasks5,6,7,8,9 using fault-tolerant quantum computers. Even with noisy intermediate-scale quantum (NISQ) devices, quantum advantage is still promising, because the model expressibility can be substantially enhanced by the exponentially large feature space carried by multi-qubit quantum states10,11,12,13.

To deploy quantum machine learning algorithms on NISQ processors, a key step is to construct a parameterized quantum ansatz that can be trained by a classical optimizer. To date, most quantum ansatzes are realized by quantum neural networks (QNN)10,14,15,16,17,18,19,20,21,22,23 that consist of layers of parameterized quantum gates, and demonstrative experiments have been carried out on classification24,25,26, clustering27,28, and generative29,30,31 learning tasks. The gate-based QNN ansatz naturally incorporates the theory of quantum circuits, but the learning performance is highly dependent on the architecture design and the mapping of circuits to experimentally operable native gates. A structurally non-optimized QNN cannot fully exploit the limited quantum coherence resource, and this is partially why high learning accuracy is hard to attain on NISQ devices without downsizing the training dataset.

There are certainly much room for performance improvement by using more hardware-efficient quantum ansatzes, e.g., via deep optimization of the circuit architecture32 and qubit mapping strategies33. Recently, a hardware-friendly end-to-end learning scheme (in the sense that the model is trained as a whole instead of being divided into separate modules) is proposed34 by replacing the gate-based QNN with natural quantum dynamics driven by coherent control pulses. This model requires very little architecture design, system calibration, and no qubit mapping. One can also jointly train a data encoder that automatically transforms classical data to quantum states via control pulses, and this essentially simplifies the encoding process because the preparation of quantum states according to a hand-designed encoding scheme is no more required. More importantly, the natural control-to-state mapping involved in the encoding process introduces nonlinearity that is crucial for better model expressibility. The idea of applying pulse-based ansatzs has drawn much attention in NISQ applications, e.g., the state preparation of quantum eigensolver35, optimization landscape investigation36, and cloud-based training37.

In this paper, we report the experimental demonstration of quantum end-to-end machine learning using a superconducting processor through the recognition of handwritten digits selected from the MNIST (Mixed National Institute of Standards and Technology) dataset38. Without downsizing the original 784-pixel images, the end-to-end learning model can be trained to achieve 98% accuracy with two qubits for the 2-digit classification and 89% accuracy with three qubits for the 4-digit task, which are among the best experimental results reported on small-size quantum processors39. The demonstrated quantum end-to-end model can be easily scaled up for solving complex real-world learning tasks owing to its inherent hardware friendliness and efficiency.

Results

Preliminaries

The basic idea of end-to-end quantum learning is to parameterize the quantum ansatz by physical control pulses that are usually applied to implement abstract quantum gates in variational quantum classifiers. In this way, a feedforward QNN can be constructed by the control-driven evolution of the quantum state \(\left\vert \psi (t)\right\rangle\), as follows40:

$$\frac{{{{\rm{d}}}}\left\vert \psi (t)\right\rangle }{{{{\rm{d}}}}t}=-\frac{{{{\rm{i}}}}}{\hslash }\left[{H}_{0}+\mathop{\sum }\limits_{m=1}^{r}{\theta }_{m}(t){H}_{m}\right]\left\vert \psi (t)\right\rangle ,$$
(1)

where H0 is the static Hamiltonian which involves the coupling between different qubits, and r is the number of pulsed control functions/channels in the quantum processor. For example, if there are M qubits for the QNN and each qubit is dictated by c control functions (e.g., flux bias or microwave driving), we have r = c × M. Here, Hm is the control Hamiltonian associated with the m-th control pulse that contains n sub-pulses over n sampling periods. The j-th sub-pulse is parameterized by θm(tj), and hence we denote the m-th control pulse by θm = [θm(t1), θm(t2), . . . , θm(tn)]. The evolution of the quantum system under all n-th control sub-pulses constructs the n-th layer of the QNN.

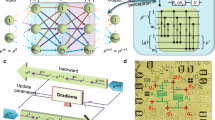
We illustrate the quantum end-to-end learning with a classification task based on the MNIST dataset. As shown in Fig. 1, an image of a handwritten digit is randomly selected from the training dataset \({{{\mathcal{D}}}}\). In the k-th iteration, the sampled image is converted to a d = 784 dimensional vector x(k), and y(k) is the corresponding label. The input data x(k) is transformed by a matrix W(k) to the control variables \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}^{(k)}={W}^{(k)}{{{{\bf{x}}}}}^{(k)}\). This constructs a classical encoding block with r channels and E sub-pulses per channel: \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}^{(k)}=[{\theta }_{1}^{(k)}({t}_{1}),...,{\theta }_{1}^{(k)}({t}_{{{{\rm{E}}}}}),...,{\theta }_{r}^{(k)}({t}_{1})...,{\theta }_{r}^{(k)}({t}_{E})]\). The generated control pulses \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}^{(k)}\) then automatically encode x(k) to the quantum state \(\left\vert {\psi }^{(k)}({t}_{E})\right\rangle\) via the natural quantum state evolution of Eq. (1).

Fig. 1: The training protocol of the quantum end-to-end learning framework.
figure 1

In the k-th iteration, a randomly selected image of a handwritten digit in the MNIST dataset is converted to a vector x(k) and then transformed by a matrix W(k) to the control variables \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}^{(k)}\) that steer the quantum state to \(\left\vert {\psi }^{(k)}({t}_{E})\right\rangle\) of the qubits in the QNN. This process encodes x(k) to \(\left\vert {\psi }^{(k)}\right\rangle\). Subsequent inference control pulses \({{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)}\) are applied to drive \(\left\vert {\psi }^{(k)}({t}_{E})\right\rangle\) to \(\left\vert {\psi }^{(k)}({t}_{E+I})\right\rangle\) that is to be measured. The parameters in W(k) and \({{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)}\) are updated for the next iteration according to the loss function \({{{\mathcal{L}}}}\) and its gradient obtained from the measurement. The circled numbers represent the specific points in the data flow and the corresponding learning performances are shown in Fig. 4. The top right is the false-colored optical image of the six-qubit device used in our experiment.

Full size image

Subsequent inference control pulses \({{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)}\), which have the same form as \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}^{(k)}\) but consist of I sub-pulses in each channel, are then applied to induce the quantum evolution from the encoded quantum state \(\left\vert {\psi }^{(k)}({t}_{E})\right\rangle\). The inference controls are introduced for improving the classification performance. Finally, the end-time quantum state \(\left\vert {\psi }^{(k)}({t}_{E+I})\right\rangle\) is measured under the appropriate experiment-available positive operator O(k) according to the classical label y(k), which gives the conditional probability (or confidence) of obtaining y(k) for a given input x(k)

$$P\left({y}^{(k)}| {{{{\bf{x}}}}}^{(k)},{W}^{(k)},{{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)}\right)=\left\langle {\psi }^{(k)}\left({t}_{E+I}\right)\right\vert {O}^{(k)}\left\vert {\psi }^{(k)}({t}_{E+I})\right\rangle .$$
(2)

The corresponding loss function is defined as

$${{{\mathcal{L}}}}\left[{W}^{(k)},{{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)},\left\{{{{{\bf{x}}}}}_{\ell }^{(k)}\right\}\right]=1-\frac{1}{b}\mathop{\sum }\limits_{\ell =1}^{b}P\left({y}^{(k)}| {{{{\bf{x}}}}}_{\ell }^{(k)},{W}^{(k)},{{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)}\right).$$
(3)

In the experiment, we select a batch of b samples in each iteration to reduce the fluctuation of \({{{\mathcal{L}}}}\) for faster convergence of the learning process. The gradient of the loss function \({{{\mathcal{L}}}}\) with respect to the encoding control \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}^{(k)}\) and the inference control \({{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)}\) can be evaluated with the finite difference method by making a small change of the each control parameter \({\theta }_{i}^{(k)}({t}_{j})\)41. The gradient of \({{{\mathcal{L}}}}\) with respect to W(k) can be derived from the gradient of \({{{\mathcal{L}}}}\) with respect to \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}^{(k)}\)34. Therefore, we can apply the widely used stochastic gradient-descent algorithm in machine learning to update W(k) and \({{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}^{(k)}\) by minimizing \({{{\mathcal{L}}}}\) on the training dataset \({{{\mathcal{D}}}}\) (see Methods for details of the algorithms)42. Once the model is well trained, one can use fresh samples from a testing dataset to examine the recognition performance of the handwritten digits.

Experiments and simulations

The end-to-end model is demonstrated in a superconducting processor, as shown in Fig. 1. All qubits take the form of the flux-tunable Xmon geometry and are driven with inductively coupled flux bias lines and capacitively coupled RF control lines43,44,45. Among the six qubits, Q1, Q2, Q4, Q5 are dispersively coupled to a half-wavelength coplanar cavity B1, and Q2, Q3, Q5, Q6 are dispersively coupled to another cavity B2. Each qubit is dispersively coupled to a quarter-wavelength readout resonator for a high-fidelity single-shot readout and all the resonators are coupled to a common transmission line for multiplexed readouts (see details of the experimental setup in Supplementary Notes I ~ III). The qubits that are not relevant to the QNN is biased far away and can be ignored from the system Hamiltonian, therefore, the static Hamiltonian of the QNN can be written in the interaction picture as

$${H}_{0}/\hslash =\mathop{\sum}\limits_{q\ne p}{J}_{qp}\left({a}_{q}^{{\dagger} }{a}_{p}+{a}_{p}^{{\dagger} }{a}_{q}\right)-\mathop{\sum }\limits_{q=1}^{M}\frac{{E}_{C,q}}{2}{a}_{q}^{{\dagger} }{a}_{q}^{{\dagger} }{a}_{q}{a}_{q},$$
(4)

where Jqp is the coupling strength between the p-th and q-th qubits mediated by the bus cavity, EC,q denotes the qubit anharmonicity, and aq is the annihilation operator of the q-th qubit.

Throughout this work, we set the encoding block with E = 2 layers followed by an inference block with I = 2 layers. As shown in Fig. 1, for the q-th qubit in the n-th (n = 1, 2, 3, 4) layer of the QNN, there are c = 2 control parameters θ2q−1(tn) and θ2q(tn), which are associated with the control Hamiltonians \({H}_{2q-1}=({a}_{q}+{a}_{q}^{{\dagger} })/2\) (rotation along the x-axis of the Bloch sphere) and \({H}_{2q}={{{\rm{i}}}}({a}_{q}-{a}_{q}^{{\dagger} })/2\) (rotation along the y-axis of the Bloch sphere), respectively. The control parameters are the variable amplitudes of the Gaussian envelopes of two resonant microwave sub-pulses, each of which has a fixed width of 4σ = 40 ns. All the quantum controls in the same time interval are exerted simultaneously. For an N-digit classification task, we take \(M=\lceil {\log }_{2}N\rceil +1\) qubits for the QNN: the classification results are mapped to the computation bases of the first \(\lceil {\log }_{2}N\rceil\) qubits (label qubits) by the majority vote of the collective measurement performed on label qubits, while one additional qubit is introduced for a better expressibility of the model. Therefore, the QNN in our experiment involves totally cM(E + I) = 8M control parameters.

We perform the 2-digit (‘0’ and ‘2’) classification task (N = 2) with Q3 and Q5 (M = 2). The working frequencies are 6.08 GHz and 6.45 GHz, respectively, which are also the flux sweet-spots of the two qubits. The effective coupling strength J35/2π = 4.11 MHz. We take Q5 as the label qubit and assign the classification result to be ‘0’ or ‘2’ if the respective probability of measuring \(\left\vert g\right\rangle\) or \(\left\vert e\right\rangle\) state is larger.

The end-to-end model is initialized with W = W0 and θIn = θ0, where all elements of W0 are 10−5 and each element of θ0 is tuned to induce a π/4 rotation of the respective qubit. The parameter update is realized as follows. Firstly, we obtain the loss function \({{{\mathcal{L}}}}\) according to Eq. (3) by measuring Q5. We perturb each control parameter in the control set {θEn, θIn} and obtain the corresponding gradient of \({{{\mathcal{L}}}}\). The \({{{\mathcal{L}}}}\) and its gradient averaged over a batch of two training samples (b = 2) are sent to a classical Adam optimizer46 for updating W and θIn. All control parameters are linearly scaled to the digital-to-analog converter level of a Tektronix arbitrary waveform generator 70002A, working with a sampling rate of 25 GHz, to generate the resonant RF pulses directly. The control pulses composed of in-phase and quadrature components are sent to each qubit with the corresponding RF control line. To obtain the classification result, we repeat the procedure and measure the label qubit for 5000 times.

In the 4-digit (‘0’, ‘2’, ‘7’, and ‘9’) classification task (N = 4), we take Q3, Q5, and Q6 (M = 3) to construct the QNN, whose working frequencies are 6.08 GHz, 6.45 GHz, and 6.19 GHz, respectively. Q3 and Q5 are measured for the classification output. The target digits correspond to the four computational bases spanned by the two label qubits. The training procedure and algorithms are the same as those for the N = 2 task.

The typical training process is shown in Fig. 2a, b. For better clarity, the curves are smoothed out by averaging each data point from its neighboring four ones. For the 2-digit (4-digit) classification task, the experimental loss function \({{{\mathcal{L}}}}\) converges to 0.14 (0.22) in 300 (500) iterations. The training loss can potentially be reduced by increasing the depth E of the encoding block34. For comparison, numerical simulations are also performed with the calibrated system Hamiltonian, the same batches of training samples, and the same parameter update algorithms. As shown in Fig. 2a, b, the simulations match the experiments well. The small deviation of the experimental data may attribute to the simplified modeling of high-order couplings between the qubits and the control pulses47, as well as the system parameter drifting.

Fig. 2: Results of training the quantum end-to-end model.
figure 2

a, b The typical training process of the end-to-end model. For better clarity, all data points are averaged over the neighboring four points. c–f The classification performance of the trained model. The horizontal labels show the digits to be classified, while the vertical labels show the majority vote of the computational basis measurement results. The hollow bars (nearly invisible) in the experimental results (c, e) correspond to the standard deviation of multiple repeated measurements. c, d Experimental and simulation results for the 2-digit classification task, respectively. The averaged accuracies for the classification are 0.986 ± 0.001 and 0.982 in the experiment and the simulation, respectively. e, f The 4-digit classification of the QNN. The averaged accuracies are 0.894 ± 0.015 and 0.889 in the experiment and the simulation, respectively.

Full size image

To examine the performance of the end-to-end learning, we experimentally test the generalizability of the trained end-to-end model with fresh testing samples (1000 for each digit), and count the frequencies of assigning these samples to different digits (see Fig. 2c–f). The measured overall accuracies (i.e., the proportion of samples that are correctly classified) are (98.6 ± 0.1)% for the 2-digit task and (89.4 ± 1.5)% for the 4-digit task, respectively, which are consistent with the simulation results (98.2% and 88.9%, respectively) based on the experimentally identified Hamiltonian.

The performance of the model also relies on the amount of entanglement gained in the quantum state. When the number of QNN layers is fixed, the quantum state gets more entangled under longer pulse length τ (includes all the E + I = 4 sub-pulses in both the encoding and the inference blocks), but coherence may be lost in the prolonged control time duration due to the inevitable decoherence. We use the experimentally calibrated parameters to simulate the 2-digit classification process under different τ and different coherence times T1 and Tϕ of the qubits (see simulation details in Supplementary Notes: The Numerical Model of the System). As shown in Fig. 3, the average confidence \(1-{{{\mathcal{L}}}}\) varies little with τ when T1 or Tϕ is sufficiently small because the coherent control is overwhelmed by the strong decoherence. For larger T1 or Tϕ (e.g., T1 = 20 μs), the average confidence initially increases with τ, but then decreases after reaching the peak. This trend clearly indicates the trade-off between the gained entanglement and the lost coherence, and thus τ as well as the number of layers should be optimally chosen for the best balance.

Fig. 3: The error analysis of the average confidence.
figure 3

a The simulated average confidence as a function of the qubit relaxation time T1 and the pulse length τ, while the qubit pure dephasing time Tϕ is infinite; (b) The simulated average confidence as a function of Tϕ and τ, while T1 is infinite.

Full size image

The end-to-end learning scheme provides a seamless combination of quantum and classical computers through the joint training of the pulse-based QNN and the classical data encoder W. To understand their respective roles in the classification, we check how the data distribution varies along the flow \({{{\bf{x}}}}\to {{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}\to \left\vert \psi ({t}_{E})\right\rangle \to \left\vert \psi ({t}_{E+I})\right\rangle \to y\) (see ① ~ ④ in Fig. 1) in the 2-digit classification process. To facilitate the analysis, we use the Linear Discriminant Analysis (LDA)48 that projects high-dimensional data vectors into two clusters of points distributed on an optimally chosen line (see details in the Supplementary Notes: Liner Discriminant Analysis). The LDA makes it easier to visualize and compare data distributions whose dimensionalities are different.

The projected clusters are plotted in Fig. 4. In each sub-figure, the distance between the centers of the two clusters is normalized, and hence we can quantify the classifiability by their standard deviations (i.e., the narrowness of distribution). As can be seen in Fig. 4a, b, the classical data encoder W effectively reduces the original 784-dimensional vector x to a 8-dimensional vector of control variables θEn, but the standard deviation is increased from 0.1658 for the original dataset to 0.2903 for the transformed control pulses. Then, the control-to-state mapping, which is both nonlinear and quantum, sharply reduces the standard deviation to 0.0919 for the encoded quantum state (Fig. 4c), while the following quantum inference block does not make further improvement (Fig. 4d). These results indicate that the classical data encoder is responsible for the compression of the high-dimensional input data, while the classification is mainly accomplished by the QNN.

Fig. 4: The projected points by using LDA, where the distance between the projected cluster centers is normalized.
figure 4

The positions of ① ~ ④ along the data flow are shown in Fig. 1. a The projected points of the original 784-dimensional handwritten digits. b The projected points of the control pulses for encoding the classical data to the quantum states. c The projected points of the quantum states after the encoding block. d The projected points of the final quantum states.

Full size image

Discussion

To conclude, our proof-of-principle experiment has clearly demonstrated the feasibility of the end-to-end quantum machine learning framework. The pulse-based QNN is experimentally easy to implement and scale up. Through joint training of the classical encoder and the QNN, high-precision classification is achieved for MNIST digits without downsizing the dataset. Our experiment indicates that the limited quantum resources on NISQ devices can be more efficiently exploited than pure gate-based quantum models.

It should be noted that no quantum advantage is claimed here over classical ML algorithms, which is still an ongoing pursuit for all types of variational quantum algorithms. When more qubits are available and the noise level is sufficiently low, quantum advantage may be approached owing to the enhanced expressive power by the exponentially scaled quantum Hilbert space. We expect that, with more elaborately designed training algorithms, the framework of quantum end-to-end learning can be applied to more complicated real-world ML applications (e.g., unsupervised and generative learning).

Methods

Algorithm for the classical optimizer

The algorithm for evaluating the loss function and the calculation of the gradient is shown in Algorithm 1. The Adam optimizer that is used in our experiment is shown in Algorithm 2.

Algorithm 1

Calculate the loss function and the gradients with respect to the model parameters

Input W, θIn, Batch of training data \(\left\{{{{{\bf{x}}}}}^{(k)},{y}^{(k)}\right\}\)

Pout, gW, gIn ← 0

\(\delta \in {{\mathbb{R}}}^{+}\)

for ℓ = 1: b do

 \({P}_{0}=P\left({{{{\bf{y}}}}}_{\ell }^{(k)}| {{{{\bf{x}}}}}_{\ell }^{(k)},W,{{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}\right)\)

 \({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}=W* {{{{\bf{x}}}}}_{\ell }^{(k)}\)

 for \(i=1:\,{{\mbox{Length}}}\,\left({{{{\bf{\uptheta }}}}}_{{{{\rm{En}}}}}\right)\) do

  θ1 = [θEn(1), …, θEn(i) + δ, … ]

  \({{{{\bf{g}}}}}_{1}(i)=\left(P\left({{{{\bf{y}}}}}_{\ell }^{(k)}| {{{{\bf{x}}}}}_{\ell }^{(k)},{{{{\bf{\uptheta }}}}}_{1},{{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}\right)-{P}_{0}\right)/\delta\)

 end for

 for i = 1: Length(θIn) do

  θ2 = [θIn(1), …, θIn(i) + δ, … ]

  \({{{{\bf{g}}}}}_{2}(i)=\left(P\left({{{{\bf{y}}}}}_{\ell }^{(k)}| {{{{\bf{x}}}}}_{\ell }^{(k)},{{{\bf{W}}}},{{{{\bf{\uptheta }}}}}_{2}\right)-{P}_{0}\right)/\delta\)

 end for

 \({{{{\bf{g}}}}}_{W}={{{{\bf{g}}}}}_{W}-{{{{\bf{g}}}}}_{1}* {{{{\bf{x}}}}}_{\ell }^{(k)\top }/b\)

 gIn = gIn − g2/b

 Pout = Pout + P0/b

end for

return Pout, gW, gIn

Algorithm 2

Adam optimizer

Input Training dataset {x, y}

sW, rW, sIn, rIn ← 0

W, θIn ← W0, θIn,0

lr = 10−3, β1 = 0.9, β2 = 0.999, ϵ = 10−8

for k = 1: N do

 \({{{{\bf{g}}}}}_{W},{{{{\bf{g}}}}}_{{{{\rm{In}}}}}={{{\bf{Algorithm1}}}}\left(W,{{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}},\left\{{{{{\bf{x}}}}}^{(k)},{y}^{(k)}\right\}\right)\)

 \({\mathbf{s}}_{w}={\beta_{1}}*{\mathbf{s}}_{w}+(1-\beta_{1})*{\mathbf{g}}_{w}\)

 \({\mathbf{r}}_{w}=\beta_{2}*{\mathbf{r}}_{w}+(1-{\beta}_{2})*{\mathbf{g}}_{w}.*{\mathbf{g}}_{w}\)

 \({{{{\bf{s}}}}}_{1}={{{{\bf{s}}}}}_{W}/\left(1-{\beta }_{1}^{k}\right)\)

 \({{{{\bf{r}}}}}_{1}={{{{\bf{r}}}}}_{W}/\left(1-{\beta }_{2}^{k}\right)\)

 \(W=W-{lr}* {{{{\bf{s}}}}}_{1}./\left(\sqrt{{{{{\bf{r}}}}}_{1}}+\epsilon \right)\)

 \({\mathbf{s}}_{\mathrm{In}}= \beta_{1}*{\mathbf{s}}_{\mathrm{In}}+(1-\beta_{1})*{\mathbf{g}}_{\mathrm{In}}\)

 \({\mathbf{r}}_{\mathrm{In}}= \beta_{2}*{\mathbf{r}}_{\mathrm{In}}+(1-\beta_{2})*{\mathbf{g}}_{\mathrm{In}}.* {\mathbf{g}}_{\mathrm{In}}\)

 \({{{{\bf{s}}}}}_{2}={{{{\bf{s}}}}}_{{{{\rm{In}}}}}/\left(1-{\beta }_{1}^{k}\right)\)

 \({{{{\bf{r}}}}}_{2}={{{{\bf{r}}}}}_{{{{\rm{In}}}}}/\left(1-{\beta }_{2}^{k}\right)\)

 \({{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}={{{{\bf{\uptheta }}}}}_{{{{\rm{In}}}}}-{{{\rm{lr}}}}* {{{{\bf{s}}}}}_{2}./\left(\sqrt{{{{{\bf{r}}}}}_{2}}+\epsilon \right)\)

end for

return W, θIn

The gradient of the loss function \({{{\mathcal{L}}}}\) for parameter update in each iteration is obtained by averaging the gradients of the conditional probability P over a batch of randomly selected input samples (b = 2). This can reduce the fluctuation of \({{{\mathcal{L}}}}\) for faster convergence in the learning process. For the inference block, the gradient gIn of \({{{\mathcal{L}}}}\) with respect to each parameter in θIn is directly obtained by rerunning the experiment with a small change in θIn and calculating the difference of P. As for the encoding block, the gradient gW with respect to the elements of the classical matrix W is needed. To reduce the experimental cost, we can equivalently calculate gW from the outer product between the measured gradient g1 with respect to the encoding controls and the input data vector.

Once the gradients with respect to the model parameters are obtained, we take Adaptive Moment Estimation (Adam)46 update algorithm to update the corresponding parameters. The Adam algorithm is popular for its efficiency and stability in stochastic optimization of learning problems. In the Adam algorithm, lr, β1, β2, ϵ refer to algorithm configuration parameters and are chosen as default empirical values. The intermediate parameters sW, sIn, rW, rIn will be passed to the next iteration so as to adaptively control the parameter updating rate.