Introduction

It is hard to overstate the power of communication in today’s society, which enjoys the benefits of technological advances due to telecommunication and the internet. These advances are a result of reliable and efficient classical communication protocols, which have been facilitated by decades of studies on data compression, error correction and physics of data transmission. As our technologies enter the quantum age, we have similarly started facing the question of how to make quantum communication reliable and efficient. Quantum communication is central to the important tasks of quantum key distribution1,2, the transfer of quantum states3 and the design of large scale quantum computers4,5. While the proposals and experimental implementations of quantum communication have made great strides in recent years6,7, the range of communication is still limited to about a few hundred kilometers7,8 in ground-based experiments. Some of the key challenges are the probabilistic nature (as well as decoherence) in optics-based models8 and fast decoherence in matter-based models8. This strongly motivates the problem of finding quantum protocols that efficiently achieve certain tasks with small communication or fight noise to reliably communicate a given amount of message.

The efficiency of a quantum communication protocol is typically captured by two quantities: the number of qubits communicated and the amount of additional resource, such as quantum entanglement, needed in the protocol. Since the foundational works of Holevo, Schumacher and Westmoreland9,10,11, great progress has been made in the understanding of optimal amount of communication and additional resources needed in a large family of quantum communication tasks. Well known results on quantum channel coding10,11,12,13,14,15,16, quantum source coding9, quantum state merging17,18 and quantum state redistribution19,20 have discovered a powerful collection of tools for quantum information processing. These tools have found applications in disciplines beyond quantum communication, such as quantum thermodynamics21,22 and black hole physics23,24. One such tool that takes a central stage in our work is that of quantum decoupling.

Notably, aforementioned works in quantum information theory are set in the asymptotic and i.i.d. (independent and identically distributed) framework of Shannon25, which allows the protocol to run over many independent instances of the input system. In practice, however, one typically does not have an access to such independent instances, limiting the scope of these results. The field of one-shot information theory addresses this problem, by constructing protocols that run on one instance of the input system. This leads to a generalization of the asymptotic and i.i.d. theory and brings information processing tasks to a more practical domain.

However, unlike the asymptotic and i.i.d. theory of quantum information, the understanding of optimal communication and additional resources is still lacking in one-shot quantum information theory. Even for the very basic task of entanglement-assisted quantum channel coding14, state-of-the-art26,27,28 one-shot protocols fail to simultaneously achieve optimal communication capacity and optimal amount of initial entanglement. The aim of this work is to introduce methods that make progress in this problem and exponentially improve upon the amount of initial entanglement needed in a family of one-shot protocols that achieve the best known communication for above tasks. In many cases, the resulting protocols have the additional property that either the encoding or the decoding operation is a quantum circuit of small depth.

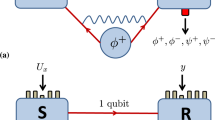
In order to lay the groundwork for our results, we revisit the existing techniques of decoupling and more recent convex-split and position-based decoding. Decoupling (Fig. 1) refers to the process of applying some quantum operation on one of the two given systems (which share quantum correlation), so as to make the two systems independent of each other. More precisely, given a quantum state ΨRC, one adds registers \(T,T^{\prime}\) in the quantum state \({\sigma }_{TT^{\prime} }\), and applies a quantum operation U on registers \(CTT^{\prime}\) such that

$${{{\rm{Tr}}}}_{T^{\prime}} ({U}^{{\dagger} }({{{\Psi }}}_{RC}\otimes \sigma _{TT^{\prime}})U)\approx {{{\Psi }}}_{R}\otimes {\omega }_{C}\otimes {\sigma }_{T}^{\prime}.$$

That is, the registers R and C are approximately independent after register \(T^{\prime}\) has been discarded. This idea has been applied in the aforementioned tasks of quantum state merging17,18,29,30,31,32, quantum state redistribution19,20,33,34 and quantum channel coding15,26,27,35, as well as randomness extraction36,37,38. The central approach in many of these works is to perform a random unitary operation17,18 and then discard a part of the system. This technique has been expanded upon in various works such as refs. 39,40,41,42. Due to the importance of decoupling technique and the limitation that random unitaries cannot be implemented with a quantum circuit of small size, there is a great interest in finding efficient circuits that achieve the same performance as a random unitary.

Fig. 1: Decoupling method.
figure 1

Process of removing the quantum correlation between two registers R and C, by means of quantum operations. The cost of performing a decoupling operation is characterized by the size of the register that must be discarded, in order to implement the operation. In Fig. a, the discarded register is \(T^{\prime}\) and the operation performed on \(CTT^{\prime}\) is a global unitary U. In Fig. b, the register J (that is eventually discarded) is maximally mixed to begin with and the operation performed is a controlled unitary. Thus, J can be viewed as a classical noise61. While the operation in Fig. b is a special kind of operation in Fig. a, the following equivalence holds due to the duality between teleportation62 and superdense coding63. For every operation in Fig. a with \(\log | T^{\prime} |\) qubits that are discarded, there is an operation in Fig. b with \(2\log | T^{\prime} |\) bits of noise. Moreover, for every operation in Fig. b with \(\log | J|\) bits of noise, there is an operation in Fig. a where \(\frac{1}{2}\log | J|\) qubits that are discarded.

Full size image

Existing methods to make decoupling efficient involve replacing random unitaries with unitary 2-designs43,44,45,46,47 which can be simulated by Clifford circuits of small depth, random quantum circuits of small depth48 and random unitaries diagonal in Pauli-X and Pauli-Z basis49. To elaborate, suppose we are given a quantum state ΨRC on two registers R and C, and we need to make C independent of R by acting on C. We must further ensure that the size of the discarded system, which is the cost of the decoupling operation (Fig. 1), is small enough, ruling out the operation that discards all of C. Note that the number of qubits of the discarded system translates to the quantum communication cost of a quantum protocol that employs decoupling. This motivates the question of minimizing the size of discarded system. The work47 shows that a quantum circuit of size \({{{\mathcal{O}}}}(\log | C| \log \log | C|)\) and depth \({{{\mathcal{O}}}}(\log \log | C|)\) suffices for this purpose, achieving the same cost as that of a random unitary. A similar circuit size of \({{{\mathcal{O}}}}(\log | C| {\log }^{2}\log | C|)\) and depth \({{{\mathcal{O}}}}({\log }^{3}\log | C|)\) is obtained in ref. 48, using elementary gates that mimic real world quantum processes. See Table 1 for a comparison of the methods.

Table 1 Parameters of various decoupling methods (Unitary 2- design47, Random X and Z basis49, Random gates48, Convex-split54, this work (Method A)).
Full size table

While the circuit size achieved by above results is impressive, the gates used in the circuit are highly quantum. More precisely, for a choice of preferred basis such as the computational basis, the gates convert any basis vector into a superposition over these vectors. Can the construction of a decoupling operation be further simplified, by only using the gates that are classical (taking basis vectors to basis vectors)? While being useful for practical implementation, such a construction would also lead to a surprising theoretical simplification: it would leave no conceptual difference between quantum decoupling and its classical counterpart of randomness extraction50,51,52.

Random permutation is a canonical classical operation known to perform randomness extraction and also decouple classical-quantum systems36,37,38. In ref. 53 (see also ref. 40) the authors used permutations to derive an analog of the decoupling theorem that however only removes quantum and not classical correlations between R and C. While the remaining classical correlation could also be removed by random permutations, the overall cost of decoupling would be larger than the cost of decoupling by a random unitary. This indicates that a decoupling method, which matches the random unitary decoupling in its cost, may involve operations that are not classical.

This is shown not to be true by the convex-split lemma54, which expresses a relation of the following form

$${{{\Phi }}}_{RCE}\approx \mathop{\sum}\limits_{i}{p}_{i}{{{\Phi }}}_{RCE}^{(i)},$$
(1)

showing how to view a given quantum state ΦRCE as a convex combination of (more desirable) quantum states \({{{\Phi }}}_{RCE}^{(i)}\) in order to achieve an information-theoretic task. It implies decoupling (of the type in Fig. 1b) when the quantum state on the left hand side (that is, ΦRCE) is a product state across R and CE. In particular, it was shown in ref. 54 that given ΨRC, if we add the quantum state \({\sigma }_{{C}_{1}}\otimes \ldots {\sigma }_{{C}_{N}}\) (for some large enough N) and randomly swap the register C with one of the registers C1, …CN, then the register R becomes independent of all the other registers; leading to decoupling with the classical operation of permutation of registers. Expressed mathematically in the form of Eq. (1), we would set E = C1C2…CN, \({{{\Phi }}}_{RCE}={{{\Psi }}}_{R}\otimes {\sigma }_{C}\otimes {\sigma }_{{C}_{1}}\otimes \ldots {\sigma }_{{C}_{N}}\), \({{{\Phi }}}_{RCE}^{(i)}={{{\Psi }}}_{R{C}_{i}}\otimes {\sigma }_{C}\otimes {\sigma }_{{C}_{1}}\otimes \ldots {\sigma }_{{C}_{i-1}}\otimes {\sigma }_{{C}_{i+1}}\otimes \ldots {\sigma }_{{C}_{N}}\) and \({p}_{i}=\frac{1}{N}\).

In this work we will solely be interested in quantum tasks where decoupling is the same as constructing an appropriate convex-split, and hence we will use the two terms interchangeably. However, we highlight that the convex-split method is more general and can be used even in situations where no decoupling exists: such as in classical or classical-quantum communication tasks28,55,56 and resource theoretic tasks57,58,59.

Since the process of swapping two registers is a ‘classical’ operation (that is, it takes basis vectors to basis vectors), the convex-split lemma of ref. 54 gives a classical unitary for performing quantum decoupling. Unfortunately, the value of N can be as large as \({{{\mathcal{O}}}}(| C|)\), where ∣C∣ is the dimension of the register C. Hence swapping the register C with a random register Ci requires a circuit of depth \({{{\mathcal{O}}}}(| C|)\), which is exponential in the number of qubits of register C. Even an alternate implementation of swap operation, by placing the registers on a three dimensional grid, would require \({{{\mathcal{O}}}}(| C{| }^{1/3})\) operations. Thus, it has so far been unknown if one can achieve quantum decoupling by efficient classical operations.

Recent works have shown several applications of the convex-split method in one-shot quantum information theory, along with the dual method of position-based decoding28. The methods have been used to obtain near-optimal communication for one-shot entanglement-assisted quantum channel coding28, near-optimal communication for one-shot quantum state splitting54 (with slight improvement of the additive \(\log \log | C|\) factor over31, for communicating the register C) and smallest known communication for one-shot quantum state redistribution60. As mentioned earlier, all these protocols use a large amount of entanglement. Other known protocols14,26,27, for entanglement-assisted quantum channel coding and33,34 for quantum state redistribution, that do not rely on these two methods use exponentially small entanglement, but their communication is not known to be near-optimal. This motivates the question of find a scheme that achieves the best of both of the lines of work.

Results

We show how to achieve near-optimal communication and the size of initial entanglement at most constant factors away from the optimal, in all the aforementioned quantum communication tasks. We further show that, in several cases, the implementation of either the encoding or the decoding operation in the protocol can be made efficient. Our results are obtained by two methods that we outline below.

Method A: Efficient decoupling procedures

As mentioned earlier, the quantity of interest in a decoupling procedure is the number of bits or qubits that are discarded to achieve the decoupling. There are two models under which decoupling is performed, see Fig. 1. The first model involves adding a quantum state, applying a global unitary (without involving the register R) and then discarding some quantum system.

The second model also involves adding a quantum state followed by a unitary, but the system that is discarded is classical and the unitary acts in a classical-quantum manner61. The two models can be converted into each other by a Clifford circuit of depth 1 and the number of qubits/bits discarded are the same up to a factor of 2, due to the well known duality between teleportation62 and superdense coding63. Additional quantum systems that are not discarded act as a catalyst for the decoupling process31,54,57,58,64. For example, the randomness used in the process of decoupling via unitary 2-design acts as a catalyst. In principle, this randomness can be fixed by standard derandomization arguments, but it leads to a loss in efficient implementation.

In this work, we consider the second model of decoupling. We construct two convex-split lemmas which immediately lead to efficient decoupling procedures for a quantum state ΨRC (recall the discussion following Eq. (1)). One of these lemmas solves the aforementioned problem of decoupling via an efficient classical operation.

  • Method A. 1: A set of unitaries \({\{{V}_{\ell }\}}_{\ell = 1}^{| C{| }^{2}}\) on a register C forms a 1-design if

    $$\frac{1}{N}\mathop{\sum}\limits_{\ell }{V}_{\ell }{\rho }_{C}{V}_{\ell }^{{\dagger} }=\frac{{{{{\rm{I}}}}}_{C}}{| C| },\quad \forall \,{{\mbox{quantum state}}}\,{\rho }_{C}.$$

    A canonical example of unitary 1-design is the set of the tensor products of Pauli-X and Z operators if the register C admits a qubit decomposition. Our first procedure shows how to achieve decoupling using a mixture of small number of \(\approx \log | C| -{{{{\rm{H}}}}}_{\min }\,{\left(C| R\right)}_{{{\Psi }}}\) unitaries from any 1-design. Here ΨRC is the quantum state on registers R and C and \({{{{\rm{H}}}}}_{\min }\,\left(C| R\right)\) is the conditional min-entropy. The additional randomness used to choose the unitaries is \(4\log | C|\) bits. We highlight that this is in stark contrast with many of the previous constructions for decoupling, which required unitaries from a 2-design. Details appear in Supplementary Discussion. This method is related to the explicit schemes presented in refs. 65,66 for quantum encryption. These works show how to achieve decoupling with a mixture of Pauli operators chosen from an explicit set. But the size of the set can be large, and hence does not directly compare with our work. The classical-quantum version of this method previously appeared in the work67.

  • Method A. 2: The second decoupling procedure enlarges the Hilbert space \({{{{\mathcal{H}}}}}_{C}\otimes {{{{\mathcal{H}}}}}_{C}\) in a manner that the resulting Hilbert space \({{{{\mathcal{H}}}}}_{G}\) has prime dimension ∣G∣ ≤ 2∣C∣2. This is possible due to Bertrand’s postulate68, which says that there is a prime between any natural number and its twice. It also introduces a register L of size ~\(N\mathop{=}\limits^{{{{\rm{def}}}}}\log | C| -{{{{\rm{H}}}}}_{\min }\,{\left(C| R\right)}_{{{\Psi }}}\). A preferred basis on \({{{{\mathcal{H}}}}}_{C}\) (such as the computational basis in the qubit representation of the registers) is chosen, which gives a basis \({\{{\left|i\right\rangle }_{G}\}}_{i = 0}^{| G| -1}\) on \({{{{\mathcal{H}}}}}_{G}\). Similarly, a preferred basis \({\{\left|\ell \right\rangle \}}_{\ell = 1}^{N}\) is chosen on \({{{{\mathcal{H}}}}}_{L}\). Following this, a unitary operation \(U=\mathop{\sum }\nolimits_{\ell = 1}^{N}{U}_{\ell }\otimes \left|\ell \right\rangle {\left\langle \ell \right|}_{L}\) is applied, where Uℓ acts on two registers \(G,G^{\prime} \equiv G\) as

    $${U}_{\ell }{\left|i\right\rangle }_{G}{\left|j\right\rangle }_{G^{\prime} }={\left|i+(j-i)\ell ({{\mbox{mod}}}| G|)\right\rangle }_{G}{\left|j+(j-i)\ell ({{\mbox{mod}}}| G|)\right\rangle }_{G^{\prime} }.$$
    (2)

    Upon tracing out register L, register R becomes independent of \(GG^{\prime}\). Furthermore, the final state on registers \(GG^{\prime}\) is maximally mixed and the register \(G^{\prime}\) is returned in the original state. As can be seen, the unitaries Uℓ are ‘classical’ as they take basis vectors to basis vectors and perform addition and multiplication modulo ∣G∣. This makes the construction of U efficient, with circuit depth \({{{\mathcal{O}}}}(\log \log | C|)\) and size \({{{\mathcal{O}}}}(\log | C| \log \log | C|)\) due to well known results in modular arithmetic69. Details appear in Supplementary Discussion.

    In the other direction, our result shows that the reversible or quantum circuit complexity (such as depth or size) of integer multiplication modulo a prime is lower bounded by the reversible or quantum circuit complexity of the ‘best’ decoupling method. This holds since integer multiplication is the most expensive step in Eq. (2). We highlight that a super-linear lower bound on the circuit complexity of integer multiplication is an outstanding open question in the area of complexity theory70,71. The aforementioned connection to decoupling may suggest attacking this problem using an entirely different avenue connected to decoupling24: scrambling of quantum information in black holes72.

Method B: Exponential improvement in entanglement

A procedure, that realizes any classical distribution as a marginal of a uniform distribution in a larger space, has been used in the context of classical correlated sampling in several works73,74,75,76,77,78,79. A counterpart of this procedure for quantum states was considered in ref. 80. Since this procedure makes the distribution uniform or ‘flat’ in its support, we will call it a flattening procedure. Let the eigendecomposition of σC be \({\sigma }_{C}={\sum }_{i}{p}_{i}\left|i\right\rangle {\left\langle i\right|}_{C}\). Append a register E through the transformation

$$\left|i\right\rangle {\left\langle i\right|}_{C}\to \left|i\right\rangle {\left\langle i\right|}_{C}\otimes \left(\frac{1}{K{p}_{i}}\mathop{\sum }\limits_{j=1}^{K{p}_{i}}\left|j\right\rangle {\left\langle j\right|}_{E}\right),$$

where K is a large enough real such that \({\{K{p}_{i}\}}_{i}\) are all integers. The existence of such a K can be ensured, for example, by an arbitrarily small perturbation in \({\{{p}_{i}\}}_{i}\), so that they all are rationals. As a result, the quantum state σC transforms to

$${\sigma }_{C}\to \frac{1}{K}\mathop{\sum}\limits_{i,j:j\le K{p}_{i}}\left|i\right\rangle {\left\langle i\right|}_{C}\otimes \left|j\right\rangle {\left\langle j\right|}_{E},$$
(3)

which is uniform in a subspace. However, ref. 80 did not provide a unitary operation to realize the above extension of σC. We show that this extension can be constructed in a unitary manner using embezzling states81. If the basis \({\{\left|i\right\rangle \}}_{i}\) can be efficiently prepared from computational basis and the eigenvalues \({\{{p}_{i}\}}_{i}\) are easy to compute, then the flattening procedure is also computationally efficient. Details appear in Supplementary Discussion. The consequences of this method are as follows, with all the tasks appearing below summarized in Fig. 2.

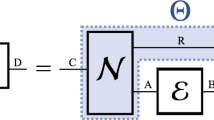
  • Entanglement-assisted classical communication over quantum channel: Consider a quantum channel \({{{{\mathcal{N}}}}}_{A\to B}\), over which we wish to communicate a message from the set {1, 2, …2R}, with small error. The work14 considered the asymptotic and i.i.d. setting for this task, involving the channel \({{{{\mathcal{N}}}}}_{A\to B}^{\otimes n}\) for large enough n. It was shown that the rate of communication \(\frac{R}{n}\) converges to

    $$\mathop{\max }\limits_{{\left|{{\Psi }}\right\rangle }_{AA^{\prime} }}{{{\rm{I}}}}\,{\left(A^{\prime} :B\right)}_{{{{{\mathcal{N}}}}}_{A\to B}({{{\Psi }}}_{AA^{\prime} })},$$

    where \({{{\rm{I}}}}\,\left(A^{\prime} \,:\,B\right)\) is the quantum mutual information. The number of qubits of entanglement in the protocol from14 was ~nS(ΨA) (the von-Neumann entropy) and the rate of communication was shown to be optimal. The work27 obtained a one-shot version of their protocol, with \(\log | A|\) qubits of pre-shared entanglement. Their communication was characterized by the quantum hypothesis testing relative entropy between the quantum state \({{{{\mathcal{N}}}}}_{A\to B}({{{\Psi }}}_{AA^{\prime} })\) and a separable state derived from \({{{\Psi }}}_{AA^{\prime} }\), which may not be optimal. The work28 introduced the position-based decoding method, showing how to achieve a communication characterized by the quantum hypothesis testing relative entropy between \({{{{\mathcal{N}}}}}_{A\to B}({{{\Psi }}}_{AA^{\prime} })\) and \({{{{\mathcal{N}}}}}_{A\to B}({{{\Psi }}}_{A})\otimes {{{\Psi }}}_{A^{\prime} }\). The achievable communication is near-optimal, due to the converse given in ref. 82. But the protocol in ref. 28 required \({{{\mathcal{O}}}}(| A|)\) qubits of entanglement. Using our flattening procedure on the quantum state \({\left|{{\Psi }}\right\rangle }_{AA^{\prime} }\), we show how to achieve the same near-optimal communication with \({{{\mathcal{O}}}}(\log | A|)\) qubits of entanglement. If the flattening procedure is efficient, then the encoding by Alice is efficient as well. Details appear in Supplementary Discussion.

    The work28 also studied entanglement-assisted classical communication through various quantum networks, shown to be near optimal in ref. 83. Our technique also exponentially improves upon the amount of entanglement in these protocols, while maintaining the achievable communication.

  • Quantum state splitting and quantum state redistribution: The task of quantum state redistribution19,20 considers a quantum state \({\left|{{\Psi }}\right\rangle }_{RABC}\), where the register R is inaccessible, registers A, C are with Alice and register B is with Bob. It is required that after communication from Alice to Bob, the register C should be held by Bob. Its special cases of quantum state splitting29 and quantum state merging17 are equivalent (up to reversal of the protocol) and quantum state splitting considers the case where register B is trivial. The work31 obtained a one-shot protocol for quantum state splitting achieving near-optimal communication up to an additive factor of \({{{\mathcal{O}}}}(\log \log | C|)\). This was improved in ref. 54 through a near-optimal protocol with communication tight up to an additive factor of \({{{\mathcal{O}}}}(1)\). While the protocol in ref. 31 required \({{{\mathcal{O}}}}(\log | C|)\) qubits of pe-shared entanglement, the protocol in ref. 54 required much larger \({{{\mathcal{O}}}}(| C|)\) qubits. Here, we show how to improve the number of qubits of pre-shared entanglement to \({{{\mathcal{O}}}}(\log | C|)\), retaining the communication cost in ref. 54. Again, we use the flattening procedure, efficiency of which ensures the efficiency of decoding operation by Bob.

    The work60 gave a protocol for quantum state redistribution with smallest known quantum communication, improving upon the prior work34. But the number of qubits of pre-shared entanglement required was exponentially larger than that in ref. 34. Similar to aforementioned results, here we give a protocol that has similar quantum communication to ref. 60 and similar number of qubits of entanglement to34. Details appear in Supplementary Discussion. We highlight that an upcoming work84 uses our flattening procedure to further improve upon60, and provides a connection between one-shot quantum state redistribution and quantum Markov chains.

Fig. 2: Quantum communication tasks.
figure 2

Figure a depicts the task of entanglement-assisted quantum channel coding, where the register M holds a message m ∈ {1, 2, …2R}. The goal is to maximize the value of R, while keeping the error in decoding small. Figure b shows the task of quantum state redistribution with entanglement assistance. The goal is to ensure that the register C is obtained by Bob using as less communication \(\log | M|\) as possible and ensuring that \({{\Psi }}^{\prime} \approx \left|{{\Psi }}\right\rangle \left\langle {{\Psi }}\right|\).

Full size image

Discussion

Method A. 1 is reminiscent of the derandomizing unitaries constructed in ref. 85, which also uses unitary 1-design for quantum encryption. But there is a difference between our setting and that in ref. 85, since the number of unitaries that we use is dependent on the conditional min-entropy of the quantum state. On the other hand, the authors of ref. 85 only aim to decouple the maximally entangled state. We may also compare Method A. 1 with the unitaries in ref. 49, which shows how to perform decoupling with random unitaries diagonal in either X or Z bases. Our construction also yields a unitary diagonal in either X or Z bases, but it is explicit (that is, not a random unitary) and uses some additional catalytic randomness.

As mentioned earlier, the construction in Method A. 2 is efficient, with circuit depth \({{{\mathcal{O}}}}(\log \log | C|)\) and size \({{{\mathcal{O}}}}(\log | C| \log \log | C|)\). This already achieves the performance of circuits based on unitary 2-designs47 (Table 1), by employing very simple operations of integer addition and multiplication. Thus, the method also improves upon the performance of ref. 48. Furthermore, the integer addition and multiplication operations (Eq. (2)) are very similar to the pair-wise independent hash functions employed in randomness extraction against classical50 and quantum side-information36,37. This provides a unified perspective on decoupling in the classical, classical-quantum and fully-quantum settings. The unitaries \({\{{U}_{\ell }\}}_{\ell }\), as defined in Eq. (2) have an interesting property that they act as a representation of the cyclic group, reflecting the property of permutation operations in the convex-split method.

In the language of resource theory of coherence, both the decoupling procedures in Method A belong to the class of Physically Incoherent Operations86. Thus, an immediate implication of our results is that quantum decoupling can be performed by incoherent unitaries. These decoupling procedures perform the same as decoupling via random unitary37,39,42, when we consider the size of discarded system. None of these results (those in Method A and the decoupling via random unitary) are optimal due to the additional effort put in making the decoupled register C uniform. Indeed, it is known that the optimum cost of decoupling is characterized by the max-mutual information, rather than the conditional min-entropy31,54,64. Method B leads to a decoupling procedure achieving this, as it reduces the task to the case of uniform (or flat) marginal.

As shown in Eq. (3), the central idea behind Method B is to flatten a non-uniform quantum state, and use resource-efficient protocols for the flattened state. The work31 used a different technique for flattening the eigenvalues of a quantum state. Their technique was to distribute the eigenvalues into bins [2−i: 2−i−1] and run a protocol within each bin. While this method can be used for quantum state splitting (with a loss of communication of \(\approx \log \log | C|\) required in transmitting the information about the bin), it is not clear how it can be used to construct a near-optimal entanglement-assisted protocol for quantum channel coding. In fact, the quantum channel coding protocol in ref. 27 also can be viewed in the light of this ‘binning’ technique. But, as mentioned, the one-shot optimality of their protocols is unknown. Our flattening method does not face this limitation and can be uniformly applied to all the quantum communication scenarios. It achieves near-optimal one-shot quantum communication for entanglement-assisted quantum channel coding. Further, our use of embezzling states in both quantum state splitting and entanglement-assisted quantum channel coding further highlights the duality between the two tasks31,87.

We end this section with some open questions. Our first question is if there exists an analog of Method B that does not require embezzling states to achieve near-optimal decoupling. An efficient scheme could lead to protocols with even smaller number of qubits of pre-shared entanglement in quantum communication tasks. Another important question is to see if the number of bits of additional randomness used in Method A can further be reduced. It is known that seed size in randomness extraction in the presence of quantum side information can be very small88 (based on Trevisan’s construction52). Since our construction treats classical side information and quantum side information in similar manner, we can hope to have similar results even in the case of quantum decoupling.

Methods

Techniques for Method A

The proofs of results presented in Method A crucially rely on the following simple identity, which was first shown in ref. 54. Below, \({{{\rm{D}}}}\,\left(.\parallel .\right)\) is the quantum relative entropy89.

$${{{\rm{D}}}}\,\left(\mathop{\sum}\limits_{i}{p}_{i}{\rho }_{i}\parallel \theta \right)=\mathop{\sum}\limits_{i}{p}_{i}\left({{{\rm{D}}}}\,\left({\rho }_{i}\parallel \theta \right)-{{{\rm{D}}}}\,\left({\rho }_{i}\parallel \rho \right)\right).$$

This relation allows us to decompose the convex combination in Eq. (1) into individual components. In addition, the proof of the decoupling result in Method A. 1 also uses the notion of pairwise independent random variables to reduce the size of additional randomness, inspired by55. The proof of decoupling result in Method A. 2 is more subtle, as it requires us to find a collection of unitaries that form an appropriate representation of the cyclic group. Our construction, that is based on modular arithmetic, is inspired by explicit constructions of pairwise independent random variables90,91.

Techniques for Method B

To implement the flattening procedure in Method B, we show the following relationships for quantum embezzlement. Let \({\xi }_{D}\mathop{=}\limits^{{{{\rm{def}}}}}\frac{1}{S}\mathop{\sum }\nolimits_{j = 1}^{n}\frac{1}{j}\left|j\right\rangle {\left\langle j\right|}_{D}\) be the marginal of the embezzling state from81, for some integer n and S being the normalization factor. Let \({\rho }_{E}\mathop{=}\limits^{{{{\rm{def}}}}}\frac{1}{b}\mathop{\sum }\nolimits_{e = 1}^{b}\left|e\right\rangle {\left\langle e\right|}_{E}\) be uniform in a support of size b. We show the existence of a unitary Ub such that

$${{{{\rm{D}}}}}_{\max }\,\left({U}_{b}\left({\xi }_{D}\otimes \left|1\right\rangle {\left\langle 1\right|}_{E}\right){U}_{b}^{{\dagger} }\parallel {\xi }_{D}\otimes {\rho }_{E}\right)\le \delta ,$$

whenever \(n \,>\, {b}^{\frac{1}{\delta }}\). Here \({{{{\rm{D}}}}}_{\max }\,\left(.\parallel .\right)\) is the quantum max-relative entropy92,93. Thus, it is possible to embezzle certain states with error guarantee in max-relative entropy, improving upon the earlier error guarantee in fidelity81. We crucially use this in our proofs, as small max-relative entropy allows us to bound other one-shot information theoretic terms.