Quantum coherence bounds the distributed discords

Abstract

Establishing quantum correlations between two remote parties by sending an information carrier is an essential step of many protocols in quantum information processing. We obtain trade-off relations between discords and coherence within a bipartite system. Then we study the distribution of coherence in a bipartite quantum state by using the relations of relative entropy and mutual information. We show that the increase of the relative entropy of discord between two remote parties is bounded by the nonclassical correlations quantified by the relative entropy of coherence between the carrier and two remote parties, providing an optimal protocol for discord distribution and showing that quantum correlations are the essential resource for such tasks.

Introduction

Quantum coherence and quantum correlations like quantum discord are valuable resources in quantum information processing^1,2,3. Stemming from the superposition rule of quantum mechanics, quantum coherence captures the feature of quantumness in a single system and plays an important role in a variety of applications ranging from thermodynamics^4,5 to metrology⁶, see⁷ for a nice review of the theory of quantum coherence and its applications. Recently, the resource theory of coherence has attracted much attention, with efforts to the quantification and manipulation of coherence^8,9,10,11,12. Coherence in multipartite systems has been also studied^13,14,15, together with its relations to quantum entanglement and quantum nonlocality^{16,17,18,19,20,21}. Interestingly, such quantum correlations also appear naturally in dynamic causal structures of quantum gravity²². The distribution of coherence in bipartite and multipartite systems has been investigated in refs. ^14,23, respectively. In¹⁴ the trade-off relation between the intrinsic coherence and the local coherence in multipartite systems has been demonstrated. In^24,25 the authors proved that the increase of relative entropy of entanglement between two remote parties is bounded by the amount of nonclassical correlations. A rigorous characterization of the distribution of coherence in multipartite systems is imperative and of paramount importance.

The quantum discord quantifies the quantum correlation in a bipartite systems and plays a central role in quantum tasks due to its potential applications in such as quantum critical phenomena^26,27,28,29 and quantum evolution under decoherence^30,31,32,33. We address the following fundamental questions: How much can the discord between sender and receiver laboratories increase under the exchange of a carrier? Is there a quantitative relation between such increase and the nonclassical correlations between the carrier and the parties?

In this article, we present a general bound on the discord gain between distant laboratories under local quantum-incoherent operations and quantum communication, which is given by the quantum coherence between them and the carrier. We first give some trade-off relations between various types of discord and coherence within a bipartite system. Then, we discuss the distribution of coherence in a bipartite quantum state into discord between subsystems and coherent in each individual subsystem, by using the relations of relative entropy and mutual information. Finally, discord distribution in multipartite state is studied, and the discord gain between distant laboratories is bounded by the amount of quantum coherence between them and the carrier.

The relative entropy of coherence of a quantum state ρ is given by ${C}^{r}(\rho )=\mathop{\min }\nolimits_{\sigma \in {{{\mathcal{I}}}}}S(\rho | | \sigma )=S({{\Delta }}(\rho ))-S(\rho )$, where $S(\rho | | \sigma )={{{\rm{Tr}}}}(\rho {\log }_{2}\rho )-{{{\rm{Tr}}}}(\rho {\log }_{2}\sigma )$ is the quantum relative entropy and ${{\Delta }}(\rho )={\sum }_{i}\left|i\right\rangle \left\langle i\right|\rho \left|i\right\rangle \left\langle i\right|$ is the dephased state in reference basis $\{\left|i\right\rangle \}$ of the system, ${{{\mathcal{I}}}}$ denotes the set of all incoherent (diagonal) states. Consider bipartite systems A and B with basis $\{{\left|i\right\rangle }_{A}\}$ and $\{{\left|i\right\rangle }_{B}\}$, respectively. The B-incoherent states with respect to $\{{\left|i\right\rangle }_{B}\}$, denoted as ${{{{\mathcal{I}}}}}_{A| B}$, have the form ${\sigma }_{AB}={\sum }_{i}{p}_{i}{\sigma }_{A}^{i}\otimes {\left|i\right\rangle }_{B}\left\langle i\right|$. A map Λ_A∣B which maps B-incoherent states to B-incoherent ones is called B-incoherent operation. With respect to B-incoherent states, the corresponding coherence is defined by ${C}_{A| B}^{r}({\rho }_{AB})=\mathop{\min }\nolimits_{{\sigma }_{AB}\in {{{{\mathcal{I}}}}}_{A| B}}S({\rho }_{AB}| | {\sigma }_{A| B})=S({{{\Delta }}}_{B}({\rho }_{AB}))-S({\rho }_{AB})$, where ${{{\Delta }}}_{B}({\rho }_{AB})={\sum }_{i}({\mathbb{I}}\otimes {\left|i\right\rangle }_{B}\left\langle i\right|)\rho ({\mathbb{I}}\otimes {\left|i\right\rangle }_{B}\left\langle i\right|)$ is the local dephasing associated with the subsystem B, ${\mathbb{I}}$ is the identity operator. Since the relative entropy does not increase under quantum operations, ${C}_{A| B}^{r}({\rho }_{AB})$ is monotonically nonincreasing under local quantum-incoherent operations and classical communication (LQICC).

With respect to the dephasing on subsystem B, the relative entropy of discord for bipartite states ρ_AB is given by³⁴, ${D}_{A| B}^{r}({\rho }_{AB})=\mathop{\min }\nolimits_{{\delta }_{AB}\in {{{{\mathcal{F}}}}}_{A| B}}S({\rho }_{AB}| | {\delta }_{A| B})$, where ${{{{\mathcal{F}}}}}_{A| B}={\sum }_{i}{p}_{i}{{{{\mathcal{F}}}}}_{A}^{i}\otimes {\left|i\right\rangle }_{B}\left\langle i\right|$ is the set of quantum-classical correlated states. A symmetric version of quantum discord with respect to both dephasing on subsystems A and B is defined by ${D}_{AB}^{s}({\rho }_{AB})=\mathop{\min }\nolimits_{{\gamma }_{AB}\in {\chi }_{AB}}S({\rho }_{AB}| | {\gamma }_{AB})$, where ${\gamma }_{AB}={\sum }_{jk}{p}_{jk}{\left|j\right\rangle }_{A}\left\langle j\right|\otimes {\left|k\right\rangle }_{B}\left\langle k\right|$, and χ_AB is the set of classical-classical correlated states. The global discord³⁵ for bipartite states ρ_AB is defined by, ${D}_{A| B}^{g}({\rho }_{AB})=\mathop{\min }\nolimits_{\{{{{\Pi }}}_{B}^{i}\}}{D}_{\{{{{\Pi }}}_{B}^{i}\}}^{g}({\rho }_{AB})$, where ${D}_{\{{{{\Pi }}}_{B}^{i}\}}^{g}({\rho }_{AB})=S({\rho }_{AB}| | {{{\Pi }}}_{B}^{i}({\rho }_{AB}))-S({\rho }_{B}| | {{{\Pi }}}_{B}^{i}({\rho }_{B}))$, ${{{\Pi }}}_{B}=\{{{{\Pi }}}_{B}^{i}\}$ is a complete projective measurement on subsystem B, see also the original definition of discord^36,37. It is evident from the above definitions that D^s(ρ_AB) ≤ C^r(ρ_AB)¹³, as this measure of discord is the minimum amount of the coherence in any product basis².

Results

Linking quantum coherence to quantum discord

Theorem 1 For any bipartite state ρ_AB, it holds ${D}_{A| B}^{g}({\rho }_{AB})+{P}_{{\rho }_{B}}\,\le \,{D}_{A| B}^{r}({\rho }_{AB})\,\le \,{C}_{A| B}^{r}({\rho }_{AB})\,\le \,{C}^{r}({\rho }_{AB})-{C}^{r}({\rho }_{A})$, where ${P}_{{\rho }_{B}}=\mathop{\min }\nolimits_{{{{\Pi }}}_{B}}S[{\pi }_{{{{\Pi }}}_{B}({\rho }_{AB})}]-S({\pi }_{{\rho }_{AB}})$ with ${\pi }_{{\rho }_{AB}}=T{r}_{B}{\rho }_{AB}\otimes T{r}_{A}{\rho }_{AB}$ the product of the reduced states, see proof in “Methods”.

If the project measurement Π_B on subsystem B is given by the reference basis $\{{\left|i\right\rangle }_{B}\}$ of the coherence for subsystem B, one can easily get that ${P}_{{\rho }_{B}}={C}^{r}({\rho }_{B})$ for relative entropy of coherence. Thus Theorem 1 shows that the summation of the global discord with local measurements on subsystem B and the coherence of subsystem B is bounded by ${D}_{A| B}^{r}({\rho }_{AB})$ and ${C}_{A| B}^{r}({\rho }_{AB})$. On the other hand, the B-incoherent state of ρ_AB, ${C}_{A| B}^{r}({\rho }_{AB})$ (or the discord with local measurements on subsystem B, ${D}_{A| B}^{r}({\rho }_{AB})$), and the coherence of subsystem A is bounded by the coherence C^r(ρ_AB) of the ρ_AB. The first two equalities in Theorem 1 hold for some optimal bases $\{{\left|i\right\rangle }_{B}^{* }\left\langle i\right|\}$ which give the minimum solution of quantum discord ${D}_{A| B}^{r}({\rho }_{B})$. Moreover, if one performs local measurements on subsystem A, similar relation can be obtained, ${D}_{B| A}^{g}({\rho }_{AB})+{P}_{{\rho }_{A}}\,\le \,{D}_{B| A}^{r}({\rho }_{AB})\,\le \,{C}_{B| A}^{{r}_{B}}({\rho }_{AB})\,\le \,{C}^{r}({\rho }_{AB})-{C}^{r}({\rho }_{B})$.

To illustrate the inequality presented in Theorem 1, let us consider two simple examples. The first one is a two-qubit separable state^38,39: ${\rho }_{AB}=\frac{1}{4}[\left|+\right\rangle \left\langle +\right|\otimes \left|0\right\rangle \left\langle 0\right|+\left|-\right\rangle \left\langle -\right|\otimes \left|1\right\rangle \left\langle 1\right|+\left|0\right\rangle \left\langle 0\right|\otimes \left|-\right\rangle \left\langle -\right|+\left|1\right\rangle \left\langle 1\right|\otimes \left|+\right\rangle \left\langle +\right|]$, where $\left|+\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )$ and $\left|-\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle -\left|1\right\rangle )$. The optimal basis $\{{\left|i\right\rangle }_{B}^{* }\left\langle i\right|\}$ which gives the minimum solution of quantum discord ${D}_{A| B}^{r}({\rho }_{B})$ is just $\{{\left|i\right\rangle }_{B}\left\langle i\right|\}$. Under this basis we have ${P}_{{\rho }_{B}}=0$, C^r(ρ_A) = C^r(ρ_B) = 0, ${D}_{A| B}^{g}({\rho }_{AB})={D}_{A| B}^{r}({\rho }_{AB})={C}_{A| B}^{r}({\rho }_{AB})\approx 0.311$, and C^r(ρ_AB) = 0.5. The first two inequalities in Theorem 1 are equalities in this case. The second one is the Werner state: ${\rho }_{AB}=(1-p)\frac{I}{4}+p\left|\psi \right\rangle \left\langle \psi \right|$, where $\left|\psi \right\rangle =\frac{1}{\sqrt{2}}(\left|00\right\rangle +\left|11\right\rangle )$ is a Bell state, p ∈ [0, 1]. The state is a separable for $0\, <\, p\,\le \,\frac{1}{3}$ with nonzero discord. The nearest classical state is just the closet incoherent state of ρ_AB⁴⁰. Under optimal basis $\{{\left|i\right\rangle }_{B}\left\langle i\right|\}$ we have ${P}_{{\rho }_{B}}=0$, C^r(ρ_A) = C^r(ρ_B) = 0, ${D}_{A| B}^{g}({\rho }_{AB})={D}_{A| B}^{r}({\rho }_{AB})={C}_{A| B}^{r}({\rho }_{AB})={C}^{r}({\rho }_{AB})$. In this case, all the inequalities in Theorem 1 become equalities.

The total correlation between systems A and B in a bipartite state ρ_AB is given by the quantum mutual information I(ρ_AB) = S(ρ_A) + S(ρ_B) − S(ρ_AB). In the following, we show that the total correlation present in a bipartite state ρ_AB is bounded, see proof in Methods.

Theorem 2 For any bipartite state ρ_AB, we have $I({\rho }_{AB})\,\le \,{I}_{T}({\rho }_{AB})+{D}_{\bar{T}| T}^{{r}_{T}}({\rho }_{AB})-{P}_{{\rho }_{T}}$, where ${P}_{{\rho }_{T}}=\mathop{\min }\nolimits_{{{{\Pi }}}_{T}}S[{\pi }_{{{{\Pi }}}_{T}({\rho }_{AB})}]-S({\pi }_{{\rho }_{AB}})$, ${I}_{T}({\rho }_{AB})=\mathop{\max }\nolimits_{\{{{{\Pi }}}_{T}^{i}\}}I({{{\Pi }}}_{T}^{i}{\rho }_{AB}{{{\Pi }}}_{T}^{i})$, T = A, B, AB, $\bar{T}$ is the complementary of T in the subsystem of AB, with ${D}_{\overline{AB}| AB}^{r}({\rho }_{AB})={D}_{AB}^{s}({\rho }_{AB})$.

The equality in Theorem 2 holds, $I({\rho }_{AB})={I}_{{{{\Pi }}}_{T}}({\rho }_{AB})+{D}_{\bar{T}| {{{\Pi }}}_{T}}^{{r}_{T}}({\rho }_{AB})-{P}_{{\rho }_{{{{\Pi }}}_{T}}}$, if the measurement Π_T on system T is just the reference basis of coherence for T, T = A, B, AB. When T = AB, one gets $I({\rho }_{AB})+{C}^{r}({\rho }_{A})+{C}^{r}({\rho }_{B})={C}^{c}({\rho }_{AB})+{D}_{AB}^{s}({\rho }_{AB})$, where C^c(ρ_AB) = I_AB(ρ_AB)³⁴ is classical correlation given by the minimal distance between ρ_AB and product states π, ${C}^{c}({\rho }_{AB})=\mathop{\min }\limits_{\pi }S({\rho }_{AB}| | \pi )$, with ρ_AB ∈ χ_AB. This means that the sum of the mutual information and the local coherence is equal to the sum of the quantum discord and classical correlations. One can also obtain that $I({\rho }_{AB})-{C}^{c}({\rho }_{AB})={D}_{AB}^{s}({\rho }_{AB})-{C}^{r}({\rho }_{A})-{C}^{r}({\rho }_{B})$, which means that the overall quantum correlations given in a bipartite state ρ_AB is equal to the quantum discord minus the coherence in each subsystem. When T = A(B), one obtains $I({\rho }_{AB})+{C}^{r}({\rho }_{B})={I}_{B}({\rho }_{AB})+{D}_{A| B}^{r}({\rho }_{AB})$, namely, the sum of the mutual information and the coherence of the measured subsystem B(A) is equal to the sum of the discord and conditional mutual information performed on subsystem B(A).

Example 1 Let us consider the Bell-diagonal states^41,42, ${\rho }_{AB}=\frac{1}{4}(I\otimes I+\mathop{\sum }\nolimits_{j = 1}^{3}{c}_{j}{\sigma }_{j}\otimes {\sigma }_{j})$, where σ_j are the standard Pauli matrices. In this case, we have $I({\rho }_{AB})-{I}_{AB}({\rho }_{AB})=I({\rho }_{AB})-{C}^{c}({\rho }_{AB})={D}_{AB}^{g}({\rho }_{AB})={D}_{AB}^{s}({\rho }_{AB})$, and $I({\rho }_{AB})-{I}_{B}({\rho }_{AB})={D}_{A| B}^{g}({\rho }_{AB})={D}_{A| B}^{r}({\rho }_{AB})$, see Methods for detailed derivations.

Discord distribution between spatially separated parties

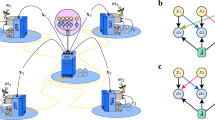
Consider two remote agents, Alice and Bob, having access to particles A and B, respectively. Alice interacts an ancilla C with her particle A and sends C to Bob. Bob interacts C with his particle B. At the end how much discord they share could be increased? What is the cost to increase the discord they share by sending an auxiliary quantum particle C? see Fig. 1.

Fig. 1: Alice and Bob have particles A and B, respectively.

a Alice interacts an ancilla C with her particle A. b C is then sent to Bob’s side. c Bob interacts C with his particle B.

Let ρ be the initial state of the particles A, B and C. The initial discord between Alice and Bob is ${D}_{AC| B}^{r}(\rho )$. If the particle C is sent to Bob’s side without any operations, the discord between the them is given by ${D}_{A| BC}^{r}(\rho )$. We first present a general relation among ${D}_{AC| B}^{r}(\rho )$, ${D}_{A| BC}^{r}(\rho )$ and the cost ${C}_{AB| C}^{r}(\rho )$ for arbitrarily given ρ. Consider the optimal projective measurement ${{{\Pi }}}_{C}^{* }=\{{\left|i\right\rangle }_{C}\left\langle i\right|\}$ on C, with pi the probability of outcome i and ${\rho }_{AB}^{i}$ the corresponding conditional states of systems AB, i.e., ${{{\Pi }}}_{C}^{* }({\rho }_{ABC})={\sum }_{i}{p}_{i}{\rho }_{AB}^{i}\otimes {\left|i\right\rangle }_{C}\left\langle i\right|$. Then we have the following result, see proof in Methods and also an example to illustrate that the increase of the relative entropy of discord between two remote parties is bounded by the nonclassical correlations quantified by the relative entropy of coherence between the carrier and two remote parties after the proof.

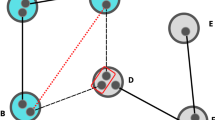
Theorem 3 For any tripartite state ρ of systems A, B and C, it holds that

$${D}_{T| \bar{T}C}^{r}(\rho )-{D}_{TC| \bar{T}}^{r}(\rho )\,\le \,{C}_{AB| C}^{r}(\rho ),$$

(1)

where T = A, B, and $\bar{T}$ is the complementary of T in the subsystem AB.

We point out that the inequality (1) holds for any dimensions of the subsystems. The implications of Theorem 1 is illustrated in Fig. 2. In particular, for tripartite pure state ${\rho }_{ABC}={\left|\psi \right\rangle }_{ABC}\left\langle \psi \right|$ from Theorem 3 we have:

$$\begin{array}{r}| S({\rho }_{A})-S({\rho }_{B})| \,\le \,S[{{\Delta }}({\rho }_{AB})],\end{array}$$

where Δ is a full dephasing operation.

Fig. 2: The area (yellow and blue) represents the discord between AC and B, while the area (red and blue) represents the quantum correlations between AB and C.

The total area (yellow, blue and red) represents the discord between A and BC. One can read off the main result: ${D}_{A| BC}^{r}(\rho )-{D}_{AC| B}^{r}(\rho )\,\le \,{C}_{AB| C}^{r}(\rho )$.

Now let α denote the initial state of A, B and C, and β the state after Alice interacts the ancilla C with particle A. As local operation on AC cannot increase the discord in the AC∣B cut, one has ${D}_{AC| B}^{r}(\beta )\,\le \,{D}_{AC| B}^{r}(\alpha )$. Then Alice sends C to Bob, who interacts C with particle B. From Theorem 3 for state β one gets ${D}_{A| BC}^{r}(\beta )\,\le \,{D}_{AC| B}^{r}(\alpha )+{C}_{AB| C}^{r}(\beta )$. This shows that the discord gained between Alice and Bob is bounded by the quantum coherence measured on C.

It is impossible to distribute the discord by LQICC. Let us first address the case of ${C}_{AB| C}^{r}(\rho )=0$, i.e., ρ is a quantum-incoherent state, $\rho ={\sum }_{i}{p}_{i}{\rho }_{AB}^{i}\otimes {\left|i\right\rangle }_{C}\left\langle i\right|$, which corresponds to classical communication from Alice to Bob. The index i embodies classical information that Alice may copy locally before sending C to Bob. Then both Alice and Bob have access to this information after C is transferred from Alice to Bob, and a local incoherent transformation can be performed by Bob depending on the index i. The process is just the one communication step for a general protocol in terms of LQICC. The protocol may also include the round of classical communication with C that is sent from Bob to Alice. Then one obtains ${D}_{B| AC}^{r}(\beta )\,\le \,{D}_{BC| A}^{r}(\alpha )+{C}_{AB| C}^{r}(\beta ).$ In this case, local classical registers can be kept or erased at any stage of the protocol. Inequality (1) gives rise to that coherence does not increase at any step of a protocol based on LQICC. If ${C}_{AB| C}^{r}(\rho )$ does not vanish, the transfer of C cannot be interpreted as classical communication, revealing the role of coherence in general quantum communication. Hence, (1) constitutes a nontrivial relaxation of the condition of monotonicity of discord under LQICC, bounding the increase of discord under local quantum-incoherent operations and quantum communication.

In order to investigate the discord distribution via a quantum-classical system, besides the coherence present in β, there must be coherence on the receiver’s side already in the initial state α. Exchanging the roles of B and C, one gets from (1), ${D}_{A| BC}^{r}(\beta )-{D}_{AB| C}^{r}(\beta )\,\le \,{C}_{AC| B}^{r}(\alpha )$. Suppose C is a classical state, i.e., ${D}_{AB| C}^{r}(\beta )=0$, we obtain the relation ${D}_{A| BC}^{r}(\beta )\,\le \,{C}_{AC| B}^{r}(\alpha )$. Note that if C is initially not correlated with AB, one further gets ${D}_{A| BC}^{r}(\beta )\,\le \,{C}_{A| B}^{r}(\alpha )$. Another interesting case ${C}_{AC| B}^{r}(\alpha )=0$. Then B is incoherent state initially, and hence $\beta ={\sum }_{i}{p}_{i}{\beta }_{AC}^{i}\otimes {\left|i\right\rangle }_{B}\left\langle i\right|$. In this case discord between Alice and Bob can only be created if C and A (B) have non-vanishing discord, in particular, only if at least one ${\beta }_{AC}^{i}$ has non-vanishing discord. Indeed, such β simply describes a situation in which Bob, upon reading the index i interacted in B, knows which states ${\beta }_{AC}^{i}$ he will end up sharing with Alice. Let us consider two examples.

Example 2 Discord distribution with non-vanishing initial discord between Alice and Bob. Let us consider the state $\rho ={\left|+\right\rangle }_{A}\left\langle +\right|\otimes {\left|0\right\rangle }_{C}\left\langle 0\right|\otimes {\left|-\right\rangle }_{B}\left\langle -\right|$, where ${\left|+\right\rangle }_{A}=\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )$ and ${\left|-\right\rangle }_{B}=\frac{1}{\sqrt{2}}(\left|0\right\rangle -\left|1\right\rangle )$. Alice applies an incoherent operation ${{{\mathcal{O}}}}({\rho }_{ACB})=p{U}_{AC}{\rho }_{ACB}{U}_{AC}^{{\dagger} }+(1-p)\frac{I}{4}\otimes {\left|-\right\rangle }_{B}\left\langle -\right|$, where I is unit operator, 0 ≤ p ≤ 1, U_AC is the CNOT gate ${U}_{AC}(\left|i\right\rangle \otimes \left|j\right\rangle )=\left|i\right\rangle \otimes \left|i\oplus j\right\rangle$. The output state is ${\rho }_{1}=p\left|{{\Psi }}\right\rangle \left\langle {{\Psi }}\right|\otimes {\left|-\right\rangle }_{B}\left\langle -\right|+(1-p)\frac{I}{4}\otimes {\left|-\right\rangle }_{B}\left\langle -\right|$, with $\left|{{\Psi }}\right\rangle =\frac{1}{\sqrt{2}}(\left|00\right\rangle +\left|11\right\rangle )$. Obviously, the discord between subsystems A and C is greater than 0 for p > 0, and the entanglement is vanished when $p\,\le \,\frac{1}{3}$. From the inequality (1), we have that the discord between A and BC is bounded by ${C}_{AB| C}^{r}({\rho }_{1})$ after A interacts with C, i.e., ${D}_{A| BC}^{r}({\rho }_{1})-{D}_{AC| B}^{r}(\rho )\,\le \,\frac{1-p}{4}\log \frac{1-p}{4}+\frac{1+3p}{4}\log \frac{1+3p}{4}-\frac{1+p}{2}\log \frac{1+p}{4}$.

Example 3 Discord distribution with vanishing initial discord between Alice and Bob. Consider the initial three-qubit state in ref. ⁴³, $\alpha =\left(\frac{1}{3}\left|{\phi }^{+}\right\rangle \left\langle {\phi }^{+}\right|+\frac{1}{6}\left|01\right\rangle \left\langle 01\right|+\frac{1}{6}\left|10\right\rangle \left\langle 10\right|\right)\otimes {\left|0\right\rangle }_{B}\left\langle 0\right|+\left(\frac{1}{6}\left|00\right\rangle \left\langle 00\right|+\frac{1}{6}\left|11\right\rangle \left\langle 11\right|\right)\otimes {\left|1\right\rangle }_{B}\left\langle 1\right|$, where $\left|{\phi }^{+}\right\rangle =\frac{1}{\sqrt{2}}(\left|00\right\rangle +\left|11\right\rangle )$ is the maximally entangled state of A and C. Alice performs a CNOT operation on A and C with A as the control qubit, and passes C to Bob. Bob performs another CNOT operation on the system BC with B as the control qubit, i.e., $\alpha{\mathop\rightarrow\limits^{{{\rm{CNOT}}}_{AC}}}\beta {\mathop\rightarrow\limits^{{{\rm{CNOT}}}_{BC}}}\gamma$. It shows that the qubit B has zero discord with A and C all the time. Nevertheless, A and C may share some discord at last, ${D}_{A| BC}^{r}(\gamma )\,\le \,\frac{1}{3}\log 2$.

In fact, one may obtain similar results for other quantum correlations such as information deficit, which quantifies the amount of information that cannot be localized by classical communication between two parties. If only one-way classical communication from party X to party Y is allowed, one has the one-way information deficit: ${{{\Delta }}}_{X| Y}({\rho }_{XY})=\mathop{\min }\nolimits_{{{{\Pi }}}_{Y}^{i}}S({\rho }_{XY}| | {\sum }_{i}{{{\Pi }}}_{Y}^{i}{\rho }_{XY}{{{\Pi }}}_{Y}^{i})$, where the minimization goes over all local von Neumann measurements $\{{{{\Pi }}}_{Y}^{i}\}$ on subsystem Y. We have

$${{{\Delta }}}_{A| BC}(\rho )-{{{\Delta }}}_{AC| B}(\rho )\,\le \,{C}_{AB| C}^{r}(\rho ),$$

(2)

see proof in “Methods”. This shows that the deficit of the bipartite partition A∣BC cannot be larger than the sum of the deficit of the partition AC∣B plus the quantum coherence across the partition AB∣C. Thus, the inequality (2) may be viewed as a type of monogamy relation satisfied by a tripartite quantum state.

Discussions

Establishing quantum correlations between two distant parties is an essential step of many protocols in quantum information processing. The purpose of the physical transmission of the carrier system is to change the amount of quantum correlations between the between remote agents. For example, the increase of the total correlations, mutual information, is bounded by the amount of communicated correlations⁴⁴, i.e., $I({\rho }_{T| \bar{T}C})-I({\rho }_{TC| \bar{T}})\,\le \,I({\rho }_{AC})\,\le \,I({\rho }_{T\bar{T}| C})$, with T = A, B, and $\bar{T}$ the complementary of T in the subsystem AB. We have investigated the trade-off relations satisfied by discord and coherence during such essential steps, via distributing the coherence in a bipartite quantum state to the discord between the subsystems, based on the relations between relative entropy and mutual information. We have identified quantum correlations as the key resource for discord distribution and derived a general bound on the discord gained between distant paries under local quantum-incoherent operations and quantum communication. Explicitly, we have proved that the discord gained between distant parties is bounded by the amount of quantum coherence between them and the information carrier, which provides a fundamental connection between quantum discord and quantum coherence and a natural operational interpretation of quantum coherence as the necessary prerequisite for the success of discord distribution. Our results may highlight further studies on quantum resources consuming in information processing and give rise to related experimental demonstrations.

Methods

Proof of Theorem 1

It can be shown that ${D}_{A| B}^{r}({\rho }_{AB})$ corresponds to the minimal entropic increase resulting from the complete projective measurement Π_B on B: ${D}_{A| B}^{r}({\rho }_{AB})=\mathop{\min }\nolimits_{{{{\Pi }}}_{B}}S[{{{\Pi }}}_{B}({\rho }_{AB})]-S({\rho }_{AB})$, where Π_B(ρ_AB) is the state after the measurement Π_B, ${{{\Pi }}}_{B}({\rho }_{AB})={\sum }_{i}({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i}){\rho }_{AB}({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i})={\sum }_{i}{p}_{i}{\rho }_{A}^{i}\otimes {\left|i\right\rangle }_{B}\left\langle i\right|$. Similarly, ${D}_{AB}^{s}({\rho }_{AB})=\mathop{\min }\nolimits_{{{{\Pi }}}_{AB}}S[{{{\Pi }}}_{AB}({\rho }_{AB})]-S({\rho }_{AB})$, where Π_AB(ρ_AB) is the state after the measurement Π_AB, ${{{\Pi }}}_{AB}\left({\rho }_{AB}\right)={\sum }_{j,k}\left({{{\Pi }}}_{A}^{j}\otimes {{{\Pi }}}_{B}^{k}\right){\rho }_{AB}\left({{{\Pi }}}_{A}^{j}\otimes {{{\Pi }}}_{B}^{k}\right)={\sum }_{jk}{p}_{jk}{\left|j\right\rangle }_{A}\left\langle j\right|\otimes {\left|k\right\rangle }_{B}\left\langle k\right|$. Note that ${C}_{A| B}^{r}({\rho }_{AB})$ is different from the relative entropy of discord which involves a minimization over all bases of B, while ${C}_{A| B}^{r}({\rho }_{AB})$ is defined for a fixed incoherent basis $\{{\left|i\right\rangle }_{B}\}$.

Under the von Neumann projective measurement ${{{\Pi }}}_{B}=\{{{{\Pi }}}_{B}^{i}\}$, the state of the system B is given by ${\rho }_{A}^{i}={{{{\rm{Tr}}}}}_{B}[({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i}){\rho }_{AB}({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i})]/{p}_{i}$, with the measurement outcome probability ${p}_{i}={{{\rm{Tr}}}}[({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i}){\rho }_{AB}]$. The conditional entropy of system A is then $S[{{{\Pi }}}_{B}({\rho }_{A| B})]={\sum }_{i}{p}_{i}S({\rho }_{A}^{i})$. Therefore, the quantum mutual information induced by the von Neumann measurement on the system B is given by:

$${I}_{{{{\Pi }}}_{B}}({\rho }_{AB})=S({\rho }_{A})-S[{{{\Pi }}}_{B}({\rho }_{A| B})].$$

The measurement-independent quantum mutual information I_B(ρ_AB) is given by:

$$\begin{array}{l}{I}_{B}({\rho }_{AB})=\mathop{\max }\limits_{{{{\Pi }}}_{B}}{I}_{{{{\Pi }}}_{B}}({\rho }_{AB})\\ \qquad\quad\,\,\,\,\,\,=\mathop{\max }\limits_{\{{{{\Pi }}}_{B}^{i}\}}I\left(({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i}){\rho }_{AB}({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i})\right),\end{array}$$

which is interpreted as the one-sided classical mutual information on subsystem B. Let ${{{\Pi }}}_{B}^{* }=\{{\left|i\right\rangle }_{B}^{* }\left\langle i\right|\}$ be the optimal basis of system B for ${D}_{A| B}^{r}$. Then we have:

$$\begin{array}{ll}{D}_{A| B}^{g}({\rho }_{AB})&=\mathop{\min }\limits_{{{{\Pi }}}_{B}}S({\rho }_{B})-S({\rho }_{AB})+\mathop{\sum}\limits_{i}{p}_{i}S({\rho }_{A}^{i})\\& \le \,S({\rho }_{B})-S({\rho }_{AB})+S[{{{\Pi }}}_{B}^{* }({\rho }_{AB})]-S[{{{\Pi }}}_{B}^{* }({\rho }_{B})]\\ &=S({\rho }_{B})+S[{{{{\rm{tr}}}}}_{B}{{{\Pi }}}_{B}^{* }({\rho }_{AB})]-S({\rho }_{AB})+S\left([{{{\Pi }}}_{B}^{* }({\rho }_{AB})]\right.\\ &\,\,\quad-\,S[{{{{\rm{tr}}}}}_{A}{{{\Pi }}}_{B}^{* }({\rho }_{AB})]-S[{{{{\rm{tr}}}}}_{B}{{{\Pi }}}_{B}^{* }({\rho }_{AB})]\\ &=S({\pi }_{\rho })-S({\rho }_{AB})+S[{{{\Pi }}}_{B}^{* }({\rho }_{AB})]-S({\pi }_{{{{\Pi }}}_{B}^{* }({\rho }_{AB})})\\ &={D}_{A| B}^{r}({\rho }_{AB})-[S({\pi }_{{{{\Pi }}}_{B}^{* }({\rho }_{AB})})-S({\pi }_{\rho })]\\& \le \,{D}_{A| B}^{r}({\rho }_{AB})-{P}_{{\rho }_{B}},\end{array}$$

where we have used $S[{{{{\rm{tr}}}}}_{A}{{{\Pi }}}_{B}^{* }({\rho }_{AB})]=S[{{{\Pi }}}_{B}^{* }({\rho }_{B})]$ and ${{{\Pi }}}_{B}^{* }({\rho }_{B})={\sum }_{i}{p}_{i}{\left|i\right\rangle }_{B}^{* }\left\langle i\right|$. Then one gets

$${D}_{A| B}^{g}({\rho }_{AB})+{P}_{{\rho }_{B}}\,\le \,{D}_{A| B}^{r}({\rho }_{AB}).$$

It is evident that ${D}_{A| B}^{r}({\rho }_{AB})\,\le \,{C}_{A| B}^{r}({\rho }_{AB})$ for any reference basis¹³. In fact, the measure of discord is the minimum coherence in any product basis². The equality holds for an optimal basis. On the other hand:

$$\begin{array}{ll}{C}_{A| B}^{r}({\rho }_{AB})&=S[{{{\Delta }}}_{B}({\rho }_{AB})]-S({\rho }_{AB})\\ &=S[{{{\Delta }}}_{AB}({\rho }_{AB})]-S({\rho }_{AB})\\& \quad\,\,-\,\left(S[{{{\Delta }}}_{AB}({\rho }_{AB})]-S[{{{\Delta }}}_{B}({\rho }_{AB})]\right)\\& \le \,{C}^{r}({\rho }_{AB})-{C}^{r}({\rho }_{A}),\end{array}$$

(3)

where Δ_AB is the completely dephasing operation.

Proof of Theorem 2

The total mutual information of a bipartite state ρ is given by the relative entropy between ρ the product state of the reduced states π_ρ = ρ_A ⊗ ρ_B, $I({\rho }_{AB})=S({\rho }_{AB}| | {\pi }_{{\rho }_{AB}})=S({\rho }_{AB}| | {\rho }_{A}\otimes {\rho }_{B})$³⁴. We have:

$$\begin{array}{ll}{I}_{B}({\rho }_{AB})&=S({\rho }_{A})-\mathop{\sum}\limits_{i}{p}_{i}S({\rho }_{A}^{i})\\ &=S({\rho }_{A})+\mathop{\sum}\limits_{i}S({{{\Pi }}}_{B}^{i}({\rho }_{B}))\\ &\quad\,\,-\,[\mathop{\sum}\limits_{i}S({{{\Pi }}}_{B}^{i}({\rho }_{B}))+\mathop{\sum}\limits_{i}{p}_{i}S({\rho }_{A}^{i})]\\ &=S({\rho }_{A})+\mathop{\sum}\limits_{i}S({{{\Pi }}}_{B}^{i}({\rho }_{B}))-\mathop{\sum}\limits_{i}S({{{\Pi }}}_{B}^{i}({\rho }_{AB}))\\ &=S\left({{{\Pi }}}_{B}({\rho }_{AB})\parallel {\rho }_{A}\otimes {{{\Pi }}}_{B}({\rho }_{B})\right)\\ &=S({\rho }_{A})+S({{{\Pi }}}_{B}({\rho }_{B}))-S({{{\Pi }}}_{B}({\rho }_{AB})),\end{array}$$

(4)

with maximization taken over measurement $\{{{{\Pi }}}_{B}^{j}\}$, where ${{{\Pi }}}_{B}({\rho }_{AB})={\sum }_{i}({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i}){\rho }_{AB}({\mathbb{I}}\otimes {{{\Pi }}}_{B}^{i})={\sum }_{i}{p}_{i}{\rho }_{A}^{i}\otimes {\left|i\right\rangle }_{B}\left\langle i\right|$ and ${{{\Pi }}}_{B}({\rho }_{B})={\sum }_{i}{p}_{i}{\left|i\right\rangle }_{B}\left\langle i\right|$.

Combining

$${D}_{A| B}^{r}({\rho }_{AB})=\mathop{\min }\limits_{{{{\Pi }}}_{B}}S[{{{\Pi }}}_{B}({\rho }_{AB})]-S({\rho }_{AB})$$

and

$$\begin{array}{l}{P}_{{\rho }_{B}}=\mathop{\min }\limits_{{{{\Pi }}}_{B}}S[{\pi }_{{{{\Pi }}}_{B}({\rho }_{AB})}]-S({\pi }_{{\rho }_{AB}})\\ \quad\,\,\,\,\,\,=\mathop{\min }\limits_{{{{\Pi }}}_{B}}S({{{\Pi }}}_{B}({\rho }_{B}))-S({\rho }_{B})\end{array}$$

we have $I({\rho }_{AB})={I}_{{{{\Pi }}}_{T}}({\rho }_{AB})+{D}_{\bar{T}| {{{\Pi }}}_{T}}^{r}({\rho }_{AB})-{P}_{{\rho }_{{{{\Pi }}}_{T}}}$, where ${I}_{{{{\Pi }}}_{T}}({\rho }_{AB})$, ${D}_{\bar{T}| {{{\Pi }}}_{T}}^{r}({\rho }_{AB})$ and ${P}_{{\rho }_{{{{\Pi }}}_{T}}}$ are the projective measurement Π_T dependent, T = A, B, AB, and $\bar{T}$ is the complementary of T in the subsystem AB. Under the optimal local measurements, one has $I({\rho }_{AB})\,\le \,{I}_{B}({\rho }_{AB})+{D}_{A| B}^{r}({\rho }_{AB})-{P}_{{\rho }_{B}}$. With a similar consideration, we can also get $I({\rho }_{AB})\,\le \,{I}_{A}({\rho }_{AB})+{D}_{B| A}^{r}({\rho }_{AB})-{P}_{{\rho }_{A}}$ and $I({\rho }_{AB})\,\le \,{I}_{AB}({\rho }_{AB})+{D}_{AB}^{s}({\rho }_{AB})-{P}_{{\rho }_{AB}}$.

Derivations in Example 1

Consider the Bell-diagonal states^41,42, ${\rho }_{AB}=\frac{1}{4}(I\otimes I+\mathop{\sum }\nolimits_{j = 1}^{3}{c}_{j}{\sigma }_{j}\otimes {\sigma }_{j})={\sum }_{ab}{\lambda }_{ab}\left|{\beta }_{ab}\right\rangle \left\langle {\beta }_{ab}\right|$, with the maximally mixed marginals (${\rho }_{A}={\rho }_{B}=\frac{I}{2}$). The density matrix of Bell-diagonal states with σ₃ representation takes the form:

$${\rho }_{AB}^{{\sigma }_{3}}=\frac{1}{4}\left(\begin{array}{llll}1+{c}_{3}&0&0&{c}_{1}-{c}_{2}\\ 0&1-{c}_{3}&{c}_{1}+{c}_{2}&0\\ 0&{c}_{1}+{c}_{2}&1-{c}_{3}&0\\ {c}_{1}-{c}_{2}&0&0&1+{c}_{3}\end{array}\right).$$

The eigenstates of ${\rho }_{AB}^{{\sigma }_{3}}$ are the four Bell states: $\left|{\beta }_{ab}\right\rangle =(\left|0,b\right\rangle +{(-1)}^{a}\left|1,1\oplus b\right\rangle )/\sqrt{2}$, with the corresponding eigenvalues ${\lambda }_{ab}=\frac{1}{4}[1+{(-1)}^{a}{c}_{1}-{(-1)}^{a+b}{c}_{2}+{(-1)}^{b}{c}_{3}]$, where a, b ∈ {0, 1}.

For Bell-diagonal states, the reduced states have no coherence in the subsystems. The relative entropy of coherence is given by:

$${C}^{r}({\rho }_{AB}^{{\sigma }_{i}})=-H({\lambda }_{ab})-\mathop{\sum }\limits_{j=1}^{2}\frac{(1+{(-1)}^{j}{c}_{i})}{2}{\log }_{2}\frac{(1+{(-1)}^{j}{c}_{i})}{4},$$

where $H({\lambda }_{ab})=-{\sum }_{ab}{\lambda }_{a,b}{\log }_{2}{\lambda }_{ab}$. The mutual information for Bell-diagonal states is given by:

$$I({\rho }_{AB})=\mathop{\sum}\limits_{a,b}{\lambda }_{ab}{\log }_{2}(4{\lambda }_{ab}).$$

The classical correlation for Bell-diagonal states is given by:

$${C}^{c}({\rho }_{AB})=\mathop{\sum }\limits_{j=1}^{2}\frac{(1+{(-1)}^{j}c)}{2}{\log }_{2}(1+{(-1)}^{j}c),$$

where $c=\max \{| {c}_{1}| ,| {c}_{2}| ,| {c}_{3}| \}$.

Before calculating ${D}_{AB}^{g}({\rho }_{AB})$, we note that from the derivation of Theorem 2, the quantum discord can be rewritten as the difference of relative entropies:

$$\begin{array}{ll}{D}_{A| B}^{g}({\rho }_{AB}) &=I({\rho }_{AB})-{I}_{B}({\rho }_{AB})\\ &=S\left({\rho }_{AB}\parallel {\rho }_{A}\otimes {\rho }_{B}\right)\\ &\quad\,-\,S\left({{{\Pi }}}_{B}({\rho }_{AB})\parallel {\rho }_{A}\otimes {{{\Pi }}}_{B}({\rho }_{B})\right)\\ &=S[{\rho }_{AB}| | {{{\Pi }}}_{B}({\rho }_{AB})]-S[{\rho }_{B}| | {{{\Pi }}}_{B}({\rho }_{B})],\end{array}$$

with the minimization taken over the measurement $\{{{{\Pi }}}_{B}^{j}\}$. Performing measurements on both subsystems A and B, one has the symmetric version ${D}_{AB}^{g}\left({\rho }_{AB}\right)$,

$$\begin{array}{ll}{D}_{AB}^{g}\left({\rho }_{AB}\right)&=\mathop{\min }\limits_{\{{{{\Pi }}}_{A}^{j}\otimes {{{\Pi }}}_{B}^{k}\}}\left[S\left({\rho }_{AB}\parallel {\rho }_{A}\otimes {\rho }_{B}\right)\right.\\ &\quad\,\,\left.-\,S\left({{{\Pi }}}_{AB}\left({\rho }_{AB}\right)\parallel {{{\Pi }}}_{A}\left({\rho }_{A}\right)\otimes {{{\Pi }}}_{B}\left({\rho }_{B}\right)\right)\right],\end{array}$$

(5)

where ${{{\Pi }}}_{AB}\left({\rho }_{AB}\right)={\sum }_{j,k}\left({{{\Pi }}}_{A}^{j}\otimes {{{\Pi }}}_{B}^{k}\right){\rho }_{AB}\left({{{\Pi }}}_{A}^{j}\otimes {{{\Pi }}}_{B}^{k}\right)$. Expressing (5) in terms of the mutual information I, we obtain

$${D}_{AB}^{g}\left({\rho }_{AB}\right)=\mathop{\min }\limits_{\{{{{\Pi }}}_{A}^{j}\otimes {{{\Pi }}}_{B}^{k}\}}\left[I({\rho }_{AB})-I({{{\Pi }}}_{AB}\left({\rho }_{AB}\right))\right],$$

(6)

which is the symmetric version of the expression for the loss of correlation based on the measurement^45,46. Remarkably, ${D}_{AB}^{g}\left({\rho }_{AB}\right)$ is equivalent to the measurement-induced disturbance⁴⁷ if the measurements performed (5) are replaced by the eigenprojectors of the reduced density operators, respectively. Moreover, Eq. (5) also provides the symmetric quantum discord considered in ref. ⁴⁸ and experimentally witnessed in ref. ⁴⁹. Eq. (5) yields:

$$\begin{array}{ll}{D}_{AB}^{g}\left({\rho }_{AB}\right)&=\mathop{\min }\limits_{\{{{{\Pi }}}_{A}^{j}\otimes {{{\Pi }}}_{B}^{k}\}}\left[S\left({\rho }_{AB}\parallel {{{\Pi }}}_{AB}\left({\rho }_{AB}\right)\right)\right.\\ &\quad\,\,\left.-\,S\left({\rho }_{A}\parallel {{{\Pi }}}_{A}\left({\rho }_{A}\right)\right)-S\left({\rho }_{B}\parallel {{{\Pi }}}_{B}\left({\rho }_{B}\right)\right)\right]\\ &\le \,S\left({\rho }_{AB}\parallel {{{\Pi }}}_{AB}\left({\rho }_{AB}\right)\right)-{P}_{{\rho }_{A}}-{P}_{{\rho }_{B}}.\end{array}$$

Specially, for some basis the symmetric extension quantum discord ${D}_{AB}^{g}\left({\rho }_{AB}\right)$ is bounded by the correlated coherence C_cc(ρ_AB) = C^r(ρ_AB) − C^r(ρ_A) − C^r(ρ_B) defined in⁵⁰.

From (6), we have the quantum discord for Bell-diagonal states:

$${D}_{AB}^{g}({\rho }_{AB})=-H({\lambda }_{ab})-\mathop{\sum }\limits_{j=1}^{2}\frac{(1+{(-1)}^{j}c)}{2}{\log }_{2}\frac{(1+{(-1)}^{j}c)}{4}.$$

We note that the one-side quantum discord, two-side quantum discord and the relative entropy of quantum discord are identical for Bell-diagonal states. It is easy to verify that the quantum discord is equal to the coherence under an optimal basis. Therefore, $I({\rho }_{AB})-{I}_{B}({\rho }_{AB})={D}_{A| B}^{g}({\rho }_{AB})={D}_{A| B}^{r}({\rho }_{AB})$ as C^r(ρ_A) = C^r(ρ_B) = 0 and $I({\rho }_{AB})-{I}_{AB}({\rho }_{AB})=I({\rho }_{AB})-{C}^{c}({\rho }_{AB})={D}_{AB}^{g}({\rho }_{AB})={D}_{AB}^{s}({\rho }_{AB})$.

Proof of Theorem 3

Let ${\rho }_{AB}^{i* }$ be the state resulted from the optimal measurement on subsystem B for ${D}_{A| B}^{r}({\rho }_{AB}^{i})$. As the state ${\sum }_{i}{p}_{i}{\rho }_{AB}^{i* }\otimes {\left|i\right\rangle }_{C}\left\langle i\right|$ is a quantum-classical state, we have:

$$\begin{array}{ll}{D}_{A| BC}^{r}(\rho )&\le S(\rho \parallel \mathop{\sum}\limits_{i}{p}_{i}{\rho }_{AB}^{i* }\otimes {\left|i\right\rangle }_{C}\left\langle i\right|)\\&=-S(\rho )-{{{\rm{Tr}}}}[\rho \log (\mathop{\sum}\limits_{i}{p}_{i}{\rho }_{AB}^{i* }\otimes {\left|i\right\rangle }_{C}\left\langle i\right|)]\\&=-S(\rho )-{{{\rm{Tr}}}}[{{{\Pi }}}_{C}^{* }(\rho )\log (\mathop{\sum}\limits_{i}{p}_{i}{\rho }_{AB}^{i* }\otimes {\left|i\right\rangle }_{C}\left\langle i\right|)]\\&=\left[S({{{\Pi }}}_{C}^{* }(\rho ))-S(\rho )\right]+\left[-S({{{\Pi }}}_{C}^{* }(\rho ))\right.\\ & \left.-\,{{{\rm{Tr}}}}\left({{{\Pi }}}_{C}^{* }(\rho )\log \left(\mathop{\sum}\limits_{i}{p}_{i}{\rho }_{AB}^{i* }\otimes {\left|i\right\rangle }_{C}\left\langle i\right|\right)\right)\right]\\&={C}_{AB|C}^{r}(\rho )+S\left(\mathop{\sum}\limits_{i}{p}_{i}{\rho }_{AB}^{i}\otimes {\left|i\right\rangle }_{C}\left\langle i\right|\right.\\&\qquad\qquad\qquad\qquad\,\left.\times\parallel \mathop{\sum}\limits_{i}{p}_{i}{\rho }_{A:B}^{i* }\otimes {\left|i\right\rangle }_{C}\left\langle i\right|\right)\\&={C}_{AB| C}^{r}(\rho )+\mathop{\sum}\limits_{i}{p}_{i}S({\rho }_{AB}^{i}\parallel {\rho }_{AB}^{i* })\\ &={C}_{AB| C}^{r}(\rho )+\mathop{\sum}\limits_{i}{p}_{i}{D}_{A| B}^{r}({\rho }_{AB}^{i})\\&={C}_{AB| C}^{r}(\rho )+{D}_{A| BC}^{r}({{{\Pi }}}_{C}^{* }(\rho ))\\&={C}_{AB| C}^{r}(\rho )+{D}_{AC| B}^{r}({{{\Pi }}}_{C}^{* }(\rho ))\\ &\le \,{C}_{AB| C}^{r}(\rho )+{D}_{AC| B}^{r}(\rho ),\end{array}$$

where the first inequality is due to that the quantum-classical state ${\sum }_{i}{p}_{i}{\rho }_{A:B}^{i* }\otimes {\left|i\right\rangle }_{C}\left\langle i\right|$ cannot be better than optimal state for the sake of ${D}_{A| BC}^{r}(\rho )$, the second equality holds since ${{{\rm{Tr}}}}(\sigma \log {{\Pi }}(\tau ))={{{\rm{Tr}}}}({{\Pi }}(\sigma )\log {{\Pi }}(\tau ))$ for all projective measurements Π, and for all σ and τ⁴⁴, the fourth equality is due to the optimality of ${{{\Pi }}}_{C}^{* }$ for ${C}_{AB| C}^{r}(\rho )$, the fifth equality is due to the chain rule for relative entropy⁵¹, the last two equalities are due to the fact that the relative entropy of coherence satisfies the “flags” condition ref. ⁵², i.e., ${D}_{FX| Y}^{r}\left({\sum }_{i}{p}_{i}{\left|i\right\rangle }_{F}\left\langle i\right|\otimes {\rho }_{XY}^{i}\right)={\sum }_{i}{p}_{i}{D}_{X| Y}^{r}({\rho }_{XY}^{i})={D}_{X| YF}^{r}\left({\sum }_{i}{p}_{i}{\rho }_{XY}^{i}\otimes {\left|i\right\rangle }_{F}\left\langle i\right|\right)$. From the above consideration, the cost for sending the particle C from Alice to Bob is bounded by ${C}_{AB| C}^{r}(\rho )$, ${D}_{B| AC}^{r}(\rho )-{D}_{BC| A}^{r}(\rho )\,\le \,{C}_{AB| C}^{r}(\rho )$.

Example. Consider the state $\rho ={\left|+\right\rangle }_{A}\left\langle +\right|\otimes {\left|0\right\rangle }_{B}\left\langle 0\right|\otimes {\left|0\right\rangle }_{C}\left\langle 0\right|$, where ${\left|+\right\rangle }_{A}=\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )$, and the incoherent operation $\varepsilon (\rho )=\frac{1}{2}({U}_{CN}\otimes {I}_{B})\rho ({U}_{CN}^{{\dagger} }\otimes {I}_{B})+\frac{1}{8}I$ on the subsystem AC, where I_B is identity operator on the subsystem B, U_CN is the CNOT gate, ${U}_{CN}(\left|i\right\rangle \otimes \left|j\right\rangle )=\left|i\right\rangle \otimes \left|i\oplus j\right\rangle$ on the the subsystem AC. Alice applies the incoherent operation ε on initial state ρ and passes the qubit C to Bob, who then performs another CNOT operation ${U}_{CN}^{\prime}$ on the subsystem BC with C as the control qubit. The resulting state is:

$$\begin{array}{l}{\rho }_{ABC}^{\prime}=\frac{3}{8}(\left|000\right\rangle \left\langle 000\right|+\left|111\right\rangle \left\langle 111\right|)\\ \qquad\quad\,\,\,\,\left.+\,\frac{1}{4}\left|000\right\rangle \left\langle 111\right|+\left|111\right\rangle \left\langle 000\right|\right)\\ \qquad\quad\,\,\,\,+\,\frac{1}{8}(\left|011\right\rangle \left\langle 011\right|+\left|100\right\rangle \left\langle 100\right|).\end{array}$$

Taking concurrence E_C as an entanglement measure, we have ${E}_{C}({\rho }_{A| BC}^{\prime})\ge {E}_{C}({\rho }_{AB}^{\prime})=\frac{1}{4}$, where we have used the formula that the concurrence of a two-qubit mixed state ρ is ${E}_{C}(\rho )=\max \{0,\,{\lambda }_{1}-{\lambda }_{2}-{\lambda }_{3}-{\lambda }_{4}\}$, with λ₁, λ₂, λ₃ and λ₄ being the square roots of the eigenvalues of ρ(σ_y ⊗ σ_y)ρ^⋆(σ_y ⊗ σ_y) in nonincreasing order, σ_y is the Pauli matrix, and ρ^⋆ is the complex conjugate of ρ. That is to say, the final state ${\rho }_{ABC}^{\prime}$ is entangled and the discord of the final state ${\rho }_{ABC}^{\prime}$ is nonzero, ${D}^{r}({\rho }_{A| BC}^{\prime}) \,>\, 0$, although the discord of the initial state ρ is 0. Therefore, the discord strictly increases by the transfer of a separable carrier. Since the coherence between the carrier and the two remote parties is given by ${C}^{r}({\rho }_{AB| C}^{\prime})=0.182$, from the inequality (1) in Theorem 3 one has that the increase of the discord is bounded by the coherence between the carrier and the two remote parties, i.e., $0 \,<\, {D}^{r}({\rho }_{A| BC}^{\prime})\,\le \,{C}^{r}({\rho }_{AB| C}^{\prime})=0.182$.

Derivation of (2)

Let $\sigma ={\sum }_{i}{{{\Pi }}}_{B}^{i}\rho {{{\Pi }}}_{B}^{i}$ be the state from the local measurement ${{{\Pi }}}_{B}=\{{{{\Pi }}}_{B}^{i}\}$ on the B part of ρ, which minimizes the relative entropy of σ and ρ such that

$${\Delta}_{AC|B}(\rho )=S(\rho||\sigma).$$

Assume state ρ₁ is the closest C-incoherent state to ρ, namely,

$${C}_{AB| C}^{r}(\rho )=S(\rho | | {\rho }_{1}).$$

Suppose ${{{\Pi }}}_{C}=\{{{{\Pi }}}_{C}^{i}\}$ is the local measurement such that ${\rho }_{1}={\sum }_{i}{{{\Pi }}}_{C}^{i}\rho {{{\Pi }}}_{C}^{i}$. One has ${\sigma }_{1}={\sum }_{i}{{{\Pi }}}_{C}^{i}\sigma {{{\Pi }}}_{C}^{i}$. Since ${{{\rm{Tr}}}}(\rho \log {\rho }_{1})={{{\rm{Tr}}}}({\rho }_{1}\log {\rho }_{1})$ and ${{{\rm{Tr}}}}(\rho \log {\sigma }_{1})={{{\rm{Tr}}}}({\rho }_{1}\log {\rho }_{1})$, we have

$$S(\rho | | {\sigma }_{1})=S(\rho | | {\rho }_{1})+S(\rho_{1} | | {\sigma }_{1}).$$

As the relative entropy does not increase under quantum operations, S(Λ(ρ)∣∣Λ(σ)) ≤ S(ρ∣∣σ), we have S(ρ₁∣∣σ₁) ≤ S(ρ∣∣σ). Then

$$S(\rho | | {\sigma }_{1})\,\le \,{C}_{AB| C}^{r}(\rho )+{{{\Delta }}}_{AC| B}(\rho ).$$

By the definition of deficit, we have Δ_A∣BC(ρ) ≤ S(ρ∣∣σ₁), and

$${{{\Delta }}}_{A| BC}(\rho )-{{{\Delta }}}_{AC| B}(\rho )\,\le \,{C}_{AB| C}^{r}(\rho ).$$