Introduction

Quantum technology enables applications ranging from fundamentally secure cryptography1 to quantum teleportation2,3 and ultimately the quantum internet as enabled by the distribution of global-scale entanglement resources4,5,6. Quantum correlations, created in quantum networks, can be harnessed to enhance the efficiency of distributed information processing, i.e. by reducing communication cost; this is exemplified in the use of shared entanglement in communication complexity problems (CCPs)7,8,9. This will be of interest in near-term quantum computing platforms where many medium-sized nodes are linked to scale up the computational capabilities10,11, where CCP will naturally reside.

Distributed computing represents a highly versatile method of solving demanding tasks by taking a global target function and splitting the input among multiple users. The users act on their inputs locally to solve a global problem with some communication allowed between each of the users. CCP provides the necessary framework in evaluating the ultimate performance of these architectures, notably evaluating the minimum communication overhead needed to achieve the task12,13,14. Recent developments of CCPs have adopted the use of non-classical resources7, and an updated definition for evaluating the complexity of a problem. One might also be interested in obtaining the highest probability of successfully evaluating the target function, with a fixed amount of communication8,15,16,17,18,19. In spite of Holevo’s theorem20—showing that quantum states cannot reduce the cost of transmitting a classical message—if our aim is to compute a function of it, as in the classic CCP setting, quantum resources such as entanglement can demonstrate an improvement. Proof-of-principle experiments have been realised using photonic Bell states21, GHZ states22, and entanglement of high-dimensional systems23,24.

We remark that while in this work we focus on entanglement-based CCPs, there is a class of protocols in which the quantum improvement is obtained not via entanglement but from prepare-and-measure type schemes25,26,27,28. Notable experiments of this kind include the quantum fingerprinting protocols29,30 and multi-user encoding on non-classical states of light13,14,31. For a broad review of the topic, which includes a discussion of the resources underpinning the quantum advantages in CCPs, see ref. 8. More recently, the combination of both entanglement and quantum communication has also started to be considered32,33,34. Remarkably, it has been proven that quantum advantages in CCPs can be mapped to the violation of Bell inequalities19,35,36, thus establishing an important link between two key concepts of computer science and quantum theory. Moreover, it is widely believed that communication complexity should scale with the size of the input data. Interestingly, this non-triviality of a CCP can be seen as an informational principle for why Nature cannot be more non-local than what is achievable within quantum theory37,38,39.

The connection between Bell inequalities and communication complexity has only been proven for the standard notion of Bell non-locality, which contrasts quantum mechanics with local hidden-variable (LHV) models. In this standard scenario, one considers a number of separate parties who share a common source of correlations but cannot communicate—an arrangement that is severely limiting, particularly in the context of CCPs. The study of Bell non-locality has, however, produced much more general and stronger notions of non-locality40,41,42,43,44; these include scenarios that allow subsets of parties involved in a Bell experiment to communicate, while the classical description now considers non-local hidden-variable (NLHV) models. So far the connection between CCPs and this generalised Bell non-locality has not been investigated. That is precisely our aim.

Here we show that NLHV models define a new and more general class of CCPs. As opposed to the standard scenario, where each party has an exclusive part of the input data required to compute the desired function, in the generalised case the input data can be distributed in arbitrary manners. Every NLHV model defines a specific pattern in which the input data is distributed among the parties, see Fig. 1a. Moreover, every full correlator Bell inequality bounding the classical correlations in such NLHV models not only defines a target function in the CCP but also the corresponding probability of success in trying to compute it with a restricted amount of communication between the parties. Thus, the violation of these Bell inequalities is a necessary and sufficient condition for a quantum advantage in generalised CCPs. This establishes the general connection between this form of nonclassicality emerging from NLHV models and a relevant quantum information task. We experimentally investigate a three-party CCP task with a causal structure inspired by the guess-your-neighbour-input (GYNI) non-local game, and demonstrate an increased winning probability when using quantum resources that violate the associated Bell-like inequality. This exemplifies the need to consider the underlying causal structures when defining the Bell-like inequalities for generalised CCPs.

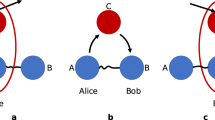
Fig. 1: Distributed computation in a CCP scenario.
figure 1

a A central agent allocates resources among a network of n users who independently produce outcomes to solve a collective task. Each user i receives yi and a subset xi of the variables \(\left\{{x}_{1},\cdots \ ,{x}_{n}\right\}\) according to some underlying causal structure indicated by the shaded pink region. Each user processes their input data along with shared correlations and broadcast a one-bit message mi to all others before they compute a function f(x1, …, xn, y1, …, yn). When allowing for quantum resources, shared quantum correlations that violate a Bell-like inequality bounding the corresponding NLHV model provide an advantage in the probability of success of the task over its classical counterpart. b Causal structure of the three-party GYNI scenario41,49 experimentally investigated. The input of each party xi is communicated to its neighbour to the right (or alternatively, to the left). The variable λ stands for pre-shared (classical) correlations shared among the parties and used to produces respective outcomes, ai. c Causal structure of Svetlichny’s scenario40 as discussed in Supplementary Methods.

Full size image

Results

Bell scenarios with non-local hidden-variable models

In a standard Bell scenario, each of n distant parties receives an input xi and produces an output ai (with i = 1, …, n). A local hidden-variable description implies that the observed probability distribution p(a1, …, an∣x1, …, xn) = p(a∣x) can be decomposed as

$$p({{{\bf{a}}}}| {{{\bf{x}}}})=\mathop{\sum}\limits_{\lambda }p({a}_{1}| {x}_{1},\lambda )\ldots p({a}_{n}| {x}_{n},\lambda )p(\lambda ),$$
(1)

where λ is a classical random variable accounting for all correlations observed between the measurement outcomes of the distant parties. In turn, in a quantum description, Born’s rule implies that

$$p({{{\bf{a}}}}| {{{\bf{x}}}})=Tr\left[\left({M}_{{a}_{1}}^{{x}_{1}}\otimes \ldots \otimes {M}_{{a}_{n}}^{{x}_{n}}\right)\rho \right],$$
(2)

where \({M}_{{a}_{i}}^{{x}_{i}}\) are measurement operators and ρ describes the quantum state shared between the parties. As shown by Bell45, there are quantum correlations (2) that cannot be written as (1). This is the phenomenon known as Bell non-locality and is witnessed by the violation of Bell inequalities35,45, where linear constraints on the probabilities should be respected by any distribution of the form (1).

In spite of its importance, the usual Bell scenario is rather restrictive, in that no communication can take place between the parties. Alternatively, one can think of an external agent that generates a sequence of values of n random variables \(\left\{{x}_{i}\right\}\) and sends (possibly overlapping) subsets of this sequence to each of the n parties involved in the Bell test. In this more general scenario the ith party can receive a total of li inputs that we label as \({x}_{i,j}\in \left\{{x}_{i}\right\}\) with j = 1, …, li and xi,1 = xi. Let the set of inputs of party i be organised in a vector xi = {xi,j∣j = 1, …, li}. A classical description is then given by a NLHV model

$$p({\bf{a}}| {\bf{x}})=\mathop{\sum}\limits_{\lambda}p(a_1| {\bf{x}}_1,\lambda)\ldots p(a_n|{\bf{x}}_n,\lambda)p(\lambda),$$
(3)

that can be graphically represented by a directed acyclic graph where each measurement outcome ai has a set of parents xi,j. See Fig. 1b and Fig. 1c for examples.

Analogously to Eq. (2), the set of quantum correlations in this extended Bell scenario is described as

$$p({{{\bf{a}}}}| {{{\bf{x}}}})=Tr\left[\left({M}_{{a}_{1}}^{{{{{\bf{x}}}}}_{1}}\otimes \ldots \otimes {M}_{{a}_{n}}^{{{{{\bf{a}}}}}_{n}}\right)\rho \right],$$
(4)

that is, the measurement settings of each party may now depend on subsets of \(\left\{{x}_{i}\right\}\) and might have an overlap for different parties. From a broad perspective, we are imposing a given causal structure to the experiment, one in which parts of the input of a given party can also be known by other distant parties. Similarly to the usual Bell’s theorem, we will be interested in whether: (i) there are quantum correlations, Eq. (4), that do not have a classical description as in Eq. (3); and (ii) this nonclassicality can be harnessed in the processing of information, in particular in CCPs.

The answer to the first question will inherently depend on the specific causal structure under analysis but positive examples are known40,41,42,43,44,46,47,48 and will be explored in more detail below. Preceding this, a general answer to the second question is the central theoretical result of this paper.

Communication complexity and Bell inequalities

Without loss of generality, in a usual CCP involving n participants16, each party i receives two bits—xi and yi—and can broadcast to all other parties just a one-bit message. As an example of such a CCP, one can consider that the parties want to schedule an appointment, their local inputs represent their availability in different time slots and thus the function they want to compute relates to finding a time slot when all of them are available. However, one can think of more general scenarios where the schedule (or part of it) from one of the participants is known to the others. Having this in mind in our generalised CCP each party i has access to the random variables \({{{{\bf{x}}}}}_{i}=\left\{{x}_{i,j}| j=1,\ldots ,{l}_{i}\right\}\subset \left\{{x}_{i}| i=1,\ldots ,n\right\}\) and yi, where xi, yi ∈ { ± 1} (see Fig. 1a). The values of the variables xi are drawn from a joint probability distribution q(x1, …, xn), while the yi’s are independently drawn from a uniform distribution. Furthermore, the parties are also allowed to share correlated systems and use their measurement outcomes ai ∈ { ± 1} in the execution of the protocol. Here, we follow closely the conceptual framework of the seminal results in ref. 16, which provides a general connection between LHV models and CCPs. As in ref. 16, the goal is for each party to evaluate a binary function f(x1, . . . , xn, y1, . . . , yn) = f(x, y) = f given by

$$f({{{\bf{x}}}},{{{\bf{y}}}})={y}_{1}\ldots {y}_{n}S[Q({x}_{1},\ldots ,{x}_{n})],$$
(5)

where Q = Q(x1, …, xn) is a function of all inputs, and \(S[Q]=\frac{Q}{| Q| }\) is the sign function, with the restriction that each party i can only broadcast a single bit \({m}_{i}={m}_{i}({x}_{i,1},\ldots ,{x}_{i,{l}_{i}},{y}_{i},{a}_{i})\) to every other party j. If party i guesses Gi(x, y) for the function f(x, y), its probability of success is given by

$${{{{\mathcal{P}}}}}_{i}=\frac{1}{{2}^{n}}\mathop{\sum}\limits_{\begin{array}{c}{x}_{1},\ldots ,{x}_{n}\\ {y}_{1},\ldots ,{y}_{n}\end{array}}q({{{\bf{x}}}})P({G}_{i}({{{\bf{x}}}},{{{\bf{y}}}})=f({{{\bf{x}}}},{{{\bf{y}}}})),$$
(6)

where P(Gi(x, y) = f(x, y)) = 1 if Gi(x, y) = f(x, y) and 0 otherwise.

Consider now a general Bell inequality of the form

$${B}_{n}=\mathop{\sum }\limits_{{x}_{1},\ldots ,{x}_{n}=-1}^{1}Q({x}_{1},\ldots ,{x}_{n}){E}_{{x}_{1},\ldots ,{x}_{n}}\le {B}_{n}^{C},$$
(7)

where Q(x1, …, xn) is the coefficient of \({E}_{{x}_{1},...,\,{x}_{n}}\), which stands for the full correlation function

$${E}_{{x}_{1},\ldots ,\,{x}_{n}}={P}_{{x}_{1},\ldots,\,{x}_{n}}\left(\mathop{\prod }\limits_{i=1}^{n}{a}_{i}=1\right)-{P}_{{x}_{1},\ldots ,\,{x}_{n}}\left(\mathop{\prod }\limits_{i=1}^{n}{a}_{i}=-1\right),$$
(8)

and \({B}_{n}^{C}\) is the classical bound associated with a given causal structure described by the NLHV decomposition in Eq. (3). Then, our main theoretical result is to show that a violation of such a Bell inequality is necessary and sufficient to lead to a quantum advantage in a CCP related to the computation of the function in Eq. (5). This is stated in the following theorem, the proof of which is elaborated in the Methods and Supplementary Methods.

Theorem 1

Given a Bell inequality of the form (7), the optimal classical probability of success \({{{{\mathcal{P}}}}}_{i}^{C}\) of party i computing the function

$$f({{{\bf{x}}}},{{{\bf{y}}}})={y}_{1}\ldots {y}_{n}S[Q({x}_{1},\ldots ,{x}_{n})],$$
(9)

is limited by

$${{{{\mathcal{P}}}}}_{i}^{C}\le \frac{1}{2}+\frac{{B}_{n}^{C}}{2{{\Gamma }}},\ \ \ \forall i;$$
(10)

with \({{\Gamma }}=\mathop{\sum }\nolimits_{{x}_{1},\ldots ,{x}_{n}=-1}^{1}| Q({x}_{1},\ldots ,{x}_{n})|\). Moreover, using the correlations shared between the parties there is a protocol achieving

$${{{{\mathcal{P}}}}}_{i}=\frac{1}{2}+\frac{{B}_{n}}{2{{\Gamma }}},\ \ \ \forall i;$$
(11)

thus showing that a violation of the Bell inequality (7) is both necessary and sufficient for an advantage in the CCP.

This result shows that every full correlator Bell inequality that displays a quantum violation is associated with a CCP with quantum advantage, even in scenarios where the parties can communicate. As detailed in the Methods and Supplementary Method, to achieve the probability of success (11) we provide a protocol, which we prove to be optimal for classical and quantum systems, in which the message mi communicated from one party to all others has the form mi = yiai, that is, the product of its input yi with the measurement outcome ai. Interestingly, as we show next, there are inequalities that do not show quantum violations in standard Bell scenarios, that, however, is violated if such communication is allowed. In order to illustrate the theorem, we present a Bell inequality along with its corresponding CCP, associated with a tripartite Bell scenario with communication-related to the guess-your-neighbour’s-input (GYNI) scenario49. We then proceed to implement this scenario experimentally. As a second illustration of the Theorem, we introduce the ‘Svetlichny’ scenario40 in the Supplementary Methods.

Guess-your-neighbour’s-input scenario

The causal structure for this scenario (see Fig. 1b), akin to the guess-your-neighbour’s-input game49, was introduced in ref. 41, leading to a new type of multipartite non-locality. Classical correlations (3) are bounded by the inequality41

$${B}_{G}=\mathop{\sum }\limits_{{x}_{1},{x}_{2},{x}_{3}=-1}^{1}{Q}_{G}({x}_{1},{x}_{2},{x}_{3}){E}_{{x}_{1}{x}_{2}{x}_{3}}\le {B}_{G}^{C},$$
(12)

with \({B}_{G}^{C}=6\) and \({Q}_{G}({x}_{1},{x}_{2},{x}_{3})=1-\frac{(1-{x}_{1})(1-{x}_{2})(1-{x}_{3})}{4}\). Following the causal structure in Fig. 1b and general prescription of the CCP, party 1 broadcasts a bit m1(x1, x3, y1, a1), party 2, m2(x1, x2, y2, a2), and party 3, m3(x2, x3, y3, a3).

According to the Theorem, the classical probability of success in computing the associated function is \({P}_{Suc}^{C}\le 7/8=0.875\). As shown in ref. 41, a quantum violation of this inequality is not possible if party i only has access to the input xi. If, however, the three parties share a GHZ state of the form \(\left|\,{{\mbox{GHZ}}}\,\right\rangle =(\left|000\right\rangle +\left|111\right\rangle )/\sqrt{2}\), and are able to choose their measurements according to the GYNI causal structure depicted in Fig. 1b, the inequality (12) can be violated up to BG ≈ 7.39. This results in a higher probability of success, PSuc ≈ 0.962, a quantum advantage in this CCP. As shown in the Supplementary Methods, resorting to a generalisation of the NPA hierarchy50 (a secondary but still relevant technical contribution of our results), this is the optimal quantum value.

Experimental implementation

We experimentally investigate the GYNI scenario by producing a tripartite GHZ state encoded in the polarisation of telecom-wavelength photons (see Fig. 2). We measure the correlation terms defined by inequality (12) to demonstrate that the experimentally observed state can violate the inequality, which is both necessary and sufficient for a quantum advantage in the CCP. For each correlation term, we implement the optimal measurement settings in Alice, Bob and Charlie’s polarisation analysers and record the photon statistics for all 23 outcomes to evaluate the expectation values as shown in Fig. 3. See Methods for details on the optimal measurement settings. From our measurements we obtain a correlation value of BG = 7.023 ± 0.036, representing a violation of the inequality (12) by 28 standard deviations with respect to the classical bound of \({B}_{G}^{C}=6\). Using Eq. (11), the observed violation translates to a probability of correctly computing the CCP in this GYNI scenario of PSuc = 0.9389 ± 0.0049.

Fig. 2: Experimental layout.
figure 2

a Conceptual layout of the three-user GYNI protocol. The tripartite GHZ state is distributed among the three users who locally measure their photon based on input bits {xi, xj}. To compute the target function, each user broadcasts a one-bit message using their measured outcome and a local bit, yi. b We create the GHZ state using two polarisation-entangled photon-pair sources and a linear-optics fusion gate. Each source is implemented with an aperiodically poled KTP crystal embedded in a Sagnac loop that is optically pumped bidirectionally using a picosecond mode-locked laser, see Methods for details. Down-converted photons are separated from the pump laser using dichroic mirrors (DM) and interference filters (IF) then fibre coupled into single mode fibres. One photon from each source non-classically interferes on a polarising beamsplitter (PBS) creating the three-photon GHZ state conditioned on measuring the forth photon as a Trigger. Each user performs projective measurements on their qubit using a quarter-wave plate (QWP), half-wave plate (HWP), and PBS. Single photons are detected using superconducting nanowire single-photon detectors (SNSPD) and time-tagged for coincidence measurements within a 1 ns window.

Full size image
Fig. 3: Experimental results.
figure 3

Experimentally measured correlation terms belonging to the non-local Bell inequality in the GYNI scenario, \({E}_{{x}_{1}{x}_{2}{x}_{3}}\) where {x1, x2, x3} = ± 1. Orange bars represent the theoretical values assuming the optimal measurement settings while yellow bars show the experimentally observed values. We evaluate the inequality and report a correlation value of BG = 7.023 ± 0.036. Errors as estimated by Monte Carlo sampling, using N = 200 runs and assuming Poissonian statistics, are omitted as they are to small too be visible.

Full size image

We implement the tripartite GYNI protocol in a faithful round-by-round execution to verify the general connection between CCPs and NLHV models established in this work. In each round of the protocol, we distribute a GHZ state to three users, and use the NIST randomness beacon51 to generate randomised input data (x1, x2, x3, y1, y2, y3). Each user receives their input bits {xi, xj, yi}, updates their polarisation analysers with their respective measurement settings \({M}^{({x}_{i},{x}_{j})}\). Since the generation of the GHZ state is non-deterministic, we post-select on the first four-fold detection coincidence event for each round. This heralds successful distribution of the resource state and enables us to record the outcome ai of each player—see Methods for details. Finally, every user announces their one-bit message, mi = yi ⋅ ai, evaluates a guess for the round and compares the joint result with the value of the target function, \(f({{{\bf{x}}}},{{{\bf{y}}}})={y}_{1}{y}_{2}{y}_{3}\left(1-\frac{(1-{x}_{1})(1-{x}_{2})(1-{x}_{3})}{4}\right)\), obtaining a pass/fail for the round.

We perform the protocol for a total of 10,100 rounds and observe successful outcomes for 9403 rounds, corresponding to a probability of success of PSuc = 0.9310. The experimentally measured probability of success is slightly smaller than the estimated value obtained by the measured violation of the inequality. This is likely due to drifts in the setup when performing the protocol over a large number of rounds. For the round-by-round execution we collected 2 days worth of statistics, whilst the measurements pertaining to the inequality violation were recorded in less than an hour. One of the main limitations in our measurement rate is the use of motorised stages for rotating the waveplates. As a result the majority of the data acquisition time is currently due to the time needed to update the measurement settings. Our implementation of the protocol obtained a probability of success beyond what is achievable when parties only have access to classical shared resources, i.e. \({P}_{Suc}^{C}\le 0.875\), unambiguously demonstrating the quantum advantage as it was defined in ref. 16.

Discussion

Generalisations of Bell’s theorem to more complex causal networks and in particular those involving communication between the parties are attracting growing attention. On one side they unveil new48,52 and sometimes stronger40,42 kinds of quantum non-locality. On the other hand, the practical use of this nonclassicality in the processing of information has so far been limited to specific cases, such as device-independent entanglement quantification53, closing attacks in multipartite cryptographic protocols54, and game theory55. Here we proposed a general approach by showing that non-local hidden-variable models introduce a new class of communication complexity problems that contain previous versions16 as special cases. The Bell inequalities bounding classical correlations in such models can be mapped to the functions to be computed in the associated communication problem. Further, the violations of these inequalities provide a necessary and sufficient condition for a quantum advantage over the best possible classical protocol. Our results are theoretically proven in full generality and validated for a specific scenario in an experiment based on a high-fidelity tripartite GHZ state, demonstrating a quantum violation of the Bell inequality (12), akin to the guess-your-neighbour-input scenario41,49.

Our implementation of the protocol in its entirety—using randomised measurement settings on a round-by-round basis—demonstrates the advantage in a CCP task when using non-locality as a quantum resource. Future quantum networks will enable the implementation of increasingly sophisticated CCP related tasks over distances, e.g. linking a cluster of network nodes. Here the entanglement resources are produced in the telecom regime, enabling low-loss transmission in optical fibres connecting network nodes. Additionally, the investigation of different CCP tasks associated with “network-friendly” multipartite entangled states such as graph states would further provide utility in more generalised scenarios.

In spite of the generality of our results a few relevant questions still require further in-depth analysis. As we show here, the violation of a full correlator Bell inequality is a necessary and sufficient condition for a quantum advantage, even in NLHV models related to Bell scenarios with communication. But for which NLHV models are such violations possible? Initial attempts41 have provided partial answers in the case where the quantum correlations are nonsignalling, that is, the quantum measurements do not make use of the inputs of other parties. The answer to the more general case remains open. Further, we have focused here on full correlator Bell inequalities and it is known that, in the more general case, the violation of Bell inequalities does not necessarily lead to quantum improvements in standard CCPs56. In view of that, analysing under which conditions quantum advantages in generalised CCPs can also be connected with Bell inequalities involving marginals and more measurement outcomes is an interesting question for future research.

Methods

Entangled photon source

We employ two parametric down-conversion (PDC) sources to create the polarisation-encoded GHZ state. Each source consists of a 30 mm aperiodically poled KTP (aKTP) crystal designed to produce spectrally pure photon pairs at 1550 nm in the Type-II configuration57. This is achieved through an optimised domain engineering technique, where aperiodic poling achieves a non-linear Phase Matching Function (PMF) that approximates a Gaussian, resulting in near-optimal bi-photon spectral purity58. This approach allows our photon sources to operate without lossy narrowband filters—the interference filters have nominal full-width-half-maximum bandwith of 8.8 nm—allowing higher heralding and collection efficiencies while maintaining high visibility non-classical interference as required for producing multi-photon states efficiently. Our crystals are designed for matching a transform-limited Sech-shaped pump spectrum with a pulse duration of 1.3 ps. The domain engineered crystal is embedded in a Sagnac loop, which generates polarisation-entanglement between the photon pair. A lens with a 50 cm nominal focal length is used to focus the pump field into each crystal, leading to a source brightness of ~2400 pairs mW−1 s−1 and heralding efficiencies of ~60%. With 50 mW of pump power we witness interference visibility of 94.2 ± 1.5% between photons generated from independent sources without any filtering. In addition, the picosecond laser is spatially multiplexed attaining 320 MHz repetition rate. This is implemented using two free-space delay loops using 50:50 beamsplitters (BS) and mirrors. This allows the peak power per pulse to be reduced to lower the probability of unwanted multi-photon events at the same pump power.

One photon from each source interferes non-classically on a PBS such that conditional on measuring one photon in each output detector set; Alice (A), Bob (B), Charlie (C), and Trigger (T), the quantum state of the overall four-photon system is,

$${\left|{{\Psi }}\right\rangle }_{A,B,C,T}=\frac{\left|HVVH\right\rangle +{e}^{i\vartheta }\left|VHHV\right\rangle }{\sqrt{2}},$$
(13)

where \(\left|H\right\rangle \equiv \left|0\right\rangle\) and \(\left|V\right\rangle \equiv \left|1\right\rangle\) in the logical basis encoding59. We note the phase shift ϑ is intrinsic to the optical components in our setup and can be compensated by local operations on any one of the entangled qubits. Our setup uses standard polarisation measurement analysers—which consists of a QWP, HWP, and PBS where the output modes are fibre coupled to SNSPDs—to perform arbitrary projective measurements on each qubit.

To obtain the three-qubit GHZ state for this experiment we project the Trigger photon onto the state, \(\left|\vartheta \right\rangle \doteq (\left|H\right\rangle +{e}^{-i\vartheta }\left|V\right\rangle )/\sqrt{2}\), which ensures entanglement among the remaining photons and simultaneously implements the phase correction. Detecting a photon after the PBS projects the remaining three photons onto the following state,

$${\left|{{\Psi }}\right\rangle }_{A,B,C}=\frac{\left|HHH\right\rangle +\left|VVV\right\rangle }{\sqrt{2}},$$
(14)

up to a local bit-flip which is implemented in the respective user’s measurement stage with the use of the polarisation fibre controller. We perform quantum state tomography and reconstruct the density matrix to characterise the general properties of the GHZ state. We observe the fidelity to the ideal state to be \({{{\mathcal{F}}}}=0.9508\pm 0.0031\) and a state purity of \({{{\mathcal{P}}}}=0.9255\pm 0.0058\). Uncertainties are reported for one standard deviation and obtained by Monte Carlo sampling using 200 runs, assuming Poissonian statistics.

Our linear-optics setup produces the multipartite entangled state non-deterministically, with a success probability of PSuc = 1/2. Nonetheless, provided one photon is detected at the measurement stages of Alice, Bob, Charlie, and the Trigger, we obtain the state in (13). Thus, in the round-by-round implementation we post-select on four-fold coincidence events to record an outcome for the round. We implement this using the fast coincidence logic to record only the first valid four-fold event after the polarisation analysers are set. Then, as per the protocol, the next round proceeds by updating the measurement stage settings.

Measurement settings

In our experiment the measurement setting in each round for each user is determined by two input bits {xi, xj}, distributed as per the GYNI scenario. As such, each user has four possible projective measurement settings, \({M}^{({x}_{i},{x}_{j})}\), as shown in Table 1.

Table 1 Optimal projective measurement settings for each player in three-user GYNI CCP scenario.
Full size table

The correlators, \({E}_{{x}_{1}{x}_{2}{x}_{3}}=\langle {A}_{{x}_{1}{x}_{3}}{B}_{{x}_{1}{x}_{2}}{C}_{{x}_{2}{x}_{3}}\rangle\), measured in our experiment are expressed in conventional notation in which the subscript indices, denote the local variable xi assigned to each user prior to distribution to their neighbour. As such we make use of Table 2 to determine the measurements that is performed by each user.

Table 2 Measurement settings for measurements of each correlator term in the three-user GYNI inequality.
Full size table

Our measurement apparatus allows us to perform arbitrary projective measurements by using the HWP and QWP to rotate the measurement basis. Placement of detectors behind both outputs of the PBS enables us to obtain outcomes spanning the full basis set.

Calculating correlations

In the experiment each user’s measurement stage is accompanied by two detectors to measure both outputs of the PBS. This allows us to directly sample the joint outcomes for a given basis defined by the measurement settings of each user. For example to evaluate the correlator E+++ we set the measurement waveplates to implement \({M}_{1}^{(+,+)},{M}_{2}^{(+,+)},\) and \({M}_{3}^{(+,+)}\), for Alice, Bob, and Charlie, respectively. We record the three-fold coincidence events according to the outcome detector patterns and evaluate,

$$\begin{array}{ll}{E}_{+++}&=\langle {M}_{1}^{(+,+)}{M}_{2}^{(+,+)}{M}_{3}^{(+,+)}\rangle \\& =\frac{{C}_{+++}-{C}_{++-}-{C}_{+-+}+{C}_{+--}-{C}_{-++}+{C}_{-+-}+{C}_{--+}-{C}_{---}}{{C}_{+++}+{C}_{++-}+{C}_{+-+}+{C}_{+--}+{C}_{-++}+{C}_{-+-}+{C}_{--+}+{C}_{---}},\end{array}$$
(15)

where Cijk are the number of coincidences, and indices {i, j, k} ∈ { + , − } denote the outcome for Alice, Bob, and Charlie, respectively. Finally, we note that the other correlators are evaluated in the same way following the measurement settings outlined previously.

Sketch of the Theorem’s proof

The full proof of (10) is rather lengthy and presented in the Supplementary Methods. Here we focus on (11). First, notice that full correlators can be written as

$$E({x}_{1},\ldots ,\,{x}_{n})=S[Q]\left[2{P}_{{x}_{1},\ldots ,\,{x}_{n}}\left(\mathop{\prod }\limits_{i=1}^{n}{a}_{i}=S[Q]\right)-1\right].$$
(16)

Inequality (7) can then be rewritten as

$$\mathop{\sum }\limits_{{x}_{1},\ldots ,\,{x}_{n}=-1}^{1}{q}^{* }({x}_{1},\ldots ,\,{x}_{n})\times {P}_{{x}_{1},\ldots ,\,{x}_{n}}\left(\mathop{\prod }\limits_{i=1}^{n}{a}_{i}=S[Q({x}_{1},\ldots ,\,{x}_{n})]\right)\le \frac{1}{2}+\frac{{B}_{n}}{2{{\Gamma }}}.$$
(17)

in which \({q}^{* }({x}_{1},\ldots ,\,{x}_{n})=\frac{| Q({x}_{1},\ldots ,\,{x}_{n})| }{{{\Gamma }}}\). In what follows we will set q(x1, …, xn) = q*(x1, …, xn), thus connecting the probability distribution q(x1, . . . , xn) governing the variables x1, . . . , xn with the coefficients Q(x1, . . . , xn) defining the Bell inequality (7).

The protocol proceeds as follows. Each party i chooses a measurement to perform from the set \(\left\{{x}_{i,j}| j=1,\ldots ,{l}_{i}\right\}\), obtaining outcome ai. Each party, then, broadcasts to all other parties the message mi = aiyi ∈ { ± 1}. In the final step all parties make the same guess about the function f to be computed, given by

$${G}_{i}=\mathop{\prod }\limits_{j=1}^{n}{m}_{j}={y}_{1}\ldots {y}_{n}{a}_{1}\ldots {a}_{n},\ \ \ \forall i.$$
(18)

A comparison between the guess of each party (18) and the function (5) to be computed shows that, given a sequence of inputs x1…xn, y1…yn, the success probability is independent of y1, …, yn and given by \({P}_{{x}_{1},\ldots ,\,{x}_{n}}(\mathop{\prod }\nolimits_{i = 1}^{n}{a}_{i}=S[Q({x}_{1},\ldots ,\,{x}_{n})])\). Hence, since the variables x1, …, xn are sorted according to a distribution q(x1, …, xn) and variables y1, ..., yn are uniformly sorted, the final probability of success is

$${P}_{Suc}=\mathop{\sum }\limits_{{x}_{1},\ldots ,{x}_{n}=-1}^{1}q({x}_{1},\ldots ,{x}_{n})\times {P}_{{x}_{1},\ldots ,{x}_{n}}\left(\mathop{\prod }\limits_{i=1}^{n}{a}_{i}=S[Q({x}_{1},...,{x}_{n})]\right).$$

A comparison with (17) leads directly to (11).