Introduction

Tailoring defects is a primary pathway to structure-property engineering in materials1,2,3,4,5,6. In particular, in polycrystalline materials the grain boundaries (GB) constitute a network of disordered regions percolating through the bulk and dominating many properties. Understanding how solute atoms partition to GBs is critical to alloy design due to the ability to control material structure and properties7,8,9,10,11,12,13 via both thermodynamic14,15,16,17 and kinetic18,19,20,21 stabilization of the GBs.

Equilibrium GB segregation states are often modeled with the classical McLean isotherm22:

$$\frac{{\bar{X}}^{{\rm{GB}}}}{1-{\bar{X}}^{{\rm{GB}}}}=\frac{{X}^{{\rm{C}}}}{1-{X}^{{\rm{C}}}}\exp \left[-\frac{\Delta {\bar{F}}_{{\rm{eff}}}^{{\rm{seg}}}}{{k}_{{\rm{B}}}T}\right]$$
(1)

where \({X}^{{\rm{C}}}\) is the solute concentration in the crystals that is in equilibrium with the GB at an average solute concentration \({\bar{X}}^{{\rm{GB}}}\). The free energy of segregation, \(\Delta {\bar{F}}_{{\rm{eff}}}^{{\rm{seg}}}\) is a combination of the segregation energy and excess entropy of segregation (or the vibrational, magnetic, electronic and other degrees of freedom changes upon solute segregation), i.e., \(\Delta {\bar{F}}_{{\rm{eff}}}^{{\rm{seg}}}=\Delta {\bar{E}}_{{\rm{eff}}}^{{\rm{seg}}}\)-T\(\Delta {\bar{S}}_{{\rm{eff}}}^{{\rm{seg}}}\). These quantities represent the changes of energy and entropy when the solute segregates from a bulk site to a grain boundary site, and a negative segregation free energy indicates a preference for solute enrichment. The enthalpic term or P∆V is assumed to be small for solids and neglected in this work23.

While the simplicity of the McLean isotherm has enabled its usage in a wide range of situations24,25,26,27,28, it neglects the atomistic nature of GBs, which involves a broad range of local atomic environments29,30,31,32,33,34. Collapsing the true spectral nature of GB sites to single-value effective quantities in Eq. (1) can cause artificial concentration31,35, grain size36 and temperature dependences28; Eq. (1) turns out to be merely a fitting function, and is only valid over the narrow range of concentrations and temperatures for which it is fitted. A better approach to GB segregation is to acknowledge the fundamental physics of GB site competition that defines it, and instead treat grain boundary site equilibrium at site type ‘i’ with a local per-site segregation energy (\(\Delta {E}_{i}^{{\rm{seg}}}\)), entropy (\(\Delta {S}_{i}^{{\rm{seg}}}\)), or free energy (\(\Delta {F}_{i}^{{\rm{seg}}}\))29:

$$\frac{{X}_{i}^{{\rm{GB}}}}{1-{X}_{i}^{{\rm{GB}}}}=\frac{{X}^{{\rm{C}}}}{1-{X}^{{\rm{C}}}}\exp \left[-\frac{\Delta {E}_{i}^{{\rm{seg}}}-T\Delta {S}_{i}^{{\rm{seg}}}}{{k}_{{\rm{B}}}T}\right]=\frac{{X}^{{\rm{C}}}}{1-{X}^{{\rm{C}}}}\exp \left[-\frac{\Delta {F}_{i}^{{\rm{seg}}}}{{k}_{{\rm{B}}}T}\right]$$
(2)

Such calculations for site-wise quantities in polycrystals were not computationally feasible even in the recent past, but due to computational advances, there has been progress in this vein such as the tabulation of \(\Delta {E}_{i}^{{\rm{seg}}}\) spectra for a great many alloys based on both interatomic potentials37 and first principles calculations38. Critical to that effort is the use of data science or machine learning methods, which help traverse the many millions of GB sites in a polycrystal.

The recent availability of GB segregation energy spectra now allows alloy designers to evaluate Eq. (2) for a wide range of dilute binary alloys. However, the site-wise excess entropy, \(\Delta {S}_{i}^{{\rm{seg}}}\), has been mostly neglected and rarely discussed in the past literature due to the extensive computation needed to evaluate it, especially for large polycrystalline structures. Entropic effects cannot generally be neglected at finite temperatures and are considered critical for future alloy design efforts25,26,39. The existing literature for this site-wise quantity consists of data for only a few alloy systems and from small coincidence site lattice (CSL) boundaries which cannot fully represent complex grain boundary networks40,41,42,43,44,45,46,47,48,49,50.

With recent advances in computation of vibrational entropy using multiscale approaches to the harmonic approximation45,51,52,53, and in the use of data science sampling methods34,37,38 via local atomic environment descriptors54,55, the tools to address GB segregation entropy more broadly are now all in place. We have therefore developed a rapid assessment framework for the polycrystalline \(\Delta {E}_{i}^{{\rm{seg}}}\)-\(\Delta {S}_{i}^{{\rm{seg}}}\) spectra to quantify the extent of vibrational effects using the isotherm of Eq. (2). This is the goal of the present work: to exhaustively explore segregation entropy for common FCC transition metals (Ag-, Al-, Au-, Cu-, Ni-, Pd- and Pt-based alloys) that have published interatomic potentials56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102. In addition to providing considerably broader views on the role of entropy in GB segregation, such methods also produce a large quantitative atlas of segregation energy and entropy, for the interpretation of experiments and new efforts in alloy design.

Results and discussion

Accelerated model and validation

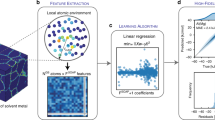
We first summarize our process in Fig. 1, which begins with site sampling (Fig. 1a–d). Our sampling process is inspired by prior work in which a small number of sites is selected to represent the full distribution of GB sites in a polycrystal37,38. Here we begin with a pure solvent 20 × 20 × 20-nm polycrystalline structure from ref. 37, then further anneal it using the corresponding interatomic potential, resulting in the structure in Fig. 1a. The GB sites are characterized via local atomic environment (LAE) descriptors, with each LAE vector containing 1015 smooth overlap of atomic positions (SOAP)54,55 elements (Fig. 1b shows only one example SOAP component). Next, we apply principal component analysis (PCA) for SOAP vector dimensionality reduction as shown in Fig. 1c. The explained-variance ratios indicate that the 1015 features can be easily collapsed to the first ten PCA components while capturing all the essential features of the local atomic environments.

Fig. 1: Entropy estimation workflow.
figure 1

a The polycrystals used in this work were obtained from the database in ref. 37 and further annealed and relaxed. b SOAP feature vectors are constructed for grain boundary site samplings via principal component analysis140,141,142 c and sampled via K-means clustering143,144 d. The sites near K-means centers are used to calculate substitutional segregation energy e and vibrational entropy f for spectral fitting in g and h, exemplified here for Ni(Zr)102.

Full size image

To sample the site distribution in an efficient and representative manner, we apply K-means clustering to select 500 GB sites for per-site segregation energy (relaxation in Fig. 1e) and entropy calculations (Fig. 1f). We fit segregation energy spectra directly by minimizing negative log-likelihood functions (without, e.g., per-site linear regression with local atomic environments as used elsewhere37,38). We show an example of such a segregation energy spectrum in Fig. 1g fitted with a skew-normal distribution with skewness (α), position (µ), and size (σ) parameters31,103,104:

$${P}_{i}(\Delta {E}_{i}^{{\rm{seg}}})=\frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{{\left(\Delta {E}_{i}^{{\rm{seg}}}-\mu \right)}^{2}}{2{\sigma }^{2}}\right]{\rm{erfc}}\left[\frac{\alpha \left(\Delta {E}_{i}^{{\rm{seg}}}-\mu \right)}{\sqrt{2}\sigma }\right]$$
(3)

For the site entropy distribution, we employ additional methods. For the 500 sites selected above, we perform the excess entropy calculation from ref. 51 based on a full harmonic calculation around the solute site, coupled to a local harmonic approximation45,53,105 at greater distances, an approach that balances computational efficiency with accuracy (details are listed in Method and Supplementary Material 1). We then calculate sample means (\({\boldsymbol{\mu }}\)) and covariance matrices (\({\boldsymbol{\Sigma }}\)) amongst the energies and entropies of the sampled sites, casting the full distribution as a bivariate Gaussian:

$${P}_{i}({\boldsymbol{x}}=\left[\Delta {E}_{i}^{{\rm{seg}}},\Delta {S}_{i}^{{\rm{seg}}}\right])=\frac{1}{2\pi \sqrt{\left|{\boldsymbol{\Sigma }}\right|}}\exp \left[-\frac{1}{2}{\left({\boldsymbol{x}}-{\boldsymbol{\mu }}\right)}^{T}{{\boldsymbol{\Sigma }}}^{{\boldsymbol{-}}{\bf{1}}}\left({\boldsymbol{x}}-{\boldsymbol{\mu }}\right)\right]$$
(4)

In Fig. 1h, we plot an example kernel density estimate for the segregation energy and entropy from 500 GB sites for Ni(Zr)102.

An important feature of the distribution in Fig. 1h is that there is a correlation between site energy and entropy; this is known as the ‘compensation effect’ in literature on GB segregation106. As we have demonstrated in ref. 51, this correlation permits substantial simplification of the mathematics of Eq. (2), because it allows information about site energy (which is easily computed) to be projected into information about site entropy (which is not). Such mapping can be conducted accurately with a linear energy-entropy compensation40,51:

$$\Delta {S}_{i}^{{\rm{seg}}}=\chi \Delta {E}_{i}^{{\rm{seg}}}+{\Delta S}_{0}^{{\rm{solute}},{\rm{GB}}}$$
(5)

where \(\chi\) and \({\Delta S}_{0}^{{\rm{solute}},{\rm{GB}}}\) are system-specific parameters that characterize the correlation between site energy and entropy, and which we can aspire to tabulate for many materials. Typically, in correlated systems such as this, sample correlations stabilize close to the true population value when conducting random sampling at less than N = 500107; we use N = 500 and the application of K-means clustering should converge more quickly than random sampling, so we expect high accuracy for the estimation of \(\chi\) and \({\Delta S}_{0}^{{\rm{solute}},{\rm{GB}}}\). To validate this expectation we report root mean squared errors (RMSE) of this approach with respect to a randomly sampled 500-site validation set in Supplementary Material 3.

Having established the framework in Fig. 1, we turn our attention to validating the accelerated model against full spectra computed exhaustively on full polycrystals. We show example spectra for a 13 × 13 × 13-nm Ni(Pt)58 system in Fig. 2a. The full lines in blue represent the 500-sample distribution derived from the accelerated sampling model, plotted atop the dashed lines corresponding to the full spectrum of about 50,000 GB sites; the agreement is very good. The projected spectra, on both the energy and entropy axes, also show good agreement between the two. In a practical sense, spectra such as these provide all the information needed for a rigorous prediction of grain boundary segregation for dilute alloys, which can be encoded in the form of the distribution functions. In the large grain size limit (\({X}^{{\rm{C}}}\,\approx \, {X}^{{\rm{tot}}}\), the total system solute content), grain boundary concentration can be evaluated by integrating the site density function of Eq. (4) weighted by local concentration (\({X}_{i}^{{\rm{GB}}}\)) of Eq. (2):

$${\bar{X}}^{{\rm{GB}}}=\int \int d\triangle {E}_{i}^{{\rm{seg}}}\,d\triangle {S}_{i}^{{\rm{seg}}}{P}_{i}{X}_{i}^{{\rm{GB}}}$$
(6)
Fig. 2: Validating the accelerated model.
figure 2

Segregation energy-entropy spectrum of Ni(Pt)58 obtained from the accelerated model and a full 13 × 13 × 13-nm system are plotted atop one another for comparison in a. The spectra can be well modeled with a bivariate Gaussian distribution and used to calculate the GB concentrations shown in b in the large grain size limit with Xtot = 1 at.%.

Full size image

In Fig. 2b, we show outputs of such calculations estimated from the spectra in Fig. 2a for 1 at.% solute loading, and demonstrate the similarity between the accelerated and full spectrum. We have performed this kind of exhaustive validation for several Ni-based systems (Pd, Ag, Au, and Cu), and obtained reasonable accuracy of grain boundary concentrations as shown in Supplementary Material 1 (errors are below 5% relative to the full spectra).

With this validation we proceed with confidence in the methods, and turn our attention to the assessment of the spectra for dilute FCC binary alloys for which there are published interatomic potentials56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102. More details of the method are described in the method section and Supplementary Material 1. The segregation energy spectra are listed in Supplementary Material 2, and the energy-entropy spectra are listed in Supplementary Material 3. The dataset shown in this work is published in the repository108.

Segregation energy and entropy spectra

A major outcome of the workflow in Fig. 1 is that we can now very quickly estimate full, polycrystalline grain boundary segregation spectra, inclusive of both energy and entropy terms, with just a small number of computations on true polycrystals, amplified by data science principles. As an example, we show the full spectra for several Cu-based systems in Fig. 3. This includes systems with a wide range of behaviors, with different distribution centers, different widths and different degrees of energy-entropy correlation (ρ). The spectra for all of the systems explored in this work are presented in Supplementary Material 2, 3, along with the bivariate normal fitting parameters that allow reconstruction of the full distribution on the basis of Eq. (4). This collection of 155 binary GB segregation spectra is one of the most exhaustive of its kind, and should permit detailed comparison with experimental data, new efforts in alloy design, and, as we shall see below, further commentary on the nature of excess entropy in grain boundary segregation problems.

Fig. 3: Energy-entropy grain boundary spectra of Cu-based alloys.
figure 3

Density plots of solute segregation energy and excess vibrational entropy from the accelerated model of Fig. 1 are shown for the systems with the largest correlation (ρ) or energy-entropy ‘compensation effect’ for a given solute. See Supplementary Material 3 for the full data for all systems, and fitting parameters that can be used to reproduce these distributions.

Full size image

One challenge with GB segregation spectra generally is that their accuracy is only as great as that of the interatomic potentials from which they derive. Taking Cu(Ag) as an example binary system, we show \(\Delta {E}_{i}^{{\rm{seg}}}\)-\(\Delta {S}_{i}^{{\rm{seg}}}\) spectra from three different interatomic potentials58,60,61 proposed in the literature in Fig. 4a–c. Their corresponding isotherms at 1 at.% total solute content as a function of temperature are calculated via Eq. (4) and plotted in Fig. 4d–f, both with and without site-wise excess entropies. These isotherms depict how site-wise spectra unfold into the average GB concentrations often measured in experiments, and to what extent vibrational entropic effects play a role in grain boundary segregation (or i.e., the ratio between \({\bar{X}}_{{\rm{w}}/\Delta {S}_{i}^{{\rm{seg}}}}^{{\rm{GB}}}\) and \({\bar{X}}_{{\rm{w}}/{\rm{o}}\Delta {S}_{i}^{{\rm{seg}}}}^{{\rm{GB}}}\)). The spectra along with the isotherm solver in the Supplementary Material can be used to calculate a dilute isotherm of interest. However, the results in Fig. 4 also provide a note of caution about any results based on the use of interatomic potentials, as the three nominally identical alloys in Fig. 4 have rather different predicted GB segregation spectra, and expect different levels of GB solute enrichment as a result. The inclusion of disordered structures in, for instance, metallic glass and grain boundary potentials, and other more accurate methods such as machine learning potentials109,110 may yield more accurate forces required for accurate entropy calculations.

Fig. 4: Cu(Ag) segregation behavior.
figure 4

Spectra for three Cu(Ag) systems58,60,61 based on different published interatomic potentials are shown in a–c with their corresponding spectral segregation isotherm in d–f both with and without excess entropies. The choice of potential has a significant impact on the output of segregation models, especially as regards the site excess entropy and the compensation effect. See Supplementary Material 3 for the full spectral information.

Full size image

The Importance of excess entropy on segregation

Although it is common to neglect excess entropy in GB segregation analysis, this is generally only appropriate at the lowest temperatures. The present survey of many alloy systems highlights the fact that there are significant entropic contributions due to the spectrality of GB site free energies. This is apparent in the Cu(Ag) system shown in Fig. 4 where in Fig. 4f the GB concentration can be much lower due to the compensation effects which penalize the negative tail of segregation distribution51, and thus affect how solute redistributes with increasing temperature31. To amplify this point, in Fig. 5, we show the isotherm normalized errors, \(\beta\), defined as:

$$\beta ={\rm{|}}{\bar{X}}_{{\rm{w}}/\Delta {S}_{i}^{{seg}}}^{{\rm{GB}}}-{\bar{X}}_{{\rm{w}}/{\rm{o}}\Delta {S}_{i}^{{seg}}}^{{\rm{GB}}}{\rm{|}}/{\bar{X}}_{{\rm{w}}/\Delta {S}_{i}^{{\rm{seg}}}}^{{\rm{GB}}}$$
(7)

where \({\bar{X}}_{{\rm{w}}/\Delta {S}_{i}^{{\rm{seg}}}}^{{\rm{GB}}}\) and \({\bar{X}}_{{\rm{w}}/{\rm{o}}\Delta {S}_{i}^{{\rm{seg}}}}^{{\rm{GB}}}\) indicate equilibrium grain boundary solute concentration predicted with and without excess entropies in Eq. (2). This quantity, \(\beta\), is essentially the relative contribution of excess entropy to the grain boundary concentration. The figure shows that excess entropy is very important to accurate predictions: even at moderate temperatures, most systems differ more than ~15% (medians lie above 0.15 in Fig. 5) from the true segregation state. At higher temperatures where entropy becomes more important, this error becomes much higher, with some cases having more than 100% error at \(\beta\)>1. There are several edge cases in the uppermost quartile such as Cu(Ag) in Fig. 4f for which GB concentrations can be overestimated by more than a factor of two, affecting alloy design criteria such as nanocrystalline stability111,112.

Fig. 5: Excess entropic effects in GB segregation prediction.
figure 5

A boxplot showing the distribution of all 155 alloy systems and the importance of excess site entropy on GB segregation; the y-axis shows the isotherm prediction errors when excess entropies are excluded, normalized by the GB concentration predicted with excess entropies. For this computation the bulk concentration is taken as 1 at.% in the large grain limit (i.e., \({X}^{{\rm{C}}}\,\approx\, {X}^{{\rm{tot}}}\)). The box lower and upper bounds denote the first and third quartiles respectively, with the centerlines representing the medians. The whiskers extend by 1.5 times the interquartile range beyond the box bounds.

Full size image

Grain boundary segregation spectra and enthalpy-entropy relationship

In prior works40,51, per-site GB segregation energy and entropy have been found to be strongly correlated for a few dilute Ni-based systems, as suggested by the compensation effect of Eq. (5). With more access to data for 155 alloy systems, the present work permits evaluation of that linear relationship more broadly. Looking at the example Cu-based systems in Fig. 3, we find that essentially all systems exhibit positive correlations of the kind expected; all of the distribution functions slant at least somewhat to the right. Some of the interatomic potentials show quite high correlations (two-thirds of the example systems in Fig. 3 have ρ > 0.7); the other systems such as Cu(Al)65, Cu(Co)96 and Cu(Cr)80 are exceptions, with correlations as low as 0.24.

Looking at all of the systems represented in Supplementary Material 3, we find that positive energy-entropy correlations are indeed typical; the only exceptions of Ni(Co)91 and Ni(Cu)82 are essentially uncorrelated and by happenstance can be fitted with a slightly negative slope with a low magnitude of order \(\chi\) ~ 10−5 1/K, suggesting negligible excess entropies in both systems. The generally positive correlations are in agreement with the previously reported data for both atomistic simulations40,113,114 and experimentally-realized macroscopic compensation effects26,115.

The energy-entropy compensation effect has been discussed in an experimental context by using the classical McLean isotherm of Eq. (1) and fitting it to experimental measurements of GB segregation for many materials26,115. The result is indeed a linear correlation of the form of Eq. (5), not in a site-wise fashion, but as a broad average trend across the literature; see for example the review in ref. 25. The availability of site-wise data for 155 alloys permits a first comparison of the aggregated trends across all alloys, which we perform in Fig. 6. Here we plot all 155 \(\chi\) and \({\Delta S}_{0}^{{\rm{solute}},{\rm{GB}}}\) (i.e., the compensation slope and intercept, respectively) from all the present computed alloy systems, along with those from the aggregated experimental literature data from ref. 26. There are two slopes representing experimental data, as there are two clusters of results in the literature, which have been suggested to correspond to substitutional (blue ▲) and interstitial (red ×) GB segregation, respectively, in Fe-based alloys. Note that the present computations are strictly based on substitutional segregation, although it is instructive to see both substitutional and interstitial experimental trends in Fig. 6.

Fig. 6: Atomistic vis-à-vis macroscopic compensation effects.
figure 6

Atomistic compensations (\(\chi\) and \({\triangle S}_{0}^{{\rm{solute}},{\rm{GB}}}\)) are plotted along with the macroscopic compensation slopes and intercepts from ref. 25 estimated from multiple substitutional and interstitial solute segregation in α-iron summarized in refs. 162,163. Error bars for 155 atomistic \(\chi\) and \({\triangle S}_{0}^{{\rm{solute}},{\rm{GB}}}\) are calculated from 80% sample bootstrapping.

Full size image

The comparison in Fig. 6 suggests a rather remarkable disagreement: the site-wise compensation slope for a given system is often an order of magnitude lower than the experimental McLean effective energy-entropy compensation (~10−4 1/K for per-site spectra vis-à-vis ~10−3 1/K for bulk substitutional compensation in refs. 25,116). In other words, the experimental data predict substantially higher entropic effects and associated temperature dependences of GB segregation (if applied to any single site). This disagreement is caused by a mathematical artifact in the use of Eq. (1) with experimental data: the collapsing of spectral GB quantities to a single effective McLean segregation energy is known to result in artificial temperature dependences of the fitted segregation quantities28,117. When Eq. (1) is fitted to experimental data, the effective segregation enthalpies and entropies, in turn, produce artificially large compensation effects; the neglect of spectrality misses the true physics of temperature-dependent site selection, and in turn requires artificially high ‘average’ entropies in order to fit the data.

Thus, at the atomic site-level, the true ‘compensation effect’ in GB segregation is remarkably small compared to expectations based on prior experimental literature. By extension, it is also somewhat surprising how important that very small compensation effect is: we still observe many systems with drastic entropic effects in Fig. 5. This occurs because the role of entropy is more complex in a spectral system, affecting which sites are occupied in subtle ways, and preferentially compensating the negative tail of the segregation energy distribution. For demonstration we show how solute atoms occupy Al(Mg)70, Ni(Pt)58 and Ni(P)99 grain boundaries in Fig. 7a–c respectively. These three systems represent three different magnitudes of the compensation slope χ. Al(Mg) in 7a has a small χ and a low melting point, resulting in near-constant free energy distributions with temperature. As a result, the negative tail is populated at all temperatures, and hence there are negligible entropic effects. Conversely, there is very strong compensation of the negative tails in 7b and 7c as temperature rises for the systems with moderate (Ni(Pt)58) to large χ (Ni(P)99). The most energetic segregation sites simply disappear due to the strong effects of site entropy, leading to very strong temperature dependence of segregation, and thus very high apparent segregation entropy of the system on average. This effect of the shifting free energy spectrum lies at the heart of the discrepancy between theory and experiment in Fig. 6: the lack of a spectrum in the experimental data analysis requires the use of a multifold inflation on the role of excess entropy.

Fig. 7: Solute occupancy of segregation spectra.
figure 7

The density of segregation sites is shown (on the basis of full free energies) as a function of temperature (dashed lines), as well as the solute occupancy of those sites (site density times local concentration \({X}_{i}^{\rm{GB}}\)) for 1% solute content in a–c. Spectra are shown for a Al(Mg)70, b Ni(Pt)58 and c Ni(P)99, which have three quite different values of the energy-entropy compensation parameter χ, whose effects penalize the negative tail of the distributions.

Full size image

The results in Figs. 6 and 7 provide a note of caution in the use of averaged quantities for GB segregation problems; neglecting the full spectral nature of the problem can give energy and entropy quantities that are off significantly from the true, physical values they are expected to have. This calls for innovation in the approach to interpreting GB segregation experiments. Such experiments are not trivial, and fitting just a single segregation spectrum requires tremendous experimental data118. With recent advances in nanoscale resolution characterization tools119,120,121,122,123,124 and the spectral framework now better established29,31,51, we hope that both future experimental effort and more accurate free energy estimations will allow us to accurately determine spectra of GB segregation. A similar note of caution should be applied to the theoretical viewpoint as well; although spectral forms like the ones used here have a sound physical motivation, they too can miss important details relevant to the interpretation of experiments. For example, the framework and results presented here are limited to dilute limit segregation within the harmonic approximation. Anharmonicity may become large, and grain boundary structural transformations and complexion energies may play major roles at high temperatures124,125,126,127,128,129,130. Solute-solute interactions are not discussed here, but should in principle also be included via the frameworks described elsewhere35,131,132. Thus, the significant gap between experiment and theory in Fig. 6 needs more concerted attention from both the experimental and theoretical points of view, but clearly should be resolved with a spectral view of segregation.

In summary, dilute polycrystalline grain boundary segregation vibrational entropy spectra have been estimated and tabulated for 16 Ag, 22 Al, 10 Au, 35 Cu, 51 Ni, 11 Pd and 10 Pt-based binary alloys. These entropy spectra are very dependent on the fitting of the corresponding interatomic potential, but in aggregate they speak to a positive correlation between segregation energy and excess entropy as expected physically. These energy-entropy compensation slopes are mostly positive in agreement with the past theoretical literature. However, the spectra here show large discrepancies compared to experimental compensation effects; the experiments unfortunately have strong artificial entropic effects from neglecting the spectrality of segregation energy and entropy, instead forcing a fit with average or effective thermodynamic quantities. This work thus significantly encourages the usage of spectral isotherm models for more accurate descriptions of GB segregation.

Methods

Polycrystalline structures

To quantify segregation energy and vibrational entropy of intergranular site solute segregation, we use the polycrystals published in refs. 38,133. We anneal at 0.4 of the melting temperature for 100 ps then quench to 0 K at 2 K/ps via Nose-Hoover thermostat/barostat at zero pressure followed by relaxation with the FIRE134,135 algorithm, using as termination criterion that the force norm of all atoms lies below 10−6 eV/Å. Both annealing and relaxation are conducted using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) software package136,137,138,139.

Statistical and data science framework

After obtaining the base elemental polycrystals, we follow a statistical procedure in the spirit of refs. 37,38. We first characterize atoms using the smooth overlap of atomic positions (SOAP) descriptor via QUIPPY54,55 with \({r}_{{\rm{SOAP}}}^{{\rm{cut}}}=6\) Å, \({n}^{\max }={l}^{\max }=12\) and Gaussian width \({\sigma }_{{\rm{SOAP}}}=1\) Å, resulting in 1015 SOAP features. Dimensionality reduction is carried out with principal component analysis140,141,142. K-means clustering143,144 is then applied to sample 500 sites for calculating segregation energy and vibrational entropy. Ten bulk sites are chosen randomly from amongst those sites more than 3 nm from any grain boundary site identified by Adaptive Common Neighbor Analysis145,146 implemented in the OVITO software package147.

Vibrational entropy estimation

We employ the multiscale algorithm developed in our previous work of ref. 51. The free energy is calculated via43,45,53:

$$F={U}_{0}+{k}_{{\rm{B}}}T\mathop{\sum }\limits_{i}^{3N}\mathrm{ln}\left[2\sinh \left(\frac{h{v}_{i}}{2{k}_{{\rm{B}}}T}\right)\right]$$
(8)

with \({U}_{0}\) the potential energy from the interatomic potential and the summation conducted over the eigenvalues obtained from dynamical matrices calculated with LAMMPS148,149 and \(T=0.6{T}_{{\rm{melt}}}\). Vibrational free energy of segregation is defined via the double difference:

$${\Delta F}_{{\rm{vib}},i}^{{\rm{seg}}}=\left({F}_{{\rm{GB}},i}^{{\rm{solute}}}-{F}_{{\rm{GB}},i}^{{\rm{pure}}}\right)-\left({F}_{{\rm{bulk}}}^{{\rm{solute}}}-{F}_{{\rm{bulk}}}^{{\rm{pure}}}\right)-\Delta {E}_{i}^{{\rm{seg}}}$$
(9)

where superscripts ‘solute’ and ‘pure’ denote whether the site is occupied by a solute or a solvent atom. The subscript indicates the site (GB, ‘i’ for a GB site type i and ‘bulk’ from the average of 10 bulk sites). We include details of such calculations in Supplementary Material 1. Note that while the entropy changes of harmonic oscillators converge at high temperatures, there could be anharmonicity, volumetric effects and grain boundary transitions not incorporated in this study43,51,126,129.

Spectral segregation isotherm

A Jupyter notebook is implemented with the Python libraries103,150,151,152,153,154,155,156,157,158,159 and is provided for readers to calculate segregation isotherms equivalent to Figs. 4 and 5 for the tabulated alloys. At finite grain sizes, the following solute balance equation is solved160:

$${X}^{{\rm{tot}}}=\left(1-{f}^{{\rm{GB}}}\right){X}^{{\rm{C}}}+{f}^{{\rm{GB}}}{\bar{X}}^{{\rm{GB}}}$$
(10)

where \({\bar{X}}^{{\rm{GB}}}\) can be calculated via the isotherm of Eq. (2) with the rearranged form of \({X}_{i}^{{\rm{GB}}}\):

$$\begin{array}{l}{\bar{X}}^{{\rm{GB}}}=\int \int d\Delta {E}_{i}^{{\rm{seg}}}\,d\Delta {S}_{i}^{{\rm{seg}}}{P}_{i}(\Delta {E}_{i}^{{\rm{seg}}},\Delta {S}_{i}^{{\rm{seg}}})\\\qquad\qquad{\left[1+\frac{1-{X}^{{\rm{C}}}}{{X}^{{\rm{C}}}}\exp \left(\frac{\Delta {E}_{i}^{{\rm{seg}}}-T\Delta {S}_{i}^{{\rm{seg}}}}{{k}_{{\rm{B}}}T}\right)\right]}^{-1}\end{array}$$
(11)

and \({f}^{{\rm{GB}}}\) is the grain boundary atomic fraction which scales with grain sizes (d)36,161. The commonly used form of \({f}^{\rm{GB}}\) is:

$${f}^{{\rm{GB}}}=1-{\left(\frac{d-t}{d}\right)}^{3}$$
(12)

with t as the grain boundary thickness. We note that with increasing temperature, \(\Delta {S}_{i}^{{\rm{seg}}}/{k}_{{\rm{B}}}\) becomes significant vis-à-vis \(\Delta {E}_{i}^{{\rm{seg}}}/{k}_{{\rm{B}}}T\) and hence alters solute equilibrium at finite temperatures. The isotherms used here also neglect solute-solute interactions and short-range ordering at grain boundaries.

Details on numerical implementations can be found in Supplementary Material 4. The large grain limit of Eq. (11) is used throughout the paper without the finite size correction of Eqs. (10) and (12). The finite GB form is included in the supplemental Jupyter notebook for use with nanocrystalline alloys.