Introduction

Ferroelectric materials have found many interesting applications in electronic and memory devices, and understanding and engineering their properties is a topic of great interest in condensed matter physics and materials science1,2,3,4,5,6. Ferroelectricity can be realized in materials with broken spatial inversion symmetry, for example by relying on second-order Jahn–Teller distortions occurring in systems composed of elements with d0 electronic configurations7, or on the presence of lone pair ns2 configurations, e.g., in heavy elements2.

Oxides represent an interesting class of materials where ferroelectricity has been realized. While there are only few transition metal oxides with partially filled d-orbitals8,9, some layered oxide perovskites structures exhibit a ferroelectric behavior due to the geometric arrangements of layers10,11,12,13. An emerging route to stabilize a polar phase in oxides is the utilization of symmetry breaking in oxygen-deficient perovskites (ABO3−δ), for example brownmillerites where oxygen vacancies are perfectly ordered14,15,16,17.

In oxides with the ABO3 perovskite structure shown in Fig. 1, oxygen vacancies with long-range order are formed along specific crystallographic directions, leading to the transformation of BO6 octahedral units into BO4 tetrahedral chains. Depending on how these chains are “twisted” (see Fig. 2) polar structures may be formed; however, in many instances such structures18,19,20,21 are metastable or only marginally stable18,22,23,24, thus limiting their use in devices.

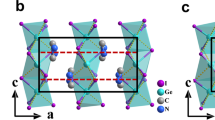
Fig. 1: Structures of oxygen-deficient perovskites.
figure 1

Schematic illustration of the RFeO3 perovskite (left), R1/3A2/3FeO2.67 Grenier (middle), and AFeO2.5 brownmillerite structure (right). R-ions and A-cations are omitted for clarity, and vacancy sites are drawn as gray dots. Note that the stacking sequence of the Grenier phase is OOTOOT…, with two octahedral (O) layers sandwiched between tetrahedral (T) layers, and that of the browmillerite phase is OTOTOT….

Full size image
Fig. 2: Arrangements of tetrahedral chains and corresponding distortion patterns in oxygen-deficient phases.
figure 2

a Twisting of tetrahedral chains in oxygen-deficient perovskites with ordered oxygen vacancies. Symmetry breaking in b Grenier and c brownmillerite phases due to the twisting of tetrahedral chains. We omitted A-cations, and R-ions for clarity, and oxygen atoms are depicted as yellow circles. Note the difference in space group, given below each structure, depending on the twisting of the chains. In high symmetry, nonpolar phases, the chains are in undistorted positions. In polar phases, all tetrahedral chains are aligned, while in antipolar phases two nearest tetrahedral layers exhibit opposite chain twisting. Other distortion patterns induced by chain twisting and observed in large unit cells are discussed in Supplementary Discussion 7.

Full size image

One promising oxygen-deficient perovskite is the so-called Grenier phase, whose oxygen deficiency (δ = 1/3) is smaller than that of brownmillerites (δ = 0.5)25,26,27. Grenier and brownmillerite phases differ by the stacking and periodicity of tetrahedral chains (Fig. 1) formed by oxygen vacancies. While brownmillerite solids have been extensively investigated for a variety of applications, e.g. as possible constituents of neuromorphic devices or as ionic conductors28,29,30,31,32, Grenier phases are much less studied33,34,35,36,37,38,39,40. However, recent experiments observed a spontaneous polarization coexisting with antiferromagnetism in R1.2Ba1.2Ca0.6Fe3O8 (R= Gd, Tb)41, pointing at the possibility of realizing stable polar Grenier phases and hence interesting ferroelectric materials, which could be used, for example, as neuromorphic devices9,42.

In this work, using first principles calculations we predict that tunable ferroelectricity can be realized in oxygen-deficient R1/3A2/3FeO2.67 (=RA2Fe3O8) perovskites with ordered oxygen vacancies. In particular we show that polar Grenier and antipolar brownmillerite phases may be realized, with the polarization determined by cooperative distortions that can be tuned by the choice of the cations. Specifically, larger A alkali-earth cations, e.g., Ba and smaller R rare-earth elements, e.g., Tb, lead to a maximum in the spontaneous polarization of the solid and to a minimum in the energy barriers required to induce a switch in the sign of the polarization.

Results

Using first principles calculations based on Density Functional Theory (DFT), we investigated the properties of R1/3A2/3FeO2.67 solids as a function of the rare-earth element R and cation A. We considered A = Ca, Sr, and Ba and lanthanides from La to Tm, which are known to form RFeO3 perovskite structures43,44,45,46,47,48,49. We excluded Yb and Lu from our study as those elements were found to lead to metallic Grenier structures.

Ferroelectricity from cooperative distortions

We start by considering Nd1/3Ca2/3FeO2.67 and CaFeO2.5 as representative compounds with the Grenier and brownmillerite structure, respectively, because these materials have been investigated in several experiments22,34,38,40. In these systems, the oxidation state of Fe is 3+; Fe has a high-spin d5 electronic configuration, leading to antiferromagnetic (AFM) Fe–Fe coupling, based on Goodenough–Kanamori–Anderson (GKA) superexchange rules50,51,52. Hence in our calculations we constrained Nd1/3Ca2/3FeO2.67 and CaFeO2.5 to have G-type AFM order in all brownmillerite and Grenier phases, consistent with the findings of previous studies19,40,41,53,54,55 (see Supplementary Discussion 2 for details on magnetic ordering).

In Fig. 2, we show how different twisting of tetrahedral chains leads to polar, nonpolar or antipolar structures18,19,20,27. Our total energy calculations for Nd1/3Ca2/3FeO2.67 and CaFeO2.5 show that polar structures can only be stabilized for Grenier phases, while antipolar structures can only be stabilized in browmillerite phases (see Table 1). These results point at the key role of oxygen vacancy concentration (δ) in oxygen-deficient perovskites (ABO3−δ) to obtain the desired ferroelectric behavior, specifically, a δ value of 1/3 is required to realize polar phases.

Table 1 Energy differences [ΔE, meV per formula unit (f.u.)] referred to the ground state energies for prototypical oxygen-deficient perovskites.
Full size table

Interestingly, we find that cooperative distortions are responsible for the stabilization of a polar (antipolar) phase in Grenier (brownmillerite) structures. In particular, as shown in Fig. 3, rotations (bending) of octahedral units lead to antipolar (polar) structures in browmillerite, while the opposite happens in Grenier phases, where rotations (bending) of the units lead to polar (antipolar) structures.

Fig. 3: Distortion patterns in polar and antipolar phases.
figure 3

Octahedral distortions in polar and antipolar phases of a Grenier (R1/3A2/3FeO2.67) and b brownmillerite (AFeO2.5) structures. Red and blue spheres indicate R-ions and A-cations, respectively. Oxygen atoms are represented as yellow circles.

Full size image

One may intuitively understand the emergence of ferroelectricity in Grenier phases by drawing an analogy between cooperative distortions and gear motion, as shown in Fig. 4. Upon rotation of octahedral and twisting of tetrahedral units, the apical oxygen atoms of the octahedral units move in opposite directions, whereas the ones in the tetrahedral units move in the same direction (Fig. 4a, b). We may then view octahedral layers as rotating gears, and tetrahedral layers as sliding gears. Hence ferroelectricity arises from the combination of the rotational and sliding motion of octahedra and tetrahedra, respectively. This combined motion gives rise to a polarization along the c-direction (see Fig. 5a), parallel to the tetrahedral layer. This motion is realized by a single \({{{\Gamma }}}_{3}^{-}\) mode in the nonpolar phase, which is also responsible for the displacement of the R- and A-ions along the tetrahedral chain direction. The polarization is the primary order parameter in the Grenier phases and this ferroelectricity mechanism is proper (see Supplementary Fig. 10). We note that these cooperative distortions occur without any displacement of Fe atoms from the center of the polyhedral units, consistent with the general trend observed for systems with partially filled d-orbitals8. We also investigated the stability of the polar Grenier phase, by computing the phonon dispersion curves of Nd1/3Ca2/3FeO2.67 and La1/3Ca2/3FeO2.67 polar phases (see Supplementary Figs. 10 and 11). We found one small imaginary frequency (≤10i cm−1), close to the zone center, corresponding to a phonon mode propagating along the b-direction in Fig. 5a, perpendicular to the polarization direction (along the c-axis in Fig. 5a). This instability likely arises due to numerical noise when calculating the phonon dispersion, and we expect it to disappear in a larger unit cell (see Supplementary Discussion 7). The characteristics of this mode indicate that a distortion of the unit cell used here in the b-direction is necessary to obtain a stable structure. Although we could not use the unit cell including all distortions along the b-axis (which, in the case of Nd1/3Ca2/3FeO2.67 would include 870 atoms), our results on the physical properties of the polar Grenier phases are robust, since no distortion occurs in the polarization direction.

Fig. 4: Cooperative distortions and gear motions.
figure 4

Cooperative distortions of polyhedral units in perovskite, brownmillerite, and Grenier phase: a rotation of octahedra and b twisting of tetrahedral chains. Stable distortion patterns in c RFeO3 perovskite, d R1/3A2/3FeO2.67, and e AFeO2.5, where octahedral and tetrahedral layers are shown as rotational and sliding gears, respectively. For brownmillerite, there is a single rotational gear (octahedral layer) between sliding gears (tetrahedral layers) and the two nearest sliding gears move in opposite direction. In Grenier phases, the additional rotational gear (arising from the different octahedral layer stacking) leads to an opposite rotation, and the sliding gears move in the same direction.

Full size image
Fig. 5: Polarization and switching barrier in Nd1/3Ca2/3FeO2.67.
figure 5

a Layer-by-layer projection of the polarization in the Nd1/3Ca2/3FeO2.67 Grenier phase based on Born effective charge calculations [Eq. (1)]. b Total energy difference between two polar phases with opposite polarizations as a function of the polarization obtained using the Berry phase method.

Full size image

Having identified which structural motifs lead to polar phases, we calculated the spontaneous polarization of the solids using DFT+U and the Berry-phase method which allows one to carry out calculations in periodic boundary conditions56,57. For Nd1/3Ca2/3FeO2.67 we obtained 2.24 μC cm−2 using the PBE functional, a value which is insensitive to the choice of the U value, with variations within 0.11 μC cm−2 when U is varied between 4 to 7 eV. (Supplementary Discussion 1). We found that the geometries optimized with the PBEsol functional exhibit small variations relative to those computed with PBE (small reduction in the unit cell volume <5%), and hence the polarization computed with PBE and PBEsol are similar (2.25 μC cm−2). This value is smaller than that reported experimentally41 for R1.2Ba1.2Ca0.6Fe3 O8 (R = Tb, Gd), most likely due to the difference of R and A cations, as discussed in the next section. In Fig. 5b, we show the difference in polarization between the nonpolar and the polar phases. Assuming that the path identified here is indeed the lowest energy path, we find that the energy barrier to switch the sign of the polarization is 263 meV per f.u. for Nd1/3Ca2/3FeO2.67. This barrier is larger than that found in SrFeO2.5 (~ 150 meV per f.u.23), possibly because of smaller R-ions and A-cations.

In order to better understand the mechanism leading to ferroelectricity, it is useful to analyze the contributions of each layer to the total polarization. To this end, we plot the layer polarization along the polar (z) direction in Fig. 5a, computed by summing, for each constituent ion (n), the products of Born effective charges (BEC; Z*) and the displacement relative to the atomic coordinates in the nonpolar phase (Δu):

$${P}_{z}=\frac{e}{{{\Omega }}}\mathop{\sum}\limits_{n}{Z}_{zx,n}^{* }{{\Delta }}{u}_{x,n}+{Z}_{zy,n}^{* }{{\Delta }}{u}_{y,n}+{Z}_{zz,n}^{* }{{\Delta }}{u}_{z,n}.$$
(1)

Here e is the electron charge and Ω is the volume of the unit cell, and x, y, and z are directions defined for individual atoms parallel to the a-, b-, and c-directions of the polar phase in Fig. 5a. As shown in Fig. 5a, the tetrahedral chains give rise to local dipole moments, with additional, significant contributions of opposite sign from CaO layers (negative contribution) and NdO layers (positive contribution). Our layer polarization results are qualitatively different from those of the model suggested in ref. 41, which predicts positive contributions to the polarization from all atomic layers and contributions from RO and AO layers smaller than those found here. In the model of ref. 41, all apical oxygen atoms are displaced in the same direction.

We note that in Eq. (1) we found a considerable contribution to the value of the polarization from the off-diagonal components of the BEC tensor (\({Z}_{zx}^{* }\) and \({Z}_{zy}^{* }\)) (see Supplementary Table 1). The BEC tensor is defined as \({Z}_{ij}^{* }=\frac{{{\Omega }}}{e}\frac{\delta {P}_{i}}{\delta {u}_{j}}=\frac{1}{e}\frac{\delta {F}_{i}}{\delta {E}_{j}}\), where P and u represent polarization and displacement, while F and E are force and electric field, respectively. The indices i and j denote Cartesian coordinates56. Specifically, when including off-diagonal elements we obtain a value for the layer polarization sum of 3.48 μC cm−2, whereas in the absence of off-diagonal terms the summation yields 8.98 μC cm−2 due to an overestimation of the polarizations of the FeO tetrahedral layer. We note that upon cooperative distortions, tetrahedra rotate round the apical oxygen atoms (oxygens belonging to the CaO layers); as a consequence, the Fe and O atoms in the tetrahedral layers are considerably displaced along the b-directions; in particular Fe and O atoms are displaced by 0.21 and 0.68 Å, respectively, and they contribute to the polarization along the c-direction through the \({Z}_{zy}^{* }\) component of the BEC tensor. The discrepancy between values of the polarization obtained with the Berry phase (2.24 μC cm−2) and the BEC (3.48 μC cm−2) method is attributed to numerical factors, including a possibly different convergence of the two methods with system size, and different k-meshes and cutoff energies used in the two cases. However, the polarization values from the two methods are within a factor of two and hence consistent with each other. In the following we will use values obtained with the Berry phase method.

The ferroelectricity found here in Nd1/3Ca2/3FeO2.67 Grenier phases originates from the presence of two octahedral layers between pairs of tetrahedral layers, i.e., the emergence of ferroelectricity is critically dependent not only on oxygen deficiency but also on the stacking of layers, which differs from the stacking found in brownmillerite composed only of one octahedral layer between pairs of tetrahedral ones. Our results also indicate that any even number of intercalated octahedral layers would lead to the stabilization of a polar phase. However, to the best of our knowledge, there is no compound with a number of intercalated octahedral layers larger than two (as in Grenier structures); hence we consider Grenier structures as the optimal solution for designing ferroelectricity in the class of materials studied here, and in the next section we consider only solids with the Grenier stacking.

Cation size-effect in ferroelectricity

We now turn to discuss the effect of the size of R-ions and A-cations in determining the ferroelectric properties of R1/3A2/3FeO2.67. In Fig. 2 we consider a cation ordering in which the R-ions are located between the octahedral layers because our total energy calculations as a function of cation orderings in Nd1/3Ca2/3FeO2.67 showed that the rare earth preferably occupies the A-site in octahedral units (see Supplementary Discussion 4). The ordering chosen here is also consistent with the cation occupancies reported in the literature for La1/3Sr2/3FeO2.67 and Nd1/3Ca2/3FeO2.6740.

In Fig. 6, we show the total energy difference between polar and nonpolar phases as a function of R and A. For all R1/3A2/3FeO2.67 systems we find that the polar phase is more stable than the antipolar one and small-size R and A contribute to the stabilization of the polar phase. The systems with the smallest cations (R = Tm, A = Ca) exhibit the largest energy differences between different phases, and the polar phase is 123 and 320 meV per f.u. lower than antipolar and nonpolar phases, respectively. On the other hand, for larger cations (e.g., R = La, A = Ba) we find that these energy differences almost vanish (they are less than 1 meV per f.u.), indicating that in the Grenier structure all phases are nearly degenerate. As mentioned above, even smaller R-ions, e.g., Yb or Lu, yield a R1/3A2/3FeO2.67 metallic phase. However, also in this case we find that the polar distortion persists in the Grenier structure, confirming the geometric origin of ferroelectricity.

Fig. 6: Cation-dependent energy differences between distortion patterns in Grenier structure.
figure 6

a Energy difference between nonpolar, antipolar and polar phases in Grenier structures of R1/3Ca2/3FeO2.67 as a function of R-ions. b Total energy difference between nonpolar, antipolar, and polar phases as a function of A-cation and R-ions. Two-dimensional projections for A = Sr and Br are provided in Supplementary Fig. 5.

Full size image

Interestingly, we find that for all R-ions, only the polar phase can be stabilized. In Fig. 6, we show that the energy difference between antipolar and nonpolar phases is not sensitive to the size of the R-ion, since the local geometries surrounding the element R are similar in the nonpolar and antipolar phases, whose main difference is the twisting of the tetrahedral chains. For example in systems with A = Ca shown in Fig. 6a, the energy difference between nonpolar and antipolar phases shows a weak variation from 197 meV per f.u. for R = Tm to 224 meV per f.u. for R = La. On the other hand, the energy differences between nonpolar, polar, and antipolar phases vary substantially as a function of the A cation. The energy difference decreases by 50% when going from from Ca to Sr, and is again halved in the case of Ba.

Based on our results on total energy differences and the layer-by-layer projection of the polarization presented in Fig. 5a, we identify three major geometrical descriptors for the emergence of the polarization in Fig. 7a, b: the twist angle of tetrahedral chains (θtwist) and the displacements of R − O pairs along the polar direction (Δuz,R−O) and of A − O pairs (Δuz,A−O). We found that these geometrical parameters undergo substantial variations, depending on the choice of R and A (see Supplementary Discussion 6). For example, for Nd1/3Ca2/3FeO2.67 (small cation), Δuz,R−O = 0.45 Å and Δuz,A−O = 0.47 Å, while for La1/3Sr2/3FeO2.67 (large cation), those values are smaller, 0.14 and 0.19 Å, respectively, as shown in Fig. 7b. On the other hand, the difference in θtwist is relatively small, with the angle of Nd1/3Ca2/3FeO2.67 being 51.5∘ and that of La1/3Sr2/3FeO2.67 48.7∘.

Fig. 7: Geometric descriptors of the polar R1/3A2/3FeO2.67 phases and the effect of cation size in polarization.
figure 7

a Twist angle (θtwist) of tetrahedral chains in polar Grenier phase of Nd1/3Ca2/3FeO2.67. b Atomic structure and polar displacements in RO and AO layers in polar Grenier phases of Nd1/3Ca2/3FeO2.67 and La1/3Sr2/3FeO2.67. c Spontaneous polarization of R1/3A2/3FeO2.67 as a function of the rare-earth ion calculated using the Berry phase method.

Full size image

In Fig. 7c, we show the polarization as a function of R and A, exhibiting a maximum for R = Tm and A = Ba. This cation selection gives rise to the largest Δuz,R−O and smallest Δuz,A−O, which in turn maximize the spontaneous polarization. We note that the value found here for the polarization is lower than the values reported experimentally: The experimental polarization of R1.2Ba1.2Ca0.6Fe3O8 (R = Gd, Tb) ranges from 23.2 to 33.0 μC cm−2 41, while the computed polarization with the same choice of R-ions, Gd and Tb, in R1/3Ba2/3FeO2.67 is 12.6 and 13.4 μC cm−2, respectively. Different reasons may be responsible for this discrepancy. From a theoretical standpoint, the absolute value of P is expected to depend on the choice of the functionals58, and the trend shown in Fig. 7, more than the absolute values, should be considered to define a reliable roadmap for ferroelectric design. It is noteworthy though that the polarization values computed here are not sensitive to the choice of the U value (see Supplementary Discussion 1). We also note that the chemical formula of R1.2Ba1.2Ca0.6Fe3O8 (R = Gd, Tb) reported experimentally deviates from that of the stoichiometric R1/3A2/3FeO2.67 considered here, and may involve cation disorder. We conclude that smaller R such as Tm and larger A such as Ba are optimal choices for enhancing ferroelectricity of polar Grenier structures. In addition, given that the primary switching barrier is formed between the polar and nonpolar phases, we find that small A-cations like Ca lead to a high energy barrier. This trend of smaller cations driving larger atomic displacements is consistent with that found in other perovskite-like structures59,60. While our results show that the energy barrier also changes depending on the choice of R, the polarization value does not substantially vary when R is smaller than Gd (Fig. 7c). Specifically, changing R from the smallest member (Tm) of the set to the slightly larger Tb in R1/3Ba2/3FeO2.67 would decrease the spontaneous polarization from 14.8 to 13.4 μC cm−2. For A = Sr and Ca, the decrease in polarization is 0.30 and 0.26 μC cm−2, respectively. This small variation of P indicates that several R elements such as Tb, Dy, and Ho may be chosen to obtain a similar ferroelectric behavior in Grenier structures.

Discussion

Using the results of first-principles calculations we proposed that Grenier structures arising from oxygen-vacancy ordering in 3D oxide perovskites are interesting materials to realize ferroelectricity. In Grenier structures polar phases are stabilized by the cooperative motion of octahedral and tetrahedral units, with the twisting motion of tetrahedral chains playing a key role in forming local dipole moments. We considered in particular R1/3A2/3FeO2.67 solids, where the oxidation state of Fe is +3, and whose composition is optimal to grow Grenier rather than brownmillerite structures61. We investigated the emergence of ferroelectricity in R1/3A2/3FeO2.67 as a function of the size of the rare-earth and alkali-earth elements, and provided a strategy to choose optimal elements to obtain polar phases. Interestingly, Grenier structures can also be present in superlattices. For example in ref. 62, the introduction of oxygen vacancies in \({({{{{\rm{LaFeO}}}}}_{3})}_{2}/({{{{\rm{SrFeO}}}}}_{3})\) superlattices was shown to form polar domains. Despite a different ratio of La to Sr compared to the ratios considered here, it is reasonable to expect that Grenier phases formed at interfaces may be responsible for the polar domains observed in the films.

We emphasize that the ferroelectricity in Grenier phases is a proper mechanism, at variance from the improper ferroelectricity in other layered perovskites. For example, in the Ruddlesden–Popper and Dion–Jacobson phases12,63, with even number of octahedral layers, and a hybrid improper mechanism is responsible12,13,64 for ferroelectricity. However, there are similarities in the geometrical distortions responsible for ferroelectricity in Grenier phases and other layered perovskites. On the other hand, the geometrical distortions giving rise to the spontaneous polarization in Grenier phases and BaTiO3, which both exhibit proper ferroelectricity, are different. The ferroelectricity of Grenier phases also differs from that of oxygen-deficient oxides with defect-like vacancies, e.g. in SrMnO3−δ and SmFeO3−δ65,66.

Overall, our work suggests that Grenier phases can be a rich platform for materials phenomena arising from breaking inversion symmetry in solids. The geometrically driven ferroelectric behavior observed in Grenier phases can be extended to other d-electron configurations by adjusting the R/A ratio or incorporating different transition metals. Notably, oxides containing elements such as Mn, Al, Ga, and In, which are known to be compatible with tetrahedral coordination, can form Grenier or brownmillerite structures21,33,67,68. By exploring the chemistry of polar Grenier phases, we anticipate exciting opportunities to realize materials with various properties. For example, polar metals can be realized by employing small R-ions, e.g., Yb and Lu. In addition, the coexistence of antiferromagnetic order with ferroelectricity41,69 may lead to a magnetoelectric coupling that switches polarization with applied magnetic field. This line of inquiry could pave the way for utilizing Grenier phases in energy-efficient computing devices, where the inherent hysteresis of ferroelectricity can help realize nonvolatile memories for neuromorphic devices9,42.

Methods

Calculation details

We performed density function theory (DFT) calculations with the generalized gradient corrected functional proposed by Perdew–Burke–Ernzerhof (PBE)70, and using the plane wave code Quantum ESPRESSO (QE)71,72,73, with a U parameter74 for Fe of 6.5 eV. This U value was determined by matching the experimental band gap of the SrFeO2.5 brownmillerites75. We find the calculated total energies and polarization values are relatively insensitive to the choice of U (see Supplementary Discussion 1). We used projected augmented wave (PAW) pseudopotentials from the PSlibrary76, except for La where we used the Rare Earth PAW datasets77. For rare-earth elements, f-electrons were considered as part of the core and we used pseudopotentials having 11 valence electrons. assuming a 3+ charge state of each element. We used a kinetic energy cutoff of 75 Ry for wavefunctions and 300 Ry for the charge density. The Brillouin zone was sampled with a 3 × 8 × 8 k-grid for Grenier structures whose unit cell size is \(6{a}_{{{{\rm{pc}}}}}\times 2\sqrt{2}{a}_{{{{\rm{pc}}}}}\times 2\sqrt{2}{a}_{{{{\rm{pc}}}}}\), where apc denotes the pseudocubic lattice parameter of perovskites. The cell parameters and atomic coordinates were optimized with a threshold of 3 × 10−4 Ry/Bohr (~0.01 eV/Å) on the atomic forces. Phonon band structures were calculated with the frozen phonon method by using the Phonopy package78 with a 2 × 2 × 2 supercell. Born effective charges were obtained from density functional perturbation theory calculations. Due to the high computational cost of phonon calculations, we used an energy cutoff of 50 Ry and a 1 × 3 × 3 k-grid. We carried out calculations for R1/3A2/3FeO2.67 solids with different choices of R and A elements:R is a lanthanide elements from La to Tm, where RFeO3 solids are known to form perovskite structures43,44,45,46,47,48,49; A = Ca, Sr, and Ba. When comparing the size of rare-earth cations, we used 8-coordinate ionic radii79, similar to nickelate perovskite studies80,81. Although the R cations are expected to be 12-fold coordinated in cubic perovskites, the nickelates possess GdFeO3-type distortions, which reduce the R cation coordination. Visualization of atomic structures was done with the VESTA package82.