Automated classification of big X-ray diffraction data using deep learning models

Abstract

In current in situ X-ray diffraction (XRD) techniques, data generation surpasses human analytical capabilities, potentially leading to the loss of insights. Automated techniques require human intervention, and lack the performance and adaptability required for material exploration. Given the critical need for high-throughput automated XRD pattern analysis, we present a generalized deep learning model to classify a diverse set of materials’ crystal systems and space groups. In our approach, we generate training data with a holistic representation of patterns that emerge from varying experimental conditions and crystal properties. We also employ an expedited learning technique to refine our model’s expertise to experimental conditions. In addition, we optimize model architecture to elicit classification based on Bragg’s Law and use evaluation data to interpret our model’s decision-making. We evaluate our models using experimental data, materials unseen in training, and altered cubic crystals, where we observe state-of-the-art performance and even greater advances in space group classification.

Introduction

The response of materials at extreme pressures strongly depends on their atomic arrangements and crystal structure. Determination of the crystal structure of solid and liquid materials is essential for understanding their mechanical, electromagnetic, and thermodynamic properties^1,2,3. Powder x-ray diffraction (XRD) is the golden standard for material characterization, where it produces a pattern that encodes information about the crystal symmetry, lattice parameters, types, and packing of atoms at nanoscale domains^4,5. However, current indexing techniques require human intervention and contextual insights from verified materials^5,6,7,8,9,10. Rietveld Refinement process requires manual tuning and adjustments such as peak indexing and parameter initialization for trial-and-error iterations^11,12. These parameters are initialized using known contextual knowledge such as expected material symmetries, beam source, crystal, temperature, and grain size. The parameters are then optimized using a best-fit iterative procedure to replicate the original experimental diffraction pattern. Automatic classifying software such as TREOR lacks the accuracy needed for reliable automated material characterization as it ultimately relies on human intervention^13,14. Furthermore, initialization steps can be extremely difficult to establish with the presence of a small number of impurity phases that cause overlapping peaks with the main phase¹³. Characterizing materials that have no available contextual knowledge makes classification even more difficult, time-consuming, and inaccurate. On the data collection side, recent advances in ultrafast synchronous X-ray diffraction and spectroscopy measurements generate big datasets from millions of measurements; far over what human experts can manually analyze^{15,16,17,18,19}. Moreover, advances in computational power have allowed for substantially more accurate simulations for materials in unexplored conditions. Therefore, with the critical need for adaptive and automated analysis of XRD data, we developed generalized deep learning models for crystal system and space group classification given an XRD pattern.

Deep learning (DL) is a powerful machine learning method that can classify a myriad of data^20,21,22. DL models have outperformed traditional rule-based methods in many areas, such as image classification²³, control²⁴, and natural language processing²⁵ enabling new capabilities in high-throughput data analysis^22,26. With many variables affecting the shape of an XRD pattern, such as the material’s phase or crystal lattice, it is difficult to characterize a material if no comparable structures are known. However, DL models can overcome this issue¹ because of the thousands of tunable parameters that are optimized using big data—allowing models to make predictions based on learned representations from the data. Still, for a model to correctly characterize materials and material transformations, the model must be generalized, i.e., have the ability to accurately classify a wide array of materials beyond the training data. Herein, we will also discuss and analyze models’ generalizability by their capacity to uphold high performance across a variety of inorganic crystalline materials.

There have been previous works on developing various machine learning and DL methods for diffraction data analysis^17,27 for different purposes such as pattern decomposition, cluster analysis^28,29,30,31, crystal structure classification³², structure-property relationships³³, and phase mapping^34,35,36. Park et al.¹³ introduced convolutional neural network (CNN) models trained on simulated XRD patterns (synthetic data) for classifying crystal systems, and space groups. Contemporary models use standard DL architectures because they proved to be sufficient on the synthetic data, however, the generalizability of Park et al.’s model was only tested on two experimental patterns and even failed on one of them. Similarly, Vecsei et al.³⁷ trained a deep neural network (DNN) and a CNN, but also evaluated their model’s performance on the RRUFF experimental dataset. This dataset is a collection of experimentally verified high-quality spectral data from well-characterized minerals³⁸. Their best model, the CNN, tested at 86% accuracy on crystal system classification for their synthetic patterns, but this performance dropped to 56% when evaluated on the RRUFF data. Vecsei et al.³⁷ also achieved better results from the DNN model over CNN. Other works trained similar models to classify smaller subsets of crystal symmetry classes¹⁸ or a narrow specific group of materials datasets^1,18,39. Therefore, there is still a critical need for a robust model that can classify dynamic and/or unseen real XRD data from diverse materials.

The focus of our work is to develop a generalized model that is robust enough to classify the crystal system (7-way classification) and space group (230-way classification) of materials encountered in cutting-edge material design. In this paper, we implemented three main strategies to develop such a model. First, we generated an augmented synthetic dataset that is comparable to real experimental XRD data. This enhances the model’s ability to classify patterns irrespective of noise, small peak shifts due to atomic impurities, grain size, and pattern variations due to instrumental parameters. Second, we designed architectures and tuned hyper-parameters to develop models that best fit XRD analysis. Here, models are designed with the explicit purpose of instilling scientific classification strategies that are based on real physics. In addition, we used an adaptation technique to teach our model to account for experimental factors that are not captured in synthetic data. Lastly, we used three evaluation datasets that represent materials dissimilar to those encountered in the training data to explore the model’s classification strategy. The first evaluation dataset is the experimental RRUFF dataset. The second dataset is a collection of materials with enhanced magnetic properties selected from the Materials Project that were not used to train the model or part of the training data^40,41. The third is the Lattice Augmented dataset; a set of synthetically generated patterns from materials whose crystal lattice sizes are manually changed. Each of these datasets is used to evaluate the capabilities of our models outside of synthetic data. We also elucidate the relationship between model architecture and the classification process based on Bragg’s Law. In addition, we have made our entire model development pipeline (from data generation to model development) available in our Data and Code availability section. It should also be noted that past studies and this work are focused on data generated assuming a Cu source, however, the beam source can be specified by the user to develop a compatible model.

Results

Training data

A total of 204,654 crystallographic information files have been retrieved from the Inorganic Crystal Structures Database⁴². Incomplete or duplicated structures were removed for a final count of 171,006 entries (hereafter called 171k). We used the original 171k files to create 7 synthetic datasets as outlined in the methods. These synthetic datasets, numbered 1–7, have a unique set of Caglioti parameters and noise implementations. The supplementary material illustrates seven different XRD patterns, each corresponding to a set of Caglioti parameters. However, these are not the datasets used to train the models but instead are used to create the 3 training datasets. The first training dataset is named the baseline dataset, which is just synthetic dataset 1 at 171k data points. The second training dataset is the mixed dataset, which was randomly sampled without replacement from synthetic datasets 1–4, for a total of 171k data points. The last training dataset is our large dataset which is a combination of all 7 synthetic datasets for a total of 1.2 million data points. We use the baseline, mixed, and large training datasets to train models. More details on the criterion for pattern engineering processes, noise implementations, and Caglioti parameters for the synthetic datasets are provided in Methods.

Although our baseline training dataset houses over 171k data points, not all classes are equally represented. Figure 1a illustrates the relative distribution of crystal systems and space groups within the original 171k crystals. For example, triclinic crystals (7904 data points) have much less representation than orthorhombic crystals (38,604 data points) which have the largest representation.

Fig. 1: Crystal system and space group distributions.

Crystal system and space group distribution of the datasets used in this study. We have the a 171k dataset, b the RRUFF dataset, and c the Materials Project (MP) dataset. Inner circle is crystal system number, name, and count. Outer circles show space groups with a large count.

Evaluation data

Our model’s performance on training data is not reported, as all models converge to ~98% accuracy. Contemporary model performances are similar and only reported on synthetic datasets or a small subset of materials^13,19,37. Therefore, to test the model’s capabilities in material development and if the model is well generalized, we applied it to three additional evaluation datasets that were not engaged within the training process.

The first evaluation dataset is the RRUFF dataset from the RRUFF project, a collection of experimental XRD data not seen by the model³⁸. This dataset will test the model’s ability to classify real materials whose diffraction patterns are affected by experimental conditions⁴³. The RRUFF dataset includes 908 entries and the class distribution for this dataset is shown in Fig. 1b. Figure 2 compares a pattern generated by our pipeline and a pattern from the RRUFF dataset that was experimentally recorded. It should be noted that the experimental XRD patterns provided by RRUFF have peak locations and intensities that are not simply replicated in synthetic data. Therefore, this dataset will examine our model’s performance on real experimental data that are difficult to characterize because of the pattern changes that arise from the instrument of choice, impurities, grain size, preferred crystal orientation, and other external factors^44,45.

Fig. 2: Diffraction pattern comparison.

Comparison of Axinite XRD patterns from two sources: ICSD and RRUFF. The structural chemical formula is shown. The synthetic profile was generated through our pipeline using the peak shape 1 function, while the RRUFF pattern was experimentally recorded. Only the 2theta range from 0 to 45° is shown. Although peak positions are similar, there is significant noise in peak intensities due to difference in impurities and as a result many overlapping peaks.

The second evaluation dataset is the MP Dataset, which contains 2253 inorganic crystal materials obtained from the Materials Project database. The materials were chosen by Shen et al.⁴⁰ because of their potential for enhanced electromagnetic properties. The data distribution is shown in Fig. 1c. We used our data generation pipeline to produce the XRD patterns of the selected materials. This evaluation dataset contains a different distribution than that of the RRUFF dataset and baseline training dataset and will further test the model’s performance on distinctive materials that the model has no prior knowledge of.

The third evaluation dataset is the Lattice Augmentation dataset. Here, we test our model’s performance on synthetic cubic material patterns with manually expanded or compressed lattice constants. By deviating lattice constants, cubic structures still maintain a cubic symmetry but will induce translational shifts in their diffraction patterns. This is because relative intensities and distances between peaks elucidate the crystal symmetry in an XRD pattern and not the angle at which the X-ray beam contacts and diffracts. For a scientifically sound model, it must be able to classify XRD patterns based on the relative location and intensity of the peaks and not the exact location of the peaks. Therefore, this dataset will test a model’s ability to make accurate predictions irrespective of crystal lattice size, usually observed in time-resolved experiments. This property is specifically important for in-situ dynamic compression experiments in which it is critical for a model to be able to distinguish peak shifting due to pure compression of a material system that does not necessarily cause a phase transformation^46,47,48. In addition, peak shifts are characteristics of alloying in materials and will test a model’s ability to account for alloying effects^49,50,51. To generate a Lattice Augmentation dataset, we take all 29k cubic crystals from the 171k original crystals and compress/expand them by a specified percentage. After their sizes are augmented, we generate the synthetic pattern with our data generation pipeline. We used this procedure to augment crystals down to 80% and up to 120% of their original size. This will generate 409k data points.

Ultimately, all three evaluation datasets are used to test a model’s performance on unseen data. Maintaining high performance on these indicates that the model is well generalized for real-world applications.

Model development

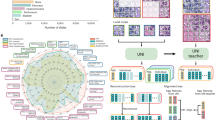
The training data are fed into our supervised deep learning algorithms for training among seven crystal systems and 230 space group classes. In this section, we consider three architectures, two of which are the standard convolutional neural network (SCNN) architecture, Fig. 3a, and the multi-layer perceptron (MLP) dense network, Fig. 3b, the same as architectures used in works by Park¹³ and Vecsei³⁷. The third is the no-pooling convolutional neural network (NPCNN), where the average pooling layers are removed. MLP architectures are inspired by human neurons, where each neuron is a linear equation with adjustable parameters and each connection is a non-linear function to normalize the information. CNNs function in much the same manner, but instead, each neuron is a ‘filter’ so that it can be iterated over the entire data range, leading to smaller model architectures. The SCNNs are referred to as ‘standard’ because their architecture was originally used for image classification, and to distinguish them from the more specialized NPCNN. The NPCNN uses the same parameters as the SCNN but removes the pooling layers that down-sample the information from the filter. Model hyperparameter specifications are shown in Fig. 3 and further detailed in methods.

Fig. 3: Model Architectures.

Model architecture specifications used. We have a Standard convolutional neural network (SCNN) and b multi-layer perceptron (MLP) architectures. The input is the XRD pattern, and the output is the desired classification: 1-of-7 crystals systems or 1-of-230 space groups. The No-Pooling Convolutional Neural Network (NPCNN) has the same specifications as the SCNN, but with removed pooling layers.

Using purely synthetic data in model development

Our baseline models were developed using the baseline dataset. The MLP and SCNN models have ~96% accuracy in 7-way classification and 94% accuracy in 230-way classification, meaning the model has fully learned the synthetic training dataset. Models released as recently as last year^13,18,19,37 have also converged on a testing accuracy of up to 98% on their respective synthetic datasets. All the studies emphasize their respective architecture as the reasoning behind their state-of-the-art performance^13,19.To evaluate our model’s performance outside of synthetic data, we tested our models on the experimental RRUFF dataset. However, as seen in Fig. 4, the performance on the RRUFF dataset was alarmingly low at 7-way accuracies of 12% and 22% from the SCNN and MLP models respectively. 230-way accuracies followed similar trends at 12% and 17% for SCNN and MLP respectively. The low performance from the MLP and SCNN models, and by extension all contemporary models evaluated on synthetic data, indicates that they are not well generalized to make predictions on data outside of synthetic data.

Fig. 4: RRUFF Experimental Performance.

Model performances on RRUFF dataset. Y-axis is the accuracy, and x-axis is the dataset used to train the model. Left is the 7-way, or crystal system, performance. Right is the 230-way, or space group, performance. Each model is color coded where blue is the standard convolutional neural network (SCNN), orange is the multi-layer perceptron (MLP), and in green is the no-pooling convolutional neural network (NPCNN).

Using mix and large datasets for training

Sample thickness, crystal orientation, and experimental conditions can affect peak broadness, location, and intensity. Therefore, we used the mixed and large datasets to train a model to classify irrespective of these external factors. By using the mixed dataset, we observed an increase in 7-way accuracy at 35% and 64% for the CNN and MLP respectively. 230-way accuracies are also reported and have similar trends at 22% and 53%, Fig. 4. With the mixed dataset being limited to 171k data points, it could equally be limited in capturing the variability that is observed in real-world crystals. The large dataset uses several more peak shape functions and noise implementations, however, models trained on the large dataset only gained an average marginal 4% increase in performance for the SCNN and MLP respectively, Fig. 4. This means that the mixed dataset sufficiently captures variations implemented in the XRD patterns. We will explore how to adapt models to these patterns in a more holistic manner in the Domain Adaptation section. Nevertheless, our mixed and large datasets teach the model to be invariant to—or irrespective of—external parameters. Data variations increase model generalizability and help maintain high performance in real-world applications.

Pooling ablation

CNNs in previous studies use standard architectures which include a series of down-sampling functions called pooling layers^13,37. The layers allow for smaller models; however, information down-sampling can lead to misclassification, and pooling layers themselves have also been shown to cause overfitting^52,53,54. Many of the beneficial properties of pooling layers, such as dimension reduction, enlarging the receptive field, and learning invariance features have been achieved with convolutions alone^{55,56,57,58,59}. For tasks like image segmentation and object detection, where local information is crucial, state-of-the-art networks often omit pooling layers to achieve better performance^60,61. Removing the pooling layers from SCNNs will prevent information compression and will enable the model to extract contextual information from locally spaced peaks. This is the basis for our NPCNNs–SCNNs with pooling layer ablations.

In this comparison, we look at models trained on the large dataset and evaluated on the RRUFF dataset. The NPCNN increased to 74% accuracy on the 7-way classification. For reference, the SCNN and MLP had 7-way accuracies of 40% and 67%, respectively, Fig. 4. This trend is exacerbated in the 230-way classification, where we see a large increase from the SCNN to NPCNN at 28% and 66% respectively, Fig. 4. Ultimately, the NPCNN now supersedes the MLP as the best model and has improved performance. We also analyze some specific cases in the RRUFF dataset and have added these insights to our supplementary materials. A more detailed reasoning as to why we observe this trend is in the Elucidating Model Properties section.

Domain adaptation via data inclusion (souping)

In this section, we train models by using data from the domain source we are trying to adapt. Here we adapt to the experimental domain by including RRUFF data in the training algorithm. For these models, we include 50% of the RRUFF data into the large dataset to create our final training dataset: ‘Souping Large Dataset”. The remaining 50% of the RRUFF data is used to test performance. Souping the model adapts it to uncertainties arising from experimental conditions like the beam source-subject-detector distances, temperature, pressure, crystallite size, or impurities^45,62. Thereby, the model learns to differentiate peak intensity/position changes due to experimental conditions, polycrystal properties, or a newly observed atom symmetry. This adaptation is similar to the experience an experimental scientist gains by working with the same instrument or the same type of materials repeatedly. The results of souping models are shown in Fig. 4. Again, the NPCNNs have the best performance at 86% 7-way accuracy, followed by MLP and CNN. 230-way accuracies saw similar trends at 77% accuracy for the NPCNN. It is also important to note that there are only 452 experimental data points and 1.2 million synthetic data points in this large souping dataset, but the model was still able to extract valuable classification insights from the experimental data. These insights allowed the model to adapt to new parameters that can affect peak shapes, including but not limited to, defects and impurities.

The improved accuracy shows that the model learned new classification strategies from architecture optimization. However, the confusion matrix on the RRUFF data reveals bias in all models towards space groups with the highest count in the training dataset, Fig. 5. Here, the y-axis is the actual classification, and the x-axis is the model’s predictions. We observe that space group two crystals are erroneously predicted to be space group 6, 8, 9, and 11–15 because they have the largest distribution in the original 171k data, as shown in Fig. 1a. Thus, if the diffraction pattern is difficult to characterize, then the model assumes it is a space group with the highest probability of appearing. This flawed justification leads to higher accuracy but faulty classification reasoning and ultimately stems from an out-of-distribution classification. In other words, the model is characterizing materials that it has little training in classifying. This is a well-known phenomenon in DL, here caused by an uneven distribution of classes in the training dataset. It should be noted that a similar issue is present for other overrepresented classes (space group 62, 139, etc.), albeit to a lesser degree. However, a confusion matrix on a small portion of data is not enough to determine if the model’s accuracy was compromised due to class imbalance. Accuracy is often used to understand model performance, but it does not give a full understanding of a model’s decision-making process as it fails to determine if the accuracy was affected by biases and assumptions. In the F1 Score and Bias section, we further analyze the effect of class imbalance as it can have a negative effect on performance. We will also discuss various methods to counteract this issue. Since models gained a significant performance boost using the ‘Large Souping Dataset’, the models will be fixed to these hyperparameters and there will be no further training.

Fig. 5: RRUFF and MP dataset Confusion Matrix.

Confusion Matrix for NPCNN trained on the Souping Large Dataset evaluated on two datasets. The datasets are the a RRUFF dataset and b MP dataset. Only space groups 1–19 are shown. Model erroneously predict many patterns as space group 2, 12, 14, and 15. These space groups are also overrepresented in the training data.

Testing model performance on the MP dataset

The Materials Project dataset is a collection of crystals chosen because of their potential in energy storage technologies. It has a distribution of space groups different than that of the RRUFF and training dataset and is shown in Fig. 1c. For instance, there is a larger representation of Trigonal crystals present whereas the RRUFF dataset has zero representation of this class. The patterns were generated using our pattern generation pipeline but the CIFs were sourced from the Materials Project database. The models here are all trained using the Large Souping Dataset discussed in the previous section. The performance of this dataset will test the model on unseen materials with entirely different structures and class distributions. To evaluate performance, we use the models trained on the large souping dataset. Figure 6 shows accuracy results for 7-way classification of the MLP, CNN, and NPCNN models which are 54%, 75%, and 67%. The 230-way accuracies are at 25%, 45%, and 36% respectively. In this instance, the NPCNN is superseded by the SCNN model. This performance shift arises from the larger architecture of the NPCNN models, making it less robust to the materials introduced here. However, they suffer from the same out-of-distribution problem that was observed in the RRUFF results. The bias towards space groups 12, 14, and 15 are visualized in Fig. 5, the confusion matrix of the NPCNN model on the MP dataset. We further analyze the implications of this observed class imbalance in the F1 Score and Bias section.

Fig. 6: Materials project performance.

Model performance on the materials project (MP) dataset. 7-way and 23-way accuracy is the crystal system and space group classification respectively. Here, the standard convolutional neural network (in blue) is outperforming the no-pooling convolutional neural network and multi-layer perceptron models (in green and orange respectively).

We also analyzed the MP Dataset to further understand the discrepancy in performance compared to other evaluation datasets. We found that the MP dataset has a lower average unit cell volume at 205 (+/−110) ${\dot{A}}^{3}$ and lower number of atom sites at 13.42 (+/−6.87) compared to the ICSD dataset average of 1186 (+/−3800) ${\dot{A}}^{3}$ and 22.18 (+/−27) average atom sites. Per Bragg’s law, which establishes an inverse relationship between atomic plane distance and diffraction angle, smaller unit cell volumes produce peaks at higher angles. However, we cut off the 2θ angle resolution to 5–90°, and therefore our models use low-angle XRD peaks. Consequently, the more important peaks at higher angles (that appear in the MP dataset patterns) are less seen by our pre-trained models. Because the NPCNN has no pooling layers, it extracts more information from peaks, placing more importance on these low-angle peaks, when in fact, they should be placed on high-angle peaks. Furthermore, the low number of atom sites, and in turn the lower number of peaks given for data extraction, makes it much more difficult for the NPCNN. Conversely, the SCNN’s pooling layers prevent the model from extracting positional information, which makes it invariant to translation. This places less emphasis on peak locality, enabling feature extraction even with limited resolution, which played a significant role in its better performance compared to the NPCNN. However, it is worth noting that the performance difference between the SCNN and NPCNN was not considerably distinct when compared to other evaluation datasets.

Performance on lattice augmentation dataset

Volumetric compression of cubic crystals does not change its symmetry and therefore classification should remain consistent across all augmentations within the Lattice Augmentation Dataset. The MLP and NPCNN models trained on the Souping Large Dataset were used in this study, where Fig. 7 shows the results. For example, the MLP model has 88% accuracy on cubic crystals that were 80% of their original size. Both models have exceptional accuracy across all deviations, even at extreme ends, and the trend continues in that the NPCNN still leads. Although performances vary through the entire range, the highest accuracies are observed for sizes that are closest to the original size at 98% and 102%. These smaller deviations are a closer representation of how they emerge in alloy materials⁵⁰ or in compression experiments that do not induce a phase change^46,49. This also elucidates a broader classification strategy: classification based on peak relations: using relative peak intensities and distances to make crystal system and space group predictions per Bragg’s Law. Further discussions are in the Elucidating Model Properties section.

Fig. 7: Lattice augmentation performance.

Performance of MLP and the NPCNN models on the Lattice Augmentation dataset. For example, on crystals that were 80% of their original size, the MLP model has an accuracy of 88%, while the NPCNN model has 94% accuracy.

F1 score and bias

We have repeatedly discussed the presence of overrepresented space groups and crystal systems in our original 171k data. In this section, we analyze our model’s predictive power using the F1 score metric, which is the harmonic average of precision and recall rates⁶³. Achieving a good F1 score indicates two crucial aspects of the model’s performance: first, its ability to maintain precision by refraining from continuously assuming only higher-represented classes, and second, its recall ability to correctly classify the unique instances of lesser-represented classes. The F1 score on the RRUFF evaluation dataset from models trained on the Large Souping Dataset are 0.859, 0.753, and 0.568 for the NPCNN, MLP, and SCNN respectively Fig. 8. These scores align with the accuracy, demonstrating their consistency. Moreover, the MP results also follow similar trends. Despite the apparent overrepresentation of certain crystal systems, our model’s robust performance in both accuracy and F1 Scores showcases its ability for nuanced decision-making. However, there is still a clear imbalance in the data, and solving this imbalance will improve model performance. One method is data duplication of lesser represented classes to create a more balanced training dataset. Another method is to introduce a loss function that penalizes the model more on lesser represented classes, thereby increasing model performance when encountering more divergent patterns, such as those found in the MP evaluation dataset.

Fig. 8: F1 Score on RRUFF and MP datasets.

F1 Score for the RRUFF and MP evaluations datasets. Model are trained using the Large Souping Dataset. The F1 Scores and in agreeance with our reported accuracy in Figs. 6 and 4.

We can also gain additional insights by analyzing the relationship between accuracy on the MP dataset and class count in the training data. Here we use the SCNN trained on the Souping Large Datset. Figure 9 is a scatterplot that graphs the accuracy of each space group, where the size of each bubble (i.e. space group) is proportional to its total count in the training data. Although there is bias observed from the confusion matrix, there is variability when it comes to performance and representation. Space groups with less than 2500 data points are sporadic in their performance but the model was still able to accurately classify these lesser-represented space groups. Ultimately, there is a clear relationship between bias and class representation, a consequence of overfitting that can be fixed by duplicating lesser-represented classes in the training data. Furthermore, the model is still able to accurately classify space groups that it has little experience with. This attribute is valuable since material design efforts are developing increasingly divergent microstructures, where models can leverage a small number of data points.

Fig. 9: Scatterplot on MP performance.

Scatter plot of standard convolutional neural network performance on the MP dataset. Y-axis is the accuracy and x-axis is the space group. The size of each circle is the count of the space group in the original 171k dataset. For example, space group 62 has an accuracy of 63%, with a count of over 12,500 synthetic patterns in the 171k dataset.

Discussion

The quality of training data is as important as the quality of the architecture, and a more holistic representation of the data will generate better, more robust models for real-world applications. As such, our data augmentation, via peak shape variation and merging experimental data into the training algorithm, produces better results in all of our evaluation datasets.

Although there are many studies on the quality of the training data^13,18,19,37 and feature importance^{1,18,19,36,51}, there are none to study the effect of deep learning architecture on pattern analysis. Here, we elucidate the relationship between model architecture and performance. In XRD pattern analysis, the 2-theta angle at which peaks emerge depends on the symmetry of the crystal lattice. This means that in isolation, the peak location does not provide enough information for classification. Two materials of the same symmetry group, but of different sizes, will produce dissimilar peak locations. Therefore, their relative peak intensities, distances, and ordering elucidate their symmetry.

Hence, deducing the degree to which CNNs and MLPs use local properties is critical for model development and future works. To do so, we first present the properties of deep learning layers in Fig. 10a: translational equivariance, permutation invariance, positional reasoning, receptive field, and state if or how the layer elicits these properties. The receptive field is the length of the segments that the model analyzes, Fig. 10b. Permutation invariance allows for consistent classification when the ordering of the data is changed, Fig. 10c. Translational equivariance is a property that allows models to correctly classify an object in an image, say a cat, even if it’s shrunk, expanded, or translationally shifted in any direction, Fig. 10d. Note that not all properties allotted to the three layers are exhaustive to the complete reasoning strategy spectrum of individual models. For example, local non-equivariant MLPs are indeed possible, and this is the reason we restricted this taxonomy to individual layer operations. We will individually discuss how the models’ reasoning emanates from these properties, relates to our observed empirical results, and the implications of their success or failure on XRD reasoning.

Fig. 10: Model architecture taxonomy.

Layer taxonomy and the resulting positional reasoning. a Each property of an individual layer. b Receptive fields and its data segmentation. c Permutation invariance property from pooling layers. d Translation equivariance gained from a convolutional layer.

First, we discuss the receptive field, which refers to the length of the segments that the model analyzes. Convolutional kernels and pooling layers are applied on local regions of 2theta angles, whereas dense layers span the full range. This process is shown in Fig. 10b. The convolutional local property induces spatial impartiality across local regions of an input. Thus, the kernel has no concept of absolute angle, but still processes the relative values of the regions that it is applied to—relative peak relationships. The operation is local to a small region and delocalized to an absolute position (2theta angle). As the receptive field of a CNN’s neurons increases with each application of convolution, the reasoning of the model grows potentially more global. In contrast, the MLP layer is analogous to single kernels that span the global context. In that way, its reasoning specializes in the absolute points in the input. It is also called a “fully-connected layer”. As expected, the architecture that is presumed to emphasize local relationships between peaks performs better. Ultimately, our SCNNs and NPCCNs are the best fit for diffraction analysis because they tend to reason based on local relationships between peaks.

Second, we discuss permutation invariance, via average pooling, which allows models to be immune to peak re-orderings entirely Fig. 10c. This property is observed to decrease the model performance on evaluation XRD data. Although a convolutional kernel has a relativistic view of peak positions; average pooling erases positional information altogether via mean-reduction. Conversely, a dense layer specializes in weights to each absolute position. Comparing the performances of permutation-invariant pooling and order-preserving no-pooling demonstrates the importance of peak positional ordering, that is, which symmetries are present in the diffraction pattern. Information lost because of pooling layers will lose relevant local information, and presumably the reason why the SCNN consistently performed worse than the MLP in past studies. The pooling layer helps the SCNN remain translationally equivariant but lose peak ordering information. Removing the pooling layer helps the NPCNN remain translationally equivariant, but also retain peak ordering information. As observed in our results, NPCNN architecture is critical for model performance.

Lastly, we discuss translation equivariance which is defined as a functional symmetry across translations. That is, a translation on the input results in an analogous translation on the output (feature-map) of the neural network. See Fig. 10d for a visualization of this equivariance. Reasoning in this manner allows a neural network to be “unfazed” by small shifts in the relative peak positions of the XRD pattern. Both the convolutions in NPCNN and SCNN architectures intrinsically have this critical property while the MLP does not. This property is tested in the lattice size augmentation experiment, where lattice deviations of the same crystal structure generate similar patterns but translationally shift along the 2theta axis. As expected, the translation equivariant model, NPCNN, performs better than the non-equivariant model, MLP.

By analyzing these properties, we observe how a model’s positional reasoning affects performance. The MLP models use absolute peak positions as a basis of classification and therefore lose the emphasis on relative properties, lowering overall performance. The SCNN has no positional information, which is not a desirable property in XRD analysis, as shown by its consistently lower performance in the evaluation datasets. The NPCNN model has relative peak reasoning, in other words, it uses relative peak intensities and distances to derive the crystal system or space group. This reasoning falls most in line with real-world XRD analysis.

Ultimately, we have developed a generalized convolutional neural network to classify the crystal system and space group of a wide array of materials by generating high-quality training data, optimizing model architecture specifically for XRD pattern analysis, and implementing domain adaptation methods.

First, we developed a data generation pipeline for the production of large XRD datasets that incorporates experimental effects on diffraction patterns. Our pipeline also has the capability of simulating materials that undergo alloying and/or dynamic experimentation, neither of which were ever used to train, or evaluate, a model in previous works. Our data augmentation techniques generate patterns that account for many experimental factors such as sample thickness, grain size, impurities, preferred crystal orientation, and other external instrumentational factors. This higher quality data taught our models to discern pattern changes due to factors that are not encountered in synthetic data, which until this work was unaccounted for.

Second, our No-Pooling Convolutional Neural Network can characterize materials based on relative-and-local reasoning between indexed peaks, a fundamental characterization approach based on Bragg’s Law. Because our models were trained based on physics-based classification, we observed increased performance across all of our evaluation datasets, most notably, on crystal structures that are representative of alloying, compression, or expansion. Our models can be advanced to account for dynamic material transformations and experimental effects which is a key critical component of cutting-edge materials characterization and design.

In addition, we used domain adaptation to achieve new classification strategies in our models and improve performance on unseen experimental data. Our models learned classification strategies on a much lower fraction of experimental examples and applied those insights to unseen experimental XRD patterns. Domain adaptation adapted our model to external factors that affect pattern shapes it would not otherwise see under conventional training methods.

Lastly, by evaluating unseen materials, we observe that our models can learn how to classify said data from relatively few data points. This property is most important when evaluating out-of-distribution data or increasingly divergent materials, both of which are commonly encountered in material development research.

With the higher quality training data, optimized model architecture, and adaptive learning technique, we observed state-of-the-art performance from our convolutional neural networks.

Furthermore, because DL models are inexpensive to run, they also offer instantaneous feedback when implemented in an experimental setting. These properties are not only useful for material exploration and design but also for eliciting materials phase transformation behaviors from big data via in situ XRD experiments. At extreme pressures, phase transformations and plastic deformations are tremendously difficult to characterize because of the vast amounts of data; however, with our automated and validated models, we can fully unlock these insights.

Future works should focus on developing models that induce relative peak analysis but be careful to preserve crucial peak ordering information. New models could also generate data that is agnostic to the beam source by incorporating momentum transfer Q instead of 2θ which will ensure compatability across beam sources⁶⁴. The distribution of classes is also an issue but can be resolved by duplicating lower-represented classes. The methods outlined here can also be used to develop models for other spectroscopy characterization techniques, such as Raman and nuclear magnetic resonance. These methodologies are similar in that they measure intensity with respect to some frame of reference (Raman shift/ppm), therefore, architectures are easily compatible.

Methods

1D XRD pattern generation

To generate synthetic powder XRD patterns we use Bragg’s Law to calculate peak locations and use the Lorentz multiplier, polarization factor, and structure factor to calculate peak intensities⁶². There are two major factors to determine the Bragg angle: (1) interplanar distance, and (2) wavelength. Braggs’ law is the relation between the diffraction angle (Bragg angle), ${\theta }_{{hkl}}$, interplanar distance, ${d}_{{hkl}}$, and the wavelength, $\lambda$, as:

$$\sin {\theta }_{{hkl}}=\frac{\lambda }{2\cdot {d}_{{hkl}}}$$

(1)

Since we have a fixed wavelength, we calculated planar distances ${d}_{{hkl}}$ using the unit cell parameters. The interplanar distance is a function of the unit cell parameters ($a,b,{c},\alpha ,\beta ,\gamma )$ and Miller indices ($h,k,l$) which allows us to describe every set of crystallography plane. The general equation to calculate planar distance is:

$$\begin{array}{ll}\frac{1}{{d}_{{hkl}}^{2}}=\left[\frac{{h}^{2}}{{a}^{2}{\sin }^{2}\alpha }+\frac{2{kl}}{{bc}}\left(\cos \beta \cos \gamma -\cos \alpha \right)+\frac{{k}^{2}}{{b}^{2}{\sin }^{2}\beta }\right.\\\qquad+\,\frac{2{hl}}{{ac}}\left(\cos \alpha \cdot \cos \gamma -\cos \beta \right)+\frac{{l}^{2}}{{c}^{2}{\sin }^{2}\gamma }\\\qquad\left.+\,\frac{2{hk}}{{ab}}\left(\cos \alpha \cdot \cos \beta -\cos \gamma \right)\right]/\left(1-{\cos }^{2}\right.\alpha -{\cos }^{2}\beta -{\cos }^{2}\gamma\\\qquad\left. +\,2\cdot \cos \alpha \cdot \cos \beta \cdot \cos \gamma \right)\end{array}$$

(2)

The diffraction pattern has multiple Bragg angles, which lead to multiple Bragg peaks, and each has its peak intensities.

The peak intensities are affected by structural factors and external factors. In our synthetic data generation, we used structure factors, which depend on the atomic structure of the crystal. The overall equation for intensities is:

$${I}_{{hkl}}=K\times {L}_{\theta }\times {P}_{\theta }\times {\left|{F}_{{hkl}}\right|}^{2}$$

(3)

Where $K$ is a scaling factor, ${L}_{\theta }$ is the Lorentz multiplier, ${P}_{\theta }$ is the polarization factor, ${F}_{{hkl}}$ is the structure factor. The Lorentz multiplier and polarization factor are merged as the Lorentz polarization factor:

$${LP}=\frac{1+{\cos }^{2}2\theta }{\cos \theta \cdot {\sin }^{2}\theta }$$

(4)

The structure factor is determined by the distribution of atoms in the unit cell as:

$${F}_{{hkl}}=\mathop{\sum }\limits_{j=1}^{n}{g}_{j}\cdot {f}_{j}\cdot \exp (2\pi i(h\cdot {x}_{j}+k\cdot {y}_{j}+l\cdot {z}_{j}))$$

(5)

Where $n$ is the total number of atoms in the unit cell, ${g}_{j}$ is the population and occupation factor, ${f}_{j}$ is the atomic scattering factor, and $x,{y},{z}$ are the fractional coordinates of the ${j}^{{th}}$ atom. The normal atomic scattering factors are represented as follows:

$${f}_{j}\left(\sin \theta /\lambda \right)=\mathop{\sum }\limits_{i=1}^{4}{a}_{i}\exp \left(-{b}_{i}\cdot {\sin }^{2}\theta /{\lambda }^{2}\right)+c$$

(6)

The scattering factors of chemical elements and ions can be referenced from the International Tables for Crystallography, Vol. C⁶⁵ .

Once positions and intensities are calculated we use a peak shape function to give the data the appearance of experimental data. In manual methods, the parameters within the peak shape functions are determined using a best-fit approach to simulate the correct observed symmetry and composition. In our pipeline, we adopt the Gauss peak shape which is described as:

$$y\left(x\right)=G\left(x\right)=\frac{{C}_{G}^{\frac{1}{2}}}{\sqrt{\pi }H}\cdot \exp \left(-{C}_{G}\cdot {x}^{2}\right)$$

(7)

Here ${C}_{G}=4\mathrm{ln}2$ and $x=(2{\theta }_{i}-2{\theta }_{k})/{H}_{k}$, where ${2\theta }_{i}$ is the Bragg angle of the ${i}^{{th}}$ point of the powder diffraction pattern, and $2{\theta }_{k}$ is the ideal Bragg angle of the ${k}^{{th}}$ Bragg reflection. Full widths at half maximum, $H$, give the appearance of Gaussian peaks. It is calculated using the three free variables U, V, and W in the Caglioti formula as⁴⁴:

$$H={\left(U\cdot {\tan }^{2}\theta +V\cdot \tan \theta +W\right)}^{\frac{1}{2}}$$

(8)

Dataset

In experimental data, the shape of the peaks depends on external factors. Here in this work, four sets of Caglioti parameters are used to generate 4 synthetic datasets, each with differing peak shapes. Three additional synthetic datasets were generated by randomly amplifying the recorded intensities with noise between 0.2 and 2% of its original intensity. Note that the noise amplification is added before the intensities are normalized, therefore we maintain an intensity range from 0 to 1000. In total, we generated seven synthetic datasets where details on the chosen parameters for each dataset are shown in Table 1.

Table 1 Synthetic datasets specifications.

Ultimately, these datasets represent materials of varying experimental conditions⁴⁵. For direct comparison with experimental data and previous literature^13,37, we fixed the wavelength at the copper Kα line (λ = 1.54 Å) and displayed our results as a function of 2θ. We set the range from 5^◦ < 2θ < 90^◦ with a spacing of 0.01^◦. We also have trained models on the large range of 5^◦ < 2θ < 180^◦ but did not observe a significant performance improvement. Therefore, to be consistent with experimental data, we used the smaller 2θ range. In addition, we normalize the patterns such that the largest peak intensity is always one thousand.

Deep learning architecture

The SCNN is composed of 3 convolutional layers with output channels [80, 80, 80], kernel sizes [100, 50, 25], strides [5, 5, 2], and no padding. Each layer has a number of neurons that collect information from the previous layer. This information is converted into a specific value by an activation function to be transferred to neurons in the next layer. The rectified linear unit (ReLU) activation function is used in our models, following each convolutional layer is a dropout probability of 30% that arbitrarily skips some neurons when computing the gradients for training. Consistent with Vescei’s work³⁷, we include an average pooling layer after each convolution with kernel sizes [3, 3, 3] and strides [2, 1, 1]. The final neural feature maps are flattened via concatenation and processed by a 3-layer ReLU-activated MLP with output dimensions [2300, 1150, number of classes] and dropout probability of 50% during training after each ReLU activation, consistent with Park¹³ and Vecsei³⁷.

The NPCNN is composed of 3 convolutional layers, with output channels [80, 80, 80], kernel sizes [100, 50, 25], and strides [5,5,2]. After each convolutional layer, there is a dropout probability of 30% and the average pooling layers are removed. The feature map is flattened and processed by the same 3-layer MLP featured in the SCNN.

Our MLP model consists of 5 ReLU-activated layers with output dimensions [4000, 3000, 1000, 800, number of classes] and dropout probabilities of [60%, 50%, 40%, 30%] after each ReLU activation during training, also consistent with Park¹³ and Vecsei³⁷. In all cases, the loss function that is minimized is softmax-cross-entropy. We use a batch size of 256 during training and the Adam optimizer to minimize the loss function.

The performance of the models depends upon their architecture and the choice of hyper-parameters such as the numbers of convolutional, pooling, and fully connected layers, the number of neurons in each layer, the size and number of convolutional filters with their stride size, and the rate of dropout¹³. Here, the accuracy is the total number of correct predictions over the total number of predictions. We proposed the models performing best on the RRUFF evaluation dataset after testing a large variety of hyperparameters.

Our code is built on top of Pytorch and the UnifiedML deep learning library⁶³. The complete source code for our models has been provided in Data availability.