Introduction

Magnetic translational symmetry of crystals in the presence of an external magnetic field1,2 manifests as a fractal form of the energy spectrum that resembles recurring replicas of butterflies, known as Hofstadter butterflies3,4,5,6,7,8,9. Although a strong magnetic field is generally required, Hofstadter butterflies have recently been observed owing to advances in two-dimensional van der Waals materials10,11,12,13,14,15,16,17,18. The magnetic field required to produce replicas of the Landau levels could be significantly reduced by the large-scale synthesis of a van der Waals superlattice with a macroscopic unit cell. For this crucial development, the Hofstadter butterflies have been experimentally realized in a graphene superlattice19,20,21,22,23,24, magic-angle twisted bilayer graphene (TBG)25,26, and twisted double-bilayer graphene27.

Notably, the link with the magnetic translational symmetry and symmetry-protected topological phases of matter has been revealed recently28,29,30,31,32,33,34,35,36,37. In a general lattice model with multiple sites per unit cell, the Hofstadter energy spectrum becomes approximately replicative under the addition of the flux periodicity, E(ϕ) ≈ E(ϕ + Φ), which constitutes the additional flux translational symmetry via the unitary transformation of the Hamiltonian, H(ϕ), as,

$${{{\mathcal{U}}}}({{{\bf{A}}}})H(\phi )\,{{{{\mathcal{U}}}}}^{{\dagger} }({{{\bf{A}}}})\approx H(\phi +\Phi ),$$
(1)

where \({{{\mathcal{U}}}}({{{\bf{A}}}})={\sum }_{{{{\bf{R}}}}}{c}_{{{{\bf{R}}}}}^{{\dagger} }{c}_{{{{\bf{R}}}}}\exp (i\frac{e}{\hslash }\int\nolimits_{{{{{\bf{r}}}}}_{0}}^{{{{\bf{R}}}}}{{{\bf{A}}}}\cdot d{{{\bf{r}}}})\) with \(\int(\nabla \times {{{\bf{A}}}})\cdot d{{{\bf{S}}}}=\Phi ,{c}_{{{{\bf{R}}}}}^{{\dagger} }\) (cR) is a creation (annihilation) operator of an electron at R in the real space, A is the vector potential, and S is the unit cell area. Remarkably, the effective time-reversal symmetry \({{{\mathcal{UT}}}}\) is restored at a half-flux periodicity \(\phi =\frac{1}{2}\Phi\)30, allowing for the existence of diverse topological states of matter protected by symmetries28,29,30,31,32.

In this work, we study the higher-order topological insulator (HOTI) phases of Hofstadter butterflies in TBG. Archetypal HOTIs have been studied with respect to symmetry protection28,30. By contrast, the replica HOTIs that we find here recur in the form of quasiperiodic replicas without explicit symmetry protection. Instead, they rely on the self-similar nature of Hofstadter butterflies. We prove that the full lattice model of TBG possesses the exact flux periodicity at all commensurate angles, which rigorously characterizes the band topological protection in the presence of the magnetic field. Two original HOTIs exist at time-reversal invariant fluxes (TRIFs) ϕ = 0 and \(\phi =\frac{1}{2}\Phi\), where ϕ = − ϕ (mod Φ). In addition, replicas HOTIs recur at the specific fluxes \(\phi =\frac{p}{2{N}_{{{{\rm{rep}}}}}}\Phi (p\in {\mathbb{Z}};p\,\ne \,{N}_{{{{\rm{rep}}}}}{\mathbb{Z}})\) [Fig. 1b; See Eq. (3) for the definition of Nrep]. To quantitatively diagnose HOTIs, we extend the concept of real-space topological markers38,39,40,41,42,43 to the HOTI version. Similar to the original HOTIs, replica HOTIs are characterized by localized HOTI markers and corner modes. The origin of the replica HOTIs is attributed to the reduced interior area of the Peierls path because of the interlayer hopping in TBG.

Fig. 1: Replica HOTI states in TBG.
figure 1

a Atomic structure of TBG. S denotes the smallest area enclosed by a Peierls path for TBG at θ=21.8∘. For comparison, we illustrate the corresponding area for graphene \({S}_{\min }^{{{{\rm{G}}}}}\) and the area of the graphene unit cell SG, where \(S=\frac{1}{7}{S}_{\min }^{{{{\rm{G}}}}}=\frac{1}{42}{S}^{{{{\rm{G}}}}}\). b Schematic of re-entrant exact HOTI and replica HOTI phases as a flux ϕ function. Red and blue colors indicate the exact HOTI and replica HOTI phases, respectively. The kx and ky are pseudo-momenta, well defined in the presence of the magnetic translational symmetry under arbitrary rational flux.

Full size image

Results and discussion

Lattice model and symmetries

We use the Moon-Koshino tight-binding model for TBG44

$$H=\mathop{\sum}\limits_{ij}{t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j}){c}_{{{{{\bf{R}}}}}_{i}}^{{\dagger} }{c}_{{{{{\bf{R}}}}}_{j}}+h.c.,$$
(2)

where the hopping integral tij(Ri − Rj) is modeled as an exponentially decaying function of Ri − Rj44 (see Methods). Magnetic flux ϕ is introduced using the Peierls substitution45: \({t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j})\to {t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j})\exp \left(i\frac{e}{\hslash }\int\nolimits_{{{{{\bf{R}}}}}_{j}}^{{{{{\bf{R}}}}}_{i}}{{{{\bf{A}}}}}_{0}\cdot d{{{\bf{r}}}}\right)\), where A0 is the vector potential in the Landau gauge (see Methods). We consider the atomic structure of TBG in the hexagonal space group #177, generated by twisting the AA-stacked bilayer graphene about the hexagonal center with the twist angle \({\theta }_{m,n}=\arccos \frac{1}{2}\frac{{m}^{2}+{n}^{2}+4mn}{{m}^{2}+{n}^{2}+mn}\) (\(m,n\in {\mathbb{Z}},m\ne n\)) (Fig. 1a). This construction of TBG preserves C6z, C2x, and C2y rotational symmetries. The twist lowers the discrete translational symmetry, leading to the translational symmetry of the moiré lattice with the enlarged unit cell area by NL = m2 + n2 + mn times. In the presence of a uniform perpendicular magnetic field, a flux translational symmetry emerges, which locally restores crystalline symmetries for specific fluxes. For example, for \(\phi =\frac{1}{2}\Phi\), combination of C2x and unitary matrix \({{{\mathcal{U}}}}\) leaves the system invariant. Therefore, \({{{\mathcal{U}}}}{C}_{2x}\) is preserved at \(\phi =\frac{1}{2}\Phi\) because \(\frac{1}{2}\Phi =-\frac{1}{2}\Phi\) (mod Φ).

Hofstadter butterflies

For the nearest-neighbor tight-binding model of graphene, the flux periodicity is given as the magnetic field strength B = Φ0/SG, where \({\Phi }_{0}=\frac{h}{e}\) is the flux quantum and SG is the graphene unit cell area11,44,46. However, when next neighbor hoppings are introduced, the minimal loop along the allowed hoppings, namely, the minimal Peierls path, has decreased inner area \({S}_{\min }^{{{{\rm{G}}}}}=\frac{1}{6}{S}^{{{{\rm{G}}}}}\) (Fig. 1a), leading to an increased flux periodicity. A stronger magnetic field of \(B={\Phi }_{0}/{S}_{\min }^{{{{\rm{G}}}}}=6{\Phi }_{0}/{S}^{{{{\rm{G}}}}}\) is required to implement the full flux quantum into the decreased inner area \({S}_{\min }^{{{{\rm{G}}}}}\) of the minimal Peierls path. Consequently, the entire cycle is completed by repeating six times modulated quasiperiodic replicas of the nearest-neighbor graphene spectrum30.

For TBG, we show the existence of the exact flux periodicity at the twist angle θm,n, dictated by,

$${N}_{{{{\rm{rep}}}}}\equiv {S}_{\min }^{{{{\rm{G}}}}}/{S}_{\min }^{{{{\rm{TBG}}}}}=\frac{{N}_{L}}{\gcd ({z}_{1},{z}_{2},{z}_{3})}\in {\mathbb{Z}},$$
(3)

where gcd indicates the greatest common divisor and z1 = m2 − n2, z2 = 3m2, z3 = 2m2 − mn − n2 (see Supplementary Note 2). For θ = 21. 8∘(m = 1, n = 2), Nrep = 7 corresponds to the area of the minimal Peierls path, \({S}_{\min }^{{{{\rm{TBG}}}}}\equiv S=\frac{1}{7}{S}_{\min }^{{{{\rm{G}}}}}=\frac{1}{42}{S}^{{{{\rm{G}}}}}\) (see Fig. 1a). As a result, a self-similar pattern is rendered by 42 replicas of the original graphene spectrum, only having the nearest-neighbor hopping term.

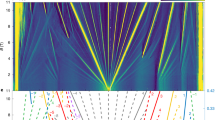
Figure 2 shows the calculated Hofstadter butterflies for both graphene and TBG by using the kernel polynomial method (see Methods). Quasi-periodicity is exhibited, as our tight-binding model includes electron hopping beyond the nearest neighbors. For example, in the graphene spectrum (Fig. 2a), the quasi-periodicity of \(\frac{1}{6}\Phi\) is displayed by having similar patterns recurring at every integer multiple of \(\frac{1}{6}\Phi\). Similarly, for TBG spectrum (Fig. 2b), a quasi-periodicity of \(\frac{1}{42}\Phi\) occurs as expected. Moreover, the energy spectrum that resembles the graphene spectrum in Fig. 2a recurs at every integer multiple of \(\frac{1}{7}\Phi\). This modulation of the graphene spectrum by \(\frac{1}{7}\Phi\) is weaker than that of \(\frac{1}{42}\Phi\) because the interlayer hopping is relatively weaker in TBG compared to next-nearest-neighbor intralayer hopping. Therefore, the quasi-periodicity of \(\frac{1}{7}\Phi\) is more prominent than that of \(\frac{1}{42}\Phi\) in TBG spectrum.

Fig. 2: Hofstadter butterflies of the atomistic tight-binding model of TBG.
figure 2

a, b Hofstadter spectrum of TBG a without and b with interlayer coupling calculated by using the kernel polynomial method (see Methods). Red dashed lines indicate the system’s half and full flux periodicity. Blue dashed lines indicate quasi periodicities at \(\phi =\frac{p}{14}\Phi (p=1,2,\ldots ,6)\). In b, the red and green solid lines denote the highest occupied and lowest unoccupied states, respectively. c–j Magnified view of b at specific flux values c ϕ = 0, d \(\phi =\frac{1}{2}\Phi\), e \(\phi =\frac{1}{14}\Phi\), f \(\phi =\frac{1}{7}\Phi\), g \(\phi =\frac{3}{14}\Phi\), h \(\phi =\frac{2}{7}\Phi\), i \(\phi =\frac{5}{14}\Phi\), and j \(\phi =\frac{3}{7}\Phi\), where \(\varepsilon =\frac{1}{1680}\Phi\).

Full size image

The computed spectrum exhibits symmetries of Hofstadter butterflies (Fig. 2b). Translational flux symmetry is displayed in the recurring patterns at ϕ and ϕ = ϕ + Φ. Moreover, the C2x symmetry that is broken under the flux gives rise to the mirror-symmetric spectrum about TRIFs (both ϕ = 0 and \(\phi =\frac{1}{2}\Phi\)). The Hamiltonian is transformed under the C2x operator as

$${C}_{2x}H(\phi ){C}_{2x}^{{\dagger} }=H(-\phi ).$$
(4)

Combined with the unitary matrix \({{{\mathcal{U}}}}\), we obtain

$${{{\mathcal{U}}}}{C}_{2x}H\left(\frac{1}{2}\Phi +\phi \right){({{{\mathcal{U}}}}{C}_{2x})}^{{\dagger} }=H\left(\frac{1}{2}\Phi -\phi \right).$$
(5)

Therefore, the energy eigenvalues for ϕ and − ϕ about TRIFs are equivalent.

Exact HOTIs

The proposed tight-binding model reproduces the HOTI phase of TBG well at zero flux, showing good agreement with previous studies47,48. Consequently, the system harbors localized states at the corner of a diamond-shaped flake under an open boundary condition (OBC) (Fig. 3b). In energy space, two corner states reside inside the spectral gap of the bulk (Fig. 3a). In general, these two (in-gap) corner states can have different energies owing to the finite-size effect, in which they spatially overlap and cause hybridization48.

Fig. 3: Characterization of HOTI states.
figure 3

a Energy spectrum of TBG with θ = 21. 8∘ in OBC. Red Data points indicate corner states. b Topological corner state in OBC. The colored circle indicates the phases of eigenstate components. c Zak phase calculated using c2x = + 1 bands along the rotation-invariant ky = 0 line in periodic boundary condition. d HOTI marker χ+(r) for c2x = + 1 states in OBC. Here, χ+(r) is normalized to its maximum value.

Full size image

The bulk gap at ϕ = 0 is ~9 meV. This leads to a spectral gap of approximately 236 meV for a flake width of ~ 11 nm (2800 atoms). The HOTI at ϕ = 0 is under multiple protection conditions47,48. Two distinct topological invariants exist: the second Stiefel-Whitney number ω249,50,51,52,53,54,55 and \({{\mathbb{Z}}}_{2}\) rotation-winding number56,57,58, protected by space time-reversal symmetry [\({({C}_{2z}{{{\mathcal{T}}}})}^{2}=1\)] and rotation symmetry C2x, respectively. The combined symmetry \({({C}_{2z}{{{\mathcal{T}}}})}^{2}=1\) imposes the reality condition on the Hamiltonian, leading to the real-valued corner state (Fig. 3b). The C2x rotation-resolved Zak phase ν± along the rotation-invariant line ky = 0, where ± denotes the rotation eigenvalue c2x = ± 1, gives rise to a nontrivial \({{\mathbb{Z}}}_{2}\) rotation-winding number (Fig. 3c).

We suggest a HOTI marker given by \({\chi }^{\pm }({{{\bf{r}}}})=-\left\langle {{{\bf{r}}}}\right\vert {{\widetilde{C}}{\,}_{2x}^{\pm }}{P}^{\pm }\hat{X}{Q}^{\pm }\left\vert {{{\bf{r}}}}\right\rangle\), where \({\widetilde{C}}{\,}_{2x}^{\pm }={P}^{\pm }{C}_{2x}{P}^{\pm }\) is a projected symmetry operator, and \(\hat{X}\) is a position operator (see Methods). Here, P±(Q±) is the projection operator to the occupied (unoccupied) c2x = ± 1 subspaces. In OBC, χ±(r) successfully diagnoses the rotation-winding number in real space: χ±(r) dictates the nontrivial rotation-winding number by being localized along the edge of the flake (Fig. 3d), whereas in the trivial case, it is delocalized over the entire geometry (see Supplementary Fig. 3). Interestingly, the corner state appears at the boundary between the opposite signs of each HOTI marker χ±(r). The sum of the opposite HOTI markers χ+(r) + χ−(r) is zero, which indicate a trivial winding number. The HOTI marker can be applied to symmetry-breaking perturbations, as demonstrated in TBG under the uniform magnetic field.

To study the effect of the magnetic field on the HOTI states, we track the corner states by investigating their spectral flow at fixed filling30 (see red and green lines in Fig. 2b). At zero flux, the highest occupied (HO) and lowest unoccupied (LU) states are identified as corner-localized states (Fig. 3b). They adiabatically evolve as a flux function and undergo a series of discontinuity transitions at specific fluxes. This discontinuity is indicative of a topological change due to bulk gap change30,31. Indeed, we reveal that HO and LU states at the discontinuity transitions are quantum Hall chiral edge states (see Supplementary Note 4).

Remarkably, we find a reentrance of the HOTI phase at \(\phi =\frac{1}{2}\Phi\), characterized by edge-localized marker χ+(r) (Fig. 4a). χ+(r) decays exponentially along the bulk as \(\exp [-\alpha (x-{x}_{0})]\) with α = 0.52, which is identical to that of the exact HOTI state at zero flux (Fig. 4b) (see also Supplementary Note 3 for the detailed quantitative analysis). The re-entrant HOTI phase relies on composite symmetry \({{{\mathcal{U}}}}{C}_{2x}\) exactly preserved at \(\phi =\frac{1}{2}\Phi\) because \(({{{\mathcal{U}}}}{C}_{2x})H(\frac{1}{2}\Phi ){({{{\mathcal{U}}}}{C}_{2x})}^{{\dagger} }=H(\frac{1}{2}\Phi )\) from \({C}_{2x}H(\frac{1}{2}\Phi ){C}_{2x}^{{\dagger} }=H(-\frac{1}{2}\Phi )\) and \(H(\phi +\Phi )={{{\mathcal{U}}}}H(\phi ){{{{\mathcal{U}}}}}^{{\dagger} }\). Note that the corner boundary modes of the re-entrant HOTI phase are localized at the corner, but the node appears slightly more concentrated off the corner (Fig. 4a) (see also Supplementary Fig. 4 for the reason of the nodal structure of the corner states).

Fig. 4: Characterization of replica HOTI states.
figure 4

a, d–i Real-space distribution of the corner states (the highest occupied eigenstates) and HOTI markers χ+(r) for various fluxes a \(\phi =\frac{1}{2}\Phi\), d \(\frac{1}{14}\Phi\), e \(\frac{1}{7}\Phi\), f \(\frac{3}{14}\Phi\), g \(\frac{2}{7}\Phi\), h \(\frac{5}{14}\Phi\), and i \(\frac{3}{7}\Phi\). In a, the colored circle indicates the phases of eigenstate components. Due to the mirror symmetry about the flux ϕ = Φ/2, the eigenstates and markers at \(\phi =\frac{p}{14}\Phi (p=1,2,\ldots ,6)\) are the same as those at \(\phi =\frac{14-p}{14}\Phi\). b, c Line profiles of χ+(r) along the arrow indicated in a. Here, \({\phi }_{1}=\frac{1}{21000}\Phi\) and x0 is the corner position.

Full size image

Replica HOTIs

In addition to the exact HOTIs at TRIFs (ϕ = 0 and \(\phi =\frac{1}{2}\Phi\)), replicas of the original HOTIs are found at the \(\frac{1}{7}\Phi\) quasi-periodic counterparts of TRIFs. We employ HO and LU states as indicators of a replica of the original HOTI. We find that they are positioned within the spectral gap at the specific fluxes of quasi-periodicity \(\phi =\frac{p}{14}\Phi (p\in {\mathbb{Z}};p\ne 7{\mathbb{Z}})\) (Fig. 2e–j). A close inspection reveals that HO and LU states show oscillatory behavior of HO and LU energies as a function of flux, which originates from the Aharonov-Bohm tunneling in the presence of an external magnetic flux. Notably, the oscillation is a finite-size effect rather than a characteristic behavior of corner states, as is evident in the oscillations of other states near HO and LU states.

To demonstrate the characteristics of the replica HOTIs, we plot the HO states in the left panels in Fig. 4d–i. The real-space distribution arguably shows the corner-localized states, supporting the HOTI phases. Nonetheless, these states exhibit stark contrast to the corner states of the exact HOTI at zero flux in that they are complex-valued functions, while the exact HOTI hosts real-valued corner states (Fig. 3b). The complex-valued wave functions manifest the broken reality condition \([{({C}_{2z}{{{\mathcal{T}}}})}^{2}=1]\) at finite fluxes, implying that the Stiefel-Whitney characterization is inapplicable. Furthermore, these quasiperiodic fluxes also break the C2x and \({{{\mathcal{U}}}}{C}_{2x}\) symmetries, which were utilized to characterize the exact HOTIs at TRIFs.

Remarkably, the HOTI marker can be defined without the protecting symmetries, enabling the evaluation of rotation-winding numbers. We find that the HOTI marker can quantitatively characterize the corner states in the presence of flux, that is, under rotational-symmetry C2x breaking. At a small flux \({\phi }_{1}=\frac{1}{21000}\Phi\), the eigenstate shows the remaining localized corner state, and the corner state is characterized by the marker χ+(r) which is sufficiently localized along the entire edge despite the small permeated values towards the bulk (Supplementary Figure 3). Quantitatively, χ+(r) exhibits an exponential decay as \(\exp [-\alpha (x-{x}_{0})]\) with α = 0.10, which is smaller than α = 0.52 of the exact HOTIs due to the symmetry breaking (Fig. 4b). The exponential localization of χ+(r) from the edge for the corner states is in stark contrast to a linear delocalization ∝ − β(x − x0) of χ+(r) along the whole geometry for the trivial state that occurs at, for example, ϕ = 13ϕ1 (Fig. 4b). Such localization characteristics of the markers serve as a hallmark to identify nontrivial bulk topology, which fundamentally originates from the action of the projected symmetry operator, as in the generic topological crystalline insulating phases protected by spatial symmetries42,43 (see also Methods for the detailed explanation for the real-space behavior of the HOTI marker).

Our HOTI marker captures the replica HOTI phases as well, at \(\phi =\frac{p}{14}\Phi (p\in {\mathbb{Z}};p\ne 7{\mathbb{Z}})\) (Fig. 4d–i). χ+(r) at \(\phi =\frac{p}{14}\Phi\) show robust edge localization, consistent with the corner-localized eigenstates. The line profiles of χ+(r) (Fig. 4c) exhibit exponential decay (see also Supplementary Fig. 6). The replica HOTIs can be viewed as the copies of exact HOTIs disordered by the fractional flux quantum acquired when electrons travel through the minimal Peierls path because the composite symmetry \({{{{\mathcal{U}}}}}_{0}{C}_{2x}\) becomes exact when the interlayer coupling is turned off.

We also verify that replica HOTIs generally appear at other large angles. Figure 5 shows the HO states and HOTI markers at the other twist angles θ = 13. 2∘(m = 2, n = 3) and 9. 4∘(m = 3, n = 4). We find that both the corner localized states in real space and the localization behavior of the calculated HOTI markers support the existence of the replica HOTI states at the flux \(\phi =\frac{p}{2{N}_{{{{\rm{rep}}}}}}{\Phi }_{m,n}(p\in {\mathbb{Z}};p\ne {N}_{{{{\rm{rep}}}}}{\mathbb{Z}})\) where the flux periodicity is given by Φm,n = NrepΦG with the flux periodicity of graphene ΦG. Here, Nrep = 19 and 37 for θ = 13. 2∘ and 9. 4∘, respectively. We note that the localization strength of the HOTI markers (see the line profiles in Fig. 5) is weakened as we decrease the twist angle because the bulk gap is significantly reduced (see Supplementary Fig. 9).

Fig. 5: Replica HOTI states at other large angles.
figure 5

a–c Real-space distribution of corner states (the highest occupied eigenstates), HOTI marker χ+(r) and its line profile for the twist angles a θ1,2 = 21.8∘, b θ2,3 = 13.2∘, and c θ3,4 = 9.4∘. For the geometry in the open boundary condition, the 10 × 10 unit cell is used for the angles θ = 21.8∘, 13.2∘, and 9.4∘, which contains 2800, 7600, and 14,800 atoms, respectively. Here, we represent the replica HOTIs at a \(\phi =\frac{1}{14}{\Phi }_{1,2}\), b \(\phi =\frac{1}{38}{\Phi }_{2,3}\), and c \(\phi =\frac{1}{74}{\Phi }_{3,4}\) where Φm,n is the flux periodicity at given integers m and n.

Full size image

We find that the out-of-plane rotational symmetry C2x is essential to realize the re-entrant exact and replica HOTI phases in TBG under a magnetic field. In contrast to our model, there is no re-entrant corner state at half-flux periodicity in the magic-angle TBG model30 with only \({C}_{2z}{{{\mathcal{T}}}}\) symmetry, where the flux pumps corner states into the bulk. The disappearance of the corner states at half periodicity confirms the inapplicability of the Stiefel-Whitney characterization for the HOTI states in the presence of a magnetic field. This indicates that additional crystalline symmetry, such as C2x, is required to protect the corner states in TBG under a strong magnetic field.

In summary, we have demonstrated that HOTIs can occur without explicit protecting symmetries because of the self-similarity of Hofstadter butterflies as replicas of original HOTIs. We expect the distinct symmetry dependence of replica HOTIs can lead to distinct physical properties from the exact HOTIs (see Supplementary Note 6 for the detailed discussion). The HOTI marker is an invaluable tool for studying HOTI states in various situations beyond conventional methods using periodic boundary conditions. It offers the distinct advantage of being able to readily identify the HOTI phase, even at a small magnetic field in the open boundary condition. This is particularly advantageous compared to momentum-space methods relying on periodic boundary conditions, as they are computationally demanding at low magnetic fields, with their computational cost scaling inversely with the strength of the magnetic field. The exponents of our HOTI marker allows for quantitative analysis, which can be potentially useful for future study such as many-body disordered HOTIs. The observation of the replica HOTI at the fixed filling requires a huge magnetic field B ~ 105T, but replica topology may occur at different filling near low fields. Therefore, establishing an exact relationship between discrete scale invariance and band topology in this quantum fractal will be exciting future research with direct experimental implications. Additionally, a critical challenge that needs to be tackled in order to realize the observation is ensuring the stability of large TBG flakes under high magnetic fields. It would also be interesting to explore the Coulomb repulsion effect on replica phases at smaller angles, where the role of Coulomb repulsion is crucial59,60,61,62,63,64. With much progress in synthesis of moiré materials65,66,67,68,69,70 and measurement of Hofstadter energy spectrum33,71, our results can pave the way for studying replica topology under magnetic field in generic moiré multilayer67,68,69 and moiré quasiperodic70 systems that host multiple interaction scales.

Methods

Tight-binding model

We employ the Moon-Koshino tight-binding model for twisted bilayer graphene in ref. 44, which is written as

$$H=\mathop{\sum}\limits_{ij}{t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j}){c}_{{{{{\bf{R}}}}}_{i}}^{{\dagger} }{c}_{{{{{\bf{R}}}}}_{j}}+h.c.,$$
(6)

where \({c}_{{{{{\bf{R}}}}}_{i}}^{{\dagger} }\) (\({c}_{{{{{\bf{R}}}}}_{j}}\)) is a creation (annihilation) operator of an electron at the lattice site Ri, and tij(Ri − Rj) is the hopping integral between the sites Ri and Rj. The hopping integral is given by

$$-{t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j})={V}_{pp\pi }\left[1-{\left(\frac{{{{\bf{d}}}}\cdot \hat{{{{\bf{z}}}}}}{d}\right)}^{2}\right]+{V}_{pp\sigma }{\left(\frac{{{{\bf{d}}}}\cdot \hat{{{{\bf{z}}}}}}{d}\right)}^{2}.$$
(7)

Here, the hopping parameters are given as a decaying function of a hopping distance d = ∣d∣ = ∣Ri − Rj∣

$${V}_{pp\pi }={V}_{pp\pi }^{0}\exp \left(-\frac{d-{a}_{0}}{\delta }\right)\quad \,{{\mbox{and}}}\,\quad {V}_{pp\sigma }={V}_{pp\sigma }^{0}\exp \left(-\frac{d-{d}_{0}}{\delta }\right),$$
(8)

where a0 ≈ 1.42Å is the bond length of graphene, d0 ≈ 3.35Å is the interlayer distance, and δ = 0.319a0 is the decay length. Here, we set \({V}_{pp\pi }^{0}=-2.7\) eV and \({V}_{pp\sigma }^{0}=0.82\) eV, which reproduce the band structure of 21.8∘ twisted bilayer graphene with a bulk gap ~ 9 meV in a HOTI state47,48. Our tight-binding model under a periodic boundary condition (see atomic geometry used in Supplementary Figure 1) has 14 occupied pz orbital bands that consist of the same number of c2x = + 1 and c2x = − 1 bands, where c2x is an eigenvalue of a twofold rotational symmetry operator C2x about the x-axis. This implementation of the model successfully reproduces the nontrivial rotation-winding number (Fig. 3c) in line with the previous DFT results47. For the calculations of Hofstadter butterflies and topological markers, we use the flake geometry with an open boundary condition (see Supplementary Fig. 1).

To study the effect of the magnetic field, we incorporate a magnetic flux ϕ into the hoppings as an additional phase via Peierls substitution45:

$$\begin{array}{rcl}{t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j})&\to &{t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j})\exp \left(i\frac{e}{\hslash }\int\nolimits_{{{{{\bf{R}}}}}_{j}}^{{{{{\bf{R}}}}}_{i}}{{{{\bf{A}}}}}_{0}\cdot d{{{\bf{r}}}}\right)\\ &=&{t}_{ij}({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j})\exp \left[i\frac{e}{\hslash }\frac{\phi }{2{S}_{\min }}({x}_{i}+{x}_{j})({y}_{j}-{y}_{i})\right],\end{array}$$
(9)

where the vector potential \({{{{\bf{A}}}}}_{0}=B(0,x)=\frac{\phi }{{S}_{\min }}(0,x)\) for \({{{\bf{B}}}}=B\hat{z}\) and \({S}_{\min }\) is the interior area of the minimal Peierls path. We prove that our twisted bilayer graphene lattice has exact flux periodicity (see Supplementary Note 2). The Hofstadter energy spectrum of our system is thus periodic under the translation by a magnetic flux quantum \(\Phi =\frac{h}{e}\) because the Hamiltonian can be gauge transformed according to30

$$H(\phi +\Phi )={{{\mathcal{U}}}}({{{\bf{A}}}})H(\phi ){{{{\mathcal{U}}}}}^{{\dagger} }({{{\bf{A}}}}).$$
(10)

The unitary matrix \({{{\mathcal{U}}}}({{{\bf{A}}}})={\sum }_{{{{\bf{R}}}}}{c}_{{{{\bf{R}}}}}^{{\dagger} }{c}_{{{{\bf{R}}}}}\exp (i\frac{e}{\hslash }\int\nolimits_{{{{{\bf{r}}}}}_{0}}^{{{{\bf{R}}}}}{{{\bf{A}}}}\cdot d{{{\bf{r}}}})\) (r0: a fixed lattice site) is defined for the vector potential A( ≠ A0) that leads to the flux quantum \({\int}_{{S}_{\min }}(\nabla \times {{{\bf{A}}}})\cdot d{{{\bf{S}}}}=\Phi\).

Kernel polynomial method

Hofstadter butterflies of twisted bilayer graphene can be efficiently calculated by using the kernel polynomial method72. The essential idea of the kernel polynomial methods is to expand the density of states ρ(E) (E: energy) in terms of Chebyshev polynomials as,

$$\rho (E)=\pi \sqrt{1-{E}^{2}}\mathop{\sum }\limits_{n=0}^{M}{\mu }_{n}{U}_{n}(E),$$
(11)

where Un(E) is the second kind n-th Chebyshev polynomials,

$${U}_{n}(E)=\frac{\sin [(n+1)\arccos (E)]}{\sin [\arccos (E)]}.$$
(12)

Here, μn is the moment for an operator \(\hat{O}(E)\), which reads

$${\mu }_{n}=\frac{2}{{\pi }^{2}}\int\nolimits_{-1}^{1}dE\,\hat{O}(E){U}_{n}(E).$$
(13)

The targeting density of states operator \(\hat{\rho }(E)\) is given by

$$\hat{\rho }(E)=\frac{1}{N}\mathop{\sum }\limits_{k=1}^{N}\delta (E-{E}_{k}).$$
(14)

After putting \(\hat{\rho }(E)\) into μn, we obtain

$$\begin{array}{rcl}{\mu }_{n}&=&\frac{2}{{\pi }^{2}}\int\nolimits_{-1}^{1}dE\,\hat{\rho }(E){U}_{n}(E)\\ &=&\frac{2}{{\pi }^{2}}\frac{1}{N}\mathop{\sum }\limits_{k=1}^{N}{U}_{n}({E}_{k})\\ &=&\frac{2}{{\pi }^{2}}\frac{1}{N}\mathop{\sum }\limits_{k=1}^{N}\left\langle k\left\vert {U}_{n}(H)\right\vert k\right\rangle \\ &=&\frac{2}{{\pi }^{2}}{{{\rm{Tr}}}}({U}_{n}(H)).\end{array}$$
(15)

A stochastic approach is employed to obtain the trace by introducing the R-number of random vectors \(\left\vert r\right\rangle\), instead of (potentially unknown) exact eigenvectors:

$${{{\rm{Tr}}}}({U}_{m}(H))\simeq \frac{1}{R}\mathop{\sum }\limits_{r=1}^{R}\left\langle r\left\vert {U}_{m}(H)\right\vert r\right\rangle ,$$
(16)

where R is set to a sufficiently large value to attain the converged density of states. Then, we take advantage of a recursive relation for the polynomial,

$${U}_{m+1}=2H{U}_{m}-{U}_{m-1},$$
(17)

to rewrite the trace as

$${{{\rm{Tr}}}}({U}_{m}(H))\simeq \frac{1}{R}\mathop{\sum }\limits_{r=1}^{R}{\langle r| r\rangle }_{m},$$
(18)

where

$${\left\vert r\right\rangle }_{m}={U}_{m}(H)\left\vert r\right\rangle \quad \,{{\mbox{and}}}\,\quad {\left\vert r\right\rangle }_{m+1}=2H{\left\vert r\right\rangle }_{m}-{\left\vert r\right\rangle }_{m-1}.$$
(19)

As a result, the density of states is obtained as

$$\rho (E)=\frac{2}{\pi }\sqrt{1-{E}^{2}}\mathop{\sum }\limits_{n=0}^{M}{g}_{m}^{M}{{{\rm{Tr}}}}({U}_{m}(H)){U}_{n}(E),$$
(20)

where \({g}_{m}^{M}\) is the Jackson kernel,

$${g}_{m}^{M}=\frac{1}{M+1}\left[(M-m+1)\cos \frac{m\pi }{M+1}+\sin \frac{m\pi }{M+1}\cot \frac{\pi }{M+1}\right],$$
(21)

which is introduced to reduce the Gibbs oscillation72.

HOTI topological marker

Topological marker is a local quantity in real space that characterizes the topological phases38,39,40,41,42. The local Chern marker was first introduced as a topological marker whose spatial average in bulk in thermodynamic limit corresponds to the Chern number of the system38. The topological marker was then generalized to the topological crystalline insulating (TCI) phases, in which the topological states are protected by the spatial symmetries42. The generalized topological marker \({{{{\mathcal{T}}}}}_{G}({{{\bf{r}}}})\) related to the symmetry G is given by

$${{{{\mathcal{T}}}}}_{G}({{{\bf{r}}}})=\left\langle {{{\bf{r}}}}\right\vert \widetilde{G}{{{\mathcal{F}}}}(P)\left\vert {{{\bf{r}}}}\right\rangle ,$$
(22)

where \(\widetilde{G}=PGP\) is a projected symmetry operator and a function \({{{\mathcal{F}}}}(P)\) encodes the types of topological invariants. For example, \({{{\mathcal{F}}}}(P)\propto P[\hat{X},P]\) and \(P[[\hat{X},P],[\hat{Y},P]]\) for 1D winding39 and 2D Chern numbers38, respectively, where \(\hat{X}\) and \(\hat{Y}\) are position operators.

We extend the topological marker to a HOTI version in our twisted bilayer graphene system. The extension is straightforward because the HOTI phase in twisted bilayer graphene is protected by the C2x rotation symmetry resolved winding number, the rotation-winding number. Let us first see the topological marker χ(r) for the C2x symmetry, which is given by

$$\chi ({{{\bf{r}}}})\equiv {{{{\mathcal{T}}}}}_{{C}_{2x}}({{{\bf{r}}}})=\left\langle {{{\bf{r}}}}\right\vert {\widetilde{C}}_{2x}P[\hat{X},P]\left\vert {{{\bf{r}}}}\right\rangle =-\left\langle {{{\bf{r}}}}\right\vert {\widetilde{C}}_{2x}P\hat{X}Q\left\vert {{{\bf{r}}}}\right\rangle ,$$
(23)

where we used the relation Q = 1 − P in the last equality. By projecting the projection operators to the C2x rotation ± subspaces as P = P+ + P− and Q = Q+ + Q−, we obtain

$$\begin{array}{rcl}\chi ({{{\bf{r}}}})&=&-\left\langle {{{\bf{r}}}}\right\vert {\widetilde{C}}_{2x}P\hat{X}Q\left\vert {{{\bf{r}}}}\right\rangle \\ &=&-\left\langle {{{\bf{r}}}}\right\vert ({P}^{+}{C}_{2x}{P}^{+}+{P}^{-}{C}_{2x}{P}^{-})({P}^{+}\hat{X}{Q}^{+}+{P}^{-}\hat{X}{Q}^{-})\left\vert {{{\bf{r}}}}\right\rangle \\ &=&-\left\langle {{{\bf{r}}}}\right\vert ({P}^{+}{C}_{2x}{P}^{+}\hat{X}{Q}^{+}+{P}^{-}{C}_{2x}{P}^{-}\hat{X}{Q}^{-})\left\vert {{{\bf{r}}}}\right\rangle \\ &\equiv &{\chi }^{+}({{{\bf{r}}}})+{\chi }^{-}({{{\bf{r}}}}),\end{array}$$
(24)

where we used the condition P+P− = Q+Q− = PQ = 0. The C2x rotation-resolved topological marker χ±(r) serves as the real space local expression of the rotation-resolved Zak phase ν±.

Real-space behavior of HOTI marker

To understand the real-space behavior of the HOTI marker, we first consider the localization property of the topological markers for TCI phases. The topological markers for TCI phases feature the exponential localization from the subspace restricted by the spatial symmetries42,43. It is different from the case of the typical Chern insulators without symmetries where the localization sites of the topological marker are all the sites within the bulk38,40,41. In a TCI phase, protected by a spatial symmetry G, the eigenvalues of G classify the eigenstates of the Hamiltonian \(\{\left\vert {u}_{i}\right\rangle \}\) and thus the projection matrix for occupied states \(P={\sum }_{n\in occ.}\left\vert {u}_{n}\right\rangle \left\langle {u}_{n}\right\vert\) at the symmetry-invariant subspace \({{{\mathcal{S}}}}\). As a result, the bulk topology of a TCI phase is encoded by the projection matrix P at the invariant subspace \({{{\mathcal{S}}}}\), which allows the introduction of the real-space topological invariant, the topological marker \({{{{\mathcal{T}}}}}_{G}({{{\bf{r}}}})\) in Eq. (22). It is proven that the topological marker \({{{{\mathcal{T}}}}}_{G}({{{\bf{r}}}})\) exhibits the exponential localization from the fixed points \({{{{\bf{r}}}}}_{S}(\in {{{\mathcal{S}}}};{{{\mathcal{S}}}}=\{{{{\bf{r}}}}| G{{{\bf{r}}}}={{{\bf{r}}}}\})\) of the spatial symmetry G as42

$$| {{{{\mathcal{T}}}}}_{G}({{{\bf{r}}}})| < {{{\mathcal{O}}}}({e}^{-| {{{{\bf{r}}}}}_{S}-{{{\bf{r}}}}| /\zeta })\quad {{{\rm{when}}}}\quad | {{{{\bf{r}}}}}_{S}-{{{\bf{r}}}}| \gg \zeta .$$
(25)

Here the length scale ζ is rough in the order of the inverse gap/localization strength. We note that the localization property is fundamentally arising from the action of the projected symmetry operator \(\widetilde{G}\): the projection matrix P is exponentially localized for the insulators73,74,75 and the symmetry G restricts the localization site of the markers42,43. The localization property is more general than the exponentially localized Wannier functions because the topological marker is localized even in the presence of a nonzero Chern number, which prohibits the construction of localized Wannier functions.

In the case of C2x winding number, the presence of the projected symmetry operator \({\widetilde{C}}{\,}_{2x}^{\pm }\) gives rise to the exponential localization of the HOTI marker χ±(r) from the edge. The absence of the winding number allows for the C2x specification of the winding number, revealing the presence of the C2x-protected metallic edge states. As in the case of the known HOTI phases characterized by C2x winding number47,48, the corner state is the Su-Schrieffer-Heeger type domain wall state, arising from the gap opening of the edge states. The edge is the bulk of the corner states in the HOTI state. Due to the action of the projected symmetry operator \({\widetilde{C}}{\,}_{2x}^{\pm }\), our HOTI marker of HOTI states exhibits exponential localization from the edge rE as

$$| {\chi }^{\pm }({{{\bf{r}}}})| < {{{\mathcal{O}}}}({e}^{-| {{{{\bf{r}}}}}_{{{{\rm{E}}}}}-{{{\bf{r}}}}| /\zeta })\quad {{{\rm{when}}}}\quad | {{{{\bf{r}}}}}_{{{{\rm{E}}}}}-{{{\bf{r}}}}| \gg \zeta .$$
(26)

On the contrary, HOTI trivial cases do not show such localization behavior from the edge. Instead, they are linearly delocalized over the entire geometry ( ∝ the position operator \(\hat{X}\)) which follows from the form of the C2x-marker formula proportional to \(\hat{X}\) in Eq. (24).