Introduction

Silica crystals are a class of oxide materials that are used in a plethora of applications owing to their eco-friendly nature and their rich polymorphism that allows them to display widely different properties. For example, α-quartz is piezoelectric whereas α-cristobalite has a negative Poisson ratio. Zeolites add to the exceptional polymorphism of silica. The porosity of zeolites1,2,3,4,5,6 makes them outstanding as selective catalysts7,8,9,10,11,12, adsorbents13,14, and membranes15,16,17 in the gasoline industry, hydrocarbon separations, and desalination, respectively, with potential applications in aquaculture18 and photocatalysis19,20. High-pressure phases of silica include stishovite, a dense polymorph that is octahedrally coordinated and is of interest from a geological perspective, since it occurs in silica rich parts of subducted oceanic slabs and crystal fragments in the Earth’s mantle. There are about 240 zeolite frameworks recognized by the International Zeolite Association21 and plenty of hypothetical structures compiled into several databases. Given these large number of zeolite frameworks and polymorphs, it is important to develop models that can enhance our understanding of their properties and applications.

Molecular dynamics (MD) simulations represent an elegant way of capturing structure-property relationship at the nanoscale, as well to probe the mechanisms of growth and phase transitions materials. While ab initio techniques and first-principles calculations can be used22,23 to get an understanding of a system, they quickly become computationally expensive given the large unit cells of silica polymorphs and the number of possible configurations. Furthermore, ab initio simulations of silica are often limited by length-time scales, that circumscribe them for the dynamics of small clusters24,25. Faster models are required to access longer time scales and accurately capture the dynamical evolution of the structural features like the angular distribution between the tetrahedral units and even features such as charge distribution, when subject to external stimuli26,27,28.

It is therefore not surprising that have been several attempts over the past three decades to develop interatomic potential models that can elucidate dynamics and structural characteristics of silica polymorphs. The majority of empirical silica force fields are based on pairwise interactions, i.e., without an explicit three-body term, and differ in the type of charge assigned to capture the electrostatic interactions. Typically, the charge computation methodologies involve either shell–core or the rigid-ion models29. There have been extensive studies that compare the performance of different atomistic models for silica, including those using partial charges that suggest that even without the three-body term the predictions of these models across various polymorphs can be fairly reasonable when compared to experiments30.

For more details, we refer the reader to the review in ref. 29, which summarizes the performance of partial, formal charge and molecular mechanics type potentials. Amongst the various atomistic models based on pairwise interactions including partial charges, the one of van Beest, Kramer, and van Santen (BKS)31 seems to perform the best in capturing the energetic ordering of the select few silica polymorphs considered in their study while reasonably describing amorphous properties at ambient conditions, despite having been fitted primarily to α-quartz. Several notable silica models are a slight modification or reparameterisation of the existing BKS form, such as the CHIK32 and PSO33 models. Despite sharing the same functional form, the CHIK parameterization outperforms the original BKS in its description of amorphous systems. The improvement has been attributed to the additional silicon-silicon Buckingham-type interactions absent in the original BKS. Other attempts to improve upon the BKS model have been based on fine tuning of the silicon partial charge. These include the SHIK model34 that shares with CHIK significantly lower partial charges compared to those in the original BKS. It was concluded from these models that there must be a trade-off between the various structural, energetics and elastic properties depending on the choice of partial charges. Other studies aimed at incorporating more flexibility translated into more complex formalisms that implement polarization terms, charge transfer, and explicit three-body effects35,36,37,38. Despite several attempts at reparameterization and improved formalisms, the above potentials typically describe only a subset of the crystalline and amorphous forms, and often lack a fully accurate description of the relative energetic ordering of different polymorphs observed in the experiments. Recent improvements in machine learnt potentials39,40,41, such as the Gaussian Approximation Potential (GAP42) model, allow for higher flexibility and improvements in the predictions of the solid-amorphous phase properties. However, this gain in accuracy and flexibility comes at a 50 to 100 times increase in computational cost. Hence, it is desirable to retain the computationally effective models that can capture the physics of silica with interpretable interatomic potentials.

Historically, the development and reparameterization of interatomic potentials involve the use of optimization techniques that can efficiently navigate through the often high-dimensional parameter search space43,44,45. This is often a time-consuming and nontrivial process. For classical potential models with few to tens of parameters, the techniques used for optimization are primarily based on local optimization or gradient-based information46,47. These impose a requirement that the gradients of the objective function are well-defined. This approach can be efficient and has been a popular method for optimization32. Nonetheless, local optimization techniques remain limited in the search space that they can efficiently explore. Global optimization techniques, in contrast, have recently found tremendous success48,49,50,51. These techniques include genetic algorithms (GA), particle swarm, or Bayesian optimization which have been employed to explore a much wider parameter search space and obtain optimal set of parameters that perform well on several different physical, mechanical and thermodynamic properties52,53. A drawback of such global optimization techniques is that they often require a large number of evaluations (e.g., populations and generations in GA) to converge to an optimal solution54. The sluggish nature of the convergence combined with the solution quality tends to be poor, especially in higher dimensional search spaces. The search procedure can also become much more complicated when the aim is to fit multiple objectives (e.g., lattice constants, cohesive energies and elastic constants of a multitude of polymorphs55. In such cases, the search algorithms tend to either be biased towards a certain subset of properties depending on the selection of individual weights or depend on the preference of the user (in case of pareto-type) to pick an optimal parameter set from the pareto front56. The emergence of ML-based optimization techniques such as reinforcement learning (RL)-based search algorithms can help overcome this issue, especially when dozens of properties (for tens of different polymorphs) need to be concurrently captured57,58,59.

Here, we introduce a multireward reinforcement learning based workflow that allows us to reparameterize the coefficients of the BKS model and significantly improve its performance in capturing the properties of silica polymorphs. We employ a hierarchical reward system that eliminates the property bias associated with weight selection during the search process. This allows us to concurrently capture and improve the relative energetic ordering amongst the polymorphs, their lattice parameters, densities, cohesive energies as well as elastic constants compared to the available experimental training and test datasets. We show that in the BKS formalism, the improvements in capturing the crystal properties come at the expense of liquid and amorphous properties. To address this limitation, we introduce the ML-BKS formalism that includes an additional repulsive WCA-type interaction that allows for capturing the liquid and amorphous properties without sacrificing the improvements in those of the crystal polymorphs. We compare the performance of these two models to several existing, empirically fitted interatomic potentials and discuss the origin of the improvements. We find that the inclusion of Si–Si interaction allows us an additional degree of freedom which significantly improves the overall performance of the ML-BKS model. We also discuss, more generally, the criteria for evaluating the quality of interatomic potentials in terms of their computational cost, predictive power, and the need for better formalisms to overcome the limitations of existing empirical potential models.

Results and discussion

We build upon our recently developed multireward reinforcement learning workflow60 and train a physics-based model with BKS formalism to an available experimental dataset of 21 silica polymorphs, including 17 silica zeolites (see “Methods”). In the methods, we first describe the functional forms used in our work, and then explain our multireward hierarchical reinforcement learning workflow. The RL method is used to navigate through 16-dimensional BKS potential surface. We also discuss a formalism of machine learnt BKS (ML-BKS) which includes an additional WCA-type repulsive interaction that enables the model to describe both the crystals and the liquid and amorphous phases of silica. Finally, we provide details on the atomistic simulations used for property evaluation of the various crystalline silica polymorphs as well as liquid/amorphous phases. Below, we discuss the application of our c-MCTS RL workflow to develop and parameterize silica models.

c-MCTS-trained optimal parameter set

We deploy the hierarchical c-MCTS workflow to optimize the parameters of the BKS force field with an expanded training dataset that includes the experimental densities, energetics, and structural features of 21 different silica polymorphs. c-MCTS is able to successfully navigate through the 16-dimensional parameter space and arrive at the optimal set of parameters (Table 1). The evolution of the best objective score is shown in Supplementary Fig. 1 (see Supplementary Information). We observe that the objective function, which represents the difference between the model and target properties, has a sharp drop within the first 1000 evaluations. This fast convergence is due to the hierarchical multireward scheme implemented in this work.

Table 1 ML-BKS-Solids model parameters for crystalline silica polymorphs obtained in this work.
Full size table

The initial ranges chosen for each of the parameter sets are quite broad as seen from Supplementary Table S1—an advantage of the hierarchical multireward scheme is that it rank-orders the multiple properties depending on the choice of the user and sets a threshold for the evaluation of each of the different properties (of several polymorphs in this case). However, it is typical to include structural features such as lattice parameters and density first followed by energetics (cohesive energy) and subsequently equations of state, elastic constants, etc. This is to ensure that the target elastic constants and other properties are mapped to the correct polymorph and allows the algorithm to exploration of search space where the parameter sets correspond to sub-optimal solutions. In other words, the c-MCTS algorithm avoids getting trapped in a sub-optimal minima. As a result, the objective or cost function shows a rapid decrease in the score. Subsequently, once the solution approaches a decent minimum, there is a rather slower decay in the objective score as the algorithm starts to exploit more near the search space to approach the best possible minimum for the defined objective. It takes around 10,000 total evaluations to reach this minimum. The final optimal set of parameters corresponding to this minimum is reported in Table 1.

We compare the normalized objective score obtained in this work with other parameterizations of the BKS models (see Supplementary Fig. 2). We note that the ML-BKS-Solids model has a lower objective score on our experimental training dataset compared to the existing parameterizations. A quick comparison of the ML-BKS-Solids model parameters with other parameterizations of BKS model are shown in Table 2. Unlike the existing force-field models (BKS, SHIK, CHIK, PSO-1, PSO-2) that have a fixed cutoff distance for all Van der Waals interactions, the optimal ML-BKS-Solids has 11 Å, 5.5 Å, 7.4 Å for Si–Si, O–O, and Si–O Buckingham interactions, respectively. These cut-offs are thus all different in the optimal parameter set. A more detailed discussion on the comparison of the different model parameters and their predictions is provided in “Discussion”.

Table 2 Comparison of the electrostatic and Buckingham parameters in the ML-BKS-Solids and ML-BKS models developed in this work and previous parameterizations.
Full size table

Predictions of crystal properties of silica polymorphs

We first assess the performance of the trained ML-BKS-Solids model on its ability to predict the experimentally determined cohesive energies, densities, Si–O–Si and O–Si–O angles across 21 different silica polymorphs. In general, we compare the calculated structure, energetics and mechanical properties of α-quartz and the other silica polymorphs with experiments. α-quartz is the thermodynamically stable phase of quartz under ambient conditions. It is trigonal with a 9-atom unit cell and P3121 space group symmetry. This phase has been exhaustively studied in the past and represents one of the main sources of data for parametrization of silica interatomic potentials. We use as initial models the structure corresponding to the experimental X-ray resolved unit cells for each polymorph and subject them to an energy minimization process at constant pressure, allowing for the optimization of all the lattice parameters. The cohesive energies for α-quartz as well as the relative energies of the various polymorphs with respect to the α-quartz are also compared. For the structural properties, we compare the densities as well as the bond distances Si–O, Si–Si and the angles between Si–O–Si and O–Si–O triplets. These properties allow us to assess the structural features predicted by the different force fields relative to those determined in experiments. The training dataset includes the lattice and energies of the 21 polymorphs, which allow us to capture the global features. In addition, their densities and angular distributions ensure the learning of the local environment. While the four properties in Fig. 1 are the quantities used to optimize the model parameters, we have also characterized the elastic properties, structure factor, and melting point to showcase the robustness of the model (see "Testing of ML-BKS model", below). The optimized parameter set is shown in Table 3.

Fig. 1: Multireward RL workflow to train the silica models.
figure 1

The training set consists of the experimental structure and energetics of 21 silica polymorphs, including 17 zeolites. The multireward technique gives the choice to tune the parameters based on the relative importance of the target desired properties. The global optimization is performed using Monte Carlo Tree Search (MCTS) while the parameter set satisfying all the different stages of objectives is fed into Simplex for local optimization. More details are presented in the Methods section.

Full size image
Table 3 Full set of parameters of the ML-BKS model, developed for simulations of the amorphous and crystalline polymorphs of silica.
Full size table

Figure 2 compares the predictions made by the ML-BKS-Solids model with those of other silica force fields, including the recently developed machine learning potential GAP42. The relative cohesive energies of the various polymorphs with respect to α-quartz are plotted on the LHS of Fig. 1a, and the corresponding absolute errors are plotted on the RHS. Figure 2a shows that while the general trend is correctly captured by the original BKS as well as the CHIK parameterization, these models show high error in the relative cohesive energies, in the 0.1–0.2 eV atom−1 range, for highly metastable polymorphs when compared to the experiments. The PSO-1 and PSO-2 parameterizations that used particle swarm-based optimization improve the predictions, resulting in errors in cohesive energies within 0.1 eV atom−1. The ML-BKS-Solids significantly improves the predictions, resulting in errors much below 0.03 eV atom−1 and perfect agreement with the experimental relative energy ordering of the polymorphs. The GAP42 model also has low errors of about 0.02 eV atom−1 for most polymorphs, but does not capture the experimental ordering for the least stable or highly metastable silica polymorphs such as the pure silica zeolites CHA, FAU, MEI, and ISV.

Fig. 2: Comparison of select properties and structural features of silica polymorphs predicted by different models.
figure 2

a Relative cohesive energy with respect to α-quartz, b Density, c Si–O–Si angle, d O–Si–O angle. All the properties were computed at 300 K in order to compare with the reference experimental values from ref. 69. ML-BKS-Solids (abbreviated here as M-B-S) is the model developed in this work. Table shows the absolute error (AE) or relative percent error (RE) with respect to the experimental values.

Full size image

Figure 2b compares the density predictions of the various models, including ML-BKS-Solids. It can be noted that all models present similar deviations from the experimental densities; the performance of the models is comparable for this property, with errors in the 10–20% range. We find that the original BKS model, which imposes a higher partial charge on the atoms (Table 2), captures the trend of the curve of experimental densities, but underpredicts this property for the lower-density silica polymorphs. Although the under-prediction of density could be attributed to the partial charge assigned to the silicon atom, it must be noted that an increase in the Si–O-Si angle (Fig. 2c) results in a higher margin of error. We conclude that the large magnitude in partial charges results in greater repulsive forces that favor open structures. This leads to lower densities than in the experiments. Note that the CHIK model is similar to the BKS model and also suffers from under-prediction of the density. It is counterintuitive that the CHIK model performs worse than the original BKS despite featuring a lower partial charge. We attribute this to the additional Si–Si interactions considered by the CHIK model. Therefore, the CHIK model needs to be much “softer” than the original BKS to compensate for the effect of added Si–Si repulsive forces. It should be noted that the increased accuracy in the cohesive energies comes at the cost of higher errors in densities. Next, we observe that PSO-2, which is slightly lower on the partial charge than BKS displays the same behavior as BKS, with only a slight improvement in density predictions. While the energetics have improved in PSO-2, we find that the ordering of energies of the polymorphs is sacrificed. Similarly, we note that PSO-1, which has a much lower partial charge (i.e., is soft), shows an improvement in density prediction with a better cohesive energy ordering. ML-BKS-Solids has the lowest partial charge amongst the models considered, i.e., it is much softer compared to models reported previously. It performs as well as the PSO-1 model for the densities but has a much lower error in cohesive energies, while improving the relative energetic ordering. The success of ML-BKS-Solids suggests that Si–Si interactions must also be considered for a better representation of both energy and density.

We further inspect the angular distribution for all the polymorphs in the training set. Figure 2c, d corresponds to the intra-tetrahedral O–Si–O and inter-tetrahedral Si–O–Si angles, respectively, represented as the weighted average of the angular distributions in each polymorph. Figure 2d shows that, the intra-tetrahedral angle O–Si–O is fairly well and similarly predicted by all the models, with very low error that suggests that this angle is less sensitive to the imposed partial charges. For the BKS model, the largest errors for the Si–O-Si angle is 10° for the high-density polymorphs. The CHIK parameterization slightly improves with maximum errors of 7°. Interestingly, the PSO parameterization shows higher errors in the Si–O–Si angle, even for low-density polymorphs. The Gaussian approximation potential GAP42 model generally shows low error, except for a few polymorphs such as FER (10°), CFI (6°) and MWW (7°). The predictions of the ML-BKS-Solids model are the more accurate among all the BKS-type models considered in this work, and comparable to those of the much more expensive GAP42 model. This result supports the hypothesis that a lower partial charge reduces the magnitude of repulsive forces that otherwise might lead to a more open (i.e., lower-density) structure. Moreover, ML-BKS-Solids captures best the density of the high-density polymorphs without sacrificing the accuracy for the lower-density zeolites.

Predictions of ML-BKS-Solids model for amorphous silica

We next evaluate the ability of the optimized ML-BKS-Solids to model amorphous silica. We perform the simulations at around 1500 K (see “Methods”) in order to check the stability of the force field to the Buckingham catastrophe at high temperatures, as well as to compare the structural characteristics of amorphous silica. We find that although the ML-BKS-Solids model performs very well in capturing the properties of the crystalline polymorphs, it is dynamically unstable at 1500 K i.e., fails in simulating the amorphous structures at higher temperatures such as 1500 K and beyond. We find that the failure originates in Buckingham’s catastrophe: the soft nature of the ML-BKS-Solids model allows it to enter the unphysical short-range region of steeply attractive Si–Si interactions of the Buckingham’s potential (Fig. 3a). The O–O interactions shown in Fig. 3b and the Si–O interactions shown in Fig. 3 for the ML-BKS-Solids do not seem to have this issue (Fig. 3b, c).

Fig. 3: Potential energy for the three pairwise interactions across different models with BKS formalism.
figure 3

a Si-Si interaction, b O-O interaction, and c Si-O interaction as a function of the interatomic distance.

Full size image

We then investigate the origin of such erroneous force predictions by the ML-BKS-Solids model at high temperatures. Figure 3a shows that the potential energy curve for Si–Si interactions in the ML-BKS-Solids model has a maximum at 1.8 Å and the Si–Si interaction is attractive at shorter distances. Though the equilibrium bond length of Si atoms is around 3.2 Å, we find that the relatively low charges on the silicon atoms enables Si–Si bond distances at high temperatures (see the radial distribution function shown in Supplementary information). The unphysical attraction of the potential energy curve for these atoms at short distances destabilizes simulations of the amorphous phases. We note that such features are absent in the original BKS and PSO parameterization, because they have larger partial charges that push the region of unphysical attraction to extremely small interatomic distances (Fig. 3). Although the other parameterizations such as BKS and even PSO models have a maximum at 1.2 Å for Si–O interaction, such distances are not effective sampled at moderately high temperatures and do not impact the dynamical stability. However, at high pressures, such parameterizations might also result in unphysical forces due to the absence of repulsive regimes at short Si–O distances.

ML-BKS formalism to model both crystal polymorphs and amorphous silica

To address the cause of dynamic stabilities at high temperatures and to adequately represent the structural/dynamical properties of liquid/amorphous phase, we modify the functional form of the ML-BKS- Solids model to include an additional repulsive term that prevents the sampling of the configurations with much shorter Si–Si bond lengths. We model this repulsive interaction with the Weeks–Chandler–Andersen potential (WCA, see Eq. (4)). By placing the WCA repulsion for the Si–Si interaction at σ = 2.8 Å, the Si–Si potential becomes purely repulsive at short distances (Fig. 4a), without affecting the Si–Si interactions in the region that is accessed by the silica crystals. The result is a model that does not impact the ML-BKS-Solids predictions for the crystals while improving the predictions for the liquid phase because it prevents the unphysical attraction that fails the Buckingham potential at shorter distances. We term this hybrid ML-BKS-Solids/WCA model as ML-BKS, and demonstrate below that it efficiently simulates both solids and liquid phases of silica.

Fig. 4: Comparison of the pairwise potential energies and radial distribution functions of the liquid in the ML-BKS and ML-BKS-Solids models.
figure 4

Panels on the left present the pairwise a Si-Si, b O-O, and c Si-O interaction energy plots, comparing ML-BKS parameterization with WCA repulsion between Si atom, and the ML-BKS solids that does not have WCA terms. Panels on the column on the right present the corresponding d Si-Si, e O-O, and f Si-O radial distribution functions for liquid silica at 2000 K.

Full size image

Figure 4 represents the Si–Si, Si–O, and O–O pairwise potential interactions as a function of the corresponding interatomic distance. The addition of the repulsive interaction clearly eliminates the Buckingham catastrophe that ails ML-BKS-Solids. The figure shows that the correction applied to the Si–Si interactions does not affect other pairwise interactions, and the equilibrium bond distances match with the experimental values. We note that the addition of the WCA term in the ML-BKS potential serves the same purpose as the D r−24 term used in models such as CHIK, PSO-1, and PSO-2, but with the advantage that it can be implemented using a Lennard–Jones potential (see Eq. (4)). Moreover, owing to the r−12 dependence it does not require extremely small time steps in the integration of the equations of motion to conserve the energy.

We aim to develop a model that concurrently captures the properties of both the crystalline polymorphs as well as amorphous/liquid phases. Figure 4 RHS presents the radial distribution functions, 5, for Si–Si, Si–O, and O–O interactions in the ML-BKS model; the dashed vertical lines show the position of the first peaks determined from experimental methods61,62. In Fig. 5, we compare the experimental structure factor S(q) of amorphous silica62 and the predictions of the ML-BKS model. The model represents well the intensity and positions of the peaks in the structure factor S(q)42. We conclude that ML-BKS accurately captures the structure of amorphous silica. The performance of the ML-BKS is on-par or better than several of the existing models based on similar formalism—one can refer to the work in ref. 42 to draw a comparison on the structural factor of glassy silica predicted by other notable parameterizations of the classical force fields of silica.

Fig. 5: Structure factor of silica glass at 300 K.
figure 5

The experimental curve from ref. 62 is shown in blue, and the prediction of the ML-BKS model in orange.

Full size image

Next, we want to ensure that the ML-BKS has not compromised the predictions of the crystal properties. In Fig. 6, we compare the various crystal properties as we did for ML-BKS-Solids in Fig. 2. The corresponding errors in the prediction between the ML-BKS-Solids and the ML-BKS models remain low and unchanged, confirming that the crystal properties are unaffected by the addition of the WCA term. This is not surprising because the unphysical interactions at interatomic distances (less than 1.8 Å) were sampled only at high temperatures in the amorphous phase and are irrelevant for crystal phases of silica. Thus, the ML-BKS-Solids and ML-BKS model predictions of crystal properties are similar. For the low-temperature simulations (e.g., at 300 K) of crystalline silica polymorphs, one can safely omit the WCA functional form and use the ML-BKS-Solid model.

Fig. 6: Comparison of the predictions of the two models of this study, ML-BKS-Solids and ML-BKS, and the experimental properties.
figure 6

a cohesive energy relative to quartz, b density, c Si–O–Si angles, and d O–Si–O angles. Here M–B–S refers to ML-BKS-Solids.

Full size image

Testing of ML-BKS model

We next present a comprehensive evaluation of the elastic constants, phonon dispersion and thermodynamic properties of silica polymorphs using ML-BKS as well as other silica force fields.

Elastic constants

First, the elastic constants of α-quartz were computed using the ML-BKS model. While the experimental, BKS and CHIK elastic constants are available in the literature32, the predictions for PSO-1 and PSO-2 models were not available and were computed in this work. Elastic constants were part of the training set in the development and optimization of both BKS and CHIK force fields,. However, it is worth noting that neither of the PSO models were optimized for α-quartz and they primarily considered the mechanical properties of amorphous silica.

Figure 7 shows the comparison of the elastic constants for the various models relative to the experiments. If the agreement between model and experimental value were perfect, then the values would coincide with the center of the spider plot. The greater the deviation, the farther from the center of the spider plot. The corresponding percentage mean absolute errors in the various elastic constants are also tabulated in Fig. 7. We note that the original BKS performs quite well and the errors are generally less than 30% for most elastic constants except the shear ones (C12 ~ 48% and C13 ~ 40%). ML-BKS improves upon these predictions without sacrificing the other elastic constants except C14 ~ 40%. We note that other models such as PSO-1, CHIK, and even the GAP42 potential have much higher errors for C12 and/or greater than 100% for C13. Elastic constants of PSO-2 were already reported33 to be erroneous and hence were not included in the comparison. It appears that the higher accuracy of BKS and ML-BKS is a result of closer agreement to the Si–O–Si angles to the reference values across different crystals. Moreover, we do not observe any explicit influence of partial charges on the mechanical predictions made by ML-BKS. Overall, the ML-BKS captures quite well the elastic constants of α-quartz when compared to experiments.

Fig. 7: Elastic Properties of α-quartz computed using different models.
figure 7

Spider plots indicate the deviation with respect to experiment and the Table shows the percentage absolute errors. Each concentric circle corresponds to a 25% error.

Full size image

Melting of cristobalite

To estimate the melting temperature of cristobalite, we heat a simulation cell containing only cristobalite from 300 to 3000 K and monitor the enthalpy as a function of temperature. Figure 8a shows that there is a jump in enthalpy at around 2200 K that corresponds to the melting of cristobalite, confirmed by visual inspection of the simulation trajectory. This melting is not in equilibrium, but one-phase melting that should involve significant superheating for the nucleation of the liquid phase. Considering that the experimental melting temperature of cristobalite is 1999 K63 we use the enthalpy spike around 2000 K to estimate the enthalpy of melting. We find that the melting enthalpy is 11.25 KJ/mol, 26% larger than the experimentally reported value of 8.9 ∓ +− 1 KJ/mol. The original BKS model strongly overestimates the melting temperature of cristobalite, resulting in one-phase melting at temperatures over 4400 K64 at same heating rate.

Fig. 8: Solid–liquid and interface of β-cristobalite in simulations with ML-BKS.
figure 8

a Corresponds to the change in enthalpy with temperature at a heating rate of 1.7 K/ps, b corresponds to the change in enthalpy of the solid–liquid interface system with temperature, snapshot of the interface c at 1400 K, d 1480 K, e 1500 K in simulations with a heating rate 2.2 K/ps.

Full size image

To fine tune the melting temperature of cristobalite in the ML-BKS model, we perform MD simulations for the two-phase cristobalite-amorphous system described previously, and track ratio of crystal and amorphous (by following the position of the solid–liquid interface, see methods) as the system is heated at a rate of 2200 K/ns (see “Methods”). Figure 8b shows the temperature evolution of the enthalpy for the two-phase system, where we can observe the slight change in the slope around 1500 K. To accurately assess the melting temperature, we have tried using slower heating kinetics by accessing longer time scales up to 10 ns at 1400 K (Fig. 8c). We find that the interface remained intact after 10 ns at 1400 K, as seen in the snapshot shown in (Fig. 8c). The crystal-amorphous interface begins to undergo a rapid transformation at 1480 K, as seen in Fig. 8d. The transformation to an amorphous phase is complete at 1500 K (Fig. 8e). For comparison, the two-phase melting of cristobalite in the BKS model occurs at 3600 K64. However, we do not observe growth of cristobalite at temperatures below 1500 K; the dynamics is too sluggish compared to the time scales accessible to the simulations. We note that spontaneous growth of cristobalite has never been observed in molecular simulations of any model. The only example of growth of cristobalite, using the Takada65 force field, has been achieved using metadynamics simulations66.

Phonon dispersion

An important metric to ascertain the predictive power of any force field, especially for crystalline solids, is to compare the phonon dispersion relations with experiments or ab initio calculations. Phonon dispersions are defined as the reciprocal space k dependence of the frequencies, ω(k,j), of the normal modes for all branches j and selected directions in the crystal. Typically, the number of phonon branches, j = 1, 2, …, 3r, is equal to the number of degrees of freedom in the primitive unit cell. Every point on the phonon dispersion curve ω(k,j) corresponds to a frequency of a phonon, which can be visualized as a dynamical wave of length λ = 1/k, propagating along the k/k direction. Atoms in this wave vibrate with frequency ω(k,j). The high-symmetry directions Γ − X, X–M, M − Γ and Γ − R connect the high-symmetry points Γ − X = (0, 0, 0), X = (1/2, 0, 0), M = (1/2, 1/2, 0), R = (1/2, 1/2, 1/2) of the primitive cubic Brillouin zone.

Figure 9 compares the experimental67 and ML-BKS phonon dispersion for α-quartz. Our ML-BKS model displays high accuracy and the acoustic branches closely matches previous experimental data. The predictions are an improvement over the previous parameterizations, including the original BKS models and are on-par with the CHIK parameterization which also predicted phonon dispersion quite well. Other parameterizations such as the Broughton and the Vashishta potentials have the acoustic branches scaled by a somewhat constant factor compared to experimental results. In our case, the predictions and slope of the various acoustic branches at the Γ point are in good agreement compared to experiments but show a deviation near the K point. The recently developed ML potential GAP42 shows the highest accuracy, with only a very slight deviation near the K point (see Supplementary Fig. S5). Overall, the ML-BKS model provides a reasonable description of the phonon dispersion properties of α-quartz.

Fig. 9: Phonon dispersion of α-quartz predicted by ML-BKS compared to the experiments.
figure 9

The experimental results are shown with dashed black lines, and the predictions of ML-BOP with red lines.

Full size image

Conclusions

In this work, we introduce a parameterization and a new formalism for the BKS potential for silica using a multireward reinforcement learning algorithm. The models from this work, ML-BKS-solids and ML-BKS, represent improvements over the existing BKS parameterizations in their ability to describe the energetics and relative ordering of a wide range of cristalline silica polymorphs with respect to α-quartz, including the 17 silica zeolites for which the energetics are available from experiments. We have also assessed the structure of these 21 silica polymorphs, as well as the elastic constants and phonon dispersion of α-quartz, the melting of cristobalite, and the structural characteristics of the amorphous phase. Although the discussion below focuses on silica polymorphs, the arguments are generally applicable to other zeolitic and hierarchical materials. A summary of the comparison of the performance of the ML-BKS to all popular existing models of silica, including the recently developed machine learnt GAP42 model is shown in Fig. 2 (see Supplementary Information). We find that our parameterization of BKS improves upon the already good predictions of the original BKS model. In particular, the structural features (density, Si–O–Si and O–Si–O angles) and elastic constants are predicted quite well by the BKS-type BKS, CHIK, and PSO-2 potentials. The more complex GAP42 model also shows excellent predictions and can achieve a more comprehensive description of the phase stability than the BKS-type models. The ML-BKS model performs on-par with GAP42, and even displays improved predictions of phase stability of compact and porous silica polymorphs relative to α-quartz.

We note that ML-BKS-Solids and ML-BKS are based on rather simple analytical potentials, which results in computationally efficient evolution of their dynamics. ML-BKS-Solids has the same functional form as the original BKS, CHIK, SHIK and PSO models. However, the performance of the ML-BKS-Solids for crystalline solids is significantly improved. Note that one of the main differences between previous BKS-type models and ML-BKS is the reduction in the effective charge on the atoms, from 2.4 e to around 1.785 e for Si (half these values for O). Thus, the ML-BKS model is much “softer” compared to the original BKS as well as CHIK (1.91 e), and PSO-2 models (2.35 e) that typically do well on crystalline and amorphous systems. In general, we note that “hard” models, i.e., with higher Si partial charges, tend to underpredict the densities and overpredict the cohesive energies of the polymorphs30. We hypothesize that the higher magnitude of partial charges causes greater repulsive forces that leads to a much more open structure i.e., atoms are pushed away leading to lower-density predictions in comparison to the experimental values. Consequently, the cohesive energies of the hard BKS-type parameterizations tend to be underestimated, which is consistent with the increased repulsion. The soft ML-BKS parameterization addresses both of these limitations and thus provides an improved description of the structure and energetics of the various polymorphs. Interestingly, the PSO-1 model (charge +1.79  for Si) parameterized using particle swarm is as soft as the ML-BKS models, but tends to perform poorly in predicting crystalline properties, especially the elastic constants and phonons. This suggests that the non-electrostatic pairwise interactions are more optimal in ML-BKS compared to the PSO-1 parameterization. The GAP42 model has a more flexible functional form and predicts silica properties in very good agreement with experiments, which is particularly impressive considering that its training data was not experimental data but a SCAN-derived dataset. The ML-BKS model performs on-par with the GAP42 model but with a much simple two-body interaction, which is quite remarkable and computationally advantageous.

We note that BKS, CHIK, SHIK, PSO-1, PSO-2, and the ML-BKS-Solids models developed in this work have all the same Buckingham plus coulomb form, but their performances are widely different. The training datasets and parameterization strategies utilized for the different models result in the different optimal sets of parameters, shown in Supplementary Table 1. Capturing the crystal properties of the different polymorphs with a single model is nontrivial; it customarily requires defining multi-objective cost functions which typically present the challenge of defining weights for each of the individual properties. This can induce bias in that a subset of polymorphs and/or properties are fit better than the others. The multireward hierarchical scheme of this work overcomes this bias and defines the cost function analogous to stagewise rewards in computer games. As a result, the MCTS decision tree is able to explore and exploit regions of the parameter space that favor higher rewards, i.e., a better fit to as many polymorph properties as possible for the defined functional form. The MCTS algorithm is able to effectively navigate around sub-optimal regions in the parameter space by growing other branches of the tree effectively utilizing the trade-off mechanism between exploration and exploitation. MCTS simultaneously explores potentially better pathways to reach the optimal point in a search space, and exploits pathways that have the greatest estimate value of the multireward cost function. This combination of exploration and exploitation, together with an appropriate trade-off mechanism between them, represents a powerful strategy of identifying optimal parameter sets for a given functional form.

We also note that the fixed functional form of BKS potentials impose limitations. Although the predictions of the ML-BKS-Solids model are a significant improvement over the existing parameterizations for the crystalline silica polymorphs properties when compared to experiments, we find that ML-BKS-Solids is unstable for the modeling of the liquid phase. We systematically compare the various pairwise interactions and conclude that the dynamic instability arises from the lack of repulsive interactions at short distances in the Si–Si interaction of ML-BKS-Solids. Such issues with dynamical stabilities have also been observed in prior parameterizations of BKS-type models, and the PSO models include a D r−24 term to avoid them. Here, we opt for the addition of a computationally efficient, shifted LJ repulsive term analogous to the WCA functional form for the Si–Si interaction. The resulting formalism of Buckingham plus coulomb plus WCA is termed ML-BKS and is shown to capture the amorphous properties very well when compared to experiments, without sacrificing the improvements obtained in the crystalline properties for the ML-BKS-solid potential.

Despite the improvements, there is always an upper limit that can be attained with simple, pairwise functional forms such as BKS. Further improvements in the structure and energetics for the wide range of silica polymorphs would require more flexibility in the functional form, such as for example, via the incorporation of explicit three-body interactions. In this respect, the recent developments in machine learnt potentials such as GAP42 offer encouraging prospects. It should however be noted that the computational cost of GAP42 is still 10 to 100 times higher than that of simple pairwise interaction potentials. Symbolic regression approaches such as genetic programming can allow for search of two-body and/or short-range three-body corrections to the existing BKS functional form. Such an approach would retain the computational efficiency of ML-BKS while incorporating more flexibility.

An advantage of the ML-BKS models, however, lies in their simplicity and interpretability, since the functional form is based on the physics of molecular interactions (electrostatics plus van der Waals interactions). While physical models are less flexible than neural networks, they also impose constraints that ensure that they can work well in scenarios beyond those presented by the training dataset. To further ensure reliable model predictions, we have performed short timescale MD equilibration on-the-fly during our training workflow. This helps to relax the initial structures and obtain time-averaged predictions with the associated uncertainties. Moreover, we used a large enough simulation box size to address any inconsistencies between the predicted vs. target structures and densities arising from finite size effects.

The ML-BKS all-atom model could be used to understand the phase behavior and mechanical properties of silica polymorphs. However, the slow dynamics of breaking and reforming bonds in silica requires accessing long simulation time scales, that could only be achieved with shorter-range and/or coarser-grained models. Combined with the recent developments in powerful machine learning potentials such as GAP42, the ML-BKS model along with future coarser-grained models would allow for prediction of structural evolution and dynamical properties of silica polymorphs across a wide range of applications.

Methods

Functional form

We utilize two types of formalisms for our study. First, we aim to reparameterize the BKS-type functional form (we term that optimized ML-BKS-Solids). Next, we describe a modification to this BKS functional form to include an additional term similar to the WCA formalism68 (we name that ML-BKS). The two are briefly described below:

$${V}^{ML-BKS-Solids}({r}_{ij})={V}^{BKS}({r}_{ij})$$
(1)
$${V}^{ML-BKS}({r}_{ij})={V}^{BKS}({r}_{ij})+{V}^{WCA}({r}_{ij})$$
(2)

in which, VBKS constitutes short-range Van der Waals interactions in the usual Buckingham form plus a long-range Coloumbic term with partial charges while VWCA models the repulsive component of a Lennard–Jones interaction

$${V}^{BKS}({r}_{ij})=\mathop{\sum}\limits_{i\ne j}{q}_{i}{q}_{j}/{r}_{ij}+{A}_{ij}exp(-{r}_{ij}/rh{o}_{ij})-{C}_{ij}/{r}_{ij}^{6}$$
(3)
$${V}^{WCA}({r}_{ij})=\left\{\begin{array}{ll}\mathop{\sum}\limits_{i\ne j}{V}^{LJ}({r}_{ij})-{V}^{LJ}({2}^{1/6}\sigma )\quad &{r}_{ij}\le {2}^{1/6}\sigma \\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.$$
(4)
$${V}^{LJ}({r}_{ij})=4\epsilon [{(\sigma /{r}_{ij})}^{12}-{(\sigma /{r}_{ij})}^{6}]$$
(5)

The VWCA term is added only to the Si-Si interactions, to prevent the well-known catastrophic collapse that originates in the highly attractive nature of Buckingham potential at very short distances. We use the Ewald summation for long-range Coulombic (cutoff of 11 Å) while the short-range interactions are determined as part of the training process.

Training data

The parameters of the ML-BKS-Solids and ML-BKS model are trained against experimental data available for 21 silica polymorphs69. This training data consists of the various polymorph structures, densities, and relative cohesive energies tagged to 21 experimentally realized silica polymorphs. The energetics were obtained from enthalpies of formation of the crystals obtained through high-temperature calorimetry70. All this data has been reported at standard conditions.

Test data

To test the optimized models, we compare the elastic constants for α-quartz reported in ref. 32. This work compares predictions made by the original BKS and the reparameterized CHIK model to an experimental reference. In this work, we additionally computed the elastic constants for the PSO-based model and make a comparison with the predictions of our ML-trained models. The procedure to compute elastic constants is described in the molecular modeling section. In addition, our test dataset includes the experimental enthalpy of melting of cristobalite at its experimental melting point63 which allows us to compare thermodynamic predictions of our models at high temperatures.

Multireward reinforcement learning workflow

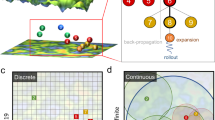
We utilize the reinforcement learning (RL)-based workflow described in Fig. 1. Our RL approach is based on the use of a decision tree, i.e., Monte Carlo Tree Search (MCTS). The MCTS tree consists of several nodes, each of which contains a unique BKS parameter set. In the RL approach, the main idea is to grow those tree branches that contain nodes with promising parameter sets. To achieve this, the head node of the MCTS tree is initialized randomly with a ML-BKS-Solids or ML-BKS parameter set and then the four stages of MCTS are executed iteratively using a learning policy with modifications to enable operation in a continuous search space as described in our recent work71.

Having defined the objective evaluation strategy, we now provide an overview on our optimization engine, the Monte Carlo Tree Search (MCTS) algorithm. Our c-MCTS algorithm iterates over four stages- selection, expansion, simulation, and backpropagation. In the selection stage, we select a node (a parameter set) with the highest score based on the learning policy. This first step usually involves initializing the head node of the tree. About 50 leaf or child nodes are initialized in our search. Next, there are playouts that assign rewards to the parameter set as described in the feedback description. Now the score is fed into an equation usually referred to as the “learning policy”. Here, we use the popular upper confidence bound (UCB) as the learning policy, with important modifications to suit efficient optimization in the continuous potential energy surface as opposed to the traditional discrete design space.

$${{{\rm{UCB}}}}({\theta }_{j})=\mathop{\sum}\limits_{{H}_{{{{\rm{stage}}}}}}-\min ({r}_{1},{r}_{2},\ldots ,{r}_{{n}_{i}})+c\cdot f({\theta }_{j})\cdot \sqrt{\frac{ln{N}_{i}}{{n}_{i}}}$$
(6)

The learning policy contains two parts, one is focused on exploitation or achieving minimum error score while the other is related to the exploration and is based on the ratio of parent-to-child node visits made by the MCTS agent. The latter term contains an exploration constant, a hyper-parameter that balances the exploitation-vs-exploration trade-off. Next, in the expansion stage, child nodes are added to the selected node such that their parameter values are small perturbations to that of the parent node. We note that the region of the space explored reduces with the increase in tree depth, which helps in the convergence of the algorithm71. In the simulation stage, playouts are conducted for the newly generated child nodes to evaluate their performance and the scores of all relevant parent and child nodes are updated in the backpropagation stage. More details on the UCB policy are added to the S1 section of the suporting information.

Next, we discuss about the objective function or the definition of the rewards used in the MCTS workflow. Feedback is an important aspect of any learning process and hence we enhance the learning by returning hierarchical rewards to the RL workflow, as illustrated in Fig. 1. We draw analogies from computer games and introduce a rewards scheme where the objectives are evaluated based on an hierarchical manner where error for multiple properties are evaluated stagewise depending on a typically increasing level of difficulty. All the multiple objectives or rewards are evaluated using LAMMPS72. Initially, the agent makes a heuristic guess of the model parameters within the specified bounds of the high-dimensional space. The property evaluations are ordered according to their simulation cost as demonstrated in Fig. 1. The reward for the first stage (the lattice parameters of the 21 silica polymorphs) is evaluated and if the constraint on the relative error is satisfied, the agent moves to evaluate the reward for the successive stages (cohesive energy, densities, etc. of all polymorphs) one at a time. The rewards from each stage are accumulated and the overall reward is fed back to the agent. Thus, the reward value for a BKS parameter set is higher if it successfully completes multiple stages. Hence, we identify each of the target properties as an individual stage (see Fig. 1). This type of setting allows the user to set the order of property evaluation along with different error criteria. Our initial gateway of lattice constants was chosen so that we first predict the correct structure for each of the polymorphs and then map their properties to the structures. If the cohesive energies are made the initial gateway, then the algorithm may accurately predict the cohesive energies but the corresponding structures that the energies would be mapped to might be different. In principle, if this mapping were unique, then the hierarchy would not matter. However, in some cases, where there is a many-to-one mapping, then it is preferable to keep the structure as the initial gateway to make it easier to map the properties that are lower in the hierarchy onto the correctly predicted structures.

Our hierarchical rewards approach offers several advantages. One is the early rejection of parameter sets without having to evaluate all the properties, thus saving time and computing power. Another is the ability to tune the search space to simultaneously identify and map regions of good parameters relative to the most desired properties. For instance, Fig. 1 has the first two properties marked as “yes” meaning the parameter set is well within the range of the error criterion defined by the user. A cumulative reward is computed for both of them—note that this eliminates the need to evaluate all the properties and one can assign a penalty based on the extent of error. This way we save on the number of calculations made in each of the iteration made by the optimizer. It should be noted that this saves a lot more computations when we loop across each of the 21 polymorphs from the training dataset. Clearly, this leaves a faster and smarter feedback to the optimizer allowing it to carry out more iterations unlike in the workflows with all the properties evaluated without a stage cutoff. This way as the optimizer samples through the search space, it tends to target the search space such that the high-reward stages still yield at least the same accuracy while improving the subsequent stages. Another added advantage is the elimination of property bias as we do not need to set any weights to the rewards computed at each stage in order to train a property better. Instead we simply alter the training order of properties. More details on the hyperparameters and the LAMMPS computations are provided in the Supplementary Information60.

To summarize, based on the cumulative rewards score returned by learning policy (which is a balance of exploration and exploitation of the search space), the best-scored head-leaf node is selected, this completes the first c-MCTS stage. Next stage is the expansion of such leaf or parent node with a certain number of child nodes (in this study, five child nodes were generated per parent). This is followed by a simulation stage, which involves evaluation of every child node using the learning policy described in detail above by perturbing the parameters within the search bounds of that node. The last stage involves back-propagating the scores until the head or parent-leaf node is selected. Backpropagation keeps a track of the number of times a child node is visited and the chances of it being exploited diminish if it has lower rewards despite a higher number of visits. This allows the algorithm to learn and explore newer regions and helps identify the next best head node that needs to be expanded or the child node with next best score available in the tree. The global optimization of the parameter sets is thus achieved through a multireward MCTS scheme which is followed by a Simplex algorithm73 for a subsequent local optimization to derive the final set of best parameters.

Molecular modeling

The RL workflow for training and testing force-field parameters needs the target properties for the rewards to be predicted. These properties are further used to learn the exploration of the search space. All the property evaluations for the crystalline and amorphous phases are performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)74. Prior to the computation of any property, the corresponding starting configurations are minimized via the conjugate gradient technique with force and energy tolerances equal to 10−4 eV Å−1 and 10−4 eV, respectively. A barostat with P = 1 bar, a time step of 1 fs and a 3 × 3 × 3 supercell was used in all the simulations.

For the crystalline polymorphs (obtained from IZA database), the minimized system is relaxed using the model parameters using box/relax and subsequently equilibrated at 300 K in the NVE ensemble for 10 ps. Then the target properties—lattice, density, cohesive energy, Si–O–Si and O–Si–O angles are evaluated in order to assess the quality of the parameter set within the multireward decision tree workflow. The lattice parameters are retrieved from the equilibrated box dimensions while the cohesive energy for each polymorph is computed by normalizing the potential energy of the system with the total number of atoms in the simulation cell. We must note that cohesive energies are always computed relative to the most stable polymorph, i.e α-quartz, and the relative energetic ordering is compared w.r.t. experiments69. We use a cutoff radius of 10 Å with a shell thickness of 0.01 Å for the calculation of the angular distribution functions. The angles are obtained by computing the Angle Distribution function (ADF) of the relaxed structures. To evaluate the elastic constants, each relaxed crystal structure is subjected to both positive and negative deformations along all directions to compute the derivative of the pressure tensor with respect to the strain, which is used to construct the elastic constant matrix. The phonon dispersion is obtained using the Finite displacement method through the Phonopy75 package.

We perform MD simulations to evaluate the structure and enthalpy of amorphous silica. To obtain an amorphous configuration, we heat the cristobalite crystal to a temperature of 5000 K and then cool it back to 300 K. For the original BKS model, the one-phase melting of crystobalite occurs above 4400 K64. Therefore, in the process of preparing the glass sample, we heated it up to 5000 K which ensures the complete melting of the crystal. The amorphous system is then replicated to obtain a large enough system size with about 12,000 atoms that is used for MD simulations. We measure the enthalpy of melting for cristobalite around 2000 K, because the experimental melting temperature of this mineral is 1999 K. The simulation cell of the crystal is replicated to size similar to that in the amorphous simulation. Both the crystal and amorphous systems are then slowly heated from 300 K to a temperature of 2500 K in an NPT ensemble and then equilibrated for 1 ns at that temperature. The enthalpy of melting is computed as the difference in the enthalpy per atom in the simulations of the amorphous and cristobalite phases identifying the jump in the potential energy (see “Results”). We also estimate the melting point through heating of a two-phase amorphous and solid β-cristobalite separated by a flat interface. The two-phase system is created by dividing the crystal simulation cell-sized 5.2 nm × 5.5 nm × 16 nm into two regions along the z axis. The positions of the atoms in one half are fixed using the setforce command in LAMMPS resulting in zero forces, while the other half was heated to 3000 K in NPT ensemble (p = 1 bar) with anisotropic barostatting over 1 ns and subsequently equilibrated at the same temperature (3000 K) for another ns. This procedure results in the amorphization of the unfixed block. Next, the system is cooled to 300 K. This two-phase system is then evolved in the NPT ensemble, removing the setforce constraint and integrating the equations of motion of all atoms. The temperature of the simulation is increased linearly to the target temperature i.e., from 300 to 2500 K, over 1 ns. The structural characteristics are evaluated to determine the melting point.

Silica glass is created using melt-quench simulations starting from β-cristobalite (4000 SiO2 units). We heat the crystal from 300 to 3000 K over 1 ns, at 1 bar in an NPT ensemble and then rapidly cool the configuration to room temperature in order to obtain the glass. This is then held at 300 K and 1 bar for 3 ns in a NPT ensemble in order to generate trajectories necessary to evaluate the structure factor.